Solving a Hard Instance of Suspicious Behaviour Detection with Sparse
Binary Vectors Clustering
Eric Filiol and Abhilash Hota
Laboratoire de Virologie et de Cryptologie Op
´
erationnelles, ESIEA, Laval, France
Keywords:
Machine Learning, Clustering, Sparse Binary Vector, Malicious Behaviour, Infrastructure Security.
Abstract:
In this article we present a study dealing with the problem of detecting a very small subset of suspicious and
malicious behaviours represented by sparse binary vectors in a population of individuals significantly larger.
The main problem lies in the fact that malicious behaviours, in the case of sparse vectors, are difficult to
distinguish from normal behaviours. Despite the fact that vectors are apparently strongly unbalanced, this
property cannot be exploited since the objects to classify (behaviours) do not exhibit strongly enough frequen-
cies discrepancy. It is not possible to work on detection directly and it is therefore necessary to go through
a preliminary phase of vector partitioning (representing normal or malicious behaviour) to select a reduced
subset concentrating with a high probability most of the vectors corresponding to malicious behaviours. We
have been working on a set of anonymized real data from terrorism-related cases.
1 INTRODUCTION
An essential goal in security relates to the ability of
distinguishing malicious objects (attackers, malware,
events...) from normal (benign) objects (users, legi-
timate programs, normal events...). Since a few year
machine-learning and data analysis provide interes-
ting and often powerful tools to achieve this goal in
the field of (cyber)security. Once the objects have
been carefully modelled by the right objects, a lot of
algorithms nowadays are available to solve this ques-
tion efficiently and accurately. Among many other,
modelling object by means of Boolean vectors has
proved to be very powerful. In this case, we consi-
der attributes (features) seen as categorical variables
and the corresponding bit value describes the pre-
sence or the absence of the relevant attribute. Then
simple similarity measures enables either the identi-
fication of homogeneous subsets of objects (supervi-
sed techniques like clustering) or to identify a given
unknown object as being closer to one particular fa-
mily of known objects than to any other.
However malicious objects adapt and strive to
evade the known detection techniques. Optimally
either they mimic as much as possible normal objects
or they limit the leak of information that could be use-
ful for their detection. They can also force the analyst
to face complexity issue that makes the detection far
more difficult.
In this paper, we are going to address an unu-
sual problem where all classical approaches (Aggar-
wal, 2015, Chap. 6 & 7) are not working. This me-
ans that they do not provide better results than would
a random approach. When considering the specific
case of unbalanced binary data clustering (i.e data
exhibit disparities in observed frequencies) (He and
Garcia, 2009) we did not obtain better or more sa-
tisfying results. Despite the fact that ou data ap-
pear strongly unbalanced (we consider 16-bit binary
vectors having constant Hamming weight of 5 then
P[attibute
i
= 1] =
5
16
), the unbalancedness property
here is not relevant in our specific cases study. We
came to the conclusion that the difficulty relates more
to the vector sparsity than to the vector attributes un-
balancedness. Behaviours (vectors) are described as
a collection of basic actions/properties that are reali-
zed or not (attributes). Due to operational constraints
(Section 3), only a reduced number of attributes can
be collected at a time (sparsity). Moreover the num-
ber of behaviours recorded are close enough to the
maximal number of possible behaviours. Our pro-
blem consists then in clustering behaviours that do not
exhibit exploitable frequencies discrepancies, at least
by known unbalanced binary data clustering techni-
ques.
The problem comes from the analysis/detection of
terrorist behaviours in a population. A French govern-
mental security entity has provided us with a database
Filiol, E. and Hota, A.
Solving a Hard Instance of Suspicious Behaviour Detection with Sparse Binary Vectors Clustering.
DOI: 10.5220/0007347206350644
In Proceedings of the 5th International Conference on Information Systems Security and Privacy (ICISSP 2019), pages 635-644
ISBN: 978-989-758-359-9
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
635

of binary vectors that describe behaviour patterns for
a number of individuals. Due to the sensitivity of the
data, we got only an anonymized version of the actu-
ally collected vectors.
The main interest of this study was to be aware
that in a few cases we cannot find an optimal, ideal
solution (it does not clearly exist). However, the ope-
rational view can orientate new approaches that are
suitable and admissible for the people working on the
field. In our case, the aim was no longer to extract
a subset of “positive” vectors (potentially suspicious
behaviours) as usual approaches strive to but to par-
tition the dataset in a suitable enough way to make
detection then possible by a subsequent, intelligence-
driven step. It is worth mentioning that only this latter
step is able to confirm which vector relates to a suspi-
cious actor or not as soon as the analyst can work on
a significantly reduced subset. So we have to switch
from a classical clustering problem to a dataset refi-
ning problem.
The paper is organized of follows. After presen-
ting the state-of-the-Art in binary vector clustering
applied to the security domain, Section 3 formali-
ses the problem by considering sparse binary vectors.
Then Section 4 explains how which techniques we
have combined to extract a reduced subset from the
initial set without loosing to much information about
the malicious behaviours. Section 5 presents the re-
sults which have been obtained on a set of real data
and on sets simulating this set. Finally we conclude
in Section 6.
2 STATE-OF-THE-ART IN
SECURITY
Clustering techniques find a wide variety of applica-
tions in information security including anomaly de-
tection, vulnerability characterization, etc. We pro-
pose to summarize the state-of-the-art regarding ca-
tegorical data (binary) clustering when applied to the
security field.
2.1 Clustering Binary Vectors
M
¨
unz, Li and Carle (M
¨
unz et al., 2007) describe the
use of clustering for anomaly detection in network
traffic. They present a flow-based anomaly detection
scheme using k-means clustering. The initial training
data consists of unlabelled network flow records con-
taining both normal and anomalous traffic. These re-
cords are transformed into feature datasets which are
then clustered into normal and anomalous traffic. The
centroids of these clusters are then used in distance-
based anomaly detection in new network flow data.
Nalavade and Meshram (Nalavade and
B. Meshram, 2014) investigate clustering appro-
aches for network intrusion detection. Intrusion
detection systems using data mining approaches
enable us to search patterns and rules in large amount
of audit data. Classification-based data mining
models for intrusion detection have often proven
ineffective due to dynamic patterns in network data.
They experiment with k-means clustering algorithm
on the KDD dataset and measure the performance
based on detection rates and false positive rate with
different cluster values.
Syarif, Prugel-Bennett and Wills (Syarif et al.,
2012) describe the advantages of using the anomaly
detection approach over the misuse detection techni-
que in detecting unknown network intrusions or at-
tacks. They investigate five different clustering algo-
rithms: k-Means, improved k-Means, k-Medoids, EM
clustering and distance-based outlier detection algo-
rithms. They show that misuse detection techniques,
which implemented four different classifiers (na
¨
ıve
Bayes, rule induction, decision tree and nearest neig-
hbour) failed to detect network traffic, which contai-
ned a large number of unknown intrusions. Anomaly
detection,on the other hand, showed better results, es-
pecially with distance-based outlier detection algo-
rithms.
Wazid (Wazid, 2014) investigates the feasibility
of using clustering techniques for security in wireless
sensor networks. He proposes a hybrid anomaly de-
tection technique based on k-means clustering. He
shows the effectiveness in detecting misdirection and
blackhole attacks.
Riadi et.al.(Riadi et al., 2013) describe the use of
clustering techniques to characterize types of attacks
for forensics. Network data, including packets rele-
vant to the attacks being investigated are stored in a
log file. This data is grouped using k-means clustering
technique into three categories and mapped based on
source and target. They thus propose a framework for
forensic investigations.
Li, Venter and Eloff (Li et al., 2004) describe a
way to categorize vulnerabilities in the CVE data-
base and present a method to cluster the vulnerabi-
lities using self-organizing feature maps.
K-anonymization techniques have become impor-
tant in many data privacy solutions. A key require-
ment is to ensure data anonymization while avoiding
information loss. Byun et.al.(Byun et al., 2006) pro-
pose an approach using clustering techniques. They
formulate a k-member clustering problem, prove that
the problem is NP-hard and present a greedy algo-
ForSE 2019 - 3rd International Workshop on FORmal methods for Security Engineering
636

rithm with a complexity of O(n
2
). They also propose
extension to reduce classification errors.
Pai (Pai, 2015) (and its references) applies clus-
tering techniques to the malware detection problem
with the goal of classifying malware as part of a fully
automated detection system. Clusters are computed
using K-means and EM clustering algorithms, with
scores obtained from Hidden Markov Models.
2.2 Unbalanced Binary Data Clustering
As explained in the introduction, solving our problem
deals more with vectors sparsity that with the fact that
underlying attributes exhibits strong frequencies dis-
crepancy. A lot of papers have been published regar-
ding machine learning techniques of unbalanced data.
The interested reader may refer to (He and Garcia,
2009; Krawczyk, 2016) (and their respective biblio-
graphy).
2.3 Clustering Sparse Binary Vectors
A number of approaches have been applied to the
specific problem of clustering sparse binary vectors.
Distance-based approaches have been quite popular
along with other techniques like EM based approa-
ches, subspace clustering, spectral clustering, etc.
Choi, Cha and Tappert (Choi et al., 2010) sur-
vey binary similarity and distance measures. The ef-
fectiveness of many clustering techniques often co-
mes down to selecting the right distance metric and as
such this study stays relevant regardless of techniques
used. They study 76 measures and show correlations
through hierarchical clustering.
Jian et.al (Jian et al., 2018) study similarity ana-
lysis of categorical data that is not independent and
identically distributed (non-IID) and propose a Cou-
pled Metric Similarity (CMS) for unsupervised lear-
ning which flexibly captures the value-to-attribute-to-
object heterogeneous coupling relationships. The si-
milarities are learnt in terms of intrinsic heterogene-
ous intra- and inter-attribute couplings and attribute-
to-object couplings in categorical data and CMS are
shown to flexibly adapt to IID to non-IID data. They
further incorporate CMS into spectral clustering and
k-modes clustering.
Conventional clustering techniques have of-
ten proven ineffective when dealing with high-
dimensional spaces because of the inherent sparsity
of the data points. Gan and Wu (Gan and Wu, 2004)
propose an iterative algorithm called SUBCAD for
clustering high dimensional categorical data sets, ba-
sed on the minimization of an objective function for
clustering. They further propose an objective function
that determines the subspace associated with each
cluster. They go on to prove various properties of this
objective function and propose a fast algorithm to find
the subspace associated with each cluster.
Su and Su (Su and Su, 2017) study the cluste-
ring problem for categorical data and propose a met-
hod to find distinctive features in categorical data-
sets. Their model works by comparing pooled within-
cluster mean relative difference and then partitioning
the data upon such features and deriving the subspace
of the subgroups.
Mahdi, Abdelrahman and Bahgat (Mahdi et al.,
2018) propose a new similarity measure for catego-
rical datasets. The Probability of the Weights of
Overlapped items (PWO) estimates the goodness of
clusters. The goal is to maximize frequent items
within clusters and minimize items overlapping bet-
ween clusters. An F-Tree clustering model is used to
compare the effectiveness of PWO with other measu-
res.
Ordonez (Ordonez, 2003) proposes three variants
of the K-means algorithm to cluster binary data stre-
ams including On-line k-means, Scalable k-means,
and Incremental k-means. Incremental k-means is
presented as a scalable solution that finds higher qua-
lity clusters in less time. A mean-based initialization
and incremental learning are used to obtain higher
quality clusters.
3 FORMALISATION OF THE
PROBLEM
In this section we are going to formalize the problem
we have to address when considering the very speci-
fic operational constraints of the underlying environ-
ment. Contrary to usual set clustering problem (see
Section 2) where objects to be classified are rather
easy to partition, in our case the usual techniques do
not work efficiently enough to do better than a random
partitioning.
Our dataset A is made of binary vectors of size 16.
Thus A = {v
0
, v
1
, . . . , v
N
}. Each of these vectors v
i
is
representing either a likely malicious behaviour or a
normal behaviour in the following way, considering a
set of attributes of interest B = {b
0
, b
1
, . . . , b
15
}. For
confidentiality purposes, we do not know what each
attribute b
i
is representing. Only an arbitrary labelling
has to be considered. Each Boolean value for attribute
b
i
is modelling a “basic” behaviour in a “complex”
behaviour v
j
. Thus to summarize:
∀ j ∈ {0, 1, . . . , N} v
j
= (v
0
j
, v
1
j
, . . . , v
15
j
)
Solving a Hard Instance of Suspicious Behaviour Detection with Sparse Binary Vectors Clustering
637

v
i
j
=

1 if basic behaviour b
i
is observed
0 otherwise
Due to operational (technical, legal) constraints of
the surveillance and intelligence system, only 16 dif-
ferent attributes can be considered and only 5 attri-
butes can be collected for a given individual j at a
time (for one set only, denoted D
1
, however 6 attri-
butes have been collected). So the Hamming weight
of the corresponding vector H[v
j
] = 5 (or H[v
j
] = 6
for set D
1
). From a pure combinatorial point of view
there are only 4,368 such vectors (resp. 8,008 for set
D
1
). Feedbacks from the field shows that the number
of actually collected vector may be very close from
this theoretical upper bound, unless a manual, intel-
ligence driven preprocessing step is performed. Mo-
reover, the same behaviour pattern can be recorded
many times both for suspicious and non suspicious
individuals. As a consequence discriminating mali-
cious behaviours from non malicious ones become a
hard task for two main reasons:
• each vector is containing a limited amount of in-
formation due to its sparsity and due to the limited
number of attributes that are considered,
• each of the basic behaviours b
i
is not malicious in
itself since it may equally be realised (v
i
j
= 1) or
not (v
i
j
= 0). It implies that discriminating malici-
ous complex behaviours from non malicious ones
cannot be performed directly. In fact the actual
malicious state must be related to the environment
in which individuals evolve and operate.
As far as the last point is concerned, it is then impossi-
ble to work on the full initial dataset to identify the in-
dividuals that potentially behave in a suspicious way.
Indeed each vector has to be interpreted in connection
with the collecting environment. However, this final
step becomes “easy” (by a subsequent step) as soon as
the dataset has a reduced size. So here the aim is no
longer to cluster data with the hope to get one cluster
containing all the malicious instances (plus a limited
number of non malicious ones). Instead we wish to
obtain a partition P = {A
1
, A
2
, . . . , A
k
} of the set A
such that at least one of the cluster contains at least
half of the malicious instances (that will be identified
as such in the subsequent, intelligence-driven step).
Let us denote A
1
i
the cluster which contains most
of the target vectors (malicious behaviours). The key
parameters are k, the number of final clusters, |A
i
| the
size of the different subset of P and |A
1
i
|, the size of
the target cluster. It is considered that is k ≥ 4 and
|A
1
i
| ≈
|A|
k
while in average |A
j
| ≈
|A|
k
for j 6= i, then
the results are operationally admissible and viable.
4 REDUCED SUBSET
EXTRACTION PROBLEM
Firstly we consider three approaches to cluster our
datasets: the leading eigenvector method, the correla-
tion explanation techniques and the classical k-Means
technique applied on sentence vectors. Then we deve-
lop a combined clustering step using a majority voting
scheme with these three approaches.
4.1 The Leading Eigenvector Method
The leading eigenvector method (Newman, 2006) has
proved to be quite effective in community detection.
It uses the eigenvectors of matrices to detect commu-
nity structure in large networks.
The data is preprocessed prior to the actual cluste-
ring. This step is relatively simple since there are no
missing values. Also, since these are binary vectors,
scaling is not needed. At this stage we run some pre-
computations to figure out thresholds to be used while
creating graphs using the datasets. These thresholds
are based on two comparisons:
1. The number of equal corresponding elements be-
tween any two feature vectors. The workflow
using this comparison will be referred to npsum
01
in this document. If we consider vectors v
i
and
v
j
then it consists in considering the Hamming
weight of v
i
&v
j
where v denotes the bitwise nega-
tion of vector v and & denotes the bitwise AND.
2. The number of corresponding elements of any two
feature vectors both being equal to 1. In this case,
if the corresponding elements are both 0, they are
simply ignored. The workflow using this compa-
rison will be referred to npsum
1
in this document.
It is equivalent of the dot product of the two vec-
tors.
The following example describes how the threshold
values were computed. Let us consider three vectors
from the dataset D
1
(length 16, weight 6):
• v
0
= (0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0)
• v
1
= (0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0)
• v
2
= (0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0)
Then weights W
i j
are computed for possible edges
between all vector pairs i and j and we have:
• For npsum
01
, W
01
= 14 −W
02
= 12 −W
12
= 12
• For npsum
1
, W
01
= 5 −W
02
= 4 −W
12
= 4
The clustering is then done in two stages each con-
sisting of a 50 % split of the dataset being considered.
Each stage consists of the following steps (terms and
techniques are those used in (Newman, 2006)):
ForSE 2019 - 3rd International Workshop on FORmal methods for Security Engineering
638

1. Build the undirected graph using predetermined
threshold values. For that purpose we use Net-
workx (Aric Hagberg, 2018) in Python.
2. Compute the adjacency matrix for this graph.
3. Compute the modularity matrix.
4. Compute the eigenvalues and corresponding ei-
genvectors for the modularity matrix.
5. Assign clusters based on signs of the elements of
the eigenvector corresponding to the most positive
eigenvalue.
The process was applied with npsum
1
and npsum
01
as described previously. For three of the resulting
datasets there was no difference in the results. For
the fourth one npsum
01
gave slightly better results in
terms of preserving the original positives in the fi-
nal clustering. The threshold value remains consistent
across the two stages.
Two graphs were built for each dataset, one with a
threshold value equal to 12 and the other with a thres-
hold value equal to 14. For each pair of feature vec-
tors, if the npsum value exceeds the threshold, an edge
is created between the nodes representing the two fe-
ature vectors. This allows us to minimize the number
of edges without losing any useful information.
An adjacency matrix is a square matrix used to
represent a finite simple graph. The elements of the
matrix indicate whether pairs of vertices are adjacent
or not in the graph. For the purposes of this analysis,
only unweighed adjacency matrices are considered.
The following function takes a NetworkX graph and
computes the adjacency matrix, returning it as a scipy
(Jones et al., 01 ) sparse matrix.
Modularity is a measure of the structure of a net-
work. A network with high modularity has dense
connections between nodes within communities while
sparse connections between nodes in different com-
munities.
For any two nodes i and j corresponding to binary
vectors v
i
and v
j
respectively,
• k
i
and k
j
denote the expected degree of each node
• P
i j
denotes the number of expected edges between
node i and node j.
We begin with the constraint that the expected degree
is equal to the actual degree of the node taken from
the adjacency matrix. Thus summing the columns of
the adjacency matrix gives us the expected degree for
each node in the graph.
Let m denote the total number of edges in the
graph. Then P
i j
is given by
P
i j
=
k
i
× k
j
m
Given an adjacency matrix A, we can now com-
pute the corresponding modularity matrix B such that
B
i j
= A
i j
− P
i j
At this stage the eigenvalues and corresponding ei-
genvectors are computed for the modularity matrix B.
Cluster assignment is now done based on the sign of
the elements of the eigenvector corresponding to the
most positive eigenvalue.
4.2 The Correlation Explanation
Method
Correlation Explanation aims at learning a hierarchy
of abstract representations of complex data by opti-
mizing an information-theoretic objective (Steeg and
Galstyan, 2014; Ver Steeg and Galstyan, 2014). Let
X denote a discrete random variable while P(X) deno-
tes a probability distribution over X and |X| denotes
the cardinality of the set of values that X may take
and is always finite. Assuming n random variables,
G ⊆ N
n
= {1, 2, . . . , n} and X
G
is the corresponding
subset of random variables. Let us denote H(X ) the
entropy of X and I(X
1
: X
2
) as the mutual information
between the two random variables X
1
and X
2
(Cover
and Thomas, 2006).
The measure of mutual information used in this
method is known as total correlation (Watanabe,
1960), multi-information (Studen
´
y and Vejnarov
´
a,
1998) or multivariate mutual information (Kraskov
et al., 2005). It is defined as
TC(X
G
) =
∑
i∈G
(H(X
i
) − H(X
G
)
The extent to which another variable Y explains the
correlations in X can be measured by how much
the total correlation is reduced (Steeg and Galstyan,
2014).
TC(X;Y ) = TC(X ) − TC(X|Y )
=
∑
i=N
n
(I(X
i
: Y ) − I(X : Y ))
(1)
Optimizing over Equation 1 is thus equivalent to sear-
ching for a latent factor Y . Let Y be a discrete random
variable that can take k values. This optimization may
be represented as
max
p(y|x)
TC(X;Y ), |Y | = k
This can now be extended to account for multiple
latent factors Y
1
, Y
2
, . . . , Y
m
:
max
G
j, p(y
j
|xG
j
)
m
∑
j=1
TC(XG
j
;Y
j
), |Y
j
| = k, G
j
∩ G
j
0
6= j
= 0
For our datasets, we choose 2 hidden units with 4 di-
mensions each for the computations.
Solving a Hard Instance of Suspicious Behaviour Detection with Sparse Binary Vectors Clustering
639

4.3 K-means Clustering on Sentence
Vectors
For this third technique, we consider the Word2Vec
tool which has been introduced by Mikolov et al (Mi-
kolov et al., 2013; Goldberg and Levy, 2014). This
tool has played a major role in recent developments in
natural language processing. It is a group of related
models which is used to produce word embeddings
and therefore it gives us a way to represent words in
terms of vectors in a real space, while preserving the
linguistic context.
The process involves the following steps:
1. Assign a character corresponding to each of the
16 positions, since we have 16-bit binary vectors.
2. For every vector, we keep the words correspon-
ding to ones.This gives us 6-word sentences (or
patterns) corresponding to each vector in the da-
taset, thus forming our working corpus.
3. We now compute word vectors using Word2Vec
for this corpus.
4. Sentence vectors, which are computed as the
averaged word vectors for each sentence, form a
new representation for the original binary vector
dataset.
5. Since the dataset is now represented in a real
space, we can now use classical clustering met-
hods like k-means.
4.4 Final Processing by Majority Vote
Once the three previous clustering techniques have
been applied to our dataset, we explore the possibility
of combining the partitions we have obtained through
these different methods. The aim is to get a better
clustering. This attempt is based on a simple majority
vote.
For that purpose, all pairs of vectors are taken and
each of the three methods is checked to count the to-
tal number of times the two vectors were kept in the
same cluster. If the count is greater than or equal to
2, we keep the two vectors in the same final cluster.
Since the clusters obtained via the three methods lie
on different spaces with different centroid, we cannot
simply vote on cluster labels. Thus, for each pair of
vectors, we see how many methods keep them in the
same cluster.
5 EXPERIMENTAL RESULTS
We have been provided with four datasets to analyse
denoted D
1
, D
2
, D
3
, D
4
respectively. Let us precise
Table 1: Dataset parameters.
Dataset Dataset size # malicious vectors
D
1
4,692 5
D
2
3,802 20
D
3
3,804 5
D
4
3,809 51
that dataset D
1
has binary vectors of weight 6 (there
are 8,008 such vectors at most). It is a special case
provided by the French police forces. Table 1 sum-
marizes the parameters for these four datasets.
5.1 Leading Eigenvector
The best results are obtained with npsum
01
. The
structure of the graph (density) and the resulting ad-
jacency and modularity matrices strongly depends on
the threshold value we consider. Figures 1 and 2 show
the number of edges in the graph modelling each da-
taset for different threshold values. from the analysis
of Figures 1 and 2 we clearly see that only threshold
values greater or equal to 12 are likely to provide the
expected results. In other words, the graph density is
not too high in order to have a chance to get a suf-
ficient number of connected components correspon-
ding to the expected partition. On the other side, a
too small threshold (less than 8) would provide also
a sparse graph but with too many connected compo-
nents. As a consequence the useful information would
be spilled up and wasted.
Once the clustering step (see Section 4.1) has been
applied we obtain four clusters. Table 2 summarizes
the results. We can see that dataset D
1
and D
4
give the
best results for a threshold value of 14 while datasets
D
1
and D
4
give better results with a threshold value of
12. As a general decision rule, the best cluster appears
to be obtained by taking the largest cluster at the end
of clustering phase 1 and then the smallest cluster at
the end of the clustering phase 2.
5.2 The Correlation Explanation
Method
We applied the clustering in two steps as in the pre-
vious method. We obtain the results presented in Ta-
ble 3.
As a general rule, we can decide to keep the largest
cluster but with a residual error of 0.25. However it is
admitted that the four resulting clusters can be post-
processed in parallel.
ForSE 2019 - 3rd International Workshop on FORmal methods for Security Engineering
640

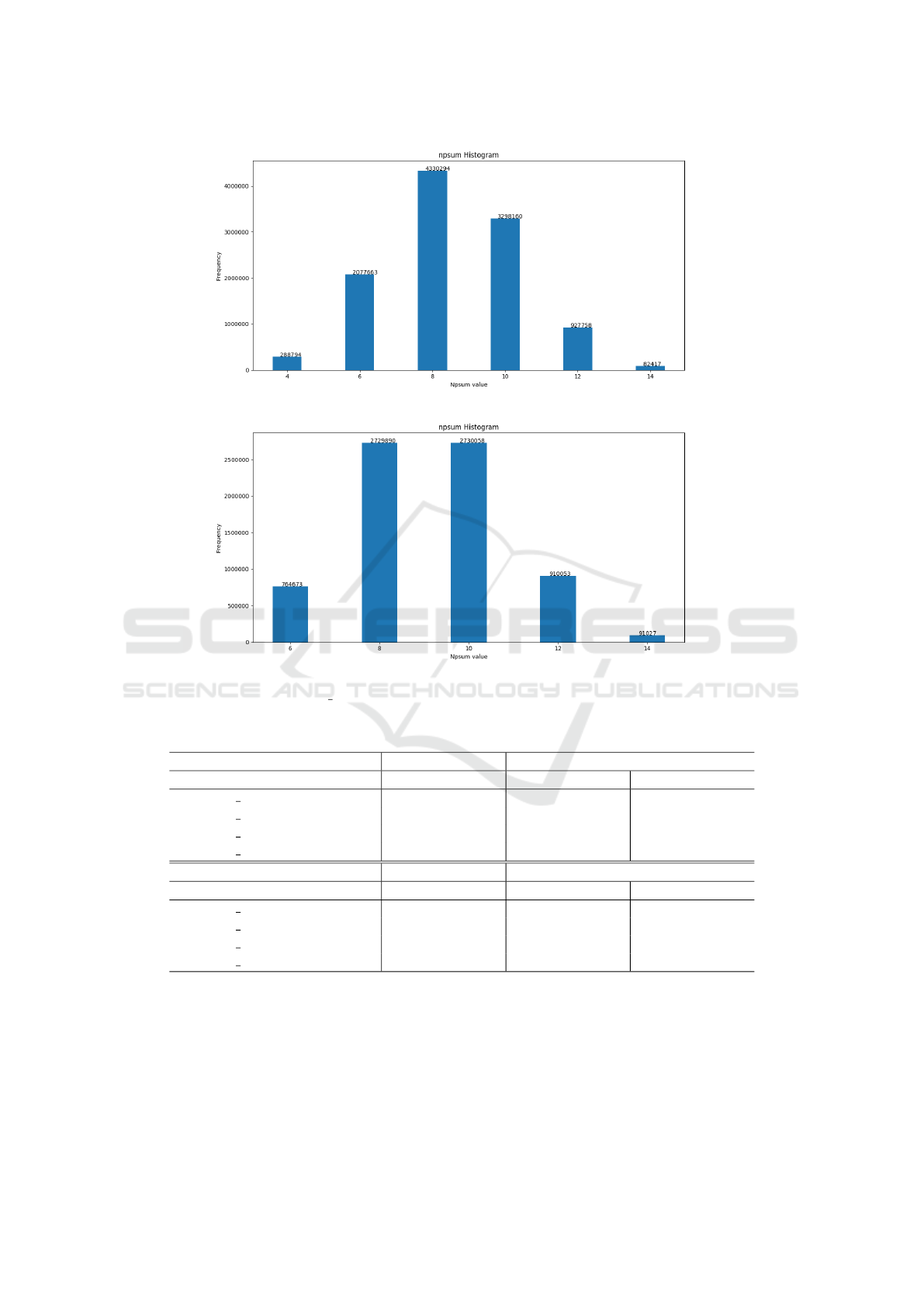
D
1
D
2
Figure 1: npsum 01 Thresholds value vs Number of Edges (datasets D
1
and D
2
).
Table 2: Partition of datasets with npsum
01
threshold of 12 (top) and 14 (bottom) (leading eigenvector technique).
D
1
- T12 D
2
- T12 D
3
- T12 D
4
- T12
Positives Total Positives Total Positives Total Positives Total
Cluster 0 0 5 1195 7 944 0 920 29 932
Cluster 0 1 0 1126 0 937 1 967 6 991
Cluster 1 0 0 1203 13 904 4 938 0 945
Cluster 1 1 0 1168 0 1017 0 979 16 941
D
1
- T14 D
2
- T14 D
3
- T14 D
4
- T14
Positives Total Positives Total Positives Total Positives Total
Cluster 0 0 0 1160 1 936 0 925 0 974
Cluster 0 1 0 1167 9 958 3 931 17 927
Cluster 1 0 4 1150 0 996 2 910 12 998
Cluster 1 1 1 1215 10 913 0 1038 22 910
5.3 K-means Clustering on Sentence
Vectors
We applied the clustering in two steps as in the two
previous method. We obtain the results presented in
Table 4. As a general rule, we can decide to keep the
smallest cluster.
5.4 Final Processing by Majority Vote
According to the procedure described in Section 4.4,
the majority vote scheme has been applied on the four
datasets with the following results presented in Ta-
ble 5. Extracting a general decision rule is not pos-
sible from this majority vote procedure, However, it
Solving a Hard Instance of Suspicious Behaviour Detection with Sparse Binary Vectors Clustering
641

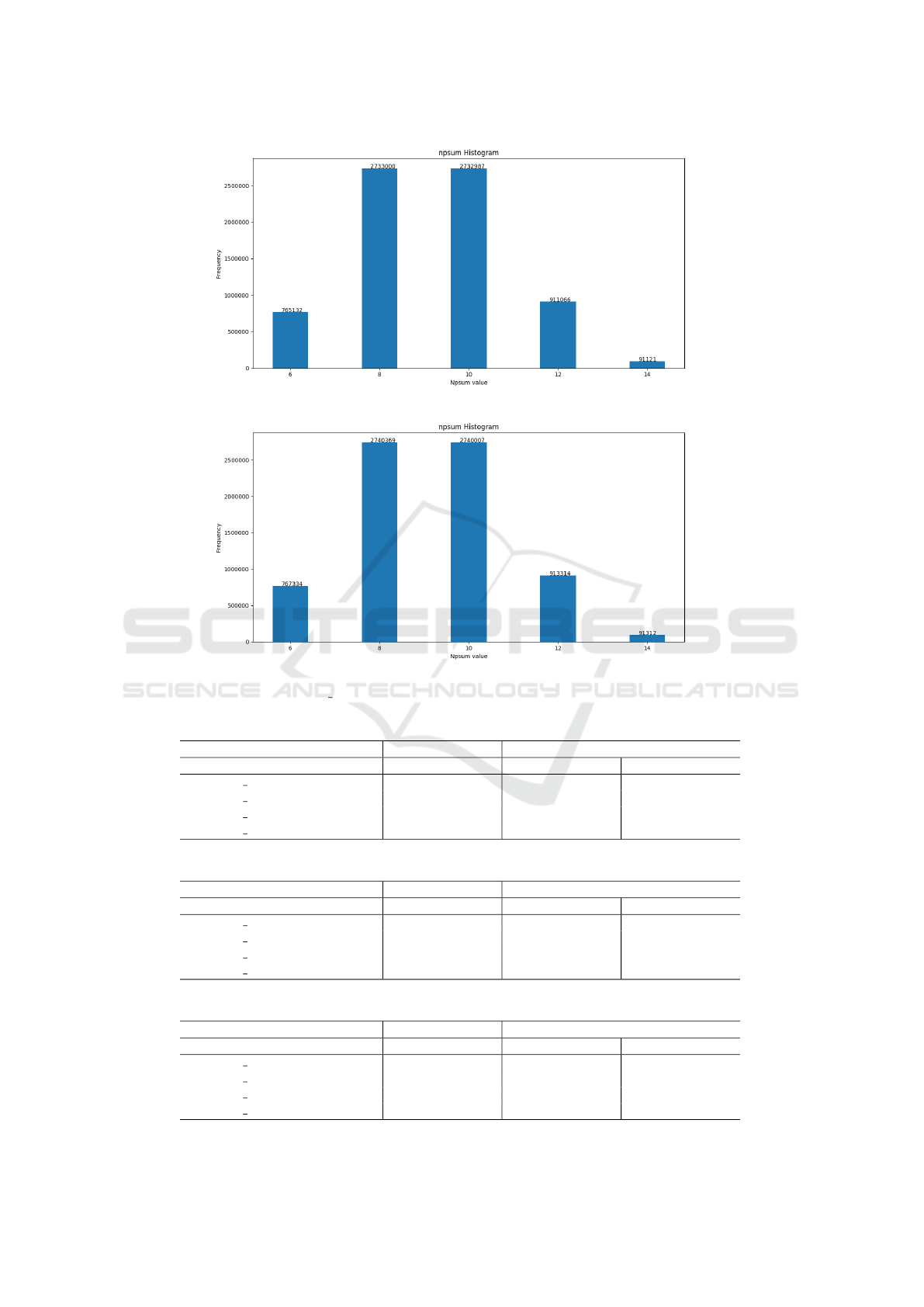
D
3
D
4
Figure 2: npsum 01 Thresholds value vs Number of Edges (datasets D
3
and D
4
).
Table 3: Partition of datasets with the correlation explanation technique.
D
1
D
2
D
3
D
4
Positives Total Positives Total Positives Total Positives Total
Cluster 0 0 5 1001 14 1203 0 880 0 1180
Cluster 0 1 0 1781 5 617 5 1190 5 1125
Cluster 1 0 0 745 0 863 0 619 15 625
Cluster 1 1 0 1165 1 1119 0 1115 31 879
Table 4: Partition of datasets with the K-means clustering on sentence vectors technique.
D
1
D
2
D
3
D
4
Positives Total Positives Total Positives Total Positives Total
Cluster 0 0 3 857 0 912 0 918 35 858
Cluster 0 1 0 1384 16 796 2 1108 12 893
Cluster 1 0 0 1134 4 1201 0 922 0 920
Cluster 1 1 2 1317 0 893 3 856 4 1138
Table 5: Partition of datasets with the cluster ensemble.
D
1
D
2
D
3
D
4
Positives Total Positives Total Positives Total Positives Total
Cluster 0 0 3 918 0 1141 0 586 47 1068
Cluster 0 1 0 1334 10 1134 0 513 0 951
Cluster 1 0 0 1132 7 614 4 745 0 661
Cluster 1 1 2 1308 3 913 1 1960 4 1129
ForSE 2019 - 3rd International Workshop on FORmal methods for Security Engineering
642

worth mentioning that when applied, positive vectors
are more concentrated in a cluster. It was precisely
one strong result to achieve.
6 CONCLUSION
In this paper we have addressed the problem of clus-
tering sparse binary vectors in the field of security.
Since the vectors we have to deals with cannot be ef-
ficiently clustered by known techniques, the aim was
to find a procedure that would systematically clus-
ter data in such a way that one cluster would con-
tain most of the positive vectors describing potentially
suspicious terrorist activity. With such a cluster, it is
then possible to perform an intelligence-driven post-
processing step that is tractable while it is not on the
initial sets.
The study presented here considers only four data-
sets which could be of course considered as non signi-
ficant on such a reduced number of cases. Our techni-
ques has been transferred to the police entity which
was requested this study. Their feedback show that
our techniques is still valid and robust when conside-
ring vectors of larger length but still sparse.
We hope this study will draw attention from ot-
her researchers that would be interested to investigate
with other approaches. This is the reason why we
have been authorized to share the four datasets used
in this study. Anyone interested can contact the first
author.
REFERENCES
Aggarwal, C. C. (2015). Data Mining - The Textbook.
Springer.
Aric Hagberg, Dan Schult, P. S. (2014–2018). Networkx:
Software for complex networks. https://networkx.
github.io/.
Byun, J.-W., Kamra, A., Bertino, E., and Li, N. (2006). Ef-
ficient k -anonymization using clustering techniques.
Technical report, Purdue University.
Choi, S.-S., hyuk Cha, S., and Tappert, C. (2010). A survey
of binary similarity and distance measures. Journal of
Systemics, Cybernetics and Informatics, pages 43–48.
Cover, T. M. and Thomas, J. A. (2006). Elements of In-
formation Theory (Wiley Series in Telecommunicati-
ons and Signal Processing). Wiley-Interscience, New
York, NY, USA.
Gan, G. and Wu, J. (2004). Subspace clustering for high di-
mensional categorical data. SIGKDD Explor. Newsl.,
6(2):87–94.
Goldberg, Y. and Levy, O. (2014). word2vec explained:
deriving mikolov et al.’s negative-sampling word-
embedding method. CoRR, abs/1402.3722.
He, H. and Garcia, E. A. (2009). Learning from imbalan-
ced data. IEEE Transactions on Knowledge and Data
Engineering, 21(9):1263–1284.
Jian, S., Cao, L., Lu, K., and Gao, H. (2018). Unsupervised
coupled metric similarity for non-iid categorical data.
PP:1–1.
Jones, E., Oliphant, T., Peterson, P., et al. (2001–). SciPy:
Open source scientific tools for Python. [Online;
accessed August 2018].
Kraskov, A., Stgbauer, H., Andrzejak, R. G., and Grassber-
ger, P. (2005). Hierarchical clustering using mutual
information. EPL (Europhysics Letters), 70(2):278.
Krawczyk, B. (2016). Learning from imbalanced data: open
challenges and future directions. Progress in Artificial
Intelligence, 5(4):221–232.
Li, Y. L., Venter, H., and Eloff, J. (2004). Categorizing vul-
nerabilities using data clustering techniques. In Eloff,
J., Venter, H., Labuschagne, L., and Eloff, M., editors,
Proceedings of the 3rd Conference in Information Se-
curity for South Africa. ISSA Press.
Mahdi, M. A., Abdelrahman, S. E., and Bahgat, R. (2018).
A high-performing similarity measure for categorical
dataset with sf-tree clustering algorithm. International
Journal of Advanced Computer Science and Applica-
tions, 9(5).
Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013).
Efficient estimation of word representations in vector
space. CoRR, abs/1301.3781.
M
¨
unz, G., Li, S., and Carle, G. (2007). Traffic anomaly de-
tection using kmeans clustering. In In GI/ITG Works-
hop MMBnet.
Nalavade, K. and B. Meshram, B. (2014). Evaluation of k-
means clustering for effective intrusion detection and
prevention in massive network traffic data. 96:9–14.
Newman, M. E. J. (2006). Finding community structure
in networks using the eigenvectors of matrices. Phys.
Rev. E, 74:036104.
Ordonez, C. (2003). Clustering binary data streams with
k-means. In Proceedings of the 8th ACM SIGMOD
Workshop on Research Issues in Data Mining and
Knowledge Discovery, DMKD ’03, pages 12–19, New
York, NY, USA. ACM.
Pai, S. (2015). A comparison of clustering techniques for
malware analysis. Technical report, San Jose State
University.
Riadi, I., Istiyanto, J. E., Ashari, A., and Subanar (2013).
Log analysis techniques using clustering in network
forensics. CoRR, abs/1307.0072.
Steeg, G. V. and Galstyan, A. (2014). Discovering structure
in high-dimensional data through correlation explana-
tion. CoRR, abs/1406.1222.
Studen
´
y, M. and Vejnarov
´
a, J. (1998). The Multiinforma-
tion Function as a Tool for Measuring Stochastic De-
pendence, pages 261–297. Springer Netherlands, Dor-
drecht.
Su, J. and Su, C. (2017). Clustering categorical data ba-
sed on within-cluster relative mean difference. Open
Journal of Statistics, 7:173–181.
Solving a Hard Instance of Suspicious Behaviour Detection with Sparse Binary Vectors Clustering
643

Syarif, I., Prugel-Bennett, A., and Wills, G. (2012). Unsu-
pervised clustering approach for network anomaly de-
tection. In Benlamri, R., editor, Networked Digi-
tal Technologies, pages 135–145, Berlin, Heidelberg.
Springer Berlin Heidelberg.
Ver Steeg, G. and Galstyan, A. (2014). Maximally
Informative Hierarchical Representations of High-
Dimensional Data. ArXiv e-prints.
Watanabe, S. (1960). Information theoretical analysis of
multivariate correlation. IBM J. Res. Dev., 4(1):66–
82.
Wazid, M. (2014). Hybrid anomaly detection using k-
means clustering in wireless sensor networks. Crypto-
logy ePrint Archive, Report 2014/712. https://eprint.
iacr.org/2014/712.
ForSE 2019 - 3rd International Workshop on FORmal methods for Security Engineering
644