
Reinforcement Learning Approach for Cooperative Control of
Multi-Agent Systems
Valeria Javalera-Rincon
1
, Vicenc Puig Cayuela
2
, Bernardo Morcego Seix
2
and
Fernando Orduña-Cabrera
1
1
Advanced Systems Analisys and Ecosystem Services and Management Programs, International Institute for Applied
Systems Analysis, Schlossplatz 1, A-2361, Laxenburg, Austria
2
Advanced Control Systems Group, Universitat Politècnica de Catalunya (UPC), Rambla Sant Nebridi, 10,
08222 Terrassa, Spain
Keywords: Distributed Control, Intelligent Agents, Reinforcement Learning, Cooperative Agents.
Abstract: Reinforcement Learning (RL) systems are trial-and-error learners. This feature altogether with delayed
reward, makes RL flexible, powerful and widely accepted. However, RL could not be suitable for control of
critical systems where the learning of the control actions by trial and error is not an option. In the RL literature,
the use of simulated experience generated by a model is called planning. In this paper, the
planningByInstruction and planningByExploration techniques are introduced, implemented and compared to
coordinate, a heterogeneous multi-agent architecture for distributed Large Scale Systems (LSS). This
architecture was proposed by (Javalera 2016). The models used in this approach are part of a distributed
architecture of agents. These models are used to simulate the behavior of the system when some coordinated
actions are applied. This experience is learned by the so-called, LINKER agents, during an off-line training.
An exploitation algorithm is used online, to coordinate and optimize the value of overlapping control variables
of the agents in the distributed architecture in a cooperative way. This paper also presents a technique that
offers a solution to the problem of the number of learning steps required to converge toward an optimal (or
can be sub-optimal) policy for distributed control systems. An example is used to illustrate the proposed
approach, showing exciting and promising results regarding the applicability to real systems.
1 INTRODUCTION
RL is a well-known and formally studied family of
learning techniques. Moreover, depending on the
formulation of the problem and the richness of
experience data, the chances of convergence are high.
One of the main characteristics of RL is that the
agents learn by trial and error discovering which
actions yield the maximum reward by trying them.
However, it is also this characteristic what makes RL
unsuitable for controlling critical time-varying
systems where good performance is crucial all the
time, and the cost of this learning curve of the agent
can be too high.
Currently, some algorithms implement planning
techniques such as Dyna-Q and Prioritized Sweeping.
Some examples of applications of Dyna-Q algorithm
are (Tateyama et al. 2007), (Hwang et al. 2015) and
(Hwang et al. 2017). Moreover, for Prioritized
Sweeping see (Zajdel 2018) and (Desai and Patil
2017). In these cases, the planning techniques are
used to simulate experience generated by a model.
Here two planning techniques are introduced aiming
to work cooperatively and coordinated getting a
heterogeneous multi-agent architecture for Large
Scale Systems (LSS).
These planning techniques were specially
developed to fit into the LINKER Architecture (LA)
introduced in (Javalera 2016) as the MA-MPC
architecture. First descriptions and applications of
this architecture were presented in (Javalera et al.
2010), and the use of this architecture and
methodology to the Barcelona Drinking Water
Network is described in (Morcego et al. 2014). In all
these applications the agents implement a control
technique called "Model Predictive Control (MPC),"
therefore the name of the architecture. However, this
work is called LINKER architecture, since the
algorithms and architecture can be applied to other
types of agents as well, not just MPC.
Reinforcement learning (RL) works based on
experience, which, in LA is used aiming to reduce the
80
Javalera-Rincon, V., Cayuela, V., Seix, B. and Orduña-Cabrera, F.
Reinforcement Learning Approach for Cooperative Control of Multi-Agent Systems.
DOI: 10.5220/0007349000800091
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 80-91
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

requirement of iterative methods, facilitating that the
system behaves almost like a reactive system with
reduced response time. Another relevant feature of
RL exploited by the LINKER Architecture is that it
explicitly considers the whole problem of a goal-
directed agent interacting with an uncertain
environment. Moreover, this is in contrast with many
approaches that consider sub-problems without
addressing how they might fit into a larger picture.
Even more, this is important for the LINKER
Architecture because it is distributed control
architecture of LSS, where some of its control
variables overlap between sub-systems; this issue is
aboard in the next section.
This paper aims to explain how using the
proposed learning techniques and the LINKER
Architecture, and is possible to integrate agents of a
distributed system with LINKER agents trained with
the proposed planning techniques. Each LINKER
agent calculates the value of shared variables between
overlapping systems looking for the global optimum
of the relation and coordinating its process with the
other agents of the system obtaining an overall good
performance. This work also proposes a solution that
makes possible to achieve the benefits of RL
techniques in critical systems that cannot afford to
pay the learning curve of a learner agent. Even more,
this is made using a meaningful reinforcement given
by the distributed agents that try the actions in its
internal model in offline training. Once all the
functions learned are evaluated and approved, the
LINKER agents use an online optimization algorithm
that can also have adaptation properties.
Another contribution of this paper is to compare
two learning techniques. In the first one, the actions
used in training are dictated by a teacher that, in this
case, is the centralized MPC (Model Predictive
Control) controller. In second one a learning
technique where actions are randomly selected. The
LINKER agent explores actions trying and evaluating
it, through the interaction with the agents that directly
control the model. An illustrative example is
developed using both techniques.
The structure of the paper is as follows: Section 2
introduces the problem statement. Section 3 presents
the model driven control and the model driven
integrated learning. Section 4 presents the planning
by instruction while Section 5 presents the planning
by exploration. Section 6 uses an application case
study to illustrate the performance of the proposed
architecture and approaches. Finally, Section 7
summarizes the main conclusions and describes the
future line of research.
2 PROBLEM STATEMENT
In order to describe the learning techniques
mentioned above, it is necessary to explain the
underlying problem, which is the distributed control
problem that the LINKER architecture addresses.
This architecture is applied to a LSS.
In order to control an LSS in a distributed way,
some assumptions have to be made on its dynamics,
i.e. on the way the system behaves. Let us assume first
that the system can be decomposed into n sub-
systems, where each sub-system consists of a subset
of the system equations and the interconnections with
other sub-systems. The problem of determining the
partitions of the system is not addressed in this work.
The set of partitions should be complete. This means
that all system states and control variables should be
included at least in one of the partitions.
Definition 1. System partitions. P is the set of
system partitions and is defined by
(1)
Where each system partition (subsystem)
,
is described by a model. In this example, a
deterministic linear time-invariant (LTI) model is
used to represent a drinking water distribution
network; this type of model can also be used for other
type of LSS where there is a network of connected
nodes and an element that flows in the network that
should be distributed to fulfill certain demands. This
model is expressed in discrete-time as follows
(2)
The model describes the topology and dynamics
of the network. Variables x, y, u, d are the state,
output, input and disturbance vectors (for this case,
the demands) of appropriate dimensions,
respectively; A, B, C and D are the state, output, input
and direct matrices, respectively. Sub-indexes u and
d refer to the type of inputs the matrices model, either
control inputs or exogenous inputs (disturbances).
Control variables are classified as internal or shared
variables.
Reinforcement Learning Approach for Cooperative Control of Multi-Agent Systems
81
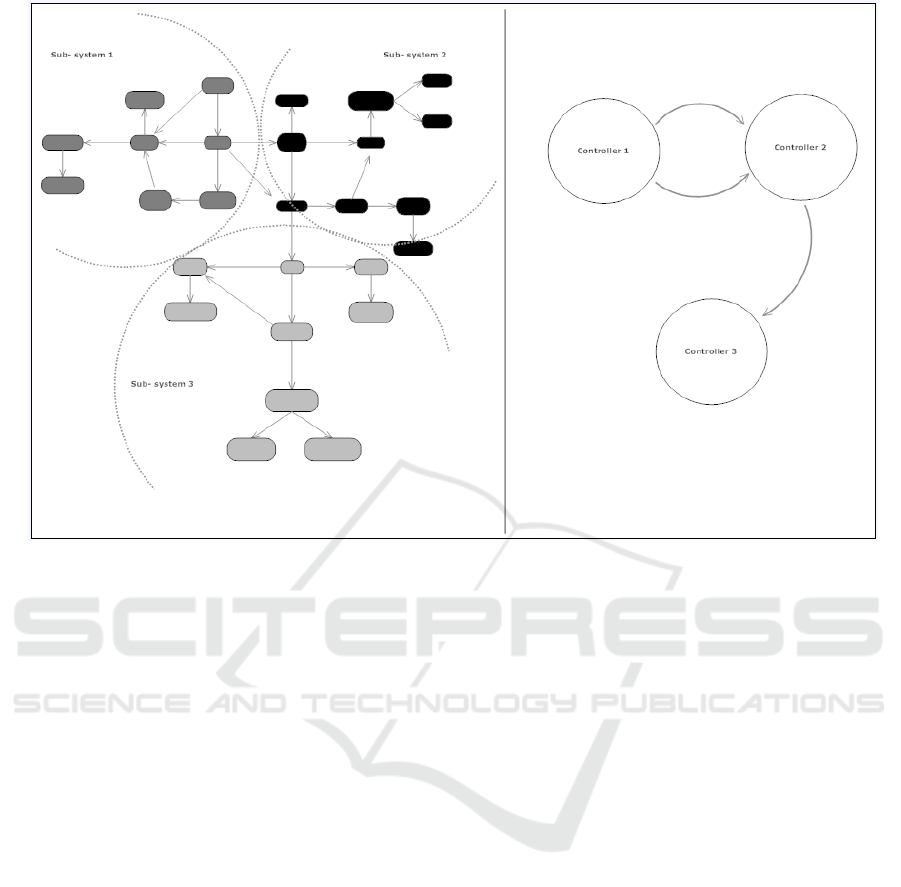
Figure 1: The problem of distributed control.
Definition 2. Internal Variables. Internal variables
are control variables that appear in the model of only
one subsystem in the problem. The set of internal
variables of a partition i is defined by equation 3:
}
(3)
Definition 3. Shared Variables. Shared variables are
control variables that appear in the model of at least
two subsystems in the problem. Their values should
be consistent in the subsystems they appear. They are
also called negotiated variables because their values
are obtained through a negotiation process.
is the
set of negotiated variables between partitions i and j,
defined by equation 4
(4)
Each subsystem i is controlled by a controller (agent)
using:
the model of the dynamics of subsystem i given
by eq. (2);
the measured state x
i
(k) of subsystem i;
the exogenous inputs d
i
(k) of subsystem i over a
specific horizon of time;
As a result, each agent calculates directly the
internal control actions, u
i
(k), of subsystem i. Figure.
1 on the left shows a sample system divided into three
partitions. Subsystem 1 has two shared variables with
sub-system 2 and subsystem 2 has one shared variable
with sub- system 3. The relations that represent those
variables are shown on the right as lines. The problem
consists in optimizing the manipulated variables of
the global system using a distributed approach, i.e.
with three local control agents that should preserve
consistency in the shared variables. In order to solve
the problem described above, a new framework has
been developed. This framework comprises a
methodology, the so called the LINKER
methodology and the architecture. The methodology
helps to implement the architecture
3 A MODEL DRIVEN CONTROL
AND A MODEL DRIVEN
INTEGRATED LEARNING
The LINKER architecture integrates a model driven
control and a model driven learning process. In order
to perform the negotiation of the shared variables, the
Linker agent learns to think globally, by means of an
offline training where negotiator and agents interact
and accumulate meaningful experience. This offline
training is made using a model of each sub-system
environment computing value functions (Q-tables)
whose optimality and efficiency are proved in the
experimentation phase, in order to be used later in the
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
82
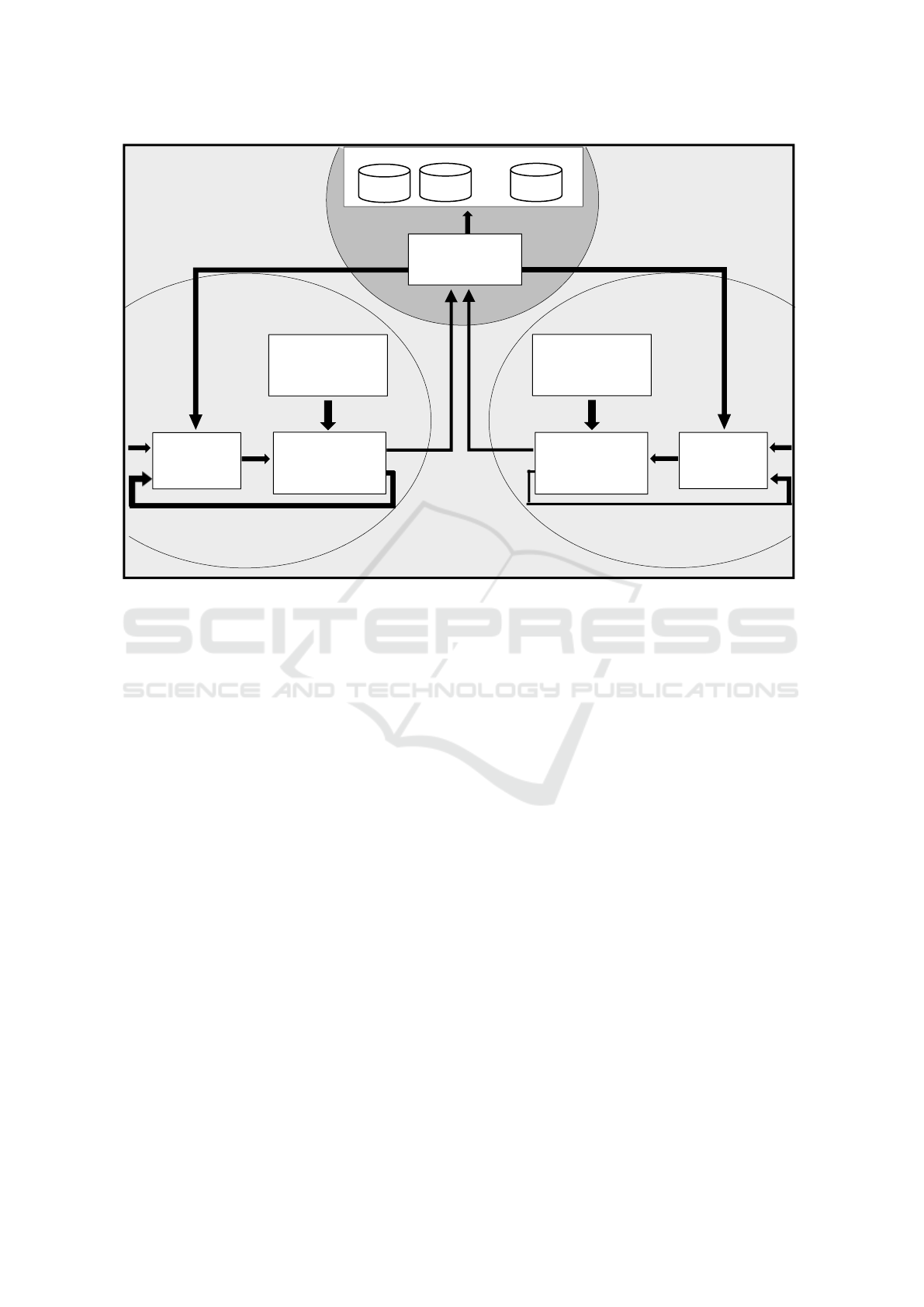
Figure 2: Integration of the models of agents in the planning process.
negotiation process. This allows eliminating iterative
communication between agents in the negotiation
process, increasing efficiency, decreasing time of
response and making it safe to implement.
Figure 2 shows the integration of the models in the
agents in the planning process. The Linker agent
assigns the values of V to the related agents. Each
related agent has its own reference, disturbance model
and plant model according to Eq. 2. The local
controller takes V as constraints, computes vector c and
applies the control action to the plant model producing
y and e. e is an error vector that indicates to the Linker
how good the actions (V) were. In order to evaluate that,
it is necessary to calculate the state of both agents. This
is made based in the cost function of the agents, as for
example,
s1= Hpi=0J(i)= Hpi=0Jx (i)+ Hpi=0 Ju(i)
(5)
s2= Hpi=0J(i)= Hpi=0Jx (i)+ Hpi=0 Ju(i)
(6)
where
and
(7)
The reward (r), is calculated using the states of
both MPC agents with the equation:
(8)
where represents the reward r and is a constant
that satisfies:
(9)
Given that s
1
and s
2
represents a sum of quadratic
errors (5), (6), the reward will be always positive.
With a smaller sum of errors the reward will be larger
and vice versa. s
1
and s
2
have to be discretized in order
to be use in
(10)
that is the function that updates each Q-table where
the parameters rates past experience.
The purpose of this three-dimensional matrix is to
map the state agent 1 (
) and the state of agent 2 (
)
to a single action. The coordination feature of the
Linker agent lies on the fact that, in exploitation, the
Linker agent will map to an optimal (or sub-optimal)
action every
and
eliminating with this conflicts
between agents assigning the value of shared
variables.
The Linker uses this simulated experience and
updates the Q-values in the Q-tables, one for each
shared variable of the vector V in order to improve its
policy. All this process is implemented through the
PlannigByInstruction and PlanningByExploration
Q
v1
Q
v2
Q
vn
…
Local
controller
Disturbance
Model 1
agent1
agent2
LINKER
V
V
d
r
1
c
y
d
r
2
y
c
e
2
Local
controller
Plant Model 2
Disturbance
Model 2
Plant Model 1
e
1
Planning
Reinforcement Learning Approach for Cooperative Control of Multi-Agent Systems
83

behaviors of the Linker that will be explained in
further detail in next section.
The integration of RL with the LTI model in this
approach offers high cohesion to the system. The
support that the LTI model (2) offers is deterministic,
descriptive and highly trusted. So, the integration of
these techniques coupled by the implementation of
the methodology makes the planning process efficient
and reliable.
The policy obtained is evaluated in the
experimentation phase. The fact that the policy is
obtained offline is a very important characteristic of
this approach due to the critical nature of LSS. The
use of a standard trial-and-error technique of RL
would make the implementation of this approach
unfeasible. If the learning process is driven from real
experience in the plant, the system will be unfeasible
most of the time at the beginning of the process and
the actuators can be damaged. That is why, in this
framework, in order to arrive to the implementation
phase, the optimality of the obtained policy has to be
tested beforehand.
4 PLANNING BY INSTRUCTION
In contrast to some IA learning methods, like
supervised learning, in this work, the term instruction
refers to the way in which the action is selected in the
learning process, and not to the type of the feedback
used. So, PlannigByInstruction behavior (PBIB) is a
learning behavior that implements a specific
combination of choosing actions and providing
feedback.
4.1 Description of the Approach
The purpose of this learning behavior is to obtain an
optimal policy (Q), constructing a knowledge base
based on the evaluation of actions given by a teacher.
This teacher has to be a trustable controller, like a
centralized MPC or the actions taken by a human
expert. These actions are simulated in the model
system and the result (states s
a1
and s
a2
, (5), (6)) is
evaluated obtaining a reward (r) (8) that is used to
obtain the new Q-value (10). n
it
iterations are made
for the complete control horizon with random initial
conditions. This behavior is performed offline in the
training phase of the LINKER methodology.
Assuming that there is a single negotiation variable,
the PlanningByInstruction behavior algorithm
describes the training algorithm that the NA executes
in order to update its Q-table by this learning behavior
In this algorithm, s
a1
and s
a2
represents the states
(5), (6) of agent1 and agent2 (the two agents that
share that particular negotiation variable). V
a1
and V
a2
are the internal representations of the shared variable
in Agent1 and Agent2 (sub-indices a1 and a2
respectively) for k instant. teacherAction is the action
dictated by the teacher.
Define , n, s
a1
← random, s
a2
← random,
controlHorizon, teacherAction (1-control horizon), k=1
loop while iterations ≤ n
loop while k ≤ controlHorizon
V
a1
(k) ← teacherAction (k)
V
a2
(k) ← teacherAction (k)
s
a1
← send V
a1
(k) to agent1, agent1 set the
action V
a1
(k) and calculates its internal variables,
apply all the controls (actions) obtained (and
given) for step k to its LTI model of its partition
and calculates s
a
using
(5)
.
s
a2
← send V
a2
(k) to agent2, agent2 set the
action V
a2
(k) and calculates its internal variables,
apply all the controls (actions) obtained (and
given) for step k to its LTI model of its partition
and calculates s
a2
using
(6)
.
r ← - s
a1
- s
a2
Q (s
a1
’, teacherAction (k)’, s
a2
’ )← r +α Q(s
a1
,
teacherAction (k), s
a2
)
s
a1
’← s
a1
s
a2
’← s
a2
k=k+1
end loop
iterations=iterations+1
end loop
5 PLANNING BY EXPLORATION
Learning by exploration is the main type of learning
technique used in RL. It is based on trying random
actions from a deterministic and finite set, in order to
obtain a feedback that represents how good the taken
action was. Learning by exploration in LSS can be a
difficult task because of the size and complexity of
these systems. The PlanningByExploration behavior
(PBEB) implements learning by exploration
combined with selective feedback. The use of
selective feedback reduces drastically the time of
training needed in order to obtain an optimal policy
(Q) and the difficulty to find a good parameterization
of the learning process in the experimentation phase.
The purpose of this learning behavior is to obtain an
optimal policy (Q), constructing a knowledge base
based on the exploration of a deterministic and finite
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
84
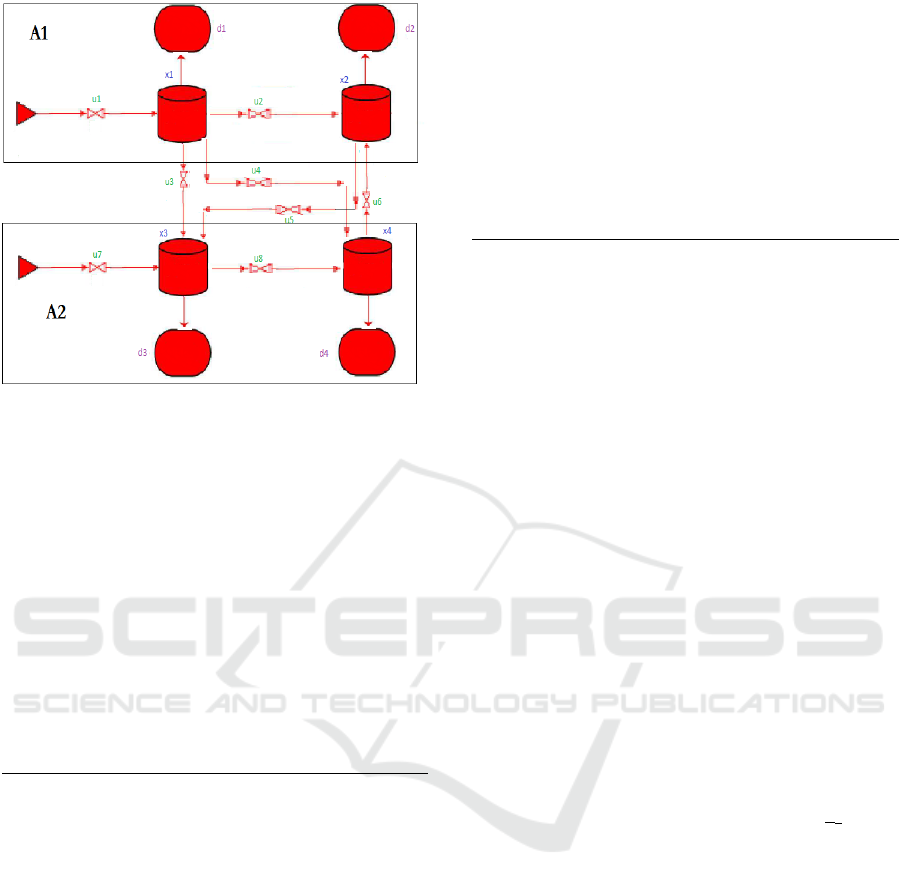
Figure 3: Water network considered as case study.
set of actions. These actions are simulated in the model
system and the result (states s
a1
and s
a2
) is evaluated
and only in case a feasible solution for both agents
(agent1 and Agent2) is found, the feedback is selected
for leaning. For those cases, a reward (r) is obtained
and used to calculate the new Q-value (10). n
it
iterations are made for the complete control horizon
with random initial conditions. This behavior is
performed offline in the training phase of the LINKER
methodology. Assuming that there is a single
negotiation variable, the PlanningByExploration
behavior algorithm describes the training algorithm
that the LINKER executes in order to update its Q-
table by this learning behavior:
Define , n, s
a1
← random, s
a2
← random,
controlHorizon, k=1
loop while iterations ≤ n
loop while k ≤ controlHorizon
a ← random (a) A Q (s
1
′,a, s
2
′)
V
a1
(k) ← a
V
a2
(k) ← a
s
a1
← send V
a1
(k) to agent1, agent1set the action
V
a1
(k) and calculates its internal variables, apply
all the controls (actions) obtained (and given) for
step k to its LTI model of its partition and
calculates s
a1
using
(5)
.
s
a2
← send V
a2
(k) to agent2, agent2set the action
V
a2
(k) and calculates its internal variables, apply
all the controls (actions) obtained (and given) for
step k to its LTI model of its partition and
calculates s
a2
using
(6)
.
if agent1 and agent2 have a feasible solution
r ← - s
a1
- s
a2
Q (s
a1
’, a’, s
a2
’ )← r +α Q(s
a1
, a, s
a2
)
s
a1
’← s
a1
s
a2
’← s
a2
else
s
a1
’← random
s
a2
’← random
end if
k=k+1
end loop
iterations=iterations+1
end loop
6 ILLUSTRATIVE APPLICATION
This section shows an example of the optimization of
a water distribution network using the proposed
architecture. The partitioning of the network obeys a
geographical criterion, so it has been divided in two
partitions, north and south (see Figure 3). The tanks
x
1
and x
2
will belong to the north sector where a local
control is required. The tanks x
3
and x
4
will belong to
the south sector, with its corresponding local
controller.
There are two supply sources and four demand
points, one for each tank. Typically the demands have
a sinusoidal behavior throughout the day that try to
emulate the actual demand behavior. The system shall
operate in a distributed way but looking for global
optimum in the controlled tank levels, satisfying the
demand points of both subsystems, and avoiding
collisions or conflicts among them.
It is expected that the performance of the tank
levels follow a reference variable in time, but without
performing drastic actions in the actuators. The target
control is defined as follows: For each tank (x
1
, x
2
, x
3
,
x
4
) there is a given reference that describes the
desirable behavior of the levels of these tanks. These
levels will be achieved through the manipulation of
the control variables (u
1
, u
2
,…,u
8
) with minor
variations over time.
6.1 Using PBIB
6.1.1 Training
Figure 4 shows a representation of the Q-values
calculated in different phases of the training of the
variable u
5
. The Q-table contrast the error of M
1
and
M
2
(or the discretize state of each agent) with the
action taken.
In order to use only positive errors, in Fig. 4,
errors range from 0 to 200. Negative errors range
from 0 to 99, 100 corresponds 0 and from 101 to 200
Reinforcement Learning Approach for Cooperative Control of Multi-Agent Systems
85
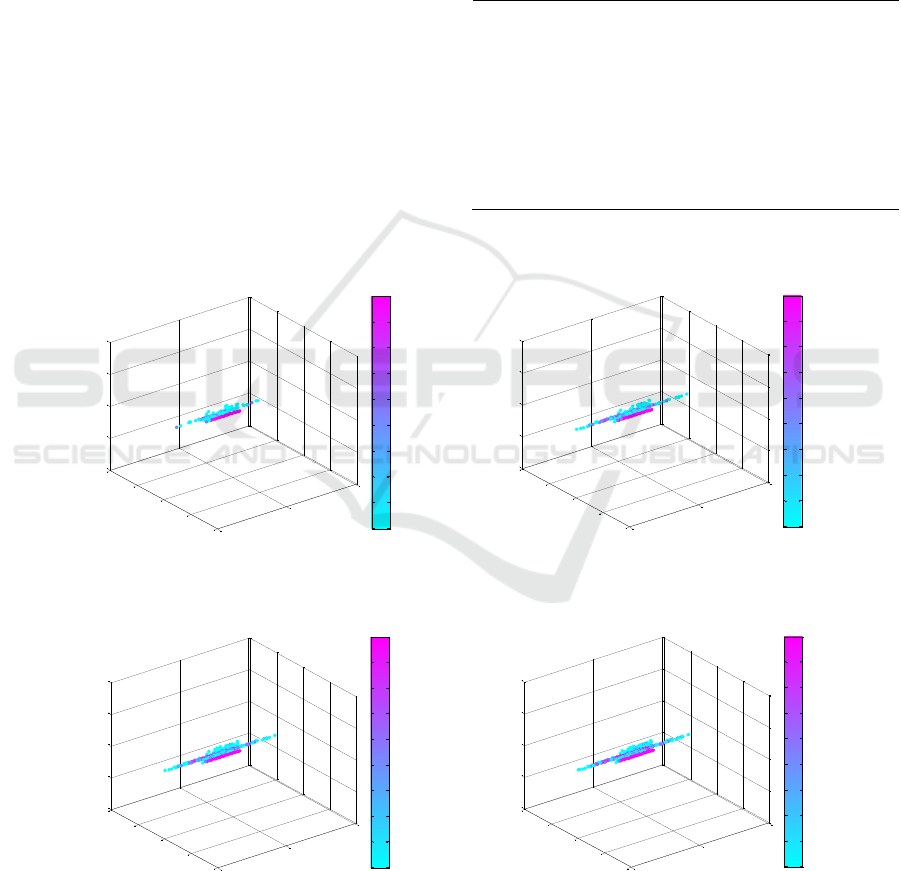
are range the positive errors. Actions are ranging from
0 to 100. As it can be appreciated in the figure, the
states visited in this training tend to be denser near the
optimum state (100). This is because all the actions
were dictated by the teacher, the centralized system.
Making a comparison between sub-figures (a), (b), (c)
and (d) it can be seen that the Q-values cloud is
spreading on the axis of the actions and becomes
denser as the training progresses. It is important to
notice that the only random factor in this training
(using PBIB) are the initial states of A
1
and A
2
. The
fact that in this training instructed learning is used
makes it fast and efficient. The Q-values stored in these
Q-tables represents meaningful and evaluated experi-
ence (because of the accumulation of the rewards).
It can be noticed that between section c and d of
the Fig. 4 there is not much difference. This is one of
the factors that can show that no more iterations are
needed. Additionally, the results of the exploitation
phase are necessary in order to determinate that the
training phase is finished. Similar results are obtained
for the rest of the Q-tables. A training based on PBIB
can be also used as a good start (or seed) before a non-
instructed learning technique.
6.1.2 Simulation
As it was mentioned before, in order to know if the
training phase is finished it is necessary to evaluate
the Q-tables making test and exploiting. In order to
do that, the greedy behavior has to be implemented.
The algorithm of greedy behavior is shown below.
Q (s
1
,a, s
2
) s S, a A
observe initial state, s
1,
s
2
loop
a ←max a ′ A Q (s
1
′,a, s
2
′)
s
1
← send V
a1
(k) to agent 1
s
2
← send V
a2
(k) to agent 2
s
1
←s
1
′
s
2
← s
2
′
end loop
This algorithm observes the state of the agents s
1
and s
2
(in a discretized way) and maps it to the action
Q-table Negotiation variable u
5
training of 50
iterations
(a)
Q-table Negotiation variable u
5
training of 100
iterations
(b)
Q-table Negotiation variable u
5
training of 200
iterations
(c)
Q-table Negotiation variable u
5
training of 300
iterations
(d)
Figure 4: Different phases of the training using PBIB of the variable u5.
0
50
100
0
50
100
150
200
0
50
100
150
200
Action
QTable Negotiator 1 - Variable u5
Error Agent 1
Error Agent 2
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
x 10
7
0
50
100
0
50
100
150
200
0
50
100
150
200
Action
QTable Negotiator 1 - Variable u5
Error Agent 1
Error Agent 2
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
x 10
7
0
50
100
0
50
100
150
200
0
50
100
150
200
Action
QTable Negotiator 1 - Variable u5
Error Agent 1
Error Agent 2
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
x 10
7
0
50
100
0
50
100
150
200
0
50
100
150
200
Action
QTable Negotiator 1 - Variable u5
Error Agent 1
Error Agent 2
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
x 10
7
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
86
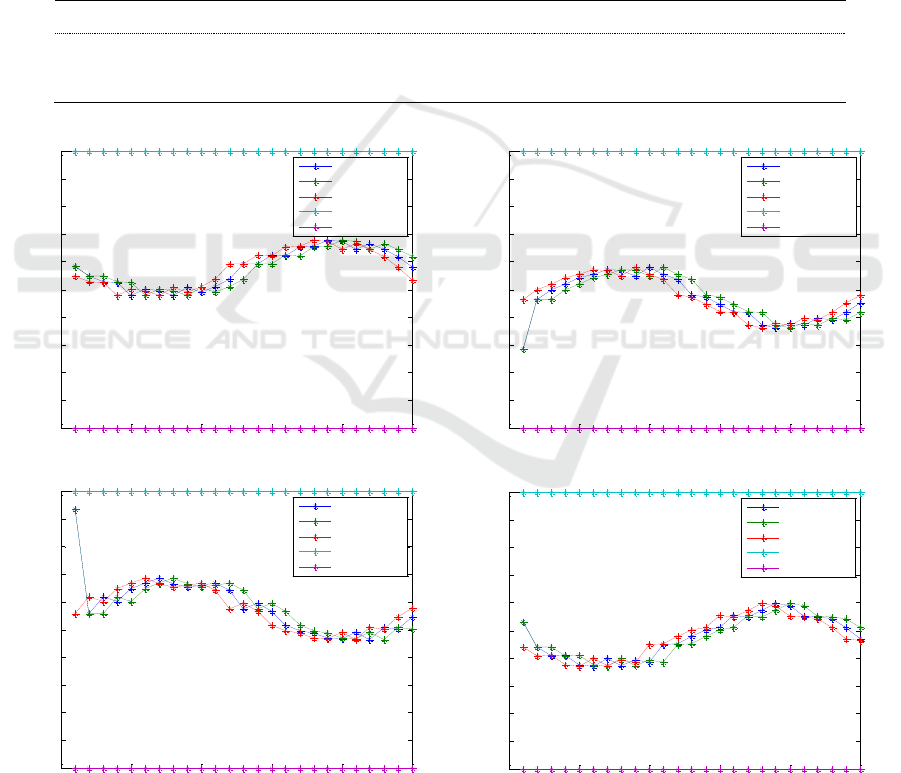
that maximizes the accumulated Q-value. Figure 6
shows the resulting actions of the shared variables
applied in the simulations shown above. It can be
notice that the ones calculated by the Linker (blue)
vary les over time than the ones calculated with a
centralized MPC (green). This is archived without
sacrificing performance.
6.1.3 Performance Analysis and Validation
Table 1 shows the average absolute error of the output
of 30 simulations. The first column was calculated
with a training of 50 iterations, next ones with 100
iterations, 200 and 300 iterations. The sum of the
error A
1
and error A
2
provides the total error. It can
be seen how the error in the LINKER system (the first
three) decreases as the iterations of the training
progresses. Also it can be noticed that between 200
and 300 iterations there is not much difference in the
error. The analysis of this table and the differences
between the resulting Q-tables is useful to establish
when the training is completed. The results shown in
Figure 5 show, that the LINKER system using
Instructed learning by implementing the
PlanningByInstruction behavior (PBIB) has a better
performance than the centralized MPC solution from
iteration 200.
Table 1: Accumulative ∆u between trainings.
50 it
100 it
200 it
300 it
tralized MPC
4,666e-05
6,333e-05
5,000e-05
6,333e-05
LINKER
0,0140833
0,0153533
0,0116933
0,0155466
Figure 5: Results of the Linker agents (blue) compared with the centralized MPC (green) solution. The red line is the reference,
purple x min, cyan x max.
0 5 10 15 20 25
0
1
2
3
4
5
6
7
8
9
10
Time (hr)
Volume (m3)
Agent 1 - Output x1
MA-MPC
Cetralize MPC
Reference
x Max
x Min
0 5 10 15 20 25
0
1
2
3
4
5
6
7
8
9
10
Time (hr)
Volume (m3)
Agent 1 - Output x2
MA-MPC
Cetralize MPC
Reference
x Max
x Min
0 5 10 15 20 25
0
1
2
3
4
5
6
7
8
9
10
Agent 2 - Output x3
Time (hr)
Volume (m3)
MA-MPC
Cetralize MPC
Reference
x Max
x Min
0 5 10 15 20 25
0
1
2
3
4
5
6
7
8
9
10
Agent 2 - Output x4
Time (hr)
Volume (m3)
MA-MPC
Cetralize MPC
Reference
x Max
x Min
Reinforcement Learning Approach for Cooperative Control of Multi-Agent Systems
87

Table 2: Average of absolute error between increasing
iterations during training with PBIB.
50
it
100
it
200
it
300
it
A
1
62,36
24,04
18,07
17,14
A
2
60,11
24,23
17,20
17,37
LINKER
(PBIB)
122,47
48,27
35,27
34,49
Centralized
MPC
45,91
44,08
45,04
44,71
Table 2 shows the accumulative ∆u objective
applied by the LINKER and the centralized MPC
solution in 30 simulations. The first column was
calculated with a training of 50 iterations, next ones
with 100, 200 and 300 iterations.
The results of this example shows that a system with
multiples dependences between its components can
be governed efficiently using distributed agents and,
even more, it can increase its performance using the
LINKER architecture implementing instructed
learning by the PBIB behavior.
It can also be observed that the actions calculated
by the LINKER (the shared variables) vary less over
time without sacrificing performance. But the
accumulative control effort is minor compared with
the centralized MPC.
Other experiments have been carried varying the
weights of the parameters
and
of Eq. (7).
Making the same changes in the teacher (the
centralized MPC) and performing a new training, the
Linker adapts to the new parameterization providing
similar results than ones obtained with the ones used.
6.2 Using PBEB
6.2.1 Training
The training implements the PlanningByExploration
behavior. Many experiments were made in this phase.
First experiments were made using just explorative
learning. Then, the PlanningByExploration behavior
(PBEB) was implemented varying the number of the
iterations in the training. Then, PBEB with selective
penalization of reward was implemented. All
training was made for the complete control horizon
(24 hrs.) for each shared variable. Random initial
conditions were set for each complete horizon.
During training, the Q-table for each shared variable
was filled with the Q-values calculated for all states
visited.
The learning behavior PlanningByExploration,
selects the actions that leads to a feasible solution of
the related MPC agents. In this experiment, PBEB
with selective penalization of reward was
implemented applying a penalization in the opposite
case, this means that if there is no feasible solution for
the local agents, a negative reward was assigned (-
1000). This negative reward ensures that the Q-value
of state-action-state that leads to critical states stays
low and accelerates drastically the training process
allowing the LINKER system to improve the
centralized MPC solution from the iteration 20 (see
Table 3).
Table 3: Comparison of the average absolute error between
local agents, LINKER system and centralized MPC
solution with trainings of 20, 50 and 100 iterations.
20 it
50 it
100 it
A1
17,2429
15,8219
16,3230
A2
18,3069
17,5714
16,3808
LINKER
35,5499
33,3932
32,7038
Centralized
MPC
45,3116
43,7657
42,8805
The experimentation made on this example shows
that using just using exploration, the system cannot
recover from states related to unfeasible solutions. In
addition, these states have high frequency of visits
because it is more likely that the random action
selected were not the good one. This affects
negatively the learning process because the
accumulation of many small rewards becomes in
larges Q-values.
In order to solve that issue, selective feedback
was applied. This reduces drastically the iterations
needed using just exploration and the Q-values
result more reliable. Moreover, the use of a negative
reward in the selected actions that lead to unfeasible
states also provide a huge improvement. After
assigning the negative reward, s’1
and
s’
2
are set to
random in order to continue the learning process
effectively.
With these conditions a training of 100 iterations
was carried out. Figure 6 (a) shows a color
representation of the Q-values calculated in the
learning process. The Q-table allows to present the
error of A
1
and A
2
(or the discretize state of each
agent) with the action taken. In order to use only
positive errors, the errors are scaled from 0 to 200.
Negative errors are scaled from 0 to 99, 100 is 0
while values from 101 to 200 correspond to positive
errors. Actions are ranging from 0 to 100. The
figure compares the Q-tables obtained using PBEB
(a) and (PBIB) (b). From Figure 6 (a), it can be
noticed that the cloud of data spreads all over the
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
88
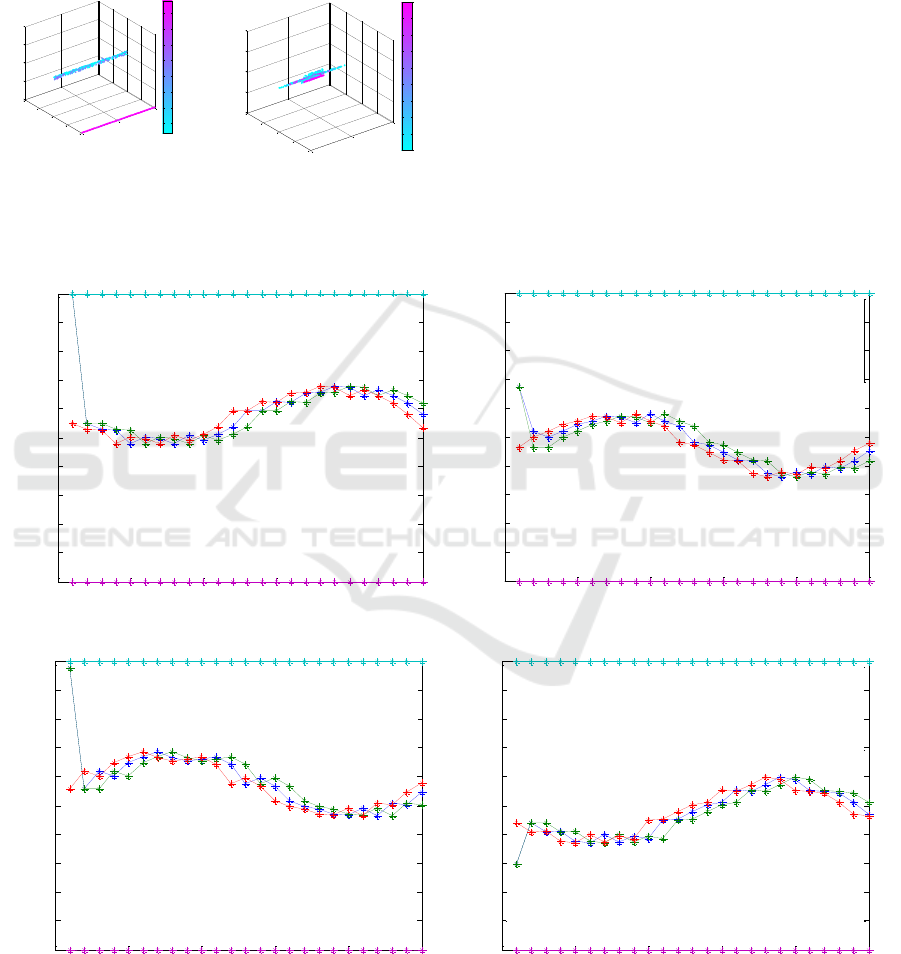
action axis, meaning that all actions were explored.
Fig. 6 (b) shows the Q-table of shared variable u
5
with a training of 300 iterations using PBIB. In this
Q-table, the cloud of Q-values is more compact
because its training only tried the actions dictated by
the teacher (in this case, centralized MPC).
Figure 6: Comparison of the resulting Q-Tables of the
variable u5 using PBEB (a) and PBIB(b).
6.2.2 Simulation
In other to know if the training phase is finished it is
necessary to evaluate the elements of the Q-table by
means of testing and exploiting. The simulation
process implements the greedy behavior (described
above).
The simulation results presented in Figure 7 allow
to compare the LINKER using PBEB (blue line) and
the centralized solution (green line) with the same
random initial conditions and references (red line),
obtained after a training of 100 iterations using PBEB
with selective penalization of reward explained
above. Notice that the reference is variable in time.
The parameters of MPC agents and the centralized
MPC system are the same.
From Figure 7, it can be noticed that both approach
force the system to track the reference.
Figure 7: Results of the MPC agents (blue) compared with the centralized MPC (green) solution. The red line is the reference,
purple x min, cyan x max.
(a)
(b)
0
50
100
0
50
100
150
200
0
50
100
150
200
Action
QTable Negotiator 1 - Variable u5
Error Agent 1
Error Agent 2
500
1000
1500
2000
2500
3000
3500
4000
0
50
100
0
50
100
150
200
0
50
100
150
200
Action
QTable Negotiator 1 - Variable u5
Error Agent 1
Error Agent 2
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
x 10
7
0 5 10 15 20 25
0
1
2
3
4
5
6
7
8
9
10
Time (hr)
Volume (m3)
Agent 1 - Output x1
MA-MPC
Cetralize MPC
Reference
x Max
x Min
0 5 10 15 20 25
0
1
2
3
4
5
6
7
8
9
10
Time (hr)
Volume (m3)
Agent 1 - Output x2
MA-MPC
Cetralize MPC
Reference
x Max
x Min
0 5 10 15 20 25
0
1
2
3
4
5
6
7
8
9
10
Agent 2 - Output x3
Time (hr)
Volume (m3)
MA-MPC
Cetralize MPC
Reference
x Max
x Min
0 5 10 15 20 25
0
1
2
3
4
5
6
7
8
9
10
Agent 2 - Output x4
Time (hr)
Volume (m3)
MA-MPC
Cetralize MPC
Reference
x Max
x Min
Reinforcement Learning Approach for Cooperative Control of Multi-Agent Systems
89

6.2.3 Performance Analysis and Validation
Many simulations were made to assess the
performance of the extended proposed approach.
Table III shows the comparison of the average
absolute error (with respect to the reference) of 30
simulations in the training process of the best Q-
tables found, the ones obtained using PBEB with
selective penalization of reward. Columns show the
results of a training of 20, 50 and 100 iterations with
random reference and initial conditions. From this
table, it can be noticed that the LINKER solution
improves the centralized solution since the first 20
iterations of the training and keeps improving slightly
as iterations increase.
It was observed that the actions calculated by the
Linker (the shared variables) vary less over time
without sacrificing performance. But, the
accumulative control effort is grater compared
with the centralized MPC. Other experiments were
made increasing or decreasing the negative reward
but for this problem the best negative reward was -
1000.
7 CONCLUSION
This article describes three behaviors that
implemented in the LINKER architecture, they
manage to separate the learning process of the
optimization process, eliminating with this the cost
of the number of learning steps necessary to
converge towards an optimal (or can be sub -
optimal) policy.
Explorative training is usually exhaustive. In this
work this complexity is reduced applying selective
feedback (using PBEB) but the combination of the
use of negative reward for the selected feedbacks not
just improves the results compared to the centralized
MPC but also the PlanningByInstruction Behavior
(PBIB) and decrease drastically the iterations
needed in the training phase. Table 4 shows the
average absolute error with respect to the reference
of 30 simulations of the PBEB with selective
penalization of reward and the PBIB. Random initial
conditions and random references were use. The
random cases calculated for PBEB with selective
penalization of reward were different than the ones
calculated for PBIB. The training of the PBEB with
selective penalization of reward, involves 100
iterations while in the case of the PBIB uses 300
iterations.
Table 4: Errors between PBEB with selective penalization
of reward and PBIB.
PBEB selective
reward
PBIB
A
1
16,3230
24,04
A
2
16,3808
24,23
LINKER
32,7038
48,27
Centralized MPC
42,8805
44,08
Table 5 shows the average
obtained using the
LINKER and the centralized MPC solution in the
same experimentation conditions that those used to
obtain the results presented in Table 4.
Table 5: Comparison of the J_∆u between the PBEB with
selective penalization of reward and PBIB.
PBEB
PBIB
Centralized MPC
0,0001
6,333e-05
LINKER
0,0107
0,0153533
Thus, the experimentation results obtained in this
example show that PBEB with selective penalization
of reward is a more efficient learning technique than
PBIB due to the reduction of the error and the
iterations needed in training.
The training of the PBEB with selective
penalization of reward and the LINKER framework
was successfully applied into a more realistic case of
study, the Barcelona drinking water network (DWN)
case study (Morcego et al. 2014) and (Javalera et al.
2019). This DWN in managed by Aguas de
Barcelona, S.A. (AGBAR).
ACKNOWLEDGEMENTS
This work was financed by the National Council of
Science and Technology (CONACyT) and PRODEP
of Mexico.
REFERENCES
Desai, R. M. and Patil, B. P., 2017. Prioritized Sweeping
Reinforcement Learning Based Routing for MANETs.
Indonesian Journal of Electrical Engineering and
Computer Science, 5(2), pp.383–390.
Hwang, K., Jiang, W. and Chen, Y., 2017. Pheromone-
Based Planning Strategies in Dyna-Q Learning. IEEE
Transactions on Industrial Informatics, 13(2), pp.424–
435.
Hwang, K.-S., Jiang, W.-C. and Chen, Y.-J., 2015. Model
learning and knowledge sharing for a multiagent system
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
90

with Dyna-Q learning. IEEE transactions on
cybernetics, 45(5), pp.964–976.
Javalera, V., 2016. Distributed large scale systems: a multi-
agent RL-MPC architecture. Universidad Politécnica
de Cataluña. Available at: http://digital.csic.es/
handle/10261/155199.
Javalera, V., Morcego, B. and Puig, V., 2010. Negotiation
and Learning in distributed MPC of Large Scale
Systems. In Proceedings of the 2010 American Control
Conference. pp. 3168–3173.
Javalera, V., et al. Cooperative Linker for the distributed
control of the Barcelona Drinking Water Network
Proceedings of the International Conference of Agents
and Artificial Intelligence. 2019.
Morcego, B. et al., 2014. Distributed MPC Using
Reinforcement Learning Based Negotiation:
Application to Large Scale Systems. In J. M. Maestre
& R. R. Negenborn, eds. Distributed Model Predictive
Control Made Easy. Dordrecht: Springer Netherlands,
pp. 517–533.
Tateyama, T., Kawata, S. and Shimomura, T., 2007.
Parallel Reinforcement Learning Systems Using
Exploration Agents and Dyna-Q Algorithm. In SICE
Annual Conference 2007. pp. 2774–2778.
Zajdel, R., 2018. Epoch-incremental Dyna-learning and
prioritized sweeping algorithms. Neurocomputing, 319,
pp.13–20
Reinforcement Learning Approach for Cooperative Control of Multi-Agent Systems
91
