Project Portfolio Selection Considering Return-risk Evaluation and

Multiple-Criteria Decision Analysis

Guilherme Augusto Barucke Marcondes

National Institute of Telecommunications (INATEL), Santa Rita do Sapuca

ı-MG, Brazil

Keywords:

Project Portfolio Selection, Mean-Gini, Multi-Criteria Decision, PROMETHEE.

Abstract:

Companies often face a challenge when they need to select their projects for execution because the resources

are not enough for all of them. For supporting decision, they need to employ some form of selecting the

best portfolio to run. There are several proposals in the literature, many allowing an evaluation of efﬁciency

between expected return and risk. However, these proposals indicate a list of efﬁcient portfolios, but not

the one best suited for execution. On the other hand, multi-criteria analysis methods allow a more speciﬁc

indication, but they are difﬁcult to be executed when the number of projects increases. This work seeks to

cover this gap by proposing a selection method that combines the return-risk assessment using mean-Gini

approach, complemented by the application of the multi-criteria decision method PROMETHEE II. The result

is the objective indication of the best project portfolio to be executed by the company.

1 INTRODUCTION

Frequently, companies have a list of projects to be

executed. But, due to resource constraints, they are

forced to select a subset of them (Abbassi et al.,

2014). This need for decision has been one of the

critical problems of project management (Jafarzadeh

et al., 2015). Decision makers need to prioritize

projects and deﬁne the best subset to be executed

(Perez and Gomez, 2014). The subset of projects can

be viewed as a portfolio.

Portfolio analysis may manage the risk in a set of

assets to establish which one offers the greatest re-

turn for a certain level of risk or the lowest risk for

a deﬁned level of return. These portfolios are called

efﬁcients. Project portfolios can be evaluated in the

same way of asset portfolios (Eilat et al., 2006).

Markowitz (1952) was a pioneer in proposing an

optimum strategy for maximizing return and min-

imizing risk of portfolios candidates for selection.

Based on his work, an efﬁcient frontier of portfolios

can be found by comparing expected return mean and

the correspondent variance for each portfolio (MV

portfolio). However, MV portfolio has reliable results

only when return are normally distributed or decision

maker utility function are quadratic (Feldstein, 1969).

In this way, while MV portfolio has been well ex-

plored by works as Levy and Levy (2014); Zopouni-

dis et al. (2014), other ones propose alternatives.

The work of Shalit and Yitzhaki (1984) presented

an alternative for portfolio selection by comparing

return mean and Gini coefﬁcient of portfolios under

evaluation (MG portfolio). Its application is less re-

strictive than MV. Investment portfolio selection us-

ing MG can de viewed in Alessandra Cillo (2014).

The same approach applied to project portfolio selec-

tion was used in the works of Ringuest et al. (2004)

and Gemici-Ozkan et al. (2010).

Resources scarcity is a reality in companies (Perez

and Gomez, 2014). In the same sense, Dutra et al.

(2014) state that, in general, there is no enough re-

source for all projects. It highlights the importance

of selecting the best set of projects (portfolio) to be

executed.

Projects selection must be done, naturally, before

knowing their returns. Decision makers decide based

on estimations, which leads to uncertainty, even if

good tools are applied (Kitchenham and Linkman,

1997). In this case, it is important to consider uncer-

tainty in project portfolio selection (Marcondes et al.,

2017).

Project Management Body of Knowledge Guide

(PMBOK



) from Project Management Institute rec-

ommends triangular distribution for dealing with un-

certainty in projects (PMI, 2013). It allows consid-

ering worst-case, most-likely and best-case estima-

tion for projects, using a range of value in evalua-

tions (instead of point values). Still in PMI (2013),

264

Marcondes, G.

Project Portfolio Selection Considering Return-risk Evaluation and Multiple-Criteria Decision Analysis.

DOI: 10.5220/0007350802640269

In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 264-269

ISBN: 978-989-758-352-0

Monte Carlo simulation is indicated as a tool for

uncertainty evaluation, which is usually used when

mathematical model is difﬁcult (or impossible) to

be treated (Bertrand and Fransoo, 2002; Better and

Glover, 2006).

In despite of return estimation based methods for

project portfolio selection, as in MV and MG portfo-

lios, in general, there are several conﬂicted criteria to

be evaluated. For supporting this kind of decision, the

literature offers the Multi-Criteria Decision Making

(MCDM) approaches (Behzadian et al., 2010). Pref-

erence ranking organization method for enrichment

evaluation (PROMETHEE) is an MCDM method for

ranking ﬁnite set of options under evaluation, among

conﬂicted criteria. Its application is increasing, based

on the number of published papers in literature (Be-

hzadian et al., 2010).

As PROMETHEE application compares, in all cri-

teria, options pair-by-pair, it can be cumbersome, de-

pending on the number of projects to be evaluated.

For instance, if one evaluates ten projects, there are

1,023 possible portfolios (not considering the option

of no project selected). If twenty projects, the number

of portfolios is 2,047.

Based on it, this work proposes a new method for

selecting a project portfolio to be executed. It applies

ﬁrst MG portfolio to reach an efﬁcient portfolio list

(the ones which are in MG efﬁcient frontier), con-

sidering uncertainty of estimations by Monte Carlo

simulation (implemented by Python language). For

indicating the best option, over the efﬁcient portfo-

lios, PROMETHEE II is applied. At the end, decision

maker has a ranking of portfolios, indicating from the

best to the worst, for choosing.

The research approach was based on simulation

with a real set of project. M

akinen and Vilkko (2014)

and Marcondes et al. (2018) applied simulation as a

tool for portfolio selection.

The remainder of this paper is organized as fol-

lows. Section 2 presents MG portfolio selection and

PROMETHEE II method. Section 3 explains how to

use triangular distribution for considering uncertainty

in selection. Proposed method is presented in Section

4 and its application using a real projects dataset in

Section 5. Finally, Section 6 concludes this work.

2 PROJECT PORTFOLIO

SELECTION

2.1 Mean-Gini

Mean-Gini portfolio selection considers estimation

of portfolio return for indicating an efﬁcient fron-

tier. Based on return distribution, one can calculate

its mean, indicating expected return, and Gini coefﬁ-

cient, indicating risk.

Expected return of a portfolio depends on ex-

pected return of each project included in it. Project

expected return is the expected value of its return ran-

dom variable. Portfolio expected return (R

) (or port-

folio mean), can be found by Equation (1).

∑

j=1

(1)

where:

• r

is the expected return of project j;

• w

∈ {0, 1} represents the decision of exclude or

include project j in portfolio, respectively.

Gini coefﬁcient is a statistical dispersion measure.

In general, it is largely applied to measure inequality

in income distribution for nation’s residents. Shalit

and Yitzhaki (1984), although its original purpose,

presented an application of Gini coefﬁcient for port-

folio risk analysis. Their application is an alternative

of variance application. Ringuest et al. (2004) state

Gini coefﬁcient is a simple measure and easy to be

applied in decision making process.

Gini coefﬁcient can be calculate by (Shalit and

Yitzhaki, 1984):

Γ = 2cov[R, F (R)] (2)

where:

• R is the portfolio return random variable;

• F (R) is its cumulative probability distribution.

and Γ

denote the return mean and Gini co-

efﬁcient, respectively, for portfolio i, in MG sense, a

portfolio II is dominated by a portfolio I, if and only

if (Ringuest et al., 2004):

> R

(3a)

and

6 Γ

(3b)

where at least one of these two conditions (3a) or (3b)

must be satisﬁed as inequality.

Project Portfolio Selection Considering Return-risk Evaluation and Multiple-Criteria Decision Analysis

265

Non-dominated portfolios are kept in efﬁcient

evaluation, and dominated ones discarded (not ef-

ﬁcient, compare to any other portfolio). Non-

dominated portfolios are considered efﬁcient. They

compose the efﬁcient frontier.

2.2 MCD PROMETHEE

Often, decision makers must select among options

based on several criteria that can be conﬂicting. For

this situation, literature offers the Multi-Criteria Deci-

sion Making (MCDM) approaches (Behzadian et al.,

2010). Preference ranking organization method for

enrichment evaluation (PROMETHEE) is an MCDM

outranking method when evaluating, among con-

ﬂicted criteria, a ﬁnite set of alternatives.

There are some PROMETHEE options.

PROMETHEE II is the chosen one when com-

plete ranking of alternatives is needed. It can offer

a ﬁnal list of alternatives, ranked from the best to

the worst, based on the deﬁned criteria and weights

assigned to them. The comparison for each criterion

must be made pair by pair, starting by calculating

the deviation (difference between their values). The

difference of each criterion must be applied to a

preference function (there are six basic types to be

chosen, depending on the kind of comparison is

done).

PROMETHEE II considers:

• A a set of n alternatives to be compared in j dif-

ferent criteria ( j = 1, ..., k);

• g

(a) the evaluation (value) of alternative a (a ∈

A) in criterion j;

• d

(a, b) the difference between alternatives a and

b (a, b ∈ A) in criterion j;

• F

(a, b)] the result of preference function ap-

plied to d

(a, b);

• w

the weight of criterion j.

It is based on ﬁve steps, as following (Behzadian

et al., 2010):

1. Calculate the deviations between a pair of criteria

(pair by pair):

(a, b) = g

(a) − g

(b) (4)

2. Apply the preference function:

(a, b) = F

(a, b)] for j = 1, ..., k (5)

3. Calculate the global preference index (π):

∀a, b ∈ A ⇒ π(a, b) =

∑

j=1

(a, b) (6)

4. Calculate the outranking ﬂows (positive φ

and

negative φ

−

) for each alternative:

(a) =

n − 1

∑

x∈ A

π(a, x) (7)

−

(a) =

n − 1

∑

x∈ A

π(x, a) (8)

5. Calculate the net outranking ﬂows for each alter-

native:

φ(a) = φ

(a) − φ

−

(a) (9)

After all steps, φ(a) for each alternative can be

compared. The higher the value of φ(a), the better

the alternative. At the end, the evaluation results in

the ranking among alternatives, facilitating the choice

for the decision maker.

PROMETHEE II is easy to be applied for rank-

ing projects criteria and its application is increasing,

based on the number of published papers in literature

(Behzadian et al., 2010). Based on it, it was chosen

for this work.

3 UNCERTAINTY ON PROJECTS

As Eilat et al. (2006), when proceeding portfolio se-

lection, uncertainty must be considered. A bad per-

formance on selection can occur due to parameters

uncertainty, mainly if it is considered that return esti-

mation is difﬁcult (DeMiguel and Nogales, 2009). In

fact, the impact of estimation error in choosing the op-

timal portfolio was discussed in several works, show-

ing it represents an important role in project selection

(Lim et al., 2011; Marcondes et al., 2017).

Three point estimation is recommended by PMI

(2013). For it, instead of estimating only one value,

they are three: worst-case (a), most-likely (b), and

best-case (c) outcomes. With them, one can construct

a triangular distribution, as presented in Figure 1, as

frequently applied in projects uncertainty evaluation

(Marcondes et al., 2018).

4 PROPOSED METHOD

The method proposed in this paper is based on MG

portfolio selection and PROMETHEE II. The purpose

is to indicate a portfolio to be executed by the com-

pany. There are some steps, as presented in Figure 2,

detailed described as following.

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

266

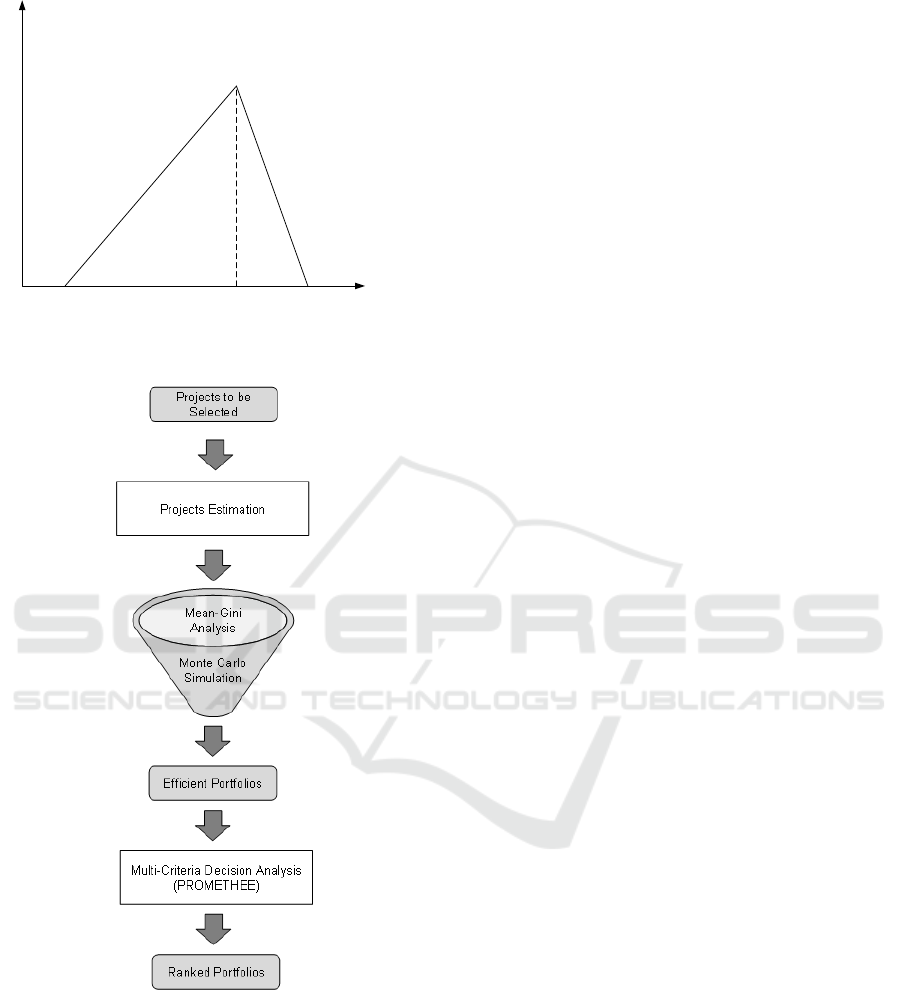
Probability Density Function

Random Variable

a bc

Figure 1: Triangular distribution based on three point esti-

mation.

Figure 2: Proposed Method.

1. Projects Estimation

Specialists use three-point estimation for estimat-

ing projects parameters and deﬁne worst-case,

most-likely, and best-case outcomes for return.

After that, for each project a triangular distribu-

tion is obtained.

They must also estimate information for

PROMETHEE II application, classifying the

projects in criteria as, for instance, strategic

importance, market position, innovation, and so

on.

2. Mean-Gini Analysis

All portfolio possibilities are identiﬁed and mean-

Gini comparison is started. Portfolios return mean

and Gini coefﬁcient are calculated and compared,

using Monte Carlo simulation. If a portfolio is

identiﬁed as dominated (not efﬁcient), it is dis-

carded for future comparisons.

At the end of this step, there will be a list of efﬁ-

cient portfolios.

3. Multi-Criteria Decision Analysis

Over the list of efﬁcient portfolios, PROMETHE

II is applied. φ(a) is calculated for each project,

and after that, for each efﬁcient portfolio (by sum-

ming up all φ(a) of each project constituting it).

Then, the list is ranked (from the highest to the

lowest value of φ(a)) and the decision maker can

choose portfolio to be executed.

After mean-Gini evaluation, decision maker has a

list of efﬁcient portfolio. However she/he must de-

cide for just one portfolio to be executed. Several

criteria must be consider for this decision. In the

proposed method, considering all criteria established

by the company, multi-criteria decision is applied for

ranking the portfolios. After these steps, decision

maker has a ranking for choosing the portfolio to be

executed.

5 APPLICATION IN REAL

PROJECTS

The method proposed in this paper was applied in

a real set of software development projects, from a

service provider company. The estimation process

involved three software engineers (specialists) with

more than 10 years of experience on software devel-

opment working as software architects and develop-

ers. Table 1 presents return three-point estimation for

eight projects.

For proceeding PROMETHEE II evaluation, the

following characteristics were deﬁned, and a weight

distribution established:

• Competitiveness Improvement (weight - 0,5):

considering the capacity of project for improv-

ing company competitiveness (from 1 - low to 4

- high);

• Market Potential (weight - 0,3): considering the

capacity of project for improving market share or

market penetration (from 1 - low to 4 - high);

Project Portfolio Selection Considering Return-risk Evaluation and Multiple-Criteria Decision Analysis

267

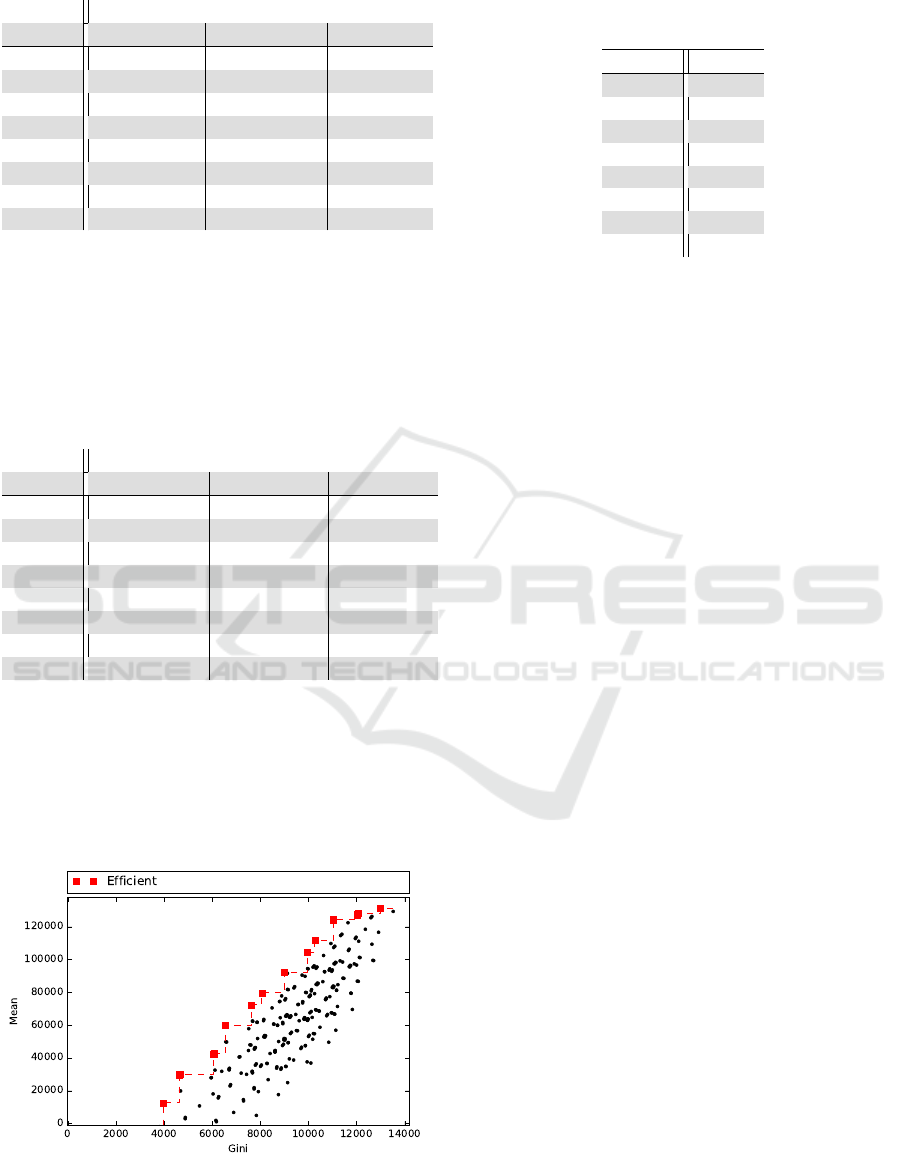
Table 1: Projects Return Information.

Return

Project Worst-Case Most Likely Best-Case

A -19,830 10,420 20,760

B -20,540 5,170 9,930

C 4,990 31,080 59,870

D -20,510 10,120 19,490

E 9,920 30,260 49,790

F -3,120 10,480 30,750

G 0 20,000 40,000

H 9,950 29,680 49,640

• Degree of Innovation (weight - 0,2): considering

how innovative the project is (from 1 - low to 4 -

high).

Table 2 summarizes the specialists evaluation for

each project characteristics.

Table 2: Projects Characteristcs.

Characteristics

Project Comp. Imp. Market Pot. Innovation

A 1 1 4

B 1 3 2

C 4 2 3

D 1 1 1

E 2 4 3

F 4 2 3

G 2 3 2

H 3 2 1

Based on Tables 1 and 2 informations, the sim-

ulation was run. From a total of 255 portfolios, it

was selected 15 efﬁcient portfolios. Figure 3 presents

a graphical with these partial result: all inefﬁcient

portfolios in black circles, efﬁcient portfolios in red

squares and efﬁcient frontier in dashed line.

Figure 3: Efﬁcient Frontier.

In the sequence, over these 15 efﬁcient portfolios

PROMETHEE II was run. For each project, φ(a) was:

Table 3: Projects Characteristcs.

Project φ(a)

A -1.800

B -1.267

C 2.467

D -3.400

E 1.400

F 2.467

G 0.067

H 0.067

The ﬁnal ranking of portfolio was (the sequence

of letters indicates which projects are included in the

portfolio):

1 CEFGH 9 FH

2 CEFH 10 F

3 ACEFGH 11 EGH

4 EFGH 12 EH

5 CEGH 13 E

6 EFH 14 ACDEFGH

7 EF 15 H

8 CDEFGH

The ranking indicates that portfolio CEFGH is the

best option for being executed. It is efﬁcient (for its

level of return mean, there is no one with lower risk;

for its risk level, there is no one with higher return

mean) and it has the highest φ(a) value. Complimen-

tary, this portfolio has the fourth highest return mean

value and the best return/risk ratio.

6 CONCLUSIONS

Presently, deﬁne the project portfolio to be executed

is a challenge for companies. In general, they don’t

have enough resources to execute all projects.

Several project portfolio selection method are pro-

posed in literature. The ones based on efﬁcient fron-

tier evaluation compares return and risk. Indicating a

list of efﬁcient portfolios.

However, over this list, decision makers need to

choose only one. Several criteria must be applied

(highest return, best relation return/risk, strategic re-

sults, and so on). When several criteria must be con-

sidered at the same time, it is important to use a suit-

able tool for this.

Based on this, this work proposes a method for

project portfolio selection combining efﬁciency (re-

turn and risk) evaluation and multi-criteria decision

PROMETHEE II in a sequence. The ﬁrst one works

as a pre-selection for applying the second one. The

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

268

result is an objective ranked list of portfolios to be se-

lected. Supporting decision maker in her/his decision.

For future works, the author has the following list:

• Before applying PROMETHEE II, over efﬁcient

portfolios some ﬁlters can be used: minimum ex-

pected return, minimum return/risk rate, or other;

• Additionally to return and risk information, some

constraints must be considered: people limit, time

limit, equipment (or other resources) limit, and so

on;

• Survey with some companies about the use of this

method in project portfolio selection.

REFERENCES

Abbassi, M., Ashraﬁ, M., and Tashnizi, E. S. (2014). Se-

lecting balanced portfolios of R&D projects with in-

terdependencies: A cross-entropy based methodology.

Technovation, 34(1):54–63.

Alessandra Cillo, P. D. (2014). Mean-risk analysis with en-

hanced behavioral content. European Journal of Op-

erational Research, 239(3):764–775.

Behzadian, M., Kazemzadeh, R. B., and Albadvi, A. A. M.

(2010). Promethee: A comprehensive literature re-

view on methodologies and applications. European

Journal of Operational Research, 200(1):198–215.

Bertrand, J. W. M. and Fransoo, J. C. (2002). Operations

management research methodologies using quantita-

tive modeling. International Journal of Operations &

Production Management, 22(2):241–264.

Better, M. and Glover, F. (2006). Selecting project port-

folios by optimizing simulations. The Engineering

Economist, 51(2):81–98.

DeMiguel, V. and Nogales, F. J. (2009). Portfolio selec-

tion with robust estimation. Operations Research,

57(3):560–577.

Dutra, C. C., Ribeiro, J. L. D., and de Carvalho, M. M.

(2014). An economic-probabilistic model for project

selection and prioritization. International Journal of

Project Management, 32(6):1042–1055.

Eilat, H., Golany, B., and Shtub, A. (2006). Constructing

and evaluating balanced portfolios of R&D projects

with interactions: A DEA based methodology. Euro-

pean Journal of Operational Research, 172(3):1018–

1039.

Feldstein, M. S. (1969). Mean-variance analysis in the the-

ory of liquidity preference and portfolio selection. The

Review of Economic Studies, 36(1):5–12.

Gemici-Ozkan, B., Wu, S. D., Linderoth, J. T., and Moore,

J. E. (2010). R&D project portfolio analysis for

the semiconductor industry. Operations Research,

58(6):1548–1563.

Jafarzadeh, M., Tareghian, H. R., Rahbarnia, F., and Ghan-

bari, R. (2015). Optimal selection of project portfo-

lios using reinvestment strategy within a ﬂexible time

horizon. European Journal of Operational Research,

243(2):658–664.

Kitchenham, B. and Linkman, S. (1997). Estimates, uncer-

tainty, and risk. IEEE Software, 13(3):69–74.

Levy, H. and Levy, M. (2014). The beneﬁts of differen-

tial variance-based constraints in portfolio optimiza-

tion. European Journal of Operational Research,

234(2):372–381.

Lim, A. E., Shanthikumar, J. G., and Vahn, G.-Y. (2011).

Conditional value-at-risk in portfolio optimization:

Coherent but fragile. Operations Research Letters,

39(3):163–171.

akinen, S. J. and Vilkko, M. K. (2014). Product portfolio

decision-making and absorptive capacity: A simula-

tion study. Journal of Engineering and Technology

Management, 32:60–75.

Marcondes, G. A. B., Leme, R. C., and de Carvalho, M. M.

(2018). Framework for integrated project portfolio se-

lection and adjustment. IEEE Transactions on Engi-

neering Management. In press.

Marcondes, G. A. B., Leme, R. C., Leme, M. S., and

da Silva, C. E. S. (2017). Using mean-Gini and

stochastic dominance to choose project portfolios with

parameter uncertainty. The Engineering Economist,

62(1):33–53.

Markowitz, H. M. (1952). Portfolio selection. Journal of

Finance, 7:77–91.

Perez, F. and Gomez, T. (2014). Multiobjective project port-

folio selection with fuzzy constraints. Annals of Op-

erations Research, 236:1–23.

PMI (2013). A Guide to the Project Management Body of

Knowledge. Project Management Institute, Atlanta,

EUA, 5 edition.

Ringuest, J. L., Graves, S. B., and Case, R. H. (2004).

Mean-Gini analysis in R&D portfolio selection. Eu-

ropean Journal of Operational Research, 154(1):157–

169.

Shalit, H. and Yitzhaki, S. (1984). Mean-Gini, portfolio

theory, and the pricing of risky assets. The Journal of

Finance, 39(5):1449–1468.

Zopounidis, C., Doumpos, M., and Fabozzi, F. J. (2014).

Preface to the special issue: 60 years following Harry

Markowitz’s contributions in portfolio theory and op-

erations research. European Journal of Operational

Research, 234(2):343–345.

Project Portfolio Selection Considering Return-risk Evaluation and Multiple-Criteria Decision Analysis

269