Semantic Differencing of Statecharts for Object-oriented Systems

Imke Drave, Robert Eikermann, Oliver Kautz and Bernhard Rumpe

Software Engineering, RWTH Aachen University, Aachen, Germany

Keywords:

Semantics, Semantic Differencing, Model Reasoning, Statecharts, UML.

Abstract:

Statecharts are well-suited to describe the behavior of objects in object-oriented systems. Effective statechart

evolution analysis for detecting errors and exploring design alternatives requires to reveal the semantic dif-

ferences from one statechart to another. Previous work has not produced approaches to semantic differencing

of statecharts for object-oriented systems. This paper deﬁnes a syntax and a semantics for reduced UML/P

statecharts and presents an explicit semantics-preserving translation from statecharts to ﬁnite automata. This

enables to reduce semantic statechart differencing to language inclusion checking between ﬁnite automata.

The translation is formally deﬁned and proven to be correct. This paper further introduces operators for hid-

ing and matching events to compare statecharts semantically on different levels of abstraction. The result is a

sound and complete method for semantic differencing of statecharts and abstraction methods, which ultimately

facilitates semantic statechart evolution analysis.

1 INTRODUCTION

Statecharts model the behavior of reactive systems

and have originally been introduced in (Harel, 1987).

The UML/P (Rumpe, 2016) is a variant of the UML

targeting implementability and code generation. The

UML/P focuses on modeling object-oriented systems

and is speciﬁcally suited for Java as target language.

The behavior of an UML/P statechart models a

high-level view on the behavior of objects of a class.

With this, it abstracts from low-level implementation

details. The states of the statechart correspond to con-

trol states of objects. The behaviors modeled by a

statechart abstract from data states. Nevertheless, data

states can be manipulated within reactions of a state-

chart but they do not inﬂuence the statechart’s behav-

ior with respect to its control ﬂow.

We formally deﬁne a reduced abstract syntax for

UML/P statecharts and a semantics mapping based

on possible execution traces, which represent the be-

haviors of the statechart. We assume that the set of

a statechart’s control states is representable by a ﬁ-

nite set and that each statechart only contains ﬁnitely

many transitions. The semantic difference from one

statechart SC

to another statechart SC

is deﬁned

as the set δ(SC

,SC

) of all behaviors in the seman-

tics of SC

that are no members in the semantics of

. Each behavior b ∈ δ(SC

,SC

) is thus a behav-

ior modeled in statechart SC

that is not modeled in

statechart SC

. The behavior b is interpretable as a

possible behavior of an object that behaves as speci-

ﬁed with SC

, which is no behavior of any object that

behaves as speciﬁed with SC

. It represents a possi-

ble observation of reactions to environmental inputs

(method calls) of an object. This paper further de-

ﬁnes a translation from statecharts to ﬁnite automata.

The translation enables to reduce semantic differenc-

ing of statecharts to language inclusion checking be-

tween the automata, which is a well-known decidable

problem (Hopcroft et al., 2006). Two statecharts may

be inequivalent on one level of abstraction but equiva-

lent on another. We present two statechart abstraction

methods that enable to compare statecharts semanti-

cally on different levels of abstraction.

The next section recaps details about UML/P stat-

echarts in the context of modeling object oriented sys-

tems. Section 3 presents a motivating example for

semantic differencing of statecharts. Subsequently,

Section 4 presents formal preliminaries grounding our

approach. Then, Section 5 presents a reduced abstract

syntax and a semantics for statecharts. Based on this,

Section 6 presents a method for semantic differenc-

ing of statecharts based on a translation to ﬁnite au-

tomata. Then, Section 7 presents abstraction meth-

ods. Finally, Section 8 discusses related work, before

Section 9 concludes.

272

Drave, I., Eikermann, R., Kautz, O. and Rumpe, B.

Semantic Differencing of Statecharts for Object-oriented Systems.

DOI: 10.5220/0007351902720280

In Proceedings of the 7th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2019), pages 272-280

ISBN: 978-989-758-358-2

2 UML/P STATECHARTS

UML/P statecharts (Rumpe, 2016) are intended to de-

scribe the behavior of objects in object-oriented sys-

tems. States in UML/P statecharts are interpreted as

control states (Rumpe, 2016). With this, a statechart

abstracts from the actual data states of objects during

runtime. An object’s state is divided into its control

state and its data state, determined by the values as-

signed to its attributes. UML/P statecharts abstract

from implementation details by abstracting from the

possibly inﬁnite set of actual data states with ﬁnitely

many control states. Each control state represents a

class of possibly inﬁnitely many data states. In stat-

echarts, initial states correspond to the object’s ini-

tial control state after the constructor has been called.

As modern garbage collectors delete detected un-

reachable objects, there are no explicit ﬁnal states in

UML/P statecharts (Rumpe, 2016). Transitions be-

tween states correspond to the execution of methods.

A transition is taken upon the occurrence of its stim-

ulus event, provided that the object’s control state is

equal to the transition’s source state. In UML/P state-

charts, the occurrence of a stimulus event corresponds

to calling a method of an object (including its argu-

ments). The reaction of the object to a method call

is modeled by the transition’s reaction. A reaction

is a sequence of statements, e.g., method calls or at-

tribute assignments, which are executed in the body

of the method corresponding to the stimulus (Rumpe,

2016). UML/P statecharts abstract from object re-

cursion, i.e., transitions including reactions that call

other public methods (stimuli) of the same object. It

may nevertheless appear in private methods as long as

the statechart’s control state is not manipulated. The

above interpretation of statecharts and the abstraction

from recursion enable a simplifying transformation

to a statechart normal form as described in (Rumpe,

2016). This transformation eliminates, for example,

hierarchically nested states. We will deﬁne an abstract

statechart syntax based on the simple normal form to

facilitate a semantics mapping deﬁnition.

3 EXAMPLE

Webshops usually provide virtual carts. Customers

add items to a cart by selecting items offered on prod-

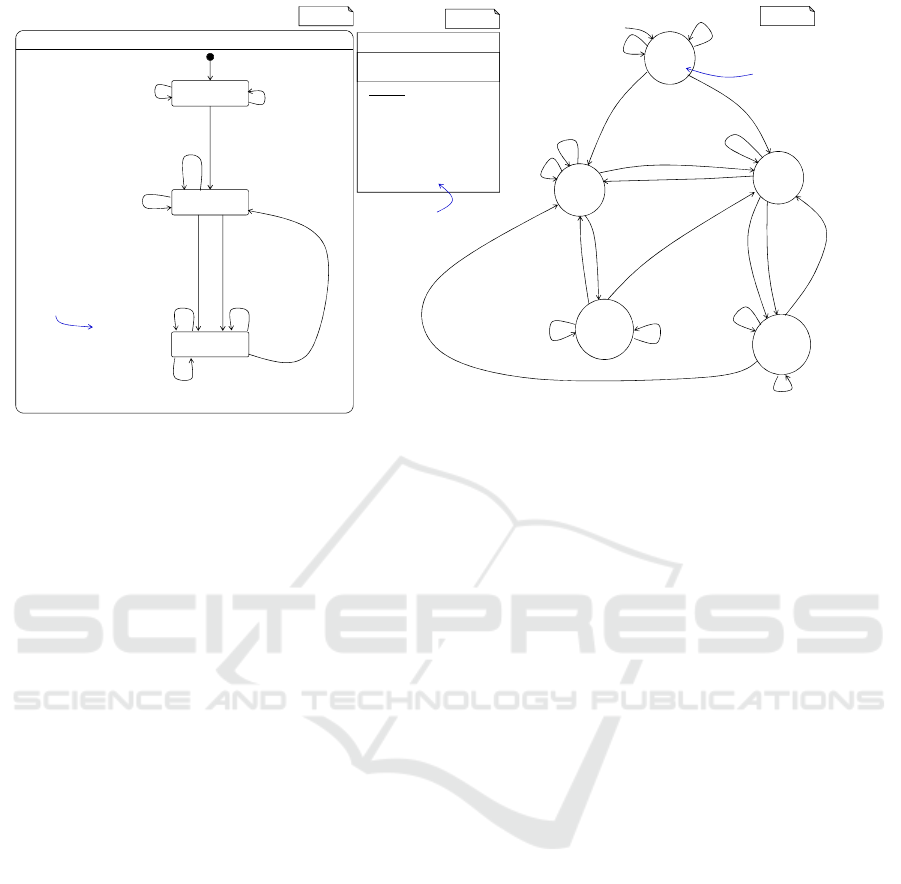
uct sites. Figure 1 depicts a statecharts describing a

webshop system’s behavior when processing orders.

On the left, statechart SC models the behavior of ob-

jects of the Order class speciﬁed by the class dia-

gram in the middle. Our analysis performs a trans-

formation into a nondeterministic ﬁnite automaton as

shown on the right of Figure 1. After construction,

an order object resides in the Created-state, where

it is not yet paid. A place-order button executes the

place() method, which triggers the execution of re-

questPay(price) setting the paid attribute of the or-

der, before it takes the Placed state. Once placed, the

customer may either cancel or re-place() and pay the

order. Shipment is initiated by tryShip(), which will

only trigger the transition to Completed if paid==true,

since the webshop explicitly requires that only paid

orders are shipped. If so, the system executes ship(),

which sends the ordered items to the customer. In

case a customer cancels her order, a cancellation re-

quest is sent to the system. As modeled by SC, can-

celing an order is also possible after the order has al-

ready been shipped. A webshop developer now no-

tices that canceling orders after shipping lead to neg-

ative ratings for the webshop. The developer decides

to inhibit canceling shipped orders. To this effect, she

modiﬁes the statechart SC by replacing the request-

Cancel() reaction in state Completed by a new method

illegalCancel(), which notiﬁes the customer that a can-

cellation of the order is not possible. The statechart is

updated to suit the new requirement. The developer

wants to understand how the syntactic change inﬂu-

enced the statechart’s semantics. She thus uses our

method for semantic statechart differencing. It turns

out that the updated version of SC has incomparable

semantics to the original, i.e., there exists a behav-

ior modeled in SC that is not possible after the up-

date and vice versa. The developer is presented with

two witnesses that are concrete examples of seman-

tic differences: A witness for the semantic difference

from the original statechart to the statechart after re-

placing requestCancel() by illegalCancel() is (place(),

paid=requestPay(price)), (tryShip(), ship()), (cancel(),

requestCancel()). Vice versa, a witness for the se-

mantic difference from the changed SC to the original

SC is the behavior (place(), paid=requestPay(price)),

(tryShip(), ship()), (cancel(), illegalCancel()).

4 PRELIMINARIES

The empty word is denoted by ε. An alphabet is a

non-empty ﬁnite set A satisfying ε /∈ A. A

∗

denotes

the set of all ﬁnite sequences (words) over an alphabet

A. For every alphabet A, ε ∈ A

∗

holds. Let u,v ∈ A

∗

be words. u · v (or uv) denotes the result of appending

the word v to the word u. |u| denotes the length of u

where |ε| = 0. u.i denotes the (i + 1)-th symbol in u

with |u| > i. For a symbol s ∈ A, we denote by s : u

the result of prepending s to u. d(u) denotes the result

from deleting the ﬁrst symbol from u 6= ε. For a set

Semantic Differencing of Statecharts for Object-oriented Systems

273

Order

Created

[paid==false]

place() /

paid=requestPay(price);

[paid == true]

tryShip() /

ship()

Completed

Placed

cancel() /

requestCancel()

[paid==true]

tryShip() /

ship()

place() /

paid=requestPay(price);

cancel() /

requestCancel()

place() / paid=

requestPay(price)

[paid==false]

tryShip()

cancel()

tryShip()

UML/P SC

[paid == false]

tryShip()

developer replaces

requestCancel() by

illegalCancel()

Completed,

false

Placed,

false

Placed,

true

Created,

false

Completed,

true

place() / paid=

requestPay(price)

place() / paid=

requestPay(price)

place() / paid=

requestPay(price)

tryShip() /

ship()

tryShip() /

ship()

place() / paid=

requestPay(price)

place() / paid=

requestPay(price)

place() / paid=

requestPay(price)

place() / paid=

requestPay(price)

place() / paid=

requestPay(price)

NFA(SC)

cancel() /

requestCancel()

cancel() /

requestCancel()

cancel() /

requestCancel()

cancel()

tryShip()

paid value

Order

-boolean paid

-int price

+Order()

+Boolean place()

+Boolean tryShip()

+Boolean cancel()

-Boolean requestPay(price)

-ship()

-requestCancel()

-illegalCancel()

added during

development

place() / paid=

requestPay(price)

cancel() /

requestCancel()

place() / paid=

requestPay(price)

Figure 1: Statechart modeling the behavior of a webshop system, the associated class, and the corresponding nondeterministic

ﬁnite automaton (NFA).

of symbols B ⊆ A, we denote by u ↓ B the result of

removing all occurrences of the symbols contained in

B from u. For all u ∈ A

∗

and B ⊆ A, the operator is

recursively deﬁned by the following equation:

u ↓ B =







ε if u = ε

u.0 : (d(u) ↓ B) if |u| > 0 ∧ u.0 /∈ B

d(u) ↓ B if |u| > 0 ∧ u.0 ∈ B

We lift functions m : A → A mapping elements of a

set A to elements of the same set to words u ∈ A

∗

over A in a point-wise manner, i.e., m(ε) = ε and

m(u) = m(u.0) : m(d(u)) for all ε 6= u ∈ A

∗

An nondeterministic ﬁnite automaton (NFA) (e.g.,

(Hopcroft et al., 2006)) is a tuple (Q,Σ,δ,Q

,F)

where Q is a ﬁnite set of states, Σ is an alphabet,

δ ⊆ Q × Σ × Q is the transition relation, Q

is a set

of initial states, and F is a set of ﬁnal states. Let

A = (Q,Σ,δ,Q

,F) be an NFA. A run of A on a word

w = w

,...,w

∈ Σ

∗

is a ﬁnite sequence of states

r = r

,...,r

∈ Q

∗

satisfying r

∈ Q

, r

∈ F and

i+1

) ∈ δ for all 0 ≤ i < n. The NFA A ac-

cepts a word w iff a run of A on w exists. The language

recognized by A is deﬁned as L (A) = {w ∈ Σ

∗

| A

accepts w}, i.e., all words accepted by A. There are

well-known algorithms to check whether the language

recognized by one NFA is included in the language

recognized by another NFA (Hopcroft et al., 2006).

5 STATECHART SYNTAX AND

SEMANTICS

A complete deﬁnition of a modeling language con-

sists of the following parts (Cengarle et al., 2009;

onniger and Rumpe, 2011): Concrete Syntax, ab-

stract syntax, reduced abstract syntax, semantic do-

main, and semantic mapping.

The concrete syntax is a model’s representation

that the user interacts with. A deﬁnition of the graph-

ical and a textual concrete syntax for statecharts as

used in this paper is available in (Rumpe, 2016). This

paper’s approach abstracts from a concrete syntactic

representation. The abstract syntax is a reduced and

compact representation of the concepts that can be

modeled using the concrete syntax. For every model

in the concrete syntax, there must exist a model in

the abstract syntax that the model is mapped to. Dif-

ferent models in the concrete syntax may be mapped

to the same model in the abstract syntax. The re-

duced abstract syntax is a subset of the abstract syn-

tax of a modeling language. It only includes a sub-

set of the abstract syntax without losing expressibil-

ity. Normal forms of propositional formulas are ex-

amples for reduced abstract syntaxes. A reduced ab-

stract syntax eases the deﬁnition of the semantics of a

language (Cengarle et al., 2009). Section 5.1 presents

a reduced abstract syntax for UML/P statecharts. A

translation from the abstract syntax (including hier-

archy, OR-states, epsilon-transitions, entry and exit

actions) to the reduced abstract syntax is described

in (Rumpe, 2016). The semantic domain contains the

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

274

elements of the semantics of a model. In this pa-

per, the semantic domain for statecharts is a set of

all ﬁnite sequences of stimuli/reaction tuples. Each

sequence represents a behavior as a trace of method

calls. The stimuli represent methods called on an ob-

ject of a statechart’s class and the reactions contain

method calls performed by the object. The semantic

mapping relates the elements of the reduced abstract

syntax to elements of the semantic domain. In this

paper, the semantic mapping maps each statechart to

the set of possible behaviors of its class’s objects.

5.1 Reduced Abstract Syntax

State hierarchies in UML/P statecharts can be elimi-

nated by a transformation (Rumpe, 2016). Therefore,

in the following we assume statecharts to be ﬂat and

their set of control states to be ﬁnitely representable.

Thus, the types of variables used on guards must also

be ﬁnitely representable. Examples for ﬁnite types

are the primitive types short, int, and boolean. Let E

denote a countable inﬁnite set of events. For exam-

ple, the set E may contain all expressions for calling

methods or attribute assignments. The following de-

ﬁnes the reduced abstract syntax for ﬂat statecharts:

Deﬁnition 1 (Statechart). A statechart is a tuple

(I, O, S,T,S

) where

• I,O ⊂ E with I ∩ O =

0 are ﬁnite sets of input and

output events,

• S is a ﬁnite set of states,

• T ⊆ S × S × I × O

∗

is a ﬁnite set of transitions,

• S

⊆ S is a set of initial states.

Notation. Let t = (src,tgt,st,ev) ∈ T be a tran-

sition. Then, src(t) = src denotes the transition’s

source state, trg(t) = tgt denotes the transition’s tar-

get state, st(t) = st denotes the transition’s stimulus,

and r(t) = ev denotes the transition’s reaction.

We assume that each statechart models the behav-

ior of instances of a class in an object-oriented sys-

tem. Each state of the statechart is a control state

that represents a possibly inﬁnite set of actual data

states. For instance, a statechart’s class may contain

several attributes. The statechart abstracts from the

data states of objects of the class (i.e., assignments to

the attributes) as it only contains control states. Al-

though the data state may be manipulated via execut-

ing transitions, it never inﬂuences the behavior of the

statechart. If the assignment to an attribute is meant to

inﬂuence a statechart’s behavior, it must be explicitly

encoded as control state. The set of initial states mod-

els the possible initial control states of objects of the

statechart’s class after their creation. The set of input

events of a statechart contains expressions represent-

ing the public methods of the statechart’s class. Out-

put events represent statements in the bodies of these

methods. These are, for example, statements for call-

ing private methods of the same class, statements for

calling methods of attributes of the class, or attribute

assignments. Recursion in statecharts induces several

semantic ambiguities (Rumpe, 2016). Therefore, the

set of input events is required to be disjoint to the set

of output events, which prevents recursion on state-

chart model level. However, recursive method calls

may appear, for example, inside private methods.

5.2 Behavior Semantics

UML/P statecharts can be interpreted as NFAs with

input and output alphabets. With this, the execution

of a transition is an atomic process, which cannot be

interrupted: When a statechart receives an event, it

takes a transition with the corresponding stimulus and

must execute the transition’s reaction before receiv-

ing the next event is possible. Immediately after exe-

cuting the reaction, the statechart switches its state to

the transition’s target state. Further, in UML/P stat-

echarts, events in reactions of transitions cannot trig-

ger further transitions, i.e., no recursion is allowed on

statechart level. The following deﬁnition formalizes

the intuition behind the notion of execution:

Deﬁnition 2 (Execution). An execution of a state-

chart SC = (I,O,S, T, S

) is a ﬁnite alternating se-

quence s

,...,s

(n ≥ 0) of states and transi-

tions ending in a state such that

1. s

∈ S

2. s

∈ src(t

i+1

) for all 0 ≤ i < n, and

3. s

∈ trg(t

) for all 0 < i ≤ n.

Ex(SC) denotes the set of all executions of SC.

With the above deﬁnition, a statechart execution

starts in one of the statechart’s initial states. Then, the

statechart iteratively executes a transition starting at

its current state and then enters the transition’s target

state. A transition may end in any of the statechart’s

states, i.e., there are no explicit ﬁnal states. This re-

ﬂects that unreferenced objects in an object-oriented

system may be garbage collected, which is a process

that does not depend on an object’s state.

Executions comprise the internal state changes of

a statechart that are invisible to its environment. The

behavior of an execution only captures the visible

events while the statechart performs the execution:

Deﬁnition 3 (Behavior). Let SC = (I,O,S,T,S

) be

a statechart. The behavior beh(ex) of an execu-

tion ex = s

,...,s

∈ Ex(SC) of the state-

Semantic Differencing of Statecharts for Object-oriented Systems

275

chart SC is deﬁned as the sequence beh(ex) =

(st(t

),r(t

)),..., (st(t

),r(t

)) ∈ (I × O

∗

)

∗

With the above, a behavior of an execution is the

sequence of tuples of stimuli and reactions of the tran-

sitions occurring in the execution. The semantics of a

statechart is the set of all behaviors of the statechart.

Deﬁnition 4. The semantics JSCK of a statechart SC

is the set of all behaviors of all executions of SC, i.e.,

JSCK = {beh(ex) | ex ∈ Ex(SC)}.

6 SEMANTIC DIFFERENCING

OF STATECHARTS

This section formally introduces semantic differenc-

ing of statecharts and presents a method that can be

performed on push-button basis.

Deﬁnition 5 (Semantic Difference). The semantic

difference of a statechart SC

to a statechart SC

deﬁned as δ(SC

,SC

) = JSC

K \JSC

With this, the semantic difference contains all be-

haviors modeled in one statechart that are not mod-

eled in another statechart. If δ(SC

,SC

) =

0, then

the Statechart SC

is a reﬁnement of the statechart

, i.e., SC

has no behavior that SC

does not have.

Therefore, the former statechart contains less under-

speciﬁcation as the latter. In model-driven develop-

ment, statecharts are naturally reﬁned in reaction to

receiving additional requirements.

As the semantics of a statechart is typically an inﬁ-

nite set, checking whether δ(SC

,SC

) =

0 is, in gen-

eral, not trivial. In the following, we present a sound

and complete method to check whether one statechart

reﬁnes another statechart. In case of non-reﬁnement,

the method yields an element w ∈ δ(SC

,SC

), which

is a concrete witness for a behavior possible in the

one statechart that is not possible in the other state-

chart. To this effect, we present a translation from

statecharts to NFAs and reduce statechart reﬁne-

ment checking to language inclusion checking be-

tween NFAs. As language inclusion checking be-

tween NFAs is fully automatable, we obtain an au-

tomated method for semantic statechart differencing.

6.1 Mapping Statecharts to Automata

For every statechart, there exists an NFA such that the

language accepted by the NFA is equal to the set of

behaviors of the statechart. The following deﬁnition

explicates the construction of such an NFA:

Deﬁnition 6. Let SC = (I, O, S,T, S

) be a statechart.

The NFA NFA(SC) associated to SC is deﬁned as

NFA(SC) = (S, Σ, δ, S

,S) where

• Σ = I × (

t∈T

{r(t)}),

• δ = {(u, (st,r),v) | (u,v,st,r) ∈ T } ⊆ S ×Σ × S.

As T is ﬁnite,

t∈T

{r(t)} is also ﬁnite. Thus, as

additionally I is ﬁnite, Σ is ﬁnite. Further S and S

⊆ S

are ﬁnite. Therefore, NFA(SC) is a well-deﬁned NFA.

With Deﬁnition 6, every NFA input symbol corre-

sponds to a stimulus/reaction tuple of the statechart.

The recognized language of an NFA associated to a

statechart equals the statechart’s semantics.

Theorem 1. For every statechart SC, it holds that

JSCK = L (NFA(SC)).

Proof. Let SC = (I,O,S, T, S

) be a statechart and let

NFA(SC) = (S, Σ, δ, S

,S).

⊆: Let e = s

,...,s

∈ Ex(SC) be an ex-

ecution of SC. We need to show that beh(e) ∈

L (NFA(SC)). By deﬁnition of execution, we have:

1. s

∈ src(t

i+1

) for all 0 ≤ i < n, and

2. s

∈ trg(t

) for all 0 < i ≤ n.

From this and the deﬁnition of δ, we can conclude

,(st(t

i+1

),r(t

i+1

)),s

i+1

) ∈ δ for all 0 ≤ i < n. By

deﬁnition of execution, it holds that s

∈ S

. As every

state in NFA(SC) is accepting, we can conclude that

,...,s

is a run of NFA(SC) on the word beh(e) =

(st(t

),r(t

)),..., (st(t

),r(t

)) ∈ L (NFA(SC)).

⊇: Let r = r

,...,r

∈ S

∗

be a run of A on a

word w = (a

),(a

),...,(a

) ∈ Σ

∗

. We need

to show that w ∈ JSCK. As r is a run on w, it holds that

∈ S

and (r

,(a

i+1

),r

i+1

) ∈ δ for all 0 ≤ i < n.

By deﬁnition of δ, this implies (r

i+1

) ∈

T for all 0 ≤ i < n. Now let t

i+1

= (r

i+1

)

for all 0 ≤ i < n. This above implies that r

∈ src(t

i+1

)

for all 0 ≤ i < n. Further, the above implies r

∈ trg(t

)

for all 0 < i ≤ n. By deﬁnition of execution, we can

conclude that e = r

,...,r

is an execution of

SC. As e is an execution of SC, it holds that beh(e) =

(st(t

),r(t

)),..., (st(t

),r(t

)) ∈ JSCK is a behavior of

SC. Observing st(t

) = a

and r(t

) = b

for all 0 < i ≤

n, we obtain (a

),(a

),..., (a

) ∈ JSCK.

Figure 1 shows the reachable part of the NFA

associated with the webshop-order statechart intro-

duced Figure 1. The attribute paid used in guards

is expanded into the state space. For each of the

transitions with the stimulus place() and the reac-

tion paid=requestPay(price) in the statechart, there ex-

ist multiple transitions with the respective label from

each respective state in the NFA. For each of these

states, there exists one transition with the respective

label to the NFA state where the value of paid is as-

signed to false and one transition with the respective

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

276

label to the NFA state where the value of paid is as-

signed to true. This is the case, because the value as-

signed to the paid attribute in the transitions’ reactions

cannot be predetermined.

With Theorem 1, semantic differencing of state-

charts can be reduced to language inclusion checking

between NFAs. Thus, reuse of well known algorithms

from automata theory is possible (e.g., (Hopcroft

et al., 2006)). Given two statecharts SC

and SC

it holds that δ(SC

,SC

) =

0 iff L (NFA(SC

)) ⊆

L (NFA(SC

)). For checking whether there exist el-

ements in the semantic difference of a statechart to

another statechart, we can thus construct the NFAs as-

sociated to the statechart before performing language

inclusion checking on the NFAs. In case language in-

clusion checking yields a counterexample in form of

a word accepted by the one automaton that is not ac-

cepted by the other automaton, the word can be used

as a witness for a behavior of the one statechart that is

no behavior of the other statechart. The witness can

be presented to a user to facilitate ﬁnding the syntactic

statechart elements causing the presence of witnesses.

7 ABSTRACTION

Two statecharts may be equivalent on one level of ab-

straction but inequivalent on another abstraction level.

A statechart developer may be aware that two state-

charts differ on one level of abstraction. At the same

time, the developer could be interested in comparing

the statecharts on another abstraction level where they

might be equivalent. This is especially useful if the

developer wants to focus on comparing some aspects

of the statecharts but wants to abstract from others.

For example, a developer might be interested

in applying semantic differencing to two statecharts

while abstracting from calls of private methods in re-

actions. This corresponds to event hiding as intro-

duced in Section 7.1.

Similarly, at an early development stage, the argu-

ments passed to a method, which is called in a re-

action of a transition, might be unknown. In later

development stages, the arguments might be known.

As a consequence, the developer changes all events

that correspond to the method calls with unknown pa-

rameters to events where the arguments are all expli-

cated. This implies that the statechart where the ar-

guments are explicated is not equivalent to the state-

chart where the arguments are not explicated. The de-

veloper might want to abstract from the arguments to

check whether the two statecharts are equivalent pro-

vided that the method is called with the same argu-

ments. This corresponds to event matching as intro-

duced in Section 7.2. Combinations of event hiding

and matching methods are also possible.

7.1 Event Hiding

Two statecharts describing the behavior of the same

class may behave equally when observed from the

outside but may still have incomparable semantics.

For example, the statecharts may call different private

methods of their class but the same methods of other

classes. Sometimes, it is required to abstract from in-

ternal method calls to check whether statecharts have

the same externally visible behaviors. This can be

achieved by hiding:

Deﬁnition 7 (Hiding). Let SC = (I,O,S,T,S

) be

a statechart and let H ⊆ O be a set of output

events. Hiding the events of H in SC yields the

statechart SC ⇓ H = (I, O \ H, S,T

) where T

{(src,trg,st, re ↓ H) | (src,trg,st,re) ∈ T }.

Thus, hiding events from a statechart effectively

removes them from the reactions of the statechart’s

transitions. An important property of the hiding op-

erator is that it strictly induces an abstraction with re-

spect to reﬁnement: If one statechart is a reﬁnement

of another statechart before hiding events, then the

statechart is still a reﬁnement of the other statechart

after hiding the same events in both statecharts.

Theorem 2. Let SC = (I, O, S, T, S

) and SC

) be two statecharts and let H ⊆ O

be a set of output events. If JSCK ⊆ JSC

K, then

JSC ⇓ HK ⊆ JSC

⇓ HK.

Proof. Let SC, SC

, and H be given as above. Assume

JSCK ⊆ JSC

K holds.

Let b ∈ JSC ⇓ HK be a behavior of the state-

chart SC ⇓ H. Then, there exists an execution e =

,...,s

∈ Ex(SC ⇓ H) such that beh(e) = b.

By deﬁnition of ⇓, we have that for all 0 < i ≤ n

there exists a transition t

= (src

,trg

,st

,re

) ∈ T

such that t

= (src

,trg

,st

,re

↓H). Since e is an

execution of SC ⇓ H and by deﬁnition of ⇓, it fol-

lows that e

= s

,...,s

∈ Ex(SC) is an exe-

cution of SC. Thus, beh(e

) ∈ JSCK is a behavior

of SC. By assumption JSCK ⊆ JSC

K, it holds that

beh(e

) ∈ JSC

K. Therefore, there exists an execu-

tion α = s

,...,s

∈ Ex(SC

) such that beh(α) =

beh(e

). By deﬁnition of ⇓, we obtain that α

,...,s

∈ Ex(SC

⇓ H) where r(u

) = r(u

)↓H and

st(u

) = st(u

) for all 0 < i ≤ n. Thus, beh(α

) ∈

JSC

⇓ HK. Observing that r(u

) = r(u

)↓H = re

↓H

and st(u

) = st(u

) = st

for all 0 < i ≤ n, we ob-

tain that b = (st

,re

↓H), ...,(st

,re

↓H) = beh(α

) ∈

JSC

⇓ HK.

Semantic Differencing of Statecharts for Object-oriented Systems

277

7.2 Event Matching

The events used in the transitions of one statechart

may contain more details than the events used in the

transitions of another statechart. For example, a state-

chart developed in an early development stage may

not contain the exact arguments that are passed to

each method. In this case, reactions in the statechart’s

transitions may include events that represent the name

of the method without providing details about its ar-

guments. These arguments may be speciﬁed in a later

development stage. As a consequence, the events in

the reactions are changed by explicating the details

about which arguments are passed to the method. A

developer might be interested in whether the changes

imply reﬁnement when abstracting from the argu-

ments passed to the method. Then, we must abstract

from the method arguments by matching the events

including arguments to the events without arguments:

Deﬁnition 8 (Matching). Let SC = (I, O, S,T,S

) be

a statechart and let m : E → E be a function that

maps events to other events. Matching the events in

SC according to m yields the statechart SC ⊕ m =

,S,T

) where

• I

= {m(i) | i ∈ I},

• O

= {m(o) | o ∈ O}, and

• T

= {(s,t, m(st),m(re)) | (s,t,st, re) ∈ T }.

Thus, matching replaces all occurrences of an

event in a statechart by the event that it is mapped

to by the matching function. Event matching induces

an abstraction in context of statechart reﬁnement: If

a statechart reﬁnes another statechart before applying

a matching, then the statechart obtained from apply-

ing the matching to the former statechart reﬁnes the

statechart obtained from applying the same matching

to the latter statechart:

Theorem 3. Let SC = (I, O, S, T, S

) and SC

) be two statecharts and let m : E → E

be a function that maps events to other events. If

JSCK ⊆ JSC

K, then JSC ⊕ mK ⊆ JSC

⊕ mK.

Proof. Let SC, SC

and m be given as above. As-

sume JSCK ⊆ JSC

K holds. Let b ∈ JSC ⊕mK be

a behavior of the statechart SC ⊕ m. Then, there

exists an execution e = s

,...,s

∈ Ex(SC ⊕

m) such that beh(e) = b. By deﬁnition of ⊕,

we have that for all 0 < i ≤ n there exists a

transition t

= (src

,trg

,st

,re

) ∈ T such that t

(src

,trg

,m(st

),m(re

)). Since e is an execu-

tion of SC ⊕ m and by deﬁnition of ⊕, it fol-

lows that e

= s

...,s

∈ Ex(SC) is an ex-

ecution of SC. Thus, beh(e

) ∈ JSCK is a be-

havior of SC. By assumption JSCK ⊆ JSC

K, it

holds that beh(e

) ∈ JSC

K. Therefore, there exist

an execution α = s

,...,s

∈ Ex(SC

) such that

beh(α) = beh(e

). By deﬁnition of ⊕, we obtain

that α

= s

,...s

∈ Ex(SC

⊕ m) where r(u

) =

m(r(u

)) and st(u

) = m(st(u

)) for all 0 < i ≤ n.

Thus, beh(α

) ∈ JSC

⊕ mK. Observing that r(u

) =

m(r(u

)) = m(r(t

)) = m(re

) = r(t

) and st(u

) =

m(st(u

)) = m(st(t

)) = m(st

) = st(t

) for all 0 < i ≤

n, we obtain that b = (st(t

),r(t

)),..., (st(t

),r(t

)) =

beh(α

) ∈ JSC

⊕ mK.

8 RELATED WORK AND

DISCUSSION

Related work divides into different statechart seman-

tics and behavior speciﬁcations as well as model

checking of statecharts.

Statecharts have originally been introduced

in (Harel, 1987). Since then, many statechart se-

mantics have been proposed. A survey (Eshuis,

2009) compares three established and commonly

used semantics: STATEMATE (Harel et al., 1988;

Harel and Naamad, 1996; Harel and Politi, 1998),

a ﬁxpoint semantics based on (Pnueli and Shalev,

1991), and an UML semantics, which resembles the

behavior description for Rhapsody statecharts (Harel

and Gery, 1997; Harel and Kugler, 2004).

In general, the three semantics induce different

statechart behavior interpretations (Eshuis, 2009). All

the three semantics rely on the notion of step. A state-

chart performs a step in reaction to an occurring input

event. In all the three semantics, when an event oc-

curs, a statechart takes a transition, produces several

events and may again react to the produced events (ei-

ther immediately or delayed). This induces several

semantical problems (Rumpe, 2016). In contrast, a

UML/P statechart always executes exactly one tran-

sition in response to an occurring event. One tran-

sition cannot trigger another transition by deﬁnition.

This further eases comprehension and code genera-

tion (Rumpe, 2016). Another difference of the three

step semantics to the UML/P semantics is that the for-

mer permit feedback loops between communicating

statecharts, i.e., allow to model recursion. With this,

the three step semantics are more tailored towards

modeling implementation details, whereas UML/P

statecharts abstract from data states and are tailored

towards modeling high-level concepts.

In contrast to the statecharts supported by the

UML semantics (Eshuis, 2009), the UML/P seman-

tics also support underspeciﬁcation: With UML/P

statecharts, it is possible to model multiple default

(initial) states and to model multiple transitions with

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

278

the same stimulus originating from the same state. In

contrast, statecharts supported by the UML seman-

tics are by deﬁnition not underspeciﬁed. The default

states of composite states are always unique. Fur-

ther, ambiguities in the transition relation are elim-

inated by using priorities (Eshuis, 2009). Model-

ing underspeciﬁed statecharts is especially useful in

early development stages where most of the system

requirements are unknown. When additional require-

ments become known in later development stages, un-

derspeciﬁcation can be removed by changing the re-

spective statechart syntactically to restrict the possible

system behaviors accordingly. Then, semantic differ-

encing facilitates developers in detecting whether the

new statechart version is indeed a reﬁnement of its

predecessor version.

A method to verify statecharts against computa-

tion tree logic formulas is introduced in (Zhao and

Krogh, 2006). The method is generic and thus appli-

cable to a general statechart class. The approach is

based on step-semantics and assumes that statecharts

exhibit bounded behaviors. Extending the approach

could yield semantic differencing methods for state-

charts with bounded behaviors under step semantics.

In (Maggiolo-Schettini et al., 1996), statecharts

are translated to labeled transition systems, which

represent their semantics. Based on the translation,

several equivalence relations for statecharts are de-

ﬁned. The semantics used in the approach is a vari-

ant of the semantics described in (Pnueli and Shalev,

1991). Transfering the equivalence relations to our

approach is interesting for the development of further

abstraction methods.

Another approach (Meng et al., 2004) that con-

siders reﬁnement of statecharts uses a coalgebraic se-

mantics inspired by the operational semantics intro-

duced in (Latella et al., 1999). The approach uses

another semantics than the one in this paper and does

not describe an automated method for checking re-

ﬁnement. However, the paper introduces eight reﬁne-

ment rules that are correct by construction. Devel-

oping such rules for statecharts using this paper’s se-

mantics is interesting future work.

9 CONCLUSION

This paper formally deﬁned a reduced abstract syntax

for UML/P statecharts modeling the behavior of ob-

jects in object-oriented systems. We further deﬁned

a semantics for statecharts based on the behaviors in-

duced by taking transitions during statechart execu-

tions. Subsequently, this paper presented a semantics-

preserving translation from statecharts to NFAs. The

translation enables to reduce semantic differencing of

statecharts to language inclusion checking between

NFAs, which is fully automatable. Afterwards, this

paper deﬁned event hiding and event matching as two

abstraction methods that enable to apply semantic dif-

ferencing to statecharts on different levels of abstrac-

tion. The result is a fully automated semantic differ-

encing method for a statechart variant that supports

underspeciﬁcation. For future work, we plan to in-

vestigate the method’s performance. The method ul-

timately facilitates semantic evolution analysis for de-

velopers of statecharts specifying the behavior of ob-

jects in object-oriented systems.

REFERENCES

Cengarle, M. V., Gr

onniger, H., and Rumpe, B. (2009).

Variability within Modeling Language Deﬁnitions. In

Conference on Model Driven Engineering Languages

and Systems (MODELS’09).

Eshuis, R. (2009). Reconciling statechart semantics. Sci-

ence of Computer Programming, 74(3).

onniger, H. and Rumpe, B. (2011). Modeling Language

Variability. In Workshop on Modeling, Development

and Veriﬁcation of Adaptive Systems.

Harel, D. (1987). Statecharts: A Visual Formalism for

Complex Systems. Science of Computer Program-

ming, 8.

Harel, D. and Gery, E. (1997). Executable Object Model-

ing with Statecharts. In International Conference on

Software Engineering.

Harel, D. and Kugler, H. (2004). The Rhapsody Seman-

tics of Statecharts (or, On the Executable Core of the

UML). In Integration of Software Speciﬁcation Tech-

niques for Applications in Engineering.

Harel, D., Lachover, H., Naamad, A., Pnueli, A., Politi, M.,

Sherman, R., and Shtul-Trauring, a. (1988). State-

mate: A Working Environment for the Development

of Complex Reactive Systems. In Proceedings of the

10th International Conference on Software Engineer-

ing.

Harel, D. and Naamad, A. (1996). The STATEMATE Se-

mantics of Statecharts. ACM Transactions on Soft-

wware Engineering Methodology, 5(4).

Harel, D. and Politi, M. (1998). Modeling Reactive Systems

with Statecharts: The Statemate Approach. McGraw-

Hill, Inc.

Hopcroft, J. E., Motwani, R., and Ullman, J. D. (2006). In-

troduction to Automata Theory, Languages, and Com-

putation (3rd Edition). Addison-Wesley Longman

Publishing Co., Inc., Boston, MA, USA.

Latella, D., Majzik, I., and Massink, M. (1999). Towards

a Formal Operational Semantics of UML Statechart

Diagrams. In Formal Methods for Open Object-Based

Distributed Systems.

Semantic Differencing of Statecharts for Object-oriented Systems

279

Maggiolo-Schettini, A., Peron, A., and Tini, S. (1996).

Equivalences of Statecharts. In International Confer-

ence on Concurrency Theory.

Meng, S., Naixiao, Z., and Barbosa, L. S. (2004). On Se-

mantics and Reﬁnement of UML Statecharts: A Coal-

gebraic View. In International Conference on Soft-

ware Engineering and Formal Methods.

Pnueli, A. and Shalev, M. (1991). What is in a Step: On

the Semantics of statecharts. In Theoretical Aspects

of Computer Software.

Rumpe, B. (2016). Modeling with UML: Language, Con-

cepts, Methods. Springer International.

Zhao, Q. and Krogh, B. H. (2006). Formal Veriﬁcation of

Statecharts Using Finite-State Model Checkers. IEEE

Transactions on Control System Technology, 14(5).

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

280