
Polyp Classification and Clustering from Endoscopic Images using
Competitive and Convolutional Neural Networks
Avish Kabra
1
, Yuji Iwahori
2
, Hiroyasu Usami
2
, M. K. Bhuyan
1
, Naotaka Ogasawara
3
and Kunio Kasugai
3
1
Indian Institute of Technology Guwahati, Assam, 781039, India
2
Chubu University, 487-8501, Japan
3
Aichi Medical University, 1-1 Yazakokarimata, Nagakute, Aichi, 480-1195, Japan
Keywords:
Competitive Learning, Deep Learning, Convolutional Neural Networks.
Abstract:
Understanding the type of Polyp present in the body plays an important role in medical diagnosis. This paper
proposes an approach to classify and cluster the polyp present in an Endoscopic scene into malignant or
benign class. CNN and Self Organizing Maps are used to classify and cluster from white light and Narrow
Band (NBI) Endoscopic Images . Using Competitive Neural Network different polyps available from previous
data are plotted with the new polyp according to their structural similarity. Such kind of presentation not only
help the doctor in it’s easy understanding but also helps him to know what kind of medical procedures were
followed in similar cases.
1 INTRODUCTION
According to the WHO, Cancer is the second lead-
ing cause of death globally, and is responsible for
an estimated 9.6 million deaths in 2018. Globally,
about 1 in 6 deaths is due to cancer . This report
verifies that Late-stage presentation and inaccessi-
ble diagnosis and treatment are common reasons for
these deaths. In 2017, only 26 percent of low-income
countries reported having pathology services gener-
ally available in the public sector. More than 90 per-
cent of high-income countries reported treatment ser-
vices are available compared to less than 30 percent
of low-income countries.
This provides a vast area of research so that diag-
nosis can be made easy and accessible. Many meth-
ods have been developed to know the existence of a
polyp in an Endoscopic scene but the automatic clas-
sification of these into different classes is still com-
plex (Y.Iwahori and K.Kasugai, 2013). This paper
proposes a method to know whether the polyp de-
tected in a patient’s body is benign or malignant be-
cause the first step after being diagnosed with a tumor
is to find it’s class. In short, the meaning of malig-
nant is cancerous and the meaning of benign is non-
cancerous that is why it is very important to have a
proper verification and to decide the further treatment
Figure 1: (i)White light Benign (ii)StainNBI Benign.
Figure 2: Malignant (i)StainNBI (ii)White Light.
path. A timely understanding of the tumor can prevent
deaths.
446
Kabra, A., Iwahori, Y., Usami, H., Bhuyan, M., Ogasawara, N. and Kasugai, K.
Polyp Classification and Clustering from Endoscopic Images using Competitive and Convolutional Neural Networks.
DOI: 10.5220/0007353204460452
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 446-452
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 LITERATURE SURVEY
Present methods of image clustering mostly involve
use of K-means algorithm and X-means algorithm
(Coleman and Andrews, 1979). Using Self Organiz-
ing Maps with zero radius can provide similar results
but with increased radius we can perform space ap-
proximation which will provide us with the minimum
number of points that cover as much data as possible.
The main issue with previous methods is that clus-
ters do not know about the existence of other clus-
ters therefore they tend to behave independently. Us-
ing SOM, we can enable more cooperative behaviour
among these clusters. Due to this cooperation the
cluster centres are more efficiently distributed. Even
if some data points are removed, our model will give
a good understanding about the shape of our original
data. As the feature map spreads out over space, this
method can generate smaller dataset which will keep
the useful properties of the original dataset.(Zhao and
Ma, 2014)
We used both CNN and Competitive Neural Net-
works to develop a self organizing map of the polyp
data-set. This map consists of polyps from many pre-
vious cases along with the tumor of present patient.
These polyps are positioned on the 2-D map accord-
ing to their level of similarity. Such representation
enables us to carefully examine the polyp and com-
pare it with the other data. The lesser it’s distance is
from the other polyp, more are it’s chances of simi-
larity. This representation not only enables us to find
it’s class efficiently but can also be further modified
to predict possible treatment procedures based on the
previous cases in which the decisions were taken by
actual doctors.
3 DATA-SET
The Data-set used for the experimentation purposes is
’Polyp-CVC-CliniDB (Bernal, 2015).
Figure 3: Content of CVC-ClinicDB database.
CVC-ClinicDB is a database of frames extracted
from colonoscopy videos. These frames contain sev-
eral examples of polyps. In addition to the frames,
it consists of the ground truth for the polyps.This
ground truth consists of a mask corresponding to
the region covered by the polyp in the image.CVC-
ClinicDB database consists of two different types of
images: Original images and Polyp mask. CVC-
ClinicDB is the official database used in the training
stages of MICCAI 2015 Sub-Challenge on Automatic
Polyp Detection Challenge in Colonoscopy Videos.
Figure 4: Correspondence between number of frames and
video sequences in CVC-ClinicDB.
4 PROPOSED METHODS
This paper proposes two methods to classify and clus-
ter the Endoscopic polyp images. One method is us-
ing self organizing map. This method uses princi-
ples of competitive learning. Competitive learning
is a form of learning in artificial neural network in
which nodes compete for the right to respond to a sub-
set of the input data. Competitive learning works by
increasing the specialization of each node in the net-
work. In contrast to other standard Neural networks, it
only has input and output layers. There are no hidden
layers in between, instead there is a SOM layer. Train-
ing is done by competitive learning where the weights
associated with output layer nodes compete for acti-
vation. Therefore we can understand a high dimen-
sional data in less dimensions and these observations
can be classified into clusters. The second method in-
volves use of CNN. A new CNN model was generated
to classify Stain Narrow Band Endoscopic images
into Benign and Malignant classes.Images are pre-
processed using combination of Bilateral and Guided
filter which are then used as inputs to the network.
4.1 Convolutional Neural Network
A Convolutional Neural Network (CNN) is com-
prised of one or more convolutional layers (often with
a subsampling step) and then followed by one or more
fully connected layers as in a standard multilayer neu-
ral network. The architecture of a CNN is designed
to take advantage of the 2D structure of an input im-
age. This is achieved with local connections and tied
Polyp Classification and Clustering from Endoscopic Images using Competitive and Convolutional Neural Networks
447
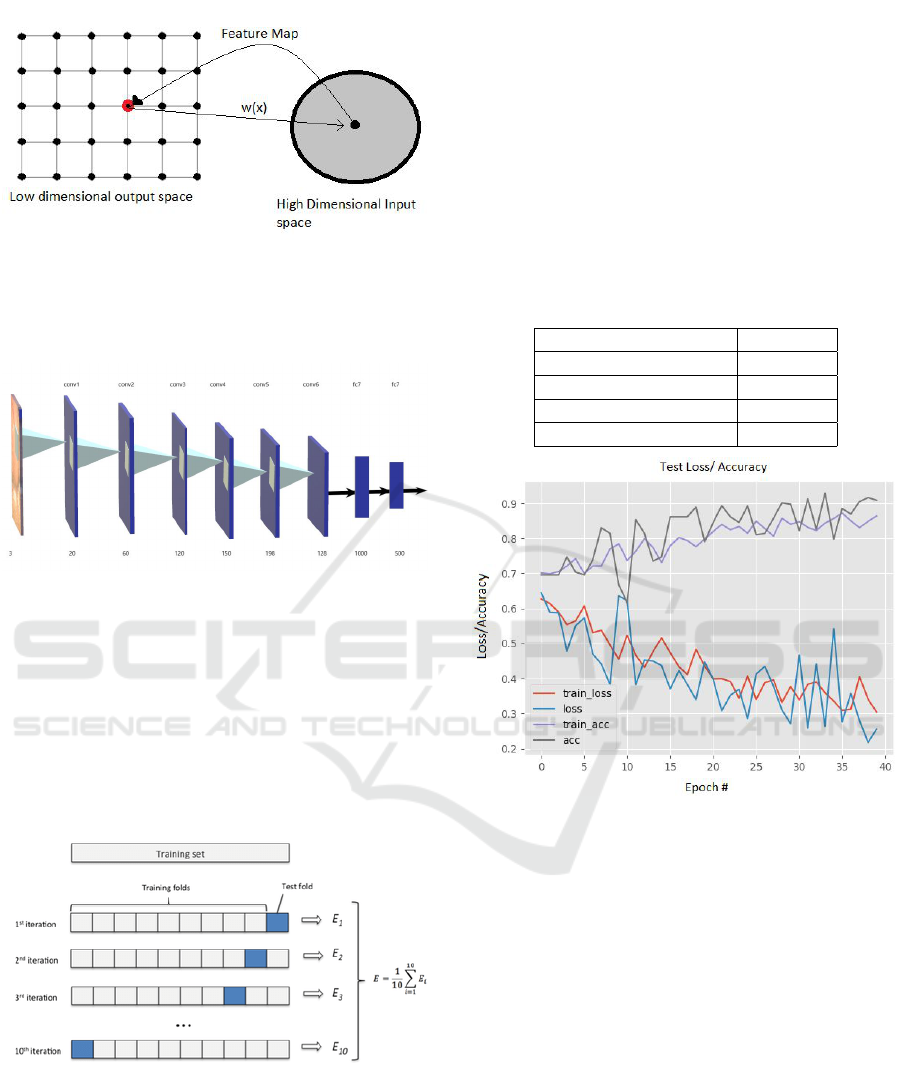
Figure 5: Working of SOM.
weights followed by some form of pooling which re-
sults in translation invariant features.(A. Krizhevsky
and Hinton, 2012)
Figure 6: Designed Neural Network structure.
A self designed and trained layer structure as
shown in figure 4 was used to classify Benign and
Malignant polyps. Input images were processed us-
ing smoothing filters and edges were detected. This
network was trained using 500 images of both kinds.
K-fold cross validation (Burman, 1989) was used on
this set. k-fold cross validation is a procedure used to
estimate the skill of the model on new data. In this
case we used 10-fold cross validation.
Figure 7: 10-fold cross validation.
In k-fold cross-validation, the original sample is
randomly partitioned into k equal sized subsamples.
Of the k subsamples, a single subsample is retained
as the validation data for testing the model, and the
remaining subsamples are used as training data. The
cross-validation process is then repeated k times, with
each of the k subsamples used exactly once as the val-
idation data. The k results can then be averaged to
produce a single estimation. The advantage of this
method over repeated random sub-sampling is that all
observations are used for both training and validation,
and each observation is used for validation exactly
once.
Results when compared with other pre-existing
networks were found to be less accurate than this net-
work. Accuracy of around 91 percent was achieved
while no other model could give accuracy of more
than 90 percent.
Table 1: Accuracy using different network architectures.
Network Architecture Accuracy
Lenet 82.7%
VGG 16 79.3%
VGG 19 87.8 %
Proposed Architecture 90.8%
Figure 8: Results using CNN.
4.2 Self Organizing Map
The SOM algorithm (Kohonen, 2013) is based on
competitive learning. It provides a topology preserv-
ing mapping from the high dimensional space to neu-
rons. Our brain is subdivided into specialized areas,
they specifically respond to certain stimuli i.e. stim-
uli of the same kind activate a particular region of the
brain. The idea is transposed to a competitive learning
system where the input space is ”mapped” in a small
(often rectangular) space with the following princi-
ple: similar individuals in the initial space will be pro-
jected into the same neuron or, at least, in neighboring
neurons in the output space (preservation of proxim-
ity). Neurons usually form a two-dimensional lattice
and forms a mapping from high dimensional space
onto a 2-dimensional plane in our case.Topology pre-
serving property means that the mapping preserves
the relative distance between the points. Points that
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
448

are near each other in the input space are mapped
to nearby map units in the SOM. The SOM can thus
serve as a cluster analyzing tool of high-dimensional
data. Also, the SOM has the capability to generalize.
Generalization capability means that the network can
recognize or characterize inputs it has never encoun-
tered before.
4.2.1 Learning Algorithm
Figure 9: Forming of Map.
These following steps are implemented so that the
weight vectors can represent the input data.
Step I: Randomly initialize the weights.
Step II: From the Input data, randomly choose a
point (marked in circle).
Step III: Find the weight vector which is closest
to the point chosen in previous step. This is consid-
ered as the winning neuron.
Step IV: The winning neuron and it’s closest
neighbouring neuron move closer to this chosen
point. Neurons which are closer to this point are
supposed to take larger steps than their neighbouring
neurons.
Step V: These steps are repeated many times
and it results in the weight vectors to settle into stable
zones that represent the patterns in the input data.
The step size for updating the weights and the
amount of weights to be updated decreases across
iterations
For finding the Best matching unit, we iterate
through all the nodes and compare the Euclidean dis-
tance between every node’s weight vector and present
input vector. Node with weight vector closest to in-
put vector is termed as the best matching unit for that
particular input. This Euclidean distance can be cal-
culated using:
dist =
s
n
∑
i=0
(V
i
−W
i
)
2
where V is current input vector and W is node’s
weight vector.
Once this best matching unit is decided, we find all the
other node’s which are in it’s neighbourhood because
in next step all their weights will be altered. Number
of node’s coming in a BMU’s neighbourhood depends
on the radius of neighbourhood chosen. This area of
neighbourhood will keep on shrinking with every iter-
ation. This property is visualized by the exponential
decay function.
σ(t) = σ
o
e
−t/λ
where σ
o
denotes the width of the lattice at time t=0,
λ denotes the time constant and t represents current
iteration of the loop.
Figure 10: Shrinking of radius.
This radius will keep shrinking until only one neu-
ron that is the BMU is present inside the neighbour-
hood. Weight vector of every node present inside the
current neighbourhood is updated using
W (t + 1) = W (t) + θ(t)L(t)(V (t)−W(t))
where t is the time step, L is the learning rate which
decays with time using
L(t) = L
o
e
−t/λ
Now practical use suggests that not only the Learn-
ing rate should decay with iteration but also it’s effect
should decrease as the distance from the best match-
ing unit increase. There should barely be any effect
at edges of the neighbourhood. To fade the amount
of learning with increasing distance Gaussian decay
function is used. θ defines the amount of influence on
learning rate of a node with distance ’dist’ from BMU
will have.
θ(t) = e
−dist
2
/2σ(t)
2
)
Polyp Classification and Clustering from Endoscopic Images using Competitive and Convolutional Neural Networks
449
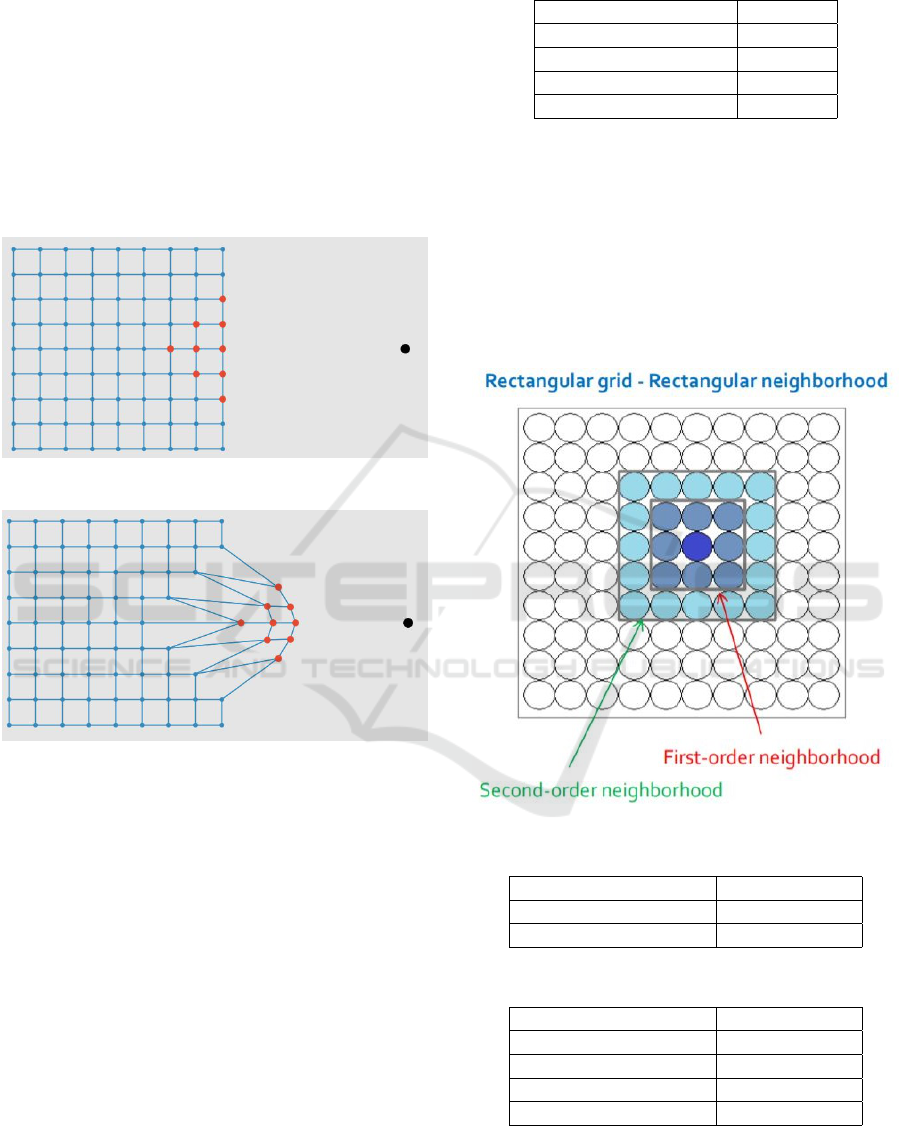
Neuron grid that is used is 2 dimensional rectangular
grid. Therefore each neuron is connected directly to 4
other neurons which are it’s close neighbours. Every
neuron possess two properties that is connection to
other neurons and position. Connections are defined
before the start of training and that remain same in all
the iterations whereas the positions keep on changing.
Positions of these neurons were initialized randomly.
At the end of every iteration the position of the win-
ning neuron and all the neurons in it’s neighbourhood
are updated.
Figure 11: Feature map before training.
Figure 12: Feature map after training.
5 RESULTS
5.1 Using CNN
Around 500 images of Benign and Malignant Polyps
were used as input to Neural networks after neces-
sary pre-processing. Different kinds of architectures
of neural networks were used to compare the results.
K-fold Cross Validation was used on this set. k-
fold cross validation is a procedure used to estimate
the skill of the model on new data. In this case we
used 10-fold cross validation. Accuracy achieved us-
ing these networks is shown in Table 1. Maximum
accuracy was achieved using the proposed Network
structure while minimum accuracy was achieved us-
ing VGG16.
Table 2: Accuracy using different network architectures.
Network Architecture Accuracy
Lenet 82.7%
VGG 16 79.3%
VGG 19 87.8 %
Proposed Architecture 90.8%
5.2 Clustering
5.2.1 Implementation
The grid structure proposed in our method is Rectan-
gular grid - Rectangular neighbourhood. The notion
of neighborhood is essential in SOM, especially for
the updating of weights and their propagation during
the learning process.
Figure 13: Rectangular grid.
Table 3: Image data statistics for 2 class clustering.
Image Type No. of samples
White Light Benign 104
White Light Malignant 92
Table 4: Image data statistics for 4 class clustering.
Image Type No. of samples
White Light Benign 60
White Light Malignant 60
Stain NBI Benign 60
Stain NBI Malignant 60
The further the neighbouring neuron is from win-
ning neuron, smaller it’s learning rate will be and
smaller the std parameter, smaller will be learning rate
for neighbouring neurons.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
450

Parameters used for the Competitive Neural network:
i) Initial Learning Radius: 6
ii) Reduce radius after: 5 Epochs
iii) std = 1
iv) reduce std after: 5 Epochs
v) step= 0.1
vi) Reduce step after: 5 Epochs
5.2.2 Formation of Clusters
Figure 14: Clustering of White Light Benign and Malignant
polyp.
Figure 15: Clustering of White Light Benign, Malig-
nant,Stain NBI Benign , Malignant Polyp.
Where square represents StainNBI Benign, pentagon
is StainNBI Malignant, cross represent White Light
Benign and Circle shows White Light Malignant.
Each Cell in this heatmap has a number associ-
ated with it which represents it’s average distance to
neighbour clusters. This number can be interpreted
from the color bar. White color means that this clus-
ter is far from it’s neighbours.
Figure 16: 4-class original cluster.
Figure 10 and 11 shows the formation of clusters
according to the similarity in the structure of in-
put polyps. Different symbols are used to represent
polyps belonging to different classes. Polyp struc-
tures which are predicted to be of similar shapes tend
to remain closer than those with different shapes. Fig-
ure 12 contains original images from the reduced data
set. This figure can be used to carefully understand
the relation between a new polyp data with those
which occurred in past.
6 CONCLUSION
Thus the CNN Architecture proposed in this paper
can be used for efficient classification of Benign and
Malignant Polyps from the Endoscopic scene. Such
kind of automatic classification can lead to easy di-
agnosis of tumor at early stage and further course of
treatment can be decided effectively. Figure 12 shown
above can be further used for real time treatment pre-
diction if proper data is provided.
Further development in this approach can be made
so that a doctor can see similar past cases and makes
a judgment depending on the outcomes of previous
decision thus decreasing the chances of fatality. The
kind of treatment given in previous cases can also be
provided as input to facilitate automatic prediction of
course of treatment using the information on how the
actual doctor proceeded in the previous cases of sim-
ilar polyp structure
Polyp Classification and Clustering from Endoscopic Images using Competitive and Convolutional Neural Networks
451

ACKNOWLEDGMENT
Iwahori’s research is supported by JSPS Grant-in-Aid
for Scientific Research (C) (17K00252) and Chubu
University Grant.
REFERENCES
A. Krizhevsky, I. S. and Hinton, G. E. (2012). Ima-
genet classification with deep convolutional neural
networks,. Advances in neural information pro- cess-
ing systems.
A. Sharif Razavian, H. Azizpour, J. S. and Carlsson, S.
(2014). Cnn features off-the-shelf: an astounding
baseline for recognition. Proceedings of the IEEE
Conference on Computer Vision and Pattern Recog-
nition Workshops.
Ahmed, N. (2015). Recent review on image clustering. IET
Image Processing.
Bernal, J., S. F. J. F.-E. G. G. D. R. C. . V. F. (2015).
Wm-dova maps for accurate polyp highlighting in
colonoscopy: Validation vs. saliency maps from
physicians. computerized medical imaging and graph-
ics.
Burman, P. (1989). A comparative study of ordinary cross-
validation, v-fold cross-validation and the repeated
learning-testing methods.
Coleman, G. B. and Andrews, H. C. (1979). Image segmen-
tation by clustering. Proceedings of the IEEE.
J. Bernal, F. J. Sanchez, F. E. G. and Rodriguez, C. Cvc
clinicdb.
Kohonen, T. (2013). Essentials of the self-organizing map.
Neural networks : the official journal of the Interna-
tional Neural Network Society.
Nath, S. S., Mishra, G., Kar, J., Chakraborty, S., and Dey,
N. (2014). A survey of image classification methods
and techniques. In 2014 International Conference on
Control, Instrumentation, Communication and Com-
putational Technologies (ICCICCT).
Simonyan, K. and Zisserman, A. (2014). Very deep con-
volutional networks for large-scale image recognition.
arXiv preprint arXiv:1409. 1556.
Tajbakhsh, N. (2016). Convolutional neural networks for
medical image analysis: Full training or fine tuning?
In IEEE Transactions on Medical Imaging.
Y.Iwahori, T.Shinohara, A. R. S. M. and K.Kasugai (2013).
Automatic polyp detection in endoscope images using
a hessian filter. In MVA.
Zhao, Z. and Ma, Q. (2014). A novel method for image
clustering. In 2014 10th International Conference on
Natural Computation (ICNC).
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
452
