Definition and Efficient Construction of Encrypted k–anonymization
Scheme
Masayuki Yoshino
1
, Takayuki Suzuki
1
, Ken Naganuma
1,2
and Hisayoshi Sato
1
1
Hitachi, Ltd. Research & Development Group, Center for Technology Innovation-Systems Engineering, Kanagawa, Japan
2
The University of Tokyo, Chiba, Japan
Keywords:
Encrypted Database, k–anonymization, Searchable Symmetric Encryption, Domain Generalization Hierarchy.
Abstract:
In this paper, we propose an encrypted k–anonymization scheme (EAS) to k–anonymize an encrypted database
using a domain generalized hierarchy while maintaining the encryption state. Preparation of the domain gen-
eralized hierarchy is optional; the proposed EAS can generate domain generalized hierarchies using a Huff-
man code tree from a database encrypted with searchable encryption. As a result, the user can delegate
k–anonymization processing to a third party organization such as the cloud while retaining the confidential-
ity of the database without preparing a generalized hierarchy. In addition, third-party organizations that are
entrusted also have the advantage to eliminate possible of misconduct such as information leakage. In a stan-
dard computer experiment, we performed a generalization process, which is the major procedure for our EAS.
The generalization process takes around 168 seconds only to achieve k–anonymity with k = 3 on 1, 000, 000
records consisting of 4 attributes. As a consequence, this high-speed performance means our EAS is applicable
to not only batch processing but also real-time processing.
1 INTRODUCTION
Numerous studies have proposed technology to make
individual identification hard, i.e., anonymize per-
sonal information. In these studies, k–anonymity is
known as a representative index that quantifies the
specific difficulty of identifying an individual (Sama-
rati and Sweeney, 1998; Samarati, 2001; Sweeney,
2002b). k–anonymity means that “the value of the
record must be converted so that there are more than
(k − 1) records that all have the same attribute val-
ues” . Finding an optimal solution that satisfies k–
anonymity is known to be a computationally hard
problem, and some of computationally hard prob-
lems are even proven to be NP Hard (Meyerson and
Williams, 2004). Therefore, a k–anonymization tech-
nique that gives up finding an optimal solution and
obtains an approximate solution to work in polyno-
mial time is widely used in practice (Sweeney, 2002a;
LeFevre et al., 2005; LeFevre et al., 2006; Wang et al.,
2004).
On the other hand, due to the progress of In-
ternet of Things (IoT) technology in recent years,
accumulated data has increased, and single systems
have nearly reached their limit to store and manage
this data. Therefore, in collaboration with external
systems such as clouds that have abundant compu-
tational resources, more data management is being
outsourced. One of the key primitives is search-
able encryption, which realizes an encrypted data
management system such as an encrypted database
and encrypted file storage to protect sensitive infor-
mation including personal data from being seen by
not only system intruders but also cloud administra-
tors. Searchable encryption is a cryptographic tech-
nique that enables matching of two kinds of encrypted
data while maintaining encryption. Although encryp-
tion requires a secret key, the matching process does
not. Several searchable encryption methods have
been proposed (Boneh et al., 2004; Boneh and Wa-
ters, 2007; Curtmola et al., 2006; Song et al., 2000;
Yoshino et al., 2011) that are classified into secret key
cryptosystems and public key cryptosystems. In this
paper, we target large-scale data and adopt the sym-
metric key cryptosystem (Yoshino et al., 2011), which
is superior to high-speed processing.
Methods have been proposed to have external or-
ganizations conduct data anonymization processing
while protecting privacy and utilizing data. For ex-
ample, in the methods of Gentry (Gentry, 2009) and
Ducas and Micciancio (Ducas and Micciancio, 2015),
arbitrary arithmetic processing can be executed while
Yoshino, M., Suzuki, T., Naganuma, K. and Sato, H.
Definition and Efficient Construction of Encrypted k–anonymization Scheme.
DOI: 10.5220/0007354702930300
In Proceedings of the 5th International Conference on Information Systems Security and Privacy (ICISSP 2019), pages 293-300
ISBN: 978-989-758-359-9
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
293

encrypting data so that anonymization processing can
be delegated safely. However, in these methods, the
overhead required for arithmetic processing in the en-
crypted state is still far from the practical level, so
even anonymization of small databases is not realis-
tic
1
.
1.1 Our Contribution
We point out that outsourcing the anonymization pro-
cess may lead to information leakage, thus we pro-
pose an encrypted k–anonymization scheme (EAS).
Our contributions are briefly described as follows.
• We define the EAS played by a user and a server
that can k–anonymize given encrypted data with-
out a secret key, and define a semantic security
model for EAS; an honest-but-curious server will
not learn any useful information about the given
encrypted database.
• We propose a construction of EAS and prove its
security. We design EAS using domain gener-
alization hierarchies, however the user does not
need to prepare them. By combining genera-
tion technique for domain generalization hierar-
chy from database (Harada et al., 2012), and
searchable symmetric encryption technique for an
encrypted database (Kamara and Lauter, 2010;
Yoshino et al., 2011; Popa et al., 2012), our con-
struction is equipped with a method to generate
domain generalization hierarchies from search-
able encrypted database. Furthermore, our con-
struction is proved to be secure under the security
model.
• We implemented the proposed EAS on a general-
purpose PC and carried out experiments, where a
generalization technique achieving k–anonymity
with k = 3 takes 168 seconds on 1, 000, 000
records consisting of 4 attributes. Thanks to the
high-speed processing, the proposed EAS is ap-
plicable to not only batch processing but also real-
time processing.
2 PRELIMINARY
2.1 Table Notation
First, we define a plaintext table P T in a database to
be k–anonymized.
1
To execute the 1-NAND operation on a general-
purpose computer, Gentry’s method takes about 30 minutes
whereas Ducas and Micciancio’s method takes about 1 sec-
ond.
• Let table P T be a combination of (A , C) where
A is an array of n attributes (a
1
, . . . a
n
) and C is an
array of n columns (C
1
, . . . C
n
).
• Each attribute a
i
contains a word w called as
quasi-identifier, which is selected from a dictio-
nary D
a
: w ∈ D
a
.
• Each column C
i
consists of m cells (c
1,i
, . . . c
m,i
).
Each cell c
i, j
contains a word w, which is selected
from a dictionary D
ci
: w ∈ D
ci
.
Let an encrypted table ET be a same structure as P T
except that each attribute a
i
∈ A and each cell c
i, j
∈ C
j
contains an encrypted word ew.
2.2 k-anonymization Techniques
k–anonymization is a de-identification technique to
achieve k–anonymity, which is an index to quan-
tify the difficulty of individual identification proposed
by Samarati and Sweeney in 1998 (Samarati and
Sweeney, 1998). To satisfy k–anonymity, the value
of the record must be converted so that there are
more than (k − 1) records that all have the same at-
tribute values. This conversion process is called re-
coding and can be roughly divided into a local re-
coding method and a global recoding method. Since
the local recoding method calculates the distance be-
tween records for grouping, many calculations are re-
quired. Although precise recoding is performed, due
to the high calculation volume, usage tends to be lim-
ited to use cases with a small number of records.
On the other hand,many global recoding methods use
auxiliary information called a generalized hierarchy
2
,
do not calculate distance, and regularly perform re-
coding. High speed is an advantage and is suitable
for k–anonymization targeting large-scale data. Since
this paper deals with large-scale data, we use a global
recoding method with high speed.
In the global recording method, each attribute to
be anonymized is associated with a domain gener-
alized hierarchy (DGH) from which the values can
be generalized to form a group of at least k tuples
with identical values (Sweeney, 2002a). Examples
of DGH and k–anonymized tables are given in Fig-
ures 1 and 2, respectively. The lowest values of DGH
are called leaf nodes, and the highest node of DGH
is called the root node. Relationships are defined be-
tween nodes from leaf nodes to root nodes. The upper
node holds the generalized value of the lower node.
Figure 1 shows the leaf node at the lowest level, which
is the nationality unit {(Japan, China), (Russia, Eng-
land, Germany) }, the more generalized regional unit
2
There is k–anonymization technology without a gener-
alized hierarchy such as (LeFevre et al., 2006).
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
294

{Asia, Europe }, and the top root, which is located
in the most generalized unit {*}. Figure 2 shows the
two attributes (occupation and nationality) associate
with their DGH. Figure 2 shows P T where the com-
binations of four attributes are 2-anonymity, i.e., there
are at least 2 identical records for every four attribute
combinations. We refer to the k–anonymized P T as
kP T and the k–anonymized ET as kE T .
Japan
China Russia England Germany
Asia Europe
*
Researcher
Student Sales Engineer
Researcher or Student
Sales or Engineer
*
NationalityOccupation
Figure 1: Example of DGH.
Researcher or Student Asia * 19**
Sales or Engineer Europe * 20**
Sales or Engineer Europe * 20**
Researcher or Student Asia * 19**
Sales or Engineer Europe * 20**
Nationality Gender Birth dateOccupation
Figure 2: Example of kP T with k = 2.
2.3 Searchable Symmetric Encryption
In this paper, we use searchable symmetric encryp-
tion SSE as cryptographic primitives. An SSE scheme
has two phases called as a store phase, which is per-
formed once, and a search phase, which is performed
a polynomial number of times. In the store phase, an
user encrypts all data and stores them on a server. In
the search phase, the user sends a trapdoor of a word
w, the server returns the encrypted word ew, which is
matched by a comparison function for a trapdoor of a
word and an encrypted word.
Formally, the searchable symmetric encryption
SSE consists of five polynomial-time algorithms
SSE = (Gen, Enc, Trpdr, Cmpr, Dec) as follows (Curt-
mola et al., 2011):
• (sk, pp) ← Gen(1
λ
): is a probabilistic algorithm
that takes security parameter λ as input and out-
puts a public parameter pp and a secret key sk.
• ew ← Enc(sk, w): is a probabilistic algorithm that
takes a secret key sk and word w as input and out-
puts an encrypted word ew. We sometimes write
ew ← Enc(sk, w) where w is a set of w and ew is
a set of ew.
• td(w
′
) ← Trpdr(sk, w
′
): is a deterministic algo-
rithm that takes a secret key sk and a word w
′
as
input and outputs a trapdoor td(w
′
). We some-
times write td(w
′
) ← Trpdr(sk, w
′
) where w
′
is a
set of w
′
and td(w
′
) is a set of td(w
′
).
• 0 or 1 ← Cmpr(ew, td(w
′
)): is a deterministic al-
gorithm that takes encrypted word ew and a trap-
door td(w
′
) as input and outputs either 1 (if w =
w
′
) or 0 (if w ̸= w
′
) with provability 1 − ε(λ) and
ε is a negligible function.
• w ← Dec(sk, ew): is a deterministic algorithm that
takes a secret key sk and encrypted word ew as
input and outputs a word w.
In SSE, the server should learn almost no informa-
tion on w and w
′
. Let L
1
(w) denote the information
that the server can learn in the store phase, and let
L
2
(w, w
′
) denote that in the search phase.
Most SSE reveals L
1
(w) = (. . . , |w
i
|, . . .) and
a dictionary D such that w
i
∈ D, and L
2
(w, w
′
)
consists of search result {(i, j)|w
i
= w
′
j
, w
i
∈
w, w
′
j
∈ w
′
} and the search pattern such that
searchpattern((w
′
1
, . . . w
′
q
), w
′
) = (b
1
, . . . b
q
) where
b
j
= 1 if (w
′
j
= w
′
) and b
j
= 0 if (w
′
j
̸= w
′
). The
search pattern caused by deterministic Trpdr algo-
rithm.
We introduce definitions of semantic security
against an adversary in (Curtmola et al., 2006). The
security is defined by using two games: Real
SSE,A
is
played by an adversary A and a challenger C, and
Ideal
SSE,A,S
is played by A, C and a simulator S.
Definition 1.
((Curtmola et al., 2006)) Let SSE =
(Gen, Enc, Trpdr, Cmpr, Dec) be a searchable sym-
metric encryption, and consider the following prob-
abilistic experiments where A is an adversary, C is a
challenger, S is a simulator and L
1
and L
2
are leak-
age algorithms:
Real
SSE,A
(λ) : The adversary A chooses a set of
word w and sends it to the challenger C. C be-
gins by running Gen(1
λ
) to generate a secret key
sk and a public parameter pp and send them to
A. A outputs a set of word w and receives ew
from C by ew ← Enc(sk, w). A gives a polyno-
mial number of words w to C, and receives trap-
doors td(w
′
) ← Trpdr(sk, w
′
) from C. Finally, A
returns a bit b, which is output by the experiment.
Ideal
SSE,A,S
(λ) : The adversary A chooses a set of
word w and sends it to the challenger C. C sends
L
1
(w) to the simulator S. S generates ew from
L
1
(w), and send it to C. C relays ew to A. A
gives a polynomial number of words w to C. C
Definition and Efficient Construction of Encrypted k–anonymization Scheme
295

sends L
2
(w, w
′
) to S. S generates a set of trap-
door td(w
′
) from L
2
(w, w
′
) and sends them to C.
C relays them to A. Finally, A returns a bit b,
which is output by the experiment.
We say that SSE is (L
1
, L
2
)-secure against chosen-
keyword attacks if for all PPT adversaries A, there
exists a PPT simulator S such that
Pr[Real
SSE,A
(λ) = 1]−Pr[Ideal
SSE,A,S
(λ) = 1] ≤ negl.
3 DEFINITION
We begin by reviewing the formal definition of an en-
crypted k–anonymization scheme. The participants
include a user that wants to store sensitive informa-
tion P T on an honest-but-curious server in such a
way that (1) the server will not learn any useful in-
formation about P T and (2) the server is given the
ability to k–anonymize E T and return kE T to the
user.
3.1 Encrypted k –anonymization Scheme
In this subsection, we define an encrypted k–
anonymization scheme.
Definition 2. EAS consists of five polynomial time al-
gorithms.
EAS = (Gen, Enc, Trpdr, Annmz, Dec)
such that
• K ← Gen(1
λ
): is a probabilistic algorithm, which
is run by the user. It takes security parameter λ as
input and outputs a secret key K.
• ET ← Enc(K, P T ): is a probabilistic algorithm
run by the user. It takes a secret key K and a table
P T as input and outputs an encrypted table E T .
• td(w
′
) ← Trpdr(K, w
′
): is a deterministic algo-
rithm run by the user. It takes a secret key K and
a set of word w
′
and outputs a set of trapdoor
td(w
′
).
• kE T or ⊥ ← Annmz(ET , td(w
′
), kv): is a de-
terministic algorithm run by the server to k–
anonymize an encrypted table E T with selected
attributes. It takes an encrypted table E T , a set
of trapdoor td(w
′
), an integer kv. If it is not pos-
sible to generate an encrypted k–anonymized ta-
ble kET , then output is ⊥. Otherwise, it outputs
kE T with provability 1 − ε(λ) and ε is a negligi-
ble function.
• kP T ← Dec(K, kE T ): is a deterministic algo-
rithm run by the user. It takes a secret key K and
an encrypted k–anonymized table k E T and out-
puts a k–anonymized table kP T .
We say that an EAS satisfies correctness if for any
K output by Gen(1
λ
), any P T , any set of word w
′
in
P T , and any positive integer kv,
kE T or ⊥
= Annmz(Enc(K, P T ), Trpdr(K, w
′
), kv) (1)
and
kP T = Dec(K, kET ), (2)
where Equation (1) holds with provability 1 − ε(λ)
and ε is a negligible function, and Equation (2) holds
with probability 1.
Similar with SSE, EAS has two phases called as
a store phase and which is performed once, and an
anonymization phase, which is performed a polyno-
mial number of times. In the store phase, an user
generates a plain table, encrypts it and stores it on a
server. In the search phase, the user selects attributes
on the table, and sends a trapdoor and an integer k
for k–anonymization. The server k–anonymized the
encrypted table and send it to the user.
Definition 3. EAS played by a user U and a server S
consists of two phases:
• Store phase
1. U generates a secret key K ← Gen(1
λ
).
2. U encrypts a plain table P T by ET ←
Enc(K, P T ).
3. U gives an encrypted table E T to S .
• Anonymization phase
1. U selects s attributes from A.
2. U generates a trapdoor set td(w
′
) ←
Trpdr(K, w
′
) and send them and an inte-
ger kv to S .
3. S receives td(w
′
) and kv, gener-
ates an encrypted k–anonymized table
kE T ← Annmz(E T , td(w
′
), kv) and give kE T
to S .
4.
U gets a k–anonymized table kP T by P T ←
Dec(K, kET ).
3.2 Security Definition
Let L
A
(w| all w
i
∈ w are stored in attributes or cells
of P T ) denote the information that the server can
learn in the store phase, and we abbreviate this leak-
age information L
A
(w) as for simplicity. Further-
more, let L
B
(w| all w
i
∈ w are stored in attributes or
cells of P T , w
′
, kv) denote that in the anonymization
phase, and we abbreviate this leakage information as
L
B
(w, w
′
, kv) for simplicity. Using these leakage in-
formation, we next define the semantic security of
EAS.
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
296

Definition 4. Let EAS =
(Gen, Enc, Trpdr, Annmz, Dec) be an EAS, and
consider the following probabilistic experiments
where A is an adversary, C is a challenger, S is a
simulator and L
A
and L
B
are leakage algorithms:
Real
EAS,A
(λ) : The adversary A chooses a plain ta-
ble P T and sends it to the challenger C. C begins
by running Gen(1
λ
) to generate a secret key K and
send it to A. A outputs a plain table P T and re-
ceives ET from C by E T ← Enc(K, P T ). A re-
peats the following Step 1–3 polynomial times.
1. A selects attributes of P T .
2. A gives a polynomial number of words w
′
for
the attributes to C.
3. A receives trapdoors td(w
′
) ← Trpdr(K, w
′
)
from C.
Finally, A returns a bit b, which is output by the
experiment.
Ideal
EAS,A,S
(λ) : The adversary A chooses a plain
table P T and sends it to the challenger C. C
sends L
A
(w) to the simulator S. S generates E T
from L
A
(w), and send it to C. C relays E T to
A. A repeats the following step 1–3 polynomial
times.
- A selects attributes of P T .
- A sends a polynomial number of words w
′
for the attributes to C. C sends L
B
(w, w
′
, kv)
to S. S generates trapdoors td(w
′
) from
L
B
(w, w
′
, kv) and sends them to C.
- A receives them from C.
Finally, A returns a bit b, which is output by the
experiment.
We say that EAS is (L
A
, L
B
)-secure against chosen-
keyword attacks if for all PPT adversaries A, there
exists a PPT simulator S such that
Pr[Real
EAS,A
(λ) = 1]−Pr[Ideal
EAS,A,S
(λ) = 1] ≤ negl.
4 EAS CONSTRUCTION
k–anonymization techniques are roughly classified
into methods that use a generalized hierarchy, often
called global recoding, and methods that do not, of-
ten called local recoding. If the purpose of anony-
mous data is clear, it is more advantageous to use a
generalized hierarchy that can clarify the policies of
anonymization. Section 4.1 describes a concrete EAS.
In practice, generalized hierarchies are troublesome to
create. Section 4.3 describes an algorithm to generate
a domain generalization hierarchy from E T .
4.1 EAS Construction using SSE
We now present our EAS construction.
• K ← Gen(1
λ
): generate a secret key
sk ←SSE.Gen(1
λ
) and output K = sk.
• ET ← Enc(K, P T )
1. encrypt each word in all attributes and cells of
P T .
- ew ← SSE.Enc(K, w) for all w ∈ A ∪ C
2. output the table consisting of ew as E T .
• td(w
′
) ← Trpdr(K, w
′
):
1. select attributes from A. Without losing gen-
erality, we assume that (a
1
, . . . a
s
) are selected
from A for simplicity.
2. generate trapdoors of each word in the selected
attributes and the corresponding columns.
- td(w
′
) ← SSE.Trpdr(K, w
′
) for all w
′
∈ a
1
∪
. . . a
s
∪ D
c1
∪ . . . D
cs
.
- ew
′
← SSE.Enc(K, w
′
) for all w
′
∈ D
c1
∪
. . . D
cs
.
3. output the set of td(w
′
) and ew
′
as td(w
′
).
• kE T or ⊥ ← Annmz(td(w
′
), E T , kv):
1. for all j ∈ [1, s]
(a) find an attribute a
i
such that
SSE.Cmpr(ew
i
, td(w
′
j
)) = 1 for i ∈ [1, n]
where ew
i
is stored in an attribute a
i
. If the a
i
is not found, output ⊥ and stop.
(b) replace ew stored in all cells in C
j
with ew
′
if
Cmpr(ew, td(w
′
)) = 1 holds for all w
′
∈ D
c j
.
(c) count frequency f (w
′
) of each trapdoor such
that f (w
′
) =
∑
ew∈C
i
Cmpr(ew, td(w
′
)) for all
w
′
∈ D
c j
and all ew stored in C
j
, and gener-
ate a domain generalization hierarchy by Al-
gorithm 1 described in Section 4.3.
2. this generalization step depends on selected
generalization algorithms. Here we give it
based on the algorithm proposed by Wang et
al. (Wang et al., 2004).
(repeat the following step (a)–(c) until k-
anonymity is satisfied or one node in every do-
main generation hierarchy is left)
(a) select two leaf nodes among
DGH
1
, . . . DGH
s
with the smallest infor-
mation entropy lost by generalization to
the nearest parent node, i.e. two leaf nodes
containing ew
′
1
or ew
′
2
are selected by using
the measure of information entropy and the
parent node contains (ew
′
1
or ew
′
2
).
(b) replace a value on the cells to that of the
parent node, i.e. ew
′
1
and ew
′
2
in the cells are
replaced with (ew
′
1
or ew
′
2
).
Definition and Efficient Construction of Encrypted k–anonymization Scheme
297

(c) delete the two leaf nodes from a DGH se-
lected at Step 2 .(a) and set the parent node as
a new leaf node of the DGH.
3. if the table is satisfied with k–anonymity for
the selected attributes, shuffle record order ran-
domly, and output it as k E T . Otherwise, out-
put ⊥.
• kP T ← Dec(K, k E T ):
1. decrypt each word in all attributes and cells of
kE T .
- w ← SSE.Dec(K, ew) for all ew ∈ A ∪ C
2. output the table as kP T .
Step 2.(a)–(c) applies the greedy method proposed
by Wang et al. (Wang et al., 2004). The method se-
quentially selects optimal anonymization target data
in accordance with a given generalized hierarchy.
Through this sophisticated anonymization process, it
is expected to output higher quality anonymous data
than the method of LeFerve et al.(LeFevre et al.,
2005), which is a representative global re-encoding
method and performs rough anonymization process-
ing.
4.2 Security
We define w
′
[s]
consists of words for queries of k–
anonymization with s attributes: w
′
[s]
= {w
′
| all w
′
stored in (a
1
, . . . a
s
) and w
′
∈ D
c1
∪ . . . D
cs
}.
Theorem 1. If SSE is (L
1
, L
2
)-secure against chosen-
keyword attacks, then the proposed EAS construc-
tion is (L
A
, L
B
)-secure against chosen-keyword at-
tacks such that L
A
(w) = L
1
(w), and L
B
(w, w
′
[s]
, kv) =
L
1
(w
′
[s]
), L
2
(w, w
′
[s]
) and kv.
Proof. Let S
′
be a simulator of the (L
1
, L
2
)-secure
SSE scheme. We construct a simulator S of EAS,
which achieves (L
A
, L
B
)-secure as follows.
(Store phase) In Ideal
EAS,A,S
, S takes L
A
(w) = L
1
(w)
as input. S runs S
′
(L
1
(w)) and gets its output ew
from S
′
. S constructs E T from ew and sends it to C.
(Anonymization phase) In Ideal
EAS,A,S
, S takes
L
B
(w, w
′
[s]
, kv) as input. S runs S
′
(L
2
(w, w
′
i
|w
′
i
stored
in a
i
)), S
′
(L
2
(w, w
′
i
| all w
′
i
∈ D
ci
)) for i = 1, . . . s,
and get its trapdoor td(w
′
) respectively. S runs
S
′
(L
1
(w
′
i
| all w
′
i
∈ D
ci
)) for i = 1, . . . s, and get its
trapdoor ew
′
respectively. S constructs kET by
EAS.Annmz(td(w
′
), E T , kv), and send kE T to
C.
4.3 Generation of Domain
Generalization Hierarchy
We design Algorithm 1, which generate domain
generalization hierarchies from searchable encrypted
database. This work is inspired by the research of
Harada et al., which use a data compression rule such
as Huffman code (Huffman, 1952) to create a domain
generalization hierarchy from a table P T (Harada
et al., 2012).
Algorithm 1: Generation of Domain Generalization
Hierarchy.
INPUT: trapdoor set td(w
′
i
), attribute a
i
, column C
i
,
frequency set
f
(
w
′
i
)
;
OUTPUT: domain generalization hierarchy DGH
i
;
1. extract all ew
′
from td(w
′
i
) and set each ew
′
as a value
of leaf nodes of DGH
i
2. store each combination of ew
′
and a frequency
f (w
′
) in a list Q in ascending order of f (w
′
), i.e.
(ew
′
1
, f (w
′
1
)), (ew
′
2
, f (w
′
2
)), . . . with f (w
′
1
) ≤ f (w
′
2
) ≤
. . . .
3. (repeat the following (a)–(d) until the number of nodes
in the list Q is 1)
(a) retrieve two nodes with the lowest and the 2nd low-
est frequencies such as ew
′
1
, ew
′
2
, and delete them
from the list Q.
(b) create a new parent node of children ew
′
1
and ew
′
2
such as (ew
′
1
or ew
′
2
)
(c) assigns frequency of the parent node to the sum of
frequencies of the child nodes. e.g. frequency of the
node (ew
′
1
or ew
′
2
) is f (w
′
1
) + f (w
′
2
).
(d)
add the parent node to the list Q and sort it again.
4. the last attribute value in list Q is taken as the root node.
Output this tree as the domain generalization hierarchy
DGH
i
On the basis of the results of aggregation, up-
per nodes of the generalized hierarchy are gradually
formed from nodes with low appearance frequency.
The appearance frequency of the upper node is the
sum of the appearance frequencies of the lower nodes,
and so that the degree of generalization is not too
strong, Huffman code or the like is used. Also, an
upper node generalizing lower nodes is represented
by a logical sum (or) of values of lower nodes.
In this paper, for simplicity, we ignore the order
relation of attributes and use Huffman code for gen-
eralized hierarchy. In the case of handling numeric
column such as age and geographical information, in-
stead of Huffman code and SSE, one can apply Hu-
Tucker code (Hu and Tucker, 1971) and order pre-
serving encryption to maintain the order relation.
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
298

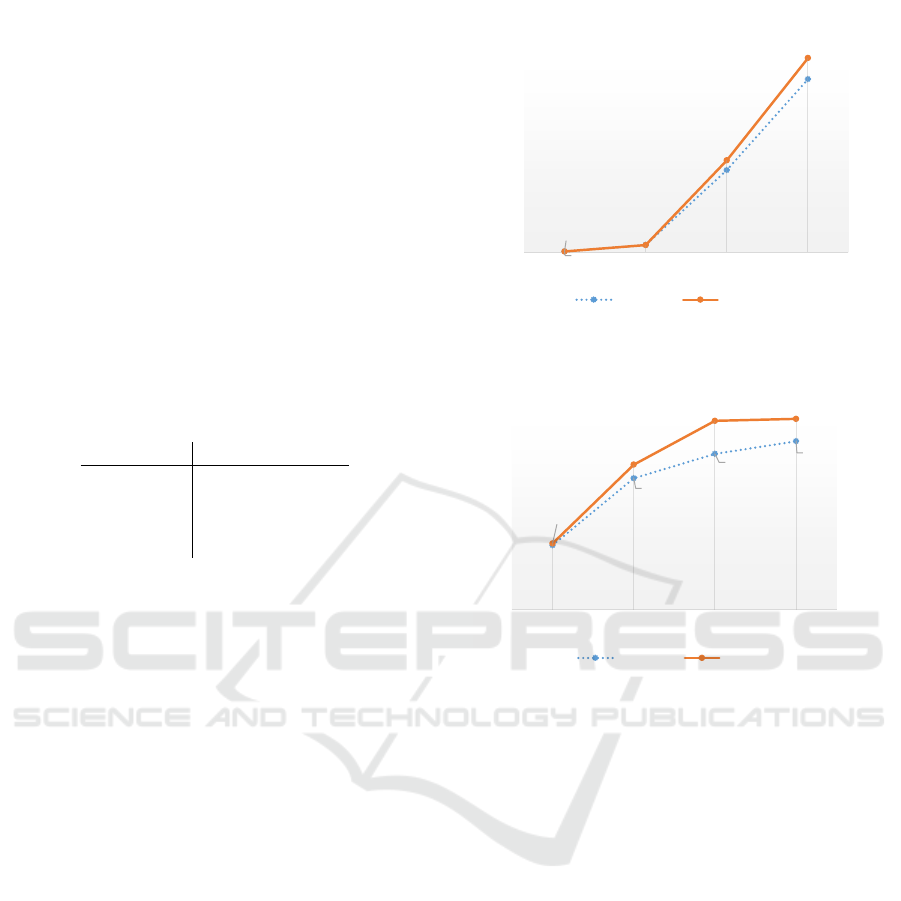
5 EXPERIMENTAL
PERFORMANCE EVALUATION
We implement the proposed scheme to utilize 256-
bit AES and SHA-256 for SSE (Yoshino et al., 2011).
The performance is evaluated on a conventional com-
puter, which is equipped with 3.4 GHz Core i7 6700
CPU, 32GB memory, Cent OS 7.4, and JVM 1.8.0.
To measure the mounting performance for data scal-
ability, we generated dummy data, which is shown in
Table 1. Three attributes (occupation, gender, and ad-
dress) are randomly selected in these value ranges,
and the last attribute (birth date) is sampled from
statistics based on Japanese population estimates (Bu-
reau, 2016).
Table 1: Test Dataset Consisting of Attributes and Possible
Values.
attribute possible value
occupation integer in [1, 24]
gender female or male
address 5000 types
birth date DD/MM/YYYY
Performance of the Enc, Trpdr, or Dec function
of the proposed EAS depends on SSE.Enc, SSE.Trpdr,
or SSE.Dec, respectively, and the running time in-
creases linearly to data size of P T , E T , or message
space. Thus, we measure the last function Annmz of
the proposed EAS, in which running time is not eas-
ily estimated. The generalization process consisting
of Step 2.(a)–(c) is the major process for Annmz. Fig-
ure 3 shows performance of the generalization pro-
cess on the dummy data with 4 attributes and k = 3.
It takes about 440 milliseconds for 10
3
records, about
6 seconds for 10
4
records, about 80 seconds for 10
5
records, and about 168 seconds for 10
6
records. Com-
pared with the case of the plaintext (Wang et al.,
2004), the generalization step of the proposed EAS
is comparable and almost equivalent. Annmz has a
branch process: if domain generation hierarchies are
not given, then Step 2 generates them. Figure 4
shows the generation time of the generalized hierar-
chy: about 77 milliseconds to 229 milliseconds for
10
3
to 10
6
records. That is negligible compared with
the generalization time.
6 CONCLUSION
We pointed out that outsourcing k–anonymization
processes may lead to information leakage, thus we
defined an encrypted k–anonymization scheme (EAS)
and a semantic security model of EAS. Furthermore,
433.877
6006.994
71086.054
150111.391
440.767
5976.579
79593.499
168447.332
0
20000
40000
60000
80000
100000
120000
140000
160000
180000
1000 10000 100000 1000000
plain data encrypted data
[records]
[ms]
Figure 3: Performance on 3–anonymization
77.305
157.574
186.757
201.908
79.419
173.886
226.306
228.667
0
50
100
150
200
250
1000 10000 100000 1000000
plain data encrypted data
[records]
[ms]
Figure 4: Performance on DGH Generation
we give a construction of EAS and prove the security
under the semantic security model. Finally, we im-
plemented the proposal on a general-purpose PC and
demonstrated its efficiency. As a consequence, our
high-speed EAS makes it feasible not only to prevent
information leakage from database but also to gain the
advantage that even the server can prevent unintended
observation of the given database.
REFERENCES
Boneh, D., Di Crescenzo, G., Ostrovsky, R., and Per-
siano, G. (2004). Public key encryption with keyword
search. In Advances in Cryptology – EUROCRYPT,
pages 506–522. Springer.
Boneh, D. and Waters, B. (2007). Conjunctive, subset, and
range queries on encrypted data. In Theory of Cryp-
tography Conference, pages 535–554. Springer.
Bureau, S. (2016). Ministry of internal affairs and commu-
nications. Government of Japan.
Curtmola, R., Garay, J., Kamara, S., and Ostrovsky, R.
(2006). Searchable symmetric encryption: Improved
definitions and efficient constructions. In Proceedings
Definition and Efficient Construction of Encrypted k–anonymization Scheme
299

of the 13th ACM Conference on Computer and Com-
munications Security, CCS, pages 79–88, New York,
NY, USA. ACM.
Curtmola, R., Garay, J., Kamara, S., and Ostrovsky, R.
(2011). Searchable symmetric encryption: improved
definitions and efficient constructions. Journal of
Computer Security, 19(5):895–934.
Ducas, L. and Micciancio, D. (2015). FHEW: bootstrapping
homomorphic encryption in less than a second. In
Advances in Cryptology – EUROCRYPT, pages 617–
640.
Gentry, C. (2009). Fully homomorphic encryption using
ideal lattices. In Proceedings of the Annual ACM Sym-
posium on Theory of Computing, STOC, pages 169–
178, New York, NY, USA. ACM.
Harada, K., Sato, Y., and Togashi, Y. (2012). Reducing
amount of information loss in k-anonymization for
secondary use of collected personal information. In
SRII Annual Global Conference, pages 61–69. IEEE.
Hu, T. C. and Tucker, A. C. (1971). Optimal computer
search trees and variable-length alphabetical codes.
SIAM Journal on Applied Mathematics, 21(4):514–
532.
Huffman, D. A. (1952). A method for the construction of
minimum-redundancy codes. Proceedings of the IRE,
40(9):1098–1101.
Kamara, S. and Lauter, K. (2010). Cryptographic cloud
storage. In International Conference on Financial
Cryptography and Data Security, pages 136–149.
Springer.
LeFevre, K., DeWitt, D. J., and Ramakrishnan, R. (2005).
Incognito: Efficient full-domain k-anonymity. In Pro-
ceedings of the ACM SIGMOD International Confer-
ence on Management of Data , pages 49–60. ACM.
LeFevre, K., DeWitt, D. J., and Ramakrishnan, R. (2006).
Mondrian multidimensional k-anonymity. In Proceed-
ings of the International Conference on Data Engi-
neering (ICDE), pages 25–25. IEEE.
Meyerson, A. and Williams, R. (2004). On the complexity
of optimal k-anonymity. In Proceedings of the ACM
SIGMOD-SIGACT-SIGART Symposium on Principles
of Database Systems, pages 223–228. ACM.
Popa, R. A., Redfield, C. M. S., Zeldovich, N., and Bal-
akrishnan, H. (2012). Cryptdb: Processing queries
on an encrypted database. ACM Communications,
55(9):103–111.
Samarati, P. (2001). Protecting respondents identities in mi-
crodata release. IEEE Transactions on Knowledge and
Data Engineering, 13(6):1010–1027.
Samarati, P. and Sweeney, L. (1998). Protecting privacy
when disclosing information: k-anonymity and its
enforcement through generalization and suppression.
Technical report, technical report, SRI International.
Song, D. X., Wagner, D., and Perrig, A. (2000). Practical
techniques for searches on encrypted data. In Pro-
ceedings of the IEEE Symposium on Security and Pri-
vacy, pages 44–55. IEEE.
Sweeney, L. (2002a). Achieving k-anonymity privacy pro-
tection using generalization and suppression. In-
ternational Journal of Uncertainty, Fuzziness and
Knowledge-Based Systems, 10(05):571–588.
Sweeney, L. (2002b). k-anonymity: A model for protecting
privacy. International Journal of Uncertainty, Fuzzi-
ness and Knowledge-Based Systems, 10(05):557–570.
Wang, K., Philip, S. Y., and Chakraborty, S. (2004).
Bottom-up generalization: A data mining solution to
privacy protection. In Proceedings of the IEEE Inter-
national Conference on Data Mining.
Yoshino, M., Naganuma, K., and Satoh, H. (2011). Sym-
metric searchable encryption for database applica-
tions. In International Conference on Network-Based
Information Systems (NBiS), pages 657–662. IEEE.
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
300