
Goal-conditioned User Modeling for Dialogue Systems using Stochastic
Bi-Automata
Manex Serras
1
, Mar
´
ıa In
´
es Torres
2
and Arantza del Pozo
1
1
Speech and Natural Language Technologies, Vicomtech, Paseo Mikeletegi 57, Donostia-San Sebastian, Spain
2
Speech Interactive Research Group, Universidad del Pa
´
ıs Vasco UPV/EHU, Campus of Leioa, Leioa, Spain
Keywords:
Dialogue Systems, Stochastic Bi-Automata, User Modeling.
Abstract:
User Models (UM) are commonly employed to train and evaluate dialogue systems as they generate dialogue
samples that simulate end-user behavior. This paper presents a stochastic approach for user modeling based
in Attributed Probabilistic Finite State Bi-Automata (A-PFSBA). This framework allows the user model to
be conditioned by the dialogue goal in task-oriented dialogue scenarios. In addition, the work proposes two
novel smoothing policies that employ the K-nearest A-PFSBA states to infer the next UM action in unseen
interactions. Experiments on the Dialogue State Tracking Challenge 2 (DSTC2) corpus provide results similar
to the ones obtained through deep learning based user modeling approaches in terms of F1 measure. However
the proposed Bi-Automata User Model (BAUM) requires less resources both of memory and computing time.
1 INTRODUCTION
Developing task-oriented Spoken Dialogue Systems
(SDS) using machine learning approaches requires
high amounts of dialogue samples from which Dia-
logue Managers (DM) learn optimal strategies. As
manual compilation and labeling of dialogue samples
is highly resource demanding, a common approach is
to develop an User Model (UM) that simulates the be-
havior of real users from a small amount of annotated
dialogue corpora. UMs are also commonly used to
evaluate the performance of DMs and/or to optimize
their policy in Reinforcement Learning (RL) scenar-
ios (Schatzmann et al., 2006; Eshghi et al., 2017;
Ga
ˇ
si
´
c et al., 2010; Ga
ˇ
si
´
c et al., 2017; Chen et al.,
2017; Serras et al., 2017). UMs are expected to main-
tain coherence throughout the dialogue and to imitate
the behavior of real users. In addition, they must also
have some degree of variability in order to generate
unseen or not-likely interactions.
Multiple methodologies have been proposed in the
literature to build UMs. Initial approaches (Eckert
et al., 1997; Levin et al., 2000; Pietquin, 2005) used
N-grams, but the resulting models were not capable
of capturing the dialogue history and, thus, lacked
coherence. With the aim of generating more co-
herent dialogues, several stochastic approaches such
as Bayesian Networks (Pietquin and Dutoit, 2006)
and networks of Hidden Markov Models (Cuay
´
ahuitl
et al., 2005) have been explored. Another popular
statistical UM is the Hidden Agenda model (Schatz-
mann et al., 2007), in which the user goal is prede-
fined as an agenda of constraints and pieces of infor-
mation to be requested to the system and updated at
each dialogue turn. Other approaches have exploited
the analogies between user simulation and imitation
learning using inverse reinforcement learning (Chan-
dramohan et al., 2011). Recently, neural network
approaches have been proposed for user simulation
(Layla et al., 2016; Crook and Marin, 2017; Serras
et al., 2019), showing to be capable of accounting for
both, the whole dialogue history and the goal of the
user. Although promising, neural implementations re-
quire specific hardware to train and run efficiently. An
alternative approach to build UMs is to use a stochas-
tic model, such as the Attributed Probabilistic Finite
State Bi-Automata (A-PFSBA) (Torres, 2013). Previ-
ous work has successfully employed this framework
to develop both UMs and DMs (Orozko and Torres,
2015; Ghigi and Torres, 2015; Serras et al., 2017;
Serras et al., 2018). However, the UMs explored so
far following the A-PFSBA formulation are simple
models that do not include user related attributes nor
goal conditioning. In addition, they have not been for-
mally evaluated, so the full potential of the A-PFSBA
framework for user simulation remains unexplored.
In this paper, the original definition of the A-
PFSBA framework is enhanced with explicit goal en-
128
Serras, M., Torres, M. and del Pozo, A.
Goal-conditioned User Modeling for Dialogue Systems using Stochastic Bi-Automata.
DOI: 10.5220/0007359401280134
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 128-134
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

coding in order to allow the development of goal-
conditioned UMs. Also, this work proposes two
novel smoothing policies that employ the K-nearest
A-PFSBA states to infer the next UM action in un-
seen interactions. The proposed model and policies
are then validated and compared to recently proposed
neural architectures in terms of quality and perfor-
mance.
The paper is structured as follows: Section 2 intro-
duces the A-PFSBA framework. In Section 3, the pro-
posed Bi-Automata User Model (BAUM) is formally
defined over the A-PFSBA framework. First, the
way in which goal conditioning is implemented is de-
scribed. Then, the two novel K-nearest state smooth-
ing policies are introduced. Section 4 presents the ex-
perimental setup and evaluates the proposed BAUM
on the DSTC2 dataset. Finally, Section 5 summarizes
the conclusions and sets the future work.
2 ATTRIBUTED PROBABILISTIC
FINITE STATE BI-AUTOMATA
FRAMEWORK
In this section, dialogue interaction is defined as a bi-
language that can be modeled by an A-PFSBA.
A dialogue z can be viewed as a sequence of sys-
tem and user actions. Let d ∈ Σ be the finite alpha-
bet of user actions decoded by a Natural Language
Understanding module and a ∈ ∆ the finite alphabet
of system actions. Then, a dialogue z = z
1
...z
|z|
is
represented as a bi-string over the extended alphabet
Γ ⊆ (Σ
≤m
× ∆
≤n
) where z
i
is of the form (d
i
: ε) for
the user turns and of the form (ε : a
i
) for the system
turns, being ε the empty symbol.
In this framework, the probability of a sys-
tem action a
i
given by a DM can be defined as
P(a
i
|z
0
...z
i−1
) and the probability of the user action
as P(d
i
| z
0
...z
i−1
, G) where G is the goal of the user
in the dialogue
1
. As the dialogue becomes larger, it
is intractable to maintain all the previous interactions
to condition the probability of a
i
and d
i
. A common
practice is to encode the transitive content (e.g. bus
departure, desired food) of the dialogue in a sum-
mary space (Ga
ˇ
si
´
c et al., 2010; Serras et al., 2017;
Casanueva et al., 2017). In the A-PFSBA framework
this is achieved using the attribute alphabet ω ∈ Ω.
These attributes are inferred from the bi-string z at
each step.
1
Because the goal of the system is usually to satisfy the
user’s goal in every interaction, it is often ignored
The A-PFSBA formulation aims to maximize the
probability of model M to generate a given sample of
dialogues Z, being z each of the dialogues that com-
pose sample Z.
ˆ
M = arg max
M
P
M
(Z) = arg max
M
∏
z∈Z
P
M
(z)
The A-PSFBA model can then be defined as
ˆ
M =
(Σ, ∆, Ω, Γ, Q, δ, q
0
, P
f
, P) where:
• Σ is the alphabet of user’s decoded actions, d ∈ Σ.
• ∆ is the alphabet of system actions, a ∈ ∆.
• Ω is the alphabet of dialogue attributes ω
i
∈ Ω.
• Γ is an extended alphabet Γ ⊆ (Σ
≤m
× ∆
≤n
) that
contains the combination of the user decoded and
the system actions.
• Q = Q
S
∪ Q
U
is the set of system and user states
labeled by bi-strings and attributes: [(d
i
: a
i
), ω
i
] ∈
Γ × Ω.
• q
0
∈ Q
S
is the unique initial state: [(ε : ε), ε] where
ε is the empty symbol.
• δ ⊆ Q × Γ × Q is the union of two sets of transi-
tions δ = δ
S
∪ δ
U
as follows:
– δ
S
⊆ Q
S
× Γ × Q
U
is the set of system tran-
sitions of the form (q, (ε : a
i
), q
0
) where q ∈
Q
S
, q
0
∈ Q
U
and (ε : a
i
) ∈ Γ.
– δ
U
⊆ Q
U
× Γ × Q
S
is the set of user transitions
of the form (q, (d
i
: ε), q
0
) where q ∈ Q
U
, q
0
∈
Q
S
and (d
i
: ε) ∈ Γ.
• P
f
: Q → [0, 1] is the final-state probability distri-
bution.
• P : δ → [0, 1] defines the transition probability
distributions P(q, b, q
0
) ≡ P(q
0
, b | q) ∀b ∈ Γ and
q, q
0
∈ Q such that:
P
f
(q) +
∑
b∈Γ,q
0
∈Q
P(q, b, q
0
) = 1 ∀q ∈ Q
where transition (q, b, q
0
) is completely defined by
the initial state q and the transition action b. Thus,
∀q ∈ Q, ∀b ∈ Γ, |{q
0
: {(q, b, q
0
)}| ≤ 1
Then, every dialogue bi-string z is modeled as a
sequence of bi-automata states (q
0
, q
1
, ..., q
|z|
) where
q
0
is the initial empty state. More details of the frame-
work can be found at (Torres, 2013; Orozko and Tor-
res, 2015; Ghigi and Torres, 2015; Serras et al., 2018).
3 BI-AUTOMATA USER MODEL
Given the formulation of the previous section, a
BAUM can be formally defined as a function that iter-
ates over the current state q
t
and returns a user action
Goal-conditioned User Modeling for Dialogue Systems using Stochastic Bi-Automata
129
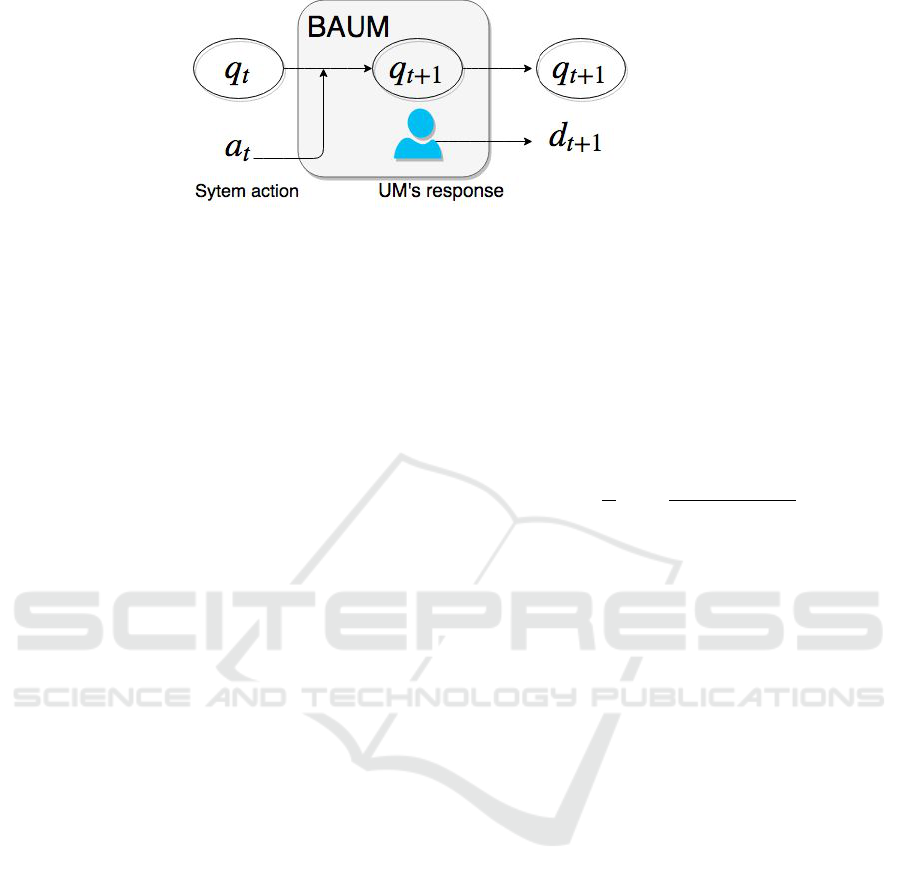
Figure 1: BAUM diagram, where the UM iterates the state to q
t+1
and returns an action d
t+1
.
d
t+1
given a system action a
t
(Serras et al., 2017):
UM
Π
: Q × ∆ → Σ × Q
Π
UM
(q
t
, a
t
,
ˆ
M, Dist) → d
t+1
, q
t+1
where
ˆ
M is the A-PFSBA model inferred from the
dialogue samples, Dist is a distance function between
the user states and Π
UM
is the policy function that
chooses the next action to perform.
The BAUM works as follows: starting from a
dialogue state q
t
it receives a system action a
t
, then
the dialogue state is updated to q
t+1
. From this state,
and using the set of possible user actions, the policy
Π
UM
chooses the next user action d
t+1
.
3.1 Goal-conditioning the States of the
A-PFSBA
Following the Hidden Agenda notation of (Schatz-
mann et al., 2007), the user goal G can be represented
as a set of constraints C and requests R. Dialogue con-
straints specify requirements of the goal to achieve
(e.g. restaurant type) while requests specify desired
pieces of information to retrieve (e.g. address, phone
number, etc.). Both can be represented as lists of slot-
value pairs. The behavior of the BAUM can be con-
ditioned to a given dialogue goal by encoding C and
R as A-PFSBA attributes Ω. As a result, Ω
G
⊂ Ω
can be defined as the union of two sets of attributes
Ω
C
∪ Ω
R
= Ω
G
, where Ω
C
corresponds to the slots
given as constraints and Ω
R
corresponds to the slots
the user has to request about, as depicted in Figure 2.
3.2 Smoothing Policies for Unseen
States
To generalize to new unseen states q
0
6∈ Q, a smooth-
ing strategy needs to be defined that willl redirect the
dialogue interaction to a seen state q ∈ Q. Previous A-
PFSBA implementations used a nearest state smooth-
ing approach, in which the dialogue interaction was
redirected to the state with minimum distance. In this
paper, a novel K-Nearest Smoothing State (K-NSS)
approach is proposed, where the next user action is
chosen using a selection procedure that employs the
K nearest states according to the distance Dist.
Being Q
K
= {q
1
, ..., q
j
, ..., q
K
} the set of the K
states q ∈ Q closest to the unseen state q
0
, let D
j
be
the set of user actions that can be performed from q
j
.
Then, the score for each user action of the multiset
d ∈ ∪
K
j=1
D
j
can be calculated as:
score(d) =
1
K
∑
q
j
∈Q
K
1
β + Dist(q
0
, q
j
)
P(d| q
j
)
where P(d|q
j
) is the probability of choosing the user
action d to transition from the state q
j
and Dist(q
0
, q
j
)
is the distance between the unseen state q
0
and the
candidate state q
j
. β is a parameter to avoid numerical
errors for zero distances. Using this scoring function,
the following two novel smoothing policies have been
derived:
• K-NSS Maximum Score Action (MSA) policy:
where the next user action d
t+1
is defined as the
action with maximum score of the multiset
d
t+1
= arg max
d∈∪
K
j=1
D
j
score(d)
For those cases where multiple user actions d
have the same maximum score, the combination
of those actions is set as d
t+1
.
• K-NSS Thresholded Score Action (TSA) policy:
where the maximum score constraint is relaxed
with a given threshold θ. In this case, the next user
action d
t+1
is the combination of all those unique
candidate user actions of the multiset d ∈ ∪
K
j=1
D
j
whose score score(d) is above a given threshold θ
defined at tuning phase:
d
t+1
= {d ∈ ∪
K
j=1
D
j
|score(d) ≥ θ}
4 SETUP AND EXPERIMENTS
This section describes how the BAUM was designed
and trained on the DSTC2 corpus and shows the re-
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
130

{food = international,
area = None,
price = cheap}
Dialogue Constraints
[1, 0, 1]
Information to Request
{food = False,
area = False,
address = True,
signature = True}
[0, 0, 1, 1]
To Vector
To Vector
Concatenation
[1, 0, 1, 0, 0, 1, 1]
Goal Attributes
Figure 2: Example of a Dialogue Goal encoded as the concatenation of Constraint attributes Ω
C
and Request attributes Ω
R
.
Table 1: Overall results at dialogue act level.
BAUM NSS BAUM K-NSS MSA BAUM K-NSS TSA Reg. Bi-LSTM (Serras et al., 2019)
DSTC2 Dev Precision 0.68 0.71 0.67 0.70
Recall 0.69 0.67 0.72 0.72
F1 0.68 0.69 0.70 0.71
DSTC2 Test Precision 0.70 0.75 0.68 0.71
Recall 0.70 0.69 0.76 0.73
F1 0.70 0.72 0.72 0.72
sults achieved. The proposed model and policies are
compared to a recent Deep Learning (DL) approach
(Serras et al., 2019).
4.1 Experimental Framework
The presented approach has been tested on the Dia-
logue State Tracking Challenge 2 (DSTC2) corpus.
The second edition of the DSTC series (Henderson
et al., 2013) focused on tracking the dialogue state of
a SDS in the Cambridge restaurant domain. For such
purpose, a corpus with a total of 3235 dialogues was
released
2
. The organizers used Amazon Mechanical
Turk to recruit users who interacted with a spoken
dialogue system where each user was given a sce-
nario with a goal to be completed interacting with the
system. The goals defined in such scenarios followed
the agenda approach of (Schatzmann et al., 2007).
As a result, the constraints and requests of the user
goal are explicitly annotated for each dialogue in the
corpus.
Following the methodology of (Serras et al.,
2019), the user and system actions are represented
at semantic level, using dialogue acts (i.e. intents
of the user/system as inform, request, etc.) and
slots that represent intent-related information with
their corresponding values (i.e. food=japanese,
where food is the slot and japanese its value). In
addition, every slot value is replaced with an is goal
or not goal token, depending on whether it matches
any given constraint value set in the goal, in order to
2
http://camdial.org/∼ mh521/dstc/
reduce data sparsity.
The train/development/test set partitions of
1612/506/1117 dialogues are given explicitly in the
corpus. The final evaluation has been performed over
the test set in terms of Precision, Recall and F1-score
as in (Layla et al., 2016; Schatzmann et al., 2006;
Cuay
´
ahuitl et al., 2005; Quarteroni et al., 2010).
These metrics allow comparing the dialogue acts of
real and simulated users, measuring the behavior and
consistency of the model.
4.1.1 Encoding the Dialogue History
The dialogue history is encoded in the attributes of
the DSTC2 corpus. Each slot of the goal constraints
C is assigned one of the following three attribute val-
ues: (1) the initial Null value, (2) the User Commu-
nicated value, for cases in which the user informs the
system about the slot and (3) the System Understood
value, that is triggered when the system understands
the slot correctly.
In addition, the attribute of each slot of the goal re-
quests R is assigned one of the following values: (1)
the Null initial state, (2) the User Requested value,
that is activated when the user requests about a slot
and the (3) System Informed value, activated when
the system gives the requested information. The value
of these attributes is inferred from the dialogue inter-
action using simple rules.
Goal-conditioned User Modeling for Dialogue Systems using Stochastic Bi-Automata
131

Table 2: Overall results at slot-value level.
BAUM NSS BAUM K-NSS MSA BAUM K-NSS TSA Reg. Bi-LSTM (Serras et al., 2019)
DSTC2 Dev Precision 0.57 0.59 0.55 0.60
Recall 0.57 0.54 0.62 0.63
F1 0.57 0.57 0.58 0.62
DSTC2 Test Precision 0.56 0.61 0.55 0.60
Recall 0.56 0.56 0.64 0.64
F1 0.56 0.58 0.59 0.62
Table 3: Relative comparison of performance.
BAUM Reg.Bi-LSTM no GPU Reg. Bi-LSTM (Serras et al., 2019)
Train time Ref 93046×Ref 3323×Ref
Eval time - Dev Ref 65.7×Ref 1.43×Ref
Mem. consumption Ref 29.9×Ref 3.3×Ref GPU
53×Ref RAM
4.1.2 Smoothing Distance
The A-PFSBA states are represented as binary vectors
and the distance between two A-PFSBA states q
1
, q
2
is defined as the euclidean distance between the sys-
tem actions and the attributes of both states.
Dist(q
1
, q
2
) =
q
(ω
1
− ω
2
)
2
+ (a
1
− a
2
)
2
where a
1
, a
2
are the system action representations
of each state and ω
1
, ω
2
are their attribute vectors.
This implementation differs from previous ones (Ser-
ras et al., 2017; Orozko and Torres, 2015; Ghigi and
Torres, 2015), in which the states were represented as
strings and the Levenshtein distance was used.
4.1.3 Parameter Tuning
The number of K states to be used in the smoothing
policies and the individual threshold θ of the K-NSS
TSA policy is set using the development set. To set
the value of the θ threshold for each dialogue act,
a grid search is done to maximize the individual F1
scores.
4.2 Experiments and Results
This section describes the experiments performed
over the DSTC2 corpus and the obtained results.
Table 1 shows the Precision, Recall and F1 score
achieved by BAUM on the DSTC2 development and
test sets at dialogue act level. For comparative pur-
poses, the latest DL user modeling approach based on
an ensemble of regularized Bi-LSTM (Serras et al.,
2019) is included. As it can be seen, the BAUM
framework achieves competitive results using a single
and lightweight model even in its simplest NSS form.
The proposed K −NSS variant smoothing policies im-
prove its generalization capability, with K-NSS MSA
achieving slightly lower but more precise results over-
all. On the other hand, the K-NSS TSA policy obtains
slightly higher results, but is more verbose than the K-
NSS MSA policy, as reflected in its recall score. It is
interesting to note that both, the MSA and TSA vari-
ants reach the same F1 score as the DL approach on
the test set.
Table 2 shows overall results achieved at slot value
level. As expected, performance decreases overall
given the finer granularity of the task and the pro-
posed user modeling framework and smoothing poli-
cies achieve slightly lower results than the regularized
Bi-LSTM ensemble. Nevertheless, the results are ro-
bust enough to prove the validity of the BAUM model
as a simple and lightweight alternative for user simu-
lation.
Finally, Table 3 shows a relative
3
comparison of
the memory and computation time requirements of
the bi-automata and deep learning UM approaches
with and without GPU hardware with a Theano
(Theano Development Team, 2016) backend. Predic-
tion times are nearly the same for the BAUM method
and the single GPU Reg. Bi-LSTM model, the first
one being slightly faster. However, the difference in-
creases significantly when compared against the same
model without GPU. The fact that training time is var-
ious orders of magnitude faster in BAUM, makes it
suitable for low resource environments.
5 CONCLUSIONS AND FUTURE
WORK
This paper has presented a stochastic UM approach
for goal-oriented spoken dialogue systems using A-
3
Reference values: Training - 13 s, Prediction- 150 s,
RAM - 137 MB
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
132

PFSBA. The BAUM model, employs user-specific
and goal encoding of attributes in order to capture the
coherence of interaction within its structure. In ad-
dition, two K-Nearest State Smoothing policies are
introduced and evaluated, achieving higher perfor-
mance than their single-state counterpart. The pro-
posed UM achieves results similar to current deep
learning approaches, using a lightweight model with
better performance in terms of computation time and
memory consumption.
Future work will involve developing a methodol-
ogy for the automatic inference of dialogue attributes
and testing the presented approach on other goal-
oriented dialogue corpora. In addition, the robustness
of the proposed simulated user modeling approach
will be tested regarding its applicability to train and
evaluate statistical spoken dialogue systems.
ACKNOWLEDGEMENTS
This work has been partially funded by the Span-
ish Ministry of Science under grants TIN2014-54288-
C4-4-R and TIN2017-85854-C4-3-R and by the Eu-
ropean Commission H2020 SC1-PM15 EMPATHIC
project, RIA grant 69872.
REFERENCES
Casanueva, I., Budzianowski, P., Su, P.-H., Mrk
ˇ
sic, N.,
Wen, T.-H., Ultes, S., Rojas-Barahona, L., Young,
S., and Ga
ˇ
sic, M. (2017). A benchmarking environ-
ment for reinforcement learning based task oriented
dialogue management. stat, 1050:29.
Chandramohan, S., Geist, M., Lefevre, F., and Pietquin, O.
(2011). User simulation in dialogue systems using
inverse reinforcement learning. In Interspeech 2011,
pages 1025–1028.
Chen, L., Zhou, X., Chang, C., Yang, R., and Yu, K. (2017).
Agent-aware dropout dqn for safe and efficient on-
line dialogue policy learning. In Proceedings of the
2017 Conference on Empirical Methods in Natural
Language Processing, pages 2444–2454.
Crook, P. and Marin, A. (2017). Sequence to sequence mod-
eling for user simulation in dialog systems. In Pro-
ceedings of the 18th Annual Conference of the Inter-
national Speech Communication Association (INTER-
SPEECH 2017), pages 1706–1710.
Cuay
´
ahuitl, H., Renals, S., Lemon, O., and Shimodaira, H.
(2005). Human-computer dialogue simulation using
hidden markov models. In Automatic Speech Recog-
nition and Understanding, 2005 IEEE Workshop on,
pages 290–295. IEEE.
Eckert, W., Levin, E., and Pieraccini, R. (1997). User mod-
eling for spoken dialogue system evaluation. In Auto-
matic Speech Recognition and Understanding, 1997.
Proceedings., 1997 IEEE Workshop on, pages 80–87.
IEEE.
Eshghi, A., Shalyminov, I., and Lemon, O. (2017). Boot-
strapping incremental dialogue systems from minimal
data: the generalisation power of dialogue grammars.
In Proceedings of the 2017 Conference on Empiri-
cal Methods in Natural Language Processing, pages
2220–2230.
Ga
ˇ
si
´
c, M., Jur
ˇ
c
´
ı
ˇ
cek, F., Keizer, S., Mairesse, F., Thomson,
B., Yu, K., and Young, S. (2010). Gaussian processes
for fast policy optimisation of pomdp-based dialogue
managers. In Proceedings of the 11th Annual Meeting
of the Special Interest Group on Discourse and Dia-
logue, pages 201–204. Association for Computational
Linguistics.
Ga
ˇ
si
´
c, M., Mrk
ˇ
si
´
c, N., Rojas-Barahona, L. M., Su, P.-H.,
Ultes, S., Vandyke, D., Wen, T.-H., and Young, S.
(2017). Dialogue manager domain adaptation using
gaussian process reinforcement learning. Computer
Speech & Language, 45:552–569.
Ghigi, F. and Torres, M. I. (2015). Decision making strate-
gies for finite-state bi-automaton in dialog manage-
ment. In Natural Language Dialog Systems and In-
telligent Assistants, pages 209–221. Springer.
Henderson, M., Thomson, B., and Williams, J. (2013). Dia-
log state tracking challenge 2 & 3 handbook. camdial.
org/mh521/dstc.
Layla, E. A., Jing, H., and Suleman, K. (2016). A sequence-
to-sequence model for user simulation in spoken dia-
logue systems. In Interspeech.
Levin, E., Pieraccini, R., and Eckert, W. (2000). A stochas-
tic model of human-machine interaction for learning
dialog strategies. IEEE Transactions on speech and
audio processing, 8(1):11–23.
Orozko, O. R. and Torres, M. I. (2015). Online learning of
stochastic bi-automaton to model dialogues. In Pat-
tern Recognition and Image Analysis - 7th Iberian
Conference, IbPRIA 2015, Santiago de Compostela,
Spain, June 17-19, 2015, Proceedings, pages 441–
451.
Pietquin, O. (2005). A framework for unsupervised learning
of dialogue strategies. Presses univ. de Louvain.
Pietquin, O. and Dutoit, T. (2006). A probabilistic frame-
work for dialog simulation and optimal strategy learn-
ing. IEEE Transactions on Audio, Speech, and Lan-
guage Processing, 14(2):589–599.
Quarteroni, S., Gonz
´
alez, M., Riccardi, G., and Varges, S.
(2010). Combining user intention and error modeling
for statistical dialog simulators. In INTERSPEECH,
pages 3022–3025.
Schatzmann, J., Thomson, B., Weilhammer, K., Ye, H., and
Young, S. (2007). Agenda-based user simulation for
bootstrapping a pomdp dialogue system. In Human
Language Technologies 2007: The Conference of the
North American Chapter of the Association for Com-
putational Linguistics; Companion Volume, Short Pa-
pers, pages 149–152. Association for Computational
Linguistics.
Schatzmann, J., Weilhammer, K., Stuttle, M., and Young,
S. (2006). A survey of statistical user simulation tech-
niques for reinforcement-learning of dialogue man-
Goal-conditioned User Modeling for Dialogue Systems using Stochastic Bi-Automata
133

agement strategies. The knowledge engineering re-
view, 21(02):97–126.
Serras, M., Torres, M. I., and Del Pozo, A. (2017). Online
learning of attributed bi-automata for dialogue man-
agement in spoken dialogue systems. In Iberian Con-
ference on Pattern Recognition and Image Analysis,
pages 22–31. Springer.
Serras, M., Torres, M. I., and del Pozo, A. (2018). User-
aware dialogue management policies over attributed
bi-automata. Pattern Analysis and Applications.
Serras, M., Torres, M. I., and del Pozo, A. (2019). Regu-
larized Neural User Model for Goal-Oriented Spoken
Dialogue Systems, pages 235–245. Springer Interna-
tional Publishing, Cham.
Theano Development Team (2016). Theano: A Python
framework for fast computation of mathematical ex-
pressions. arXiv e-prints, abs/1605.02688.
Torres, M. I. (2013). Stochastic bi-languages to model
dialogs. In 11th International Conference on Fi-
nite State Methods and Natural Language Processing,
FSMNLP, Proceedings, pages 9–17.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
134
