
Kohonen Map Modification for Classification Tasks
Jiří Jelínek
Institute of Applied Informatics, Faculty of Science, University of South Bohemia,
Branišovská 1760, České Budějovice, Czech Republic
Keywords: Kohonen Map, Neural Networks, Pattern Classification.
Abstract: This paper aims to present a classification model based on Kohonen maps with a modified learning
mechanism and structure as well. Modification of the model structure consists of its modification for
hierarchical training and recall. The change of the learning process is the transition from unsupervised to
supervised learning. Experiments were performed with the modified model to verify changes in the model
and compare the results with other research.
1 INTRODUCTION
A variety of methods are available for advanced data
processing, often in the field of artificial intelligence.
Their use then depends on what data we have and
what tasks we want to solve. One group of possible
tools for the implementation of machine learning or
data analysis has quite a long been a neural network.
For the learning of neural networks are used two
types of learning methods. In unsupervised learning,
we only have unrated input data that we intend to
analyze in some way. This procedure is typically used
in the early stages of data analysis when we examine
the structure of the data, its internal relationships, and
its character.
In supervised learning, we train the model not
only with the input patterns but also with the required
output. These examples of the R
n
> R
m
transformation
are used to form internal rules or model parameter
settings. This approach is suitable for tasks with the
desired transformation function, e.g., classification.
If we use a neural network, our goal is to learn the
network to be able to respond appropriately to inputs
that have not been trained with (the principle of
generalization). Therefore, two disjoint data sets -
training and testing - are typically used. The process
of using the model can thus be divided into two main
phases - the setting phase (learning) and the
production phase (recall). The production phase is the
very reason for the existence of the model, in it, the
learned settings are used for processing of previously
unseen (test) input data.
A useful but nowadays not very frequently used
model is the so-called Kohonen map, which is
designed for unsupervised learning and therefore
cluster data analysis. The big advantage of the model
is a visual representation of network activity.
The author worked with Kohonen maps
previously, and this work showed the weaknesses of
learning algorithms (esp. 2D area fragmentation) and
the limitations of unsupervised learning. On the other
hand, the solved tasks revealed that Kohonen maps
are very comfortable for use in systems with
a required visual representation of learning dynamics.
That was the primary motivation for modifying of
Kohonen network model and extending its
capabilities presented in this paper.
Therefore, a modified learning algorithm and
a multi-level model structure based on Kohonen maps
were designed. The model was experimentally used
(as the proof of concept) for the task of economic data
processing (Vochozka et al., 2017) and preliminarily
tested (Jelínek, 2018). This paper aims to present the
actual state of the model and new experiments with it
to demonstrate its usefulness.
The following chapters are organized as follows.
In Chapter 2 is briefly discussed the related work.
Chapter 3 focuses on a description of the standard
Kohonen map model and shows the parameters of it.
Chapter 4 then concentrates on the description of the
modifications that were made, and Chapter 5 focuses
on experiments with the model conducted primarily
to verify the benefits of the proposed modifications.
584
Jelínek, J.
Kohonen Map Modification for Classification Tasks.
DOI: 10.5220/0007361405840591
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 584-591
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 RELATED WORK
When we talk about neural networks for the
implementation of machine learning or data analysis,
we usually mean a neural network based on an
artificial neuron model (McCulloch and Pitts, 1943).
Probably the greatest attention was given to models
of multi-layered perceptron (Rosenblatt, 1957) and
models based on this principle and using back
propagation method of learning (Rumelhart et al.,
1986).
The multilayer artificial neural network models
have their renaissance nowadays, primarily due to the
deep learning paradigm. This approach enables the
model to learn patterns on a different level of
abstraction. However, our approach is not of this
kind. The deep learning models use the same input set
all the time; our model reduces the set in the course
of the learning process.
A typical example of the slightly different neural
network model with unsupervised learning is the
ART2 algorithm and model (Carpenter and
Grossberg, 1987), which is capable of solving cluster
analysis task, and its operation can be modified by
adjusting the sensitivity of the model to differences in
input data. The higher the sensitivity, the more output
categories or clusters the system creates.
The Kohonen map (Kohonen, 1982) was
introduced in the 1980s as most basic models of
neural networks and is classified into a group of Self-
organizing maps. In some ways, the Kohonen map
can remind us of the ART2 model. The similarity lies
in the same requirements on input data (number
vectors). Similar is also the structure of the network,
which is essentially two-layer. However, Kohonen
map used 2D second layer and is focused on the visual
interpretation of the output and is therefore useful
both for the better understanding of the task and, e.g.,
for use in a dynamic online environment. An example
of such usage can be monitoring the state of the
system and its dynamics (Jelínek, 1992).
We can find also works concentrating on
hierarchical usage of Kohonen maps. In (Rauber et
al., 2002) the hierarchy is constructed dynamically in
the case of clustering very different input patterns into
one output cell. However, our model is based on
supervised learning and uses of extended information
about correct input classification for hierarchical
reduction of the input set. Modification of Self
Organizing Maps for supervised learning based on
RBF is shown in (Fritzke, 1994), our model uses a
different approach to that problem.
3 KOHONEN MAP
The core activity of the Kohonen map is assigning
input patterns to the cells of the second layer (i.e., the
output clusters representing by these cells) based on
the similarity of patterns.
The input layer of the Kohonen map is composed
of the same number of cells as the dimension n of the
input space R
n
is. The output layer is two-dimensional
and is also referred to as the Kohonen layer. This
structure was chosen concerning output visualization.
The input and output layers are fully interconnected
from the input to the output one with links whose
weights are interpretable as the centroid of the input
patterns cluster represented by the selected cell of the
output layer. The number of output layer cells is the
model parameter.
In the production phase, test patterns are
submitted at the input of the model. Their distance
(here the Euclidean one) is calculated from the output
layer cell centroids, and the input pattern is assigned
to the output cell, from which it has the smallest
distance. Assigning the input pattern to the output cell
can be visualized in the output layer as shown in
Figure 1.
Figure 1: Kohonen layer visualized according to the number
of patterns represented by cells (the more patterns, the
darker color).
The learning of the Kohonen map is an extension
of the production phase and is iterative. During it, the
values of the weights leading to the cell representing
the pattern are modified (the winning cell, the pattern
was assigned to it) so as the weights to the cells in its
neighborhood. The centroids of all these cells move
towards the vector representing the pattern according
to the formula (1).
(1)
Kohonen Map Modification for Classification Tasks
585

In it the α is the learning coefficient for the
winning cell, usually with the value from the interval
(0,1), c
i
is the ith coordinate of the cell's centroid, and
s
i
is the ith coordinate of the given input pattern.
The values of weights leading to the neighbor
cells in Kohonen layer are modified according to the
same formula, but with a different learning
coefficient value α
ij
adjusted to respect the distance of
a particular cell from the winning one:
(2)
Coordinates i and j are taken relative to the
winning cell with position [0, 0]. The distance d
ij
from
the winning cell in these relative coordinates is then
calculated as Euclidean one. The neighborhood of the
winning cell is defined by the limit value of d
ij
<=
d
max
.
The Kohonen map also includes a mechanism to
equalize the frequency of cell victory in the output
layer. For each of them, the normalized frequency of
their victories in the representation of the training
models f
q
is calculated with the normalized value in
the interval (0; 1). This is then used to modify the
distance of the pattern from the centroid.
(3)
In the formula (3), w
pq
is the modified pattern p
distance from centroid q, d
pq
the Euclidean distance
of them and K a global model parameter to limit the
effect of the equalization mechanism. The calculated
distance w
pq
is then used in the learning process. The
described mechanism ensures that during the learning
the weights of the whole Kohonen layer will
gradually be adjusted. The size of this layer together
with the number P of input patterns determines the
sensitivity of the network to the differences between
the input patterns.
It was also necessary to choose the appropriate
criterion for determining the end of learning (Jelínek,
2018). It is based on the average normalized distance
v in the 2D layer through which the pattern “shifts”
between the two iterations as shown in the formula
(4).
(4)
The distance is calculated on the square-shaped
Kohonen layer (with N cells on the side) between the
two iterations of the input set P. The v value is
compared to the maximum allowable value v
max
indicating the average maximum shift of patterns
allowed in one iteration. For the learned model with
a frequency equalization mechanism, the v will be
only a small value.
The main parameters of the Kohonen maps are the
learning coefficient α, the way of setting the decrease
of this coefficient for the cells around the winning
cell, the size of the neighborhood given by d
max
and
the number of cells in the two-dimensional output
layer. Also, the behavior of the model influences the
value v
max
and the coefficient K in formula (3) and its
possible change over time.
4 MODEL MODIFICATIONS
Due to previous experience with the use of Kohonen
maps and their application potential, the modified
learning algorithm and the multilevel structure of the
model were designed for them. This paper presents
the current state of the model together with
experiments aimed at an examination of the benefits
of the proposed modifications.
4.1 Modified Learning Method
The goal of learning is to get an adjusted model that
is capable of specific generalization, i.e., adequate
responses to patterns that have not been trained on.
The model described above used unsupervised
learning, modification using supervised learning
applicable to classification tasks will be introduced.
At the learning stage, the first change was in the
fact that after finding the winning cell in the Kohonen
layer, the model also stores the classification of the
training patterns that were assigned to it. With the
help of a known classification of the training set, for
each output cell we can determine the percentage (or
probability) rate of output categories in that cell,
which can be used in the production phase to evaluate
the test patterns in one of these two ways (Jelínek,
2018):
Probability evaluation. We select the most likely
category, so the test input pattern is always
classified. The assumption here is the same
distribution of a priori probabilities of output
categories.
Absolute evaluation. We only evaluate a test
pattern if it is assigned to a winning cell
representing only one category. A significant
percentage of input patterns can thus be left
unclassified.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
586

Both mentioned ways are used in the production
phase of the hierarchical model (absolute evaluation
in intermediate steps, probability evaluation in the
final step where it is necessary to evaluate all
patterns). So the modified model already uses at the
production stage additional output information.
It has also been shown in the course of model
experiments, that classification task on data with
complex transformation R
n
> R
m
tend to a state where
the same classified patterns are assigned to output
layer cells that are often very distant from each other.
This phenomenon affects the overall efficiency of the
model that must respect this fragmentation.
The effort was to limit this behavior by using the
output categorization directly in the model’s learning
phase. In this case, the model is trained on data that
are a conjunction of the original input and the desired
output (classification). For example, if we have a
classification task performing the transformation R
4
>
B
1
, where B
1
represents a one-dimensional binary
space (one binary coordinate), the model will be
taught on the input set R
4
∩ B
1
. In the production
phase, the last coordinate b
1
is not used in the
calculations because the input test vectors will not
contain it (their classification is not known).
The described modification significantly changes
the model settings, but it has turned out to be
a positive change under certain conditions. The
critical factor here is to what extent the output (often
binary) classification should be projected into the
training input. If this projection is in full a binary
value and inputs from R
4
are normalized to a range (0;
1), the model settings are distorted too much, and the
model is not capable of generalizing. Therefore, the
new reduction factor u was implemented to limit this
projection according to formula (5)
(5)
where
is the value of the input of the model
(preceded by the coordinates of the original input
from the R space) and b
x
is the original classification
(b
x
= 0 or b
x
= 1 for pure binary classification). The
factor u has a value from the interval (0; 1) and
represents the next parameter of the model.
4.2 Model with Hierarchy Structure
The fundamental change in the work with the
Kohonen map is its repeated use with a different
training set. This set can be, e.g., quite uneven
regarding the representation of output categories or
too large for the actual size of the Kohonen layer. The
modified model addresses this problem by gradually
reducing this set by eliminating correctly classified
training patterns at the end of each learning iteration.
In the next iteration is a new instance of the map
already learned with a training set containing only
problematic (not yet categorized) patterns. The
underlying idea of this approach is to use Kohonen
map internal mechanisms so that the map in every
step refines its classification capabilities.
Thus, in each model step, a separate Kohonen
map is used. After learning, the cells of the Kohonen
layer are analyzed, and it is examined whether only
one output category is assigned to the given cell. If
this is the case, we can say that the map can uniquely
and correctly classify these patterns in accordance
with the desired output and they can be excluded from
the training set (Figure 2). The successful
classification is considered as:
Basic classification. Assignment of the pattern to
a cell representing only patterns of the same
category.
Strict classification. Assignment of the pattern to
a cell according to the previous bullet and
additionally adjacent to only the same
(representing the same category) or empty cells
(not representing any pattern).
The selection of one of the above classification
methods is a parameter of the model.
Figure 2: Learning phase of the modified model (Vochozka
et al., 2017).
For the real use of the proposed model, two
criteria are crucial. The first one is the criterion of
learning termination in each step (level) of
hierarchical model learning. The criterion of the
maximum average shift distance between the 2D
layer cells defined in formula (4) was used.
The second criterion is that of the overall ability
of the whole set of learned sub-models to correctly
Training
set bigger then
limit?
Learn the model to the steady state
Store the learned model
Remove correctly
evaluated patterns
from training set
Initialize new Kohonen model
Start
Yes
No
Stop
Kohonen Map Modification for Classification Tasks
587
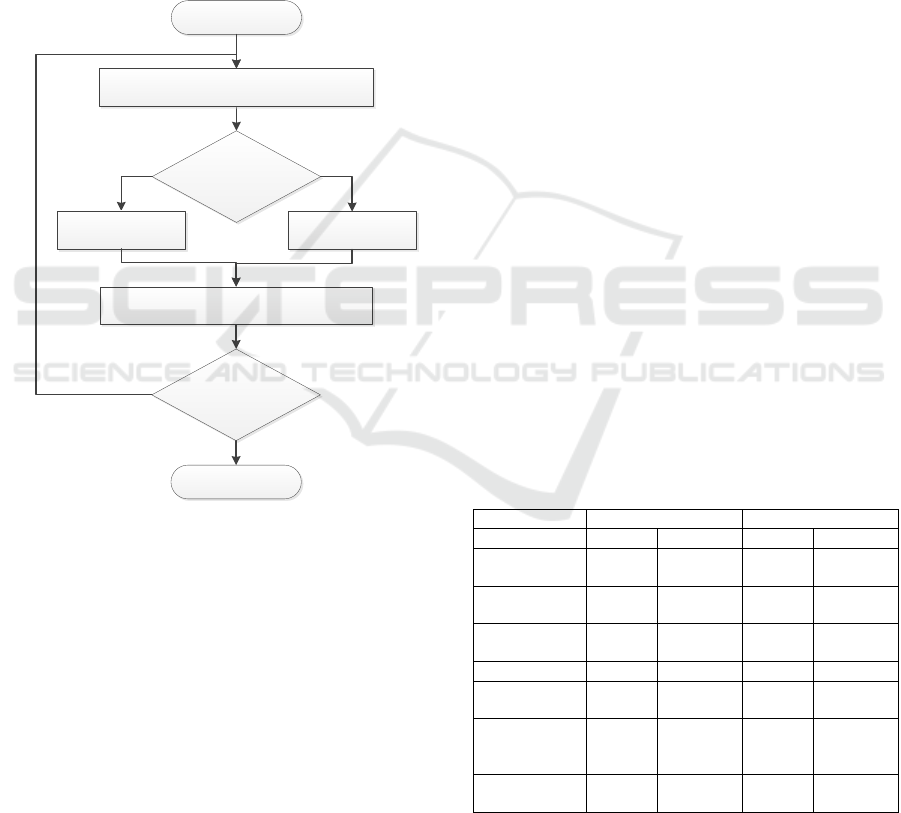
classify the training and later the test set of patterns
and can be implemented in several ways. The
minimum size of the training set, which still makes
sense for learning, was used in the model. Its higher
value reduces the number of hierarchical
classification steps but also limits the sensitivity of
the model.
In the production phase (Figure 3), the
classification method differs depending on whether
we are in the last hierarchical step or not. For the last
model in the hierarchical structure, the probability
evaluation is always used, where the pattern is
assigned to the most likely category resulted from the
learning process.
Figure 3: Production phase of the modified model
(Vochozka et al., 2017).
The modified model was set up using 11
parameters including both the Kohonen map original
ones (used in each iteration) and the other ones
characterizing the hierarchical model's operation.
5 EXPERIMENTS
The experiments carried out were aimed at
confirming the preliminary hypothesis that both
modifications of the Kohonen map model are
beneficial to the generalization quality and hence the
classification of the test set of patterns. The first
group of experiments was focused on model behavior
with artificial data; the second group concentrated on
a comparison of results on standard datasets.
The first dataset was created to represent a
complex nonlinear transformation from the input
space R
4
to the space B
1
(Jelínek, 2018). 10,000
training and test patterns were generated with random
values of the coordinates from R
4
space uniformly
generated in the interval (0; 1).
One test set and two training sets were created.
From the training sets one was for the classical
learning of the model (only inputs from R
4
) and the
other one extended with the output b
1
(the network
input dimension increased to R
5
where the fifth
coordinate was b
1
). Experiments have been optimized
for maximizing the number of adequately classified
test patterns.
As mentioned above, the model has adjustable
parameters that significantly affect its results.
Manually searching for optimal setup would be
a lengthy process, and therefore, a superstructure of
the model was used implementing an optimization
mechanism based on genetic algorithms.
Two variants of the model’s setting have been
researched. The first one focused on modified model
learning and worked with a single level of the
hierarchical model (as if the model was not
hierarchically modified). The second variant also
involved a hierarchical modification of the model
structure, and the maximum number of levels was
limited to 10.
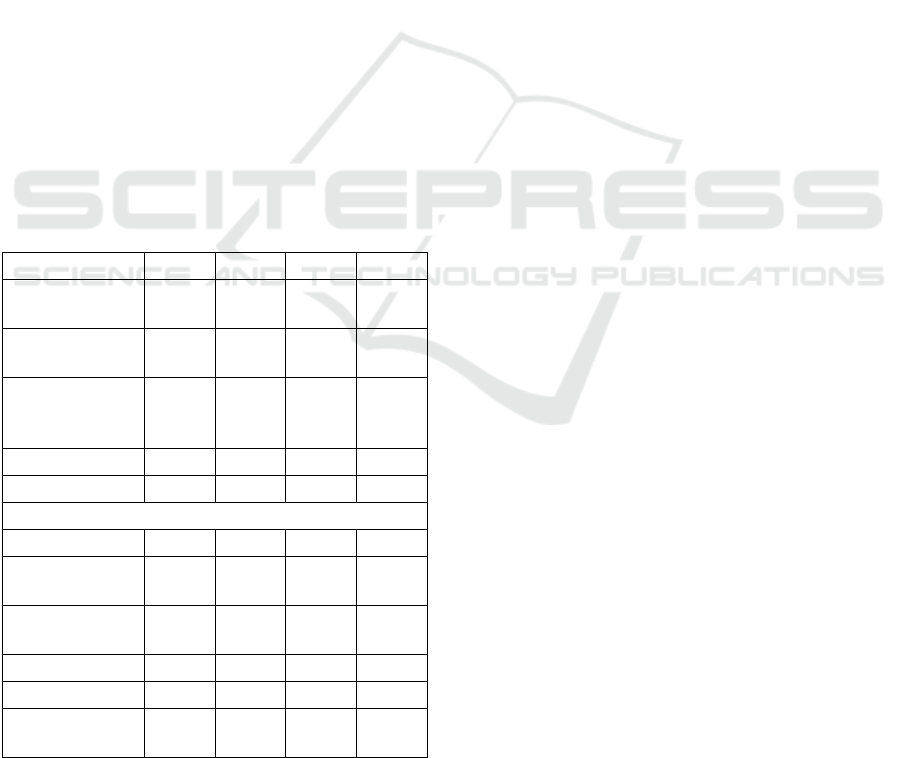
The best results are presented in the following
Table 1. These are the best from 406 experimental
settings of the model calculated by the genetic
algorithm for each variant.
Table 1: Best results for different settings (Jelínek, 2018).
Parameter
Max. 1 level
Max. 10 levels
Input
classic
extended
classic
extended
Number of
2D cells
40*40
35*35
40*40
35*35
Classification
criterion
basic
strict
strict
Strict
Reduction
factor
-
0.2
-
0.3
Real levels
1
1
10
3
Total learning
iterations
33
118
238
515
Test patterns
correctly
classified
7998
8472
7985
8643
Model
success [%]
79.98
84.72
79.85
86.43
It is clear from the table that the use of the
modified learning process brings a significant
improvement in the classification capabilities of the
network over the original learning process. The key
Load next Kohonen model in the hierarchy
Start
Yes
No
Stop
Is it the
last model?
Use probability
based evaluation
Use absolute
evaluation
Evaluate all patterns in testing set
Was it the
last model?
Yes
No
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
588

output is the finding that to achieve better results with
normalized data, the output values used for learning
(initially 0 and 1) must be reduced by the reduction
factor. Its appropriate setting was found by genetic
algorithm and was 0.2 or 0.3 (see the Reduction factor
row in Table 1).
The different number of 2D cells in different
scenarios also shows that model with extended input
set was able to obtain best results in the scenario with
fewer cells in the 2D layer, than the model with
standard input. The learning and overall performance
of the model with extended input were thus more
effective.
The sample visual outputs of the 2D network
shown in Figure 4 demonstrate the effect of modified
learning. The cells representing the patterns rated 0
are light grey, the patterns rated 1 are black. We get
"clean" colors for cells containing input patterns
included in only one category, for cells containing
patterns of different categories the color is mixed,
which respects the number of patterns in a cell with
different output categories. The influence of
additional output information on the final network
setting is quite apparent (right), and the fragmentation
from using the classical learning algorithm (left)
almost did not occur.
Figure 4: Influence of modified learning algorithm (Jelínek,
2018).
The results can still be improved by using
a hierarchical modification of the model; the added
value, however, is not so high in this case (quality
improvement of 1.71 %). The question, however, is
whether the appropriate data was used to maximize it.
In this case, the training set was evenly generated, but
the benefit could be more significant with data with
unequally represented output categories or different a
priori probabilities of them.
The second group of experiments was aimed at
comparing model results with other approaches on
standard datasets. They were obtained from the UCI
Machine Learning Repository (Dheeru and
Taniskidou, 2017). Three sets were selected with
different focus and number of input and output
attributes.
The first set is the Letter Recognition Data Set
(Lett) presented in (Frey and Slate, 1991). Input data
derive from black and white images of 26 alphabet
letters written in 20 different fonts; more images were
obtained by inserting random noise into existing ones.
Each input vector contains 16 values resulting from
the calculation of one-bit raster image values; the
output consists of a single value - the letter captured
on the figure. The set contains a total of 20 000
images. The rule-based classification method is also
presented in (Frey and Slate, 1991); the best rate of
correctly classified patterns is 82.7%.
To verify the presented model two disjoint sets
were created - for training (16000 patterns) and
testing (4000 patterns). The output was modified to
26 single-bit attributes (only one output value is one
for each letter, others are zero). Since the output is,
unlike the model description, not B
1
but B
26
, it was
necessary to select the winning attribute for the
output. The highest output attribute value does it.
Similar procedures also were used in the experiments
described below.
Experiments with this dataset did not reach the
expected values and did not achieve the reference
value mentioned in (Frey and Slate, 1991). The main
reason for this is difficult to identify, but it can be due
to the model parameter’s limits, especially in
conjunction with the R
16
> B
26
nonlinear
transformation. Inputs were pre-processed here,
which has reduced their number but has increased the
requirements on generalization capabilities of the
model too.
The second dataset was the Semeion Handwritten
Digit Data Set (Sem) described and used in
(Buscema, 1998). The set contains 1593 digital black
and white images in a 16x16 resolution. The output is
the only value identifying the digit. The article also
states the best classification using a combination of
several neural networks at 93.09%.
The input for our model was 256 binary attributes
(picture 16 x 16) and output ten binary values with the
same meaning as in the previous set and with the same
criterion for the best output selection. For the training
of the model, 1200 patterns were randomly selected,
for testing the remaining 393 ones (as recommended).
The results obtained with this dataset have already
met the expectations. The model was able to exceed
the reference value in the classification quality
(Buscema, 1998), and the influence of the extended
input data on the outputs of learning the model was
also positive.
The last used dataset was designed for testing of
accurate detection of room occupancy from data
obtained from several types of sensors. The set was
Kohonen Map Modification for Classification Tasks
589
published in (Candanedo and Feldheim, 2016) along
with an extensive set of experimental results. The data
are already divided into a training set of 8143 patterns
and two test sets (Occ 1 and Occ 2) of 2665 and 8926
patterns. The best-achieved classification results for
Occ 1 were 97.9% and for Occ 2 99.33%.
The original data were adapted for the use in our
experiment. The input was seven real normalized
values, and the output was one of two categories
(room occupied, empty).
The expected results were calculated for the
Occ 1 test set; the model again improved the best
result described in (Candanedo and Feldheim, 2016),
both for the classic and extended training set. For
Occ 2, however, the best classification was achieved
using standard input. This result has shown that the
model can achieve outstanding results even without
additional input information thanks to the hierarchical
structure of the model.
The worse outcome for the extended input can be
caused by the data character - fragmentation of
categories within the 2D layer was not significant,
and the model did not use this information. Instead, it
was forced to process more input data. Also, perhaps
a smaller size of the training set was not enough to
learn the given input-output transformation. The
results of the experiments are summarized in Table 2.
Table 2: Results of experiments on standard datasets.
Data Set
Lett
Sem
Occ 1
Occ 2
Best reference
result [%]
82.7
93,1
97.9
99.3
Best result with
classic input [%]
42.0
94.7
99.6
99.9 *
Best result with
extended input
[%]
55.0 *
96.9 *
100.0 *
97.8
Training vectors
16000
1200
8143
8143
Testing vectors
4000
393
2665
8926
Settings for best dataset result (*)
Input dimensions
16
256
7
7
Number of 2D
cells
20 * 20
40 * 40
10 * 10
20 *20
Classification
criterion
strict
strict
strict
strict
Reduction factor
0.1
0.6
0.3
0.7
Real levels
8
7
4
10
Total learning
iterations
2723
186
2887
2399
6 CONCLUSIONS
This paper introduces a modified learning algorithm
for the Kohonen map, which enables solving of
classification tasks with this network. The core of the
modification is the use of an extended training set
using the output categorization of the training patterns
for the learning process. Modifications were made
even in setting the criteria for completing model
learning (criterion of minimal pattern shift in the 2D
layer). A visual superstructure of the model was
developed to allow a detailed study of the dynamics
of the model setup process, and the obtained
knowledge could be used to better understanding of
the learning process and the nature of input data.
The second significant modification is the design
and description of the behavior of a hierarchical
classification model based on modified Kohonen
maps. The training set is gradually reduced during the
process of learning, increasing the sensitivity of the
network to differences in input data. An algorithm for
the production phase of the model was developed,
based on the learned Kohonen map sub-models.
The model was described by a set of parameters,
whose values had to be empirically determined.
Therefore, genetic algorithms have been used to find
optimal values.
Two groups of experiments were carried out with
the modified model. Experiments on artificial dataset
were focused on model in-depth behavior to verify
the benefits of the proposed modifications. They
confirmed the positive influence of the training set
extended by the outputs and the hierarchical structure
of the model for better performance of the
classification model. The overall classification
quality was improved by 6.58% on the generated data
with nonlinear randomly selected transformation
function R
4
> B
1
. The benefit of the hierarchical
structure would probably be higher when using data
unevenly covering the input space.
The experiments on standard datasets were used
to obtain result comparable with other research and to
show the practical usability of the model. Three
datasets were used in four experiments. In three of
them, the presented model exceeded the best
classification quality mentioned in the references.
Although the described model gives better results
with unprocessed data than literature references, there
is still the space for improvement of its concept. We
can find open questions in the definition and possible
dynamic modification of the neighborhood of the
winning cell, the type of distance calculation used in
the 2D layer, or the criteria for completing the
individual steps of the hierarchical learning process.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
590

It will also be necessary to examine the impact of the
input data structure on the results achieved.
REFERENCES
Buscema, M., 1998. Metanet*: The theory of independent
judges. Substance use & misuse, 33(2), 439-461.
Candanedo, L. M. and Feldheim, V., 2016. Accurate
occupancy detection of an office room from light,
temperature, humidity and CO2 measurements using
statistical learning models. Energy and Buildings, 112,
28-39.
Carpenter, G. A. and Grossberg, S., 1987. ART 2: Self-
organization of stable category recognition codes for
analog input patterns. In Applied optics, Vol. 26(23),
pp. 4919-4930.
Dheeru, D. and Taniskidou, E. K., 2017. UCI machine
learning repository. University of California, Irvine,
School of Information and Computer Sciences.
Frey, P. W. and Slate, D. J., 1991. Letter Recognition Using
Holland-style Adaptive Classifiers. In Machine
Learning, Vol 6 #2 March 91.
Fritzke, B., 1994. Growing cell structures—a self-
organizing network for unsupervised and supervised
learning. Neural networks, 7(9), 1441-1460.
Jelínek, J., 1992. Exceptional working states of power
grids. CTU - FEE, Prague. (in Czech).
Jelínek, J., 2018. Classification Model Based on Kohonen
Maps. In Proceedings of the Conference ACIT 2018,
Ternopil National Economic University, pp. 145-148.
Kohonen, T., 1982. Self-organized formation of
topologically correct feature maps. In Biological
cybernetics, Vol. 43(1), pp. 59-69.
McCulloch, W., S. and Pitts, W., 1943. A logical calculus
of the ideas immanent in nervous activity. In The
Bulletin of mathematical biophysics, Vol. 5(4), pp. 115-
133.
Rauber, A., Merkl, D. and Dittenbach, M., 2002. The
growing hierarchical self-organizing map: exploratory
analysis of high-dimensional data. IEEE Transactions
on Neural Networks, 13(6), 1331-1341.
Rosenblatt, F., 1957. The perceptron, a perceiving and
recognizing automaton Project Para. Cornell
Aeronautical Laboratory.
Rumelhart, D., E., Hinton, G., E. and Williams, R., J., 1986.
Learning representations by back-propagating errors. In
Nature, Vol. 323.9.
Vochozka, M., Jelínek, J., Váchal, J., Straková, J. and
Stehel, V., 2017. Using neural networks for
comprehensive business evaluation. H. C. Beck,
Prague, ISBN 978-80-7400-642-5 (in Czech).
Kohonen Map Modification for Classification Tasks
591
