Using Phase-type Models to Monitor and Predict Process Target

Compliance

Sally I. McClean

, David A. Stanford

, Lalit Garg

and Naveed Khan

School of Computing, Ulster University, Coleraine, BT52 1SA, U.K.

Department of Statistical & Actuarial Sciences, Western University, London, ON N6A 5B7, Canada

Faculty of Information & Communication Technology, University of Malta, Msida, Malta

School of Computing, Ulster University, Jordanstown, BT37 0QB, U.K.

Keywords:

Process Mining, Process Modelling, Phase-Type Models, Targets.

Abstract:

Processes are ubiquitous, spanning diverse areas such as business, production, telecommunications and health-

care. They have been studied and modelled for many years in an attempt to increase understanding, improve

efﬁciency and predict future pathways, events and outcomes. More recently, process mining has emerged with

the intention of discovering, monitoring, and improving processes, typically using data extracted from event

logs. This may include discovering the tasks within the overall processes, predicting future trajectories, or

identifying anomalous tasks. We focus on using phase-type process modelling to measure compliance with

known targets and, inversely, determine suitable targets given a threshold percentage required for satisfactory

performance. We illustrate the ideas with an application to a stroke patient care process, where there are mul-

tiple outcomes for patients, namely discharge to normal residence, nursing home, or death. Various scenarios

are explored, with a focus on determining compliance with given targets; such KPIs are commonly used in

Healthcare as well as for Business and Industrial processes. We believe that this approach has considerable

potential to be extended to include more detailed and explicit models that allow us to assess complex scenarios.

Phase-type models have an important role in this work.

1 INTRODUCTION

Processes are ubiquitous, spanning diverse areas

such as business, production, telecommunications and

healthcare, and have been studied and modelled for

many years in an attempt to increase understand-

ing, improve efﬁciency and predict future pathways,

events and outcomes. With the ever-increasing capa-

bility of computer systems to collect, process, store

and exchange data and the advent of the Big Data era,

the concept of Process Mining has emerged to form

a bridge between data mining and process modelling

(Van Der Aalst, 2012). Process Mining provides a

framework for service design, an under-pinning for

process improvement and a scientiﬁc basis for deci-

sion making. For example, a process can be con-

cerned with how an execution of process instances

should occur, where each execution instance of a busi-

ness process is identiﬁed as one process instance. A

process instance contains information on the tasks ex-

ecuted and the attributes observed during execution.

A process instance execution of the tasks is performed

according to the structure and deﬁnitions in the real-

world process. The process attributes typically con-

sist of information such as start time, end time, cus-

tomer name etc. and are stored in log ﬁles. Hence, a

log ﬁle typically provides an automatically produced

and time-stamped documentation of events relevant to

a particular system.

In general, process mining aims to discover, mon-

itor, and improve processes by extracting data from

event logs. This may include discovering the tasks

within the overall processes, predicting future pro-

cess trajectories, or identifying anomalous tasks and

task sequences. Such process mining activities can

build on standard approaches to data mining prob-

lems such as classiﬁcation, clustering, regression, as-

sociation rule learning, and sequence mining or more

recent approaches for Big Data, such as deep learn-

ing. However, if the structure of the process is known,

model-based approaches can also be useful for incor-

porating structural process knowledge into the analy-

sis and simplifying the problem. Thus process mining

can be use in various applications such as manufac-

McClean, S., Stanford, D., Garg, L. and Khan, N.

Using Phase-type Models to Monitor and Predict Process Target Compliance.

DOI: 10.5220/0007362200820090

In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 82-90

ISBN: 978-989-758-352-0

turing (van der Aalst et al., 2007), telecommunica-

tions (Taylor, 2015), ﬁnancial processes and health-

care (Agrawal et al., 1993).

Typically, a mathematical, symbolic or simulation

model is used to provide a simpliﬁed representation

of a process, where simulation involves using a math-

ematical model to imitate important aspects of the be-

haviour of the process and allow prediction and exper-

imentation to take place without having to disturb the

real-life set-up (McClean et al., 2011). Correctness,

conformance and performance are among the most

important issues in the study of complex processes

and systems, where process models are often used to

assess such issues. Correctness can describe quali-

tative aspects of a system, such as liveness, safety,

boundedness and fairness while compliance deter-

mines whether the observed process complies with

the theoretical one. Performance describes the quanti-

tative, dynamic, and time-dependent behaviour of the

process, such as its response time, system uptime and

throughput. In particular, our focus here is on deter-

mining whether a process is complying with targets.

For example, a business process may have targets to

fulﬁl orders in a timely manner, a hospital emergency

department often has targets to treat a set percentage

of patients within a given time limit, and service level

agreements specify agreed performance targets in the

Cloud.

Process algebras offer a means of formalising

systematic, hierarchical modelling of complex sys-

tems, but they are generally only used for qualita-

tive analysis (correctness) because they lack tempo-

ral and probabilistic semantics. Such Process Alge-

bras and Stochastic Process Algebras are high-level

modelling languages that can be used to model a sys-

tem. Stochastic extensions of process algebra fa-

cilitate both qualitative and quantitative performance

evaluation within a single, integrated modelling en-

vironment. Petri nets (Peterson, 1981) are high-

level formalisms that can also be used to model sys-

tems and are one of several mathematical modelling

languages for the description of distributed systems.

They are abstract formal methods, introduced in 1962

by Carl Adam Petri, for the description and analysis

of ﬂow of information and control in concurrent sys-

tems. Like industry standards such as UML, Petri nets

offer a graphical notation for stepwise processes that

include choice, iteration, and concurrent execution.

Unlike some industry standards, they have an exact

mathematical deﬁnition of their execution semantics,

with a well-developed mathematical theory for pro-

cess analysis and are graphically represented as col-

lections of places drawn as circles, transitions drawn

as rectangles, and arcs, which are drawn as arrows

between places. For example, Petri Nets have been

used for process support for continuous, distributed,

multi-party healthcare processes - by applying work-

ﬂow modelling to an anticoagulation monitoring pro-

tocol (McChesney, 2016). Such workﬂow modelling

has found relevance in the analysis and support of a

range of healthcare processes, e.g. Stochastic Petri

nets (Haas, 2006), including Queueing Petri nets, can

be used for quantitative performance analysis.

A Markov model is a special type of probabilis-

tic process model used to model systems where it is

assumed that future states depend only on the cur-

rent state, and not on previous events (the Markov

property). This assumption facilitates predictive mod-

elling on an individual basis (Garg et al., 2012) and

probabilistic forecasting for groups of individuals

traversing a process in parallel or during a given time

period (Gillespie et al., 2016). For example, we might

predict the most likely trajectory through the process

for a speciﬁc customer or the anticipated overall load

on a section of the total process. Higher order Markov

models may also be used if the Markov assumption

is found to be unrealistic. Continuous-time Markov

Chains (CTMCs) are also commonly used in stochas-

tic modelling where state durations are described by

exponential distributions (the Markov property). A

multi-phase (Markov) approach to process manage-

ment facilitates the study of both the speciﬁc phases

(tasks) of a process and the overall journey. In this

way, mathematical models can be developed for the

whole process with the objective of optimising perfor-

mance criteria such as waiting times, costs, or Quality

of Service goals. Such models have also been used to

ﬁnd interesting pathways (Garg et al., 2009), where

”interesting” can be interpreted, inter alia, as either

frequent, or infrequent instances.

In this paper we show how phase-type models can

be used to predict compliance of a process with com-

pletion targets. The prediction may be ab initio or

conditioned on the process already having completed

a given amount of time or reached a known termina-

tion state. A number of formulae are derived and the

ideas are illustrated for a healthcare process concern-

ing targets for patient pathways through health and

community phases.

2 BACKGROUND

Markov models have proved to be a useful repre-

sentation of process behaviour in many contexts, in-

cluding call centres (Dudin et al., 2016), sensor net-

works (Dudin and Lee, 2016), telecommunications

(Vishnevskii and Dudin, 2017), production modelling

Using Phase-type Models to Monitor and Predict Process Target Compliance

(Barron et al., 2016) and healthcare (Gillespie et al.,

2016). Phase-type models are a type of Markov model

with a number of transient states (or phases) and a sin-

gle absorbing state. Such models can be used to pre-

dict individual behaviour or to assess future resource

needs and costs. They are intuitively appealing as

they conceptualise process progression, for instance,

through acute care, into treatment, and on to rehabil-

itation. A phase type distribution (PHD) describes a

non-negative random variable (generally a duration)

generated by a Markov model where the PHD rep-

resents the duration from adnission to the transient

states of the Markov process until absorption in one of

the recurrent states. In particular, Coxian phase type

distributions (C-PHDs) are a special case of PHDs

in which a process always starts in the ﬁrst transient

state, and only sequential transitions are allowed be-

tween transient states; transition from any state to the

absorbing state is also possible (Figure 1). PHDs pro-

vide a simple description of a variable such as length

of stay (LOS) in hospital, duration of a particular ac-

tivity of daily living, or duration from order placement

to completion in a business process. PHDs also typi-

cally have the advantage of ease of parameter estima-

tion (Garg et al., 2012). In particular, Coxian phase-

type models (C-PHDs) work well for a range of set-

tings and scales, including hospitals (Fackrell, 2009),

(Tang et al., 2012), (Marshall and Zenga, 2012), and

(Grifﬁths et al., 2013), community care (Xie et al.,

2006), emergency services (Knight and Harper, 2012)

and patient activity recognition (Duong et al., 2009).

They are also intuitively appealing as, for example,

we can think of a patient as progressing through vari-

ous phases of hospital, social or community care such

as acute care, treatment, rehabilitation and long stay

(Figure 1).

Figure 1: Coxian Phase-type transition distribution.

From the technical point of view, the advantages

of using the PHDs are (i) their mathematical tractabil-

ity; (ii) parsimonious parameterization, in the case

of C-PHDs, - a general phase-type representation re-

quires a large number of parameters, with associated

difﬁculties in estimation; (iii) ﬂexibility - any distri-

bution can be approximated by a phase-type distribu-

tion with an appropriate number of parameters; and

(iv) the ease with which such representations can be

migrated to a more complex setting.

Our previous work (Garg et al., 2012) developed

a framework that classiﬁes the patient stays based on

identifying homogeneous groups, or classes, in terms

of their LOS distributions; where different admission

probabilities pertain to different classes. Classes are

characterized using appropriate covariates, which in

our case were gender, age, diagnosis and outcome.

Patients in the various classes follow separate path-

ways, with correspondingly different admission prob-

abilities for each class. Another feature of our frame-

work is that, unlike earlier work, we allow for a num-

ber of absorbing states - for example, these might

be the patient’s normal residence, a private nursing

home (PNH), or death. Such an approach allows us

to extend phase-type models to describe community

as well as hospital states thus modelling an integrated

system of stroke patient care, rather than sub-systems

of the overall care process. Generally speaking, we

can think of this model as a mixture of parallel C-

PHDs, with multiple absorbing states.

Hidden Markov models (HMMs) are similar to

phase-type models in that the system being modelled

is also assumed to be Markovian, with unobserved

(hidden) states. However, HMMs are generally more

focussed on the pathway through the Markov system

while phase-type models have a particular relevance

to duration in the transient states and have their ori-

gins in queueing theory where performance, in terms

of timeliness, is central. HMMs are especially known

for their application to temporal pattern recognition

such as speech processing (Rabiner, 1989). They

have also been extended to include parallel and hier-

archical structures, for example the hierarchical hid-

den Markov model (HHMM) (Fine et al., 1998). Such

approaches have already been used in healthcare set-

tings, in particular for patient temporal pattern discov-

ery from Australian medical claims data (Tsoi et al.,

2005). The HHMM here proﬁles the patients into sub-

behavioural groups based on similar temporal proﬁles

and medical behaviours. Another important health-

care use of HHMMs has been for activity recognition,

speciﬁcally aimed at developing automated reminder

systems for patients with dementia (Youngblood and

Cook, 2007). Here, repeated behaviours in sensorised

smart homes are observed and categorized into pat-

terns that represent the inhabitant behaviour. As for

patients moving through a health system, home-based

activities also move through a process, comprising a

sequence of smaller steps, or phases, such as treat-

ment or rehabilitation in the former case or instrumen-

tal activities of daily living (IADLs), such as taking

pills or making a cup of tea, in the latter case.

In this paper, based on our previous work (Faddy

and McClean, 2005),(Jones et al., 2018), we incorpo-

rate the covariates into the model by allowing the tran-

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

sition rates between states of the underlying Markov

model to depend explicitly on appropriate covariates.

Based on process data, the model can then be pruned

by eliminating those covariates which are not statisti-

cally signiﬁcant, on the basis of likelihood-based sta-

tistical tests. The speciﬁc functional form of this co-

variate model will be described in the next section.

We note that the approach proposed here is to use

a PHD, which may, or may not be, Coxian (C-PHD).

However in what follows we illustrate the ideas with

a speciﬁc healthcare case study where the patients

progress through successive states of health, so we as-

sume that they follow a C-PHD. Also, in general we

propose to incorporate covariates by modelling them

through an explicit functional dependency for the in-

put, exit and transition probabilities. This is also il-

lustrated in the healthcare case study.

3 PHASE-TYPE MODELS

3.1 The Basic Phase-type Model

As in (McClean et al., 2011) we employ a phase-

type model for process planning, based on Markov

phase-type models. Thus the phase-type model can

allow us to easily implement and quickly evaluate

changes in process circumstances. Frequently a C-

PHD is used and is intuitively appealing as we can

think of the process as progressing through sequen-

tial phases, without loops, before completion (Figure

1). As discussed, C-PHDs provide a simple descrip-

tion of a variable such as length of stay in hospital or

duration of an activity of daily living and also have

advantages over other types of PHDs, such as ease of

parameter estimation.

We begin by considering a basic C-PHD and then

extend the model to a general PHD with entry to any

transient state, and k absorbing states. We thus ini-

tially consider a system of k+1 states (or phases) and

a Markov stochastic process deﬁned according to the

transition probabilities deﬁned for i = 1,2,...,k − 1

P{X(t + δt) = i + 1|X(t) = i} = λ

δt + o(δt);

P{X(t + δt) = k + 1|X(t) = i} = µ

δt + o(δt).

(1)

(The latter of these equations applies as well for

i = k.) Here the rates λ

,λ

,..., λ

k−1

describe se-

quential transitions between phase S

and the subse-

quent phase S

i+1

while µ

,µ

,..., µ

describe transi-

tions from phase S

to the absorbing state S

k+1

for

i = 1, 2,. .., k (see Figure 1). If µ

> 0 for i = 1, 2,..., k

then phases S

,..., S

are transient while phase

k+1

is the unique absorbing state. Writing the ad-

mission vector as

= (α

,α

,..., α

) (2)

where α

denotes the probability of admission to

phase S

;i = 1,2,... ,k, we obtain the probability

density function (p.d.f.) for the distribution of time

until absorption as

f (x) = α

exp(Tx)t

. (3)

In the foregoing formula, t

= −T1 represents

the absorption rate vector from the various transient

states. For a C-PHD with k transient phases, the in-

ﬁnitesimal generator (rate) matrix T is null except for

the main diagonal and prime super-diagonal, which

are deﬁned for i = 1,2,.. ., k − 1 by

= −(λ

+ µ

); T

i,i+1

= λ

. (4)

Furthermore, T

= −µ

. Integrating the p.d.f, one

obtains the cumulative distribution function

(y;α,T) = 1 − α

exp(Ty)1;y ≥ 0. (5)

which represents the probability of meeting a given

time target y. Conversely, the probability of missing a

time target y is given by

(y;α,T) = α

exp(Ty)1;y ≥ 0. (6)

In this way, it is possible for us not only to quan-

tify the relative likelihoods of compliance and ex-

ceedance, but also to formulate sub-tending network

paths for the corresponding actions that would arise

in each of these cases. Using the same approach as

(Jones et al., 2018), we can ﬁnd the conditional prob-

ability of meeting (or alternatively, missing) a given

target at time y give that a known amount of time (say,

d) has already elapsed. The chance of the former is

given by

X|X>d

(y;α,T) = 1 −

exp(Ty)1

exp(Td)1

;

y ≥ d, (7)

while the chance of the latter is given by

X|X>d

(y;α,T) =

exp(Ty)1

exp(Td)1

;

y ≥ d. (8)

In like fashion, conditional means can be computed

by integrating the corresponding conditional densities

over the appropriate regions.

Using Phase-type Models to Monitor and Predict Process Target Compliance

4 CASE STUDY: STROKE CARE

In many cases there are several possible absorbing

states for termination of a process, corresponding

to different targets, In previous work we have ex-

tended the basic phase-type models to accommodate

such multiple absorbing states (McClean et al., 2011),

(Jones et al., 2018). This model pertains to care of

stroke patients using data collected over a period of 5

years. In this case we have identiﬁed 4 transient states

of the phase-type model which relate to different

types of stroke with differing severity and correspond-

ing admission probabilities for decreasing severity of

stroke. The model allows for three different types of

stroke: haemorrhagic (the most severe, caused by rup-

tured blood vessels that cause brain bleeding), cere-

bral infarction (less severe, caused by blood clots) and

transient ischemic attack or TIA (the least severe, a

mini-stroke caused by a temporary blood clot). In

this setting, there are three possible ways in which

the hospital stay can conclude: 1) upon the patient’s

demise, 2) with a transfer to a nursing home, and 3)

with a return to the patient’s usual residence. These

differing possibilities can be handled readily by re-

placing the absorption rate vector t

by a matrix of

distinct absorption rates t

deﬁned as follows:













. (9)

In (9), each column of the matrix corresponds to a dis-

tinct concluding event for the hospital stay (demise,

nursing home, and usual residence, respectively)

while each row refers to the particular transient phase

from which the absorption occurred. Each such phase

corresponds to a particular recovery stage from which

absorption occurred, with the ﬁrst corresponding to

the sickest individuals, and the last to the least sick.

The interested reader is directed to (Jones et al., 2018)

where the rational behind the four transient states and

other details are fully described.

The univariate density of time to absorption may

still be written as before, or alteratively as

(y|α,T) = α

exp(Ty)t

, y ≥ 0 . (10)

which is equivalent. If one wishes instead to deter-

mine the joint density of absorption together with

a particular concluding event (say, the jth possible

cause), the corresponding formula is given by

(y|α,T) = α

exp(Ty)t

, y ≥ 0 (11)

where e

denotes a column vector with unity in the

jth position, and zeroes elsewhere.

In this case study data were collected over a 5 year

period, on admission date, length of stay in hospi-

tal, diagnosis and discharge destination, and other co-

variates, such as age on admission and gender. The

transition rates of the model comprise both those that

depend upon the age and stroke type of the patient,

and those which do not depend on age; these depen-

dencies were previously established using statistical

analysis.

For i = 1,2, let λ

(x) be the transition intensity

from phase i to phase i + 1 for a patient who is age

x, where λ

(x) = exp(γ

+ β

x). Also, let p(x) repre-

sent the probability that a TIA stroke patient age x is

in recovery phase 4 upon admission to hospital (rep-

resenting the less severe TIAs). Consequently, a TIA

patient starts in phase 3 with probability 1 − p(x). We

assume that p(x) = exp{−exp(θ

+θ

x)}. The expo-

nential functions used in modelling λ

(x) and p(x) are

fairly standard, and ensure that their values are con-

strained to the required ranges. These functions arise

when using the log link and complementary log-log

link functions in generalized linear models (Dobson

and Barnett, 2008). As indicated in Figure 1, it is as-

sumed that µ

= ν

= 0.

We note that the routes missing from the dia-

gram in Figure 1, and corresponding zero parameters,

are determined by statistical testing based on Likeli-

hoods; for further details see (Jones et al., 2018).

4.1 Interventions to Increase

Compliance Likelihood

Another beneﬁt of the phase-type approach is that

it allows the user to explore the probabilistic conse-

quences of interventions to enhance the chances of

compliance, provided that the sequence of tasks in-

volved in the intervention can likewise be described

by a C-PHD process. Using such an approach, in

Section 3.1 we have provided formulae to predict the

probability of compliance with a given completion

target, assuming that current patterns (i.e. parameter

estimates) continue. However, an important follow-

on question is clearly: can we intervene to modify or

“restart” the process at the current point in time and

can we then predict the new probability of meeting

the target.

Following the logic behind equations (7) and

(8), the vector for the conditional probability of be-

ing in the various transient states at the interven-

tion instant d is readily seen to be given by ω

exp(Td)/[α

exp(Td)1].

Now let S denote the part of the inﬁnitesimal gen-

erator restricted to the transient states for the en-

hanced C-PHD process including the intervention

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

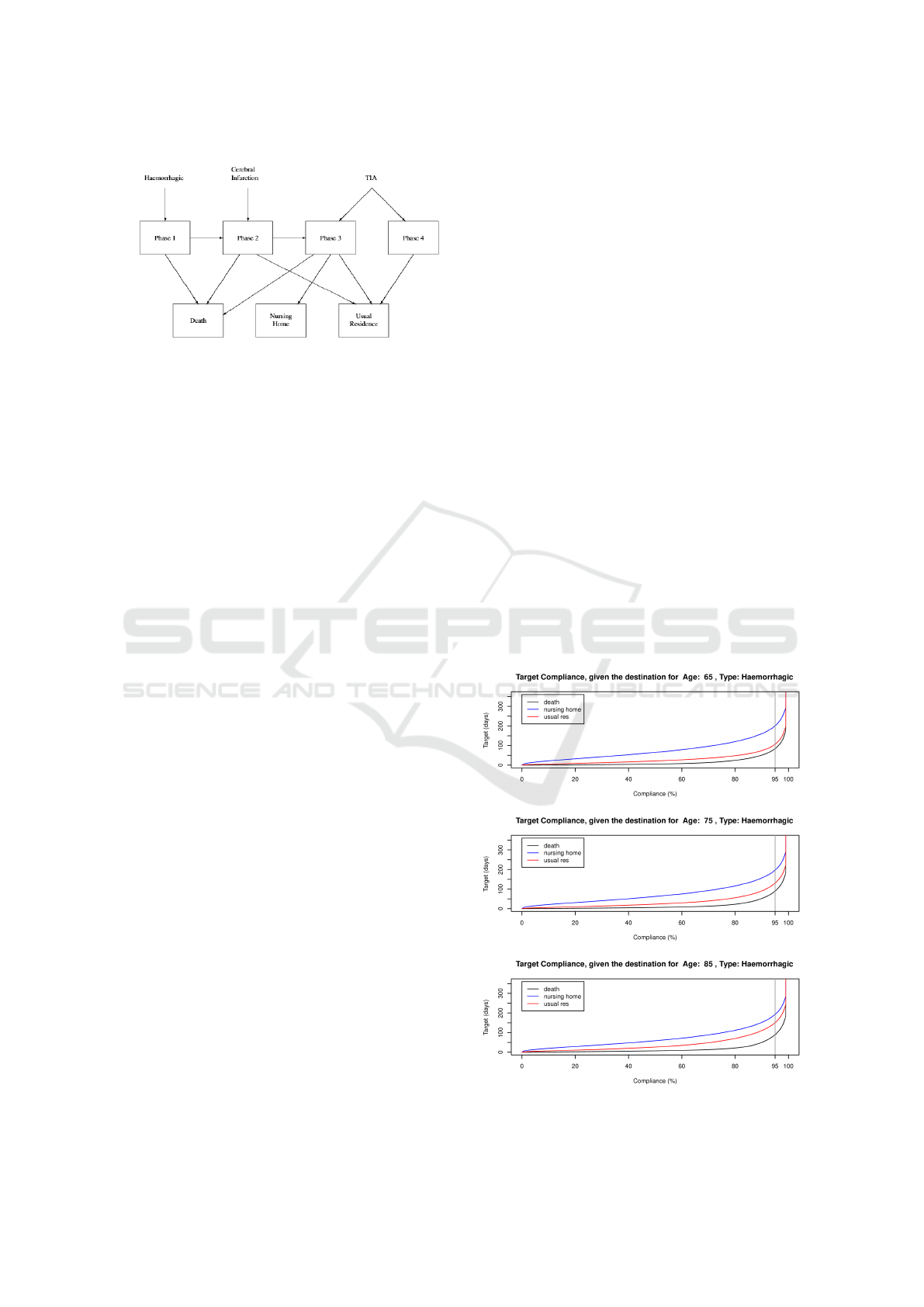
Figure 2: Stroke care transition diagram.

(which need not entail the same number of transient

states as the original process). The probability vec-

tor β for starting the enhanced process in the various

possible states β denote the vector of starting the en-

hanced process at time d in the various transient states

will be a direct function β = f (ω), such as perhaps

merely repositioning the components of ω in some

enlarged state space.

The corresponding probability of compliance by

time y given an intervention time d is then given by

X|X>d

(y;β,S) = 1 − β

exp(S(y − d))1;

y ≥ d, (12)

The other extensions can be found in like fashion. We

note here that the inverse problem of determining a

suitable target value, given a desired service level can

also be derived from this equation, by solving to ﬁnd

the target y for a .given value of F. Here F can be

thought of corresponding to a service level agreement,

where, for example, we may require 95% of jobs to

be completed within a given time. Although we can-

not solve equation (5) explicitly for y, we can instead

use a numerical approach, such as Newton-Raphson

where the estimate of y is given at the n+1st iteration

n+1

is given by:

n+1

= y

− F(y

)/F

) where

(y) = α

exp(Ty)T1;y ≥ 0, (13)

4.2 Estimating the Model Parameters

As discussed, a phase-type model typically contains

a number of parameters, representing the initial en-

trance probabilities to each state, the transition rates

between transient states and exit transition rates from

each state to the absorbing state. In addition there

are often covariates, both static (process covariates or

features) and associated dynamic covariates with in-

dividual log ﬁles. In process mining, these covariates

are extracted from the logs and can be used to im-

prove the model. Two common strategies are (1) to

use the covariates to cluster the process instances and

then use a cluster speciﬁc model to predict outcomes

and (2) to explicitly model the parameters as functions

of the covariates, thus facilitating more parsimineous

models and less data-consuming estimation (McClean

et al., 2011).

In our case study we employ the latter strategy;

this is partly due to inherently limited data in such

healthcare applications (Jones et al., 2018). The

model which we eventually decided upon represents

the smallest one to allow for sufﬁcient distinction of

the various types of stroke. It also has the desir-

able statistical property of being more parsimonious

in terms of the number of parameters to be estimated

than a larger model. Its state transition diagram is

shown in Figure 2.

4.3 Results and Discussion

Fig. 3, 4 and 5 present the choice of target as a

function of the probability of compliance for different

types of stroke and each of the modes of discharge:

death, nursing home, and usual residence. In the case

of haemorrhagic strokes,we see that, for a given prob-

ability of compliance, the target should be lowest,

with TIAs highest, representing the fact that haemor-

rhagic strokes are most severe and TIAs least severe.

Figure 3: Number of days to achieve the target compliance

for patients with Haemorrhagic stroke.

Using Phase-type Models to Monitor and Predict Process Target Compliance

Figure 4: Number of days to achieve the target compliance

for patients with Cerebral Infarction stroke.

Figure 5: Number of days to achieve the target compliance

for patients with TIA stroke.

Similarly, for discharge destination, for a given tar-

get, the probability of compliance should be lowest

for discharge to the usual residence, as an extended

period is required for such patients to pass through

the corresponding recovery phases before discharge.

This is reﬂected in the observation that for a given

probability of compliance, the target of such patients

is lowest. In the ﬁgure we have highlighted the targets

for 95% compliance as this is a typical value.

Overall, modelling can be used to characterise the

whole system of stroke patient care and the associ-

ated clinical pathways, integrating hospital and com-

munity services to provide tools for describing current

services, assessing the impact of proposed changes,

and predicting resource requirements in future sce-

narios. Our previous paper (Jones et al., 2018) fo-

cussed on developing models that use routinely avail-

able hospital discharge data to describe patient ad-

missions, movements through hospital, and discharge

modes. Such models can be used to facilitate perfor-

mance modelling, bed occupancy analysis, capacity

planning, and prediction of patient numbers in differ-

ent components of the overall care system. By using

such a model to quantify resource consumption, and

costs of such proposed interventions, we can com-

pare different solutions and determine optimal strate-

gies. Stroke patient care thus provides an important

paradigm example for healthcare process modelling,

as there are many possible interventions which strad-

dle hospital and community services. However, for

such models to be effective, a robust estimation pro-

cess and thorough evaluation is essential. Overall

length of stay in hospital and compliance with re-

lated targets are key performance indicators for hos-

pital services, and it is therefore useful to assess the

impact of key interventions, in terms of their impact

on the achievement of length of stay targets.

5 SUMMARY AND FURTHER

WORK

This paper has focussed on using process mining

to extract data on processes and learn appropriate

parameters for phase-type models where we focus

on using such models to measure compliance with

known targets or determine suitable targets given a

threshold percentage required for satisfactory perfor-

mance. We have described an application of such

phase-type models to stroke patient care, where there

are multiple outcomes for patients, such as discharge

to normal residence, nursing home, or death. Based

on these data, various scenarios have been explored,

with a focus on determining compliance with given

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

targets; such KPIs are commonly used in Healthcare

as well as for Business and Industrial processes.

Our current framework represents initial work to-

wards developing integrated models for processes,

with the aim of supporting cohesive management and

planning. However, we believe that it also has con-

siderable potential to be extended to include more de-

tailed and explicit models that allow us to assess com-

plex scenarios involving interactions between pro-

cesses. Also, our current analytic model has the ad-

vantage that the results are based on routinely avail-

able data. Another important aspect of extending our

current framework is to consider the distributions and

moments of numbers of process instances complying

with targets for multiple absorbing states, including

processes using Poisson arrivals to describe streamed

data of independent instances; costs can also be asso-

ciated with various options within the model. We plan

to explore such options in further work.

The experience gained and techniques learned are

likely to be relevant to business processes in gen-

eral. Phase-type models have an important role in this

work.

ACKNOWLEDGEMENT

This research is partly supported by BTIIC (BT Ire-

land Innovation Centre), funded by BT and Invest

Northern Ireland and by the Natural Sciences and En-

gineering Research Council of Canada (NSERC).

REFERENCES

Agrawal, R., Imieli

nski, T., and Swami, A. (1993). Min-

ing association rules between sets of items in large

databases. In Acm sigmod record, volume 22, pages

207–216. ACM.

Barron, Y., Perry, D., and Stadje, W. (2016). A make-to-

stock production/inventory model with map arrivals

and phase-type demands. Annals of Operations Re-

search, 241(1-2):373–409.

Dobson, A. J. and Barnett, A. G. (2008). An Introduction to

Generalized Linear Models. Chapman and Hall.

Dudin, A., Kim, C., Dudina, O., and Dudin, S. (2016).

Multi-server queueing system with a generalized

phase-type service time distribution as a model of call

center with a call-back option. Annals of Operations

Research, 239(2):401–428.

Dudin, S. A. and Lee, M. H. (2016). Analysis of single-

server queue with phase-type service and energy har-

vesting. Mathematical Problems in Engineering,

2016.

Duong, T., Phung, D., Bui, H. H., and Venkatesh, S.

(2009). Efﬁcient duration and hierarchical modeling

for human activity recognition. Artiﬁcial intelligence,

173(7-8):830–856.

Fackrell, M. (2009). Modelling healthcare systems with

phase-type distributions. Health care management

science, 12(1):11.

Faddy, M. and McClean, S. (2005). Markov chain mod-

elling for geriatric patient care. Methods of informa-

tion in medicine, 44(03):369–373.

Fine, S., Singer, Y., and Tishby, N. (1998). The hierarchi-

cal hidden markov model: Analysis and applications.

Machine learning, 32(1):41–62.

Garg, L., McClean, S., Meenan, B., and Millard, P. (2009).

Non-homogeneous markov models for sequential pat-

tern mining of healthcare data. IMA Journal of Man-

agement Mathematics, 20(4):327–344.

Garg, L., McClean, S. I., Barton, M., Meenan, B. J., and

Fullerton, K. (2012). Intelligent patient management

and resource planning for complex, heterogeneous,

and stochastic healthcare systems. IEEE Transactions

on Systems, Man, and Cybernetics-Part A: Systems

and Humans, 42(6):1332–1345.

Gillespie, J., McClean, S., Garg, L., Barton, M., Scotney,

B., and Fullerton, K. (2016). A multi-phase des mod-

elling framework for patient-centred care. Journal of

the Operational Research Society, 67(10):1239–1249.

Grifﬁths, J. D., Williams, J. E., and Wood, R. (2013).

Modelling activities at a neurological rehabilitation

unit. European Journal of Operational Research,

226(2):301–312.

Haas, P. J. (2006). Stochastic petri nets: Modelling, stabil-

ity, simulation. Springer Science & Business Media.

Jones, B., McClean, S., and Stanford, D. (2018). Modelling

mortality and discharge of hospitalized stroke patients

using a phase-type recovery model. Health care man-

agement science, pages 1–19.

Knight, V. A. and Harper, P. R. (2012). Modelling emer-

gency medical services with phase-type distributions.

Health Systems, 1(1):58–68.

Marshall, A. H. and Zenga, M. (2012). Experimenting with

the coxian phase-type distribution to uncover suitable

ﬁts. Methodology and computing in applied probabil-

ity, 14(1):71–86.

McChesney, I. (2016). Process support for continuous,

distributed, multi-party healthcare processes-applying

workﬂow modelling to an anticoagulation monitoring

protocol. In International Conference on Ubiquitous

Computing and Ambient Intelligence, pages 255–266.

Springer.

McClean, S., Barton, M., Garg, L., and Fullerton, K.

(2011). A modeling framework that combines markov

models and discrete-event simulation for stroke pa-

tient care. ACM Transactions on Modeling and Com-

puter Simulation (TOMACS), 21(4):25.

Peterson, J. L. (1981). Petri net theory and the modeling of

systems.

Rabiner, L. R. (1989). A tutorial on hidden markov models

and selected applications in speech recognition. Pro-

ceedings of the IEEE, 77(2):257–286.

Tang, X., Luo, Z., and Gardiner, J. C. (2012). Model-

ing hospital length of stay by coxian phase-type re-

Using Phase-type Models to Monitor and Predict Process Target Compliance

gression with heterogeneity. Statistics in medicine,

31(14):1502–1516.

Taylor, P. (2015). Autonomic Business Processes. PhD the-

sis, University of York.

Tsoi, A. C., Zhang, S., and Hagenbuchner, M. (2005). Pat-

tern discovery on australian medical claims data-a sys-

tematic approach. IEEE Transactions on Knowledge

& Data Engineering, (10):1420–1435.

Van Der Aalst, W. (2012). Process mining: Overview and

opportunities. ACM Transactions on Management In-

formation Systems (TMIS), 3(2):7.

van der Aalst, W. M., Reijers, H. A., Weijters, A. J., van

Dongen, B. F., De Medeiros, A. A., Song, M., and

Verbeek, H. (2007). Business process mining: An in-

dustrial application. Information Systems, 32(5):713–

732.

Vishnevskii, V. M. and Dudin, A. N. (2017). Queueing sys-

tems with correlated arrival ﬂows and their applica-

tions to modeling telecommunication networks. Au-

tomation and Remote Control, 78(8):1361–1403.

Xie, H., Chaussalet, T. J., and Millard, P. H. (2006).

A model-based approach to the analysis of patterns

of length of stay in institutional long-term care.

IEEE Transactions on Information Technology in

Biomedicine, 10(3):512–518.

Youngblood, G. M. and Cook, D. J. (2007). Data mining

for hierarchical model creation. IEEE Transactions on

Systems, Man, and Cybernetics, Part C (Applications

and Reviews), 37(4):561–572.

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems