A Voting Argumentation Framework: Considering the Reasoning behind

Preferences

Nikos Karanikolas

, Pierre Bisquert

and Christos Kaklamanis

1,3

Department of Computer Engineering and Informatics, University of Patras, Greece

INRA IATE/INRIA GraphIK, Montpellier, France

Computer Technology Institute and Press “Diophantus” (CTI), Patras, Greece

Keywords:

Social Choice, Argumentation, Collective Decision-Making.

Abstract:

One of the most prominent ways to reach an acceptable collective decision in normal group settings is the

employment of routines and methods of social choice theory. The classical social choice setting is the fol-

lowing: each agent involved in the decision expresses her preferences about a given set of alternatives in the

form of a linear order on them. Then, the group’s aggregated decision is the outcome of the application of

a voting rule to the input’s preferences. However, there are instances where social choice on its own cannot

provide proper solutions. For example, there are decision problems where the outcome has to be based on

the reasoning behind agents’ preferences, rather than the unjustiﬁed preferences itself. Hence, our research

motivation is the practical case where agents’ rationale is needed for the decision outcome. In this paper, we

explore how the agents’ rationale can be formulated inside the classical voting setting. Therefore, we propose

a decision-making procedure based on argumentation and preference aggregation which permits us to explore

the effect of reasoning and deliberation along with voting for the decision process. We quantify the delibera-

tion phase by deﬁning a new voting argumentation framework, that uses vote and generic arguments, and its

acceptability semantics based on the notion of pairwise comparisons between alternatives. We prove for these

semantics some theoretical results regarding well-known properties from Argumentation and Social Choice

Theory.

1 INTRODUCTION

Collective decision-making in the context of multi-

agents systems is a well-studied problem where many

possible research approaches have been proposed in

the literature for solving it. An overview of the

research approaches can be found in this survey

(Bulling, 2014). The procedure followed to reach a

group decision is a complex task, in which there are

many parameters that affect decision makers judge-

ment. The key to making a “good” collective decision

is knowing and hence, the agents (decision-makers)

should have full knowledge on the different parame-

ters that entail collective decisions.

In the decision-making literature it is widely be-

lieved that in order to conﬁrm that the chosen decision

outcome is the best one, the decision makers should

believe that this is the best outcome, and have rea-

sons to believe this. Using social choice theory we

secure the ﬁrst condition: agents express their individ-

ual preferences on the decision outcomes and voting

methods provide the means in order for agents to be-

lieve that their aggregated preference (outcome) is the

best, i.e., fairest according to their preferences. Our

motivation comes from fulﬁlling the second condition

and in order to do that we have to take into account

the reasoning behind the preferences and thus, de-

liberation and argumentation play an important role.

Hence, the scope of this paper is to fulﬁll the cen-

tral decision-making problem, which is to help deci-

sion makers produce “better” collective decision out-

comes. “Better” decisions is a very broad term and

the goal of many research papers on this domain. In

this paper, we will study on how collective decision-

making is helped with the intersection of argumenta-

tion along with deliberation in social choice theory.

Thus, we will focus on a social choice theoretic ap-

proach for multi-agent decision making enriched with

an argumentation framework.

Social choice theory can be applied to multi-agent

systems (Endriss, 2014) where voting can provide the

classical means for aggregating the individual agents’

Karanikolas, N., Bisquert, P. and Kaklamanis, C.

A Voting Argumentation Framework: Considering the Reasoning behind Preferences.

DOI: 10.5220/0007362300420053

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 42-53

ISBN: 978-989-758-350-6

preferences into a collective decision. In the origi-

nal setting we have a set of agents and a set of al-

ternatives. Each agent expresses her preference as

a total order over a set of alternatives, and then the

group’s preference is computed from the individual

preferences using a voting rule. A more analytic de-

scription of the voting problem and the social choice

fundamentals can be found in the Handbook of Com-

putational Social Choice (Brandt et al., 2016).

As previously mentioned, we believe that collec-

tive decision making should also rely on the reasoning

the agents provide when expressing their preferences.

In order to strengthen this view we can mention here

that it is common in many occasions that agents lie

in expressing preferences in favor of speciﬁc alterna-

tives when it is not possible to justify their reasons.

The same has also been noticed even if agents provide

reasoning but there is no deliberation phase. One such

example are the reviews and ratings agents provide

in sites like Google, Amazon, etc., where in some

cases the percentage of fake/questionable reviews for

a category of alternatives/products can reach 67%

Hence, it is logical to assume that the agents should

not only give their preferences but provide also a rea-

soning about their preferences so that one can de-

bate. Therefore, it is reasonable to search for a way

to interpret the preferences and the reasoning behind

them and an argumentation framework (Besnard and

Hunter, 2008; Dung, 1995) seems to be a rational ap-

proach to do that. Hence, in order to fulﬁll a col-

lective decision mechanism that considers both rea-

soning and deliberation we propose a decision-aiding

procedure which combines argumentation with com-

putational social choice.

Argumentation theory is widely used in the multi-

agent decision-making context, e.g., (Amgoud and

Prade, 2009; Gao et al., 2016; Fan and Toni, 2014)

due to its ability for reasoning with incomplete and

conﬂicting information (such as differences in opin-

ions). An argumentation framework is based on the

construction, the exchange and the evaluation of in-

teracting arguments, where various semantics are de-

ﬁned in the literature to assess the acceptability of

sets of arguments. Hence, an argumentation frame-

work where agents provide arguments with their pref-

erences can “correct” the “false” or “fake” informa-

tion that can appear. The way to measure the “false”

information included in agents’ preferences is by in-

troducing the notion of attacking power of arguments.

It is a function that quantiﬁes the attacking strength of

https://www.washingtonpost.com/business/economy/

how-merchants-secretly-use-facebook-to-ﬂood-amazon-

with-fake-reviews/2018/04/23/5dad1e30-4392-11e8-

8569-26fda6b404c7_story.html

argument(s) exposed during the deliberation phase to-

wards an argument stating an agent’s preference. For

example, if a preference argument of an agent is at-

tacked by many arguments which are revealed during

deliberation that is most likely to mean that this pref-

erence is not truthful and thus its power for the collec-

tive decision should be reduced. Therefore, we intro-

duce a method which takes into account the attacking

power of the deliberation phase to reach a collective

decision.

Concluding, it is our belief that enhancing the col-

lective decision-making procedure with a voting ar-

gumentation framework can beneﬁt the procedure in

the following ways. First, agents’ justiﬁcations for

preferences, which are depicted in the construction of

the argumentation framework, can provide the reason-

ing which can serve as the rational explanation of the

collective decision. Second, an argumentation frame-

work can model the deliberation phase prior to the ap-

plication of voting for making a group decision. This

modelling permits us to construct a preference proﬁle

that is “justiﬁed”, since it refers to the agents’ prefer-

ences and their justiﬁcations. The justiﬁed preference

proﬁle is a type of structured proﬁle which is the out-

come of a pre-voting debate phase that consists of a

deliberation procedure where agents reveal their pref-

erences and justiﬁcations. The objective is to fairly

aggregate the justiﬁed viewpoints of the agents and

hence, the justiﬁed preference proﬁle can be reported

to a voting rule for computing the decision outcome.

Our Work. Seminal to our research is the work of

(Bisquert et al., 2017) which ﬁrst presented an argu-

mentation framework based on agents’ preferences

for the voting problem from a qualitative perspec-

tive. Based on the notions of this paper we present

a novel quantitative procedure by designing a special

kind of Argumentation Framework, the Voting Argu-

mentation Framework (VAF ) and its corresponding

semantics, which are called pairwise comparison se-

mantics. The proposed semantics take into account

the deliberation

phase in terms of quantifying the

attacking power of arguments on the justiﬁcation of

the arguments produced by agents’ preferences. We

then compute the acceptability of the vote arguments

which deﬁne the new proﬁle, called the justiﬁed pref-

erence proﬁle, that takes into account the justiﬁca-

tion and deliberation phase. The justiﬁed preference

It should be noted that, similarly to (Bisquert et al.,

2017), our work does not address deliberation protocols

such as (Kok et al., 2011) directly. Indeed, we assume that

the argumentation framework is obtained as a result of a un-

speciﬁed deliberation protocol. This allows to abstract the

approach from the representation of the deliberation itself.

A Voting Argumentation Framework: Considering the Reasoning behind Preferences

proﬁle is the outcome of a quantitative argumentation

framework and its semantics and contains now all the

“corrected” preferences of the agents. Thus, a vot-

ing rule can be applied to aggregate these preferences,

which gives us the motivation to study social choice

theoretic properties for the justiﬁed preference proﬁle

and prove under which conditions they can be satis-

ﬁed. Finally, we look into properties that VAF and

its corresponding semantics should satisfy from an ar-

gumentative perspective.

Related Work. The intersection of argumentation

and deliberation in social choice theory for “better”

decision outcomes is a recently developed ﬁeld. As

already noted “better” can be deﬁned in many ways.

For example, in the work of (List et al., 2013) “bet-

ter” refers to outcomes where majority cycling can be

bypassed through single-peakedness. They show that

deliberation can protect against majority cycles by

presenting an empirical test using real data and use-

cases from Deliberative Polls. The results show that

the preferences after deliberation phase are closer,

in terms of a particular proximity function, to being

single-peaked. On the same path, i.e., decision out-

comes based on deliberation that avoid majority cy-

cling and related paradoxes, (Bisquert et al., 2017)

design a qualitative model based on an argumenta-

tion framework that is built from the justiﬁcations of

the agents pairwise preferences. They use Dung’s

“preferred” semantics to compute extensions which

provide the justiﬁed preference proﬁle. The justiﬁed

preference proﬁle is computed through a qualitative

method where the strength of votes, i.e, the number of

times that a pairwise comparison appears in the orig-

inal preference proﬁle, is not taken into account for

the aggregation. Hence, this method focuses on cases

where the decision outcome is independent of the ag-

gregation of agents’ preference relations. In our ap-

proach we instead focus on cases where the strength

of the votes are included in the collective decision.

They prove that the justiﬁed preference proﬁle per-

mits a type of structured preferences where the Con-

dorcet paradox is avoided. Another work for explor-

ing the effect of deliberation and its beneﬁts in voting

is the paper of (Fain et al., 2017). The authors in this

paper present a sequential deliberation protocol, seen

from a game-theoretic perspective, where agents ne-

gotiate in pairs and collaboratively propose outcomes

that appeal to both of them. They describe a method

where the space of preferences is deﬁned by a median

graph and prove that sequential deliberation is 1.208-

approximate to the optimal social cost on such graphs.

They also study the Pareto-efﬁciency property from a

social choice perspective and prove that the outcome

of sequential deliberation is ex-post Pareto-efﬁcient

on a median graph, i.e., that there is no other alterna-

tive that has at most that social cost for all agents and

strictly better cost for one agent.

There is also some signiﬁcant research on the in-

tersection of Social Choice and Argumentation which

is proximately related to this work. Most of the works

towards this research study the problem from an argu-

mentative perspective and deal with collective argu-

mentation. The studied problem refers to aggregating

individual argumentation frameworks to a collective

one. The aggregation mechanisms provided to com-

pute the collective frameworks rely on social choice,

which provides the means to accomplish that. A nice

example towards this research direction is the work of

(Coste-Marquis et al., 2007) for merging argumenta-

tion systems. They focus on scenarios in which some

agents are able to consider arguments not known by

other agents and disagree on the attack relation. A

three-step process is proposed where in the ﬁrst one,

each attack relation is consensually expanded to be-

come a partial system over the set of arguments. In

the second step the merging is done by generating a

class of argumentation systems that are at the short-

est “distance” of the ones in the proﬁle. In the ﬁ-

nal step the acceptable arguments are selected. An-

other example towards this direction is the research

of (Delobelle et al., 2016) where speciﬁc merging

operators based on extensions, though in combina-

tion with a framework-wise merging process. The

authors study the generation of the Argumentation

Framework resulting from a merging process. There

has been also notable research on the combination

of Judgement Aggregation, which is one of the main

problems in Social Choice, and Argumentation where

Pigozzi et al. have extensively studied the problem.

In (Pigozzi, 2006) the author proposes an aggrega-

tion procedure, called argument-based, for the case in

which the outcome is a set of arguments, combining

features of premise and conclusion-based procedures.

(Pigozzi and van der Torre, 2007) study the same

problem looking for axioms that characterize the ag-

gregation procedure and conditions such that the Con-

dorcet Paradox is avoided. They show that a condition

called premise independence of irrelevant proposi-

tional alternatives guarantees the existence of consis-

tent ways of aggregating judgments. (Caminada and

Pigozzi, 2011) employ an argumentation approach to

judgment aggregation which satisﬁes standard judg-

ment aggregation postulates and also avoids the prob-

lem of individual agents having to become committed

to a group judgment that is in conﬂict with their own

preferences. Another prominent work combining Ar-

gumentation and Voting is the one of (Leite and Mar-

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

tins, 2011) where they propose Social Abstract Ar-

gumentation Framework, which is based on Dung’s

Abstract Argumentation Framework but also incorpo-

rates social voting. They propose a class of seman-

tics for the Social Abstract Argumentation Frame-

work and prove some important properties regarding

Social Networks. An explorative survey for collective

argumentation is provided by (Bodanza et al., 2017).

On a related research path, recently, there has been

some work on the reasoning behind preferences but

not from an argumentative and social choice perspec-

tive. For example, (Dietrich and List, 2011) propose a

reason-based theory of rational choice where agents’

preferences are determined by their motivating rea-

sons and clarify the relationship between delibera-

tion for reasons and for rational choices. Another

work on the same path is the one of (Pedersen et al.,

2015) where they develop a modal logic for reason-

ing about preferences that depends on a set of motiva-

tional properties and also show that reasoning systems

and algorithms developed for modal logic can be em-

ployed for reasoning about reason-based preferences.

2 PRELIMINARIES

In the following section, we are deﬁning several no-

tions and notations that will be used later in the paper.

2.1 Social Choice Theory

We consider a set of N = {1,.. ., n} agents and a set of

alternatives A, |A| = m. Each agent i ∈ N has prefer-

ence relations () over the alternatives denoted with

x 

y which means that agent i prefers alternative x

to y. We deﬁne that each irreﬂexive preference rela-

tion satisﬁes transitivity, antisymmetry and compara-

bility and hence, the set of all the preference relations

for agent i produces a linear (strict total) order 

A, i.e., the ranking of agent i over the alternatives.

Let Ł

be the set of linear orders over A. A prefer-

ence proﬁle 

= h

,...,

i ∈ Ł

is a collection

of the linear orders for all the agents. A voting rule

is a mapping f : Ł

→ 2

\ {

0} from preference pro-

ﬁles to nonempty subsets of alternatives, which desig-

nates the winner(s) of the election. For two candidates

x,y ∈ A, and 

∈ Ł

, alternative x beats y in a pair-

wise comparison if |{i ∈ N : x 

y}| > n/2, that is,

if a (strict) majority of agents prefer x to y. The win-

ner according to the Condorcet method (Condorcet,

1785), i.e. the Condorcet winner, is an alternative that

beats every other alternative in a pairwise compari-

son. The Condorcet paradox as deﬁned by (Black,

1958) (also known as voting paradox or the paradox

of voting) is a situation in which the application of the

Condorcet method to a preference proﬁle can lead to

a voting cycle, and hence a Condorcet winner can not

be declared. A voting cycle occurs when we have 3

alternatives x,y,z such that |{i ∈ N : x 

y}| > n/2,

|{i ∈ N : y 

z}| > n/2, and |{i ∈ N : z 

x}| > n/2.

2.2 Argumentation

In order to be general with regards to the deliberation

step, we build upon the abstract argumentation frame-

work proposed by (Dung, 1995):

Deﬁnition 1. .[Argumentation framework (Dung,

1995)] An argumentation framework (AF) is a pair

(A,R), where A is a ﬁnite nonempty set of arguments

and R is a binary relation on A, called attack relation.

Let A,B ∈ A, ARB means that A attacks B.

Deﬁnition 2. .[Ranking-based semantics (Bonzon

et al., 2016)] Given an AF (A,R), a ranking-based

semantics σ associates a ranking 

on A. 

a preorder (a reﬂexive and transitive relation) on A.

For a,b ∈ A a 

b means that a is at least as accept-

able as b.

Deﬁnition 3. .[Path, attackers and defenders (Bon-

zon et al., 2016)] Given an AF (A,R), and A,B ∈ A.

A path p

B,A

is a sequence s = ha

,··· ,a

i of argu-

ments where a

= A , a

= B and ∀i < n we have that

i+1

) ∈ R. The length of the path is denoted by `

Note that `

= n. A defender of an argument A is an

argument situated at the beginning of an even-length

path leading to A. Respectively, an attacker of A is

an argument situated at the beginning of a path of odd

length. We denote the multiset of defenders and at-

tackers of A by De f

(A) = {b | ∃p

B,A

, `

∈ 2N} and

Att

(A) = {b | ∃p

B,A

, `

∈ 2N +1} respectively. The

direct attackers of A are the arguments in Att

(A).

An argument A is defended if De f

(A) 6=

Based on these notions, we can now present

the Voting Argumentation Framework combining the

strengths of social choice and argumentation.

We are assuming an odd number of agents.

A Voting Argumentation Framework: Considering the Reasoning behind Preferences

3 THE VOTING

ARGUMENTATION

FRAMEWORK

3.1 Construction of the Voting

Argumentation Framework

In order to take advantage of the reasoning capa-

bilities of AF in social choice we deﬁne our model

by constructing a special Argumentation Framework

adapted for social choice and voting. In the follow-

ing we describe the construction of this specialized

framework, which we will call Voting Argumentation

Framework, i.e, VAF .

We are going to distinguish between two types of

arguments: “vote” arguments and “generic” argu-

ments. We describe their role and the attacks that can

occur between them in the following paragraphs.

3.1.1 Vote Arguments

A vote argument A

i, j

represents the argument which

considers the total order, i.e., ranking r

produced by

agent j and the justiﬁcation provided by this agent

for each of the pairwise comparisons included in her

total order. We denote by A

= {A

i, j

,∀ j ∈ N} the set

of all the vote arguments and by A

the set of vote

arguments where the preference relation x  y occurs

in the ranking r

Vote arguments cannot be attacked by other vote

arguments, since it is natural to assume that for each

distinct agent j a different vote argument is produced

representing her preferences. Hence, two different

votes given by two different agents are not considered

inconsistent.

Example 1. Assume a decision problem with three

agents {v

} and three alternatives {c

The agents after a deliberation phase provide the fol-

lowing preferences along with a justiﬁcation:

• v

: c

 c

• v

: c

 c

• v

: c

 c

These preferences and their justiﬁcations are re-

spectively represented by vote arguments A

1,v

2,v

3,v

3.1.2 Generic Arguments

Generic arguments represent the deliberation phase

and regroup all the other possible arguments that can

arise during a debate. In particular, those arguments

are able to attack other generic arguments and vote

arguments. Indeed, giving a reason contradicting a

preference x  y of agent j triggers an attack on the

vote argument A

i, j

. We denote this generic argument

as a direct attacker of A

i, j

, i.e., da

i, j

∈ Att

i, j

The generic argument, denoted by g

i, j

, which is situ-

ated in the beginning of a path leading to A

i, j

can ei-

ther attack or defend a vote argument A

i, j

. Note that

even if the premise of an argument g

i, j

is the same

as argument g

, j

, we consider them as different ar-

guments as they correspond to the vote of a different

agent, i.e., j versus j

. Hence, a generic argument

i, j

can not have a path leading to two different vote

arguments. By k we denote the index of generic argu-

ments attacking/defending A

i, j

. We denote by G the

set of all the generic arguments and by G

i, j

the set of

generic arguments attacking A

i, j

Example 1 (cont.). Assume now that the agents enun-

ciated eight generic arguments G = {g

i,v

,...,g

i,v

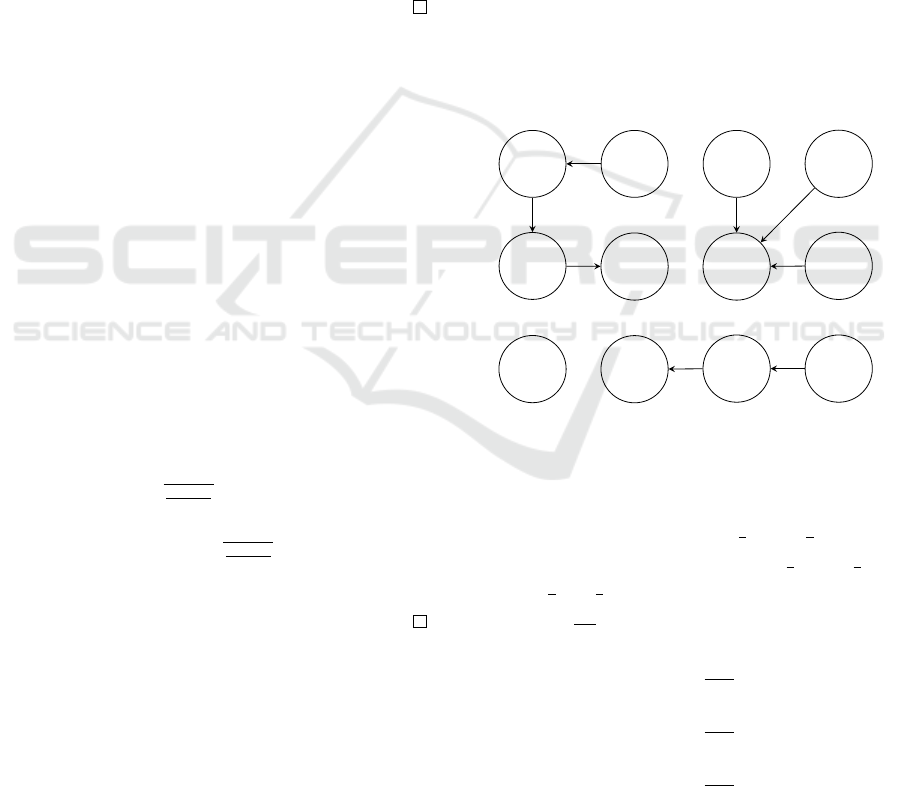
i ∈ [1, 3]. Figure 1 presents the argumentation frame-

work (A

∪ G, R), where R is represented by the ar-

rows between the arguments.

1,v

2,v

1,v

2,v

3,v

Figure 1: Voting argumentation framework of Example 1.

3.2 A Quantitative Model for Decision

Making based on the Voting

Argumentation Framework

In the following we use VAF in order to present

a quantitative model for social choice and decision

making problems that takes into account the reason-

ing behind the preferences. We start by deﬁning our

proposition for a new kind of semantics for computing

the acceptability of the vote arguments. We call them

Pairwise Comparison Semantics and can be seen as

a kind of ranking-based semantics specially adapted

to ﬁt in the voting setting. The intuition is the same

though, as each vote argument has a degree which de-

notes its strength, and hence the level of acceptability

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

in the outcome. We are then computing a new pref-

erence proﬁle taking into account the strength and the

acceptability of the vote arguments. This new proﬁle

will be thus “justiﬁed” as it is based on the outcome

of the voting argumentation framework.

3.2.1 Pairwise Comparison Semantics

Let P

i, j

the set of paths p

g,A

i, j

of attacks starting from

a generic argument g ∈ G and leading to vote argu-

ment A

i, j

. The attacking power of a generic argument

i, j

, which is the starting point of a path p

i, j

, on

a vote argument A

i, j

is denoted by ap(g

i, j

) and is

computed by the following formula.

ap(g

i, j

) =











m·(m−1)

if an odd-length path

i, j

exists

0 otherwise

Example 1 (cont.). The attacking powers of the

generic arguments that are the starting nodes of the

paths attacking the vote arguments are the following.

ap(g

1,v

) =

ap(g

2,v

) = ap(g

2,v

) = ap(g

2,v

) =

ap(g

3,v

) = 0

Note that when the attacking power of a generic

argument is 0 then this argument is defending the vote

argument. The intuition for computing the attacking

power function by the above formula is that in each

vote argument there are

m·(m−1)

pairwise comparisons

between the alternatives, where m is the number of

the alternatives. We assume that each generic argu-

ment refers to the justiﬁcation of one pairwise com-

parison each time. Hence, the weight of each vote

argument is reduced by

m·(m−1)

when it is attacked by

a generic argument. What we are actually interested

in is the effect a generic argument has on the weight

of the vote argument. Hence, the reason for denoting

positive attacking power on a generic argument only

if there exists a path of odd length starting from it,

is that having such a path affects the weight of the

vote argument as there exists an active direct attacker

on the vote argument. In the case where there ex-

ists an even path means that the direct attacker is not

active so the attacking power of the path is 0. Note

that according to Dung’s preferred semantics an even

path would defend the direct attacker of a vote argu-

ment even if an odd path exists. In our case though,

the semantics we use are not binary as Dung’s, i.e.,

an argument can either be included or excluded from

an extension, but instead we propose semantics where

the level of acceptability of an argument depends on

its weight, which is reminiscent of ranking semantics

(Bonzon et al., 2016). Hence, having an odd path

is sufﬁcient for the vote argument to decrease its ac-

ceptability value. It is reasonable to assume here that

if one wants to deﬁne the effect of the deliberation

phase, which is reﬂected through the generic argu-

ments, in a different way then the attacking power

function should be changed.

The attacking power of the set of generic argu-

ments attacking A

i, j

, denoted by ap(G

i, j

), is the

sum of all the generic arguments attacking it, hence

ap(G

i, j

) =

∑

ap(g

i, j

Example 1 (cont.). The attacking power of the set of

generic arguments attacking the vote arguments is the

following for each one of them.

ap(G

1,v

) =

ap(G

2,v

) = 1

ap(G

3,v

) = 0

Since our goal is to design an AF towards social

choice and voting we care about joining together the

vote arguments A

that correspond to the same total

order r

rather than the single vote argument A

i, j

pro-

duced by agent j itself. We call uniﬁcation (coalition)

of arguments this joining of arguments A

i, j

, who have

the same ranking r

, into a meta-argument A

with

higher weight. We deﬁne as ap(G

) =

∑

ap(G

i, j

)

the attacking power of the generic arguments attack-

ing A

. The attacking power of the whole delibera-

tion phase is deﬁned as ap(G) =

∑

ap(G

The weight of each vote argument is initially 1,

hence w(A

i, j

) = 1. A total order r

can appear |r



times in the preference proﬁle , which means that



agents have a preference order |r

|. It is easy

to see that if we sum up the initial weights of all the

vote arguments expressing votes with total order r

then we get the number of appearances of |r



in the

preference proﬁle. Hence, |r



∑

w(A

i, j

), where

j denotes an agent voting for r

For each vote argument A

i, j

we deﬁne its degree

for the acceptability semantics as

d(A

i, j

) = max



0,w(A

i, j

) − ap(G

i, j

)



Example 1 (cont.). The weight of each vote argu-

ment is initially 1, hence w(A

1,v

) = w(A

2,v

) =

w(A

3,v

) = 1. For each vote argument we compute

its degree:

A Voting Argumentation Framework: Considering the Reasoning behind Preferences

d(A

1,v

) = 1−

d(A

2,v

) = 1− 1 = 0

d(A

3,v

) = 1− 0 = 1

3.2.2 Computing the Justiﬁed Preference Proﬁle

under VAF and Pairwise Comparison

Semantics

It is possible to compute the set of “coherent pref-

erences”, i.e., the justiﬁed preference proﬁle, by us-

ing the deﬁned semantics on the voting argumenta-

tion framework. The above mentioned semantics de-

ﬁne the acceptability degree of each vote argument

in the justiﬁed preference proﬁle 

J P

under VAF .

For simplicity and onwards, when we refer to 

J P

computed by VAF and the pairwise comparison se-

mantics, we will use just the 

J P

symbol. In order

to build the 

J P

we take into account the degree of

each vote argument. For each total order r

we com-

pute the utility/acceptability uv(r

) value to denote its

strength in the 

J P

. For the computation we take into

account the acceptability degrees of each of the vote

arguments A

i, j

that refer to this total order (r

), i.e.,

the degree of meta-argument A

after the uniﬁcation.

Hence uv(r

) = d(A

) =

∑

∀ j

d(A

i, j

). It is easy to ver-

ify that uv(r

) = |r



−ap(G

). The number of times

a ranking r

appears in the justiﬁed preference proﬁle



J P

is the ratio of the utility value of r

over the sum

of all the utility values multiplied by the total number

of agents n

in 

J P

. Hence,



J P

= n

uv(r

)

∑

∀r

uv(r

)

The total number of agents in the 

J P

is computed

as following. Note that N

is the set of agents in the



J P











∑

∀r

uv(r

) if ∀uv(r

) ∈ N

∑

∀r

uv(r

)

gcd(uv(r

),∀r

∈ N

)

if ∀uv(r

) ∈ Q \ N

When it is clear in the context and for nota-

tion simplicity, we refer to gcd for denoting the

gcd(uv(r

),∀r

∈ N

), which is the greatest common

divisor of all the utility values uv(r

) that belong to

the set of agents N

in the 

J P

The need to have a integer number of agents leads

to considering the multiplication of

∑

∀r

uv(r

) by the

gcd.

Example 1 (cont.). In the following, we compute the

justiﬁed preference proﬁle 

J P

by deﬁning the num-

ber of times a ranking r

appears in it. For each to-

tal order r

we compute the utility uv(r

) taking into

account its acceptability degree. Hence, we have

that uv(r

) =

,uv(r

) = 0, uv(r

) = 1. Therefore,

∑

∀r

uv(r

) =

and gcd(1, 0,

) =

. The total num-

ber of agents n

in 

J P

is n

5/3

1/3

= 5. Therefore,



J P

= 5·

2/3

5/3

= 2



J P

= 5·

5/3

= 0



J P

= 5·

5/3

= 3

That means we have 2 agents with ranking c

 c



and 3 agents with c

 c

in the 

J P

4 PROPERTIES OF VAF UNDER

PAIRWISE COMPARISON

SEMANTICS

In this section, we are going to study some desir-

able properties that should be satisﬁed by any vot-

ing argumentation framework. Due to space restric-

tion, we omitted some proofs which can be found

at the following link: https://www.dropbox.com/s/

195fb6r8h73lmoe/icaart-app.pdf?dl=0.

4.1 VAF Desirable Properties from an

Argumentative Perspective

We will study the properties presented in the literature

of argumentation and ranking-based semantics that

make sense to be satisﬁed by a Voting Argumenta-

tion Framework and its corresponding semantics. An

overview of the desirable properties for ranking-based

semantics can be found in (Bonzon et al., 2016). We

believe that these properties should be taken into ac-

count when one wants to compute the social choice

outcome. Under this perspective, we slightly change

the deﬁnitions of the properties of Cardinality and De-

fense Precedence. Hence, we call the modiﬁed prop-

erties as Weak Cardinality Precedence and Weak De-

fense Precedence.

Deﬁnition 4 (Weak Cardinality Precedence). The

greater the number of direct attackers for a vote ar-

gument, the weaker the level of acceptability of this

argument. Given two vote arguments A,B ∈ A

s.t.

d(A) 6= 0 and d(B) 6= 0,

|Att

(A)| < |Att

(B)| ⇒ A  B.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

Theorem 1. The justiﬁed preference proﬁle com-

puted by VAF under pairwise comparison semantics

(

J P

) satisﬁes Weak Cardinality Precedence.

Proof. The degree d(A) of an argument A deﬁnes

the level of its acceptability in the framework. Thus,

it sufﬁces to show that given two vote arguments

A,B ∈ A

s.t. d(A) 6= 0 and d(B) 6= 0, if |Att

(A)| <

|Att

(B)| then d(A) > d(B).

If |Att

(A)| < |Att

(B)| then ap(G

) < ap(G

The degree of a vote argument Y is given by

d(Y ) = max



0,w(y) − ap(G

)



Since d(A) 6= 0 and d(B) 6= 0, we have that d(A) =

w(A) − ap(G

) and d(B) = w(B) − ap(G

). Also,

we have that w(A) = w(B) = 1. Summing up, we

have that d(A) > d(B).

Deﬁnition 5 (Weak Defense Precedence). For two

vote arguments with the same number of direct at-

tackers, a defended argument is ranked higher than

a non-defended argument. Given two vote arguments

A,B ∈ A

s.t. d(A) 6= 0 and d(B) 6= 0,

|Att

(A)| = |Att

(B)|,

De f

(A) 6=

0 and De f

(B) =

⇒ A  B.

Theorem 2. The justiﬁed preference proﬁle com-

puted by VAF under pairwise comparison semantics

(

J P

) satisﬁes Weak Defense Precedence.

Proof. It sufﬁces to show that given two vote argu-

ments A,B ∈ A

s.t. d(A) 6= 0 and d(B) 6= 0, if

|Att

(A)| = |Att

(B)|,De f

(A) 6=

0 and De f

(B) =

then d(A) > d(B).

Let x = |Att

(A)| = |Att

(B)| and |De f

(A)| = y,

with x,y > 0. Note that d(B) 6= 0 and |De f

(B)| = 0.

Hence, the degree of B is d(B) = w(B) − ap(G

where ap(G

) = x ·

m·(m−1)

. Also, note that d(A) 6= 0,

and hence the degree of A is d(A) = w(A)−ap(G

where ap(G

) = (x − y) ·

m·(m−1)

. From the above

conditions we have that ap(G

) > ap(G

), and

since w(A) = w(B) = 1, we conclude that d(A) >

d(B).

4.2 VAF Desirable Properties with

Respect to Social Choice

In this section we study the properties that should be

satisﬁed by a Voting Argumentation Framework and

its corresponding semantics from a social-choice the-

oretic scope.

4.2.1 Justiﬁed Preference Proﬁle Consistency

with Respect to AF

The ﬁrst property refers to the relation the Voting Ar-

gumentation framework should have with respect to

the produced justiﬁed preference proﬁle. We will

show that the following property is satisﬁed when

pairwise comparison semantics are applied to VAF

for computing the justiﬁed preference proﬁle.

Deﬁnition 6 (Justiﬁed Preference Proﬁle consistency

with respect to AF). If a uniﬁcation of vote argu-

ments A

is stronger than A

, i.e., the degree of A

is higher than A

, then the corresponding total order

should appear more times than the total order r

the justiﬁed preference proﬁle.

Example 1 (cont.: Justiﬁed Preference Proﬁle consis-

tency with respect to AF). Assume that another vote

argument A

1,v

is added to the previous voting ar-

gumentation framework. Figure 2 presents this new

VAF .

1,v

2,v

1,v

2,v

1,v

3,v

Figure 2: VAF exemplifying the Justiﬁed Preference Pro-

ﬁle consistency with respect to AF property.

We can now recompute the justiﬁed preference

proﬁle 

J P

the same way as before. We have that

d(A

) = d(A

1,v

) + d(A

1,v

) =

+ 1 =

,d(A

) =

0,d(A

) = 1. Therefore,

∑

∀r

uv(r

) =

+ 1 =

and

gcd(1,0,

) =

. The total number of agents n



J P

is n

8/3

1/3

= 8. Therefore,



J P

= 8·

5/3

8/3

= 5



J P

= 8·

8/3

= 0



J P

= 8·

8/3

= 3

Hence, now r

is the ranking with the highest degree

and it appears more times in 

J P

so the property is

satisﬁed.

A Voting Argumentation Framework: Considering the Reasoning behind Preferences

Theorem 3. The justiﬁed preference proﬁle com-

puted by VAF under pairwise comparison seman-

tics (

J P

) satisﬁes Justiﬁed Preference Proﬁle con-

sistency with respect to AF.

Proof. Let us suppose that a uniﬁcation of vote ar-

guments A

is stronger than A

, and hence the de-

gree d(A

) > d(A

) or uv(r

) > uv(r

). The corre-

sponding total order r

appears in the 

J P

, |r



J P

uv(r

)

∑

∀r

uv(r)

times while |r



J P

= n

uv(r

)

∑

∀r

uv(r)

. Given

that uv(r

) > uv(r

), we conclude that |r



J P



J P

4.2.2 Social Choice Proﬁle Consistency

The second property that we are going to check is a

new but fundamental property that quantitative vot-

ing argumentation frameworks should have. We call

it the Social choice proﬁle consistency. The intuition

behind this property is that if there is no deliberation

phase for the preferences of the agents then the out-

come of the Voting Argumentation Framework, i.e.,

the justiﬁed preference proﬁle should be the same as

the outcome of the original social choice proﬁle, since

there is no new information or conﬂicts expressed by

arguments. More formally, this property can be de-

ﬁned as follows.

Deﬁnition 7 (Social choice proﬁle consistency). The

semantics of a Voting Argumentation Framework sat-

isﬁes Social choice proﬁle consistency if when there

is no deliberation phase, i.e., no generic arguments

attacking the vote arguments, then the justiﬁed prefer-

ence proﬁle should be the same as the original social

choice proﬁle.

Theorem 4. The justiﬁed preference proﬁle com-

puted by VAF under pairwise comparison semantics

(

J P

) satisﬁes Social choice proﬁle consistency.

Proof. Let  be the social choice preference proﬁle

and 

J P

the justiﬁed preference proﬁle for the VAF

when the pairwise comparison semantics is applied.

In order to prove that VAF satisﬁes this property we

have to show that each total order r

∈ is also in-

cluded is 

J P

the same number of times.

Let r

be a given ranking included in . It sufﬁces

to show that |r



= |r



J P

, where |r



is the number

of times r

appears in  and |r



J P

the number of

times it appears in 

J P

Recall that



J P

= n

uv(r

)

∑

∀r

uv(r

)

Also, recall that uv(r

) =

∑

∀ j

d(A

i, j

) and d(A

i, j

) =

w(A

i, j

) − ap(G

i, j

Note that |r



∑

∀ j

w(A

i, j

) under pairwise com-

parison semantics and that

∑

∀ j

ap(G

i, j

) = 0 since

there are no attacks on the preferences. Hence,

uv(r

) = |r



The number of agents n

in the 

J P

∑

∀r

uv(r

)

since uv(r

) equals to |r



and therefore each uv(r

)

belongs to the set of natural numbers N. Hence,



J P



∑

∀r

uv(r

)

∑

∀r

uv(r

) = |r



4.2.3 Measuring the Effect of Deliberation on

Avoiding Voting Cycles

In this section we are going to study the impact of a

deliberation phase in social choice theory and espe-

cially on voting cycles, i.e, the Condorcet Paradox.

The intuition that triggered this study is that if there

exists an amount of ambiguous information in the

preferences of the agents the deliberation phase can

reveal it using the imposed arguments and “correct”

the misinformation on the preferences of the agents

that trigger voting cycles. In order to study this impact

we are measuring the effect of a deliberation phase in

producing a justiﬁed preference proﬁle where there

are no voting cycles. The metric that we are going to

use to measure the impact is the number of arguments

needed to attack preferences of the original proﬁle so

that no cycles exist. In other words, it is the attacking

power of the generic arguments for total order r

, i.e.,

ap(G

Theorem 5. Given that for alternatives a, b,c ∈ A, a

beats b and b beats c in both  and 

J P

, the justiﬁed

preference proﬁle computed by VAF does not pro-

duce any voting cycle when the following conditions

on the attacking power of the generic arguments hold.

∑

∈R

ap(G

) ≤

∑

∈R

ap(G

),when |R



> |R



∑

∈R

ap(G

) >

∑

∈R

ap(G

when |R



− |R



∑

∈R

ap(G

) −

∑

∈R

ap(G

)

∑

∈R

ap(G

) <

∑

∈R

ap(G

when |R



< |R



∑

∈R

ap(G

) −

∑

∈R

ap(G

) + |R



The above relations state that in order to avoid

the cycle we must have, for 3 alternatives a,b, c ∈ A

where a beats b and b beats c in  and 

J P

, the fol-

lowing conditions:

1. The attacking power for the vote arguments A

is less or equal to the attacking power for the vote

arguments A

, when the majority of agents pre-

fer a over c in the preference proﬁle .

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

2. The attacking power for the vote arguments A

is greater than the attacking power for the vote ar-

guments A

, when the difference in number of

agents preferring a  c to c  a is lower bounded

by the difference of the corresponding attacking

powers.

3. The attacking power for the vote arguments A

is less than the attacking power for the vote argu-

ments A

, when the majority of agents prefer c

over a in the preference proﬁle  and the differ-

ence in number of agents preferring c  a to a  c

is upper bounded by the difference of the corre-

sponding attacking powers.

4.3 VAF Attitude Towards Classical

Social Choice Desirable Properties

In this section we explore the behaviour of the pro-

posed approach towards classical desirable properties

from the viewpoint of Social Choice. Apart from the

properties that should be satisﬁed by a Voting Argu-

mentation Framework and its corresponding seman-

tics which are related to the Social choice outcome,

we are also referring to classical desirable properties

in order to further evaluate VAF and pairwise se-

mantics. We begin by studying the properties of ho-

mogeneity and monotonicity which both belong to the

stability category as recognized by social choice the-

orists. The properties of this category are concerned

with ensuring that the winning set remains the same

when the changes in the preference proﬁle arguably

should not modify the winning set. Our goal here is

to evaluate the effect of deliberation and argumenta-

tion in voting and investigate how the consideration of

the deliberation phase along with voting can affect the

outcome in respect with the social choice properties.

4.3.1 Homogeneity

The ﬁrst property discussed in this section is the one

of homogeneity. A method is homogeneous if the

replication

of the preference proﬁle does not change

the winning set of the alternatives. We prove the fol-

lowing positive result for our proposed method which

ensures that replicating the original instance of the

problem, i.e., the agents’ preferences and the justi-

ﬁcations, will have no effect on the decision output

as long as the voting rule used for the aggregation of

the justiﬁed preference proﬁle satisﬁes homogeneity.

This property is widely accepted among social choice

Please note that, in our context, the replication con-

cerns both the preference proﬁle and the arguments refer-

ring to this preference proﬁle.

theorists since making an exact copy of the agents’

preferences x times should not have an effect on the

winning set.

Example 1 (cont.: Homogeneity). Assume that the

original proﬁle along with its arguments is repli-

cated 2 times. The following vote arguments are

added: A

1,v

2,v

3,v

1,v

. For 

J P

have that d(A

) = d(A

1,v

) + d(A

1,v

) + d(A

1,v

) +

d(A

1,v

) =

,d(A

) = 0,d(A

) = 2. Therefore,

∑

∀r

uv(r

)

and gcd(2, 0,

) =

. The total

number of agents is n



J P

16/3

2/3

= 8. Therefore,



J P

is 5, |r



J P

is 0 and |r



J P

is 3. Hence, the

justiﬁed replicated proﬁle is the same as the original

justiﬁed proﬁle. Therefore an application of a voting

rule on both proﬁles will have the exact same winning

ranking and the property is satisﬁed.

Theorem 6. VAF satisﬁes homogeneity if the vot-

ing rule used for the aggregation of 

J P

satisﬁes also

homogeneity.

4.3.2 Monotonicity

The second property discussed in this section is the

one of monotonicity. A method is monotonic if a win-

ning alternative remains the winning one in the new

proﬁle which is created after she is moved upward

in the preferences of some of the agents. We prove

the following positive result for our proposed method

which ensures that if an alternative who is a winner

in an instance of the problem is moved upwards in

the preferences of some agents then this will have no

effect on the decision output of the new instance as

long as (1) the voting rule used for the aggregation

of the justiﬁed preference proﬁle satisﬁes monotonic-

ity, (2) the attacking power on the votes where the

winner has a better position (compared to the original

proﬁle) is equal to the attacking power on the corre-

sponding votes in the original proﬁle. This property

is also widely accepted among social choice theorists

since improving the position of a winner alternative in

some agents should not make him worse and should

remain the winner.

Theorem 7. VAF under pairwise semantics satisﬁes

monotonicity if the voting rule used for the aggrega-

tion of 

J P

satisﬁes monotonicity and the attacking

power of the w-improvement votes is equal to the at-

tacking power of the votes that change in the original

preference proﬁle.

A Voting Argumentation Framework: Considering the Reasoning behind Preferences

4.3.3 Consistency Related to Majority

In this section, we present our results about classical

properties coming from Social Choice Theory which

in general concern the consistency between the out-

comes of the given method and the majority rule.

Condorcet Consistency. One of the most mean-

ingful properties is the Condorcet consistency. This

property states that a method F satisﬁes Condorcet

consistency if whenever there is an alternative c who

beats every other alternative in a pairwise comparison

(i.e., c is the dominant alternative) then c is the winner

under F .

Theorem 8. VAF under pairwise semantics satisﬁes

Condorcet consistency if the voting rule used for the

aggregation of 

J P

satisﬁes Condorcet consistency

and the following condition holds: for any alterna-

tives a,c ∈ A



− |R



> ap(G

) − ap(G

)

where R

denotes the number or agents that rank al-

ternative x over y and ap(G

) denotes the attacking

power of the generic arguments on the arguments of

the agents that rank x over y and c is the dominant

alternative.

The theorem states that Condorcet consistency is

satisﬁed if the difference in the number of agents pre-

ferring the dominant alternative c to every other alter-

native a minus the number of agents preferring a to

c is greater than the difference of the corresponding

attacking power on the vote arguments.

Invariant loss consistency. This property is also

based on the Condorcet’s intuition and is similar to

the Condorcet consistency. It states that a method F

satisﬁes Invariant loss consistency if whenever there

is an alternative c who is beaten by every other alter-

native in a pairwise comparison then c cannot be the

winner under F .

Theorem 9. VAF under pairwise semantics satisﬁes

Invariant loss consistency if the voting rule used for

the aggregation of 

J P

satisﬁes Invariant loss con-

sistency and following condition holds: for any alter-

natives a,c ∈ A



− |R



< ap(G

) − ap(G

)

where R

denotes the number or agents alternative x

over y and ap(G

) denotes the attacking power of

the generic arguments on the arguments of the agents

that rank x over y and c is the alternative who is

beaten by every other alternative (i.e, the Condorcet

loser).

5 CONCLUSION AND FUTURE

WORK

In this paper, we have proposed a method for group

decision-making that is built upon the justiﬁed pref-

erences of the agents. Our method is able to simulate

real decision problems where the decision outcome

relies on agents’ preferences and their reasoning. Our

design choices assume and comply with a delibera-

tion phase in which a discussion is conducted among

the agents of the group so that the preferences along

with justiﬁcations are revealed. In order to do so,

we introduced a voting argumentation framework and

its corresponding semantics. We proposed a method

for computing a new preference proﬁle based on the

acceptability semantics of the vote arguments. We

proved several properties from an argumentative and

social choice theoretic point of view on the so-called

justiﬁed preference proﬁle.

In terms of future work, we plan to extend our re-

search towards the proposed modelling and charac-

terize other properties of social choice and argumen-

tation that are satisﬁed by VAF . Also, another fu-

ture step is to deﬁne another kind of acceptability se-

mantics and explore its properties. For example, it

would be interesting to design semantics that permit

us to avoid the Condorcet paradox under any case.

Furthermore, it is also appealing to design different

kinds of semantics which are specially adapted to dis-

tinctive real decision problems. Indeed, with the se-

mantics proposed in this paper, the generic arguments

have the same strength, but there are cases where

generic arguments attacking vote arguments are not

of equal importance. It is therefore a motivation to

design a semantics with graded strength of generic

arguments. It is also interesting to investigate more

on the properties from an argumentative perspective

(such as the ones deﬁned in (Bonzon et al., 2016)) for

the proposed semantics and identify which ones are

respected. Finally, it is let for future work a practical

application of this method in real decision problems.

It will be very interesting to design a real experiment

and see how the proposed method works by measur-

ing the satisfaction of the agents for the decision out-

come when their justiﬁcations are taken into account

compared to unjustiﬁed preferences where pure social

choice methods are used.

ACKNOWLEDGMENTS

The research of N. Karanikolas was implemented

with a scholarship from IKY funded by the action

“Support of Postdoctoral Researchers” from the re-

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

sources of the EP “Human Resources Development,

Education and Lifelong Learning” with priority axes

6,8,9 and is co-funded by the European Social Fund

- ESF and the Greek state.

REFERENCES

Amgoud, L. and Prade, H. (2009). Using arguments for

making and explaining decisions. Artiﬁcial Intelli-

gence, 173(3–4):413–436.

Besnard, P. and Hunter, A. (2008). Elements of Argumenta-

tion. MIT Press.

Bisquert, P., Croitoru, M., and Karanikolas, N. (2017). A

qualitative decision-making approach overlapping ar-

gumentation and social choice. In Rothe, J., editor,

Algorithmic Decision Theory, pages 344–349, Cham.

Springer International Publishing.

Black, D. (1958). Theory of Committees and Elections.

Cambridge University Press.

Bodanza, G., Tohmé, F., and Auday, M. (2017). Collective

argumentation: A survey of aggregation issues around

argumentation frameworks. Argument & Computa-

tion, 8(1):1–34.

Bonzon, E., Delobelle, J., Konieczny, S., and Maudet, N.

(2016). A comparative study of ranking-based seman-

tics for abstract argumentation. In Proceedings of the

Thirtieth AAAI Conference on Artiﬁcial Intelligence,

AAAI’16, pages 914–920. AAAI Press.

Brandt, F., Conitzer, V., Endriss, U., Lang, J., and Procac-

cia, A. D. (2016). Handbook of Computational Social

Choice. Cambridge University Press, New York, NY,

USA, 1st edition.

Bulling, N. (2014). A survey of multi-agent decision mak-

ing. KI - Künstliche Intelligenz, 28(3):147–158.

Caminada, M. and Pigozzi, G. (2011). On judgment aggre-

gation in abstract argumentation. Autonomous Agents

and Multi-Agent Systems, 22(1):64–102.

Condorcet, M. D. (1785). Essai sur l’application de

l’analyse à la probabilité de décisions rendues à la

pluralité de voix. Imprimerie Royal. Facsimile pub-

lished in 1972 by Chelsea Publishing Company, New

York.

Coste-Marquis, S., Devred, C., Konieczny, S., Lagasquie-

Schiex, M.-C., and Marquis, P. (2007). On the merg-

ing of dung’s argumentation systems. Artiﬁcial Intelli-

gence, 171(10):730 – 753. Argumentation in Artiﬁcial

Intelligence.

Delobelle, J., Haret, A., Konieczny, S., Mailly, J.-G., Rossit,

J., and Woltran, S. (2016). Merging of abstract

argumentation frameworks. In Proceedings of the

Fifteenth International Conference on Principles of

Knowledge Representation and Reasoning (KR 2016),

pages 33–42.

Dietrich, F. and List, C. (2011). A reason-based theory of

rational choice *. Noûs, 47(1):104–134.

Dung, P. M. (1995). On the acceptability of arguments and

its fundamental role in nonmonotonic reasoning, logic

programming and n-person games. Artiﬁcial intelli-

gence, 77(2):321–357.

Endriss, U. (2014). Social choice theory as a foundation

for multiagent systems. In Müller, J. P., Weyrich,

M., and Bazzan, A. L. C., editors, Multiagent Sys-

tem Technologies, pages 1–6, Cham. Springer Inter-

national Publishing.

Fain, B., Goel, A., Munagala, K., and Sakshuwong, S.

(2017). Sequential deliberation for social choice. In

R. Devanur, N. and Lu, P., editors, Web and Internet

Economics, pages 177–190, Cham. Springer Interna-

tional Publishing.

Fan, X. and Toni, F. (2014). Decision making with

assumption-based argumentation. In Black, E., Mod-

gil, S., and Oren, N., editors, Theory and Applications

of Formal Argumentation, pages 127–142, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Gao, Y., Toni, F., Wang, H., and Xu, F. (2016).

Argumentation-based multi-agent decision making

with privacy preserved. In Proceedings of the 2016 In-

ternational Conference on Autonomous Agents &

Multiagent Systems, AAMAS ’16, pages 1153–

1161, Richland, SC. International Foundation for Au-

tonomous Agents and Multiagent Systems.

Kok, E. M., Meyer, J.-J. C., Prakken, H., and Vreeswijk,

G. A. W. (2011). A formal argumentation frame-

work for deliberation dialogues. In Argumentation

in Multi-Agent Systems, pages 31–48, Berlin, Heidel-

berg. Springer Berlin Heidelberg.

Leite, J. a. and Martins, J. a. (2011). Social abstract argu-

mentation. In Proceedings of the Twenty-Second In-

ternational Joint Conference on Artiﬁcial Intelligence

- Volume Volume Three, IJCAI’11, pages 2287–2292.

AAAI Press.

List, C., Luskin, R. C., Fishkin, J. S., and McLean, I.

(2013). Deliberation, single-peakedness, and the pos-

sibility of meaningful democracy: Evidence from de-

liberative polls. The Journal of Politics, 75(1):80–95.

Pedersen, T., Dyrkolbotn, S., and Ågotnes, T. (2015). Rea-

soning about reasons behind preferences using modal

logic. Information Systems Frontiers, 17(4):713–724.

Pigozzi, G. (2006). Belief merging and the discursive

dilemma: an argument-based account to paradoxes of

judgment aggregation. Synthese, 152(2):285–298.

Pigozzi, G. and van der Torre, L. (2007). Premise in-

dependence in judgment aggregation. In Bonanno,

G., Delgrande, J., Lang, J., and Rott, H., editors,

Formal Models of Belief Change in Rational Agents,

number 07351 in Dagstuhl Seminar Proceedings,

Dagstuhl, Germany. Internationales Begegnungs- und

Forschungszentrum für Informatik (IBFI), Schloss

Dagstuhl, Germany.

A Voting Argumentation Framework: Considering the Reasoning behind Preferences