
Hyperparameter Optimization for Deep Reinforcement Learning in
Vehicle Energy Management
Roman Liessner, Jakob Schmitt, Ansgar Dietermann and Bernard B
¨
aker
Dresden Institute of Automobile Engineering, TU Dresden, George-B
¨
ahr-Straße 1c, 01069 Dresden, Germany
Keywords:
Deep Reinforcement Learning, Hyperparameter Optimization, Random Forest, Energy Management, Hybrid
Electric Vehicle.
Abstract:
Reinforcement Learning is a framework for algorithms that learn by interacting with an unknown environ-
ment. In recent years, combining this approach with deep learning has led to major advances in various fields.
Numerous hyperparameters – e.g. the learning rate – influence the learning process and are usually determined
by testing some variations. This selection strongly influences the learning result and requires a lot of time and
experience. The automation of this process has the potential to make Deep Reinforcement Learning available
to a wider audience and to achieve superior results. This paper presents a model-based hyperparameter op-
timization of the Deep Deterministic Policy Gradients (DDPG) algorithm and demonstrates it with a hybrid
vehicle energy management environment. In the given case, the hyperparameter optimization is able to double
the gained reward value of the DDPG agent.
1 INTRODUCTION
1.1 Motivation and Relevance
In recent years, machine learning has made great
progress in various domains. Particularly in the area
of supervised learning, numerous successes have
been recorded, including the image classification
(Krizhevsky et al., 2012), speech recognition (Graves
et al., 2013) and machine translation (Sutskever et al.,
2014). Deep Reinforcement Learning (DRL) gained
media attention by defeating the Go World Champion
(Silver et al., 2017) and playing ATARI games
on an advanced human level (Mnih et al., 2015).
Compared to supervised learning, reinforcement
learning is currently more the subject of research than
of industrial applications (Mania et al., 2018). The
DRL learning process requires numerous pre-defined
parameters. These ensure that the DRL algorithm can
learn on its own during the learning process through
interaction with an environment. These parameters
known as hyperparameters are for example learning
rates, neural network size, exploration and others.
They are not automatically tuned during training.
The user has to select them according to his experi-
ence. The result of the learning process and thus of
the according environment interaction as well as the
required learning time strongly depend on this choice.
A common method is the manual search for suit-
able parameters. Sufficient expertise and experience
are required to find good hyperparameter sets. How-
ever, finding the optimal hyperparameters is usually
unlikely (Chollet, 2017). The introduction of an auto-
mated hyperparameter search process offers two ma-
jor advances. First, the universal industrial applica-
tion can be advanced, as the user is not reliant on
sophisticated personal experience regarding the tun-
ing of hyperparameters. Second, the optimality-based
problem solving using DRL algorithms can be ad-
vanced into a true optimization, as only the identi-
fication of the optimal hyperparameters enable the
DRL algorithms to deliver optimal results regarding
the given task.
1.2 Related Work
Grid search is a traditional approach to find suitable
hyperparameters. A reasonable subset of values is de-
fined for each hyperparameter. Each value combina-
tion is evaluated against a defined validation problem
and finally the combination achieving the best results
is used in the actual learning task. This method is
easy to implement and a widely used approach for
the optimization of parameters. Duan et al. optimize
the hyperparameters of different RL algorithms using
134
Liessner, R., Schmitt, J., Dietermann, A. and Bäker, B.
Hyperparameter Optimization for Deep Reinforcement Learning in Vehicle Energy Management.
DOI: 10.5220/0007364701340144
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 134-144
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

conventional grid search (Duan et al., 2016). Mania
et al. apply grid search as well to fine-tune their op-
timization algorithm (Mania et al., 2018). Besides
the random parameters selection, choosing promis-
ing parameter combinations based on Bayesian meth-
ods represents an alternative approach. Barsce et al.
use a Gaussian process as underlying model of their
Bayesian method (Barsce et al., 2018). They opti-
mize the hyperparameters of the SARSA(λ) RL al-
gorithm, applied to a simple example of a blocking
maze (Sutton and Barto, 2012). Falkner et al. make
use of the Tree Parzen Estimator as a basic function
of their Bayesian optimization and combine its effec-
tiveness with the speed of the Bandit Random Search
(Falkner et al., 2018). Springenberg et al. approxi-
mate the Bayesian model with the help of neuronal
nets (Springenberg et al., 2016). Both papers exam-
ine the hyperparameter optimization of RL algorithms
using the Cartpole Swing-Up environment as example
case.
These approaches optimize the hyperparameters
of Reinforcement Learning methods which are used
to control physical systems within research demos.
This paper presents a model-based hyperparameter
optimization which is applied to an industrial real
world example. In contrast to demo problems, the
industrial application demands further requirements
such as a limitation of the time, in which the algorithm
has performed the learning process. In this contri-
bution, the hyperparameter optimization is extended
with a hard requirement on the time available for the
learning process of the DDPG algorithm in its indus-
trial application. It is shown, how well the hyperpa-
rameter optimization tunes the DDPG to achieve re-
sults, which extend the results gained with a hyperpa-
rameter set manually defined by experts, while simul-
taneously complying to the time requirements.
1.3 Structure of this Paper
Chapter two of this paper gives an introduction into
Deep RL algorithms and the hyperparameters which
are included in the optimization process. Chapter
three will provide more information on the previously
described hyperparameter optimization approaches.
Also, three methods are selected for further study in
the context of this paper, with focus on the model-
based approaches. Chapter four describes the envi-
ronment, which the Deep RL agent is interacting with
and which represents the vehicle energy management
problem. Chapter five analyses the achieved results
with the selected hyperparameter optimization meth-
ods, followed by the conclusion in chapter six.
Figure 1: Agent-Environment-Interaction of Reinforcement
Learning (Sutton and Barto, 1998).
2 BACKGROUND
2.1 Reinforcement Learning
Reinforcement Learning is a direct approach to learn
from interactions with an environment in order to
achieve a defined goal. The basic interaction is shown
in Figure 1. In this context, the learner and decision
maker is referred to as the agent, whereas the part it
is interacting with is called environment. The interac-
tion performs in a continuous form so that the agent
selects actions A
t
at each time step t, the environment
responds to them and presents new situations (in the
form of a state S
t+1
) to the agent
1
. Responding to
the agent’s feedback, the environment returns rewards
R
t+1
in the form of a numerical scalar value. The
agent seeks to maximize rewards over time (Sutton
and Barto, 1998).
Having introduced the idea of the RL, a brief ex-
planation of certain terms follows. For a detailed in-
troduction, please refer to (Sutton and Barto, 1998).
Policy: The policy, is what characterizes the agents
behavior. More formally the policy is a mapping from
states to actions.
π(a|s) = P(A
t
= a|S
t
= s) (1)
Goals and Rewards: In reinforcement learning, the
agent’s goal is formalized in the form of a special sig-
nal called a reward, that is transferred from the envi-
ronment to the agent at each time step. Basically, the
target of the agent is to maximize the total amount of
scalar rewards R
t
∈ R it receives. This means maxi-
mizing not the immediate reward, but the cumulative
reward in the long run, which is also called return.
1
In engineering applications, the agent is the controller,
the environment is the technical system to be influenced and
the action is the control signal. Nevertheless, the following
deliberately retains the established terms for reinforcement
learning in order to prevent misunderstandings and to pro-
vide the topic to a broader audience in the usual form.
Hyperparameter Optimization for Deep Reinforcement Learning in Vehicle Energy Management
135

Exploration vs. Exploitation: A major challenge
in reinforcement learning is the balance of exploration
and exploitation. In order to receive high rewards, the
agent has to choose actions that have proven to be par-
ticularly rewarding in the past. In order to discover
such actions in the first place, new actions have to be
tested. This means the agent has to exploit knowl-
edge already learned to get a reward, and at the same
time explore other actions to have a better strategy
in the future (Sutton and Barto, 1998). Various ex-
ploration strategies are available for this purpose. In
(Plappert et al., 2017), M. Plappert compares several
exploration strategies for continuous action spaces.
In numerous articles (Lillicrap et al., 2015) (Plap-
pert et al., 2017) a correlated additive Gaussian ac-
tion noise based on the Ornstein-Uhlenbeck process
(OUP) (Uhlenbeck and Ornstein, 1930) is applied.
The stochastic process models the velocity of a Brow-
nian particle with friction, resulting in temporally cor-
related values around zero. Compared to the uncorre-
lated additive Gaussian action noise, the action noise
changes less abruptly from one timestep to the next
(Lillicrap et al., 2015). This characteristic can be ben-
eficial for the control of physical actuators. M. Plap-
pert points out in (Plappert et al., 2017), that an addi-
tional action noise is not (always) mandatory in con-
tinuous action spaces. This fact will be discussed in
more detail in the following.
2.2 Deep Reinforcement Learning
After introducing the basic concepts of reinforcement
learning in the previous section, this section describes
algorithms that combine deep learning and reinforce-
ment learning.
2.2.1 Deep Q-Networks (DQN)
Mnih et al. [2013, 2015] proposed Deep Q-Networks,
which successfully learns to play Atari games directly
from pixels. In essence, DQN learns the Q-function
with deep learning networks, which is defined as:
Q
π
(s
t
, a
t
) := r(s
t
, a
t
) + E
"
T −t
∑
i=1
γ
t+i
r(s
t+1
, a
t+1
)
#
(2)
The Q-function provides the expected discounted
reward that is obtained when action a
t
is executed in
state s
t
and policy π is followed in all subsequent time
steps. The Q-function can be formulated recursively
and is also known as the Bellman equation (Sutton
and Barto, 1998):
Q
π
(s
t
, a
t
) :=r(s
t
, a
t
)+
γE
s
t+1
∼P(·|s
t
,a
t
),a
t+1
∼π(s
t+1
)
[Q
π
(s
t+1
, a
t+1
)]
(3)
Using Q, the optimal deterministic action can be
determined:
π(s) := arg max
a
Q
π
(s, a) (4)
Therefore, the policy π can be implicitly derived
from Q. When only a few actions are available, the
optimal strategy can be determined relatively easy.
In very large state spaces (as it is the case in play-
ing Atari games through pixel representation) a deep
learning network can be used to approximate the Q-
function. In this way it is possible to achieve a better
generalization by deriving unknown correlations from
previous observations. Applying the Bellman equa-
tion, the network is then trained to minimize the loss:
L = (r + γarg max
a
t+1
Q
θ
(s
t+1
, a
t+1
)) − Q
θ
(s, a))
2
(5)
For the calculation DQN stores the transition tu-
ple (s
t
;a
t
;s
t+1
;r
t
) in a replay buffer. This also stabi-
lizes the algorithm since samples are drawn uniformly
from the replay buffer and the gradient is estimated in
typical mini-batch fashion using these samples, thus
de-correlating it. Furthermore, DQN uses the concept
of a target network, that is only updated occasionally
to make the learning target (mostly) stationary (Plap-
pert et al., 2017).
2.2.2 Deep Deterministic Policy Gradient
(DDPG)
Finding the optimal action in the preceding DQN
algorithm requires an efficient evaluation of the Q-
function (see equation 4). While this is quite simple
for discrete and relatively small action spaces (all ac-
tions are calculated and those with the highest value
selected), the problem becomes unsolvable if the ac-
tion space is continuous. However, in many applica-
tions, such as robotics and energy management, dis-
cretizations are not desirable, as they have a negative
impact on the quality of the solution and at the same
time require large amounts of memory and computing
power in the case of a fine discretization. Lillicrap
et al. (Lillicrap et al., 2015) presented an algorithm
called DDPG, which is able to solve continuous prob-
lems with Deep Reinforcement Learning. In contrast
to the DQN, an actor-critic architecture is used.
The Critic still learns the Q function, which is
called Q
φ
in this context. Additionally, a second net-
work is used for the Actor π
θ
. The loss function for
the Critic is therefore:
L
critic
= (r + γQ
φ
(s
t+1
, π
θ
(s
t+1
)) − Q
φ
(s, a))
2
(6)
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
136

In contrast to DQN, DDPG uses an explicit policy,
which is defined by the actor network π
θ
. Since Q is a
differentiable network, π can be trained in such a way
that it maximizes Q:
L
actor
= −Q
φ
(s, π
θ
(s)) (7)
A more detailed description can be found in (Lill-
icrap et al., 2015).
2.3 Hyperparameter
Hyperparameters are not only part of the Deep RL al-
gorithm but also of the exploration strategy and the
environment. To demonstrate the hyperparameter op-
timization the DDPG algorithm is chosen in this con-
tribution. The DDPG (Lillicrap et al., 2015) is charac-
terized by its good results in continuous control prob-
lems (Duan et al., 2016), although being sensitive to
numerous hyperparameters (Rupam Mahmood et al.,
2018). The hyperparameters are outlined below.
2.3.1 DDPG Hyperparameter
Batch Size: Number of samples used during an up-
date (gradient descent).
Gamma: Discount factor ∈ [0, 1] defines up to
what extent future rewards influence the return in time
step t.
Actor and Critic Learning Rates: Defines the step
size in solution direction and controls how strongly
the weights of the artificial neural network are up-
dated by the loss gradient.
Number of Neurons: Layer size of the neural net-
work
Regularization Factor Critic: Method to prevent
overfitting and improve models generalization prop-
erties.
Memory Capacity: Size of the memory containing
the batch samples.
2.3.2 Exploration Hyperparameter
As previously mentioned, exploration is not always
necessary. It depends on the particular environment.
If it is uncertain, whether exploration is required or
not, the following approach can be chosen. Initially
an exploration strategy (in this case the OUP) is ap-
plied. The hyperparameter optimization presented in
this paper implicitly considers this. As soon as the ex-
ploration turns out to be unnecessary for the learning
process, the optimization process is capable of sup-
pressing the exploration. In the case of the OUP, the
standard deviation of the OUP approaches zero. The
hyperparameters of the OUP are listed below.
Mean: Mean Value of the OUP
Theta: Reversion Rate of the OUP
Sigma: Standard Deviation of the OUP
2.3.3 Environmental Hyperparameter
The environment has contextspecific hyperparame-
ters. Depending on the environment, arbitrary ones
can be included. This can be for example the training
duration. A long training duration allows the agent
to interact with his environment for a longer period
of time. However, this extends the entire RL learning
process. Short training sessions shorten the entire RL
learning process, but can cause the agent to not get to
know the environment properly and thus not be able
to exploit the full potential. The time constraint de-
scribed in chapter one is thus a hyperparameter of the
environment.
3 HYPERPARAMETER
OPTIMIZATION METHODS
As the previous chapter has shown, there are many
hyperparameters to be defined for the learning pro-
cess. This chapter discusses methods that automa-
tize this procedure. The performance of the RL algo-
rithms depends essentially on the setting of the inter-
nal parameters (Henderson et al., 2017) (Melis et al.,
2017). Suitable hyperparameters are problem-specific
and the optimal hyperparameter combination is often
not intuitive. The widespread manual choice of hyper-
parameters therefore requires expertise and is time-
consuming. Several strategies for automating param-
eter selection are listed below.
3.1 Model-free Approaches
Two intuitive approaches for determining suitable hy-
perparameters are grid and random search. Both
methods are easy to implement and often chosen for
hyperparameter optimization. Model-based search al-
gorithms can use the knowledge gained during their
processing to adapt and intensify the search in areas
Hyperparameter Optimization for Deep Reinforcement Learning in Vehicle Energy Management
137

of the search space with higher result potential. The
grid and random search algorithm do not process this
information for adaptation and are thus referenced
to as model-free strategies. The grid search consid-
ers a discrete, grid-shaped subset instead of the en-
tire parameter space. The random search selects the
hyperparameters from the equally distributed search
space. Bergstra and Bengio proved that the random
choice of hyperparameter combinations is more effi-
cient than searching a grid subset (Bergstra and Ben-
gio, 2012). The advantage of the model-free approach
is the prevention of converging into local optima. The
disadvantage is the missing restriction of the param-
eter space. Repeatedly unfavourable hyperparame-
ter combinations are chosen and the procedure is ex-
tremely time-consuming due to the curse of dimen-
sionality in large parameter spaces. Considering the
optimization of computationally intensive Deep RL
algorithms, the efficiency of the optimization process
is crucial. Model-based approaches represent a poten-
tial solution to this dilemma.
3.2 Model-based Aproaches
Compared to the model-free methods, model-based
approaches do not select hyperparameter configura-
tions randomly. Guided by an underlying model of
the parameter space which is iteratively enhanced,
they select parameters from promising areas of the
hyperparameter space, thereby making the search
more effective. The functional relationship between
hyperparameters and the performance of the RL
algorithm is unknown, therefore no gradient based
approximation method can be applied. The approach
of model-based optimization is constructing a sur-
rogate model of the hyperparameter space that can
be searched faster than the real search space. The
Bayesian optimization strategy is an approach for
model-based optimization of hyperparameters. The
model is derivative free, less prone to be caught in
local minima and characterized by its effectiveness
(Brochu et al., 2010). The surrogate model is fitted
onto the evaluated data set – Sequential Model-Based
Global Optimization (SMBO) – and the acquisition
function determines the next hyperparameter com-
bination to be evaluated, optimizing the expected
improvement. Its optimum is located in regions
of high uncertainties (exploration) and high per-
formance prediction (exploitation). This iterative
process converges the surrogate model to the real
hyperparameter space. For more detailed information
see (Lizotte, 2008) (Osborne et al., 2009). Bayesian
optimization finds suitable hyperparameters more
efficiently than the model-free grid and random
search (Bergstra and Bengio, 2012) and in some
cases surpasses the manual parameter selection of
experts (Thornton et al., 2012), (Snoek et al., 2012).
The Gaussian Process is the most commonly used
model approach for Bayesian optimization (Shahriari
et al., 2016) and is characterized by its flexibility,
well calibrated uncertainties and analytical properties
(Jones, 2001) (Osborne et al., 2009). It doesn’t
require training data, instead it is derived from sta-
tistical quantities of the examples and therefore has
a high numerical efficiency and mathematical trans-
parency (Jones, 2001) (Osborne et al., 2009). The
Gaussian Process estimates its own predictability,
correctly propagates known input errors and allows
the balance between exploration and exploitation.
If the hyperparameter number is moderate, the
Gaussian Process generates a stable surrogate model
of the parameter space. The disadvantage of the
Gaussian Process is that it is based on the inversion
of the covariance which increases the computation
effort cubically with the number of optimization
runs (Snoek et al., 2015). In contrast, the computa-
tional effort of Enesemble Methods increases linearly.
Ensemble methods consist of decision trees,
which individually represent weak learners but
collectively form a strong learner. Sequential
Model-Based Algorithm Configurations (SMAC)
differ in the way the trees are constructed and the
results are combined. Random Forest is used by
Hutter et al. as a regression model of the SMAC
algorithm. Unlike the Gaussian Process, the model
uncertainties are empirically estimated (Hutter et al.,
2011). Introduced by Breiman, Random Forests
represent a scalable and parallelizable regression
model (Breiman, 2001). The trees of the Random
Forest are trained independently with randomly
generated data sub-samples. The averaging of the
individual predictions increases the generalization
ability of the model and prevents the overfitting of the
training data. The random subsampling of the data
sets and the dimensions used as decision rules in the
nodes of the decision tree, leads to a linearly growing
computational effort with increasing dimensions and
hyperparameters (Hutter et al., 2011). As a result, the
Random Forest can be applied to high dimensional
problems where the Gaussion Process method fails
due to its cubic cost increase.
The gradient boosted trees optimization places the
trees sequentially on the residuals (prediction errors)
of the previous tree. The decision trees therefore
depend on each other. The stronger weighting of
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
138

bad predictions minimizes stepwise the deviations
between model and observed target data. Each new
tree increases the accuracy of the model.
For this paper, the three presented model-based
algorithms – Gaussian Process (GP), Random Forest
(RF), Gradient Boosted Random Trees (GBRT) – are
used for hyperparameter optimization.
4 EXPERIMENTAL SETUP
A holistic and optimal design of the energy manage-
ment of a Hybrid Electric Vehicle (HEV) for all con-
ceivable driving styles, traffic situations, and operat-
ing sites is challenging. To solve this task, a Deep Re-
inforcement Learning Energy Management was de-
veloped at the Technische Universit
¨
at Dresden (Liess-
ner et al., 2018). The energy management serves as
the object of investigation in this paper. The envi-
ronment is adopted and the hyperparameters are opti-
mized with the presented methods.
4.1 Environment
The environment consists of a driver and vehicle
model which are briefly presented below.
4.1.1 Driver Model
In order to generate realistic speed curves, the
stochastic driver model presented in (Liessner et al.,
2017) is applied. The speed curves based on a
weighted drawing are much closer to driving in real
traffic than the repeated of the same deterministic
driving cycle, which may result in a bad generaliza-
tion.
4.1.2 Vehicle Model
A simulation model of a mild hybrid vehicle serves
as the vehicle model. Its input variables are a speed
and gradient profile as well as the gear, the usage of
the electric motor and the battery cooling. The output
variables include fuel consumption, battery charge
status, derating and battery temperature.
4.1.3 Driver-vehicle-interaction
In each time step, the driver (the stochastic driver
model) is given the current vehicle velocity
k
and se-
lects the succeeding velocity
k+1
accordingly. The au-
tomatic transmission chooses a suitable gear depend-
ing on the speed and acceleration. The agent moni-
tors the choice of driver and automatic transmission
as well as the vehicle status (battery charge status
(SOC), battery temperature and derating) and controls
the electric motor and battery cooling accordingly.
4.2 Agent
Following an introduction of the environment, this
section describes the implemented agent and its in-
teraction with the environment.
4.2.1 Action a
Depending on the state (and the progress of the learn-
ing process), the agent chooses an action in each time
step. The action consists of two parts. The Agent in-
fluences firstly the performance/power/output of the
electric machine P
EM
and secondly the control of the
battery cooling C
Cool
.
a = [P
EM
, C
Cool
] (8)
4.2.2 State s
The state is a combination of state variables influ-
enced by the driver and the agent. The state observed
by the agent is thus:
s = [n
whl
, M
whl
, gear, SOC, ϑ
bat
, DR] (9)
Where n
whl
is the wheel speed, M
whl
the wheel
torque, SOC the battery state of charge, ϑ
bat
the bat-
tery temperature and DR the derating.
4.2.3 Reward r
The objective of the energy management is to mini-
mize the vehicle’s energy consumption. The achieved
energy savings can therefore be used as a reward.
r = f uel
save
(10)
4.2.4 Training and Validation Process
To prevent overfitting and to achieve good generaliza-
tion, the following training and validation strategy is
employed.
Training: In the training process, the speed curves
and vehicle initial values (SOC, battery temp, derat-
ing) vary in each run, which is comparable to driving
in real traffic. Since the speed curves and vehicle ini-
tial values differ in each training run, evaluation of
the training progress and selection of the best neural
network requires a validation process.
Hyperparameter Optimization for Deep Reinforcement Learning in Vehicle Energy Management
139

Validation: In contrast to the training process, the
validation process always uses the same, market-
specific driving cycle. It lasts 50,000 seconds and
always uses identical vehicle initial values to ensure
comparability. The approach can be compared to
driving on a test bench. The cumulated reward de-
termined in the validation is used as a measure for the
evaluation of the selected hyperparameters.
Training Duration: Since a long training process is
costly, minimizing the training time is the objective.
A time limit of one hour for the single training pro-
cess with set hyperparameters is defined, with a lim-
itation of the hyperparameter optimization iterations
to 100, thus resulting in an overall time constraint of
100 hours.
4.3 Evaluation Reference
A reference is necessary for the evaluation of the op-
timization results. The hyperparameters from the ini-
tial DDPG paper (Lillicrap et al., 2015) are defined
as reference. These are not random choices but pa-
rameters already optimized by the author (Lillicrap),
which proved good properties in various domains.
The hyperparameter optimization must therefore sur-
pass an already good parameter selection. The hy-
perparameters selected by Lillicrap are listed in Table
2. These hyperparameters are also the starting point
for the hyperparameter optimization using the model-
based methods presented in the chapter 3. The initial
hyperparameters of the environment (the duration of
the training cycle) is derived from expert knowledge.
The value corresponds to the mean value of the value
range available for the hyperparameter optimization.
5 RESULTS
5.1 Analysis of the Hyperparameter
Optimization Process
Figure 2 presents the hyperparameter optimization re-
sults for all three chosen algorithms, with the cu-
mulative fuel saving as return (cumulative rewards).
The optimization is executed with 100 iterations,
which proves sufficient to identify trends and behav-
ior specifics of the algorithms. The first iteration
is performed with the predefined hyperparameters of
the reference, followed by 20 iterations with random
choice of the hyperparameters. This initial phase is
performed as sampling of the search space. There-
after, the algorithms begin the focused search accord-
ing to their model-based behavior. The Random For-
est approach immediately achieves high scores and
expands them in the further learning process. The
GBRT shows a similar behavior whereby the maxi-
mum values are lower than in the Random Forest. The
GP shows the lowest scores in comparison. In the
range of step 50, scores around 40000 are achieved.
In the further optimization process these scores de-
crease again. Table 1 summarizes the best achieved
results for all three algorithms. The trend lines in
Figure 2 give an impression of the learning capabili-
ties of the algorithms. The Random Forest algorithms
achieves the best overall result and the steepest learn-
ing increase.
Table 1: Best Results of the Hyperparameter Optimization.
Method GP GBRT RF
Return 40018.8 45995.5 47220.2
5.2 Evaluation of the Hyperparameter
Optimization Results
At this point the performance of the optimized hyper-
parameters are analysed in comparison to the expert
hyperparameters and additionally to a random set of
hyperparameters. For this purpose, the fuel consump-
tion optimization is performed with the three sets of
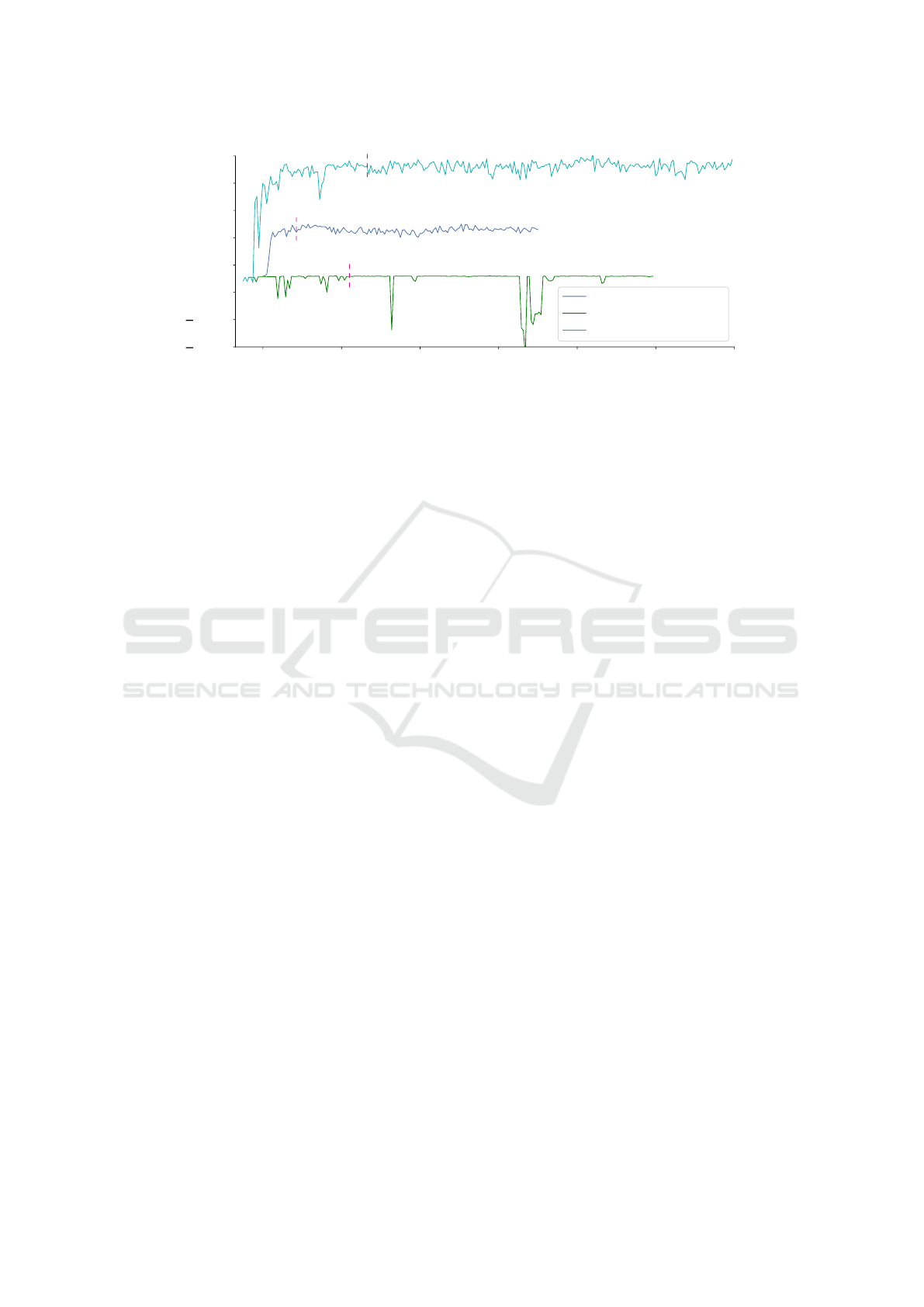
hyperparameters, which results are shown in figure 3.
In the initial phase of the executions, each optimiza-
tion fills the memory (replay buffer) of the DDPG
algorithm with sample episodes. In this phase, the
learning process has not yet begun. In the second
phase, the learning process begins, based on the sets
in the memory. In this phase, a validation run is per-
formed every 50 training sessions. The results of the
validation runs deliver the values for figure 3.
As stated before, the goal of the analysis in this
contribution is to finish the learning of the DDPG al-
gorithm within one hour for the realistic application
in industrial tasks. This hard limit has influence on
the extend of the memory, so that the DDPG can be-
gin the learning within that given time frame. This
has also been considered in the hyperparameter op-
timization before. The one hour mark is represented
by the red dashed line. As the episode size vary for
each hyperparameter set, the one hour mark differs on
the episode axis in figure 3. Nevertheless, the learn-
ing process is continued for seven additional hours af-
ter the one hour mark, to validate no additional time
would have further increased the learning results.
The random hyperparameters achieve poor re-
sults. Even a longer training time does not compen-
sate an unsuitable hyperparameter choice. This con-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
140

0 20 40 60 80 100
Iterations
0
Return
GBRT
GP
RF
50000
40000
30000
20000
10000
Figure 2: Hyperparameter Optimization Results.
firms that suitable model parameters are essential for
high performance. The reference cannot benefit from
a longer training process either. The maximum value
of 25000 is not further increased. The learning pro-
cess with the optimized hyperparameters achieves al-
most twice as high values compared to the reference
and is stable in the further training process. The re-
sults are not significantly increased after one hour,
which suggests that the hyperparameter optimization
makes good use of the time available to it.
After the reasonable choice of hyperparameters by
the Random Forest approach has been confirmed, the
individual hyperparameters will be discussed in the
following sections.
Table 2: Reference and Optimized Hyperparameters.
Hyperparameter Optimization Reference
Steps/Episode 299 500
Batch Size 1024 64
Learning Rate Actor 5.19e-05 1e-04
Learning Rate Critic 2.42e-04 1e-03
Neurons(L1/L2) 468/512 400/300
Gamma 0.99853 0.99
Regularization Critic 0.01224 0.0
Memory 1e06 1e06
Theta (EM/Bat) 0.49/ 0.20 0.15/0.15
Sigma(EM/Bat) 0.042/0.025 0.20/0.20
Return 47220.2 25003.5
5.3 Analysis of the Hyperparameters
The sensitivity of the hyperparameters are summa-
rized in figure 4. A selection of the most important
peculiarities are described below.
5.3.1 Neural Network Size
Large neural networks have good approximation
properties. Small networks can be updated faster. The
hyperparameter optimization prefers large networks
for both layers. This means that fewer episodes can
be performed in one hour. This requires a sample ef-
ficient training process, which apparently succeeds.
5.3.2 Batch Size
In (Smith et al., 2017) it is recommended to increase
the batch size in order to reduce the training time or
to achieve better results in the available time. This as-
sessment is consistent with the result of hyperparam-
eter optimization. It also prefers large batch sizes and
achieves the best result at the maximum batch size of
1024.
5.3.3 Learning Rate
The actor is more sensitive to the learning rate choice
and has a lower learning rate than the critic. While
good results are achieved even with high learning
rates for the critic, a high actor learning rate leads to
a performance breakdown.
5.3.4 Regularization
The regularization is not mandatory. The hyper-
parameter optimization reduces this value to zero.
The regularization prevents overfitting in supervised
learning. Since the overfitting is fewer explicit in the
RL, the RL can apparently omit regularization.
5.3.5 Discount Factor
The discount factor gamma determines how many fu-
ture time steps the agent considers when choosing
an action. This value strongly depends on the en-
vironment. In the energy management environment
a discount factor close to 1 allows the agent to take
actions very future oriented. A low discount factor
Hyperparameter Optimization for Deep Reinforcement Learning in Vehicle Energy Management
141
2000 4000 6000 8000 10000 12000 14000
Episodes
20000
10000
0
10000
20000
30000
40000
50000
Return
Baseline
Random Konfiguration
HPO Result
Figure 3: Comparison of the Optimized Hyperparameters to the Expert and Random Hyperparameters.
would immediately discharge the battery, thus reduc-
ing fuel consumption in the short term and causing
disadvantages in the long term. The challenge is on
the one hand to achieve savings at the moment and on
the other hand to consider the long-term impact. The
agent obviously manages this better with a higher dis-
count factor. This setup can be confirmed by expert
knowledge.
5.3.6 Exploration
The optimization result in table 2 shows that both ac-
tions require only a weak additional noise signal for
exploration. A complete avoidance of exploration is
however disadvantageous. On the one hand, the agent
receives a direct feedback for his action in each time
step. On the other hand, the influence of a battery that
is too warm or too empty has a delayed effect. Thus,
a use of the exploration in the environment seems ad-
vantageous.
6 CONCLUSIONS AND FUTURE
WORK
The research confirms the importance of the hyper-
parameters for the Deep RL learning process. The
DDPG algorithm reacts very sensitively to the choice
of hyperparameters. This can lead to the problem,
that only a single wrongly selected hyperparameter
prevents the successful learning process. A further
complication is the number of DDPG algorithm hy-
perparameters. An initial optimal manual selection of
the hyperparameters is rather unlikely. The model-
based hyperparameter optimization presented in this
paper provides an approach to solve this problem. In
this contribution, a Random Forest approach achieves
very good hyperparameters. Due to the optimization
time limit based on the application and the continuous
parameter space, the final hyperparameters are not the
one and only optimal hyperparameters. Nevertheless
the hyperparameters obtained from the optimization
lead to twice the performance compared to the origi-
nal DDPG hyperparameters (Lillicrap et al., 2015) set
by expert knowledge.
The hyperparameter optimization further supports
the decision, whether an exploration is necessary or
not. Depending on the environment, the hyperparam-
eter optimization uses the exploration in any scale
or fades it out completely. The testing of the op-
timized hyperparameters indicates the good utiliza-
tion of the time available by the Random Forest ap-
proach. Within 100 hours, very good hyperparame-
ters are generated. Using these, the learning results
in the application are of high quality, even within the
time frame of one hour. In the hybrid vehicle environ-
ment, the hyperparameter optimization automatically
sets a suitable discount factor and the environment
hyperparameter. This implies, Reinforcement Learn-
ing in combination with hyperparameter optimization
simplifies the application considerably and opens up
the framework to a wider audience.
This topic will be extended by experiments exam-
ining how the amount of time can be reduced by a
suitable parallelization. In the example, 100 runs have
been performed, each with a one-hour RL learning
process. The aim is to achieve a similar hyperparame-
ter result in a shorter time. Furthermore, hyperparam-
eter optimization will be performed for further Deep
RL algorithms like A3C, PPO and D4PG. In the liter-
ature, it is noted that these react less sensitively to the
hyperparameters. Therefore, it is interesting to exam-
ine to what extent the performance of the algorithms
can be increased by an hyperparameter optimization.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
142
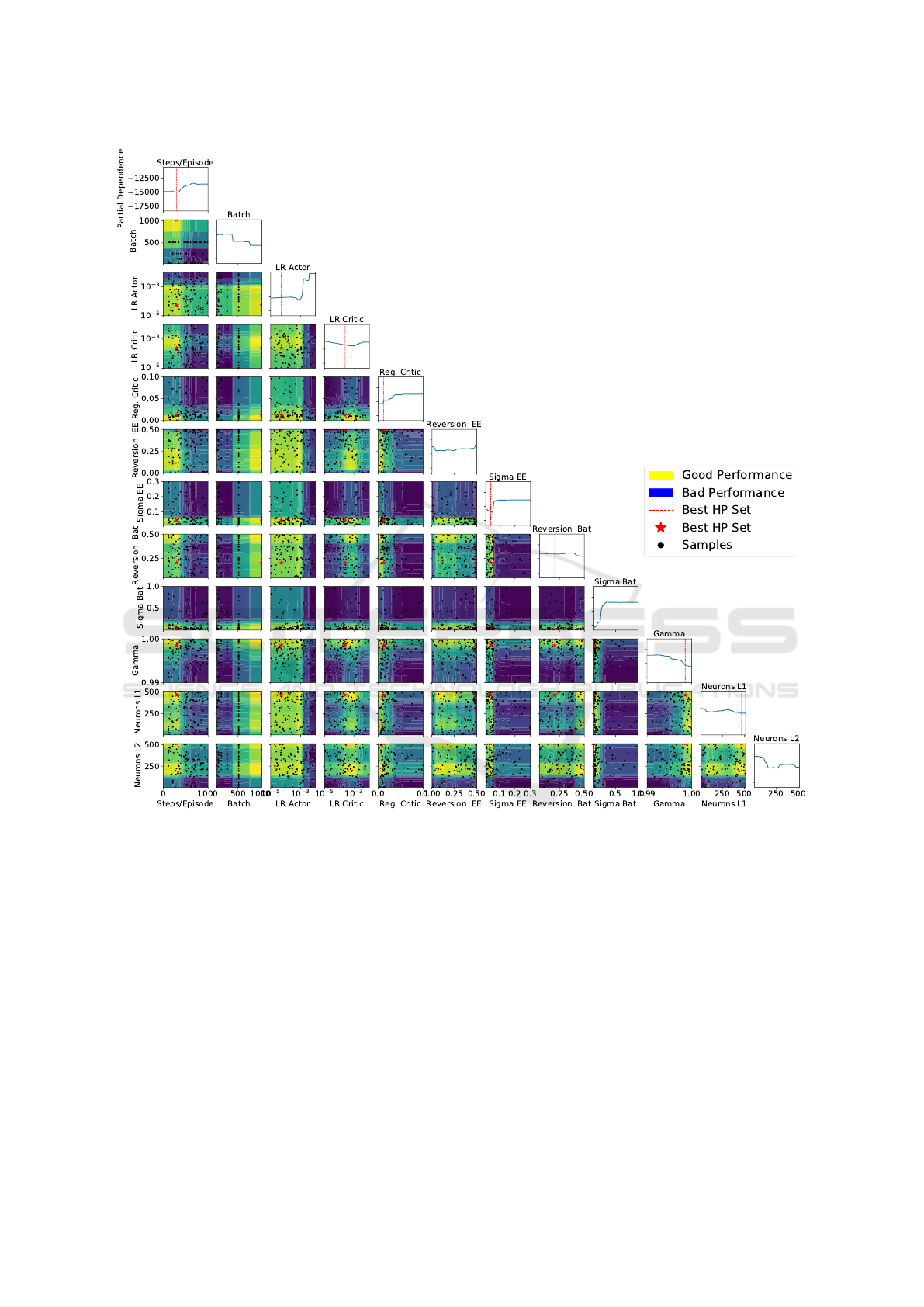
Figure 4: Sensitivity analysis of the hyperparameters. The figure shows the surrogate model of the hyperparameter optimiza-
tion for the entire hyperparameter space. It shows the individual samples, the sensitivities of the hyperparameters and the
interactions of the hyperparameters. Each row and column describes one hyperparameter. The sensitivity of the individual
hyperparameter is plotted in the diagonal. Relatively flat curves as in Reversion Bat indicate that the hyperparameter is less
sensitive. In contrast, the curves of Sigma Bat and LR Actor indicate a more distinctive sensitivity. For the selection of the
best hyperparameters, the appropriate minima are of interest.
REFERENCES
Barsce, J. C., Palombarini, J. A., and Mart
´
ınez, E. C.
(2018). Towards autonomous reinforcement learning:
Automatic setting of hyper-parameters using bayesian
optimization. CoRR, abs/1805.04748.
Bergstra, J. and Bengio, Y. (2012). Random search for
hyper-parameter optimization. J. Mach. Learn. Res.,
13:281–305.
Breiman, L. (2001). Random forests. Machine Learning.
Brochu, E., Cora, V. M., and de Freitas, N. (2010). A
tutorial on bayesian optimization of expensive cost
functions, with application to active user model-
ing and hierarchical reinforcement learning. CoRR,
abs/1012.2599.
Chollet, F. (2017). Deep Learning with Python. Manning
Publications Co., Greenwich, CT, USA, 1st edition.
Duan, Y., Chen, X., Houthooft, R., Schulman, J., and
Abbeel, P. (2016). Benchmarking deep reinforcement
learning for continuous control. In Proceedings of the
33rd International Conference on International Con-
Hyperparameter Optimization for Deep Reinforcement Learning in Vehicle Energy Management
143

ference on Machine Learning - Volume 48, ICML’16,
pages 1329–1338. JMLR.org.
Falkner, S., Klein, A., and Hutter, F. (2018). Bohb: Robust
and efficient hyperparameter optimization at scale. In
Proceedings of the 35rd International Conference on
International Conference on Machine Learning.
Graves, A., Mohamed, A., and Hinton, G. E. (2013).
Speech recognition with deep recurrent neural net-
works. CoRR, abs/1303.5778.
Henderson, P., Islam, R., Bachman, P., Pineau, J., Precup,
D., and Meger, D. (2017). Deep reinforcement learn-
ing that matters. CoRR, abs/1709.06560.
Hutter, F., Hoos, H. H., and Leyton-Brown, K. (2011). Se-
quential model-based optimization for general algo-
rithm configuration.
Jones, D. R. (2001). A taxonomy of global optimiza-
tion methods based on response surfaces. Journal of
Global Optimization, 21(4):345–383.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Proceedings of the 25th International
Conference on Neural Information Processing Sys-
tems - Volume 1, NIPS’12, pages 1097–1105, USA.
Curran Associates Inc.
Liessner, R., Dietermann, A., B
¨
aker, B., and L
¨
upkes, K.
(2017). Generation of replacement vehicle speed cy-
cles based on extensive customer data by means of
markov models and threshold accepting. 6.
Liessner, R., Schroer, C., Dietermann, A., and B
¨
aker, B.
(2018). Deep reinforcement learning for advanced
energy management of hybrid electric vehicles. In
Proceedings of the 10th International Conference on
Agents and Artificial Intelligence, ICAART 2018, Vol-
ume 2, Funchal, Madeira, Portugal, January 16-18,
2018., pages 61–72.
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,
Tassa, Y., Silver, D., and Wierstra, D. (2015). Contin-
uous control with deep reinforcement learning. CoRR,
abs/1509.02971.
Lizotte, D. J. (2008). Practical Bayesian Optimization. PhD
thesis, Edmonton, Alta., Canada. AAINR46365.
Mania, H., Guy, A., and Recht, B. (2018). Simple random
search provides a competitive approach to reinforce-
ment learning. CoRR, abs/1803.07055.
Melis, G., Dyer, C., and Blunsom, P. (2017). On the state of
the art of evaluation in neural language models. CoRR,
abs/1707.05589.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness,
J., Bellemare, M. G., Graves, A., Riedmiller, M., Fid-
jeland, A. K., Ostrovski, G., et al. (2015). Human-
level control through deep reinforcement learning.
Nature, 518(7540):529.
Osborne, M., Garnett, R., and Roberts, S. (2009). Gaussian
processes for global optimization.
Plappert, M., Houthooft, R., Dhariwal, P., Sidor, S.,
Chen, R. Y., Chen, X., Asfour, T., Abbeel, P., and
Andrychowicz, M. (2017). Parameter space noise for
exploration. CoRR, abs/1706.01905.
Rupam Mahmood, A., Korenkevych, D., Vasan, G., Ma, W.,
and Bergstra, J. (2018). Benchmarking Reinforcement
Learning Algorithms on Real-World Robots. ArXiv e-
prints.
Shahriari, B., Swersky, K., Wang, Z., Adams, R. P., and
de Freitas, N. (2016). Taking the human out of the
loop: A review of bayesian optimization. In Proceed-
ings of the IEEE.
Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I.,
Huang, A., Guez, A., Hubert, T., Baker, L., Lai, M.,
Bolton, A., et al. (2017). Mastering the game of go
without human knowledge. Nature, 550(7676):354.
Smith, S. L., Kindermans, P., and Le, Q. V. (2017). Don’t
decay the learning rate, increase the batch size. CoRR,
abs/1711.00489.
Snoek, J., Larochelle, H., and Adams, R. P. (2012). Prac-
tical bayesian optimization of machine learning algo-
rithms. In Pereira, F., Burges, C. J. C., Bottou, L., and
Weinberger, K. Q., editors, Advances in Neural In-
formation Processing Systems 25, pages 2951–2959.
Curran Associates, Inc.
Snoek, J., Rippel, O., Swersky, K., Satish, R. K. N., Sun-
daram, N., Patwary, M. M. A., Prabhat, and Adams,
R. P. (2015). Scalable bayesian optimization using
deep neural networks. In International Conference on
Machine Learning.
Springenberg, J. T., Klein, A., Falkner, S., and Hutter, F.
(2016). Bayesian optimization with robust bayesian
neural networks. In Proceedings of the 30th Interna-
tional Conference on Neural Information Processing
Systems, NIPS’16, pages 4141–4149, USA. Curran
Associates Inc.
Sutskever, I., Vinyals, O., and Le, Q. V. (2014). Sequence
to sequence learning with neural networks. CoRR,
abs/1409.3215.
Sutton, R. S. and Barto, A. G. (1998). Introduction to Re-
inforcement Learning. MIT Press, Cambridge, MA,
USA, 1st edition.
Sutton, R. S. and Barto, A. G. (2012). Reinforcement Learn-
ing: An Introduction. O’Reilly.
Thornton, C., Hutter, F., Hoos, H. H., and Leyton-Brown,
K. (2012). Auto-weka: Automated selection and
hyper-parameter optimization of classification algo-
rithms. CoRR, abs/1208.3719.
Uhlenbeck, G. E. and Ornstein, L. S. (1930). On the theory
of the brownian motion. Phys. Rev., 36:823–841.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
144
