A Belief Approach for Detecting Spammed Links in Social Networks

Salma Ben Dhaou

, Mouloud Kharoune

, Arnaud Martin

and Boutheina Ben Yaghlane

LARODEC, ISG of Tunis, Tunisia

Univ Rennes, CNRS, IRISA, France

Keywords:

Social Networks, Communities, Theory of Belief Functions, Probability.

Abstract:

Nowadays, we are interconnected with people whether professionally or personally using different social

networks. However, we sometimes receive messages or advertisements that are not correlated to the nature

of the relation established between the persons. Therefore, it became important to be able to sort out our

relationships. Thus, based on the type of links that connect us, we can decide if this last is spammed and

should be deleted. Thereby, we propose in this paper a belief approach in order to detect the spammed links.

Our method consists on modelling the belief that a link is perceived as spammed by taking into account the

prior information of the nodes, the links and the messages that pass through them. To evaluate our method,

we ﬁrst add some noise to the messages, then to both links and messages in order to distinguish the spammed

links in the network. Second, we select randomly spammed links of the network and observe if our model is

able to detect them. The results of the proposed approach are compared with those of the baseline and to the

k-nn algorithm. The experiments indicate the efﬁciency of the proposed model.

1 INTRODUCTION

Currently, a lot of researches focus on the analysis

of social networks. Some authors are interested in

the problem of predicting links (Al Hasan and Zaki,

2011), trying to predict likelihood of a future asso-

ciation between the nodes in the current state of the

graph. Other works focus on the spammers detection

in social networks such as (Zheng et al., 2015). They

investigate and analyse the behaviour of the spam-

mers. However, these researches do not deal with the

case where a link can be spammed.

Sometimes, the actors of a social network can re-

ceive messages which are uncorrelated with the type

of link that connects them. From there, it became im-

perative to be able to sort out the types of relation-

ships in the social network and therefore, allow each

actor to decide if this link is spammed and should be

removed.

In this context, we propose a new approach which,

from the information on the nodes, links and mes-

sages, makes it possible to determine if a link is

spammed and should be deleted. As we are inter-

ested in the observation of interactions in credible so-

cial network, all information about nodes, links and

messages are related. Indeed, the information on the

nodes permits to know the type of link which connects

them. From there, the type of message transiting on it

is deﬁned.

Currently, we have several information transiting

in social networks. However, most of the time, this

information may be imperfect, imprecise, uncertain,

vague or even incomplete. It becomes essential to use

formalism to model these imperfections. Historically,

the formalism of probability theory is the most com-

monly used. Nevertheless, it does not allow the mod-

elling of ignorance. Indeed, in the absence of infor-

mation, this formalism associates the same probabil-

ity with each event. In addition, due to the additivity

axiom, the probability of an event implies a value on

the probability of its complementary.

The limitations of this formalism was a motivation

for the development of new theories of uncertainty

such as the theory of possibilities (Zadeh, 1999) and

the theory of belief functions (Dempster, 1967) which

impose no relation between an event and its com-

plementary and it allow to easily model ignorance.

The theory of belief functions can be considered more

general than that of probabilities or possibilities since

we ﬁnd these as particular cases.

From there, our approach is based on the theory

of belief functions in order to model the uncertainty

and imprecision due to the different sources of in-

formation (links, nodes and messages) and combine

602

Ben Dhaou, S., Kharoune, M., Martin, A. and Ben Yaghlane, B.

A Belief Approach for Detecting Spammed Links in Social Networks.

DOI: 10.5220/0007364906020609

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 602-609

ISBN: 978-989-758-350-6

network information. We compare the proposed ap-

proach with a probabilistic method and the k-nn algo-

rithm.

This paper is structured as follows. In section 2,

we recall some basic concepts related to this work.

We propose in section 3 our belief approach to detect

spammed links. Finally, section 4 is devoted to the

experiments and section 5 concludes the paper.

2 BACKGROUND

In this section, we recall some related works and some

basis of the theory of belief functions.

2.1 Related Works

Several works have focused on the problem of predic-

tion of links or the detection of spammers in social

networks. The authors of (Al Hasan and Zaki, 2011)

present a survey of some representative link predic-

tion methods by categorising them by the type of the

models: the traditional models which extract a set of

features to train a binary classiﬁcation mode. The sec-

ond type of methods are the probabilistic approaches

which model the joint-probability among the enti-

ties in a network by Bayesian graphical models. Fi-

nally, the linear algebraic approach which computes

the similarity between the nodes in a network by rank-

reduced similarity matrices.

The authors of (Liu et al., 2015) introduced an

unsupervised link prediction method, the link sam-

ple feature representation method and the DBN-based

link prediction method for signed social networks.

As future works, the authors intend to ﬁnd other ap-

proaches for link prediction in SSNs (Signed Social

Networks). In addition, they try to ameliorate the

performance of their method and to extract more fea-

tures.

Regarding the problem of detecting spammers in

social networks, (Zheng et al., 2015) adopt the spam-

mers feature to detect spammers and test the result

over Sina Weibo. In addition, they study a set of most

important features related to message content and user

behaviour in order to apply them on the SVM based

classiﬁcation algorithm for spammer detection. Al-

though the proposed approach could achieve precise

classiﬁcation result, it takes over an hour in a process

for model training. Furthermore, in the era of big data

with huge data volume and convenient access, feature

extraction mechanism in the proposed model might

be low adaptive and take a lot of time.

The authors in (Martinez-Romo and Araujo,

2013) introduced a method based on the detection of

spam tweets in isolation and without previous infor-

mation of the user and the application of a statistical

analysis of language to detect spam in trending top-

ics. The authors present an approach to detect spam

tweets in real time using language as the primary tool.

Although the work presented is interesting, the

analysed dataset is limited and may still contain some

bias. In addition, the number of spam tweets is a

lower bound of the real number. As a future work,

the authors intend to select the most appropriate fea-

tures for use in a detection system in real time.

In (Washha et al., 2016), the authors present an

approach for detecting spammers on Twitter. In their

work, they try ﬁrst to ﬁnd to what extent it is possible

to increase the robustness of user’s and content fea-

tures used in the literature. Then, the authors were

interested to sort out if there is an accessible and un-

modiﬁable property overtime such that it can be lever-

aged for advancing the available features as well as

designing new features.

To sum up, some works in the literature focused

on the prediction of the class label of tweet such as

in (Martinez-Romo and Araujo, 2013). Other re-

searches (Washha et al., 2016; Zheng et al., 2015)

were interested on analysing the user’s proﬁle to pre-

dict whether the user is a spammer or not.

All these works are interesting either in detect-

ing spammers or predicting links in social networks.

However, the researches interested in the problem of

predicting links, focus only on how to add links to

the network when an entity disappears. As for re-

searches on the problem of spammer detection, they

focus solely on the analysis of node behaviour or the

content of the tweets.

Therefore, we propose in this paper a method

that allows the detection of spammed links in a so-

cial network. Contrary to the works of the literature

mentioned above, we suppose that the messages ex-

changed on the network are correct and that the nature

of the links can be modiﬁed according to the type of

the messages which transit on it. In addition, in this

work, we take into account the imperfections of the

informations in the social network.

We present in the following few concepts from the

theory of belief functions used in this work.

2.2 Belief Function Theory

The theory of belief functions allows explicitly the

uncertainty and imprecision of knowledge using

mathematical tools (Shafer, 1976; Dempster, 1967).

In fact, it is a suitable theory for the representation

and management of imperfect knowledge. It allows

to handle uncertainty and imprecision found in data,

A Belief Approach for Detecting Spammed Links in Social Networks

603

fuse information and make decisions.

Let Ω be a ﬁnite and exhaustive set whose ele-

ments are mutually exclusive, Ω is called a frame of

discernment. A mass function is a mapping

Ω

: 2

Ω

→ [0, 1]

such that

∑

X∈2

Ω

(X) = 1 and m

Ω

(

0) = 0 (1)

The mass m

Ω

(X) expresses the amount of belief that

is allocated to the subset X. We call X a focal element

if m

Ω

(X) > 0.

A simple support function is a mass function

which has only one focal element other than the frame

of discernment Ω. If m

Ω

(A) = a and m

Ω

(Ω) = 1 − a,

with a ∈ [0, 1] then the source has uncertain and im-

precise knowledge. The source believes partially in

A, but nothing more and A can be imprecise.

We consider the normalised conjunctive rule

called the Dempster rule (Shafer, 2016), given for two

mass functions m

Ω

and m

Ω

for all X ∈ 2

Ω

, X 6=

0 by:

Ω

⊕

(X) =

1 − k

∑

A∩B=X

Ω

(A).m

Ω

(B) (2)

where k =

∑

A∩B=

Ω

(A).m

Ω

(B) is the global conﬂict

of the combination. This rule is adapted when the

combined mass functions are reliable and indepen-

dent.

To focus on the type of relationship between two

different frames of discernment Ω and Θ, we may

use the multi-valued mapping introduced by Hyun

Lee (Lee, 2011):

) =

∑

Γ(e

)=B

Ω

) (3)

with e

⊆ Ω and B

⊆ Θ. Therefore the function Γ is

deﬁned as follow Γ : Ω → 2

The vacuous extension, being a particular case of

multi-valued mapping has the objective to transfer the

mass functions deﬁned on two different frames of dis-

cernment towards an extended frame of discernment

Ω × Θ. For that purpose, we apply the operation of

vacuous extension deﬁned by:

Ω↑Ω×Θ

(B) =



Ω

(A) if B = A × Θ

0 otherwise

(4)

In order to make decision, we use the pignistic

probability introduced by:

BetP(X) =

∑

Y ∈2

Ω

,Y 6=

| X ∩Y |

| Y |

m(Y )

1 − m(

(5)

The decision is made according to the maximum of

pignistic probabilities.

3 PROPOSED APPROACH

In social network, we can ﬁnd the case of a node that

sends certain number of messages that are not com-

patible with a small portion of links connecting it to

the other nodes of the network. Therefore, it would

be more appropriate to delete the spammed links and

keep the node in the network instead of deleting it.

In this work, we consider a spammed link any link

whose initial class has been modiﬁed because of the

incompatibility of the messages that pass through it in

all the iterations. In one iteration, the mass function

of the link is updated and it is the input of the next

iteration.

With the intention of detecting spammed links, the

proposed algorithm takes into account the informa-

tion on the links and the messages. It proceeds by

combining the extended mass functions on the prod-

uct space. Then, it transfer the obtained mass function

to the frame of discernment of the links. After that,

the pignistic probability is used to take decision on

the obtained type of link. This last is then compared

with its initial class. Finally, the modiﬁed links types

are compared in k iterations. If we obtain the same

modiﬁed link, then it is considered as spammed. Oth-

erwise, it is considered as outlier.

The proposed approach will be detailed in what

follow.

In order to model our idea, we use a belief graph

G = {V

} with: V

a set of nodes and E

a set of

edges.

In this paper, we consider three frames of discern-

ment for nodes, links and messages:

• Ω

= {ω

, . . . , ω

} for the set of nodes.

• Ω

= {ω

, . . . , ω

} for the set of links.

• Ω

= {ω

, . . . , ω

} for the set of messages.

In addition, we consider a network with N com-

munities. Each community has a speciﬁc type that has

been deﬁned according to the type of links that make

it up such as a “professional”, “friendly” or “familial”

community .

We present in the following our approach to detect

spammed links.

In order to integrate the belief on the links and on

the messages, we ﬁrst make a vacuous extension on

Ω

× Ω

for each mass of the message of M

and for

each mass of the edge of E

. Therefore, we obtain on

each message M

a mass: m

Ω

×Ω

and on each edge

i j

= (V

) between the nodes V

and V

a mass:

Ω

×Ω

i j

Then, we combine the extended mass functions

using the combination rule of Dempster:

Ω

×Ω

= m

Ω

↑Ω

×Ω

i j

⊕ m

Ω

↑Ω

×Ω

(6)

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

604

We use the multi-valued operation to transfer the

combined mass functions on Ω

× Ω

to Ω

. In fact,

a multi-valued mapping Γ describes a mapping func-

tion:

Γ : Ω

× Ω

→ Ω

(7)

We can calculate these equations by using the for-

mula:

Γ : m

Ω

) =

∑

Γ(e

)=B

Ω

×Ω

) (8)

with e

∈ Ω

× Ω

and B

⊆ Ω

Thereafter, we use the pignistic probability in or-

der to make a decision on the obtained type of links.

This operation allows to make a comparison with the

initial classes of links.

Since our algorithm is iterative, we decide that

a link is spammed and must be removed if its class

changes at all iterations.

Figure 1 summarises the process steps explained

before.

4 EXPERIMENTS

In this section, we present the results obtained after

applying our algorithm.

In this work, we use the LFR benchmark (Lanci-

chinetti et al., 2008) which is an algorithm that gen-

erates artiﬁcial networks that simulate real-world net-

works.

In these experiments, we use 4 LFR network

composed of: 99 nodes with 468 links, 200

nodes with 818 links, 300 nodes with 1227 links

and 400 nodes with 1864 links. All the net-

works have 3 communities. In addition, we con-

sider 3 frames of discernment: Ω

= {C

Ω

= {Friendly, Family, Pro f essional} and Ω

{PNC, PC, INC, IC} with PNC for Personal Not

Commercial, PC for Personal Commercial, INC for

Impersonal Not Commercial and IC for Impersonal

Commercial.

In this experiment, we consider LFR networks

with three communities. We assume that the ﬁrst

community is of type “friendly”, the second of type

“family” and the third is of type “professional”. The

type of community is deﬁned from the types of links

that make up the majority.

We start by generating the mass functions on

nodes and links according to the structure of the net-

work. For each node and each link, we generate 2

focal elements, one on the type of node/link and the

second on Ω

/Ω

by placing the largest value on the

node/link type.

Table 1: Deﬁnition of function Γ given the correspondences

between Ω

× Ω

and Ω

Γ Friendly Family Professional

PNC × ×

PC × ×

INC ×

IC ×

Then, we generate the mass functions on the mes-

sages depending on the link type. For each message

which transits on the network, we generate 2 focal el-

ements, one on the corresponding type of the message

and the second on Ω

Unlike the nodes and links of the network, we gen-

erate new mass functions on the messages at each it-

eration.

We use the passage function Γ deﬁned in table 1

to transfer the mass functions from Ω

× Ω

to Ω

In order to validate our approach, we performed

two types of experimentations:

• The ﬁrst type: adding noise on the messages only,

then adding noise on the messages in addition of

the links.

• The second: pre-selection of a number of

spammed links and see if the proposed approach

detects them.

In this work, we consider a noisy element (i.e. a

link or a message) as an element whose mass func-

tion or probability has been modiﬁed and generated

randomly. For the ﬁrst part of the experiment, we con-

sider different level of noise as follows:

• Case of noisy messages only: 20%, 40%, 50%

and 70% of messages from each community were

noisy.

• Case of noisy messages and noisy links

– 20% noisy messages and 20% noisy links.

– 40% noisy messages and 40% noisy links.

– 50% noisy messages and 50% noisy links.

– 70% noisy messages and 70% noisy links.

4.1 Baseline

In order to show the efﬁciency of our method, we have

performed an algorithm that uses the same principle

in a probabilistic version.

The probabilistic method consists of projecting

the probabilities of links and messages on the Carte-

sian frame. Then they are combined using the aver-

age. This makes it possible to know the type of the

link according to the messages which transit on it.

A Belief Approach for Detecting Spammed Links in Social Networks

605

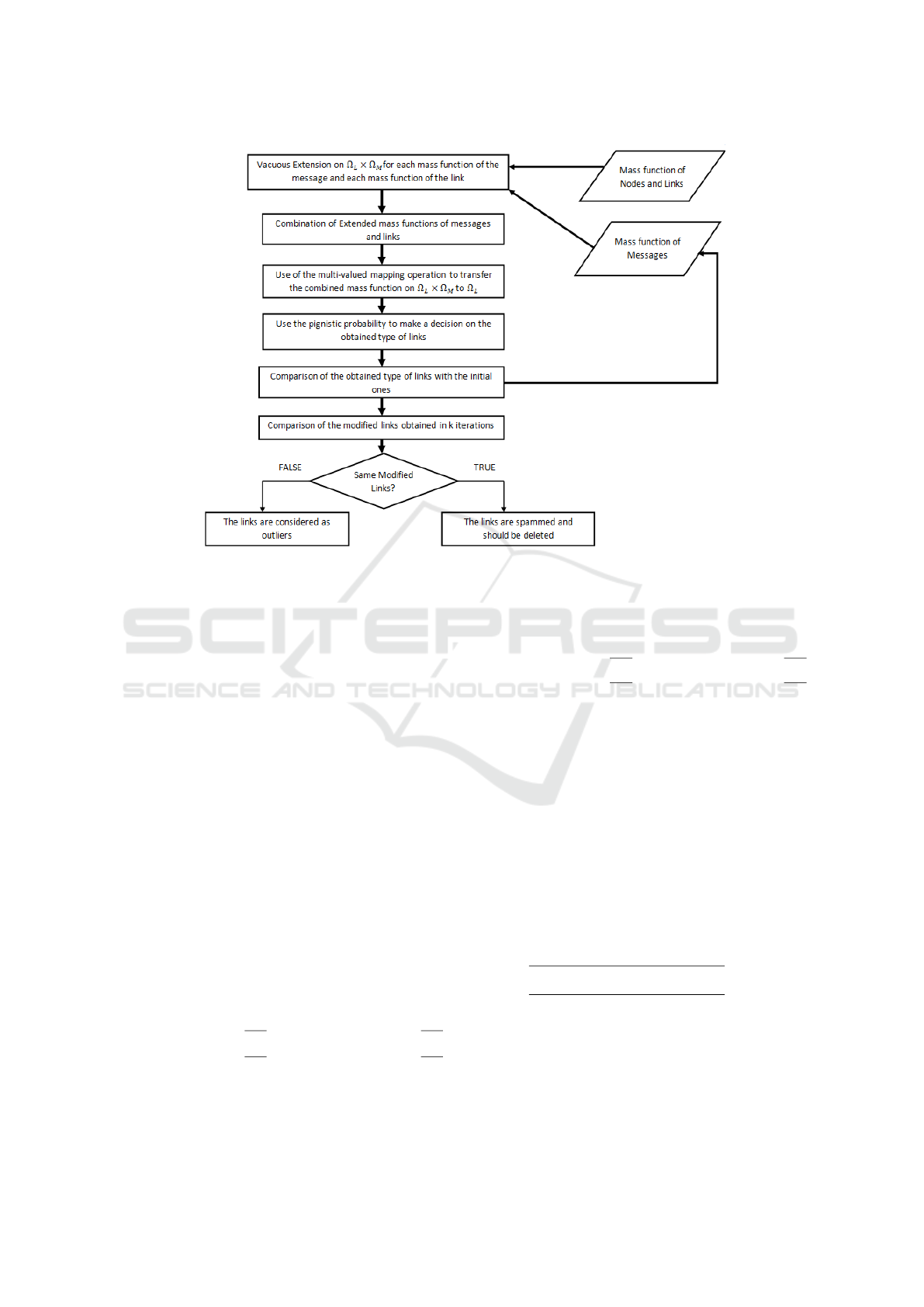
Figure 1: Process of the belief approach.

4.1.1 Extension of Probabilities in the Cartesian

Product

Let the frames of links and messages in a gen-

eral case: Ω

= {ω

, ω

, ..., ω

} and Ω

{ω

, ω

, ..., ω

The Cartesian frame is given by:

Ω

× Ω

= {(ω

, ω

), (ω

, ω

), ..., (ω

, ω

)}

Let 2 vectors of probabilities P

= (P

, P

, ..., P

)

and P

= (P

, P

, ..., P

Given that the frames of the links and messages

are independent, we need to project both probability

vectors on the Cartesian frame Ω

× Ω

in order to

combine them.

The fact that the theory of probabilities cannot

model ignorance forces us to use an equi-probability

when moving from one frame of discernment of links

or messages to the Cartesian frame.

Hence for a given probability: P

= (ω

, i =

1, ..., L, we consider the equi-probability on Ω

model the ignorance. The result is affected to each

pair of Cartesian frame containing ω

. For example:

Ω

×Ω

(ω

, ω

) =

|Ω

, . . . , P

Ω

×Ω

(ω

, ω

) =

|Ω

Ω

×Ω

(ω

, ω

) =

|Ω

, . . . , P

Ω

×Ω

(ω

, ω

) =

|Ω

. . .

By the same process, in order to consider the proba-

bility P

= (ω

, j = 1, ...,M) in the Cartesian space

Ω

× Ω

, we consider the equi-probability on Ω

model the ignorance. For example:

Ω

×Ω

(ω

, ω

) =

|Ω

, . . . , P

Ω

×Ω

(ω

, ω

) =

|Ω

Ω

×Ω

(ω

, ω

) =

|Ω

, . . . , P

Ω

×Ω

(ω

, ω

) =

|Ω

. . .

4.1.2 Calculation of the Average of the

Probabilities

Once the probabilities of the links and messages are

projected on the Cartesian frame, we proceed then to

the combination of both vectors of probabilities us-

ing the average. For example: In this work, we chose

to use the average because it has a compromise be-

haviour. Indeed, if the data contain estimation errors,

the calculation of the average makes it possible to re-

duce this rate of error. For example:

Ω

×Ω

(ω

,ω

)+P

Ω

×Ω

(ω

,ω

)

Ω

×Ω

(ω

,ω

)+P

Ω

×Ω

(ω

,ω

)

. . .

4.1.3 Projection of Obtained Averages on the

Frame of Links

In order to return to the frame of the links, we pro-

ceed to sum the average probabilities of the hypothe-

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

606

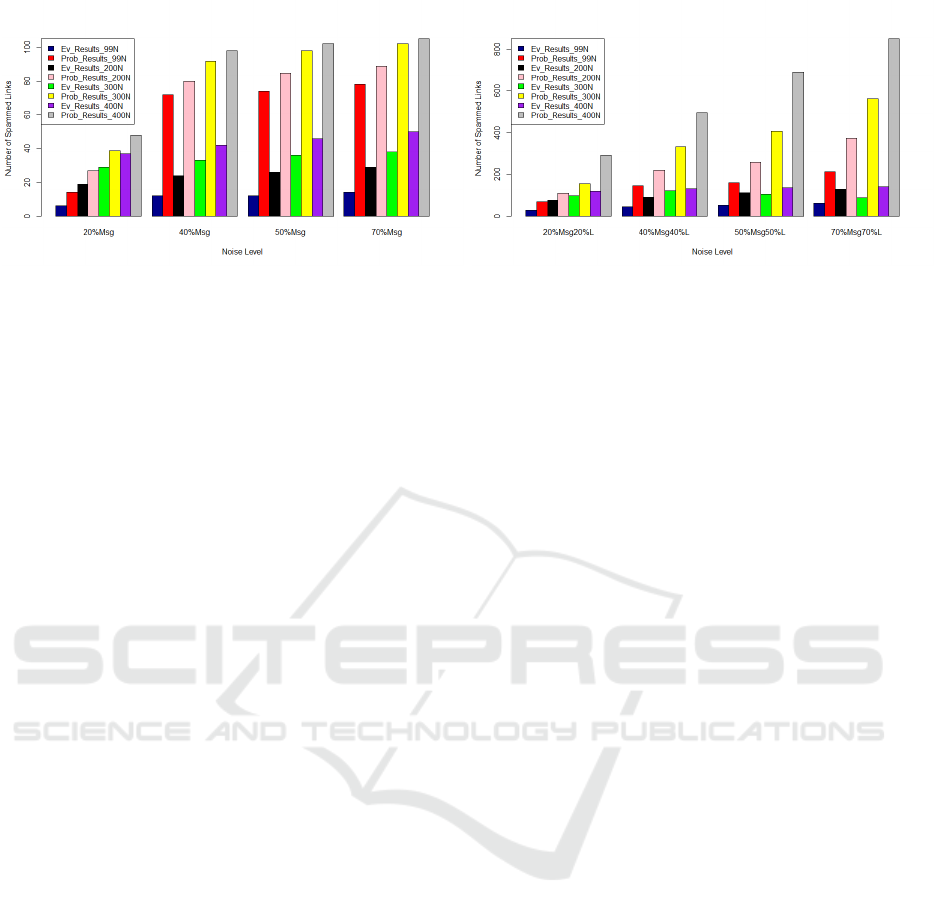
Figure 2: Spammed Links after 10 iterations: case of noisy

messages only.

ses that are related to each type of link (ω

, ω

i = 1, ..., L; j = 1, ..., M.

4.1.4 Decision Making

From each probability vector relative to each link,

we determine the current type of the given link

max(ω

), i = 1, ..., L. Hence, we compare the ob-

tained type with the initial one and decide if the link

is spammed or not.

4.2 Case of Noisy Messages Only

In this section, we present the results obtained after

adding 20%, 40%, 50% and 70% of noisy messages

in each community. The histogram given on Figure

2 shows the number of spammed links that appeared

after 10 iterations.

We notice that the more the percentage of the

noisy messages increases the more the number of

spammed links increases likewise. We also note that

in the case of the baseline a larger number of links

would be removed compared to the belief approach.

This could cause disconnection of the network.

4.3 Case of Noisy Messages and Noisy

Links

In this section, we present the results after adding

noisy links and noisy messages.

The histogram given in Figure 3 shows the num-

ber of spammed links that appeared after 10 itera-

tions while varying noise. We note that the base-

line begets the removal of a large number of network

links. As a result, the network is no longer connected.

For example, in the case of 70% noisy messages and

70% noisy links, it detects 213 links which represents

about 45.5% of the total links of the network com-

posed of 99 nodes.

Figure 3: Spammed links after 10 iterations: case of noisy

messages and links.

4.4 Detection of Spammed Links

In this section, we present the obtained accuracy re-

sults after 10 iterations. The goal of this experiment

is to test if our model manages to detect the known

spammed links. The generated mass functions on the

messages are not compatible with the spammed links

classes. We consider a LFR network composed of 99

nodes and 10 spammed links.

We will compare the obtained results given by the

proposed approach, the baseline and the k-nn algo-

rithm.

The k-nearest neighbour (Altman, 1992) is a su-

pervised learning method. Its principle is as follows:

An object is classiﬁed by a majority vote of its neigh-

bours, with the object being assigned to the class most

common among its k nearest neighbours.

It should be noted that in Figures 4, 5 and 6, the

accuracy values given by the k-nn oscillate between

0.6 and 0.69. This is because the k-nn requires learn-

ing data in contrary to the proposed approach and the

baseline. In the following, we present the results of 3

cases:

Generation of 10 messages of type PN CUPC: The

spammed links are of type “professional”. Hence, we

generate 10 incompatible messages of type “PNC U

PC”. The curves in ﬁgure 4 show that for both eviden-

tial and probabilistic approaches, only few spammed

links were detected at the ﬁrst iteration. However,

the evidential accuracy is higher than the probabilis-

tic one. For the case of the k-nn algorithm, we no-

tice that it has better accuracy results at the ﬁrst iter-

ations. Nevertheless, at the tenth iteration, we notice

that the evidential accuracy become equal to 79%. So,

we can conclude that our model is able to detect cor-

rectly more spammed links than the baseline and the

k-nn algorithm.

A Belief Approach for Detecting Spammed Links in Social Networks

607

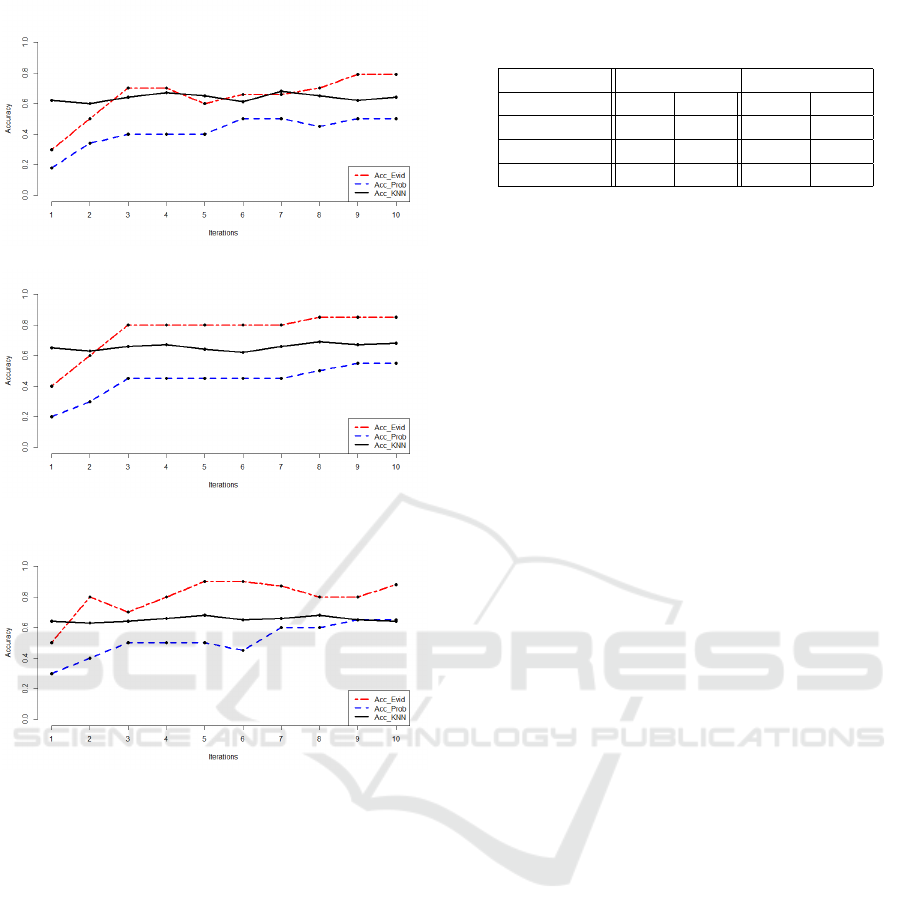
Figure 4: Accuracy Results: Case of PNCUPC.

Figure 5: Accuracy Results: Case of PNC, PC, and

PNCUPC.

Figure 6: Accuracy Results: Case of random and PNCUPC

messages.

Generation of 10 messages of type PNC, PC and

PNCUPC: We generate: 3 messages of type PNC,

3 of type PC 4 of type PNCU PC.

In Figure 5 we can note a clear improvement of

detection of spammed links at the tenth iteration. In-

deed, the evidential accuracy results given by the pro-

posed approach is equal to 85%.

Generation of 10 messages of type PNCUPC and

random: We generate: 6 random messages and 4

messages of type PNCUPC. We specify that in the

case of random message, the focal element can be ev-

erywhere except on the empty set in the case of the

proposed model.

Figure 6 shows that even when we have a portion

of random messages generated on spammed links, our

model always gives the best results of accuracy at the

tenth iteration.

Table 2: Precision/Recall Results at 1

and 10

iterations.

Method Precision Recall

It-1 It-10 It-1 It-10

Belief-App 0.36 0.85 0.366 0.87

Baseline 0.23 0.65 0.25 0.67

k-nn 0.55 0.6 0.39 0.4

4.4.1 Evaluation of the Algorithm in Terms of

Precision and Recall

In this section, we will present the obtained precision

and recall results of the proposed approach, the base-

line and the k-nn algorithm in the case of an LFR net-

work composed of 200 and 400 nodes.

We remind that precision is the fraction of relevant

instances among the retrieved instances while recall

is the fraction of relevant instances that have been re-

trieved over the total amount of relevant instances.

Case of LFR network 200 Nodes: We will start by

spamming 20 links of type “professional”, 20 links of

type “friendly” and 20 links of type “family”.

For each type of links, 20 incompatible message

were generated:

• For the case of the “professional” link, we gener-

ate messages of type “PNC”, “PC” and “PNC U

PC”.

• For the case of the “friendly” and “family” links,

we generate messages of type “IC”, “INC” and

“IC U INC”.

Table 2 shows a comparison of the obtained results

in terms of precision and recall measures in the case

of the proposed approach, the baseline and the k-nn.

We represent the obtained values at the ﬁrst and tenth

iteration. We note that the results given by the k-nn at

the ﬁrst and tenth iterations are close. This is due to

the fact that this algorithm requires learning data un-

like the evidential and probabilistic methods. There-

fore, the methods do not compare the same thing. We

notice also that our algorithm gives better results than

the baseline and the k-nn algorithm.

Case of LFR Network 400 Nodes: In this experi-

ment, 600 links were spammed. We will present the

obtained results at the ﬁrst and tenth iteration.

Table 3 shows that the proposed approach gives

better results in terms of precision and recall com-

pared to the baseline and the k-nn algorithm. We re-

mind that the closeness of the results given by the k-nn

at the ﬁrst and tenth is due to the fact that this algo-

rithm requires learning data unlike the evidential and

probabilistic methods.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

608

Table 3: Precision/recall results at the 1

and 10

iteration.

Method Precision Recall

It-1 It-10 It-1 It-10

Belief-App 0.38 0.8 0.4 0.82

Baseline 0.27 0.6 0.3 0.63

k-nn 0.5 0.51 0.41 0.43

5 CONCLUSION

The majority of researches in the literature about the

evolution in time of a social network focused more

on the prediction of entities than the removal of the

latter. In this work, we propose a belief approach that

detects spammed links in a social network. This work

will allow everyone connected to sort out the types

of its relationships in the social network and decide

which links is spammed and should be deleted.

Throughout this work, we ﬁrst recalled some re-

lated works of the literature as well as some ba-

sic notions of the theory of belief functions. Then,

we presented our method which consists of detecting

spammed links using the information of the nodes,

links and messages. In order to test our approach, we

performed two types of illustrations: ﬁrst, we added

noise on the messages only, and then we added noise

on both messages and links. Second, we selected

randomly spammed links and observed if our model

manages to detect them.

Experiments have shown that the number of

spammed links increases with the noise level. In ad-

dition, the results showed that the belief approach is

better than the probabilistic one since the latter delete

many links of the network. Furthermore, the accu-

racy, precision and recall results prove that our model

is able to detect the majority of spammed links and

gives better results than the considered baseline and

the k-nn algorithm.

As future work, we will elaborate a strategy to

deal with the outliers. Indeed, we will ﬁx a threshold

that represents the minimum number of occurrences

for a link to be considered spammed. We remind that

an outlier is a link that its initial class can be modiﬁed

but not in all iterations.

Second, we intend to test our proposed algorithm

on large and real social networks. To do so, we will

associate a simple mass function to each node, link

and message of the network based on the community

structure. In terms of scaling up, there are several

strategies that can reduce complexity such as repre-

senting only the focal elements or grouping them to-

gether if their values are negligible (Martin, 2009).

In addition, the combination rule proposed by (Zhou

et al., 2018) can be used to combine mass functions

from a large number of sources.

REFERENCES

Al Hasan, M. and Zaki, M. J. (2011). A survey of link

prediction in social networks. In Social network data

analytics, pages 243–275. Springer.

Altman, N. S. (1992). An introduction to kernel and nearest-

neighbor nonparametric regression. The American

Statistician, 46(3):175–185.

Dempster, A. P. (1967). Upper and lower probabilities in-

duced by a multivalued mapping. The annals of math-

ematical statistics, pages 325–339.

Lancichinetti, A., Fortunato, S., and Radicchi, F. (2008).

Benchmark graphs for testing community detection

algorithms. Physical review E, 78(4):046110.

Lee, H. (2011). Context reasoning under uncertainty based

on evidential fusion networks in home-based care.

Liu, F., Liu, B., Sun, C., Liu, M., and Wang, X. (2015).

Deep belief network-based approaches for link predic-

tion in signed social networks. Entropy, 17(4):2140–

2169.

Martin, A. (2009). Implementing general belief function

framework with a practical codiﬁcation for low com-

plexity. Advances and applications of DSmT for In-

formation Fusion-Collected works, 3:217–273.

Martinez-Romo, J. and Araujo, L. (2013). Detecting mali-

cious tweets in trending topics using a statistical anal-

ysis of language. Expert Systems with Applications,

40(8):2992–3000.

Shafer, G. (1976). A mathematical theory of evidence, vol-

ume 1. Princeton university press Princeton.

Shafer, G. (2016). Dempster’s rule of combination. Interna-

tional Journal of Approximate Reasoning, 79:26–40.

Washha, M., Qaroush, A., and Sedes, F. (2016). Leveraging

time for spammers detection on twitter. In Proceed-

ings of the 8th International Conference on Manage-

ment of Digital EcoSystems, pages 109–116. ACM.

Zadeh, L. A. (1999). Fuzzy sets as a basis for a theory of

possibility. Fuzzy sets and systems, 100(1):9–34.

Zheng, X., Zeng, Z., Chen, Z., Yu, Y., and Rong, C. (2015).

Detecting spammers on social networks. Neurocom-

puting, 159:27–34.

Zhou, K., Martin, A., and Pan, Q. (2018). A belief combi-

nation rule for a large number of sources. Journal of

Advances in Information Fusion, 13(2).

A Belief Approach for Detecting Spammed Links in Social Networks

609