All Together Now! The Benefits of Adaptively Fusing Pre-trained Deep
Representations
Yehezkel S. Resheff
1
, Itay Lieder
2
and Tom Hope
2
1
Intuit Tech Futures, Israel
2
Intel Advanced Analytics, Israel
Keywords:
Deep Learning, Fusion.
Abstract:
Pre-trained deep neural networks, powerful models trained on large datasets, have become a popular tool in
computer vision for transfer learning. However, the standard approach of using a single network potentially
misses out on valuable information contained in other readily available models. In this work, we study the
Mixture of Experts (MoE) approach for adaptively fusing multiple pre-trained models for each individual
input image. In particular, we explore how far we can get by combining diverse pre-trained representations
in a customized way that maximizes their potential in a lightweight framework. Our approach is motivated
by an empirical study of the predictions made by popular pre-trained nets across various datasets, finding that
both performance and agreement between models vary across datasets. We further propose a miniature CNN
gating mechanism operating on a thumbnail version of the input image, and show this is enough to guide a
good fusion. Finally, we explore a multi-modal blend of visual and natural-language representations, using a
label-space embedding to inject pre-trained word-vectors. Across multiple datasets, we demonstrate that an
adaptive fusion of pre-trained models can obtain favorable results.
1 INTRODUCTION
In many real-world scenarios arising in computer
vision applications, practitioners turn to pre-trained
deep neural networks – powerful models (Chollet,
2016; He et al., 2016; Simonyan and Zisserman,
2014; Szegedy et al., 2016) which have already been
trained on a large data set and can help jump-start a
given task. Fortunately, it turns out that image fea-
tures extracted from these pre-trained networks are
broadly applicable to other datasets and tasks (Yosin-
ski et al., 2014; Ge and Yu, 2017; Girshick et al.,
2014; Agrawal et al., 2014; Azizpour et al., 2015;
Oquab et al., 2014; Chu et al., 2016).
In practice, some form of new learning is required
in order to adapt the pre-trained model to the new
task. A common practice in such cases, especially
in settings where training data is scarce, is to either
fine-tune only the very last layer(s), or simply pro-
ceed by extracting high-level features from one of the
final layers of the model and plugging them into a lin-
ear classifier such as an SVM (Kim et al., 2016; Chu
et al., 2016; Sharif Razavian et al., 2014).
The rapid pace of deep learning research has
spawned many candidates for pre-trained networks,
with very different architectures. Newer, more ad-
vanced networks tend to have overall better perfor-
mance on a few large-scale datasets on which they
were trained, but for any given task it is unclear which
pre-trained model would work best. As confirmed by
our empirical study, the question of which pre-trained
net to employ is not simple to answer, and depends on
dataset and even on class within a dataset. Further-
more, even “older” models such as VGG (Simonyan
and Zisserman, 2014) can beat the more advanced
and modern architectures for some specific classes,
giving the old adage of “respect your elders” new
meaning. This suggests that combining multiple pre-
trained networks could be beneficial.
Our empirical findings on model (dis)agreement
across datasets and specific image classes (Section
2) suggest that it could be useful to combine these
diverse pre-trained features by customizing for each
individual image. To test this hypothesis, we em-
ploy a lightweight yet flexible Mixture of Experts
(MoE) (Masoudnia and Ebrahimpour, 2014; Eigen
et al., 2013; Shazeer et al., 2017) framework for fus-
ing multiple sources of pre-trained information (Fig-
ure 1) in a principled manner, while requiring no fine-
tuning at all. A gating mechanism differentially as-
Resheff, Y., Lieder, I. and Hope, T.
All Together Now! The Benefits of Adaptively Fusing Pre-trained Deep Representations.
DOI: 10.5220/0007367301350144
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 135-144
ISBN: 978-989-758-351-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
135

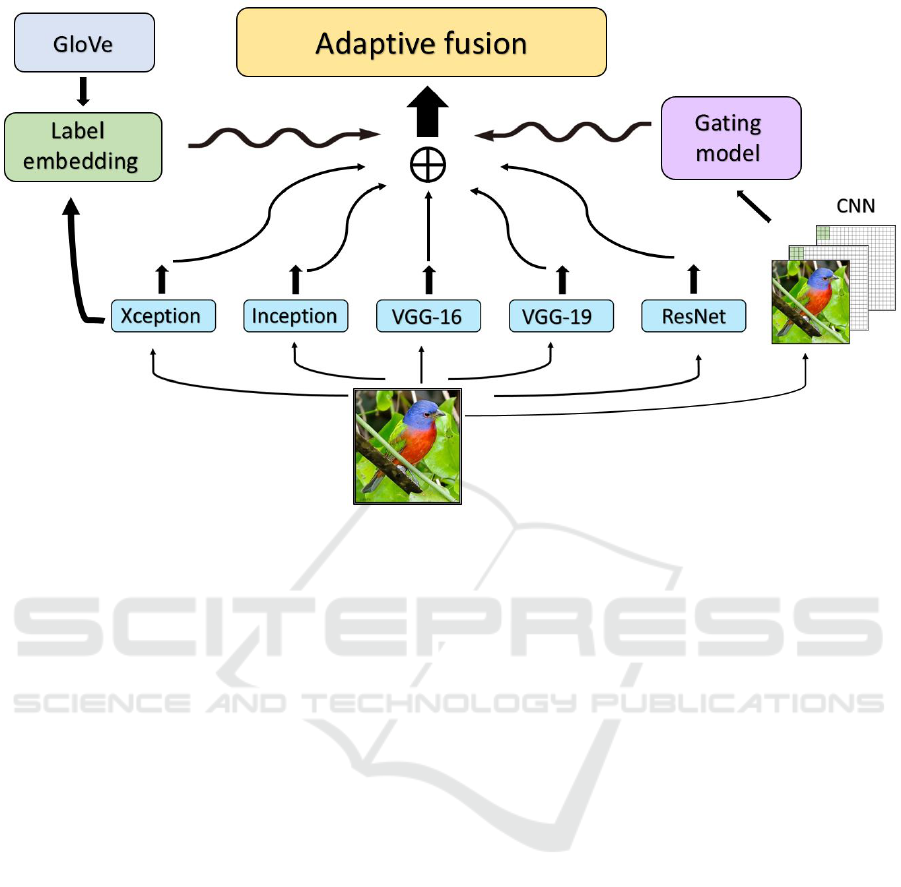
Figure 1: The overall structure of the Mixture of Experts (MoE) fusion model. Individual pre-trained representations are
gated by a dedicated CNN with thumbnail input. Label-space embedding with GloVe word vectors is used to augment the
pre-trained features prior to gating.
signs weights to the output of base-classifiers trained
on each set of pre-trained features, in a way that is
adaptable to each input image.
The generality of the MoE framework allows mul-
tiple design choices. We study several specific meth-
ods (Section 3) exploring diverse premises and struc-
tures controlling how pre-trained information is incor-
porated into the model. In one experiment, we exam-
ine whether low-level image features can help guide
our MoE’s weighting of each pre-trained set of fea-
tures, by indicating which pre-trained model is best
suited for it. We test a lightweight CNN-based gating
module, with only two small convolution layers that
process a thumbnail version of the original input im-
age. This miniature design is able to achieve excellent
results while being small enough to train and deploy
easily.
In another method, we test the multi-modal fusion
of pre-trained natural language information. In par-
ticular, we extend the CNN gating network to include
a label-space embedding of the original 1000 Ima-
geNet labels, and then initialize this embedding with
pre-trained word vectors based on class names. We
find that in some cases, incorporating this “semantic”
knowledge helps improve results.
The contribution of this paper is two-fold. First,
we systematically evaluate the transfer learning prop-
erties of multiple pre-trained models to many bench-
mark datasets, showing that there is no clear winner
and therefore we could benefit from a method to se-
lect which model to follow for a specific prediction.
Once the need to combine models is established, we
investigate and compare several methods of doing so,
and propose the thumbnail-CNN gating mechanism
as a lightweight yet effective way of adaptively fus-
ing pre-trained deep representations.
2 EXPLORING PRE-TRAINED
PREDICTIONS
In this section we conduct an empirical study of
the representations extracted from popular pre-trained
models, and explore whether there is evidence sug-
gesting they contain complementary information that
could be tapped into by a model that combines them.
We train classifiers based on features from the fi-
nal fully-connected layers of Xception, Inception V3,
VGG-16, VGG-19 and ResNet-50 and compare their
predictions across 7 datasets (Table 1), and across im-
age classes within each dataset. We explore some key
differences and similarities between the 5 pre-trained
models, by examining the agreement between them
according to various metrics and segmentations of the
datasets.
We find that while overall agreement is quite high,
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
136

there are many disparities, suggesting that this diver-
sity could be exploited by combining the “expertise”
of pre-trained nets in a dynamic, instance-level fash-
ion. These findings motivate the MoE models we
present in Section 3 and test in Section 5.
Finally, we look at cases where there is a high
level of disagreement between the individual pre-
trained models, and test the results obtained using one
of our MoE models. We find that the MoE is able
to either surpass or match the best single pre-trained
representation, showing the utility of training a model
that is able to adaptively assign a weighting to the in-
dividual pre-trained nets.
2.1 Dataset Disparities between Models
We begin by examining the agreement between the
classifiers trained on pre-trained features. We mea-
sure prediction consistency between the models with
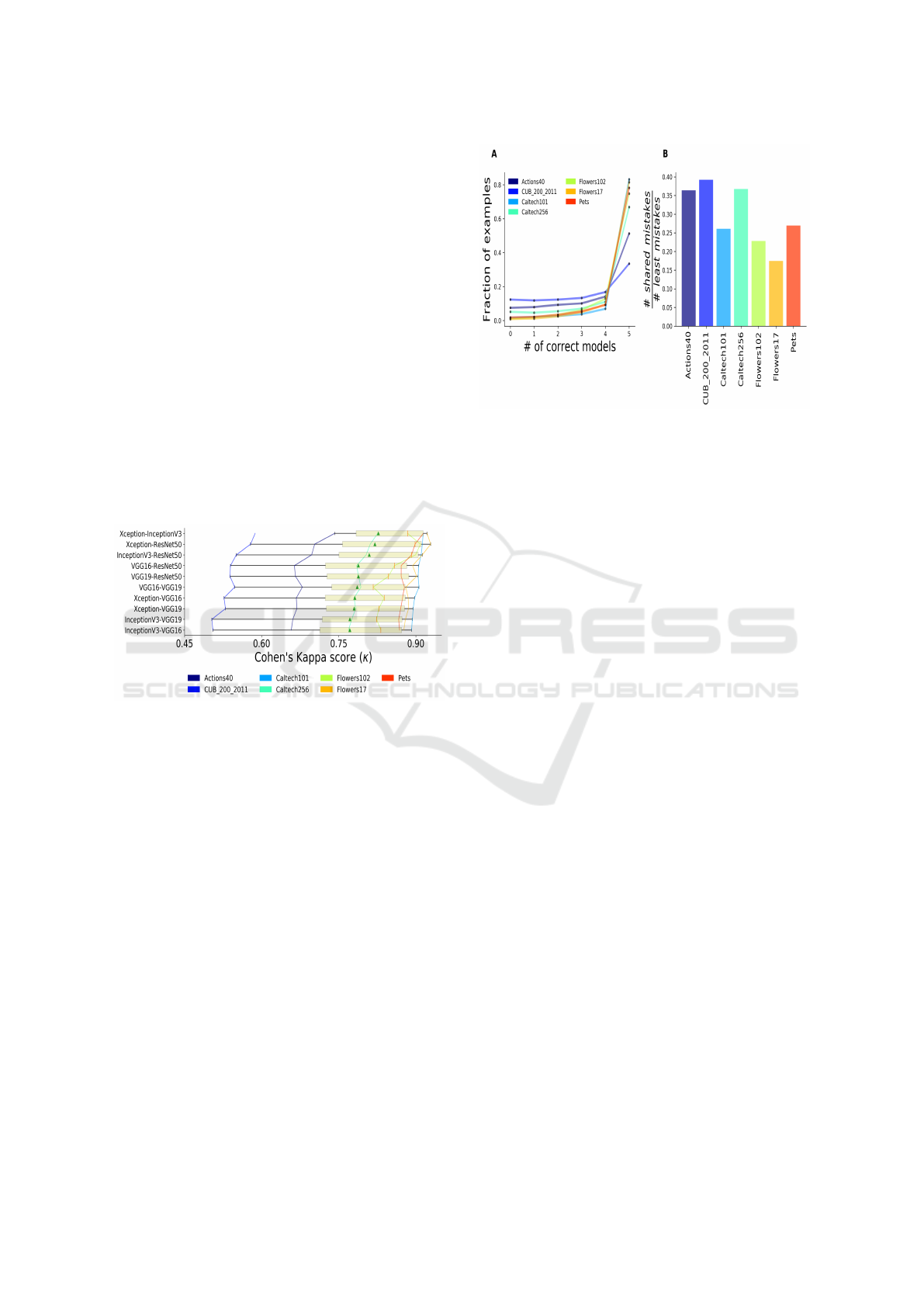
Cohen’s Kappa inter-rater agreement measure.
Figure 2: Cohen’s Kappa agreement between models. Hor-
izontal box plots show the agreement scores for each pair of
models, on each of the 7 datasets. The vertical orange line
and green triangle markers indicate the median and mean
scores.
As shown in Figure 2, the scores are high, but vary
substantially across datasets, having almost perfect
agreement between all pairs of models for 4 out of
the 7 datasets, moderate for 2 of them, and only a
somewhat fair agreement score for the CUB200 birds
dataset. The relatively low agreement in some of the
datasets suggests that models do not necessarily make
the same mistakes, and that there are non-overlapping
correct classifications. Figure 3A shows that almost
always at least some of the models are correct. If we
could learn to predict for a given example which of
the models will do well on it, we could expect a sig-
nificant boost in results. This is core notion behind
the method proposed in this paper.
Figure 3: Comparison of model errors. A The fraction of
total examples correctly predicted by each of the models.
Datasets are denoted by colors. The overwhelmingly low
proportion of examples that all models mislabel (#correct
models = 0), points to the viability of the gated Mixture of
Experts approach we suggest for this task. B: The ratio be-
tween the number of examples that all models got wrong
and the number of errors made by the best-performing
model further supports our approach.
2.2 Class-level Differences
While the examination at the dataset level revealed
some coarse differences between the pre-trained pre-
dictions, performance at the class-level is more
model-sensitive. This finding is demonstrated in
Figure 4. Each of the three columns show an ex-
ample class with corresponding F1 scores. For a
given dataset (rows), each of the examples has dif-
ferent best-performing models. For instance, in the
Caltech101 dataset (cyan), while Xception does best
at classifying the brontosaurus category, VGG-16 is
best at the water lilly category and Inception V3 wins
at wild cat. These inconsistencies challenge the no-
tion of a superior “champion” model, crowned on
some benchmark data. Additionally, we present the
F1 scores of one of the MoE models, which is gener-
ally superior to each of the individual models.
Figure 5 shows histograms of the number of
classes won (highest accuracy) by each model for the
corresponding dataset. While Xception and ResNet
dominate by this measure, there is no one model that
wins across the board, and in addition even the weaker
VGG models win for some classes of images. In
addition, the histogram with the MoE model is su-
perimposed (black), revealing that it wins the largest
number of classes in each and every dataset when in-
cluded.
Another illustration of the models’ diversity, this
time focusing on two specific classes, is shown in Fig-
All Together Now! The Benefits of Adaptively Fusing Pre-trained Deep Representations
137

Table 1: The 7 datasets used for all experiments in this paper, and their basic characteristics.
Dataset Images Labels Description
Actions40 (Yao et al., 2011) 9,532 40 Human actions
CUB200 (Wah et al., 2011) 11,788 200 Birds
Caltech101 (Fei-Fei et al., 2007) 9,146 101 Diverse Objects
Caltech256 (Griffin et al., 2007) 30,607 256 Diverse Objects
Flowers102 (Nilsback and Zisserman, 2008) 8,189 102 Flowers
Flowers17 (Nilsback and Zisserman, 2006) 1,360 17 Flowers
Pets (Parkhi et al., 2012) 7,390 37 Cats and dogs
Figure 4: F1 scores of example classes taken from each
dataset. Each of the examples has different best-performing
models. For each dataset (rows, also denoted by color), and
a specific class example (columns, label is the title), the F1
scores (y-axis) are plotted for each of the 5 individual mod-
els along with an additional embedding-based MoE model
(diagonal stripes, see Section 3) that mostly either rivals or
outperforms the best individual model.
ure 6. Some images in the action classes of texting
message and smoking have considerably high con-
fusion between them (Figure 6A and B). While all
models are quite good at distinguishing the two when
smoking is the true label (Figure 6D), the ability to
do so when texting message is the true label is signifi-
cantly worse (Figure 6C), dropping especially low for
the two VGG models, followed by ResNet-50.
The ability of each model to separate the two is
also reflected in the feature-space. Figure 6E-I shows
Figure 5: Histograms with number of classes won by each
model. There is no one model that wins across the board.
For each dataset (subplot), two superimposed histograms
show the number of times each model outperformed the
rest. Each of the colored histograms include only the 5 in-
dividual models, while the black histograms also include
the MoE model, revealing that it wins the largest number of
classes in every dataset when included.
the T-SNE (t-Distributed Stochastic Neighbor Em-
bedding) (Maaten and Hinton, 2008) 2d projection of
each of the 5 individual models. As seen, the two
classes are clearly better distinguished as two sepa-
rate clusters when viewed with the features extracted
by the two best models – Xception and Inception V3.
To wrap-up, the overall findings of this section
suggest that each model captures slightly different
behaviors, and thus has its own strengths and weak-
nesses, performing better or worse depending on the
specific class and perhaps even the specific instance
in question. The evidence presented here supports the
notion that combining the models in an adaptive way
could exploit their non-overlapping capabilities. In
the next section we test this idea with MoE methods
fusing together the multiple representations.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
138

Figure 6: Illustration of model differences in separating
two similar classes. Some models are better at distinguish-
ing high-confusion images. A,B: Illustrative images for the
two classes texting message (A) and smoking (B). C,D: The
number of predictions (y-axis) of either class (denoted by
red and blue colors respectively) by each model (x-axis)
when the true class is either texting message (C) or smoking
(D). E-I: 2D T-SNE projection of the features of examples
from the two classes (denoted by the same colors as in plots
C and D), where each point is a different instance and the
x-axis and y-axis show the first and second T-SNE compo-
nents respectively. Each plot corresponds to the features of
a pre-trained model, as indicated in the title.
3 METHODS AND MODELS
In our setting, we are interested in training a classi-
fication model by fusing information from multiple
pre-trained deep neural networks. Our goal is em-
ploying a lightweight framework that is broad enough
to enable flexible design choices for how the pre-
trained information is combined.
We thus begin by presenting a simple, general
framework adopting ideas from the rich literature on
deep Mixture of Experts (Eigen et al., 2013; Ma-
soudnia and Ebrahimpour, 2014; Shazeer et al., 2017)
models. We then present some specific variants we
study, illustrated in Figure 1, also casting previous
work in the field as a simple special case.
Let {x
(i)
,y
(i)
}
P
i=1
be our dataset consisting of im-
ages x ∈ X and the associated labels y ∈ Y . At
our disposal are K pre-trained embedding functions
Φ = {φ
1
,..,φ
K
}, where φ
i
: X → R
n
i
is an embedding
function of deep learning model i, typically trained
on datasets several orders of magnitude larger than
P. For example, φ
1
could represent the ResNet model
(He et al., 2016) trained on the ImageNet dataset
(Deng et al., 2009), φ
2
the Inception model (Szegedy
et al., 2016), and so forth. As discussed in the intro-
duction and demonstrated in Section 2, different pre-
trained networks can perform very differently for a
given input image, potentially capturing diverse as-
pects of the input. Using only one pre-trained net-
work for transfer learning thus potentially misses out
on much information that is just as easy to obtain.
Here, we utilize multiple pre-trained embeddings by
learning a probabilistic classification fusion function
f : X → ∆
|Y |
of the form:
f (x)
:
= f (x,φ
1
(x),...,φ
K
(x)). (1)
In principle, the entire set of network weights in
each φ
i
∈ Φ could be fine-tuned in tandem, generaliz-
ing the common fine-tuning setting (of one individual
φ
i
). However, even the process of fine-tuning one pre-
trained network φ
i
can often be costly, in terms of re-
quired resources and the amount of data needed, and
in training difficulty (Kim et al., 2016). A common
approach is to freeze the first l layers of φ
i
and fine-
tune only the remaining top layers. In practice, es-
pecially in low-resource scenarios, many practitioners
simply copy and freeze all but the last fully-connected
classification layer, at times replacing the final soft-
max regression with a linear SVM (Kim et al., 2016;
Sharif Razavian et al., 2014; Chu et al., 2016). This
basic method can often yield excellent results while
keeping effort minimal.
In this paper, our primary focus is to demon-
strate how a simple, principled extension of this com-
mon practice – a fusion of information extracted from
multiple pre-trained φ
i
’s – can lead to a substantial
boost in results while still being very practical and
lightweight.
To this end, we primarily focus on functions that
decompose into separate base-classifiers c : φ(x) →
∆
|Y |
, each trained on a single pre-trained representa-
tion of the images:
f (x)
:
= f (x,c
1
(φ
1
(x)),...,c
K
(φ
K
(x))) (2)
We now turn to discuss some specific realizations
we develop and explore for this fusion function. We
also show a simple extension to incorporate additional
types and sources of pre-trained information.
3.1 A Gating Mechanism for
Base-classifiers
We seek a model that is trained to combine the predic-
tions from the multiple c
i
base-classifiers while being
flexible enough to allow diverse design choices. We
All Together Now! The Benefits of Adaptively Fusing Pre-trained Deep Representations
139

begin by employing a gating mechanism, a general
method of learning a (convex) combination of these
predictions that adapts to each input image, in order
to maximize the probability of a correct labeling for a
given image.
Given the set of base-classifiers {c
i
} trained on Φ,
we construct the following classifier:
f (x) =
K
∑
i=1
a
i
(x)c
i
(φ
i
(x)), (3)
or in vector notation
f (x) = a(x)c(φ(x)), (4)
where ∀x ∈ X : a
i
(x) ≥ 0,
∑
i
a
i
(x) = 1. The learned
function a : X → ∆
K
acts as a gating mechanism,
selecting the combination of pre-trained embeddings
and models most likely to label the specific exam-
ple correctly. In this light, our function f can be
viewed as a deep mixture of experts meta-learning
model, with individual experts based on pre-trained
networks.
3.2 A Low-level CNN Gating
Mechanism
Our basic premise, based on the results in Section 2
showing model diversity, is that each individual im-
age is “suitable” for each pre-trained model φ
i
∈ Φ
to different extents, and that each φ
i
captures image
properties in a potentially different fashion. Further
building on this idea, we explore the use of extracting
low-level image features to train our gating mecha-
nism with. In particular, we experiment with a gating
mechanism based on a very small CNN model and
thumbnail versions of images:
a(x) = CNN(R(x)) (5)
where CNN : R(X ) → ∆
K
is built of only two lay-
ers with very few filters and R(x) is a resize function
mapping the original image x to a smaller version (see
Section 5). For example, we experiment with using
resized images as small as 32X32, obtaining good re-
sults. These design choices reflect the assumption that
low-level image features are sufficient to determine
the appropriateness of each of the pre-trained embed-
dings for a specific example.
In addition, the use of a very small network and
small images not only tests our ability to exploit low-
level image information for our gating function, but
also ensures a compact, lightweight model that is easy
to train and use for inference in practice.
3.3 A Feature-embedding Gating
Mechanism
A simpler gating method is to ignore the raw image
altogether, and embed all the representations from
the multiple φ
i
∈ Φ in a shared feature space. In
particular, we learn K weight matrices (fully con-
nected layers), transforming each φ
i
(x) into a lower-
dimensional vector and aggregating, before passing
through a softmax function:
˜x
i
= W
i
φ
i
(x) (6)
a(x) = softmax(m(γ([ ˜x
1
, ˜x
2
,..., ˜x
K
]))),
where W
i
is the embedding matrix corresponding to
φ
i
, γ is a point-wise non-linearity such as the ReLU
function (He et al., 2015), and m is an aggregation
function such as the mean operator.
While this method does not employ a richer model
to exploit raw image x, its advantage is in its simplic-
ity (and speed), empirically giving very good results
in our experiments.
3.4 A Fusion of Image & Label-space
Embeddings
In the above models, we use φ
i
to extract high-level
features and plug them into their respective classi-
fiers c
i
. In our case, however, each φ
i
is trained on
the ImageNet data set, with a rich set of 1000 output
classes. We seek to explore the effect of incorporating
the final softmax outputs of each φ, and whether this
added “semantic” information can enrich our fusion
of pre-trained networks. To capture rich label seman-
tics and reduce the dimensionality of the label-space,
we find a lower-dimensional embedding of the Ima-
geNet classes. Along these lines, we show how one
instance of such a label-space embedding can be used
to plug-in pre-trained word vectors in place of the em-
bedded classes. The hope is that this multi-modal fu-
sion of pre-trained information from multiple sources
could enhance our final classifier.
More technically, we learn a weighted embedding
of the label-space on which each φ
i
was trained, with
weights corresponding to the confidence scores. Let
Y
s
be the label-space of the source dataset (ImageNet)
on which each φ
i
was trained. We extend our defini-
tion of φ(x) to output both high-level vision features
and the final network predictions:
φ
i
: X → (h
i
,p
i
) ∈ R
n
i
× ∆
1000
, (7)
so that now φ
i
outputs both the original features h
i
∈
R
n
i
, along with softmax predictions vector p
i
of size
|Y
s
| (1000).
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
140

Next, we adapt our base-classifiers. We note
that each softmax predictions vector p
i
assigns a
confidence score p
k
in [0, 1] to each class k ∈
{1,...,1000}, where each class is encoded as a one-
hot binary vector v
k
. Let V be an embedding map-
ping the class vectors v
k
to a lower-dimensional
dense representation, V : v → R
300
. Finally, denote
by {k
1
,...,k
T
} the indices of the top-T confidence
scores p
k
∈ p
i
. For example, T = 5 means we se-
lect the indices corresponding to the top-5 predicted
classes.
Each c
i
now takes the one-hot vectors v
k
, embeds
them with the (trainable) V, and then takes a weighted
average of the v
k
1
,...,v
k
T
with weights correspond-
ing to confidences p
k
1
,..., p
k
T
:
˜
v =
∑
k∈{k
1
,...,k
T
}
v
k
· p
k
∑
k∈{k
1
,...,k
T
}
p
k
, (8)
where we use · to denote an elementwise product of
each element in vector v
k
with the scalar p
k
.
This weighted average embedded vector
˜
v is then
combined with the visual features h
i
, and gated via a
CNN as in Equation 5 or the method in Equation 6.
For simplicity, we experiment only with concatenat-
ing
˜
v,h
i
, but other forms of fusion are possible in this
flexible design.
3.4.1 Fusion of Pre-trained Word Vectors as
Classes
The above formulation of the label-space embedding
allows us to trivially experiment with incorporating an
external source of pre-trained information: word vec-
tors trained on massive textual corpora. In particular,
we semantically represent each class vector v
k
with
the corresponding natural-language class name. For
example, if v
3
is the one-hot vector indicating the cat
class, we use the word cat. We then replace embed-
ding V with the pre-trained GloVe (Pennington et al.,
2014) word vectors, so that the embedding of v
3
is
now the GloVe word vector for cat. (For class names
composed of more than one token, if the combination
does not exist in GloVe, we simply compute the aver-
age of tokens in the class name).
Using this idea we test whether fusing rich seman-
tic knowledge on classes, as captured in pre-trained
word vectors, can help enrich our transfer learning
model without adding much complexity to the pro-
cess.
3.5 Stacking as a Simple Special Case
We end this section showing that a recent method
(Akilan et al., ) can be cast as an instance of our gen-
eral formulation (Equation 2). Adopting notation sim-
ilar to the above, (Akilan et al., ) proposes:
f
stacked softmax
(x) = g(
1
k
∑
i
g
i
(φ
i
(x))), (9)
where all g functions represent softmax regression
classifiers fitted with respect to the class-label target
y. In the first stage individual classifiers g
i
are fitted,
then their outputs g
i
(φ
i
(x)) are averaged and used in
a second stage classifier. This stacking technique is
shown to be superior to classifiers based on individual
pre-trained embeddings, on several datasets. The au-
thors also propose replacing the average of g
i
(φ
i
(x))
with a product, which in our experiments failed to
produce worthwhile results.
Note that the raw image x is not used in Equa-
tion 9. The essential difference between Equation 9
and the MoE approach is the dynamic weighting of
base-classifiers, according to each specific example.
In other words, rather than a stacking approach with
a degenerate (constant) gate, we take a broader ap-
proach, adapting to each individual image with di-
verse design choices for the gating mechanism and
base-classifiers. In addition, as shown in Section 3.4,
our framework is able to easily incorporate further
sources of rich information, using label-space embed-
dings and pre-trained word vectors. Our experiments
show that personalization with respect to the input
images, and fusion of richer sources of information,
leads to better overall results.
4 RELATED WORK
Mixture of Experts and Ensembles. In addition to
the litany of work on transfer learning and fine-tuning
touched upon throughout the paper, our work draws
heavily on the extensive literature on Mixture of Ex-
perts (MoE). In MoE (Masoudnia and Ebrahimpour,
2014; Eigen et al., 2013; Shazeer et al., 2017), a gat-
ing model is trained to weight the outputs of “expert”
sub-models to produce a final prediction, so that each
input is assigned a different distribution over the ex-
perts. In recent work, (Zhao et al., 2017) developed a
deep MoE model to combine a set of base deep CNNs
all based on the AlexNet architecture, to recognize
atomic object classes, constructing a class ontology to
guide assignment to each base CNN. (Shazeer et al.,
2017) employed a sparsely-gated MoE with tens of
thousands of sub-networks, obtaining state-of-art re-
sults in natural language processing tasks. In work
related to MoE, (Aljundi et al., 2016) recently de-
veloped a deep neural network gating mechanism for
All Together Now! The Benefits of Adaptively Fusing Pre-trained Deep Representations
141

lifelong learning, where tasks are assumed to arrive
sequentially.
More generally, ensemble methods have been
popular in deep learning (see (Schmidhuber, 2015)
for a review), with applications in computer vision
(Antipov et al., 2016), speech recognition (Deng and
Platt, 2014), and forecasting (Qiu et al., 2014) to
name a few. Unlike work on ensembling of differ-
ent network architectures (Theagarajan et al., 2017;
Ju et al., 2017), which typically requires heavier re-
sources and large datasets, in this paper we study the
utility of a light MoE based solely on features ex-
tracted from pre-trained nets.
Combining Pre-trained Features. As discussed in
the Introduction and Section 3, there has been pre-
vious work on combining pre-trained representations
for transfer learning. Notably, in (Kim et al., 2016) a
computationally efficient SVM-based method is pro-
posed to select a subset of pre-trained features. The
selected pre-trained features are concatenated and
used in a linear model. More recently, in (Akilan
et al., ) a stacking method of individual classifiers
based on pre-trained representations is proposed, ob-
taining excellent results that beat various baselines. In
both these approaches a single global model for com-
bining the pre-trained models is learned, rather than
weighting each pre-trained net dynamically depend-
ing on the input image, as in the flexible MoE frame-
work we study that enables the exploration of more
general fusion models.
5 EXPERIMENTS
We present experiments on 7 benchmark datasets,
comparing the methods developed in Section 3 to
baseline methods for combining pre-trained models.
The datasets we selected (Table 1) are highly repre-
sentative of relatively small-sample recognition tasks,
and include diverse content from birds and flowers to
human actions. The five individual pre-trained mod-
els used in our experiments are VGG-16, VGG-19
(Simonyan and Zisserman, 2014) , ResNet-50 (He
et al., 2016) , Inception V3 (Szegedy et al., 2016)
and Xception (Chollet, 2016). These popular mod-
els are widely utilized in transfer learning. All mod-
els were implemented using the Keras Python library
with a TensorFlow backend. Results are reported for
a 50%/50% train/test cross-validation procedure. For
the MoE-Embedding method, embedding size was set
to 100. All CNN-gating models reported in Table 2
consist of two layers (32/64 filters, of size 3X3).
5.1 Individual Models
We start by comparing the performance of individual
pre-trained models. Transfer learning is conducted by
replacing the final softmax layer of the original Ima-
geNet model with a similar classification layer for the
task at hand. Only the final layer is trained. Results
(Table 2) point to no clear winner when considering
the individual models, with ResNet and Xception tak-
ing the lead most often.
5.2 Baselines and Mixture of Experts
We start with a combination (concatenation) of all
pre-trained embeddings (all + SVM in Table 2). Re-
sults indicate this outperforms all individual mod-
els only in two cases. Interestingly, the popular ap-
proach of concatenation followed by PCA (all + PCA
+ SVM) fails for all datasets (1K PCA components
were used. Results remained the same for other val-
ues of the number of components). Next, we turn to
Mixture of Experts methods.
We compare the stacking-based model (Akilan
et al., ) to our two proposed methods: MoE-
Embedding, and CNN-gated models. Each of the
two methods is used with and without the label-space
embedding extension (see Section 3.4). We present
results using CNN-gating with input images of size
32X32 and 64X64 (see supplementary material for re-
sults with additional image sizes and network sizes).
Firstly, all proposed combination methods (Table
2, bottom half) outperform all individual embedding-
based models, with a margin of up to 5%. This find-
ing is in line with the general concept of the MoE,
and the hypothesis that different information content
in the various embeddings will have an additive effect,
benefiting overall accuracy.
Secondly, CNN-gating models operating on im-
ages as small as 32X32 pixels improved on the stack-
ing method in 5/7 cases (no-LE) and 6/7 cases (LE).
With 64X64 pixels this is only marginally improved
to 6/7 for both. We interpret these results as an indi-
cation that it is very general (low-level) features of the
images that are successfully guiding the gating mech-
anism. A more thorough investigation of CNN-gating
with various image sizes, and number of layers indi-
cated that the majority of the benefit is attained al-
ready for tiny models based on thumbnail images.
Across all datasets, we significantly outperform
individual models and their concatenation. On most
datasets, we also outperfom the (Akilan et al., ) stack-
ing technique (a special case of our framework) by a
margin of about 0.5%-1.3%, corresponding to relative
error reduction of several percentage points.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
142

Table 2: Comparison of classification methods based on pre-trained embeddings. (Top panel) Individual pre-trained models
with the final softmax layer replaced and re-trained on the new labels. The “all + SVM” and “all + PCA + SVM” baselines
represent a concatenation of all 5 pre-trained representations (in the PCA case, the first 1K components) fed into a linear
SVM. (Bottom panel) Mixture of Experts (MoE) approaches for pre-trained embeddings. MoE-Stacking - see Section 3.5.
MoE-Embedding - all pre-trained representations are embedded in a common space and a final softmax layer is then applied.
MoE-CNN - see Section 3. LE/no-LE refers to label space embedding, see section 3.4. Dataset abbreviations: Actions40:
Actions, CUB-200-2011: CUB, Caltech101: C101, Caltech256: C256, Flowers17: F17, Flowers102: F102, Pets: Pets.
Method Actions CUB C101 C256 F102 F17 Pets
Inception 78.72 63.12 92.02 83.36 89.06 92.65 92.50
ResNet 75.22 63.10 92.94 76.55 93.36 92.94 90.69
VGG-16 68.42 56.60 90.62 71.96 83.96 87.94 88.39
VGG-19 69.45 56.28 90.57 72.78 83.00 88.38 87.31
Xception 80.00 67.80 92.34 85.81 90.79 90.74 93.34
all + SVM 78.56 63.86 93.57 84.93 92.38 93.38 91.72
all + PCA + SVM 74.49 56.72 90.50 80.71 91.82 94.26 89.77
no-LE
MoE-Stacking 81.56 73.13 94.05 87.01 94.46 93.97 94.42
MoE-Embedding 81.62 73.02 94.60 87.48 94.90 95.15 94.21
MoE-CNN(32) 81.91 73.01 94.49 87.26 94.63 95.00 94.07
MoE-CNN(64) 81.85 72.70 94.44 87.36 94.82 95.29 94.32
LE
MoE-embedding 81.87 73.11 94.53 87.34 94.85 94.85 94.21
MoE-CNN(32) 81.85 73.14 94.60 87.30 94.90 95.29 94.18
MoE-CNN(64) 81.64 73.28 94.62 87.36 94.92 95.15 94.32
6 CONCLUSION
In this work, we study a Mixture of Experts (MoE)
framework for fusing multiple pre-trained models in
the transfer learning setting. We perform an empir-
ical study showing the diversity of predictions made
by pre-trained model and their dependence on dataset
as well individual classes of images. We examine
multiple simple models derived from the MoE frame-
work and test several gating mechanisms that, unlike
previous work, adaptively assign varying importance
to each set of pre-trained features based on the input
image. In addition, we construct a label-embedding
method and incorporate pre-trained word vectors, ex-
ploring the effect of a multi-modal fusion of visual
and language-based information. We generalize pre-
vious work and obtain better results with a flexible,
lightweight approach, serving to demonstrate the ad-
vantage of exploiting individual-image information
for a better fusion of pre-trained models. A com-
mon approach in transfer learning is to fine-tune the
final layers of pre-trained nets. Thus, an interest-
ing future direction is to experiment with fine-tuning
multiple sets of pre-trained nets simultaneously using
the MoE framework in a scalable manner that avoids
over-fitting in the small-sample, low-resource setting.
REFERENCES
Agrawal, P., Girshick, R., and Malik, J. (2014). Analyzing
the performance of multilayer neural networks for ob-
ject recognition. In European conference on computer
vision, pages 329–344. Springer.
Akilan, T., Wu, Q. J., Safaei, A., and Jiang, W. A late fusion
approach for harnessing multi-cnn model high-level
features.
Aljundi, R., Chakravarty, P., and Tuytelaars, T. (2016). Ex-
pert gate: Lifelong learning with a network of experts.
arXiv preprint arXiv:1611.06194.
Antipov, G., Berrani, S.-A., and Dugelay, J.-L. (2016). Min-
imalistic cnn-based ensemble model for gender pre-
diction from face images. Pattern recognition letters,
70:59–65.
Azizpour, H., Sharif Razavian, A., Sullivan, J., Maki, A.,
and Carlsson, S. (2015). From generic to specific deep
representations for visual recognition. In Proceedings
of the IEEE Conference on Computer Vision and Pat-
tern Recognition Workshops, pages 36–45.
Chollet, F. (2016). Xception: Deep learning with
depthwise separable convolutions. arXiv preprint
arXiv:1610.02357.
Chu, B., Madhavan, V., Beijbom, O., Hoffman, J., and
Darrell, T. (2016). Best practices for fine-tuning vi-
sual classifiers to new domains. In Computer Vision–
ECCV 2016 Workshops, pages 435–442. Springer.
Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-
Fei, L. (2009). ImageNet: A Large-Scale Hierarchical
Image Database. In CVPR09.
All Together Now! The Benefits of Adaptively Fusing Pre-trained Deep Representations
143

Deng, L. and Platt, J. (2014). Ensemble deep learning for
speech recognition.
Eigen, D., Ranzato, M., and Sutskever, I. (2013). Learning
factored representations in a deep mixture of experts.
arXiv preprint arXiv:1312.4314.
Fei-Fei, L., Fergus, R., and Perona, P. (2007). Learning gen-
erative visual models from few training examples: An
incremental bayesian approach tested on 101 object
categories. Computer vision and Image understand-
ing, 106(1):59–70.
Ge, W. and Yu, Y. (2017). Borrowing treasures from
the wealthy: Deep transfer learning through selective
joint fine-tuning. arXiv preprint arXiv:1702.08690.
Girshick, R., Donahue, J., Darrell, T., and Malik, J. (2014).
Rich feature hierarchies for accurate object detec-
tion and semantic segmentation. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 580–587.
Griffin, G., Holub, A., and Perona, P. (2007). Caltech-256
object category dataset.
He, K., Zhang, X., Ren, S., and Sun, J. (2015). Delv-
ing deep into rectifiers: Surpassing human-level per-
formance on imagenet classification. In Proceedings
of the IEEE international conference on computer vi-
sion, pages 1026–1034.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-
ual learning for image recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 770–778.
Ju, C., Bibaut, A., and van der Laan, M. J. (2017). The rela-
tive performance of ensemble methods with deep con-
volutional neural networks for image classification.
arXiv preprint arXiv:1704.01664.
Kim, Y.-D., Jang, T., Han, B., and Choi, S. (2016). Learn-
ing to select pre-trained deep representations with
bayesian evidence framework. In Proceedings of the
IEEE Conference on Computer Vision and Pattern
Recognition, pages 5318–5326.
Maaten, L. v. d. and Hinton, G. (2008). Visualizing data
using t-sne. Journal of Machine Learning Research,
9(Nov):2579–2605.
Masoudnia, S. and Ebrahimpour, R. (2014). Mixture of ex-
perts: a literature survey. Artificial Intelligence Re-
view, pages 1–19.
Nilsback, M.-E. and Zisserman, A. (2006). A visual vo-
cabulary for flower classification. In Computer Vi-
sion and Pattern Recognition, 2006 IEEE Computer
Society Conference on, volume 2, pages 1447–1454.
IEEE.
Nilsback, M.-E. and Zisserman, A. (2008). Automated
flower classification over a large number of classes.
In Proceedings of the Indian Conference on Computer
Vision, Graphics and Image Processing.
Oquab, M., Bottou, L., Laptev, I., and Sivic, J. (2014).
Learning and transferring mid-level image represen-
tations using convolutional neural networks. In Pro-
ceedings of the IEEE conference on computer vision
and pattern recognition, pages 1717–1724.
Parkhi, O. M., Vedaldi, A., Zisserman, A., and Jawahar,
C. V. (2012). Cats and dogs. In IEEE Conference
on Computer Vision and Pattern Recognition.
Pennington, J., Socher, R., and Manning, C. (2014). Glove:
Global vectors for word representation. In Proceed-
ings of the 2014 conference on empirical methods in
natural language processing (EMNLP), pages 1532–
1543.
Qiu, X., Zhang, L., Ren, Y., Suganthan, P. N., and Ama-
ratunga, G. (2014). Ensemble deep learning for re-
gression and time series forecasting. In Compu-
tational Intelligence in Ensemble Learning (CIEL),
2014 IEEE Symposium on, pages 1–6. IEEE.
Schmidhuber, J. (2015). Deep learning in neural networks:
An overview. Neural networks, 61:85–117.
Sharif Razavian, A., Azizpour, H., Sullivan, J., and Carls-
son, S. (2014). Cnn features off-the-shelf: an as-
tounding baseline for recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition workshops, pages 806–813.
Shazeer, N., Mirhoseini, A., Maziarz, K., Davis, A., Le,
Q., Hinton, G., and Dean, J. (2017). Outrageously
large neural networks: The sparsely-gated mixture-of-
experts layer. arXiv preprint arXiv:1701.06538.
Simonyan, K. and Zisserman, A. (2014). Very deep con-
volutional networks for large-scale image recognition.
arXiv preprint arXiv:1409.1556.
Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wo-
jna, Z. (2016). Rethinking the inception architecture
for computer vision. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 2818–2826.
Theagarajan, R., Pala, F., and Bhanu, B. (2017). Eden: En-
semble of deep networks for vehicle classification. In
Computer Vision and Pattern Recognition Workshops
(CVPRW), 2017 IEEE Conference on, pages 906–913.
IEEE.
Wah, C., Branson, S., Welinder, P., Perona, P., and Be-
longie, S. (2011). The Caltech-UCSD Birds-200-2011
Dataset. Technical report.
Yao, B., Jiang, X., Khosla, A., Lin, A. L., Guibas, L.,
and Fei-Fei, L. (2011). Human action recognition by
learning bases of action attributes and parts. In Com-
puter Vision (ICCV), 2011 IEEE International Con-
ference on, pages 1331–1338. IEEE.
Yosinski, J., Clune, J., Bengio, Y., and Lipson, H. (2014).
How transferable are features in deep neural net-
works? In Advances in neural information processing
systems, pages 3320–3328.
Zhao, T., Yu, J., Kuang, Z., Zhang, W., and Fan, J. (2017).
Deep mixture of diverse experts for large-scale visual
recognition. arXiv preprint arXiv:1706.07901.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
144