
Improving the Dictionary Construction in Sparse Representation
using PCANet for Face Recognition
Peiyu Kang, Yonggang Lu, Diqi Pan and Wenjie Guo
College of Information Science and Technology, Lanzhou University, Gansu, China
Keywords: Face Recognition, Sparse Representation, PCANet, Feature Learning.
Abstract: Recently, sparse representation has attracted increasing interest in computer vision. Sparse representation
based methods, such as sparse representation classification (SRC), have produced promising results in face
recognition, while the dictionary used for sparse representation plays a key role in it. How to improve the
dictionary construction in sparse representation is still an open question. Principal component analysis
network (PCANet), as a newly proposed deep learning method, has the advantage of simple network
architecture and competitive performance for feature learning. In this paper, we have studied how to use the
PCANet to improve the dictionary construction in sparse representation, and proposed a new method for
face recognition. The PCANet is used to learn new features from face images, and the learned features are
used as dictionary atoms to code the query face images, and then the reconstruction errors after sparse
coding are used to classify the face images. It is shown that the proposed method can achieve better
performance than the other five state-of-art methods for face recognition.
1 INTRODUCTION
Face recognition technology has been developed for
a long time and a variety of methods have been
proposed (Turk and Pentland, 1991; Zhang, Chen,
and Zhou, 2005; Maksimov et al., 2006; Liu et al.,
2001). Due to the wide range of face recognition
applications, there are still many researchers
dedicated to face recognition in recent years. Facial
similarity, shape instability and facial expressions,
gestures, age and other diversity, light conditions,
facial occlusion and many factors of the outside
world increase the difficulty in face recognition
(Ghiass et al., 2012; Chen and Su, 2017).
Sparse representation (Wright et al., 2010) is a
method that commonly used for signal compression
and encoding. Sparse representation based methods,
such as sparse representation classification (SRC)
(Wright et al., 2009), have already been applied in
image recognition and led to promising results. It is
found that applying sparse representation to image
classification can both reduce the computational
complexity brought by high-dimensional data, and
improve the robustness of the method (Zhang et al.,
2010; Elad and Aharon, 2006; Mairal, Elad, and
Sapiro, 2008; Lu et al., 2015; Zhou, 2012). The
sparse representation based classification has two
steps: coding and classification. First, the query
image is coded over the features which have strong
discriminative properties between objects to be
characterized
. Then classification can be carried out
by computing the reconstruction errors using the
coding coefficirnts and the selected features. The
general form of the sparse coding model is as
follows:
2
12
min . .
α
α st y Dαε
(1)
where y is the query image, D is the dictionary
which is constructed by the selected features, α is the
encoding sparse vector of y on the dictionary D, and
ε (ε > 0) is a constant (Yang et al., 2011a).
In the SRC method, training samples are directly
used as dictionary atoms for coefficient encoding. It
classifies the query images by evaluating which
class leads to the minimal
reconstruction error. The
method is simple and easy to understand, but a large
amount of class information among the training
samples is not used. Another classical sparse
representation method is K-SVD (Aharon, Elad, and
Bruckstein, 2006), which is an iterative method that
alternates between sparse coding of the query
images based on the current dictionary and a process
Kang, P., Lu, Y., Pan, D. and Guo, W.
Improving the Dictionary Construction in Sparse Representation using PCANet for Face Recognition.
DOI: 10.5220/0007368105170523
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 517-523
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
517

of updating the dictionary atoms to better fit the
data. The update of the dictionary columns is
combined with an update of the sparse
representations, thereby accelerating the
convergence. Since sparse coding problem is
equivalent to Lasso's problem (Tibshirani, 2011),
Yang et al. propose to perform face recognition by
solving Lasso problem in Robust Sparse Coding
(RSC) (Yang et al., 2011a). The coding coefficients
are calculated by iterative improvement, and a
weight matrix is added to the face image, which
gives a very small weight to pixels with occlusion or
noisy interference. All of these methods are common
in learning a public dictionary
shared by all classes.
However, the methods of public dictionary learning
do not make full use of the relationship between
sample labels and dictionary atoms, and hence
performing classification based on the reconstruction
error associated with each class is not allowed.
Different from these works, Yang et al. proposes a
sub-dictionary learning method (Yang et al., 2011b),
which learns a structured dictionary related to class
labels. It performs classification using class-related
reconstruction errors and produces better results than
SRC.
Although sparse representation based methods
have been successfully applied in face recognition,
they depend heavily on the selected dictionary D. So
it is important to study how to improve the
dictionary construction in sparse representation.
Feature learning has been widely used in
machine learning and a variety of feature learning
methods have been proposed in recent years (Bengio
et al., 2007; Learnedmiller, Lee, and Huang, 2012).
Principal component analysis network (PCANet) is a
novel deep learning algorithm for feature learning
with the simple network architecture and parameter
settings, which can be trained very efficiently. It was
proposed by Chan et al. (Chan et al., 2015), and is a
combination of principal component analysis (PCA)
and a convolutional neural network (CNN). PCANet
uses the most basic and simple operations to
simulate the processing layers in a typical neural
network: the data adaptive convolution filter bank in
each stage is selected as the most basic PCA filter;
the nonlinear layer is set to be the simplest binary
quantization (hashing); for the feature pooling layer,
it uses only the block-by-block histogram of the
binary code, which is considered to be the final
output feature of the network. It has been shown that
even the very basic PCANet has competitive or even
better performance compared with other methods in
image classification tasks (Chan et al., 2015).
In this paper we have studied how to improve
dictionary construction in sparse representation
using PCANet, and then proposed a new method for
face recognition. As mentioned above, using the
original training samples as the dictionary atoms
could not fully exploit the discriminative
information hidden in the training samples. So
PCANet is used to learn features from original face
images, and the learned features are used as
dictionary atoms in sparse representation instead.
With the proposed improved sparse representation
based on PCANet, the reconstruction error becomes
more discriminative, which leads to a better face
recognition method.
The rest of this paper is organized as follows.
Section 2 briefly reviews some related work, Section
3 presents the proposed face recognition method
based on sparse representation and PCANet, Section
4 describes the experimental results, and Section 5
concludes the paper.
2 RELATED WORK
2.1 Sparse Representation based
Classification for Face Recognition
Wright et al. propose the sparse representation based
classification (SRC) method for face recognition
(Wright et al., 2009). Based on the assumption that
the same class training samples lie on a linear
subspace, SRC searches the representative elements
from the training sample dictionary to sparsely
represent a test sample (Yang et al., 2011a). Suppose
that there are c classes samples, and let
12
, ,...,
c
D
DD D
be the set of the training
samples, where
i
D
is the sub-set of the training
samples from the i-th class. A given unknown image
y can be represented by the linear combination of the
training samples associated with the i-th class as:
ii
yDα
(2)
where
,1 ,2 ,
, ,...,
i
iii ip
ααα α
is the representation
coefficients, it is a column vector, and p
i
is the
number of the i-th training samples.
Because there are c classes samples, the linear
representation y can also be rewritten in terms of all
the training samples as follows:
yDα
(3)
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
518
where D is the dictionary and
1
;...; ;...;
ic
αα α α
,1 , 2 ,
0,...,0, , ,..., ,0,...,0
i
ii ip
αα α
is the coefficients
vector whose entries are zero except those associated
with the i-th class. If the number of training samples
is large enough, the non-zero coefficients are sparse
relative to the length of the coefficient vector.
The coefficient vector can be estimated by
sparsely coding y on D via l1-minimization problem:
2
12
ˆ
arg min . . ααst y Dαε
(4)
Then the classification can be done via:
() argmin
i
i
identity y error
(5)
where
2
ˆ
,1,2,...
iii
error y D α ic
, and
ˆ
i
α
is the
coefficients vector associated with class i. The
implementation details of SRC can be found in
(Yang et al., 2011b).
2.2 Structures of the PCANet
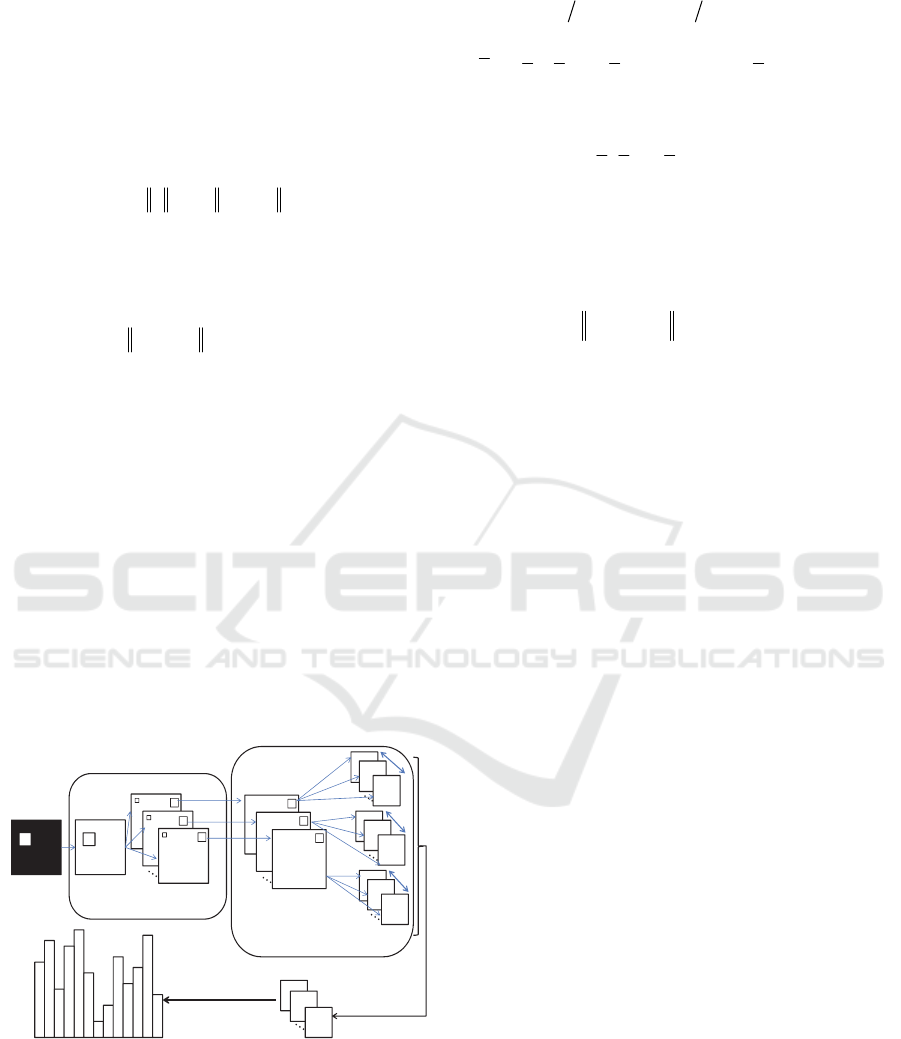
The PCANet used in the experiments has three
layers and two stages. Suppose there are N training
images
| 1, 2,...,
i
Si N
, the size of each image is
mn and the filter size of each layer is k
1
k
2
. Figure
1 shows a detailed block diagram of the two-stage
PCANet. Only the PCA filter core needs to be
learned from the training images. That is why the
PCANet can be designed and trained easily and
efficiently.
Figure 1: Detailed block diagram of a two-stage PCANet.
2.2.1 The First Stage PCA
For each pixel, a block image of size k
1
k
2
is located
around the pixel, then all the image blocks are
collected for cascading as the representation of the i-
th image
12
,1 ,2 ,
, ,...,
kk
iii imn
yyy y
, where
1
2mm k
,
2
2nn k
. We then subtract the
block mean from each block and obtain
,1 ,2 ,
, ,...,
iii imn
Yyy y
, where
,ij
y
is a mean-
removed block. For all input images, the mean of the
image are subtracted to produce the matrix:
12
12
, ,...,
kk Nmn
N
YYY Y
(6)
Supposing that the number of filters in the i-th
layer is L
i
, the purpose of the PCA is to minimize the
reconstruction error by finding a series of standard
orthogonal matrices:
1
12 1
2
min , . .
kk L
TT
L
F
U
YUUY stUU I
(7)
where U is the filter bank and
1
L
I
is identity matrix
of size L
1
L
1
. In PCANet, just the L
1
primary
eigenvectors of YY
T
are obtained. So the PCA filter
is expressed as follows:
12
12
1
,
kk
T
lkkl
W matrics eig YY
(8)
where l=1,2,…L
1
,
12
,kk
matrics vector is a function
that map
12kk
vector
to a matrix
12
kk
W
, and
T
l
eig YY
represents the l-th principal eigenvector
of YY
T
. Then, the PCA mapping output of the first
layer is calculated by:
1
, 1, 2,...,
l
iil
SSWi N
(9)
where the operation * represents the convolution of
two dimensions.
2.2.2 The Second Stage PCA
The mapping process of the second layer is basically
the same as the mapping mechanism of the first
layer. As with the blocking operation done in the
first layer, block sampling, cascading, and zero-
averaging are also performed on the input matrix
(the mapped output of the first layer) in the second
layer. The above operation is performed for each
input matrix, and finally the block sampling form of
the second layer input data is obtained:
112
12
, ,...,
L
kk Nmn
ZZZ Z
(10)
where Z represents the outputs of all the images after
convolving with
1
l
W
.
Then the eigenvectors of ZZ
T
is computed and L
2
principle eigenvectors are selected as PCA filters of
Input layer
S
i
1
1
W
1
2
W
1
i
S
2
i
S
1L
i
S
Mean
removal
PCA filters
convolution
Mean removal
2
2L
W
2
1
W
2
2
W
2
1
W
2
2
W
2
1
W
PCA filters
convolution
First stage
Second stage
2
i
R
1L
i
R
1
i
2
i
1L
i
Output layer
Binary quantization and
histogram generation
2
2L
W
2
2L
W
2
2
W
1
i
R
1
1L
W
Improving the Dictionary Construction in Sparse Representation using PCANet for Face Recognition
519

the second stage. So the PCA mapping output of the
second layer is:
2
2
, 1, 2,...
ll
iil
RSWl L
(11)
We can see that the first layer and the second
layer are very similar in structure, so it is easy to
expand PCANet into a deep network structure
containing more layers.
2.2.3 The Output Stage Hashing and
Histogram
The binary processing is performed on each output
matrix of the second layer,
2
{,
l
il
Binarify S W l
2
1, 2,..., }L
, where Binarify(x) is a binarization
function. If the x is a positive value, the function
value is 1. Otherwise, the function value is 0. In the
same pixel position of the L
2
outputs, the L
2
binary
bits are viewed as a decimal number. This converts
the L
2
outputs into a single integer-valued “image”:
2
12
1
Γ 2
L
ll l
iil
l
Binarify S W
(12)
After the above processing, each pixel value is
encoded as an integer within
2
0, 2 1
L
.
For each output matrix of the second layer, we
divide it into C blocks of size b
1
b
2
, calculate the
histogram information of each block, and then
cascade the histogram features of each block to
finally obtain the block extended histogram features:
2
1
1
2
Γ ,..., Γ
L
T
L
C
L
l
ii i
fChist Chist
(13)
where
Γ
l
i
Chist
represents the concatenated
histogram features of C blocks in decimal value map
Γ
l
i
.
When the local blocks are selected, the blocks
can be either overlapping or not. Experiments show
that non-overlapping blocks are suitable for face
recognition.
3 THE PROPOSED METHOD
Assume there are N training samples
12
Ι [Ι , Ι ,
..., Ι ]
N
. First PCANet is used to learn features from
the face images. In the proposed method, a two-stge
PCANet is used to learn features from the face
images. As mentioned above, only the PCA filter
core need to be learned from the training samples.
We need just one face dataset to learn PCA filters in
PCANet, and then such trained network can be
applied to learn features from new subjects in the
other datasets. Let
12
, ,...,
N
f
ff
be the set of the
features learned using PCANet from original
training samples. The dictionary in sparse
representation is constructed by
12
, ,...,
N
A
ff f
.
Then the sparse representation is used to code
the query face images. Using the method of
Lagrange multiplier, equation (4) is converted to the
following equivalent problem:
2
21
ˆ
min
α
α Aα y λα
(14)
where λ is the Lagrange multiplier. It’s a l1-
regularized least squares problem. In our
experiments, the l1_ls interior-point method (Koh,
Kim, and Boyd, 2007) for l1-regularized least
squares is used to solve the problem.
Once the coding coefficients are obtained, the
reconstruction error can be computed with respect to
the test sample as follows:
2
ˆ
, 1, 2,...,
iii
error y A α ic
(15)
Finally, the identity of y is the class corresponding
to the minimal reconstruction error, as given in (5).
Algorithm 1 summarizes the above procedure for the
proposed method.
Algorithm 1: Improving the Dictionary Construction in
Sparse Representation using PCANet for Face
Recognition.
Input: Training samples A
0
, testing samples B
0
, filter
size k
1
k
2
, number of filters L
1
L
2
, block size
b
1
b
2
, regularization parameter λ.
Output: Identity of test samples.
Step1: Learn PCA filters in PCANet using one face
dataset.
Step2: Produce new training samples A and test
samples B with features learning from A
0
, B
0
using PCANet.
Step3: Let A be the dictionary, using l1_ls to
compute the coding coefficients of y
i
(the i-th
sample in B) on A,
2
21
ˆ
min
i
α
α Aα y λα
.
Step4: Compute the reconstruction error:
2
ˆ
,1,2,...,
jijj
error y A α
j
c .
Step5: Output the identity of y
i
:
argmin , 1, 2,...,
ij
j
identity y error j c.
Step6: Return to step3 until all samples in B are
classified.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
520

4 EXPERIMENTS
The proposed method is verified on three publicly
available face datasets: AR, Extended Yale B, and
FERET. Experiments are conducted on computer
with Intel Core i7 CPU(3.60GHz). The proposed
method is compared with 1-nearest-neighbor (1NN),
the sparse representation based classification (SRC),
robust sparse coding (RSC), fisher discrimination
dictionary learning (FDDL), and PCANet (classify
by cosine distance). In all experiments, Principal
Component Analysis (PCA) is applied to reduce the
dimensionality.
4.1 Parameter Selection
In our experiments, a two-stage PCANet is used.
The MultiPIE
(Gross, Matthews, and Baker, 2008)
dataset has the most face images, so it is used to
learn PCA filters in PCANet, and then apply such
trained PACNet to construct dictionaries of new
subjects in the AR, Extended Yale B, and FERET
datasets for face recognition. The important
parameters in PCANet are the filter size k
1
, k
2
, the
number of filters L
1
, L
2
, and the block size b
1
, b
2
. In
order to determine the values of k
1
, k
2
, L
1
, L
2
, b
1
, b
2
,
we conduct experiments by changing the values of
k
1
, k
2
, L
1
, L
2
, b
1
, b
2
from 1 to 15 on the MultiPIE
face dataset. It is found that k
1
=k
2
=5, L
1
=L
2
=8, and
b
1
=b
2
=8 is a good choice. We set λ=0.001 in all
experiments. For the AR and FERET datasets, all
the images from one dataset are put together and
then the 5-fold cross-validation is used. The initial
samples are segmented into 5 parts, a single part is
retained as data for testing, and the other 4 parts are
used for training. Cross-validation is repeated 5
times, each part is tested once, and the average of 5-
time results is used to finally obtain a single estimate.
4.2 The AR Dataset
The AR dataset (Martinez, 1998) consists of over
4,000 images from 126 individuals (70 males and 56
females), which varies in illumination, expression
and accessories like scarves and sunglasses blocking
some part of the face. A subset containing 1,400
images of 100 subjects with 50 males and 50
females without accessory are chosen in the
experiment. Sample images of the first person are
illustrated in Figure 2. All images are resized into
6043. Dimensionality of the features is reduced to
300 by PCA for all experiments on the AR dataset.
Figure 2: Sample images of the first subject from AR
dataset.
Table 1 shows the results of 1NN, SRC, RSC,
FDDL, PCANet and the proposed method on the AR
dataset. The proposed method achieves best among
all the methods. It is at least 0.43% higher than
others.
Table 1: The classification accuracy on the AR dataset.
Methods Accuracy (%)
1NN 77.16±3.54
SRC 96.50±1.14
RSC 99.27±0.32
FDDL 76.07±7.69
PCANet 99.36±0.42
The proposed method 99.79±0.28
4.3 The Extended Yale B Dataset
The Extended Yale B dataset (Georghiades,
Belhumeur, and Kriegman, 2001) consists of 2,414
images of 38 individuals captured under various
lighting conditions controlled in laboratory. Figure 3
shows sample images of the first person under
various lighting conditions. For each subject, the
frontal illumination images (the first 6 images) are
selected as the training images and the rest for
testing. All images are resized into 54
48.
Dimensionality of the features is reduced to 200 by
PCA for all experiments on the Extended Yale B
dataset.
Figure 3: Sample images of the first subject from
Extended Yale B dataset.
Table 2 shows the classification accuracies of
1NN, SRC, RSC, FDDL, PCANet, and the proposed
method on the Extended Yale B dataset. The
proposed method has the highest classification
accuracy: 97.99%, which is at least 8.73% higher
than others.
Improving the Dictionary Construction in Sparse Representation using PCANet for Face Recognition
521

Table 2: The classification accuracy on the Extended Yale
B dataset.
Methods Accuracy (%)
1NN 42.32
SRC 48.67
RSC 53.43
FDDL 54.20
PCANet 89.26
The proposed method 97.99
4.4 The FERET Dataset
The FERET dataset (Phillips, 2000) consists of
14,051 images with different poses, illuminations
and expressions. We choose a subset containing
frontal images marked with “ba”, “bj”, and “bk”, of
which there 600 images from 200 individuals. Such
images from the subsets are given in Figure 4. All
images are resized to 7060. Dimensionality of the
features is reduced to 400 by PCA for all
experiments on the FERET dataset.
Table 3 shows the results of 1NN, SRC, RSC,
PCANet, and the proposed method on the FERET
dataset. The proposed method produces the second
highest classification accuracy: 89%, while the
PCANet produces the best result.
Figure 4: Sample images from FERET dataset.
Table 3: The classification accuracy on the FERET dataset.
Methods Accuracy (%)
1NN 35.33±3.01
SRC 65.33±4.40
RSC 50.33±4.03
PCANet 90.22±3.71
The proposed method 89±2.76
Comparing with other face datasets, the FERET
dataset is a small dataset. It has 200 individuals, but
one subject only has 3 images. So, another
experiment is done on the extended FERET dataset
by using both the original images and the mirror face
images of original samples.
According to (Xu et al., 2017), for original face
image x, its mirror face image is defined as:
,,1
m
xpq xpQq
(16)
where
1,..., ; 1,...,pPqQ
, P and Q denote the
number of rows and columns of the face image
matrix.
Table 4: The classification accuracy on the extended
FERET dataset.
Methods Accuracy (%)
1NN 56.17±1.45
SRC 76.5±1.43
RSC 61±2.27
PCANet 90.91±1.10
The proposed method 94.33±1.11
The results of 1NN, SRC, RSC, PCANet and the
proposed method on the extended FERET dataset
are showed in Table 4. The classification accuracies
of all the methods for the extended FERET dataset
become higher compared to the corresponding
results for the original FERET dataset. And the
proposed method has produced the highest
classification accuracy: 94.33%, which is at least
3.42% higher than the other methods.
In the experiments, the proposed method
produces the highest classification accuracy within
the 6 methods on AR and Extended Yale B datasets.
For the FERET dataset in which the size of the
training data in each class is very small, the
proposed method only produces the second best
result. And after increasing the size of the training
data in the FERET dataset with the mirror face
images, the proposed method can also produce the
highest classification accuracy of 94.33% on the
extended FERET dataset.
5 CONCLUSIONS
To improve the classification accuracy in sparse
representation for face recognition, in this paper, we
have proposed an improved dictionary construction
method in sparse representation using PCANet.
Extensive experiments demonstrate that the
proposed method outperforms some previous state-
of-art methods for face recognition. It is found that
that the dictionary construction is crucial for sparse
representation. Compared to the original images, the
features learned by PCANet from the images can
serve as better dictionary atoms for sparse
representation in face recognition. One disadvantage
of the method is that when the size of the training
data in each class is too small, the proposed method
does not perform satisfactorily. As shown in the
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
522

experiments, this problem can be solved by
increasing the size of the training data with the
mirror face images. Since the process of sparse
coding is very time-consuming, we will work on
improving the efficiency of the proposed method in
the future work.
ACKNOWLEDGEMENTS
This work is supported by the National Key R&D
Program of China (Grants No. 2017YFE0111900,
2018YFB1003205), and the Lanzhou Talents
Program for Innovation and Entrepreneurship
(Grants No. 2016-RC-93).
REFERENCES
Turk, M., Pentland, A., 1991. Eigenfaces for recognition.
Journal of Cognitive Neurosicence, 3(1): 71-86.
Zhang, D., Chen, S., and Zhou, Z. H., 2005. A new face
recognition method based on SVD perturbation for
single example image per person. Applied
Mathematics & Computation, 163(2): 895-907.
Maksimov, R., Gaidukovs, S., Kalnins, M., Zicans, J., and
Plume, E., 2006. A human face recognition method
based on modular 2dpca. Journal of Image &
Graphics, 42(1): 45-54.
Liu, Q., Huang, R., Lu, H., and Ma, S., 2001. Face
recognition using kernel based fisher discriminant
analysis. In IEEE International Conference on
Automatic Face and Gesture Recognition, 197.
Ghiass, R. S., Arandjelovic, O., Bendada, H., and
Maldague, X., 2013. Infrared face recognition: a
literature review. Computer Science, 1-10.
Chen, Y., Su, J., 2017. Sparse embedded dictionary
learning on face recognition. Pattern Recognition, 64:
51-59.
Wright, J., Ma, Y., Mairal, J., Sapiro, G., Huang, T. S.,
and Yan, S., 2010. Sparse representation for computer
vision and pattern recognition. Proceedings of the
IEEE, 98(6): 1031-1044.
Wright, J., Yang, A. Y., Sastry, S. S., and Ma, Y., 2009.
Robust face recognition via sparse representation.
IEEE Trans Pattern Anal Mach Intell, 31(2): 210-227.
Zhang, L., Yang, M., Feng, Z., and Zhang, D., 2010. On
the dimensionality reduction for sparse representation
based face recognition. International Conference on
Pattern Recognition, 1237-1240.
Elad, M., Aharon, M., 2006. Image denoising via sparse
and redundant representations over learned
dictionaries. IEEE Transactions on Image Processing,
15(12): 3736-3745.
Mairal, J., Elad, M., and Sapiro, G., 2007. Sparse
representation for color image restoration. IEEE
Transactions on Image Processing, 17(1): 53-69.
Lu, J., Liong, V. E., Wang, G., and Moulin, P., 2015. Joint
feature learning for face recognition. IEEE
Transactions on Information Forensics & Security,
10(7): 1371-1383.
Zhou, W., 2012. Sparse representation for face recognition
based on discriminative low-rank dictionary learning.
In IEEE Conference on Computer Vision and Pattern
Recognition, 157: 2586-2593.
Yang, M., Zhang, L., Yang, J., and Zhang, D., 2011a.
Robust sparse coding for face recognition. In
International Conference on Pattern Recognition,
625-632.
Aharon, M., Elad, M., and Bruckstein, A., 2006. K-SVD:
An algorithm for designing overcomplete dictionaries
for sparse representation. In IEEE Transactions on
signal processing, 54(11), 4311.
Tibshirani, R., 2011. Regression shrinkage and selection
via the lasso: a retrospective. Journal of the Royal
Statistical Society, 73(3): 273-282.
Yang, M., Zhang L., Feng, X., and Zhang, D., 2011b.
Fisher discrimination dictionary learning for sparse
representation. In
IEEE International Conference on
Computer Vision, 24(4): 543-550.
Bengio, Y., Lamblin, P., Dan, P., and Larochelle, H., 2007.
Greedy layer-wise training of deep networks.
Advances in Neural Information Processing Systems,
19: 153-160.
Learnedmiller, E., Lee, H., and Huang, G. B., 2012.
Learning hierarchical representations for face
verification with convolutional deep belief networks.
In IEEE Conference on Computer Vision and Pattern
Recognition, 157: 2518-2525.
Chan, T. H., Jia, K., Gao, S., Lu, J., Zeng, Z., and Ma, Y.,
2015. PCANet: a simple deep learning baseline for
image classification? IEEE Transactions on Image
Processing, 24(12): 5017-5032.
Koh, K., Kim, S. J., and Boyd, S., 2007. An interior-point
method for large-scale l1-regularized logistic
regression.
Gross, R., Matthews, I., and Baker, S., 2008. “Multi-pie,”
In IEEE Conference on Automatic Face and Gesture
Recognition.
Martinez, A. M., 1998. The AR face database. Cvc
Technical Report, 24.
Georghiades, A. S., Belhumeur, P. N., and Kriegman, D. J.,
2001. From few to many: illumination cone models for
face recognition under variable lighting and pose.
IEEE Transactions on Pattern Analysis & Machine
Intelligence, 23(6): 643-660.
Phillips, P. J., Moon, H., Rizvi, S. A., and Rauss, P. J.,
2000. The FERET evaluation methodology for face-
recognition algorithms. IEEE Transactions on Pattern
Analysis & Machine Intelligence, 22(10): 1090-1104.
Xu, Y., Li, Z., Zhang, B., Yang, J., and You, J., 2017.
Sample diversity, representation effectiveness and
robust dictionary learning for face recognition.
Information Sciences, 375(C): 171-182.
Improving the Dictionary Construction in Sparse Representation using PCANet for Face Recognition
523
