UAV Flocks Forming for Crowded Flight Environments
Rina Azoulay
1
and Shulamit Reches
2
1
Department of Computer Science, Jerusalem College of Technology, Havaad Haleumi Street, Jerusalem, Israel
2
Department of Mathematics, Jerusalem College of Technology, Havaad Haleumi Street, Jerusalem, Israel
Keywords:
Systems and Applications, Transportation Systems, UAVs, Agents, Distributed AI.
Abstract:
In this study, we consider a situation where several privately owned unmanned aerial vehicles (UAVs) are sup-
posed to travel on several routes. We develop a model for grouping them into UAV flocks that are supposed
to travel on similar routes within the same time window. Our proposed flocking protocol enables each UAV
to optimize its own preferences concerning its flights. Using this protocol enables all UAVs to enjoy freer
routes and fewer encounters with other UAVs, thus saving time and energy during their flights. The protocol
allows each UAV to create a flock or to join an existing flock to save its resources. Joining flocks in a crowded
environment can reduce the overhead caused by encountering additional UAVs in the environment. We deve-
loped a flocking protocol that allows each UAV to design its optimal route. The protocol is based on a public
on-line communication blackboard, which enables each UAV to receive information about existing flocks, join
an existing flock or build a new flock and publish it on the blackboard. In addition, we defined a strategy for
each UAV to assist in deciding which flock to join or whether to create a new flock to optimize its expected
utility. Finally, the effectiveness of the proposed algorithm is verified by means of simulations.
1 INTRODUCTION
Recently, the field of unmanned aerial vehicles
(UAVs) has gained momentum. UAVs are used to-
day for diverse tasks, and their usage has vastly grown
over the years in various fields (Valavanis and (edi-
tors), 2015) such as photography, surveillance, agri-
culture, communication, testing, and military. Future
commercial usage may also include delivery of pro-
ducts, documents and food. The decline in the price
of UAVs, among other things, has contributed to their
popularity, and it seems that their usage in the near
future will become increasingly common, resulting in
a situation of overload along their various paths.
The most significant challenge in the near future
will be to build communication protocols to enable in-
dividual heterogeneous UAVs, developed by different
companies based on various technologies, to commu-
nicate with each other. Currently, there is no such pro-
tocol. This communication would enable the UAVs
to coordinate their routes and share common routes
to avoid collisions with obstacles or other UAVs in
crowded environments and thus decrease their flight
times. This communication is essential in light of
the expected crowded and overloaded environments.
The flight of each UAV in its own direction can cause
a significant slowdown in UAVs’ progress and may
even lead to deadlocks if none of the UAVs in the cro-
wded environment can progress.
In this study we consider the problem of multiple
UAVs, each with its own goal of moving from source
location s to target location t. In crowded environ-
ments, where multiple UAVs exist, loads may occur
and thus UAVs may disturb each other. We developed
a protocol that will enable UAVs to be clustered as
flocks according to their appropriate goals and needs
such as source and destination points. The protocol
defines how flocks will be created, how different and
heterogeneous flying objects (UAVs and flocks) will
communicate with each other, and how the priority of
flocks and UAVs will be defined in cases of collisi-
ons. In addition, we have defined stable strategies for
each UAV that operates in the above environment. In
particular, the UAV will use these strategies to decide
whether to join an existing flock and which to join, or
create a new flock.
We contract a model in which individual UAVs
from different manufacturers and with different in-
terests and different sources and targets communi-
cate, in order to form flocks that serve the interests
of the individual UAVs in the flocks and maximize
their gains. We propose a model where flocks of self-
interested UAVs are created. The information about
current and future flocks is saved in a shared cloud
154
Azoulay, R. and Reches, S.
UAV Flocks Forming for Crowded Flight Environments.
DOI: 10.5220/0007369401540163
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 154-163
ISBN: 978-989-758-350-6
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

and can be viewed by all the UAVs in the given area.
Each UAV can decide whether to create a new flock,
or join an existing flock in order to maximize its own
benefits.
The algorithm we present assists the UAVs deci-
sion making processes while using the shared infor-
mation about the existing UAVs, and prior informa-
tion about the distribution of the loads in the given
environment throughout the day. The model allows
the individual UAV to decide whether to join an ex-
isting flock and thereby benefit from higher priority
of the large united flock or create a new flock and
benefit from the flexibility and shorter track length,
determined exactly according to the needs that suit it.
To summarize, an individual UAV should examine the
advantages and disadvantages of using flocks in some
or in all of its journeys, and it should make its decision
while considering the current situation (current load
and distribution of additional load) of the dynamic
environment. Unlike other studies in this field, that
deal with finding an efficient path for a given flock
of UAVs (see (Mohammadreza Radmanesh, 2018) for
an overview), or creating an efficient flying structure
in order to avoid collisions, our unique model deals
with the problem of how to form UAV flocks given
different individual UAVs, from different manufactu-
rers and with different interests and targets. It also
addresses how UAVs can communicate with each ot-
her in order to form flocks that serve the interests of
each of the individual UAVs while maximizing their
individual gains.
In order to verify the effectiveness of our model,
we present our simulation results. The simulation re-
sults prove that our model significantly improves the
flight time, especially in crowded environments.
It has already been proven (Jenhui Canny, 1987)
that computing the shortest obstacle-avoiding paths
among obstacles in three dimensions is NP-complete.
However, because the surface and the technology con-
straints allow the UAVs to fly in a very limited range
of heights, we have built our simulation in a two-
dimensional environment.
The paper is organized as follows: In Section 2
we present some of the previous works in this field.
We provide our basic model in Section 3 and we in-
troduce the flocking protocol in Section 4. The UAVs
preferences and decision-making process are detailed
in Sections 5 and 6, respectively. Our experimental
results are provided and discussed in Section 7. Fi-
nally, in Section 8 we conclude with directions for
future work.
2 RELATED WORK
Many studies present methods to allow a group of
UAVs (or robots) to move in a harmonious manner
(Panov and Yakovlev, 2017). These methods aim
to enable a group of autonomous vehicles (robots,
UAVs, or autonomous cars) to move in a stable man-
ner without collisions with the other agents in the
group. In particular, the problem of coordinating the
motion of multiple autonomous agents has been dis-
cussed in (Herbert G. Tanner and Pappas, 2003a) and
(Herbert G. Tanner and Pappas, 2003b). These stu-
dies generate a stable flocking motion for a group of
multiple vehicles while trying to imitate a group of
autonomous moving creatures such as flocks of birds
or schools of fish.
The method of building a simulated flock has been
discussed in detail by Reynolds (Reynolds, 1987).
His approach relies on several components: (1) colli-
sion avoidance: avoiding collisions with nearby flock-
mates, (2) velocity matching: attempting to match
velocities of nearby flockmates, and (3) flock cente-
ring: attempting to stay close to nearby flockmates.
Our study does not deal with the technical aspects
that enable a flock of UAVs to fly in a stable manner
without collisions between the flock members, and
instead builds a second stage of coordination between
UAVs by constructing a communication protocol that
enables them to create flocks, in a way that serves the
interests of each UAV.
The problem of assigning multiple UAVs to per-
form tasks cooperatively is a challenge that requi-
res the development of specialized algorithms. Many
studies deal with multiple robots that cooperate with
each other in order to achieve a specific mission or to
maximize their effectiveness.
In (Jenhui Chen, 2005), a communication protocol
for a sensor multi-robot system is presented in which
the energy consumption, as well as the duration of re-
aching the goal, is reduced. Yang et al. (Yanli Yang
and Minai, 2007) describe a cooperative search pro-
blem where a team of UAVs seeks to find targets of
interest in an uncertain environment. Passino et al.
(Kevin Passino, 2002) instigated the performance of
strategies for cooperative control of autonomous ae-
rial vehicles that seek to gather information about a
dynamic target environment, evade threats, and coor-
dinate strikes against targets.
Ben-Asher et al. (Yosi Ben-Asher, 2010) develo-
ped a distributed algorithm for task assignment, coor-
dination, and communication of multiple UAVs eng-
aging multiple targets in an arbitrary theater. They
aimed to maximize the ratio between the number of
intercepted targets and the number of launched muni-
UAV Flocks Forming for Crowded Flight Environments
155

tions given a fixed number of flock payloads. Coordi-
nation of UAV motion is achieved by implementing a
simple behavioral flocking algorithm utilizing a tree
topology for target list routing. In (Gurfil and Ki-
velevitch, 2007), a hierarchical algorithm was deve-
loped for autonomous formation flying, communica-
tion, and task assignment for cooperating UAVs. This
research showed, inter alia, that using communication
improves the cooperation among the flock members.
Recently, many researches have investigated the
multi-UAV path planning (Liang Yang and Xia,
2016), which is a process whereby the UAVs find
their own paths from their starting points to their des-
tinations cooperatively. Recent studies (Li and Duan,
2012; YongBo Chen and Luo, 2015; Joongbo Seo and
Tsourdos, 2017) have considered the multi-UAV for-
mation path planning in which each UAV finds its
own collision free path and simultaneously tries to
keep the formation structure of the flock to which it
belongs. Recent studies (Selim Temizer and Kuchar,
2010; Ragi and Chong, 2013; Dabbiru and Siddhabat-
hula, 2016) consider the issue of path planning and
collision avoidance using the Markov Decision Pro-
cess. The difference between our study and previous
work on UAVs’ path planning and collision avoidance
lies in the fact that we concentrate on the issue of
flocking autonomous UAVs in order to avoid poten-
tial collisions.
Swarm robotics (Bayndr, 2016; Arne Brutschy,
2014; Christopher M. Cianci, 2007; Winfield, 2008)
is an approach inspired by social insects that coordi-
nates large numbers of relatively simple robots. This
study considers groups of robots that operate without
relying on any external infrastructure or on any form
of centralized control. An important component of
this study is the communication between the members
of the group that build a system of constant feedback.
The swarm behavior involves constant change of in-
dividuals in cooperation with others, as well as the
behavior of the whole group.
There are many applications for swarm robotics.
One is in disaster rescue missions. Swarms of ro-
bots of different sizes can be sent to places that rescue
workers cannot reach safely, to detect the presence of
life via infrared sensors. Furthermore, swarm robo-
tics can be used for tasks that demand cheap designs
such as mining or agricultural foraging tasks.
In contrast to these studies in which the collabo-
ration among players in the flock aims to achieve a
common goal, or make it more efficient, our model
deals with the use of flocks to maximize the utility of
the individual UAVs. Furthermore, the protocol we
developed assists them in cooperation in a way that
is beneficial to each UAV, although each has its own
goals and targets.
3 PROBLEM DESCRIPTION
In the environment considered in this research, dyn-
amic set of UAVs exists, of a size less than or equal
to N. Each UAV u
i
must travel from a source point
S
i
to a destination point T
i
. In addition, each UAV u
i
has its time constraints, where it cannot leave S
i
be-
fore time Start
i
and it must reach point T
i
no later than
time Finish
i
.
Each UAV has the option to decide whether to tra-
vel directly from S
i
to T
i
independently, without joi-
ning other UAVs or join a flock to avoid delays caused
by other UAVs or UAV flocks that will cross its route.
Thus, it may be beneficial for a UAV to join a flock
of UAVs that have a route heading toward its destina-
tion. In the following sections, we propose a protocol
for creating flocks and stable strategies for UAVs to
decide which flock to join or attempt to create a new
flock. We call the creator of a flock the manager. The
manager of a flock is committed to its flock and de-
termines the source point and the destination point of
the flock’s flight. It is also authorized to accept anot-
her UAV to its flock or reject it. The flock manager
can restrict its flock to certain manufacturers, models,
to travel at certain heights, etc. It can also limit the
size of its flock to a maximum size, and so forth.
The goal of each UAV is to meet its constraints,
i.e., to leave starting point S
i
at time Start
i
or later, and
to reach point T
i
at time Finish
i
or earlier, while sa-
ving resources of power and flight time (including the
required travel time and waiting time in cases of col-
lisions with other flocks until other UAVs finish cros-
sing its route) and reaching the destination as early as
possible.
Also note that in cases of a possible collision of
flocks, the protocol we define provides a higher pri-
ority to the larger flock to proceed before the other
flock/s, and this could motivate UAVs to join flocks
in crowded environments, even if it might increase the
length of their total route.
In contrast to other studies in the field of UAV
flocks where the motivation of forming a flock is to
fulfill a specific task that a single UAV finds difficult
or cannot do alone, our research deals with the use
of flocks in order to achieve and optimize the goal of
every UAV.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
156

The environment studied includes the following
parameters:
• G: the identity of a group/flock of UAVs.
• L
G
: current size of flock G. There is an advan-
tage for a large flock in cases of intersections of a
number of flocks. In such cases, the smaller flock
will change its direction, or wait in its place until
the larger flock passes. In other words, the lar-
ger group has a higher priority at an intersection.
Thus, the flock’s route time decreases as the flock
size increases.
• I(size
G
i
): the expected delay due to the inter-
section of flock G with a particular flock G
i
with
a size size
G
i
. It depends on the current values of
L
G
i
and on the expected value of the number of
UAVs that will join the flocks until the departure
time. Note that if the size of flock G is greater than
the size of flock G
i
, no delay is expected because
flock G will be given priority to proceed.
• T
G
: the expected time required for the travel of
flock G, given the route s
G
to d
G
(if no inter-
section exists). T
G
depends on the distance bet-
ween s
G
and d
G
, the expected speed of the flock,
the expected wind direction, and the expected
wind speed.
• DT
G
: the flock’s required arrival time, which is
defined by the flock manager.
• s
u
and d
u
: the source and destination of the requi-
red route of UAV u.
• s
G
and d
G
: the source and destination of the ex-
pected route of flock G.
• D
u,G
: the time that will be spent due to the de-
viation of UAV u from the original UAV shortest
path to the route of the flock. When a UAV joins a
flock, it might lengthen its path if the flock’s route
is not identical to its shortest path, and this might
increase the required time. Note, however, that if
s
u
= s
G
and d
u
= d
G
, or if both s
u
and d
u
are points
inside the route of flock G, then D
u,G
= 0, because
no deviation is required to adapt the UAV route to
the flock route.
• T
u
: the expected time required for the travel given
the direct route from s
u
to d
u
(if no intersection
exists).
• [T
a
, T
b
]: time window range for the departure time
of a flock .
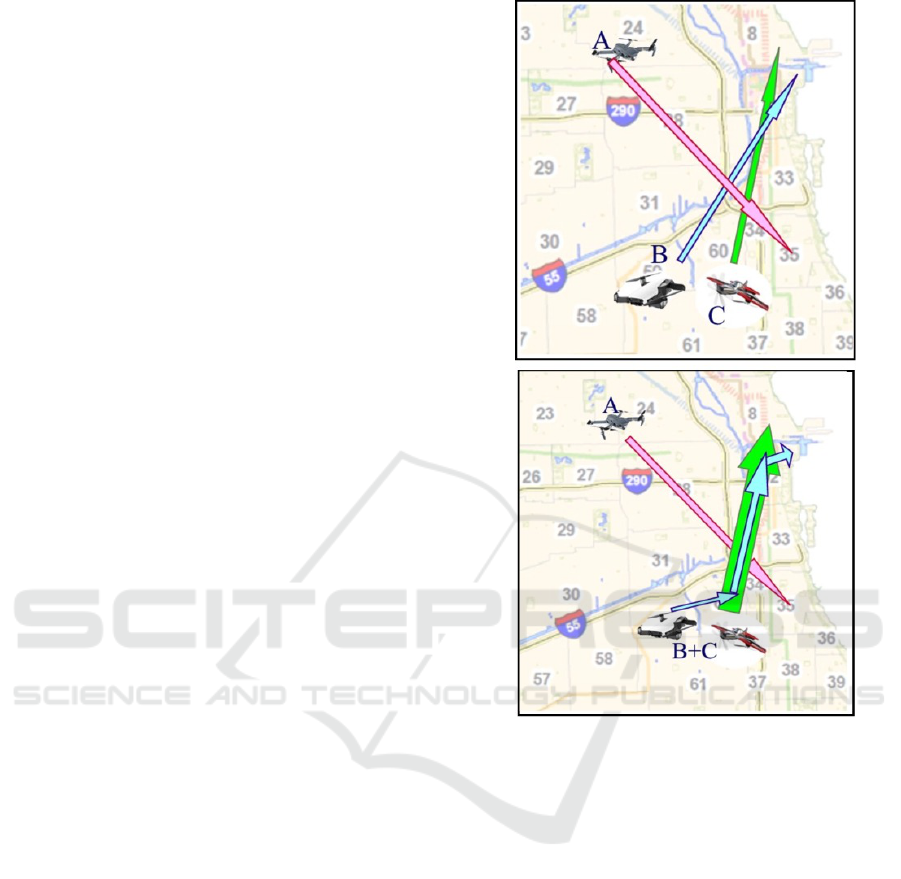
Figure 1:Up and Figure 1:Down demonstrate the
advantage of flocking in situations where multiple
UAVs act in the same loaded environment. In both
figures, three UAVs, named A, B, and C, exist, which
have similar routes within the same time window.
Figure 1: Up: demonstration of intersections between un-
flocked UAVs. Down: advantage of a flocking protocol for
the same scenario depicted in the figure above.
In Figure 1:Up, each UAV proceeds with its own
route and interacts with the two others. Then, Fi-
gure 1:Down shows a situation where a flocking pro-
tocol exists: UAVs B and C find it beneficial to form
a flock, and in this case, only one interaction occurs,
which is between A and the BC flock. UAV B has to
lengthen its route, but does not have to wait for any ot-
her UAV or flock (because the B,C flock is larger than
A, A will have to wait for B,C at their crossroad).
4 PROPOSED PROTOCOL
In this section, we will describe a communication pro-
tocol that enables the individual UAVs to estimate
the expected flight space and to plan the formation
of UAV flocks. The basic protocol is as follows: An
online blackboard exists for all UAV flocks that are
supposed to be organized in a predefined radius. Each
UAV Flocks Forming for Crowded Flight Environments
157

flock contains the following information:
• flock manager (flock creator)
• flock starting point Si and flock destination point
Ti.
• estimated departure time and estimated arrival
time.
• size of flock.
Note that the blackboard contains shared knowledge
about several departure and arrival nodes in its geo-
graphical area. In addition, the blackboard can also
share relevant information from other blackboards
about flocks that are supposed to reach its geographi-
cal area. Each UAV that wants to take a route will first
search the blackboard in order to find an appropriate
flock that matches its requirement. If such a flock is
found, the UAV sends the flock manager a request to
join it.
In addition, in case of a collision between flying
objects (flocks or UAVs), the larger flying object with
more members is given priority to proceed.
The UAV message includes:
• its contact details,
• point where it would like to join the flock,
• point where it would like to leave the flock,
• and its time constraints.
The flock manager, upon receiving the UAV mes-
sage, will decide whether to accept the UAV to the
flock or not and it will send an appropriate message
to the UAV.
If the UAV is accepted to the flock, the managers
message to it will include the time and place where
and when the UAV is supposed to join the flock (the
starting point of the flock, or a point along the flock’s
route).
1
The flock route details, i.e., the exact route
and the exact departure and arrival times, may be par-
tially defined during the flock organizing process, and
they may dynamically change with time when the
journey begins and even during the flight, if neces-
sary. Thus, the manager can continue to send updates
to the flock participants concerning the route details
until the journey is completed.
If a UAVs request to join a flock is accepted, it is
committed to the flock, and it should reach the meet-
ing point by the time that was sent to it. The UAV
may reach the flock at a different meeting point and
1
Another possibility may be a union of two flocks wai-
ting on the blackboard, which may decide to move together
on a particular route.
In this case, the estimated departure time, estimated arri-
val time, and common route will be decided together by the
flock managers and agreed upon by all participating flocks.
leave it at a different splitting point. However, during
the time that it is a member of the flock, it must keep
the flock’s direction and speed, and it must keep the
required distance from the other flock members.
If a UAV cannot find any appropriate flock, it may
create a new flock and publish it on the common
blackboard
2
. When creating a new flock, the UAV
should decide which requirements to publish such as
the starting point, the ending point, and the time win-
dow. This UAV will be the flock manager: it will
be committed to this flock and it will be responsi-
ble for accepting additional UAVs to the flock and
for keeping the flock details (route and expected time
window) up to date. The manager is authorized to
accept only UAVs of models and manufacturers that
meet the basic requirements of the flock (speed, dis-
tance, etc.). There is a possibility to join a flock du-
ring the flight. In this case, the flock’s details are al-
ready determined, and a UAV can join it by receiving
the manager’s agreement and receiving the exact joi-
ning time and place.
To summarize, the flock blackboard contains the
following details:
• For each organizing flock: (flocks that are now
being organized and not yet flying)
– flock manager’s contact details,
– expected departure time
– current flock size.
– current information about the flock’s route.
• For each airborne flock: (flocks that already began
their route)
– flock manager’s contact details,
– flock’s current point
– flock’s remaining route and estimated times.
A new UAV can do one of the following:
• view the current flocks on the blackboard.
• ask to join an existing flock (organizing or air-
borne flock).
• create a new flock.
Note that a UAV that is already a member of a
flock should be committed to it, but it can agree or
disagree to a new member joining or to merging with
another flock if this will change the flock’s route or
time.
During flight, if two or more flocks are involved
in a possible collision (intersection), the largest flock
2
According to the protocol, it may also build a rival flock
with similar route and departure time as an existing flock,
but in this case, the precedence of the rival flock will be
lower than that of the existing flock
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
158

will be given permission to proceed first. This will
motivate UAVs to join flocks and thus reduce the traf-
fic load. If both flocks are of the same size, then a
lottery will be performed to decide which flock will
be given the right of way.
We proceed by defining the UAV preferences and
expected flying time given the current knowledge
about organizing flocks and flying in flocks.
5 UAV PREFERENCES AND
EXPECTATIONS
Given the flight protocol we defined above, we pro-
ceed by describing the preferences and expected uti-
lity of a UAV that operates in an environment that uses
this protocol. In order to decide which flock to join or
whether to open a new flock, the UAV is motivated to
minimize its expected total flight time
3
.
We first assume that the UAV knows the current
information about the flocks that currently fly or the
flocks that are currently organized, using the know-
ledge in the relevant area blackboards. However, it
does not have complete information about the actual
time that each flight will require, due to unknown pa-
rameters (wind, etc.). In addition, it does not know
the exact time and place of the intersections with ot-
her flocks, and how long it will take each of them to
reach such intersections. This is due to two reasons:
(1) unknown parameters on the actual route, which
can influence the meeting location and the length of
delay that will be caused as a result; (2) the final size
of each group is dynamic and therefore not known in
advance. Thus, the UAV should evaluate the expected
time of the flight whether it will fly alone or join any
given flock. Given the list {G
1
, ..G
n
} of flocks with
departure time within the range [T
a
, T
b
], and given the
source, s
G
, destination, d
G
, the estimate time required
for the travel of flock G, T
G
, and current size L
G
i
of
each flock, attribute 5.1 defines the expected time for
flock G to complete its route.
Attribute 5.1. The expected route time of flock G is
defined as follows:
expected Route Time(G) =
T
G
+ Σ
n
i=1
expected delay time(G, G
i
)
where expected delay time(G, G
i
) is the expected
time that flock G will need to wait until flock G
i
has
passed, in a case of an intersection between the two
flocks. Note that if the size of G
i
is lower than the size
3
Other criteria which take into account other parameters,
such as route length or expected arrival time, can also be
considered.
of G, or if there will be no expected crossroad between
them, then expected delay time(G, G
i
) = 0
We will now proceed by calculating
expected delay time(G, G
i
), the expected delay
time of flock G due to an intersection with flock G
i
.
We use FL
G
i
to denote the future size of a flock in the
departure time. The future size FL
G
i
of each flock G
i
depends on its current size L
G
i
and on the distribution
of UAVs that will join it. Attribute 5.2 defines the
distribution of UAVs that are expected to join flock
G
i
during time window t = [a
t
, b
t
].
Attribute 5.2. Let JF
G
i
,t
be defined as a Poisson
random variable that represents the rate of UAV’s
that will join flock G
i
within a given time t = [a
t
, b
t
],
(JF
G
i
,t
∼ Poisson(λ
G
i
,t
)).
The expected rate λ
G
i
,t
can be estimated as the ex-
pected number of UAVs in the area aimed in the di-
rection of flock G
i
in time range t = [a
t
, b
t
], which can
be deduced from an analysis of the loads in the area
as a function of the hour. The expected rate λ
t,G
i
of
joining a flock G depends on both the path of G
i
and
the hour of the journey. There are busy hours and load
locations in which λ
G
i
,t
is very high due to the traffic
load and hours and locations in which λ
t,G
i
is lower.
Given the expected arrival rate of new UAVs and their
joining the different flocks, we will find the expected
route time of a flock.
Attribute 5.3 describes the distribution of the fu-
ture size FL
G
i
of flock G
i
at time b
t
, given its current
size L
G
i
at time a
t
and the expectation of the random
variable JF
G
i
,t
.
Attribute 5.3. Given a time window [a
t
, b
t
], the
expected size of flock G
i
at a departure time b
t
is as follows: FL
G
i
= L
G
i
+ JF
G
i
,t
where JF
G
i
,t
∼
Poisson(λ
G
i
,t
),t = [a
t
, b
t
] and L
G
i
is the size of flock
G
i
at time a
t
.
Given two flocks G
1
and G
2
with intersecting rou-
tes, JF
G
1
,t
and JF
G
2
,t
are random variables that repre-
sent the rate of UAVs joining flocks G
1
and G
2
, re-
spectively. Because flocks G
1
and G
2
have an inter-
section, we can infer that they have different directi-
ons and that the arrival rates of new UAVs to both
of them are independent. In other words, joining one
flock does not reduce the size of the other flock. As a
result, the random variables JF
G
1
,t
and JF
G
2
,t
can be
considered as independent random variables.
In Lemma 5.1, we describe the expected delay of
flock G
1
due to an intersection with another flock G
2
during its flight.
Lemma 5.1. Given two flocks G
1
and G
2
with prior
sizes L
G
1
and L
G
2
, respectively, the expected delay of
UAV Flocks Forming for Crowded Flight Environments
159

flock G
1
due to an intersection with flock G
2
is
expected delay time(G
1
, G
2
) =
Σ
∞
k
2
=0
P(JF
G
2
,t
= k
2
) · (
[Σ
L
G
2
−L
G
1
+k
2
−1
k
1
=0
P(JF
G
1
,t
= k
1
)]+
0.5 · P(JF
G
1
,t
= L
G
2
− L
G
1
+ k
2
))·
P(G
2
intersects with G
1
|JF
G
1
= k
1
, JF
G
2
= k
2
)·
I(L
G
2
+ k
2
)
where I(s) is the expected delay time for a flock
of size s, and FL
G
i
= L
G
i
+ JF
G
i
,t
for JF
G
i
,t
∼
Poisson(λ
G
i
,t
).
4
Proof. Given two flocks G
1
and G
2
with prior sizes
L
G
1
and L
G
2
, respectively, the expected delay of flock
G
1
due to an intersection with flock G
2
is
expected delay time(G
1
, G
2
) = P(FL
G
1
< FL
G
2
) ·
P(G
2
intersects with G
1
|FL
G
1
< FL
G
2
) · I(FL
G
2
).
Now, P(FL
G
1
< FL
G
2
) = P(L
G
1
+ JF
G
1
,t
< L
G
2
+
JF
G
2
,t
) = P(JF
G
1
,t
< L
G
2
− L
G
1
+ JF
G
2
,t
). Because
JF
G
1
,t
and JF
G
2
,t
are independent Poisson random va-
riables:
P(JF
G
1
,t
< L
G
2
− L
G
1
+ JF
G
2
,t
) =
Σ
∞
k
2
=0
P(JF
G
2
,t
= k
2
)
·Σ
L
G
2
−L
G
1
+k
2
−1
k
1
=0
P(JF
G
1
,t
= k
1
)
In addition, if both G
1
and G
2
are of the same size,
then a lottery is performed, and the probability of
flock G
1
to be the one that must wait till flock G
2
passes is 0.5. Thus, given the size of G
2
as L
G
2
+
k
2
, the probability of flock G
1
to be of the same
size as flock G
2
and to be the one that will wait is
0.5·P(JF
G
1
,t
+L
G
1
= L
G
2
+k
2
) and this probability is
0.5 · P(JF
G
1
,t
= L
G
2
− L
G
1
+ k
2
). Thus, the expected
delay time of G
1
can be formulated as
Σ
∞
k
2
=0
P(JF
G
2
,t
= k
2
)·
([Σ
L
G
2
−L
G
1
+k
2
−1
k
1
=0
P(JF
G
1
,t
= k
1
)]+
0.5 · P(JF
G
1
,t
= L
G
2
− L
G
1
+ k
2
))·
P(G
2
intersects with G
1
|JF
G
1
= k
1
, JF
G
2
= k
2
)·
I(L
G
2
+ k
2
)
As a result of the above lemma, the expected delay
of a single UAV due to an intersection with flock G
i
is defined as follows:
expected delay time(u, G
i
) =
Σ
∞
k=0
P(JF
G
i
,t
= k)·
P(u intersects with G
i
|JF
G
1
= k) · I(L
G
i
+ k).
4
When L
G
2
+ k
2
− L
G
1
− 1 < 0, the obtained value is 0.
Given the above expectations, we proceed by descri-
bing the decision-making process of the UAVs.
6 UAV DECISION-MAKING
PROCESS
In this section, we will describe the decision-making
process of the UAV, given its knowledge about the
environment. Let {G
1
, ..., G
n
} be flocks such that
DT
G
i
∈ [T
a
, T
b
], |d
G
i
− d
u
| < k
1
and |s
G
i
− s
u
| < k
2
for
each i ∈ 1, 2, ...n. Denote u to be the UAV that is sup-
posed to travel from s
u
to d
u
.
Let G
u
be a new flock that is organized by UAV u.
Its initial size is 1, but note that its size when starting
the flight can grow over time due to the arrival of new
UAVs that might join it once the flight is in progress.
When a UAV plans its route, it will look for a flock
that will require the shortest expected time to com-
plete its route. In order to make the process of flock
selection more efficient, the UAV can filter the rele-
vant flocks and consider only flocks with relevant at-
tributes with respect to their paths and their departure
times.
To perform this filtering, we will define the follo-
wing constants: T
a
and T
b
denote the required time
interval in which the UAV will depart, and k1 and k2
are the maximum radius of departure and arrival loca-
tions, respectively, in which the UAV will search for a
relevant flock. If the UAV will take into account also
flocks with departure or arrival locations that are not
in its area, then it can set k1 and k2 as ∞.
Given flock G
i
and UAV u, denote s
u,i
to be the
best location where UAV u can join flock G
i
, and de-
note d
u,i
to be the best location where UAV u can leave
flock G
i
, if it decides to join this flock for part of its
journey.
In addition, use Expected Route Time(F, x, y) to
denote the expected route time of flock F, during
part of its route, from source location x to destina-
tion location y. Finally, recall from Attribute 5.1 that
Expected Route Time(G
i
) is defined as the expected
route time of a new flock, which is managed by UAV
i. Attribute 6.1 defines the flock with the minimal ex-
pected root time from UAV u’s point of view.
Attribute 6.1. Denote min
G
to be defined as follows:
min
G
= min
G
i
∈{G
1
..G
n
}
{ExpectedRouteTime
u
(G
i
) +
D
u,G
i
}
where
ExpectedRouteTime
u
(G
i
) denotes the expected
time of the partial route of flock G
i
, during which UAV
u joins it, and it is evaluated as follows:
ExpectedRouteTime
u
(G
i
) =
Expected Route Time(F, s
u,i
, d
u,i
)
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
160

Attribute 6.2 describes the expected total time of
UAV u if it joins flock G
i
.
Attribute 6.2. Denote Expected Total Time(u, G
i
)
to be:
Expected Total Time(u, G
i
) =
Expected Route Time({u}, s
i
, s
u,i
)
+ Expected Route Time(G
i
∪ {u}, s
u,i
, d
u,i
)
+ Expected Route Time({u}, d
u,i
, d
i
).
Using Attribute 6.2, Attribute 6.3 describes the
UAV’s decision of whether to join an existing flock
G
i
or create a new flock and manage it.
Attribute 6.3. UAV u will decide to initiate a new
flock G
u
if
Expected Route Time(G
u
) < min
i=1..n
{Expected Total Time(u, i)}.
Otherwise, UAV u will join flock G
min
G
that minimizes
the value of Expected Total Time(u, min
G
).
The explanation for the above attributes is as fol-
lows. UAV u is interested in finding a route that will
minimize the total expected time. If it creates a new
flock, the expected required time for the total route
will be Expected
R
oute
T
ime(G
u
), and if it joins an ex-
isting flock, the most beneficial flock for it is min
G
,
which is the flock that minimizes the time it will need
to complete the entire journey, including the part it
joins the flock and the resulting deviation. Thus, the
UAV will choose the alternative that will minimize the
expected time required for its total journey.
7 SIMULATION RESULTS
In order to check the influence of flocking on the
UAV’s performance, we implemented a simulation
system that demonstrates the UAV’s arrival process
and the flocking organization protocol via a black-
board and we examined the efficiency of the propo-
sed protocol. In the following section, we present
the simulation results that compare the performance
of a flight space with flocking and without flocking.
We ran our simulation on data of taxi travels in Chi-
cago based on the Chicago smart city database
5
. The
source and destination locations, and the community
area of each location were taken from that dataset.
In addition, the mean number of trips per hour for
each source community area to each destination com-
munity area was calculated given the Chicago smart
city database. The motivation for using this database
5
https://data.cityofchicago.org
Table 1: Simulation results for the mean number of 240
UAVs per hour.
without with
flocking flocking
Average UAV route time 2.08818 1.10685
saving ratio:
47%
Average ratio of UAVs 0 31.32%
that join flocks of the UAV
Average size of flock 1 1.249
stemmed from the assumption that the distribution of
the transfer of people and journeys by means of riders
in the not too distant future can be similar to the dis-
tribution of people and journeys through current taxis.
Given that information, we ran our simulation in the
following way: For each run, the mean total number
of UAV trips per day was determined, and the mean
number of trips for each source area to each destina-
tion area was calculated. Then, for each run, the ac-
tual number of travels per day, for each source area to
each destination area, was derived from the Poisson
distribution of the number of trips for each source,
destination, and hour. Table 1 presents our results,
where the simulation was run 50 times by assuming
a Poisson distribution of required flights with mean
number of 240 UAVs per hour.
As can be observed, using flocks reduces the tra-
veling time of the UAVs by 47%. Note, however, that
the level of reduction depends on the traffic level, and
the efficiency of joining flocks increases as the mean
UAV number increases. This can be viewed in Fi-
gure 2, which shows the saving ratio due to flocking
for a mean number of 10 UAV per hour to 240 UAVs
per hour. Note that each point in the curve is based on
the average result of 50 runs of the simulation.
In order to better understand the results shown in
Figure 2, Figure 3 illustrates the average route time re-
quired for a UAV to fly independently and the average
route time required for a UAV that has the ability to
join a flock. Note that as the number of UAV per hour
increases, the environment becomes more crowded,
and the effect of the load becomes greater when the
UAVs cannot form flocks.
As depicted in the figure, the mean saving ratio
increases as the number of UAVs per hour increa-
ses. This can be easily explained by the fact that the
flocking technique is developed for crowded environ-
ments, and its importance increases as the environ-
ment becomes more crowded.
To summarize, the simulation results show that
flocking into groups can save the flight time of indivi-
dual UAVs, and the saving ratio increases as the envi-
ronments become more crowded. Thus, the flocking
protocol can be implemented by UAV designers in
UAV Flocks Forming for Crowded Flight Environments
161

Figure 2: Average saving ratio for different numbers of
UAVs per hour.
Figure 3: Average journey time with and without flocking.
order to increase flight efficiency and decrease UAV
flight time, especially in crowded flight spaces and
during busy times.
8 CONCLUSIONS
In this research, we propose a detailed protocol that
enables heterogeneous UAVs to join flocks of UAVs
that are supposed to travel on similar routes within the
same time window. The protocol is based on a com-
mon blackboard in which organizing flocks publish
their details and interested UAVs can join a flock that
matches their requirements Our model allows the in-
dividual UAV to determine the optimal route from its
point of view.
We checked our protocol by means of simulations
and found that it significantly reduces the overhead
caused by collisions of UAVs by dozens of percent in
the average flight time of UAVs in the airspace.
For future work, we intend to consider situations
where the size of the flock is limited and develop stra-
tegies that are appropriate for such situations. We
will also take into account the possibility of uniting
or splitting flocks as needed. In addition, we intend
to build a three dimensional simulation of our model.
We plan to consider the details of the path planning
process and the effect of this process on the profita-
bility of UAV flocking in crowded environments. Fi-
nally, in the future we would like to conduct expe-
riments with actual UAVs (instead of working with
simulations), in order to examine the effectiveness
of our model in real world domains including faulty
sensors and actuators and environmental uncertainties
such as wind speed.
REFERENCES
Arne Brutschy, Giovanni Pini, C. P. M. B. M. D. (2014).
Self-organized task allocation to sequentially interde-
pendent tasks in swarm robotics. Autonomous Agents
and Multi-Agent Systems, 28(1):101–125.
Bayndr, L. (2016). A review of swarm robotics tasks. Neu-
rocomputing, 172(8):292–321.
Christopher M. Cianci, Xavier Raemy, J. P. A. M. (2007).
Communication in a swarm of miniature robots: The
e-puck as an educational tool for swarm robotics.
Swarm Robotics. SR 2006. Lecture Notes in Compu-
ter Science, vol 4433. Springer, Berlin, Heidelberg.
Dabbiru, X. V. and Siddhabathula, K. (2016). Autonomous
air traffic control - collision avoidance for uav using
mdp. International Journal of Computer Science and
Information Technology and Security, 6(1).
Gurfil, P. and Kivelevitch, E. (2007). Flock properties effect
on task assignment and formation flying of coopera-
ting unmanned aerial vehicles. Proceedings of the In-
stitution of Mechanical Engineers, Part G: Journal of
Aerospace Engineering, 221(3):401–416.
Herbert G. Tanner, A. J. and Pappas, G. J. (2003a). Stable
flocking of mobile agents, part i: Fixed topology. In
Proceedings of the 42nd IEEE Conference on Deci-
sion and Control 2003, volume 2, pages 2010–2015.
AAAI.
Herbert G. Tanner, A. J. and Pappas, G. J. (2003b). Stable
flocking of mobile agents, part ii: Dynamic topology.
In Proceedings of the 42nd IEEE Conference on De-
cision and Control 2003, volume 2, pages 2016–2021.
AAAI.
Jenhui Canny, J. R. (1987). New lower bound techniques
for robot motion planning problems. In Symposium
on the Foundations of Computer Science.
Jenhui Chen, L.-R. L. (2005). Path planning protocol for
collaborative multi-robot systems. In International
Symposium on Computational Intelligence in Robo-
tics and Automation. IEEE.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
162

Joongbo Seo, Youdan Kim, S. K. and Tsourdos, A. (2017).
Collision avoidance strategies for unmanned aerial
vehicles in formation flight. IEEE Transactions on
Aerospace and Electronic Systems, 53.
Kevin Passino, Marios Polycarpou, D. J. M. P. Y. L. Y. Y. M.
F. M. B. (2002). Cooperative control for autonomous
air vehicles. Cooperative Control and Optimization,
66:233–271.
Li, P. and Duan, H. (2012). Path planning of unman-
ned aerial vehicle based on improved gravitational se-
arch algorithm. Science China Technological Scien-
ces, 55(10).
Liang Yang, Juntong Qi, D. S. J. X. J. H. and Xia, Y. (2016).
Survey of robot 3d path planning algorithms. Journal
of Control Science and Engineering.
Mohammadreza Radmanesh, Manish Kumar, P. H. G. M. S.
(2018). Overview of path-planning and obstacle avoi-
dance algorithms for uavs: A comparative study. Un-
manned Systems, 6(2):1–24.
Panov, A. I. and Yakovlev, K. (2017). Behavior and path
planning for the coalition of cognitive robots in smart
relocation tasks. Robot Intelligence Technology and
Applications, 447.
Ragi, S. and Chong, E. K. P. (2013). Uav path planning in a
dynamic environment via partially observable markov
decision process. IEEE Transactions on Aerospace
and Electronic Systems, 49.
Reynolds, C. W. (1987). Flocks, herds, and schools: A
distributed behavioral model. Computer Graphics,
21(4):25–34.
Selim Temizer, Mykel Kochenderfer, L. K. T. L.-P. and Ku-
char, J. (2010). Collision avoidance for unmanned
aircraft using markov decision processes. In AIAA
Guidance, Navigation, and Control Conference, Gui-
dance, Navigation, and Control and Co-located Con-
ferences.
Valavanis, K. P. and (editors), G. J. V. (2015). Handbook of
Unmanned Aerial Vehicles. Springer.
Winfield, E. S. . A. (2008). Special issue on swarm robotics.
Swarm Intelligence, 2(69).
Yanli Yang, M. M. P. and Minai, A. A. (2007). Multi-
uav cooperative search using an opportunistic learning
method. Journal of Dynamic Systems, Measurement,
and Control, 129(5):716–728.
YongBo Chen, JianQiao Yu, X. S. and Luo, G. (2015). Path
planning for multi-uav formation. Journal of Intelli-
gent and Robotic Systems, 77(1):229246.
Yosi Ben-Asher, Sharoni Feldman, P. G. (2010). Uav deci-
sion and control system, a patent.
UAV Flocks Forming for Crowded Flight Environments
163