Towards Automated fUML Model Veriﬁcation with Petri Nets

Francesco Bedini, Ralph Maschotta, Alexander Wichmann and Armin Zimmermann

Systems and Software Engineering Group, Technische Universität Ilmenau, Ilmenau, Germany

Keywords:

fUML, Activity Diagram, Petri net, Transformation, Model-to-Model, QVTo.

Abstract:

One of the goals of the Foundational UML Subset (fUML) is a consistent and well-deﬁned execution of UML

activity diagrams. However, the speciﬁcation is not done in a formal mathematical model and leaves room for

implementation-speciﬁc tool details. This paper shows how this may lead to problems for concurrent program

semantics. To this end, the paper introduces a transformation and basic analysis methods for activity diagrams

under the current fUML sequential execution semantics. The analysis is conducted using Petri nets, which

are mathematical models with a graphical representation to describe distributed systems. There are numerous

well-established analysis methods to validate speciﬁc desirable properties of a concurrent program including

liveliness, the absence of deadlocks, fairness, mutual exclusion, and detection of unreachable states. In this

paper, we show that the intuitive translation to Petri nets does not ﬁt the current fUML execution implemen-

tation; therefore, we introduce a new model-to-model transformation realized with QVTo, that translates a set

of the most used fUML elements to Petri nets. Moreover, we propose methods to analyze the models with the

tool TimeNET.

1 INTRODUCTION

UML activity diagrams are one of the UML’s behav-

ior diagrams; they describe how states and steps of a

process can be viewed as a ﬂow of control and data

exchange between their different actions. The spec-

iﬁcation of activity diagrams changed considerably

over time. Initially, until version 1.5 (from now on:

UML 1.x), the semantics was inherited from state ma-

chines (Arlow and Neustadt, 2002). UML 2.0 (from

now on: UML 2.x) introduced a different token-

driven semantics inspired by Petri nets and ultimately

abandoned the concept of states inside activity dia-

grams (Störrle and Hausmann, 2005).

With this fundamental change, it has become pos-

sible to model more advanced parallel executions (and

multiple calls to the same activity) that were not pos-

sible before in UML 1.x.

UML 2.x brought new elements such as object

pins, merge nodes and ﬂow ﬁnal nodes to the mod-

elers’ palette. However, the old syntax remained un-

changed for the most part, but yet with a completely

different execution semantics. Unfortunately, these

differences led to models that were syntactically valid

for both UML versions but having completely dif-

ferent results under certain circumstances (Störrle,

2005).

Behavioral semantics and execution analysis of

dynamic UML diagrams has attracted a lot of re-

search interest over the years. Partially unclear se-

mantics were found and tried to overcome. Possi-

ble approaches may either analyze properties of a

model-speciﬁed program directly or derive results via

an intermediate model and corresponding transforma-

tions (Eshuis and Wieringa, 2004).

The introduction of a Foundational UML Subset

(fUML) in 2011 aimed at a predictable interpretation

of the execution semantics of a subset of UML activ-

ity diagram elements; a token-based execution ﬂow

was introduced to precisely describe how the single

elements behave. One goal was to ensure that dif-

ferent execution tools will produce the same consis-

tent output from running the same model. The fUML

speciﬁcation assures the execution predictability due

to a sequentialized execution of the models (OMG,

2017a). However, the fUML speciﬁcation foresees

but does not strictly speciﬁes how a parallel architec-

ture should execute activity diagrams. This lack of

preciseness may lead to problems that only become

evident when executing concurrent ﬂows sequentially,

or when different tools will support concurrent execu-

tion differently, as will be presented in Section 2.3.

The fUML execution engine (OMG, 2017a) is im-

plemented to always iterate through all the output

edges of each element, and sending a token in a well-

deﬁned ﬁxed order. If the next element on the target

298

Bedini, F., Maschotta, R., Wichmann, A. and Zimmermann, A.

Towards Automated fUML Model Veriﬁcation with Petri Nets.

DOI: 10.5220/0007371402980306

In Proceedings of the 7th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2019), pages 298-306

ISBN: 978-989-758-358-2

side of the edge is ready to execute (i.e., it already re-

ceived all inputs control and data tokens), it will do so;

otherwise, another token will be sent to the next out-

put edges, if any. The order of the output edges is not

ﬁxed and is difﬁcult to predict, as it may depend on

how the user created the elements in the model, how

the modeling tool saved them, and also on the speciﬁc

execution engine implementation. Letting the parallel

execution semantics of a model depend on such tech-

nical details, that the modeler is often unaware of, will

lead to misconceptions and unexpected program be-

havior and thus counteract the intention of fUML.

As most of personal or laptop computers contain

at least two CPU cores nowadays, it is desirable and

foreseeable that the fUML execution engine will exe-

cute independent activity diagrams actions in a paral-

lel way in the future. This will help to reduce execu-

tion times, which are still signiﬁcantly higher for such

models in comparison to conventional programs (Be-

dini et al., 2017).

The fUML speciﬁcation just brieﬂy mentions the

parallel execution of diagrams, but foresees it and

its possible issues by, for example, including a must-

Isolate property for denying interleaved execution by

stating that if an execution tool uses locking to imple-

ment isolation, then it also must provide some means

to detect implementation-speciﬁc deadlock conditions

and recover from them (OMG, 2017a).

While

MergeNode

While

[true]

[false]

[true]

[false]

Figure 1: Two realizations of a do-while loop as an activity

diagram. Left: UML 1.x, Right: UML 2.x.

Figure 1 shows how a do-while loop would have

been realized in the old and new syntax. If the

UML 1.x version would be run by an fUML execution

engine, the execution would hang with a deadlock af-

ter sending the ﬁrst token to the Do action, because it

would wait for a second token coming from the deci-

sion node before being able to execute.

Moreover, the fUML speciﬁcation, being pro-

vided as a Java-like implementation, does not pro-

vide a good mathematical basis for analysis tech-

niques (Laurent et al., 2014).

For these reasons, a veriﬁcation tool for fUML

models and the execution engine is needed. With

fUML and UML’s activity diagrams based on Petri

net’s token paradigm, and aiming to take advantage of

the already existing literature and methods about Petri

nets veriﬁcation (Murata, 1989), we decided to bring

the fUML diagrams back to the origin by transform-

ing them to Petri nets. In this way, we can perform

various analyses to check that speciﬁc properties hold

within the structure of the model and during its exe-

cution, using the Petri net’s mathematical formalism

as a reliable formal basis.

One result of this paper is a Model-to-model

(M2M) transformation that respects the fUML exe-

cution semantics and provides the foundations for a

lint-like validation tool based on Petri net analysis for

fUML models. This tool will make the modeler aware

of design pitfalls and semantic ambiguities by detect-

ing possible problems that may arise when executing

the diagram sequentially or in parallel.

The following section shows the methodology,

sets the analysis’ goals and brieﬂy surveys different

Petri net analysis techniques. Some related work is

covered along the way. Section 3 shows the trans-

formation rules speciﬁc to fUML and how the trans-

formation has been realized. Section 4 gives an ap-

plication example, while results and future work are

discussed in the conclusion section. Finally, the Ap-

pendix covers the proposed set of single transforma-

tion rules.

2 METHODOLOGY

This section at ﬁrst introduces the issues that we

aim to detect in activity diagrams, followed by an

overview of the primary analysis techniques in Petri

nets that may be used for computing them. We in-

troduce a model-to-model transformation afterwards

and cover some assumptions about the original activ-

ity diagram to allow such a transformation.

2.1 Analysis Goals

Similar to the concept of soundness in the area busi-

ness process modeling (van der Aalst et al., 2000), we

want to make sure that the modeled activity diagrams

have a safe and predictable ﬂow.

For achieving this goal, we would like to analyze

activity diagrams to prove or confute some of the fol-

lowing conditions:

Deadlock is said to happen if the model reaches a

conﬁguration (state) in which no action can ﬁre

(i.e., execute).

Liveness means that the system will keep running,

requiring at least the absence of deadlocks, or the

Towards Automated fUML Model Veriﬁcation with Petri Nets

299

absence of starvation in some stricter deﬁnitions.

Both full and partial liveness covering the whole

or only parts of a model may be of interest.

Unreachable Regions — a set of elements that will

not get executed under certain circumstances, for

example, because they are located after a never-

ending loop.

Problems with concurrent programs falling into

these areas are often rooted in synchronization prob-

lems and caused by erroneous modeling. The ad-

vantage of looking for issues on a Petri net rather

than on the activity diagram directly is that the men-

tioned properties are well researched for Petri net

models, and efﬁcient algorithms for their computation

exist (Sifakis, 1978; Girault and Valk, 2003). More-

over, Petri nets have been introduced for the descrip-

tion of concurrent systems with synchronization, and

should thus be capable of capturing control ﬂow in-

formation of activity diagrams in a natural way.

2.2 Petri Net Analysis

This section will describe possible ways of mapping

the issues listed in Section 2.1 to Petri net properties

and detecting them with algorithm types known for

Petri nets.

The mentioned properties of an activity diagram

can be mapped to similar Petri net properties, pro-

vided that the behavior of the transformed model is

identical:

Deadlocks a deadlock occurs in a Petri net when no

transition can ﬁre due to the lack of (one or more)

input tokens.

Liveliness Petri net transitions and nets have sev-

eral levels of liveliness (L

: dead - L

: live) (Gi-

rault and Valk, 2003) that can be mathematically

proved.

Unreachable Regions a set of transitions that will

not ﬁre because of missing tokens in a state reach-

able by the initial net marking.

Moreover, it is possible to analyze the net’s bound-

edness to check if the amount of tokens in the net re-

mains bounded, which may otherwise point at inﬁnite

loops or wrong recursion steps.

Provided that a behavioral similar model has been

created, the next step is to compute the properties

with existing analysis methods. Reachability anal-

ysis, which consists of enumerating and analyzing

all reachable states of a net, does not scale for big-

ger models or unbounded networks with an unlimited

number of states. This issue is known as the state

space explosion problem (Valmari, 1998).

A linear algebraic analysis approach would lead to

a similar problem, resulting in many linear equations

to consider.

It would be then possible to apply some trans-

formation techniques to simplify the Petri net mak-

ing the analysis process more straightforward, but

then the difﬁculty would be ﬁnding the reducible sub-

networks and then backtracking the error to the origi-

nal element.

Synthesis methods for reducing the size of Petri

nets are NP-complete (Badouel et al., 2015) and can-

not cope with strongly coupled subsystems.

Simulating the Petri net often requires long run

times, and does not assure that all possible markings

are covered. This well-known principal problem of

simulation algorithms is similar to the test coverage

problem.

Graph theoretical analysis (for example, looking

for siphons and traps (Murata, 1989)) are inexpensive

but may detect false-positives too. For instance, activ-

ity initial and ﬁnal nodes would be detected as siphons

and traps, respectively.

For these reasons the authors argue that a graph

theoretical analysis should be preferred over the other

methods, as it is less expensive to compute and pro-

vides satisfying hints about possible problems in the

net. Those hints can then be analyzed individually

with a heuristic to ﬁlter out possible false positives.

2.3 Activity Diagram Transformation to

Petri Nets

With the UML activity diagram speciﬁcation based

on Petri nets semantics (OMG, 2017b), the trans-

formation of activity diagrams elements to Petri net

snippets should be quite natural from a conceptual

point of view. Similar transformation approaches

have been reported in the literature, although with dif-

ferent goals.

The transformation can be performed to evaluate

program performance as in (Distefano et al., 2011)

and (López-Grao et al., 2004), where UML 1.x activ-

ity diagrams are transformed to stochastic Petri nets to

evaluate their performance. This technique can also

be applied to compute other properties of the mod-

eled system. For example, system execution time and

number of resources that the system would consume

are simulated in (Andrade et al., 2009). This approach

is based on SysML activity diagrams transformed into

Time Petri nets to validate the requirements of embed-

ded systems.

Our goal and approach are more similar to the

one introduced in (Agarwal, 2013), which proposed

a method for transforming the essential elements of

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

300

HaveDinner

Think

Eat

Think

Eat

<<centralBuffer>>

Chopstick2

<<centralBuffer>>

Chopstick1

<<centralBuffer>>

Chopstick3

Chopstick

InitialNode

ForkNode

Merge1

Merge2

Figure 2: An activity diagram modeling the dining philoso-

pher problem with only two philosophers.

UML 2.x activity diagrams. The goal there is to

analyze the diagrams’ liveliness, boundedness, and

reachability for veriﬁcation purposes. The transfor-

mation methods we used are also similar to the in-

tuitive ones covered in (Staines, 2008) and (Störrle,

2004). The transformation rules we used are dis-

played in the appendix for completeness.

2.3.1 fUML Speciﬁcation Issues

To demonstrate the issues which arise by applying the

existing transformations to fUML activity diagrams,

let us consider the well-known Dining Philosopher

problem (Andrews, 1991) as a kind of benchmark for

concurrent system design. Figure 2 shows, for sim-

plicity, a section with just two philosophers (as mod-

els for concurrent processes) who are having dinner.

For simplicity, we allow in the model the philoso-

phers to take both chopsticks with one atomic action,

such that at least deadlocks cannot happen according

to the requirements of deadlocks in concurrent sys-

tems. The execution starts and two identical ﬂows

start to run. Each philosopher is thinking at the be-

ginning. Then, if both chopsticks are available, they

can eat (one at a time) and go back to thinking after-

wards.

The changes introduced by the fUML speciﬁca-

tion regarding the ﬁxed order of execution of the

model profoundly changed the semantics depicted

initially by UML 2.x, in a way that can be mislead-

ing for some modelers.

Due to the depth-ﬁrst approach and the strict

ordering intrinsically modeled in the fUML spec-

iﬁcation (inside the function ActivityNode-

Activation::sendOffers), the ﬁrst merge node

that gets executed keeps running forever, leading the

other philosopher to starvation. Which one is the ﬁrst

depends on the order how the fork node edges have

Figure 3: A Petri net representing the activity diagram in

Figure 2, obtained using the intuitive transformation.

been saved or on the order how the execution engine

internally stores them, which is a low-level technical

issue that should not inﬂuence the model behavior.

With just two philosophers, it would be possible

to solve this problem by using a decision node that

randomly picks one of its two outgoing edges instead

of the fork node. Unfortunately, this solution would

not scale with more philosophers (only one would be

allowed to eat at any time), and it requires the modeler

to include a scheduling detail in its model instead of

focusing on the high-level concurrent design of the

problem.

UML 2.x speciﬁed that concurrent execution

means that there is no required order in which the

nodes must be executed; a conforming execution of

the Activity may execute the nodes sequentially in ei-

ther order or may execute them in parallel (OMG,

2017b). fUML adheres to this speciﬁcation by execut-

ing one of them ﬁrst but never gets to execute the sec-

ond one until the ﬁrst one ﬁnishes (and that is never

going to happen in our example).

If we would transform the activity diagram in

Figure 2 to a Petri net following the intuitive trans-

formation based on the UML 2.x speciﬁcation, we

would obtain the diagram shown in Figure 3, which

would be correct concerning the original semantics of

UML 2.x, but not according to the new sequentialized

execution semantics of fUML.

Analyzing this Petri Net would not lead to dis-

covering any problem. The model executes as ex-

pected, both processes execute concurrently, and both

Towards Automated fUML Model Veriﬁcation with Petri Nets

301

Figure 4: A Petri net realizing fUML a fork and join con-

struct with a sequential execution. The three body places

are just placeholders; in reality, actions are not transformed

as a single place, but as a set of elements (as presented in

the Appendix).

Body1

Body2

Body3

Figure 5: An activity diagram showing a fork and join of

three ﬂows.

philosophers will eventually be eating. However, it

does not resemble the speciﬁed fUML behavior and

thus does not show problems arising from it. For this

reason, we introduce a different kind of transforma-

tion, to resemble fUML’s strict sequential execution

of fork node ﬂows.

2.3.2 Sequential Transformation of Fork Nodes

This section proposes an fUML-conform transforma-

tion technique for transforming fork nodes to Petri

nets. The proposed transformation replicates the

fUML sequential execution of fork nodes outgoing

ﬂows, to be able to detect problems that would happen

during the sequential execution of activity diagrams.

Figure 4 shows our proposed transformation for

the activity diagrams in Figure 5.

We introduce two additional immediate transitions

for each ﬂow that should ﬁre at the beginning and the

end of the ﬂow. For this to happen, we need one addi-

tional place (CanStart#) for all ﬂows (except the ﬁrst

one), that shall receive one token once the previous

ﬂow ﬁnishes its execution. The FlowEnd transition

takes care of placing this token.

In case a ﬂow does not end (for example when

it contains an inﬁnite loop), the CanStart place of

the following ﬂow will not receive a token, clearly

marking the remaining ﬂows as unreachable inside

the Petri net. Moreover, looking for the end (or ends)

of the ﬂows allows us to locate critical sections or

loops in the model already during the transformation

phase.

It is evident that the Flow2 and Flow3 places and

the Fork transition itself are redundant and could be

left out in this diagram without missing anything in

the ﬁnal analysis. However, to make the recognition

of the different ﬂows simpler and their structure more

systematic, we have decided to still include them in

the transformation. Additionally, when those places

are identiﬁed as traps, we can warn the user more pre-

cisely about which ﬂow will encounter problems.

Finding the ﬁnal element of a ﬂow is not trivial

and will be solved in future work. At this time, we can

simplify this task by saying that a join or ﬂow ﬁnal or

activity ﬁnal nodes would resemble, for example, an

obvious end of the ﬂow.

Another problem that arises is that the order used

during the execution is implementation-speciﬁc and

depends on different factors, such as how the elements

get saved inside the fUML model, and how the exe-

cution engine reads and stores the edges (in a FIFO or

a LIFO data structure, for example).

For example, in Figure 6 a peculiar but syntacti-

cally valid fork node with three actions is shown. De-

pending on which ﬂow gets executed ﬁrst, it is possi-

ble to obtain several different results:

A executes ﬁrst: the action A executes once, and the

activity ends, reaching the activity ﬁnal node.

B executes ﬁrst: the action B executes once and

then, depending on the internal ordering, either A

gets executed once, or C gets executed in an inﬁ-

nite loop with B (B, C, B, C. . . ).

C executes ﬁrst: results in an inﬁnite loop of C ac-

tions (C, C, . . . ).

These examples show that although the fUML

goal was to be speciﬁc enough to provide a

precise semantic for consistent execution ﬂows,

implementation-speciﬁc details can still produce dif-

ferent results while running the same model. To use

the proposed sequentialized transformation, the M2M

transformation either requires some extra knowledge

Figure 6: An activity diagram showing one fork node with

three outgoing ﬂows. Its execution heavily depends on the

speciﬁc execution engine implementation.

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

302

about the implementation-speciﬁc peculiarities of the

fUML execution engine or should produce all possi-

ble combinations and analyze all of them.

2.4 Transformation Assumptions

For the analysis, we require the following assump-

tions or limitations for activity diagrams to allow

them to be transformable:

Assumption 1. All actions must terminate and pro-

duce the outputs they are expected to provide on their

output edges, even if empty.

This restriction is necessary because the transfor-

mation loses some information about the behavioral

semantics of the original model, which is possible to

model in different ways (for example as programming

code inside a function behavior), and it is not possible

to easily transfer it into a Petri net. For this reason,

our analysis must assume that actions never hang and

always produce a token on all their outgoing edges.

Informally, the transformation cannot take a look “in-

side” the actions, and thus the signiﬁcant behavior

must be clear from the model structure.

Assumption 2. Actions should not modify at-

tributes that may get used by other actions which may

run concurrently during their execution.

For the same reasons of Assumption 1, all actions

must resemble an atomic set of operations. Activity

diagrams are high-level descriptions of a process, and

only elements that are explicitly present in a model

can be analyzed. Therefore it is important to not

hide too much logic behind actions, which can be ex-

pressed using other activity diagrams elements.

Assumption 3. Activity diagrams may consist of a

set of supported elements only. This set consists of ac-

tivity initial and ﬁnal nodes, activity input and output

parameters, ﬂow ﬁnal nodes, decision nodes, merge

nodes, fork and join nodes, central buffer nodes, data-

store nodes, actions with input and output pins and

loop nodes.

If the diagrams contain unsupported parts such as

event-related elements (i.e., send/receive signal ac-

tions and time events), they will not be transformed,

and the analysis would take place on an incomplete

diagram probably leading to wrong or at least only

partial results.

Assumption 4. The input model is syntactically

valid, which implies that all elements are correctly

connected with control or object ﬂows. As the trans-

formation considers both data and control ﬂows as

one single kind of tokens, it is essential that the origi-

nal model allows to transfer them correctly.

3 REALIZATION

To implement the transformation, we have used op-

erational QVT (QVTo), whereas for performing the

Petri net analysis, we are using the existing tool

TimeNET (Zimmermann, 2017). QVTo is an OMG

standard using an OCL-like imperative language, be-

ing still actively developed and well integrated into

Eclipse (Tikhonova and Willemse, 2015). It works

following the Query/View/Transformation paradigm,

requiring to ﬁrst selecting (query) from the original

model the elements which will be transformed, then

deﬁne how they should look like (view) in the output

model by deﬁning a transformation that realizes it.

The exogenous model-to-model transformation

from activity diagrams to Petri nets requires the

source and the destination meta-models. For UML we

used the UML ecore meta-model available from the

core Eclipse Modeling Framework (EMF), whereas

for the Petri net meta-model we have generated the

ecore meta-model from TimeNET’s internal XML

schema ﬁles (XSD) specifying stochastic Petri nets.

In TimeNET, this schema does not only describe

Extended Deterministic and Stochastic Petri nets, but

represents a model class containing the modeling

power of several well-known sub-classes like GSPNs,

DSPNs, and eDSPNs (Zimmermann, 2007) allowing

different transition ﬁring delay types. This extended

set allows us not to be restricted a priori to a single

class of Petri nets, leaving us the possibility to extend

or switch to a different subclass of Petri net when new

analysis methods are needed.

Once the input and output meta-models are avail-

able, the input model can be provided to a transforma-

tion tool, which will execute an ordered set of trans-

formation rules (also known as mappings) to produce

a Petri net model.

QVTo uses a hierarchical waterfall approach,

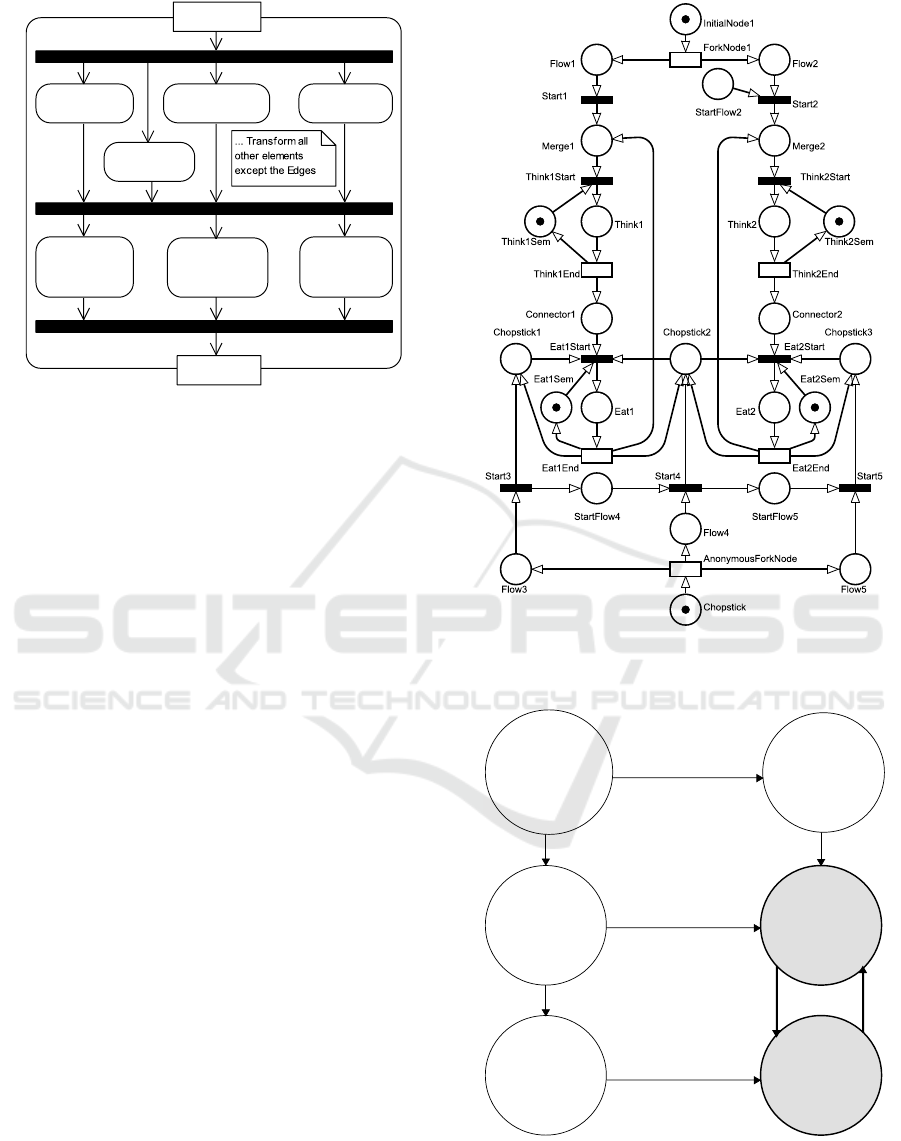
where a linear sequence of steps obtains the trans-

formed model. The transformation operates as illus-

trated in Figure 7. However, due to QVTo’s limita-

tions, the transformation is implemented sequentially

and operates as follows:

1. Transform ﬁrstly all the single activity diagram’s

nodes (for the transformation details, refer to the

Appendix).

2. Transform all edges between elements:

Towards Automated fUML Model Veriﬁcation with Petri Nets

303

Transform AD2PNm

Transform Initial

Nodes

Transform Activity

Parameter Nodes

Transform Fork

Nodes

Transform Flow

Final Nodes

Transform Edges

with additional

Places

Transform Edges

with additional

Transitions

Transform

remaining Edges

fUML Model

Petri Net Model

Figure 7: Activity diagram showing the required steps for

transforming an fUML activity diagram to a Petri net with

QVTo.

(a) transform all edges which require an extra tran-

sition (between two places);

(b) transform all edges which require an extra place

(between two transitions);

and a transition, and vice versa).

With the transformation process in place, the ac-

tivity diagrams can be now translated to Petri nets.

This transformation is not complete and loses a part

of the original model semantics, for instance the ac-

tions’ function behaviors which are internally deﬁned

as source code. On the other hand, the transformation

allows us to perform more advanced analysis on the

general structure of the diagram.

4 EXAMPLE

This section describes how the proposed sequential

Petri net transformation can detect starvation in the

philosophers problem previously described in Sec-

tion 2.3.

It is possible to apply different techniques to ana-

lyze the resulting Petri net shown in Figure 8. For ex-

ample, a structural analysis of the net shows that the

sets of places {Merge1, Think1, Connector1, Eat1}

and {Merge2, Think2, Connector2, Eat2} are traps,

denoting the presence of possible never-ending loops.

Petri net traps are sets of places which may receive

additional tokens, but will never allow them to leave

the trap.

Using the TimeNET tool, the reachability graph

(Figure 9) can be computed. It shows that there is an

Figure 8: A Petri net showing the result of the proposed se-

quentialized transformation of the fUML model in Figure 2

InitialNode, Chopstick,

Eat1Sem, Eat2Sem,

Think1Sem, Think2Sem

Flow2, Chopstick,

Eat1Sem, Eat2Sem,

Think1, Think2Sem

InitialNode,

Chopstick1,

Chopstick2,

Chopstick3, Eat1Sem,

Eat2Sem,

Think1Sem,

Think2Sem

Connector1,

Chopstick, Eat1Sem,

Eat2Sem, Flow2,

Think1Sem,

Think2Sem

Chopstick3, Flow2,

Eat1, Eat2Sem,

Think1Sem,

Think2Sem

Flow2, Chopstick1,

Chopstick2,

Chopstick3, Eat1Sem,

Eat2Sem,

Think2Sem, Think1

Think1End,

Eat1Start

Eat1End,

Think1Start

AnonymousForkNode, Start3,

Start4, Start5, Eat1Start

Think1End

AnonymousForkNode,

Start 3, Start4, Start5

ForkNode, Start1,

Think1Start

AnonymousForkNode,

Start 3, Start4, Start5

ForkNode, Start1,

Think1Start

Figure 9: The reachability graph of the Petri net shown in

Figure 8. Inside the circles, places who hold exactly one

token are listed, while transitions causing state changes are

shown on the arcs. The grey elements visualize a loop.

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

304

inﬁnite loop between two states, which hints to the

same (potential undesired) condition in the original

diagram. Moreover, as some transitions are never ﬁr-

ing in the reachability graph, some parts of the model

containing the missing transitions are unreachable

from the initial marking (Think2Start and Eat2Start

in the example).

The shown steps demonstrate that difﬁculties in

transforming an activity diagram into a Petri net arise

from the incomplete speciﬁcation of such diagrams,

but that execution-speciﬁc issues can be detected with

a correctly extended Petri net that incorporates the se-

quential fUML execution.

5 CONCLUSION

In this paper, we have developed the foundation for

a lint-like fUML activity diagram veriﬁcation, which

can be used to detect and warn modelers about er-

rors or potentially dangerous anomalies in their di-

agrams describing concurrent programs. This ap-

proach is based on two types of M2M transformations

to Petri nets: 1) an intuitive one similar to the exist-

ing literature to tackle conceptual problems, and 2) an

fUML-conform one introduced here to ﬁnd problems

caused by the sequential execution semantics speci-

ﬁed by the fUML. In particular, our method with its

different transformations, aims to detect synchroniza-

tion problems that would occur when the diagrams are

executed both concurrently and sequentially.

The sequential transformation of fork nodes al-

lowed us to verify not only models that were ob-

viously wrong (for example with disconnected ele-

ments), but also models without such problems that

in reality lead to a peculiar execution which is hard

to predict without expert knowledge of the execution

engine implementation.

As a side effect, the paper points out current limi-

tations and potentially dangerous situations of the cur-

rent fUML speciﬁcation, that would only become evi-

dent when the execution happens concurrently or with

a different static execution order.

5.1 Future Work

The next steps consist of ﬁnding a suitable algorithm

for correctly transforming all possible constellations

of fork node ﬂows; i.e., ﬁnding or deciding the ab-

sence of the end of each ﬂow. Once a reliable method

is deﬁned, it will be possible to implement the sequen-

tial transformation of fork node ﬂows.

Further work will include parallelization of the

fUML C++ execution engine developed in our group

(MDE4CPP, (Bedini et al., 2017)), automation of the

M2M transformation, and the execution of the analy-

sis techniques which are relevant to the input model.

The transformation implementation is available

online

and distributed under the MIT license.

REFERENCES

Agarwal, B. (2013). Transformation of UML Activity Dia-

grams into Petri Nets for Veriﬁcation Purposes. Inter-

national Journal Of Engineering And Computer Sci-

ence, 2(3):798–805.

Andrade, E., Maciel, P., Callou, G., and Nogueira, B.

(2009). A methodology for mapping sysml activity

diagram to time petri net for requirement validation of

embedded real-time systems with energy constraints.

In 2009 Third International Conference on Digital So-

ciety (ICDS), pages 266–271.

Andrews, G. R. (1991). Concurrent programming: prin-

ciples and practice. Benjamin/Cummings Publishing

Company San Francisco.

Arlow, J. and Neustadt, I. (2002). UML 2 and the Uniﬁed

Process: Practical Object-Oriented Analysis and De-

sign. Pearson Education, Inc., 2 edition.

Badouel, E., Bernardinello, L., and Darondeau, P. (2015).

Petri net synthesis. Springer.

Bedini, F., Maschotta, R., Wichmann, A., Jäger, S., and

Zimmermann, A. (2017). A model-driven fuml exe-

cution engine for C++. In Proceedings of the 5th In-

ternational Conference on Model-Driven Engineering

and Software Development, MODELSWARD 2017,

Porto, Portugal, February 19-21, 2017., pages 443–

450. SciTePress.

Distefano, S., Scarpa, M., and Puliaﬁto, A. (2011). From

UML to Petri Nets: The PCM-Based Methodol-

ogy. IEEE Transactions on Software Engineering,

37(1):65–79.

Eshuis, R. and Wieringa, R. (2004). Tool support for ver-

ifying uml activity diagrams. IEEE Transactions on

Software Engineering, 30(7):437–447.

Girault, C. and Valk, R. (2003). Petri Nets for System Engi-

neering. Springer.

Laurent, Y., Bendraou, R., Baarir, S., and Gervais, M.-P.

(2014). Formalization of fuml: An application to pro-

cess veriﬁcation. In International Conference on Ad-

vanced Information Systems Engineering, pages 347–

363. Springer.

López-Grao, J. P., Merseguer, J., and Campos, J. (2004).

From UML Activity Diagrams to Stochastic Petri

nets: application to software performance engineer-

ing. ACM SIGSOFT Software Engineering Notes,

29(1):25–36.

Murata, T. (1989). Petri nets: Properties, analysis and ap-

plications. Proceedings of the IEEE, 77(4):541–580.

OMG (2017a). fUML 1.3 Speciﬁcations.

https://www.omg.org/spec/FUML/1.3/PDF. on-

line.

https://github.com/MDE4CPP/AD2PN

Towards Automated fUML Model Veriﬁcation with Petri Nets

305

OMG (2017b). Uniﬁed Modeling Lan-

guage, Speciﬁcation version 2.5.1.

https://www.omg.org/spec/UML/2.5.1/PDF. on-

line.

Sifakis, J. (1978). Structural properties of Petri nets. In

Winkowski, J., editor, Mathematical Foundations of

Computer Science, pages 474–483. Springer Verlag.

Staines, T. S. (2008). Intuitive Mapping of UML 2 Activity

Diagrams into Fundamental Modeling Concept Petri

Net Diagrams and Colored Petri Nets. In 2008 15th

Annual IEEE International Conference on Engineer-

ing of Computer Based Systems (ECBS), pages 191–

200.

Störrle, H. (2004). Semantics of control-ﬂow in uml 2.0

activities. In 2004 IEEE Symposium on Visual Lan-

guages - Human Centric Computing, pages 235–242.

Störrle, H. (2005). Semantics and veriﬁcation of data ﬂow

in uml 2.0 activities. Electronic Notes in Theoretical

Computer Science, 127(4):35 – 52. Proceedings of the

Workshop on Visual Languages and Formal Methods

(VLFM 2004).

Störrle, H. and Hausmann, J. H. (2005). Towards a formal

semantics of uml 2.0 activities. In Software Engineer-

ing.

Tikhonova, U. and Willemse, T. (2015). Designing and de-

scribing qvto model transformations. In 2015 10th

International Joint Conference on Software Technolo-

gies (ICSOFT), volume 1, pages 1–6.

Valmari, A. (1998). The state explosion problem, pages

429–528. Springer Berlin Heidelberg, Berlin, Heidel-

berg.

van der Aalst, W., Desel, J., and Oberweis, A. (2000). Busi-

ness Process Management — Models, Techniques, and

Empirical Studies. LNCS 1806. Springer Berlin Hei-

delberg.

Zimmermann, A. (2007). Stochastic Discrete Event Sys-

tems — Modeling, Evaluation, Applications. Springer,

Berlin Heidelberg New York.

Zimmermann, A. (2017). Modelling and performance eval-

uation with TimeNET 4.4. In Bertrand, N. and Borto-

lussi, L., editors, Quantitative Evaluation of Systems

- 14th Int. Conf., QEST 2017, pages 300–303, Berlin,

Germany.

APPENDIX

fUML Activity Diagram to Petri Net

Transformation

This appendix shows how the QVTo transformation

translates the single fUML elements to Petri nets us-

ing the intuitive transformation.

Activity

Input

●

Activity Initial Node / Activity input parameter.

Activity

Output

Flow Final node / Activity Output Parameter. An Activity

Final node may be translated in the same way, but it would

not have the same semantic meaning as in an activity dia-

gram.

Decision/Merge nodes with 3 ﬂows.

Fork/Join nodes with 3 ﬂows (intuitive transformation).

Action

A Call Behavior/Operation Action, with incoming and out-

going data and control ﬂows. The semaphore allows to ex-

ecute the action multiple times in a loop with the correct

number of input parameters.

<<centralBuffer>>

CentralBufferNode

A Central buffer node.

<<datastore>>

DataStoreNode

A Data Store Node with one input and one output ﬂow.

<<structured>>

Loop

Test

Body

A Loop Node. According to the fUML speciﬁcation, its

Setup section must be empty.

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

306