
Enhancing Siamese Networks Training with Importance Sampling
Ajay Shrestha and Ausif Mahmood
Department of Computer Science and Engineering, University of Bridgeport, 126 Park Ave, Bridgeport, CT 06604, U.S.A.
Keywords: Siamese Networks, Importance Sampling, Dataset Optimization, Convolution Neural Networks.
Abstract: The accuracy of machine learning (ML) model is determined to a great extent by its training dataset. Yet the
dataset optimization is often not the center of the focus to improve ML models. Datasets used in the training
process can have a huge impact on the convergence of the training process and accuracy of the models. In this
paper, we propose and implement importance sampling, a Monte Carlo method for variance reduction on
training siamese networks to improve the accuracy of the image recognition. We demonstrate empirically that
our approach can achieve improvement in training and testing errors on MNIST dataset compared to training
when importance sampling is not used. Unlike standard convolution neural networks (CNN), siamese
networks scale efficiently when the number of classes for image recognition increases. This paper is the first
known attempt to combine importance sampling with siamese network and shows its effectiveness towards
getting better accuracy.
1 INTRODUCTION
Access to data is a critical factor for training robust ML
models. The explosion of smart devices, sensors, cloud
and edge computing have resulted in massive volume,
variety and velocity of data. While this has been a
tremendous boon to ML, normalizing and sanitizing
this data before utilizing them for training is a
challenge. The goal of dataset optimization is to reduce
the dimensions or the size of the dataset with the intent
of improving the accuracy and/or reducing training
time, without compromising on the quality. There are
several type of dataset optimization methods that are
currently in practice.
CNN has traditionally been the choice of network
for image recognition. It has limitations when the
number of classes become large because the number of
the output of the softmax layer needs to match the
number of classes making the network inefficient.
Siamese network addresses this shortcoming by
building a twin CNN through which the images to be
compared are passed. The input vector is then mapped
to a reduced dimension output, which is then analyzed
with a loss function that exploits the relationship or
similarity between the two images.
In this paper we marry the dataset optimization
using importance sampling with siamese network with
the goal of improving training and accuracy of the net-
work.
2 RELATED WORK
Dataset optimization including importance sampling
has been used to fine-tune the training process and
achieve both training speed-up and accuracy
improvement. Here are some of the earlier related
work.
(Zhao and Zhang, 2015) enhanced variations of
stochastic optimization (prox-SMD and prox-SDCA)
with importance sampling to reduce the variance
resulting in better convergence rate of the training.
(Katharopoulos and Fleuret, 2018) optimized the
training of CNN and RNN with importance sampling
by computing an upper bound for the gradient and
estimation for the variance reduction.
Dataset and training data in general come with lot
of noise that do not contribute to the training process
and in some cases hinder training. An effective
sampling from the full dataset is a great way to address
this concern. (Riad et al., 2018) showed that the
sampling based of word frequency compression and
speaker distribution can have a positive impact on
training.
While importance sampling and other variance
reduction methods have been used in networks before
as described above, we have not found any earlier work
showing implementation of importance sampling to
fine-tune siamese network training.
610
Shrestha, A. and Mahmood, A.
Enhancing Siamese Networks Training with Importance Sampling.
DOI: 10.5220/0007371706100615
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 610-615
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
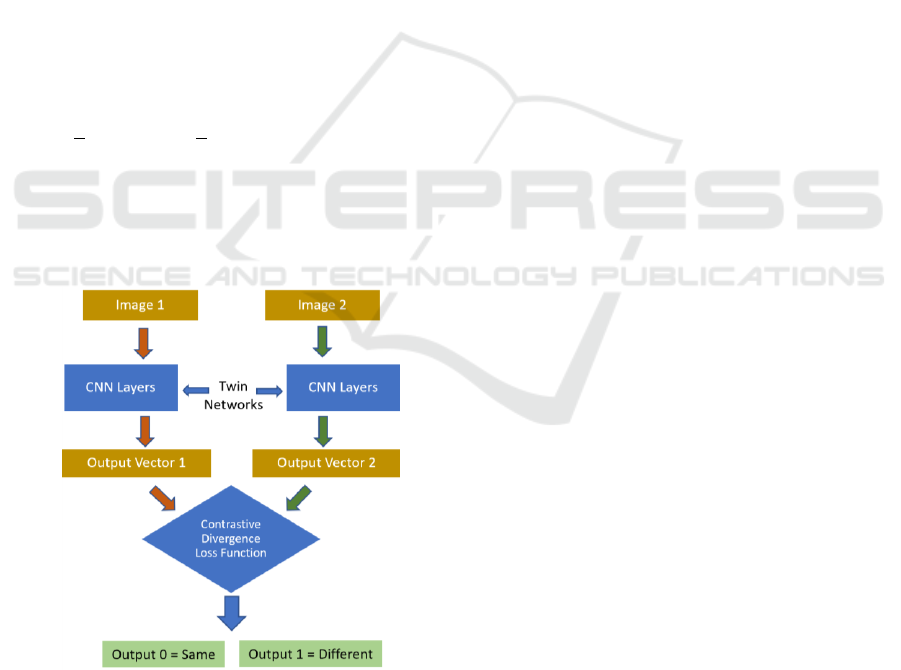
3 SIAMESE NETWORKS
Siamese networks are a variation of the CNN
architecture. As the name implies, siamese networks
use twin CNN networks with identical weights and
parameters. Two separate images are passed through
the individual networks. A dimensionality reduction
method is used to reduce and map the high dimensional
input data into a smaller dimension. Hadsell et al.
(Hadsell et al., 2006) proposed dimensionality
reduction by learning an invariant mapping (DrLIM)
method to come up with and output that is analyzed by
the loss function. The contrastive divergence loss
function indicates the degree of similarity between the
two images passed through the twin networks. Figure
1 illustrates the high-level diagram and workflow of
siamese networks.
CNN classifies images, whereas siamese networks
specifies whether the two images are the same/similar
or not. The contrastive loss function(Hadsell et al.,
2006) is as follows:
(1)
is the is the Euclidean distance between output
vectors of the twin networks. is the final output of
the network which is either 0 (indicates similar) or 1
(indicates dissimilar), and is a margin that is greater
than 0.
Figure 1: Siamese networks workflow diagram.
4 DATASET OPTIMIZATION
Dataset or training data is a key contributor to the
success of ML. It also provides an opportunity for
optimization. The size, dimensions/variables, quality,
redundancy, noise levels, variance, co-variance and
distribution of the dataset and samples impact the
training time and accuracy of the trained model. E.g.,
as the dimensions become very high, finding the
nearest neighbor instances become practically
impossible compute-wise and we have to settle for sub-
par approximates (Muja and Lowe, 2014). Here are the
commonly employed dataset optimization methods.
Optimizing datasets can help us achieve significant
speed up in the training process without compromising
on the accuracy.
4.1 Instance Selection
Instance selection is a dataset reduction method used
to decrease the training time and improve the accuracy
of the model. The number of samples in the dataset
puts a huge burden on training time of supervised
training. Instance selection reduces the number of
samples (instances) in the dataset using different
approaches based on the goal. It can also help to
remove noisy samples from the dataset that do not add
any value to or in some cases mislead the training.
Acccording to (Olvera-López et al., 2010), instance
selection can be divided into two groups: Wrapper and
Filter. The wrapper method (e.g., k-NN classifier)
discards instances that do not improve the accuracy of
the model, whereas filter methods selects instances
based on desired location, i.e., instances around
decision boundary or interior instances. Instances
around boundary could be noise or outliers and
dropping them can smoothen the decision boundary
and improve accuracy. Dropping boundary instances
could also lead to over generalization. On the other
hand, retaining all interior instances with similar
attributes might not contribute to training accuracy.
There is a directly proportional relationship
between retention rate of instances (of instance
selection method) and the accuracy of the model and
an inversely proportional relationship with training
time. (Sun and Chan, 2014) proposes RDI (Remove
Dense Instances) method that balance the two
competing constraints, such that we remove instances
from denser regions, which does not impact the
accuracy much while significantly reducing the
training time.
Instance selection itself can be an optimization prob-
lem as selecting each instance is a binary decision
problem thus giving rise to
potential subsets from
Enhancing Siamese Networks Training with Importance Sampling
611

sample instances (Bennette, 2014). Therefore, it could
be solved using metaheuristics.
4.2 Variable Selection and Dimension
Reduction
MNIST dataset includes 60k 28x28 pixel images. Each
image is a vector of 784 (28x28) variables or
dimensions. While 784 is large, it is miniscule
compared to 60k variables in gene selection problem,
where models are trained to classify whether gene
expression profiles of patients mRNA sample are
cancerous or healthy (Guyon et al., 2003). Consider
another example where blood pressure forecasting
needs to be done based on over 500k dimensions, i.e.,
the number of single nucleotide polymorphisms or
individual DNA mutations common in a population
(James et al., 2013). This can be looked at as a
dimensionality reduction problem. (James et al., 2013)
reports that once the dimensions (or features) becomes
larger than the number of samples (or observations), the
least square method doesn’t work because the mean
squared error reduces to zero even when the features
are not related.
Several ranking methods based on the contributing
factor of the variable both at individual variable level
and at a collective subset level have been proposed to
select the variables in (Guyon et al., 2003). Principal
component analysis (PCA) is another statistical
approach to reduce the dimensions. Here are three
methods described in (James et al., 2013).
4.2.1 Best Subset Selection Method
This method explores whether to include all possible
combinations of the dimensions, thus resulting in
potential subsets. Each combination has to be fit on
individual run of least squares regression, making it
computationally very expensive. There have been other
alternatives that propose only exploring a small portion
of all possible combinations of the subsets.
4.2.2 Shrinkage Method
This method attempts shrink or constraint the
coefficient estimates toward zero to fit a model with all
features. Before fitting a model, all predictors (features)
are standardized to have one standard deviation.
4.2.3 Partial Least Square (PLS)
PLS selects a new set of features using least squares
method in a supervised way by utilizing the labeled
outputs as well as the original predictors.
4.3 Monte Carlo Method
Monte Carlo method constitutes a set of algorithms
used in optimization, bayesian inference and drawing
representative samples from a probability distribution
in very high dimensional space. It is used is several
different disciplines including engineering, design,
finance, law, business, etc. In machine learning, it can
be used to approximate computationally expensive
sums and integrals in training, and in sampling
instances from large datasets. Marcov Chain Monte
Carlo (MCMC) and Importance sampling (IS) are
very popular implementation of Monte Carlo method
for sampling complex distributions.
Bayes’ theorem states the following about
posterior distribution:
(2)
Where P(X | Y) is the probability of X occurring
provided Y is true and the opposite for P(Y | X).
MCMC constructs a Markov chain with a
stationary distribution as the target distribution and
the samples produced
are revised as
(Forsyth et
al., 2001).
5 IMPORTANCE SAMPLING
Importance sampling is a variance reduction method
where the goal is to reduce the variance of the gradient
estimates of the samples. The instances that have low
variance are more likely to be sampled than the ones
with high variance in the gradient distribution. As the
name suggests, the intuition is to select samples that
are more important than the others from training and
accuracy standpoint. This is done by sampling from a
different distribution to reduce the variance of the
gradient estimation.
A probability distribution is a means for
computing expectations (expected/estimate value).
Here is the mathematical explanation of Importance
Sampling (Alain et al., 2015).
The importance sampling estimate based on
sampling from with desired distribution f
and proposed distribution .
(3)
is the normalization constant defined as:
Z
(4)
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
612

The optimal
results in the minimum variance
when:
(5)
(Chitta et al., 2015) proves the advantages of
importance sampling over another popular sampling
method (Bernoulli), where 50 points sampled from
1000 points using importance sampling represented all
10 clusters whereas Bernoulli sampling failed the same
test. In addition to sampling a good representation of
the original dataset, importance sampling also
improves the convergence of the training process by
limiting large swings in the gradient estimates (Zhao
and Zhang, 2015, Shang et al., 2018, Katharopoulos
and Fleuret, 2018). This validates the use of
importance sampling to improve the training time and
cluster quality.
6 IMPLEMENTATION
We implemented importance sampling on siamese
networks using the keras (Chollet and others, 2015)
neural network library and tensorflow (Abadi et al.,
2015) ML framework. Since the goal was to test the
validity of employing importance sampling on siamese
network, we did not optimize the network for best
performance to compete with published accuracy
results on the dataset. Rather the focus was on
demonstrating relative difference between siamese
network that uses importance sampling versus one that
doesn’t.
We started with a standard 3-layer CNN. We trained
it on MNIST dataset, both with full/uniform dataset and
then with importance sampling. We confirmed that the
training and testing accuracy were better when
importance sampling was used. Next, we saved the
indices of the sampled dataset for the next phase.
We built a siamese network. The twin networks
were setup with three fully connected layers with 784 x
1024 x 1024 x 400 nodes. The indices of the samples
selected by importance sampling were used to
complement the training. The testing errors were
compared with results from siamese network that used
the full dataset without any importance sampling. A
mini-batch of 64 samples were used for 80 epochs.
The siamese network was trained and tested on
MNIST dataset. The dataset was shuffled at every time
a mini-batch was selected for training. The trained
network was evaluated on the full test dataset.
We also used another way of picking the samples
for training and testing. The training of siamese
network differs from traditional training of CNN. A
trained siamese network is used to indicate whether the
two images passed through the twin networks are same
or different. Therefore, we trained the network
alternately with similar and differently labelled input
samples as well. Each mini-batch consisted of 50%
similar and 50% differing label samples. The testing
results were captured. Below is the flow used in the
implementation.
3
on full dataset
training and importance sampling training
Figure 2: Pseudocode for implementing importance
sampling on siamese networks.
7 RESULTS
We were able to achieve improvement on both training
and testing data when the network was fine-tuned with
importance sampling. Since our goal was to provide
evidence of relative positive impact of using
importance sampling, we did not intentionally
compare our results to state of the art.
Figure 3 shows the training and testing accuracy of
using importance sampling vs using the full dataset
with no sampling on standard CNN. This provided us
a quick validation that importance sampling improves
Enhancing Siamese Networks Training with Importance Sampling
613

Figure 3: Training loss and testing accuracy on CNN.
accuracy and gave us more confidence in using
sampled instances for siamese network as well.
Figure 4 shows the testing loss on siamese
networks with and without importance sampling fine-
tuning on regular dataset and dataset that includes 50%
similar (labels) samples.
Figure 4: Testing loss on siamese Networks.
The results demonstrate the efficacy of using
importance sampling in getting better accuracy of the
trained model.
8 CONCLUSION
We have presented a practical method to enhance the
training and accuracy of siamese network. We were
able to demonstrate that importance sampling, a
variance reduction method can successfully improve
the training and testing accuracy of the siamese
network. This the first known attempt to combine
importance sampling with siamese network. Unlike
regular CNN, siamese networks can scale to recognize
images at a very large scale with hundreds of classes
or subjects. We have empirically demonstrated the
validity of using importance sampling to fine-tune the
training. Future work on it will involve further
optimization of the importance sampling to train
siamese and other types of networks.
REFERENCES
Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z.,
Citro, C., Corrado, G. S., Davis, A., Dean, J., Devin, M.
and Others 2015. Tensorflow: Large-scale machine
learning on heterogeneous distributed systems. arXiv
preprint.
Alain, G., Lamb, A., Sankar, C., Courville, A. and Bengio,
Y. 2015. Variance Reduction in SGD by Distributed
Importance Sampling. eprint arXiv:1511.06481.
Bennette, W. D. 2014. Instance selection for model-based
classifiers. Graduate Theses and Dissertations, 13783.
Chitta, R., Jin, R. and Jain, A. K. Stream Clustering:
Efficient Kernel-Based Approximation Using
Importance Sampling. 2015 IEEE International
Conference on Data Mining Workshop (ICDMW), 14-
17 Nov. 2015 2015. 607-614.
Chollet, F. and Others 2015. Keras. https://keras.io.
Forsyth, D. A., Haddon, J. and Ioffe, S. 2001. The Joy of
Sampling. International Journal of Computer Vision,
41, 109-134.
Guyon, I., Andr, #233 & Elisseeff 2003. An introduction to
variable and feature selection. J. Mach. Learn. Res., 3,
1157-1182.
Hadsell, R., Chopra, S. and Lecun, Y. Dimensionality
Reduction by Learning an Invariant Mapping. 2006
IEEE Computer Society Conference on Computer
Vision and Pattern Recognition (CVPR'06), 2006 2006.
1735-1742.
James, G., Witten, D., Hastie, T. and Tibshirani, R. 2013.
An Introduction to Statistical Learning. New York, NY :
Springer, 103.
Katharopoulos, A. and Fleuret, F. 2018. Not All Samples
Are Created Equal: Deep Learning with Importance
Sampling. CoRR, abs/1803.00942.
Muja, M. and Lowe, D. G. 2014. Scalable Nearest Neighbor
Algorithms for High Dimensional Data. IEEE
Transactions on Pattern Analysis and Machine
Intelligence, 36, 2227-2240.
Olvera-López, J. A., Carrasco-Ochoa, J. A., Martínez-
Trinidad, J. F. and Kittler, J. 2010. A review of instance
selection methods. Artificial Intelligence Review, 34,
133-143.
Riad, R., Dancette, C., Karadayi, J., Zeghidour, N., Schatz,
T. and Dupoux, E. 2018. Sampling strategies in Siamese
Networks for unsupervised speech representation.
Computing Research Repository (CoRR),
abs/1804.11297.
0,9848
0,976
0,9969
0,9895
0,96
0,97
0,98
0,99
1
Training Accuracy Test Accuracy
3 layer CNN
No Sampling Importance Sampling
0,12
0,31
0,11
0,29
0
0,1
0,2
0,3
0,4
Regular Dataset With 50% similar
labels
Siamese Network - Testing
No Sampling Importance Sampling
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
614

Shang, F., Zhou, K., Cheng, J., Tsang, I. W., Zhang, L. and
Tao, D. 2018. VR-SGD: A Simple Stochastic Variance
Reduction Method for Machine Learning. CoRR,
abs/1802.09932.
Sun, X. and Chan, P. K. An Analysis of Instance Selection
for Neural Networks to Improve Training Speed. 2014
13th International Conference on Machine Learning and
Applications, 3-6 Dec. 2014 2014. 288-293.
Zhao, P. and Zhang, T. 2015. Stochastic Optimization with
Importance Sampling for Regularized Loss
Minimization. In: Francis, B. and David, B. (eds.)
Proceedings of the 32nd International Conference on
Machine Learning. Proceedings of Machine Learning
Research: PMLR
Enhancing Siamese Networks Training with Importance Sampling
615
