
Improving Transfer Learning Performance: An Application in the
Classification of Remote Sensing Data
Gabriel Lins Tenorio, Cristian E. Munoz Villalobos, Leonardo A. Forero Mendoza,
Eduardo Costa da Silva and Wouter Caarls
Electrical Engineering Department (DEE), Catholic University of Rio de Janeiro - PUC-Rio, Rio de Janeiro, Brazil
Keywords:
Deep Learning, Convolutional Neural Networks, Transfer Learning, Fine Tuning, Data Augmentation,
Distributed Learning, Cross Validation, Remote Sensing, Vegetation Monitoring.
Abstract:
The present paper aims to train and analyze Convolutional Neural Networks (CNN or ConvNets) capable of
classifying plant species of a certain region for applications in an environmental monitoring system. In order
to achieve this for a limited training dataset, the samples were expanded with the use of a data generator
algorithm. Next, transfer learning and fine tuning methods were applied with pre-trained networks. With the
purpose of choosing the best layers to be transferred, a statistical dispersion method was proposed. Through
a distributed training method, the training speed and performance for the CNN in CPUs was improved. After
tuning the parameters of interest in the resulting network by the cross-validation method, the learning capacity
of the network was verified. The obtained results indicate an accuracy of about 97%, which was acquired
transferring the pre-trained first seven convolutional layers of the VGG-16 network to a new sixteen-layer
convolutional network in which the final training was performed. This represents an improvement over the
state of the art, which had an accuracy of 91% on the same dataset.
1 INTRODUCTION
Vegetation monitoring can be done by farmers to dis-
tinguish plants, check planting failures and verify
vegetation health and growth. The visual distinction
of plants is useful to identify unwanted plants (weed)
that deteriorate the health of several species of vege-
tation (Aitkenhead et al., 2003). Such monitoring can
be difficult when the plantation area is large or when
it is fenced by plants. A possible solution is the use
of a remote sensing monitoring system using images
from satellites.
Some satellites use multispectral sensors which
provide images of the visible and invisible spectrum.
The reflectance of a plant at a certain wavelength de-
pends on the flux of radiation that reaches it and on
the flux that is reflected. This second variable is con-
ventionally observed in the intensity levels of a plant
image in the invisible spectrum of light, as the near
infrared spectrum is reflected by the cell structure of
plants with high magnitude, varying between differ-
ent plants (Horler et al., 1983).
The dataset analyzed in this work was obtained
through photo captures taken by the RapidEye Ger-
man satellite system, which provides multispectral
data. The dataset contains images from different areas
containing four classes of plants: agriculture, arboreal
vegetation, herbaceous vegetation and shrubby vege-
tation, present in the Serra do Cipo region in the cen-
tral area of southern Brazil (Nogueira et al., 2016).
For this task, the green, red and near-infrared bands
are appropriate for distinguishing the classes of inter-
est (Nogueira et al., 2016). Each image taken by the
satellite contains various plant species, making it nec-
essary to consult specialists for separating and classi-
fying them. Thus, a class distribution of the dataset
with 1311 multispectral scenes is obtained.
The recognition of the specie’s patterns was one of
the main difficulties discussed by the original authors
regarding the interpretation of the images contained
in the dataset, given their complex intraclass vari-
ance and interclass similarity (Nogueira et al., 2016).
These issues make the sample preparation and sep-
aration into groups costly and limited. As a conse-
quence, there are complex and unbalanced samples
so that classification algorithms such as usual ANN
(Artificial Neural Networks), SVM (Support Vector
Machine) and decision-tree provide unsatisfactory re-
sults for this task. However, literature shows that deep
learning approaches (i.e. Convolutional Neural Net-
174
Tenorio, G., Villalobos, C., Mendoza, L., Costa da Silva, E. and Caarls, W.
Improving Transfer Learning Performance: An Application in the Classification of Remote Sensing Data.
DOI: 10.5220/0007372201740183
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 174-183
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

work - CNN) and other methods (i.e. data augmenta-
tion, transfer learning and fine tuning), have a much
better performance in these cases, because they allow
to model and train a classifier, (e.g. distinguishing
vegetation) using images as inputs, even with scarcity
and complexity of data (Gu et al., 2018). In this paper,
we begin by describing CNN deep learning models
and the motivation to use transfer learning and fine-
tuning methods. Then, the solution strategy for the
classification task is presented along with approaches
called data augmentation and cross-validation, to deal
with few and unbalanced data. We also show in the-
ory and experimentally how hyperparameters for the
model, the methods and the approaches described af-
fect the training performance. In order to train the
model with different layer topologies, a statistical dis-
persion method is proposed to evaluate each convo-
lutive layer of the model and help to choose which
layers are the best to be transferred to the fine tune
model.
To increase considerably the training speed for
the CNN in a CPU, parallelism operators and a dis-
tributed learning method were used, which simulates
larger minibatches by dividing the data through work-
ers. Our experiments are then compared to baselines
and state of the art approaches, indicating superior re-
sults.
2 THEORETICAL FRAMEWORK
The convolutional neural network is a type of deep
learning architecture that has recently stood out in the
image recognition field achieving a very high accu-
racy (Gu et al., 2018). The inputs of a CNN classifier
are given by digital images, in the form of tensors,
that are brought to feature extractors. Each extrac-
tor performs operations, through filters, in parallel to
extract features from the images starting from more
generic, low-level features and culminating in higher
level features that are more specific to the dataset. A
second Neural Network is conventionally placed after
the last convolutional layer to operate as a classifier.
As the complexity of the images increases, there
is a need to change CNN hyperparameters. However,
as the number of convolutional layers, the filter size
Table 1: Original Species Samples.
Species #Samples Proportion (%)
AGR 47 3.58
FOR 962 73.37
HRB 191 14.57
SHR 111 8.46
Total 1311 100
and number of CNN filters are increased, the com-
putational cost increases significantly (He and Sun,
2015). This effect adds difficulties in experimental
research involving real applications, such as those re-
quiring rapid scenario changes
1, 2
being necessary to
explore the architecture’s parallelism capacity.
An approach called Transfer Learning (TL) may
decrease the number of required operations allow-
ing the transfer of learning, acquired in one prob-
lem, to another problem with similar characteris-
tics. What makes TL more effective is the pos-
sibility of using pre-trained networks such as VG-
GNet (Simonyan et al., 2013), GoogleNet (Szegedy
et al., 2015), ResNet (He et al., 2016) and AlexNet
(Krizhevsky et al., 2012), which stood out in the chal-
lenges of the Large Scale Visual Recognition Chal-
lenge (ILSVRC - ImageNet) for object detection and
image recognition (Russakovsky et al., 2015).
In models that require more specific classification,
as in the scope of this paper, there is a need for Fine-
Tuning (FT) the model, freezing some layers of the
pre-trained networks and constructing convolutional
layers on top of them.
3 SOLUTION STRATEGY
3.1 Preparation of Data and Data
Augmentation
The dataset used for the network training
3
was found
in the paper by (K. Nogueira et al. 2016) which
also uses the artifice of convolutional networks for
the classification of four distinct vegetative species,
as shown in Fig. 1. The resolution of each image is
64 x 64 pixels.
The dataset has unbalanced and scarce samples
making it difficult to develop the classification model.
Table 1 shows the distribution of samples between
classes.
Some approaches can be used to train neural net-
works with unbalanced data avoiding the problem of
limited generalization, such as penalizing with higher
weights the errors of classification of classes with less
1
Drive.ai, ”Building the Brain of Self-Driving Vehi-
cles”, 2018. Available: https://www.drive.ai/ [January 29,
2018].
2
Descartes Labs, ”A data refinery, built to un-
derstand our planet”, 2017. Available: https://
www.descarteslabs.com/ [August 15, 2017]
3
The dataset is available for download at http://
www.patreo.dcc.ufmg.br/2017/11/12/brazilian-cerrado-
savanna-scenes-dataset/ [December 6, 2018].
Improving Transfer Learning Performance: An Application in the Classification of Remote Sensing Data
175

Figure 1: Group of four classes: AGR, FOR, HRB and SHR.
Table 2: Balanced classes samples generated using Keras
ImageDataGenerator in each new training.
Species # Training Samples # Test Samples
AGR 1770 540
FOR 1770 540
HRB 1770 540
SHR 1770 540
Total 7080 2160
samples. Another approach makes it possible to in-
crease the amount of data of each class proportion-
ally, thus balancing the data. In this article, the sec-
ond approach was chosen to solve the problem of
data scarcity. Another advantage of the data increase
in a neural network is that it acts as a regularizer,
making the model more robust, preventing overfitting
(Cires¸an et al., 2010) and improving the performance
of unbalanced models (Chawla et al., 2002).
Through the ImageDataGenerator from the
python deep learning library keras, it becomes pos-
sible to generate new images from the dataset with
random transformations applied to an image. We
used the following transformations: width and height
displacement, shear range, zoom, horizontal rotation,
and brightness adjustment. Figure 2 illustrates four
examples of random transformations in a single im-
age. Before increasing the data, the original dataset is
divided into training and test sets, respectively, 75%
and 25% of the samples. The same sets are used in all
experiments. Then, in each new training, the original
training set is balanced, proportionally to each class,
through data augmentation. After each training, the
test set is also expanded proportionally. Table 2 illus-
trates the increase of data using the image generator
for the training and test sets.
3.2 Pre-trained Network and Transfer
Learning
The training of many-layered convolutional networks,
based on the random initialization of weights, re-
quires a high computational cost due to the amount
of parallel operations that feature extractor filters per-
form. Using pre-trained networks it is possible to
minimize this cost initializing pre-trained weights and
Figure 2: Examples of transformations performed by the
Keras ImageDataGenerator in a single image.
bias thereby reaching the convergence of the model
much earlier. There are several models of pretrained
networks such as VGGNet, GoogleNet, ResNet and
AlexNet. In this paper, the VGG-16 network was cho-
sen, because it stands out for its uniform and effective
architecture for applications involving image classifi-
cation. The sixteen layers of the VGG-16 network use
only 3 x 3 convolution order and 2 x 2 order pooling.
Convolution is an image filtering process that aims
to detect patterns creating feature maps. The pooling
process reduces the spatial size of the features discov-
ered by the convolution layers. Fig. 3 shows the ar-
chitecture of the VGG-16 networks (Gu et al., 2018).
The VGG-16 network is pre-trained using the Im-
ageNet database. This database has about fourteen
million high quality natural images with more than a
thousand labeled categories, that is, classes with their
proper titles.
Transfer learning is a technique that uses pre-
trained networks which take the generic features of
images, such as color blobs, edges and corners in the
first layers. At each subsequent layer, the character-
istics taken from the images become more and more
specific with the training datasets which can be ob-
tained, for example, from the imagenet database. Af-
ter the training step, the classification layers of the
pre-trained network (layers 14 to 16) are removed,
keeping the previous ones frozen (fixed). The images
of the target dataset are executed in this truncated net-
work in order to produce bottleneck features. These
features are used to train a new classifier and obtain
the prediction of the target dataset classes.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
176
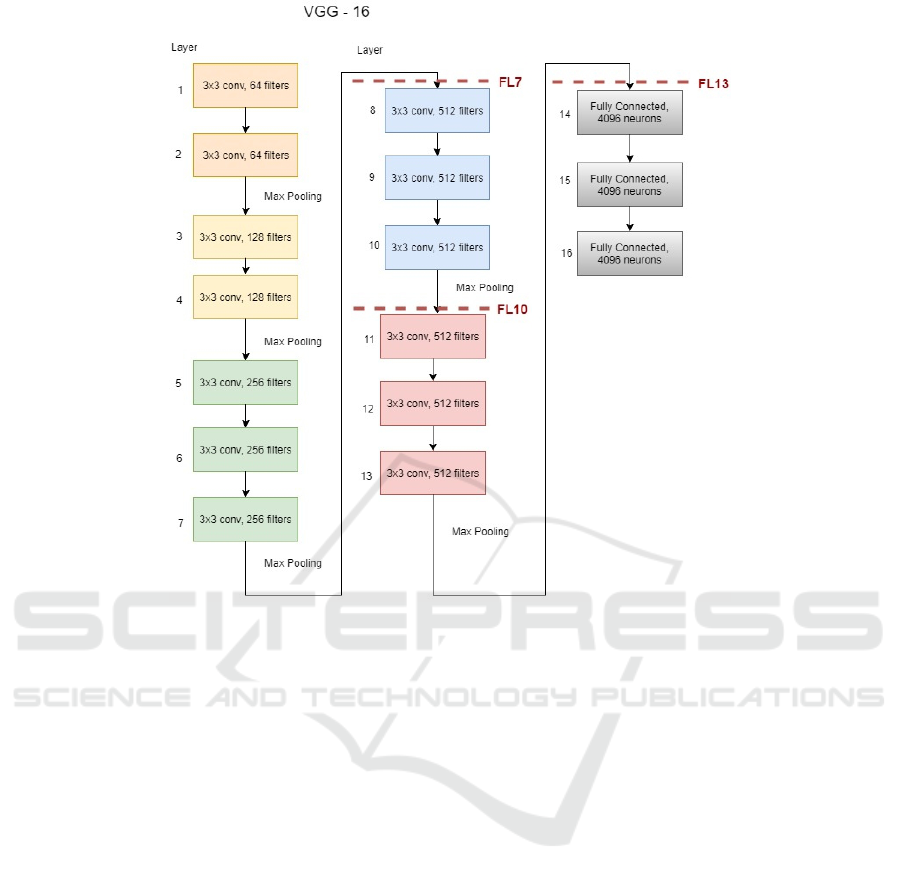
Figure 3: VGG-16 networks architecture. The codes next to the dotted lines indicate the frozen layers in the experiments.
Our target dataset has few samples, besides being
very different from the pre-trained network’s dataset,
so truncating the last layer of that network may not
be enough to obtain a satisfactory accuracy. This
is because features taken from the layers closest to
the output are not useful for the classification of the
model. One solution to this problem is fine tun-
ing which allows the lower Y layers of the transfer-
learning network to be frozen extracting characteris-
tics from these layers and after the last layer, new con-
volution and classification layers can be added. A new
training of the resulting network can be performed,
taking into account that the weights and bias of the
Y layers are fixed. Freezing more layers results in a
network with lower accuracy in exchange for a train-
ing that requires less computational complexity, as the
training of a network with less convolutional layers
demands less complexity to be calculated. In addi-
tion to the freezing of layers, the fine tuning method
is also related to the tuning of the hyperparameters of
the resulting network.
3.3 Cross-validation
In order to evaluate the learning algorithm and how it
responds to the data augmentation, a cross-validation
metric is used. The cross validation divides the sam-
ples of the increased training set into different train-
ing and validation samples by making combinations
between them. A specific case of cross-validation is
the k-Fold cross-validation method, which divides the
samples into k
f
subsets at random and without repeti-
tion, using all the data in that division. The convolu-
tional neural network model is trained k
f
times, where
in each training a single subset is selected for the
test and k
f
− 1 subsets for the training. The method
is commonly used in Machine Learning applications
with 10 folds (k
f
= 10) aiming at adjusting the gener-
alization of the algorithm (Refaeilzadeh et al., 2009).
In order to obtain a resulting accuracy, the average of
the k
f
trainings is calculated.
3.4 CNN Layer Statistical Analysis
The output of each CNN layer is a feature map. In-
terpreting the feature maps in-between the layers may
show how well and in which layers the model is learn-
ing the specific features of each class. However, they
are not trivially interpretable and consequently it is
difficult to choose the best layers to be frozen.
Some algorithms for dimensionally reduction (i.e.
PCA or t-SNE) can lead us to check whether, in a
Improving Transfer Learning Performance: An Application in the Classification of Remote Sensing Data
177

certain convolutional layer, the features of each class
was separated by reducing the dimensionally to two
features and drawing a scatter plot (Jolliffe, 2011;
Maaten and Hinton, 2008). However, in some cases,
it is difficult to verify whether the CNN has been able
to separate the features or whether the algorithm has
been able to reduce the dimension correctly. Another
algorithm that can be used to interpret the features
maps in CNNs is called DeepResolve (Liu and Gif-
ford, 2017). It is based on a gradient-ascent method
and does not require inputs by calculating a class-
specific optimal ’image’ H for each class in each layer
(Simonyan et al., 2013). This method’s output pro-
vides helpful information to analyze and decide which
layers are important to be frozen.
We propose a simpler statistical analysis of each
convolutional layer by calculating the mean of the
between-class standard deviation vector, for each
layer, which is calculated between the mean feature
maps of all classes.
Each three-dimensional feature map matrix is re-
shaped into a single dimension of vector (feature vec-
tor). The standard deviation vector previously men-
tioned is given by (1):
~
S
m
=
v
u
u
t
∑
N
n=1
~
C
n
m
−
~
C
m
2
N − 1
(1)
Where
~
C
n
m
is the mean feature vector between all
the images from class n in convolutional layer m and
~
C
m
is the mean vector between the classes in a given
layer. Those terms can be calculated by (2):
~
C
n
m
=
∑
J
n
j=1
~
F
j
n
m
J
n
~
C
m
=
∑
N
n=1
~
C
n
m
N
(2)
Where
~
F
j
n
m
denotes the feature vector from class n
in a layer m of image j and J
n
is the number of im-
ages in a given class n. Replacing the equations (2) in
equation (1), we calculate the vector
~
S
m
and the scalar
mean M
S
m
(3).
M
S
m
=
¯
~
S
m
(3)
The number of classes is four (N = 4) and the
maximum number of convolutional layers is thirteen
(m = [1, 2,..13]). It is expected that the mean of the
inter-class standard deviation in each layer (M
S
m
) in-
creases because higher layers extract more specific
features, which should therefore exhibit larger inter-
class variance. This variable could tell which is the
appropriate convolutional layer that should be frozen
and then perform a new training. For example, if the
variable decreases considerably in a given layer, this
means that the features are getting worse on the new
domain (they are too specific to the original domain),
and therefore it is not useful to freeze that layer.
3.5 Distributed Training using Large
Minibatches
In order to take advantage of the computational power
of a multi-core CPU and increase the training speed
effectively, a distributed training method was used.
The method proposed by (Goyal et al., 2018) sim-
ulates large minibatches of size kn by dividing the
batches of the dataset through k workers not compro-
mising, until a certain point, the model’s accuracy. In
order to maintain the same behavior as a regular mini-
batch of size n, the method uses a linear scaling rule
which consists in multiplying the learning rate (η) by
the number of workers (k). An assumption is made
for this rule to take effect as shown in equation 4.
∇l(x, w
t+ j
) ≈ ∇l(x, w
t
), where j < k (4)
The first term ∇l(x,w
t+ j
) represents the gradient
of the loss function for a sample x and weights w
t+ j
at
the training iteration t + j. The gradient is used in the
minibatch Stochastic Gradient Descent (SGD) with a
learning rate η and small minibatch of size n (Goyal
et al., 2018). For the large minibatch, the loss is only
calculated using the second term ∇l(x, w
t
). With the
previous assumption and setting a new learning rate
(
ˆ
η) proportional to the number workers (
ˆ
η = kη), the
SGD updates from small and large minibatch is sim-
ilar (Goyal et al., 2018). As an effect, increasing
the batch size should not substantially affect the loss
function optimization. As described by the authors,
the assumption is not true at the beginning of the train-
ing when the weights are changing quickly. To solve
this problem a gradual warmup is used, starting the
training from a base learning rate η and increasing
this value constantly until it reaches the learning rate
ˆ
η proportional to k after 5 epochs (Goyal et al., 2018).
Additionally, the learning rate is divided by 10 at the
30
th
, 60
th
and 80
th
epochs, similar to (He et al., 2016).
3.6 Experiments
The experiments performed in this work were carried
out on two Intel
R
Xeon
R
Platinum 8160 CPUs with
24 cores each (96 threads in total) and 192GB of RAM
that made possible the application of the distributed
training and considerably increase the training speed.
The implemented model was simulated in the
Keras framework with Intel
R
Tensorflow backend
that allows the use of dataflow programming. Also,
Intel
R
MKL-DNN that accelerates the Deep Learning
framework on Intel
R
processors (allowing the use of
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
178

Load Balance System Optimization
4
(LBSO) param-
eters) and the open source framework Horovod (as a
base of the distributed training) were used.
The experiments used transfer learning freezing Y
layers, denoted ”FL-Y”, and fine tuning. Freezing of
the layers below 13 (FL-13), 10 (FL-10) and 7 (FL-7)
were performed as depicted in Fig. 3. It is relevant
to notice that all the convolutional layers in the FL-13
experiment are frozen which means that fine tuning
method has no effect. For all experiments, the softmax
function was used in the output layer composed of
four neurons, which provides the degree of certainty
of an input image in relation to each of the four spec-
ified classes. The class that contains the highest value
is chosen to represent the input image.
The impacts of variations of the hyperparameters
of interest, within predefined ranges of values, on
the training time and resulting accuracy of the model
were analyzed in all experiments. These analyses
considered variations in parameters such as dropout,
number of epochs and base learning rate. Also, the
number of workers (k) and LBSO parameters such
as intra-operation parallelism (maximum number of
threads to run an operator) and inter-operation par-
allelism (maximum number of operators that can be
executed in parallel) were evaluated for the model’s
accuracy. Other parameters such as pooling size
and convolution filter size were kept fixed in order
to avoid incompatibility with the architecture of the
pre-trained networks. For k-fold cross-validation the
value of k
f
= 10 was used, which results in better per-
formance in comparison to lower values of k
f
. The
SGD optimization algorithm was used for the all the
training experiments.
Table 3 presents the range of values in which the
hyperparameters of interest were evaluated and the
optimal values obtained experimentally.
The three experiments that provided the best re-
sults from the hyparameters adjustments and freezing
of the layers below 13 (FL − 13), 10 (FL − 10) and 7
(FL −7) were selected. As discussed previously, each
convolutional layer of the pre-trained network that is
not frozen (learning not transferred) must be added in
the fine-tuning network. The three best experiments
and their topologies are shown in Table 4.
4
Boosting Deep Learning Training & Inference Per-
formance on Intel
R
Xeon
R
and Intel
R
Xeon Phi
TM
Processors, 2018. Available: https://software.intel.com/en-
us/articles/boosting-deep-learning-training-inference-
performance-on-xeon-and-xeon-phi [November 5, 2018]
Table 3: Variation of hyperparameters of Interest (keeping
the batch size fixed n = 32).
Parameter Range of Values
Min Max Optimal*
Dropout 0% 70% 50%
# Epochs 35 650 100
Base LR (η) 10
−5
10
−3
10
−5
# Workers (k) 1 12 5
Intra-op 2 48 19
Inter-op 0 4 2
Simul. Batch Size (kn) 32 384 160
Frozen Layers 7 13 7
*The optimal value is the best estimate found for the
parameter of interest
Table 4: Topologies of the FL − 13, FL − 10 and FL − 17
experiments.
FL-13 FL-10 FL-7
Convolutional Layers - 3 6
Filters - 128x3 512x6
Classification Layers 2 1 2
Neurons 512-256 512 512-256
Dropout (%) 0-0 0.3 0.5-0
4 RESULTS AND DISCUSSIONS
In order to evaluate the performance of the model with
the different analyzed topologies, the three best ex-
periment configurations of each topology were com-
pared. Additionally, the full training experiment was
done. Each experiment was performed ten times,
calculating the uncertainty of the results and obtain-
ing more precise accuracy values. Table 5 indicates
the total simulation time of the training performed,
through 10-fold cross-validation, and the resulting ac-
curacy of each experiment. It is important to note that
in the original dataset, the proportion of the class with
more samples is 73.37%. Considering this observa-
tion, it is considered that values of weighted accu-
racy around 73% are unsatisfactory, because the clas-
sifier should be better than chance. To obtain results
that are comparable to the original paper, the overall
test accuracy of the experiments was also weighted
by each class proportion. At each fold of the k-Fold
cross-validation method, the model was saved to ob-
tain the class prediction and the normalized confusion
matrix on the augmented test set. The diagonal ele-
ments of this matrix show the normalized true posi-
tive predictions of each class which are then weighted
by each class proportion and added. This procedure
is repeated k
f
times and after that the overall test ac-
curacy was calculated. Table 6 shows the confusion
matrices of experiments FL-13, FL-10 and FL-7.
In order to evaluate the training time of the exper-
iment that demands most computational power (FL-
7) varying some hyperparameters for the distributed
learning (intra-op and k) and keeping the other op-
Improving Transfer Learning Performance: An Application in the Classification of Remote Sensing Data
179

Table 5: Results FL − 13, FL − 10, FL − 7 and FL − 0.
Experiment Training Overall Test Overall Test
Time* Accuracy Accuracy
(Weighted)
FL − 13 15 min → 4 min 45.1 ± 1.9 % 79.43 ± 1.3 %
FL − 10 50 min → 12 min 81.8 ±1.4 % 76.7 ± 1.2 %
FL − 7 183 min → 37 min 97.3 ± 0.9 % 97.1 ± 1.0 %
FL − 0 567 min 55.7 ± 2.1 % 77.6 ±1.6 %
*The values indicates the decrease (→) of the training time
when using the Intel MKL-DNN as opposed to default
TensorFlow
timal values fixed (as show in Table 3), the Table 7
was generated. For all the variations expressed, the
model’s loss function presents similar behavior and
final values.
It is noted from the results presented in Tables 5
and 6 that the experiment FL-13 has high uncertainty,
regarding the achieved accuracy values and it is also
unreliable because the most predictions were just in a
single class. As noted earlier, the pre-trained network
learned from different datasets that are distinct when
compared to the dataset employed in this paper. Con-
sequently, only the lower-level features are useful for
classifying the specific vegetative species of interest
accurately.
Increasing the number of workers and intra-op, as
shown in Table 7, decreases the training time consid-
erably, but at certain point (k > 8) the model’s per-
formance decreases. Also, a proportionally low value
for intra-op in relation to k increases the training time
and, as a limitation, the multiplication of (k · Intra-op)
should be less than or equal to the number of total
threads (k · Intra-op ≤ 96). The best trade-off be-
tween performance and training time was obtained
when balancing intra-op and k values as shown in the
highlighted column in Table 7.
As discussed and described previously, it is also
possible to use a statistical method to find the most
suitable layer to be frozen and train the deep learn-
ing model. Figure 4 shows a chart that contains the
mean of the inter-class standard deviation in each
layer (M
S
m
) for each experiment.
Looking at the lightest bars, it can be seen that
after the 9
th
convolutional layer the M
S
m
value re-
mains low, which confirms that the model can’t find
useful features that distinguish the classes. So, we
may choose to freeze all layers that are part of the 9
th
layer’s max-pooling block and below, leading to the
FL − 10 model.
Alternatively, observing that M
S
m
has a maximum
at the 6
th
layer, it is logical to freeze until there.
Again, fixing the boundary to the max pooling block
leads to the FL − 7 model.
The FL −10 and FL−7 experiments provided su-
perior results compared to the FL − 13 experiment
that does not use fine tuning. The expressive gain of
accuracy of the FL − 7 and reliability (the true class
prediction is more distributed through the classes) of
the experiment FL-10 are due to the ability of the con-
volutional networks, added in these experiments, to
learn the more specific features of the dataset used,
which was expected for these configurations. In rela-
tion to the training time, it can be seen that it tripled
with the addition of three convolution layers (FL −13
experiment to FL − 10) and tripled again by doubling
the convolution layers (FL − 10 to FL − 7). This
proves the expectation of computational complexity
attributed to training a network with more convolu-
tional layers.
The superior results can also be observed when
looking at the mean interclass standard deviations in
Figure 4. Both FL − 10 (dark grey bars) and FL −
7 (black bars) show higher deviations for the deeper
layers, but only FL − 7 maintains the upward trend of
separability.
It is important to note that, for the target dataset,
freezing less and less layers results in better results,
but in addition to the computational cost, the chances
of obtaining poor results are even greater with data
augmentation. This is due to, with this decrease, the
architecture is increasingly approaching the full train-
ing model (i.e., starting from scratch) having a much
larger number of parameters to be trained and possi-
bly overfitting the model during the training (Gu et al.,
2018). In order to confirm this statement, the exper-
iment FL − 0 (training from scratch) was made and
the results are shown in table 5. For this experiment,
in the training phase, the model’s training and valida-
tion accuracies presented very high values, but in the
testing phase the overall test accuracy value was very
low, which indicates an overfitting of the data.
The baseline accuracies for this dataset predic-
tion proposed by the original authors were less than
82.5%, using different techniques as BIC (Stehling
et al., 2002), CCV (Pass et al., 1997), GCH (Swain
and Ballard, 1991) and UNSER (Unser, 1986) as seen
in Table 8.
The best accuracy obtained by the authors of the
article used as inspiration was 90.5 ± 1.8%. In the
mentioned paper, the AlexNet pre-trained network
architecture with fine tuning and layer freezing was
used, but without data augmentation (Nogueira et al.,
2016). The architecture of the AlexNet network is dif-
ferent from the one used in the present article having
a smaller number of parameters and greater complex-
ity of operations. The results obtained with VGG-16
and the auxiliary methods specified above have shown
to be promising (accuracy about 97%) in relation to
those with differentiated architecture. The possible
differences in results are related to the use of data aug-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
180
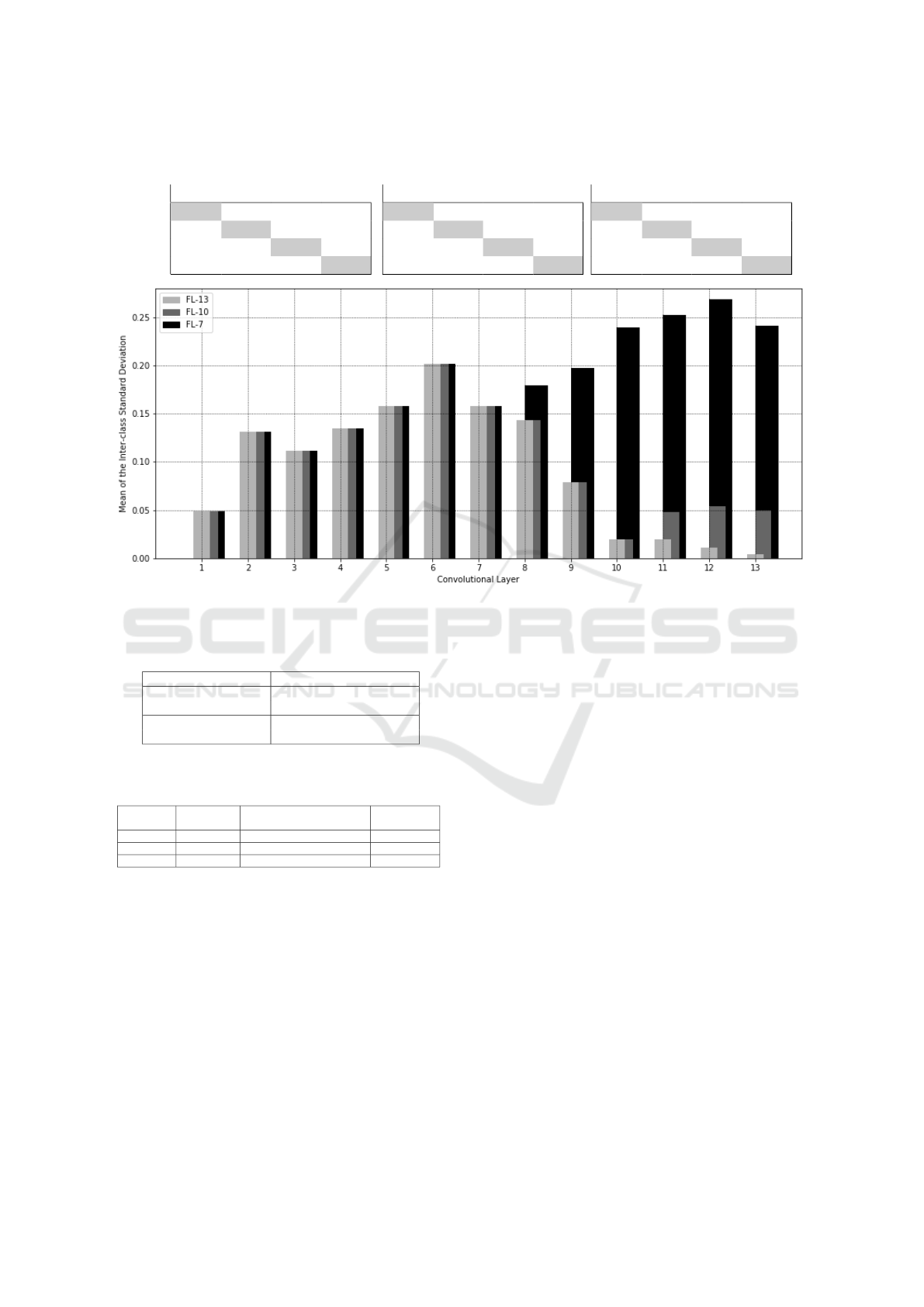
Table 6: Normalized confusion matrix FL-13, FL-10 and FL-7 experiments. The columns indicate the predict class for the
test set.
AGR FOR HRB SHR
AGR 0.3 0.26 0.26 0.19
FOR 0.01 0.99 0.00 0.00
HRB 0.26 0.21 0.23 0.30
SHR 0.20 0.29 0.23 0.28
AGR FOR HRB SHR
0.85 0.04 0.09 0.02
0.03 0.73 0.05 0.18
0.01 0.00 0.94 0.05
0.01 0.00 0.24 0.75
AGR FOR HRB SHR
0.99 0.01 0.00 0.00
0.00 0.97 0.01 0.02
0.00 0.01 0.99 0.01
0.00 0.01 0.03 0.96
Figure 4: Mean of the inter-class standard deviation (M
S
m
) in each convolutional layer for the FL-(13,10 and 7) experiments.
Table 7: Training time comparison when varying some hy-
perparameters using Intel MKL-DNN.
Hyperparameter Values
# Intra-op 20 48 19 12
# workers (k) 1 2 5 8
Simul. Batch Size (kn) 32 64 160 384
Training Time (min) 1598 903 37 69
Table 8: Comparison to baselines and deep learning models
for the test set.
Technique
Weighted
Accuracy
Technique
Weighted
Accuracy
CCV 80.6 ± 2.3% BIC 85.5 ± 1.4%
GCH 80.1 ± 2.4% Fine Tuning (original paper) 90.54 ± 1.8%
UNSER 80.3 ±0.2% Fine Tuning (FL-7) 97.1 ± 1.1%
mentation and the VGG-16 network in having fixed
parameters such as pooling size and convolution fil-
ter size. In this way, with the change of the other
hyperparameters, the impacts of these variations are
more effectively realized, resulting in a satisfactory
fine-tuning.
5 CONCLUSIONS AND FUTURE
WORK
This paper used methods that have helped convolu-
tional networks to learn more effectively the specific
characteristics of vegetative species groups. The data
augmentation method was essential in achieving ef-
fective accuracy by balancing the data to prevent over-
fitting, while transfer learning accelerated the training
process of the network, smartly, by skipping training
steps. The fine-tuning approach enabled to truncate
any layers of the transfer-learning network and the
insertion of convolutional layers, to distinguish the
classes with higher accuracy. The statistical analy-
sis proposed helps to choose which layers should be
frozen avoiding unnecessary extra experimental tests
for the correct choice.
The distributed learning (training the model by di-
viding the dataset between workers) and the tuning of
the parallel operators (LSBO parameters) have shown
the possibilities to train a convolutional network in a
CPU with high training speed. It is relevant to notice
that the maximum number of workers that resulted in
good performance is limited, perhaps due to the small
dataset.
The final result which indicates an accuracy of
about 97% is relevant for applications involving
remote sensing for the classification of vegetation
species whose images are derived from satellites.
The classification model implemented may not
work well if the camera is not multispectral, being an
essential equipment for the plant classification task.
Improving Transfer Learning Performance: An Application in the Classification of Remote Sensing Data
181

Also, for satisfactory training and inference results,
the dataset must be divided into small tiles to reduce
the number of classes present in each image.
The theoretical and experimental study of solu-
tions for implementing a classifier using unbalanced
data have great importance for future work, since
most environmental monitoring applications rely on
disproportionate class data. It is intended to apply
the concepts and experiences learned in new datasets
with more classes and more data. Also, for future
work, pixel-wise semantic segmentation deep learn-
ing models (Badrinarayanan et al., 2015; Chen et al.,
2018; Ronneberger et al., 2015) may be used to clas-
sify the plants species which makes it possible to clas-
sify whole images containing multiple classes at the
same time and without being necessary to crop them
into small tiles.
ACKNOWLEDGEMENT
This work was partially funded by a Masters Scholar-
ship supported by the National Council for Scientific
and Technological Development (CNPq) at the Pon-
tifical University Catholic of Rio de Janeiro, Brazil.
REFERENCES
Aitkenhead, M., Dalgetty, I., Mullins, C., McDonald, A.
J. S., and Strachan, N. J. C. (2003). Weed and crop dis-
crimination using image analysis and artificial intelli-
gence methods. Computers and electronics in Agri-
culture, 39(3):157–171.
Badrinarayanan, V., Kendall, A., and Cipolla, R. (2015).
Segnet: A deep convolutional encoder-decoder ar-
chitecture for image segmentation. arXiv preprint
arXiv:1511.00561.
Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,
W. P. (2002). Smote: synthetic minority over-
sampling technique. Journal of artificial intelligence
research, 16:321–357.
Chen, L.-C., Papandreou, G., Kokkinos, I., Murphy, K., and
Yuille, A. L. (2018). Deeplab: Semantic image seg-
mentation with deep convolutional nets, atrous convo-
lution, and fully connected crfs. IEEE transactions on
pattern analysis and machine intelligence, 40(4):834–
848.
Cires¸an, D. C., Meier, U., Gambardella, L. M., and Schmid-
huber, J. (2010). Deep, big, simple neural nets for
handwritten digit recognition. Neural computation,
22(12):3207–3220.
Goyal, P., Doll
´
ar, P., Girshick, R., Noordhuis, P.,
Wesolowski, L., Kyrola, A., Tulloch, A., Jia, Y., and
He, K. (2018). Accurate, large minibatch sgd: training
imagenet in 1 hour. arXiv preprint arXiv:1706.02677.
Gu, J., Wang, Z., Kuen, J., Ma, L., Shahroudy, A., Shuai, B.,
Liu, T., Wang, X., Wang, G., Cai, J., et al. (2018). Re-
cent advances in convolutional neural networks. Pat-
tern Recognition, 77:354–377.
He, K. and Sun, J. (2015). Convolutional neural networks
at constrained time cost. In Proceedings of the IEEE
conference on computer vision and pattern recogni-
tion, pages 5353–5360.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-
ual learning for image recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 770–778.
Horler, D., DOCKRAY, M., and Barber, J. (1983). The red
edge of plant leaf reflectance. International Journal
of Remote Sensing, 4(2):273–288.
Jolliffe, I. (2011). Principal component analysis. In In-
ternational encyclopedia of statistical science, pages
1094–1096. Springer.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in neural information process-
ing systems, pages 1097–1105.
Liu, G. and Gifford, D. (2017). Visualizing feature maps in
deep neural networks using deepresolve a genomics
case study. ICML Visualization Workshop.
Maaten, L. v. d. and Hinton, G. (2008). Visualizing data
using t-sne. Journal of machine learning research,
9(Nov):2579–2605.
Nogueira, K., Dos Santos, J. A., Fornazari, T., Silva, T. S. F.,
Morellato, L. P., and Torres, R. d. S. (2016). Towards
vegetation species discrimination by using data-driven
descriptors. In Pattern Recogniton in Remote Sens-
ing (PRRS), 2016 9th IAPR Workshop on, pages 1–6.
IEEE.
Pass, G., Zabih, R., and Miller, J. (1997). Comparing im-
ages using color coherence vectors. In Proceedings of
the fourth ACM international conference on Multime-
dia, pages 65–73. ACM.
Refaeilzadeh, P., Tang, L., and Liu, H. (2009). Cross-
validation. In Encyclopedia of database systems,
pages 532–538. Springer.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:
Convolutional networks for biomedical image seg-
mentation. In International Conference on Medical
image computing and computer-assisted intervention,
pages 234–241. Springer.
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S.,
Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bern-
stein, M., et al. (2015). Imagenet large scale visual
recognition challenge. International Journal of Com-
puter Vision, 115(3):211–252.
Simonyan, K., Vedaldi, A., and Zisserman, A. (2013).
Deep inside convolutional networks: Visualising im-
age classification models and saliency maps. arXiv
preprint arXiv:1312.6034.
Stehling, R. O., Nascimento, M. A., and Falc
˜
ao, A. X.
(2002). A compact and efficient image retrieval ap-
proach based on border/interior pixel classification. In
Proceedings of the eleventh international conference
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
182

on Information and knowledge management, pages
102–109. ACM.
Swain, M. J. and Ballard, D. H. (1991). Color indexing.
International journal of computer vision, 7(1):11–32.
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S.,
Anguelov, D., Erhan, D., Vanhoucke, V., and Rabi-
novich, A. (2015). Going deeper with convolutions.
In Proceedings of the IEEE conference on computer
vision and pattern recognition, pages 1–9.
Unser, M. (1986). Sum and difference histograms for tex-
ture classification. IEEE transactions on pattern anal-
ysis and machine intelligence, (1):118–125.
Improving Transfer Learning Performance: An Application in the Classification of Remote Sensing Data
183
