Spatial Kernel Discriminant Analysis: Applied for Hyperspectral Image

Classiﬁcation

Soumia Boumeddane

, Leila Hamdad

, Sophie Dabo-Niang

and Hamid Haddadou

Laboratoire de la Communication dans les Syst

emes Informatiques, Ecole nationale Sup

erieure d’Informatique,

BP 68M, 16309, Oued-Smar, Algiers, Algeria

Laboratoire LEM, Universit

e Lille 3, Lille, France

Keywords:

Kernel Density Estimation, Kernel Discriminant Analysis, Spatial Information, Supervised Classiﬁcation.

Abstract:

Classical data mining models relying upon the assumption that observations are independent, are not suitable

for spatial data, since they fail to capture the spatial autocorrelation. In this paper, we propose a new super-

vised classiﬁcation algorithm which takes into account the spatial dependency of data, named Spatial Kernel

Discriminant Analysis (SKDA). We present a non-parametric classiﬁer based on a kernel estimate of the spa-

tial probability density function which combines two kernels: one controls the observed values while the other

controls the spatial locations of observations. We applied our algorithm for hyperspectral image (HSI) classi-

ﬁcation, a challenging task due to the high dimensionality of data and the limited number of training samples.

Using our algorithm, the spatial and spectral information of each pixel are jointly used to achieve the classi-

ﬁcation. To evaluate the efﬁciency of the proposed method, experiments on real remotely sensed images are

conducted, and show that our method is competitive and achieves higher classiﬁcation accuracy compared to

other contextual classiﬁcation methods.

1 INTRODUCTION

Most statistical and machine learning methods as-

sume that data samples are independent and identi-

cally distributed (i.i.d.). This assumed pre-condition

about the independence of observations is not veriﬁed

when dealing with spatial data (Cheng et al., 2014a)

captured in many ﬁelds such as ecology, image analy-

sis, epidemiology and environmental science. In fact,

spatial data are characterized by spatial autocorrela-

tion or spatial dependency phenomenon. This charac-

teristic is deﬁned as the tendency of near observations

to be more similar than distant observations in space

(Cheng et al., 2014b). This property is formulated as

the ﬁrst law of geography : ”Everything is related to

everything else, but near things are more related than

distant things” (Tobler, 1970). For example, measure-

ments taken in neighboring sites are more likely to

be similar then those of distant locations, natural phe-

nomena vary gradually over space and objects of sim-

ilar characteristics tend to be clustered (ex: popula-

tion with similar socio-economic characteristics and

preferences,...etc) (Shekhar et al., 2009).

Ignoring this property of autocorrelation when an-

alyzing spatial data may lead to inaccurate or incon-

sistent models or hypotheses (Shekhar et al., 2015),

produce biased discriminant rules (Bel et al., 2009),

hide important insight and could even invert patterns

(Stojanova et al., 2013). An effective analysis of spa-

tial data must take into account geographic positions

of observations and the existing relationship due to

their proximity.

Several supervised learning methods modeling

spatial dependency for classiﬁcation and regression

are considered in the literature: Markov Random

Field-based Bayesian classiﬁers, which integrates the

spatial information of data via the a priori term in

Bayes rule ; The logistic spatial autoregression (SAR)

model, which models the spatial dependence directly

in the regression equation using a neighborhood rela-

tionship contiguity matrix and a weight of the spa-

tial dependency; and Geographically Weighted Re-

gression (GWR) which includes a spatial variation pa-

rameter in regression equation (Shekhar et al., 2011).

More recently, (Stojanova et al., 2013) proposed

SCLUS (Spatial Predictive Clustering System), a pre-

dictive clustering tree framework that learn from spa-

tial autocorrelated data .

Various indices are proposed to measure the spa-

tial autocorrelation, from a global or a local point of

184

Boumeddane, S., Hamdad, L., Dabo-Niang, S. and Haddadou, H.

Spatial Kernel Discriminant Analysis: Applied for Hyperspectral Image Classiﬁcation.

DOI: 10.5220/0007372401840191

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 184-191

ISBN: 978-989-758-350-6

view, such as : Moran’s I index, c index of Geary,

Cliff and Ord indices, Getis and Ord (G

et G

∗

) indices

and Local Indicators of Spatial Association (LISA)

(Shekhar et al., 2015).

We focus in this work on supervised classiﬁcation

task. We propose a new classiﬁcation algorithm for

spatially autocorrelated data, that we call SKDA, for

Spatial Kernel Discriminant Analysis. Our algorithm

is a spatial extension of classical Kernel Discriminant

Analysis rule; it is founded on a kernel estimate of

the spatial probability density function that integrates

two kernels: one controls the observed values while

the other controls the spatial locations of observations

(Dabo-Niang et al., 2014).

One potential application of our SKDA algo-

rithm is the classiﬁcation of remotely sensed hy-

perspectral images. This problem has attracted a

lot of attention over the past decade. Several stud-

ies proposed spectral-spatial classiﬁcation algorithms

which integrate spatial context and spectral infor-

mation of the hyperspectral image. This incorpo-

ration of spatial information has shown great im-

pact for improving classiﬁcation accuracy (He et al.,

2017). According to the way the spatial dimension

is incorporated, these methods can be classiﬁed into

three main categories: integrated spectral-spatial ap-

proaches, preprocessing-based approaches, and post-

processing-based approaches (Fauvel et al., 2013). A

survey about the incorporation of spatial information

for HSI classiﬁcation is presented in (Wang et al.,

2016).

The contribution of our work is double; on one

hand, we propose a spatial classiﬁcation algorithm

managing the dependency of data, on the other hand,

a spatial-spectral method is proposed for the classiﬁ-

cation of HSI with competitive results.

The remainder of the paper is organized as fol-

lows: Section 2 deﬁnes the context of this study, and

presents the background knowledge essential to the

understanding of our algorithm. Section 3 presents

our SKDA algorithm. Section 4 shows experimental

results of our method on hyperspectral image classi-

ﬁcation. Finally, section 5 summarizes the results of

this work and draws conclusions.

2 BACKGROUND

In this section, we begin by formally deﬁning the nec-

essary notations that we will adopt throughout this pa-

per. Then, present the background knowledge essen-

tial to the understanding of our algorithm.

In this work, we focus on geostatistical data, we

consider a spatial process {Z

= (X

) ∈ R

× N,i ∈

,d ≥ 1,N ∈ N

∗

}, deﬁned over a probability space

(Ω,F,P) and indexed in a rectangular region I

= {i ∈

: N ∈ N

∗

,1 ≤ i

≤ n

,∀k ∈ {1, ...,N}}. Where a

point i = (i

,...,i

) ∈ Z

is called a site, representing

a geographic position. And let ˆn = n

×n

×...×n

Card(I

) be the sample size, and f(.) the density func-

tion of X ∈ R

. Each site i ∈ I

is characterized by a

d-dimensional observation x

= (x

,...,x

In this work we are interested on supervised clas-

siﬁcation which consists of building a classiﬁer that

from a given training set containing input-output pairs

allows to predict a class Y

∈ {1, 2,..., m} of a new ob-

servation x

2.1 Bayes Classiﬁer

Bayes classiﬁer is one of the widely used classiﬁca-

tion algorithms due to its simplicity, efﬁciency and

efﬁcacy. It is a probabilistic classiﬁer which rely on

Bayes’ theorem and the assumption of independence

between the features, in other words, the classiﬁcation

decision is made basing on probabilities. It consist of

assigning an instance x to the class with the highest a

posteriori probability.

Supposing that we have m classes, associated each

with a probability density function f

where f

P(x/k) and an a priori probability π

that an obser-

vation belongs to the class k, k ∈ {1,2,..., m}. Bayes

discriminant rule is formulated as follows :

Assign x to class k

where k

= arg

max

k∈{1,2,...,m}

(π

(x))

(1)

2.2 Kernel Density Estimation

As we might notice, Bayesian methods require a

background knowledge of many probabilities, which

consists of a practical difﬁculty to apply it. To avoid

these requirements, these probabilities can be esti-

mated based on available labeled data or by mak-

ing assumptions about the distributions (Gramacki,

2018). Two classes of density estimators are recog-

nized in the literature. The ﬁrst, known as paramet-

ric methods are based upon the assumption that data

are drawn form an arbitrary well known distribution

(e.g. Gaussian, Gamma, Cauchy ... etc.) and ﬁnding

the best parameters describing this distribution . Two

commonly used techniques can be sited: Bayesian pa-

rameter estimation and maximum likelihood. How-

ever, this assumption about the form of the under-

lying density is not always possible because of the

complexity of data. In such cases, nonparametric es-

timation techniques are required. These methods do

not make any a priori assumptions about the distri-

Spatial Kernel Discriminant Analysis: Applied for Hyperspectral Image Classiﬁcation

185

bution but estimate the density function directly from

the data (Gramacki, 2018).

One of the most known non-parametric density

estimation techniques is Kernel Density Estimation

(KDE). First contributions concerning kernel estima-

tion of (Parzen, 1962) and (Rosenblatt, 1985) for spa-

tial densities are due to (Tran, 1990). A marginal den-

sity of a point x ∈ R

is deﬁned as :

f (x) =

ˆnh

∑

i∈I



x − X



,x ∈ R

(2)

Where h is a smoothing parameter called band-

width and K is a weight function, called ”kernel”

which decreases as the distance between x and X

in-

creases. This function satisﬁes the following condi-

tion:

+∞

−∞

K(x) dx = 1 (3)

Different kernel functions have been proposed in

the literature: Uniform, Triangle, Epanechnikov ...

etc.

KDE is a relevant tool for analyzing and visualiz-

ing the distribution of spatial process. Moreover, it is

one of the most common methods for hotspots map-

ping, used for crash and crimes data (Chainey et al.,

2008).

2.3 Kernel Discriminant Analysis

Replacing class densities f

in Bayes discriminant rule

(Equation 1) by its kernel density estimate given in

Equation 2 , deﬁne a new classiﬁer known as Ker-

nel Discriminant Rule , the base of Kernel Discrimi-

ant Analysis supervised algorithm. According to Ker-

nel Discriminant Rule, an observation x ∈ R

will be

assigned to the group k

which maximize

(x) .

Where

is an estimator of the a priori probabilities

, given by

ˆn

(4)

and m

is the size of the k-th class.

2.4 Spatial KDE

Kernel density estimator previously presented does

not take into account spatial autocorrelated data. In

fact, to estimate a density at a site, all the data points

are used and no speciﬁc weight is given to neighbor-

ing sites. In (Dabo-Niang et al., 2014), the authors

proposed a kernel density estimation of a spatial den-

sity function, which incorporates spatial dependency

of data. They propose a new version of (Tran, 1990)

estimator (Equation 2) which has the particularity of

taking into account not only the values of the obser-

vations but also the position of sites where the obser-

vations occurred. They established its uniform almost

sure convergence and they studied the consistency of

its mode. They proposed a spatial density estimation

of a discretely indexed spatial process i.e. a random

ﬁeld (X

,i ∈ Z

,N > 1), with values in R

,d ≥ 1 and

deﬁned over a probability space (Ω,F,P).

For each observation x

∈ R

located at a site j ∈

, this spatial density estimator is deﬁned as follows:

f (x

) =

ˆnh

∑

i∈I



− X





ki − jk



(5)

Where

• h

and h

are two bandwidths controling observa-

tions (values) and sites position respectively,

• K

and K

are two kernels respectively deﬁned in

and R, where the ﬁrst manage observation val-

ues while the second deals with spatial locations

of these observations.

• And k i − j k is the euclidean distance between

sites i and j .

In the case where I

is a rectangular grid i.e. N = 2

, Equation 5 become;

f (x

) =

ˆnh

∑

i∈I



− X





ki − jk



(6)

The incorporation of a second kernel K

allows

this estimator to give a weight to sites, which de-

crease as the distance between corresponding sites

increases. Consequently, to estimate f (x

) at a site

j, only the neighboring sites are considered because

they can bring sufﬁcient information about the distri-

bution of X

, which means that the farther a site i is

from j, the lower is the dependence between X

and

. More details about this estimator can be found in

(Dabo-Niang et al., 2014).

3 SPATIAL KERNEL

DISCRIMINANT ANALYSIS

In what follows, we propose a novel supervised spa-

tial classiﬁcation algorithm allowing a classiﬁcation

of an observation at a new site, based not only on the

observation itself but taking in consideration the posi-

tion of sites. In other words, the classiﬁcation is based

on the observations of neighboring sites. The totality

of data is exploited to achieve the classiﬁcation: the

value of the observation, the position of the new site

and training model from the nearby sites.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

186

We present a new kernel discriminant rule for

strongly mixing random ﬁelds, which means that sites

located at a proximity are more dependent than distant

sites. Thus, if a distance between two sites is high,

their values are independent and it is more likely that

they belongs to different classes.

Our classiﬁcation rule consists of assigning a new

observation x ∈ R

at a site i

to the class k

where

= arg

max

k∈{1,2,...,m}

(

(x))

Where

is estimated as follow:

(7)

Suppose that X

,...,X

kmk

are d-dimensional ob-

servations from the k-th class, spatial Kernel Density

estimate is deﬁned as follows (based on (Dabo-Niang

et al., 2014) estimator):

) =

∑

i∈I

C(X

)=k



− X





ki − jk



(8)

Where

• C(.) is the class label of an observation,

• m

is the size of k-th class in the training data

•

N is the size of the training set

The kernel function K

is a multivariate kernel with

values in R

. In this work, we suggest to deﬁne this

kernel as a multiplicative kernel, as follows:

For X = (x

,...,x

) in R

(X) = K(x

) × K(x

) × ... × K(x

) (9)

Where: K is a univariate Kernel. More speciﬁcally:



− X



= K



− X



× ...×



− X



∏

l=1



− X



We summarize in Algorithm 1 the main steps of

our SKDA technique. We precise that, in order to de-

crease the execution time of our algorithm, the term

(.) in Equation 8 is computed only when the term

(.) 6= 0. In addition, for a testing set, step 2 in Al-

gorithm 1, is executed one time.

Algorithm 1: Spatial Kernel Discriminant Analysis

algorithm.

Result:

• Classﬁcation of an observation at a new site

Input :

• X

: an observation to be classiﬁed, situated at a

site i

• A set of training data (X

) ∈ R

× {1,2,.., m},

where y

is the class label of X

Output:

• k

: the class label of X

1 foreach class k ∈ {1,2, ..., m} do

2 Compute a priori probability

(using

Equation 7)

3 Compute

) using Equation 8, based on

learning data of the k-th class

4 end

5 k

= arg

max

k∈{1,2,...,m}

(

(x))

4 EXPERIMENTAL RESULTS

4.1 Hyperspectral Images Classiﬁcation

One potential application of our algorithm on real

data would be the classiﬁcation of remotely sensed

hyperspectral images. A hyperspectral image (HSI)

is a set of simultaneous images collected for the same

area on the surface of the earth with hundreds of spec-

tral bands at different wavelength channels and with

high resolution (He et al., 2017). A HSI is represented

as a hyperspectral cube with spectral and spatial di-

mension (Figure 1). Each pixel is described by its po-

sition and a spectral vector, where its size correspond

to the number of spectral bands collected by the sen-

sor (Fauvel et al., 2013).

Hyperspectral image classiﬁcation consists of as-

signing a unique label to a pixel vector, representing

a thematic class such as forest, urban, water, and agri-

culture. These images are considered as a relevant

tool for many applications, such as ecology, geology,

hydrology, precision agriculture, and military appli-

cations (Ghamisi et al., 2017).

Using our classiﬁcation algorithm in this context

is considered as spectral-spatial classiﬁcation tech-

nique which exploits all information available in an

HSI to achieve better accuracy of classiﬁcation.

Spatial Kernel Discriminant Analysis: Applied for Hyperspectral Image Classiﬁcation

187

Figure 1: Hyperspectral image representation.

4.2 Data Set

In order to evaluate and validate the effectiveness of

our method, we carried out experiments on a widely

used real-world hyperspectral image dataset: the In-

dian Pines benchmark

. The scene represents Pine

forests of Northwestern Indiana in America in 1992.

This data set is a very challenging land-cover classi-

ﬁcation problem, due to the presence of mixed pixels

(Appice et al., 2017) and the non-proportionality be-

tween the size of different classes. In addition, the

crops (mainly corn and soybeans) of this scene are

captured in early stages of growth with less than 5%

coverage, which makes discrimination between these

crops a difﬁcult task.

This scene was captured using NASA’s Airborne

Visible/Infrared Imaging Spectrometer (AVIRIS) sen-

sor, with a size of 145 × 145 pixels, classiﬁed into

16 ground-truth land-cover classes, where each class

contains from 20 to 2468 pixels. The effective size

of this dataset is 10249 pixels after removing the im-

age background (pixels with a label equal to zero).

Each pixel is characterized by 200 spectral bands, af-

ter eliminating 20 noisy channels corresponding to the

water absorption bands. The color composite image

and the corresponding ground truth map are shown in

Figure 2.

Due to the expensive cost of manual labeling of

hyperspectral images pixels, the number of training

samples is often limited, this represent a challeng-

ing task for classiﬁcation algorithms (Ghamisi et al.,

2017). Thus, our SKDA algorithm should be capable

to well-perform even if only a few labelled samples

are available. To build the training set, we randomly

selected only 10% of pixels from each class, and the

remaining pixels forms the test set.

Available on www.ehu.eus/ccwintco/index.php/

Hyperspectral Remote Sensing Scenes

Figure 2: Indian Pines image. (a) Three-band color com-

posite. (b) Reference data. (c) Color code.

Table 1: Class labels and the number of training and testing

samples for Indian pines.

- Class Train Test Total

1 Alfalfa 4 42 46

2 Corn-no till 142 1286 1428

3 Corn-min till 83 747 830

4 Corn 23 214 237

5 Grass-pasture 48 435 483

6 Grass-trees 73 657 730

7 Grass-pasture-

mowed

2 26 28

8 Hay-windrowed 47 431 478

9 Oats 2 18 20

10 Soybean-no till 97 875 972

11 Soybean-min till 245 2210 2455

12 Soybean-clean 59 534 593

13 Wheat 20 185 205

14 Woods 126 1139 1265

15 Build-Grass-

Trees-Drives

38 348 386

16 Stone-Steel-

Towers

9 84 93

Total 1018 9231 10249

Table 1 shows the size of training and testing sets

of each class of Indian Pines scene.

4.3 Performance Comparison

To evaluate the performance of our algorithm com-

pared to other methods, we employ three widely used

classiﬁcation accuracy measures: Overall accuracy

(OA), Average Accuracy (AA) and per class accuracy.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

188

OA is deﬁned as the ratio between the number of well-

classiﬁed pixels to the size of testing set, while AA is

the average of per-class classiﬁcation accuracies.

The results of classiﬁcation depends on the train-

ing and testing sets which are randomly selected. To

reduce this effect and make the comparison fair, we

repeat each experiment 10 times with different train-

ing and testing sets and we report the mean accuracy

of these executions. We use Epanechnikov Kernel

for the two kernels K

and K

with observation band-

width h

equal to 700 and a spatial bandwidth h

of 3.

We obtained these optimal values of h

and h

band-

widths by studying their inﬂuence on overall and av-

erage classiﬁcation accuracies. In fact, we varied em-

pirically the values of these two bandwidth, and select

the combination which gave the highest OA and AA.

In this section, we present the quantitative results

achieved by our SKDA algorithm and the results of

nine different methods reported from (Zhou et al.,

2018). To have a fair comparison we use the same

ratio of training and testing set as this work. Tables 2

shows the classiﬁcation accuracy for each class, over-

all accuracy (OA) and average accuracy (AA), where

the best accuracies are in bold.

Table 2 demonstrates that our proposed SKDA al-

gorithm outperforms other methods, with an improve-

ment of Average Accuracy by 5,58%, the Overall Ac-

curacy by 3,04% and per-class accuracy till 16,11%

(expect for Wheat class) comparing to SSLSTMs ap-

proach.

It can be observed that spectral-spatial approaches

(MDA, CNN, LSTM-based methods and SKDA)

gives signiﬁcantly better accuracies then pixel-wised

methods (PCA, LDA, NWFE, RLDE) which are

based only on observations values.

Figure 3 visualize the classiﬁcation result of In-

dian pines data set using our SKDA algorithm and the

training data used for density estimation.

4.4 Inﬂuence of Parameters

Our classiﬁcation algorithm depends on two band-

widths: h

and h

, that control observation values and

spatial neighborhood respectively. In this section, we

analyze the impact of the integration of the spatial di-

mension of data in the classiﬁcation process through

the study of the inﬂuence of the spatial bandwidth h

on overall and average accuracies. We set the value

of the bandwidth h

to 700, and we vary h

from 1 to

10 and compare the results also with classical version

of Kernel Discriminant Analysis that don’t take into

account the spatial context of data (the estimation of

density is based only on the values of observations i.e

the second kernel K

is not used).

(a) Indian Pines dataset (b) Training set

= 700, h

= 3

Figure 3: Classiﬁcation visualisation.

(a) The effect of hs bandwidth on AA.

(b) The effect of hs bandwidth on OA.

Figure 4: Inﬂuence of spatial bandwidth.

Spatial Kernel Discriminant Analysis: Applied for Hyperspectral Image Classiﬁcation

189

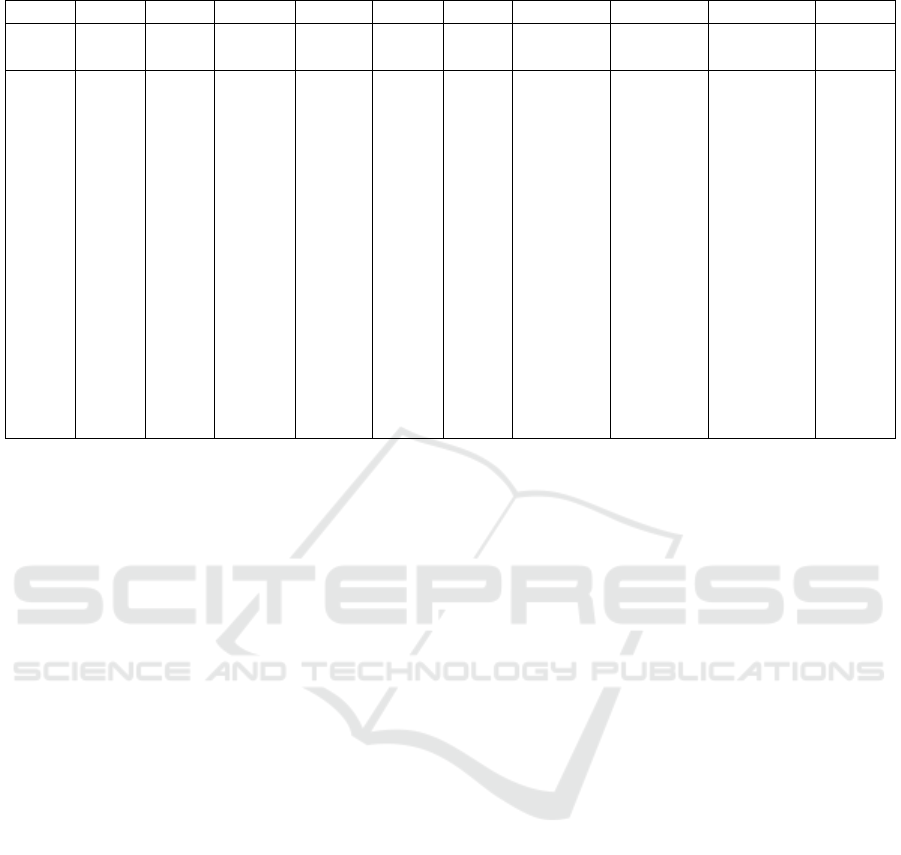
Table 2: Classiﬁcation accurracy (%) for Indian Pines data set.

Label PCA LDA NWFE RLDE MDA CNN SeLSTM SaLSTM SSLSTMs SKDA

OA 72.58 76.67 78.47 80.97 92.31 90.14 72.22 91.72 95.00 98.04

AA 70.19 72.88 76.08 80.94 89.54 85.66 61.72 83.51 91.69 97.27

1 59.57 63.04 62.17 64.78 73.17 71.22 25.85 85.85 88.78 98.57

2 68.75 72.04 76.27 78.39 93.48 90.10 66.60 89.56 93.76 96.88

3 53.95 57.54 59.64 68.10 84.02 91.03 54.83 91.43 92.42 96.59

4 55.19 46.58 59.83 70.80 83.57 85.73 43.94 90.61 86.38 96.77

5 83.85 91.76 88.49 92.17 96.69 83.36 83.45 88.60 89.79 96.78

6 91.23 94.41 96.19 94.90 99.15 91.99 87.76 90.81 97.41 99.75

7 82.86 72.14 82.14 85.71 93.60 85.60 23.20 51.20 84.80 95.38

8 93.97 98.74 99.04 99.12 99.91 97.35 95.40 99.02 99.91 99.97

9 34.00 26.00 44.00 73.00 63.33 54.45 30.00 38.89 74.44 90.55

10 64.18 60.91 69.18 69.73 82.15 75.38 71.29 88.64 95.95 96.73

11 74.96 76.45 77.78 79.38 92.76 94.36 75.08 94.62 96.93 98.74

12 41.72 67.45 64.05 72.28 91.35 78.73 54.49 86.10 89.18 96.10

13 93.46 96.00 97.56 97.56 99.13 95.98 91.85 90.11 98.48 99.02

14 89.45 93.79 93.49 92.36 98.22 96.80 90.37 98.10 98.08 99.92

15 47.77 65.54 58.50 67.10 87.84 96.54 30.49 88.59 92.85 98.33

16 88.17 83.66 89.03 89.68 94.29 81.90 62.86 64.05 87.86 96.30

Figure 4 shows overall and average accuracies as

a function of h

bandwidth. This plot proves that the

integration of the spatial dimension of data improves

drastically the classiﬁcation accuracy, and that the re-

sults obtained by our SKDA algorithm exceeds those

obtained by classical KDA. In fact, the AA increased

from 45% to 70% when spatial dependency is consid-

ered (when h

= 1). Best accuracies were obtained

when h

= 3, with an Average Accuracy of 97,27%

and an Overall Accuracy of 98,04% (as mentioned in

the previous section). However, when greater values

of h

are used, a degradation of OA and AA is cap-

tured.

This experiment proves that the choice of the spa-

tial bandwidth h

is crucial. In fact, small values

of this bandwidth are not sufﬁcient for the learning

model; while, larger values decrease the classiﬁcation

accuracy because they lead to an over-smoothing of

the density.

5 CONCLUSION

In this paper, a Kernel Discriminant Analysis algo-

rithm for spatial data named SKDA is proposed. This

supervised classiﬁcation algorithm allows taking into

consideration the spatial autocorrelation of data, and

exploiting all the available information: the observa-

tions in one hand and their positions in other hand.

Another contribution of this work is the proposition

of a new spatial-spectral hyperspectral image classi-

ﬁcation algorithm. Experimental tests on real word

dataset shows that our SKDA algorithm outperforms

other contextual classiﬁcation algorithms and proves

that the integration of the spatial dimension of data in-

creases the classiﬁcation accuracy, even with limited

number of training samples and high-dimensionality

of data. Experiments on other hyperspectral images

benchmark datasets are ongoing. Moreover, we aim

to propose an efﬁcient way for bandwidths tuning,

since the classiﬁcation accuracy depends on.

REFERENCES

Appice, A., Guccione, P., and Malerba, D. (2017). A novel

spectral-spatial co-training algorithm for the transduc-

tive classiﬁcation of hyperspectral imagery data. Pat-

tern Recognition, 63:229–245.

Bel, L., Allard, D., Laurent, J. M., Cheddadi, R., and Bar-

Hen, A. (2009). CART algorithm for spatial data: Ap-

plication to environmental and ecological data. Com-

putational Statistics & Data Analysis, 53(8):3082–

3093.

Chainey, S., Tompson, L., and Uhlig, S. (2008). The utility

of hotspot mapping for predicting spatial patterns of

crime. Security journal, 21(1-2):4–28.

Cheng, T., Haworth, J., Anbaroglu, B., Tanaksaranond, G.,

and Wang, J. (2014a). Spatiotemporal data mining.

In Handbook of regional science, pages 1173–1193.

Springer.

Cheng, T., Wang, J., Haworth, J., Heydecker, B., and Chow,

A. (2014b). A dynamic spatial weight matrix and lo-

calized space–time autoregressive integrated moving

average for network modeling. Geographical Analy-

sis, 46(1):75–97.

Dabo-Niang, S., Hamdad, L., Ternynck, C., and Yao, A.-

F. (2014). A kernel spatial density estimation allow-

ing for the analysis of spatial clustering. application

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

190

to monsoon asia drought atlas data. Stochastic envi-

ronmental research and risk assessment, 28(8):2075–

2099.

Fauvel, M., Tarabalka, Y., Benediktsson, J. A., Chanussot,

J., and Tilton, J. C. (2013). Advances in spectral-

spatial classiﬁcation of hyperspectral images. Pro-

ceedings of the IEEE, 101(3):652–675.

Ghamisi, P., Plaza, J., Chen, Y., Li, J., and Plaza, A. J.

(2017). Advanced spectral classiﬁers for hyperspec-

tral images: A review. IEEE Geoscience and Remote

Sensing Magazine, 5(1):8–32.

Gramacki, A. (2018). Nonparametric Kernel Density Esti-

mation and Its Computational Aspects. Springer.

He, L., Li, J., Plaza, A., and Li, Y. (2017). Discrimina-

tive low-rank gabor ﬁltering for spectral-spatial hyper-

spectral image classiﬁcation. IEEE Trans. Geoscience

and Remote Sensing, 55(3):1381–1395.

Parzen, E. (1962). On estimation of a probability density

function and mode. The annals of mathematical statis-

tics, 33(3):1065–1076.

Rosenblatt, M. (1985). Stationary sequences and random

ﬁelds.

Shekhar, S., Evans, M. R., Kang, J. M., and Mohan, P.

(2011). Identifying patterns in spatial information: A

survey of methods. Wiley Interdisc. Rew.: Data Min-

ing and Knowledge Discovery, 1(3):193–214.

Shekhar, S., Jiang, Z., Ali, R. Y., Eftelioglu, E., Tang, X.,

Gunturi, V. M. V., and Zhou, X. (2015). Spatiotempo-

ral data mining: A computational perspective. ISPRS

Int. J. Geo-Information, 4(4):2306–2338.

Shekhar, S., Kang, J., and Gandhi, V. (2009). Spatial data

mining. In Encyclopedia of Database Systems, pages

2695–2698. Springer.

Stojanova, D., Ceci, M., Appice, A., Malerba, D., and Dze-

roski, S. (2013). Dealing with spatial autocorrelation

when learning predictive clustering trees. Ecological

Informatics, 13:22–39.

Tobler, W. R. (1970). A computer movie simulating urban

growth in the detroit region. Economic geography,

46(sup1):234–240.

Tran, L. T. (1990). Kernel density estimation on random

ﬁelds. Journal of Multivariate Analysis, 34(1):37–53.

Wang, L., Shi, C., Diao, C., Ji, W., and Yin, D. (2016).

A survey of methods incorporating spatial informa-

tion in image classiﬁcation and spectral unmixing. In-

ternational Journal of Remote Sensing, 37(16):3870–

3910.

Zhou, F., Hang, R., Liu, Q., and Yuan, X. (2018). Hy-

perspectral image classiﬁcation using spectral-spatial

lstms. Neurocomputing.

Spatial Kernel Discriminant Analysis: Applied for Hyperspectral Image Classiﬁcation

191