Conﬂict Handling Framework in Generalized Multi-agent Path Finding:

Advantages and Shortcomings of Satisﬁability Modulo Approach

Pavel Surynek

Faculty of Information Technology, Czech Technical University in Prague,

Thakurova 9, 160 00 Praha 6, Czech Republic

Keywords:

Conﬂicts, MAPF, Token Swapping, Token Rotation, Token Permutation, SMT, SAT.

Abstract:

We address conﬂict reasoning in generalizations of multi-agent path ﬁnding (MAPF). We assume items placed

in vertices of an undirected graph with at most one item per vertex. Items can be relocated across edges

while various constraints depending on the concrete type of MAPF must be satisﬁed. We recall a general

problem formulation that encompasses known types of item relocation problems such as multi-agent path

ﬁnding (MAPF) and token swapping (TSWAP). We show how to express new types of relocation problems

in the general problem formulation. We thoroughly evaluate a novel solving method for item relocation that

combines satisﬁability modulo theory (SMT) with conﬂict-based search (CBS). CBS is interpreted in the SMT

framework where we start with the basic model and reﬁne the model with a collision resolution constraint

whenever a collision between items occurs. The key difference between the standard CBS and the SMT-based

modiﬁcation of CBS (SMT-CBS) is that the standard CBS branches the search to resolve the collision while

SMT-CBS iteratively adds a single disjunctive collision resolution constraint. Our experimental evaluation

revealed that although SMT-CBS performs better than CBS in small densely occupied instances of variants

of MAPF, it is outperformed on large sparsely occupied environments. The performed analysis shows that

individual paths in large environments of relocation instances can be found faster using simple A*-based

algorithm than by the SMT solver. On the other hand the SMT solver performs better when many conﬂicts

between items need to be resolved.

1 INTRODUCTION

Item relocation problems in graphs such as token

swapping (TSWAP) (Kawahara et al., 2017; Bon-

net et al., 2017), multi-agent path ﬁnding (MAPF)

(Ryan, 2007; Standley, 2010; Yu and LaValle, 2013),

or pebble motion on graphs (PMG) (Wilson, 1974;

Kornhauser et al., 1984) represent important combi-

natorial problems in artiﬁcial intelligence with spe-

ciﬁc applications in coordination of multiple robots

and other areas such as quantum circuit compila-

tion (Botea et al., 2018). We assume multiple dis-

tinguishable items placed in vertices of an undi-

rected graph such that at most one item is placed

in each vertex. Items can be moved between ver-

tices across edges while problem speciﬁc rules must

be observed. For example, PMG and MAPF usu-

ally assume that items (pebbles/agents) are moved

to unoccupied neighbors only. Sometimes in MAPF

it is also possible that items form a train (sequence

of items) and the entire train moves simultaneously

while only the leading item needs to enter a vacant

vertex

. TSWAP on the other hand permits only

swaps of pairs of tokens along edges while more com-

plex movements involving more than two tokens are

forbidden. The task in item relocation problems is to

reach a given goal conﬁguration of items from a given

starting conﬁguration using allowed movements.

We focus here on the optimal solving of item re-

location problems with respect to common cumula-

tive objective functions. Two cumulative objective

functions are used in MAPF and TSWAP - sum-of-

costs (Sharon et al., 2013; Miltzow et al., 2016) and

makespan (Surynek, 2014a; Yu and LaValle, 2016).

The sum-of-costs corresponds to the total cost of all

movements performed until the goal conﬁguration is

reached - the traversal of an edge by an item has unit

cost. The makespan calculates the total number of

time-steps until the goal is reached. In both cases we

trying to minimize the objective which in the case of

sum-of-costs intuitively corresponds to energy mini-

This variant of MAPF is sometimes called a parallel

MAPF or parallel PMG (Surynek, 2010).

192

Surynek, P.

Conﬂict Handling Framework in Generalized Multi-agent Path ﬁnding: Advantages and Shortcomings of Satisﬁability Modulo Approach.

DOI: 10.5220/0007374201920203

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 192-203

ISBN: 978-989-758-350-6

mization while the minimization of makespan corre-

sponds to minimization of time.

Many practical problems from robotics involving

multiple robots can be interpreted as an item reloca-

tion problems. Examples include discrete multi-robot

navigation and coordination (Luna and Bekris, 2010),

item rearrangement in automated warehouses (Basile

et al., 2012), ship collision avoidance (Kim et al.,

2014), or formation maintenance and maneuvering of

aerial vehicles (Zhou and Schwager, 2015). Examples

not only include problems concerning physical items

but problems occurring in virtual spaces of simula-

tions (Kapadia et al., 2013), computer games (Wender

and Watson, 2014), or quantum systems (Botea et al.,

2018).

The contribution of this paper consists in a thor-

ough experimental evaluation of a general frame-

work for deﬁning and solving item relocation prob-

lems based on satisﬁability modulo theories (SMT)

(Boﬁll et al., 2012; Surynek, 2018b) and conﬂict-

based search (CBS) (Sharon et al., 2015).

The framework has been used to deﬁne two prob-

lems derived from TSWAP: token rotation (TROT)

and token permutation (TPERM) where instead of

swapping pairs of tokens, rotations along non-trivial

cycles and arbitrary permutations of tokens respec-

tively are permitted. We show how to deal with all

MAPF related item relocation problems through con-

ﬂict reasoning in two algorithms suitable for this task

- SMT-CBS and CBS algorithms. Tests on various

benchmarks revealed that there is no universal win-

ner in solving item relocation problems among the

tested algorithms. While SMT-CBS turned out to be

better in small densely-populated instances, CBS ex-

hibited better performance in large environments con-

taining few items. These results are in line with pre-

vious results for the SAT-based MAPF solving where

SAT-based solvers usually perform well on small in-

stances and worse on larger ones (Surynek et al.,

2016a; Surynek et al., 2016b).

The organization of the paper is as follows. We

ﬁrst introduce TSWAP and MAPF problems formally.

Then prerequisites for conﬂict handling in item relo-

cation problems formulated in the SMT framework

are recalled, that is, we recall the CBS algorithm

and the MDD-SAT algorithm. On top of this, the

combination of CBS and MDD-SAT is developed -

the SMT-CBS algorithm. Finally, a thorough experi-

mental evaluation of CBS and SMT-CBS on various

benchmarks including both small and large instances

is presented.

2 BACKGROUND

We brieﬂy recall multi-agent path ﬁnding and token

swapping in this section.

Multi-agent path ﬁnding (MAPF) problem (Silver,

2005; Ryan, 2008) consists of an undirected graph

G = (V, E) and a set of agents A = {a

, a

, ..., a

} such

that |A| < |V |. Each agent is placed in a vertex so that

at most one agent resides in each vertex. The place-

ment of agents is denoted α : A → V . Next we are

given nitial conﬁguration of agents α

and goal con-

ﬁguration α

At each time step an agent can either move to an

adjacent location or wait in its current location. The

task is to ﬁnd a sequence of move/wait actions for

each agent a

, moving it from α

) to α

) such

that agents do not conﬂict, i.e., do not occupy the

same location at the same time. Typically, an agent

can move into adjacent unoccupied vertex provided

no other agent enters the same target vertex but other

rules for movements are used as well. An example of

MAPF instance is shown in Figure 1.

= α

A C C C D

B B A

D D D B B

Figure 1: A MAPF instance with three agents a

, a

, and

The following deﬁnition formalizes the com-

monly used move-to-unoccupied movement rule in

MAPF.

Deﬁnition 1. Movement in MAPF. Conﬁguration α

results from α if and only if the following conditions

hold: (i) α(a) = α

(a) or {α(a), α

(a)} ∈ E for all

a ∈ A (agents wait or move along edges); (ii) for all

a ∈ A it holds that if α(a) 6= α

(a) ⇒ α

(a) 6= α(a

)

for all a

∈ A (target vertex must be empty); and (iii)

for all a, a

∈ A it holds that if a 6= a

⇒ α

(a) 6= α

)

(no two agents enter the same target vertex).

Solving the MAPF instance is to search for a

sequence of conﬁgurations [α

, α

, ..., α

] such that

i+1

results using valid movements from α

for i =

1, 2, ..., µ −1, and α

= α

In many aspects, a token swapping problem

(TSWAP) (also known as sorting on graphs) (Ya-

manaka et al., 2014) is similar to MAPF. It represents

a generalization of sorting problems (Thorup, 2002).

While in the classical sorting problem we need to ob-

tain linearly ordered sequence of elements by swap-

ping any pair of elements, in the TSWAP problem we

Conﬂict Handling Framework in Generalized Multi-agent Path ﬁnding: Advantages and Shortcomings of Satisﬁability Modulo Approach

193

= τ

Figure 2: A TSWAP instance. A solution consisting of two

swaps is shown.

are allowed to swap elements at selected pairs of po-

sitions only.

Using a modiﬁed notation from (Yamanaka et al.,

2015) the TSWAP each vertex in G is assigned a color

in C = {c

, c

, ..., c

} via τ

: V → C. A token of a

color in C is placed in each vertex. The task is to

transform a current token placement into the one such

that colors of tokens and respective vertices of their

placement agree. Desirable token placement can be

obtained by swapping tokens on adjacent vertices in

G. See Figure 2 for an example instance of TSWAP.

We denote by τ : V → C colors of tokens placed

in vertices of G. That is, τ(v) for v ∈ V is a color of

a token placed in v. Starting placement of tokens is

denoted as τ

; the goal token placement corresponds

to τ

. Transformation of one placement to another is

captured by the concept of adjacency deﬁned as fol-

lows (Yamanaka et al., 2015; Yamanaka et al., 2017):

Deﬁnition 2. Adjacency in TSWAP. Token place-

ments τ and τ

are said to be adjacent if there ex-

ists a subset of non-adjacent edges F ⊆ E such that

τ(v) = τ

(u) and τ(u) = τ

(v) for each {u, v} ∈ F and

for all other vertices w ∈ V \

{u,v}∈F

{u, v} it holds

that τ(w) = τ

(w).

The task in TSWAP is to ﬁnd a swapping sequence

of token placements [τ

, τ

, ..., τ

] such that τ

= τ

and τ

i+1

are adjacent for all i = 0, 1, ..., m−1. It

has been shown that for any initial and goal placement

of tokens τ

and τ

respectively there is a swapping

sequence transforming τ

and τ

containing O(|V |

)

swaps (Yamanaka et al., 2016). The proof is based on

swapping tokens on a spanning tree of G. Let us note

that the above bound is tight as there are instances

consuming Ω(|V |

) swaps. It is also known that ﬁnd-

ing a swapping sequence that has as few swaps as pos-

sible is an NP-hard problem.

If each token has a different color we do not dis-

tinguish between tokens and their colors c

; that is, we

will refer to a token c

Observe, that the operational meaning of agents

and tokens in MAPF and TSWAP is similar. They

The presented version of adjacency is sometimes called

parallel while a term adjacency is reserved for the case with

|F| = 1.

both occupy vertices of the graph and no two of them

can share a vertex. Hence works studying relation of

both problems from the practical solving perspective

have appeared recently (Surynek, 2018a).

3 RELATED WORK

Although many works sudying TSWAP from the

theoretical point of view exist (Yamanaka et al.,

2016; Miltzow et al., 2016; Bonnet et al., 2017)

practical solving of the problem started only lately.

In (Surynek, 2018a) optimal solving of TSWAP

by adapted algorithms from MAPF has been sug-

gested. Namely conﬂict-based search (CBS) (Sharon

et al., 2012; Sharon et al., 2015) and propositional

satisﬁability-based (SAT) (Biere et al., 2009) MDD-

SAT (Surynek et al., 2016a; Surynek et al., 2016b)

originally developed for MAPF have been modiﬁed

for TSWAP.

3.1 Search for Optimal Solutions

We will commonly use the sum-of-costs objective

funtion in all problems studied in this paper. The fol-

lowing deﬁnition introduces the sum-of-costs objec-

tive in MAPF. However, analogous deﬁnition can be

introduced for TSWAP too.

Deﬁnition 3. Sum-of-costs (denoted ξ) is the sum-

mation, over all agents, of the number of time steps

required to reach the goal vertex (Dresner and Stone,

2008; Standley, 2010; Sharon et al., 2013; Sharon

et al., 2015). Formally, ξ =

∑

i=1

ξ(path(a

)), where

ξ(path(a

)) is an individual path cost of agent a

connecting α

) calculated as the number of edge

traversals and wait actions.

Observe that in the sum-of-costs we accumulate

the cost of wait actions for items not yet reaching

their goal vertices. Also observe that one swap in the

TSWAP problem correspond to the cost of 2 as two

tokens traverses single edge. Let us note that all algo-

rithms and concepts we use can be modiﬁed for dif-

ferent cummulative objective functions like makespan

or the total number of moves/swaps etc.

A feasible solution of a solvable MAPF instance

can be found in polynomial time (Wilson, 1974; Ko-

rnhauser et al., 1984); precisely the worst case time

complexity of most practical algorithms for ﬁnding

feasible solutions is O(|V |

) (asymptotic size of the

solution is also O(|V |

)) (Surynek, 2009b; Surynek,

The notation path(a

) refers to path in the form of a se-

qeunce of vertices and edges connecting α

) and α

)

while ξ assigns the cost to a given path.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

194

2009a; Surynek, 2014b; Luna and Bekris, 2011a;

Luna and Bekris, 2011b; de Wilde et al., 2014).

This is also asymptotically best possible as there are

MAPF instances requiring Ω(|V |

) moves. As with

TSWAP, ﬁnding optimal MAPF solutions with re-

spect to various cummulative objectives is NP-hard

(Ratner and Warmuth, 1986; Surynek, 2010; Yu and

LaValle, 2015).

3.2 Conﬂict-based Search

CBS uses the idea of resolving conﬂicts lazily; that is,

a solution of MAPF instance is not searched against

the complete set of movement constraints that for-

bids collisions between agents but with respect to ini-

tially empty set of collision forbidding constraints that

gradually grows as new conﬂicts appear. The advan-

tage of CBS is that it can ﬁnd a valid solution before

all constraints are added.

The high level of CBS searches a constraint tree

(CT) using a priority queue in breadth ﬁrst manner.

CT is a binary tree where each node N contains a set

of collision avoidance constraints N.constraints - a

set of triples (a

, v, t) forbidding occurrence of agent

in vertex v at time step t, a solution N. paths - a set

of k paths for individual agents, and the total cost N.ξ

of the current solution.

The low level process in CBS associated with

node N searches paths for individual agents with re-

spect to set of constraints N.constraints. For a given

agent a

, this is a standard single source shortest path

search from α

) to α

) that avoids a set of

vertices {v ∈ V |(a

, v, t) ∈ N.constraints} whenever

working at time step t. For details see (Sharon et al.,

2015).

CBS stores nodes of CT into priority queue OPEN

sorted according to ascending costs of solutions. At

each step CBS takes node N with lowest cost from

OPEN and checks if N. paths represents paths that

are valid with respect to movements rules in MAPF.

That is, if there are any collisions between agents

in N.paths. If there is no collision, the algorithms

returns valid MAPF solution N.paths. Otherwise

the search branches by creating a new pair of nodes

in CT - successors of N. Assume that a collision

occurred between agents a

and a

in vertex v at time

step t. This collision can be avoided if either agent a

or agent a

does not reside in v at timestep t. These

two options correspond to new successor nodes of N

- N

and N

that inherits set of conﬂicts from N as

follows: N

.con f licts = N.con f licts ∪ {(a

, v, t)} and

.con f licts = N.con f licts ∪ {(a

, v, t)}. N

.paths

and N

.paths inherit path from N.paths except those

for agent a

and a

respectively. Paths for a

and a

Algorithm 1: Basic CBS algorithm for MAPF solv-

ing.

1 CBS (G = (V, E), A, α

, α

)

2 R.constraints ←

3 R.paths ← {shortest path from α

) to

)|i = 1, 2, ..., k}

4 R.ξ ←

∑

i=1

ξ(N.paths(a

))

5 insert R into OPEN

6 while OPEN 6=

0 do

7 N ← min(OPEN)

8 remove-Min(OPEN)

9 collisions ← validate(N.paths)

10 if collisions =

0 then

11 return N.paths

12 let (a

, a

, v, t) ∈ collisions

13 for each a ∈ {a

, a

} do

14 N

.constraints ←

N.constraints ∪ {(a, v,t)}

15 N

.paths ← N.paths

16 update(a, N

.paths, N

.con f licts)

17 N

.ξ ←

∑

i=1

ξ(N

.paths(a

))

18 insert N

into OPEN

are recalculated with respect to extended sets of con-

ﬂicts N

.con f licts and N

.con f licts respectively and

new costs for both agents N

.ξ and N

.ξ are deter-

mined. After this N

and N

are inserted into the pri-

ority queue OPEN.

The pseudo-code of CBS is listed as Algorithm

1. One of crucial steps occurs at line 16 where a

new path for colliding agents a

and a

is constructed

with respect to an extended set of conﬂicts. Notation

N.paths(a) refers to the path of agent a.

The CBS algorithm ensures ﬁnding sum-of-costs

optimal solution. Detailed proofs of this claim can be

found in (Sharon et al., 2015).

3.3 SAT-based Approach

An alternative approach to optimal MAPF solving

as well as to TSWAP solving is represented by re-

duction of MAPF to propositional satisﬁability (SAT)

(Surynek, 2012b; Surynek, 2012a). The idea is to

construct a propositional formula such F (ξ) such

that it is satisﬁable if and only if a solution of a

given MAPF of sum-of-costs ξ exists. Moreover, the

approach is constructive; that is, F (ξ) exactly re-

ﬂects the MAPF instance and if satisﬁable, solution

of MAPF can be reconstructed from satisfying assign-

ment of the formula.

Being able to construct such formula F one can

obtain optimal MAPF solution by checking satisﬁa-

bility of F (0), F (1), F (2),... until the ﬁrst satisﬁable

F (ξ) is met. This is possible due to monotonicity of

MAPF solvability with respect to increasing values of

Conﬂict Handling Framework in Generalized Multi-agent Path ﬁnding: Advantages and Shortcomings of Satisﬁability Modulo Approach

195

Algorithm 2: Framework of SAT-based MAPF solv-

ing.

1 SAT-Based (G = (V, E), A, α

, α

)

2 paths ← {shortest path from α

) to

)|i = 1, 2, ..., k}

3 ξ ←

∑

i=1

ξ(N.paths(a

))

4 while True do

5 F (ξ) ← encode(ξ, G, A, α

, α

)

6 assignment ← consult-SAT-Solver(F (ξ))

7 if assignment 6= UNSAT then

8 paths ← extract-Solution(assignment)

9 return paths

10 ξ ← ξ + 1

common cummulative objectives such as the sum-of-

costs. In practice it is however impractical to start at

0; lower bound estimation is used instead - sum of

lengths of shortest paths can be used in the case of

sum-of-costs. The framework of SAT-based solving

is shown in pseudo-code in Algorithm 2.

The advantage of the SAT-based approach is that

state-of-the-art SAT solvers can be used for deter-

minig satisﬁability of F (ξ) (Audemard et al., 2013)

and any progress in SAT solving hence can be utilized

for increasing efﬁciency of MAPF solving.

3.4 Multi-value Decision Diagrams -

MDD-SAT

Construction of F (ξ) relies on time expansion of un-

derlying graph G (Surynek, 2017). Having ξ, the ba-

sic variant of time expansion determines the maxi-

mum number of time steps µ (also refered to as a

makespan) such that every possible solution of the

given MAPF with the sum-of-costs less than or equal

to ξ ﬁts within µ timestep (that is, no agent is outside

its goal vertex after µ timestep if the sum-of-costs ξ is

not to be exceeded).

Time expansion itself makes copies of vertices V

for each timestep t = 0, 1, 2, ..., µ. That is, we have

vertices v

for each v ∈ V time step t. Edges from

G are converted to directed edges interconnecting

timesteps in time expansion. Directed edges (u

, v

t+1

)

are introduced for t = 1, 2, ..., µ − 1 whenever there is

{u, v} ∈ E. Wait actions are modeled by introducing

edges (u

t+1

). A directed path in time expansion

corresponds to trajectory of an agent in time. Hence

the modeling task now consists in construction of a

formula in which satisfying assignments correspond

to directed paths from α

) to α

) in time ex-

pansion.

Assume that we have time expansion T EG

, E

) for agent a

. Propositional variable X

) is

introduced for every vertex v

in V

. The semantics of

) is that it is True if and only if agent a

resides

in v at time step t. Similarly we introduce E

, v

)

for every directed edge (u

, v

t+1

) in E

. Analogously

the meaning of E

u,v

) is that is True if and only if

agent a

traverses edge {u, v} between time steps t and

t + 1.

Finally constraints are added so that truth assign-

ment are restricted to those that correspond to valid

solutions of a given MAPF. The detailed list of con-

straints is given in (Surynek et al., 2016a). We here

just illustrate the modeling by showing few represen-

tative constraints. For example there is a constraint

stating that if agent a

appears in vertex u at time

step t then it has to leave through exactly one edge

, v

t+1

). This can be established by following con-

straints:

) ⇒

t+1

)∈E

u,v

), (1)

∑

t+1

|(u

t+1

)∈E

u,v

) ≤ 1 (2)

Similarly, the target vertex of any movement ex-

cept wait action must be empty. This is ensured by

the following constraint for every (u

, v

t+1

) ∈ E

u,v

) ⇒

∈A∧a

6=a

∧v

∈V

¬X

) (3)

Other constraints ensure that truth assignments to

variables per individual agents form paths. That is if

agent a

enters an edge it must leave the edge at the

next time step.

u,v

) ⇒ X

) ∧ X

t+1

) (4)

Agents do not collide with each other; the fol-

lowing constraint is introduced for every v ∈ V and

timestep t:

∑

i=1,2,...,k|v

∈V

) (5)

A common measure how to reduce the number of

decision variables derived from the time expansion

is the use of multi-value decision diagrams (MDDs)

(Sharon et al., 2013). The basic observation that

holds for MAPF and other item relocation problems

is that a token/agent can reach vertices in the dis-

tance d (distance of a vertex is measured as the length

of the shortest path) from the current position of the

agent/token no earlier than in the d-th time step. Ana-

logical observation can be made with respect to the

distance from the goal position.

Above observations can be utilized when making

the time expansion of G. For a given agent or token,

we do not need to consider all vertices at time step t

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

196

but only those that are reachable in t timesteps from

the initial position and that ensure that the goal can be

reached in the remaining σ − t timesteps. This idea

can reduce the size the expansion graph signiﬁcantly

and consequently can reduce the size of the Boolean

formula by eliminating X (a)

and E (a)

u,v

variables

correspoding to unreachable vertices u and v.

A comparison of standard time expansion and

MDD expansion in MAPF for agent (a

) is shown in

Figure 3.

Timestep 0 1 2 3

G=(V,E)

Time expansion graph for a

(TEG

), µ = 3

MDD for a

(MDD

), µ = 3, ξ = 3

0 1 2 3

Figure 3: An example of time expansion and MDD expan-

sion for agent a

The combination of SAT-based approach and

MDD time expansion led to the MDD-SAT algorithm

described in (Surynek et al., 2016a) that currently rep-

resent state-of-the-art in SAT-based MAPF solving.

4 GENERALIZATIONS OF ITEM

RELOCATION

Although the differences between MAPF and TSWAP

led to different worst case time complexities in algo-

rithms for ﬁnding feasible solutions, problems differ

only in local understanding of conﬂicts reﬂected in

different movement rules in fact. This immediately

inspired us to suggest various modiﬁcations of move-

ment rules.

We deﬁne two problems derived from MAPF and

TSWAP: token rotation (TROT) and token permuta-

tion (TPERM)

4.1 Token Rotation and Token

Permutation

A swap of pair of tokens can be interpreted as a ro-

tation along a trivial cycle consisting of single edge.

We can generalize this towards longer cycles. The

TROT problem permits rotations along longer cy-

cles but forbids trivial cycles; that is, rotations along

These problems have been considered in the literature

in different contexts already (for example in (Yu and Rus,

2014)). But not from the practical solving perspective fo-

cused on ﬁnding optimal solutions.

triples, quadruples, ... of vertices is allowed but swap

along edges are forbidden.

Deﬁnition 4. Adjacency in TROT. Token place-

ments τ and τ

are said to be adjacent in TROT if there

exists a subset of edges F ⊆ E such that components

, ...,C

of induced sub-graph G[F] satisfy fol-

lowing conditions:

(i) C

= (V

, E

) such that V

= w

, w

, ..., w

with

≤ 3 and

= {{w

, w

};{w

, w

};...;{w

, w

}}

(components are cycles of length at least 3)

(ii) τ(w

) = τ

), τ(w

) = τ

), ..., τ(w

) =

)

(colors are rotated in the cycle one position for-

ward/backward)

The rest of the deﬁnition of a TROT instance is

analogical to TSWAP.

Similarly we can deﬁne TPERM by permitting all

lengths of cycles. The formal deﬁnition of adjacency

in TPERM is almost the same as in TROT except re-

laxing the constraint on cycle lenght, n

≤ 2.as

We omit here complexity considerations for

TROT and TPERM for the sake of brevity. Again it

holds that a feasible solution can be found in polyno-

mial time but the optimal cases remain intractable in

general.

Both approaches - SAT-based MDD-SAT as well

as CBS - can be adapted for solving TROT and

TPERM without modifying their top level design.

Only local modiﬁcation of how movement rules of

each problem are reﬂected in algorithms is necessary.

In case of CBS, we need to deﬁne what does it mean

a conﬂict in TROT and TPERM. In MDD-SAT differ-

ent movement constraints can be encoded directly.

Motivation for studying these item relocation

problems is the same as for MAPF. In many real-life

scenarios it happens that items or agents enters po-

sitions being simultaneously vacated by other items

(for example mobile robots often ). This is exactly

the property captured formally in above deﬁnitions.

4.2 Adapting CBS and MDD-SAT

Both CBS and MDD-SAT can be modiﬁed for opti-

mal solving of TSWAP, TROT, and TPERM (with re-

spect to sum-of-costs but other cumulative objectives

are possible as well). Different movement rules can

be reﬂected in CBS and MDD-SAT algorithms with-

out modifying their high level framework.

Conﬂict Handling Framework in Generalized Multi-agent Path ﬁnding: Advantages and Shortcomings of Satisﬁability Modulo Approach

197

4.2.1 Different Conﬂicts in CBS

In CBS, we need to modify the understanding of con-

ﬂict between agents/tokens. In contrast to the original

CBS we need to introduce edge conﬂicts to be able to

handle conﬂicts properly in TSWAP and TROT.

Consider an example from Figure 4 that concerns

TSWAP being solved by CBS. The situation when to-

ken c

traverses from A to B and simultaneously to-

ken c

traverses from B to C cannot occur in TSWAP.

However we cannot properly branch in CBS using

vertex conﬂicts to tackle this situation. Although all

movements of c

from B into any other vertex than

A can be ruled out by vertex conﬂicts, wrong move-

ment of c

into A from a vertex other than B remains

allowed.

t → t+1

,B,t+1) or (c

,C,t+1)

t → t+1

Figure 4: A collision that leads to wrong reasoning with

vertex conﬂicts in TSWAP. Vertex conﬂict (c

,C, t) does

not properly forbid simultaneous movements from A to B

and from B to C. At some later stage in the sub-tree after

,C, t) it would be still possible that although c

cannot

move into any other vertex than A at t it can move into A

from other vertex than B which is not desirable.

Therefore edge conﬂicts have been introduced to

tackle conﬂicting situations in TSWAP and TROT

properly within CBS and SMT-CBS. An edge con-

ﬂict is triple (c

, (u, v),t) with c

∈ C, u, v ∈ V and

timestep t. The interpretation of (c

, (u, v),t) is that

token c

cannot move across {u, v} from u to v be-

tween timesteps t and t + 1.

Edge conﬂict can be used to resolve collision from

4. Instead of forbidding c

to enter any vertex other

than A at timestep t movements of c

across all edges

other than (B, A) at timestep t are forbidden. Analog-

ical collision resolution using edge conﬂicts can be

applied in the TROT problem.

Conﬂict reasoning in individual item relocation

problems derived from MAPF is described in the fol-

lowing paragraphs. Proofs of soundness of conﬂict

reasoning are omitted here.

TPERM: The easiest case is TPERM as it is least re-

strictive. We merely forbid simultaneous occurrence

of multiple tokens in a vertex - this situation is un-

derstood as a collision in TPERM and conﬂicts are

derived from it. If a collision (c

, c

, v, t) between to-

kens c

and c

occurs in v at time step t then we in-

troduce conﬂicts (c

, v, t) and (c

, v, t) for c

and c

re-

spectively.

TSWAP: This problem takes conﬂicts from TPERM

but adds new conﬂicts that arise from doing some-

thing else than swapping (Surynek, 2018a). Each time

edge {u,v} is being traversed by token c

between

time steps t and t +1, a token residing in v at time step

t, that is τ

(v), must go in the opposite direction from

v to u. If this is not the case, then a so called edge col-

lision involving edge {u, v} occurs and corresponding

edge conﬂicts (c

, (u, v),t) and (τ

(v), (v, u), t) are in-

troduced for agents c

and τ

(v) respectively.

Edge conﬂicts must be treated at the low level of

CBS. Hence in addition to forbidden vertices at given

time-steps we have forbidden edges between given

time-steps.

TROT: The treatment of conﬂicts will be comple-

mentary to TSWAP in TROT. Each time edge {u, v}

is being traversed by token c

between time steps t

and t + 1, a token residing in v at time step t, that

is τ

(v), must go anywhere else but not to u. If this

is not the case, then we again have edge collision

, τ

(v),{u,v},t) which is treated in the same way

as above.

4.2.2 Encoding Changes in MDD-SAT

In MDD-SAT, we need to modify encoding of move-

ment rules in the propositional formula F (ξ). Again,

proofs of soundness of the following changes are

omitted.

TPERM: This is the easiest case for MDD-SAT too.

We merely remove all constrains requiring tokens to

move into vacant vertices only. That is we remove

clauses (3).

TSWAP: It inherits changes from TPERM but in ad-

dition to that we need to carry out swaps properly. For

this edge variables E

u,v

) will be utilized. Following

constraint will be introduced for every {u

, v

t+1

} ∈ E

(intuitively, if token c

traverses {u, v} some other to-

ken c

traverses {u, v} in the opposite direction):

u,v

) ⇒

j=1,2,...,k| j6=i∧(u

t+1

)∈E

v,u

) (6)

TROT: TROT is treated in a complementary way to

TSWAP. Instead of adding constraints (6) we add con-

straints forbidding simultaneous traversal in the oppo-

site direction as follows:

Formally this is the same as in MAPF, but in addition to

this MAPF checks vacancy of the target vertex which may

cause more colliding situations.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

198

u,v

) ⇒

j=1,2,...,k| j6=i∧(u

t+1

)∈E

¬E

v,u

) (7)

5 COMBINING SAT-BASED

APPROACH AND CBS

Close look at CBS reveals that it operates similarly

as problem solving in satisﬁability modulo theories

(SMT) (Boﬁll et al., 2012). SMT divides satisﬁabil-

ity problem in some complex theory T into an ab-

stract propositional part that keeps the Boolean struc-

ture of the problem and simpliﬁed decision procedure

DECIDE

that decides conjunctive formulae over T .

A general T -formula is transformed to propositional

skeleton by replacing atoms with propositional vari-

ables. The standard SAT-solving procedure then de-

cides what variables should be assigned T RUE in or-

der to satisfy the skeleton - these variables tells what

atoms holds in T . DECIDE

if the conjunction of

satisﬁed atoms is satisﬁable. If so then solution is

returned. Otherwise conﬂict from DECIDE

is re-

ported back and the skeleton is extended with a con-

straint forbidding the conﬂict.

The above observation let us to the idea to imple-

ment CBS in the SMT manner. The abstract propo-

sitional part working with the skeleton will be taken

from MDD-SAT except that only constraints ensur-

ing that assignments form valid paths interconnect-

ing starting positions with goals will be preserved.

Other constraints for collision avoidance will be omit-

ted initially. Paths validation procedure will act as

DECIDE

and will report back a set of conﬂicts

found in the current solution. We call this algorithm

SMT-CBS and it is shown in pseudo-code as Algo-

rithm 3 (it is formulated for MAPF; but is applicable

for TSWAP, TPERM, and TROT after replacing con-

ﬂict resolution part).

The algorithm is divided into two procedures:

SMT-CBS representing the main loop and SMT-CBS-

Fixed solving the input MAPF for a ﬁxed cost ξ. The

major difference from the standard CBS is that there

is no branching at the high level. The high level SMT-

CBS rougly correspond to the main loop of MDD-

SAT. The set of conﬂicts is iteratively collected during

entire execution of the algorithm. Procedure encode

from MDD-SAT is replaced with encode-Basic that

produces encoding that ignores speciﬁc movement

rules (collisions between agents) but on the other hand

encodes collected conﬂicts into F (ξ).

The conﬂict resolution in standard CBS imple-

mented as high-level branching is here represented

by reﬁnement of F (ξ) with disjunction (line 20).

Branching is thus deferred into the SAT solver. The

Algorithm 3: SMT-CBS algorithm for solving MAPF.

1 SMT-CBS (Σ = (G = (V, E), A, α

, α

))

2 con f licts ←

3 paths ← {shortest path from α

) to

)|i = 1, 2, ..., k}

4 ξ ←

∑

i=1

ξ(paths(a

))

5 while True do

6 (paths, con f licts) ←

SMT-CBS-Fixed(con f licts, ξ, Σ)

7 if paths 6= UNSAT then

8 return paths

9 ξ ← ξ + 1

10 SMT-CBS-Fixed(con f licts, ξ, Σ)

11 F (ξ)) ← encode-Basic(con f licts, ξ, Σ)

12 while True do

13 assignment ← consult-SAT-Solver(F (ξ))

14 if assignment 6= U NSAT then

15 paths ← extract-Solution(assignment)

16 collisions ← validate(paths)

17 if collisions =

0 then

18 return (paths, con f licts)

19 for each (a

, a

, v, t) ∈ collisions do

20 F (ξ) ← ¬X

) ∨ ¬X

)

21 con f licts ←

con f licts ∪ {[(a

, v, t), (a

, v, t)]}

22 return (UNSAT,con f licts)

presented SMT-CBS process builds in fact equisatis-

ﬁable formula to that built by MDD-SAT. The advan-

tage of SMT-CBS is that it builds the formula lazily;

that is, it adds constraints on demand after conﬂict oc-

curs. Such approach may save resources as solution

may be found before all constraint are added.

6 EXPERIMENTAL EVALUATION

We performed an extensive evaluation of all presented

algorithms on standard synthetic benchmarks (Bo-

yarski et al., 2015; Sharon et al., 2013). A represen-

tative part of results is presented in this section.

6.1 Benchmarks and Setup

We used the implementation of SMT-CBS in C++ on

top of the Glucose 4 SAT solver (Audemard et al.,

2013; Audemard and Simon, 2009) that ranks among

the best SAT solvers according to recent SAT solver

competitions (Balyo et al., 2017). The standard CBS

has been re-implemented from scratch since the orig-

inal implementation written in Java does support only

grids but not general graphs (Sharon et al., 2015) that

we need in our tests. Regarding MDD-SAT we used

a version applicable on TSWAP, TPERM, and TROT

Conﬂict Handling Framework in Generalized Multi-agent Path ﬁnding: Advantages and Shortcomings of Satisﬁability Modulo Approach

199

that is implemented in C++ (Surynek et al., 2016a).

All experiments were run on a Ryzen 7 CPU 3.0 Ghz

under Kubuntu linux 16 with 16GB RAM

Figure 5: Example of 4-connected grid, star, path, and

clique.

We divided the experimental evaluation into two

categories of tests. The ﬁrst part of experimental eval-

uation has been done on diverse instances consisting

of small graphs: 4-connected grid of size 8 × 8 and

16 × 16, random graphs containing 20% of random

edges, star graphs, paths, and cliques (see Figure 5).

Initial and goal conﬁgurations of tokens/agents was

set at random in all tests. We used a clique, a random

graph, a path, and a star consisting of 16 vertices.

The second part of experimental evaluation took

place on large 4-connected maps taken from Dragon

Age (Sharon et al., 2015; Sturtevant, 2012) - three

maps we used in our experiments are shown in Fig-

ure 7. In contrast to small instances, these were only

sparsely populated with items. Initial and goal con-

ﬁguration were generated at random again.

We varied the number of items in relocation in-

stances to obtain instances of various difﬁculties; that

is, the underlying graph was not fully occupied -

which in MAPF has natural meaning while in token

problems we use one special color ⊥ ∈ C that stands

for any empty vertex (that is, we understand v as

empty if and only if τ(v) = ⊥). For each number of

items in the relocation instance we generated 10 ran-

dom instances. For example, a clique consisting of 16

vertices gives 160 instances in total.

The timeout in all test was set to 60 seconds. Pre-

sented results were obtained from instances ﬁnished

under this timeout.

6.2 Comparison on Small Graphs

Tests on small graphs were focused on the runtime

comparison and evaluation of the size of encodings in

case of MDD-SAT and SMT-CBS. Part of results we

obtained is presented in Figures 6, 8, and 9 - mean

runtime out of 10 random instances is reported per

each number of items. Surprisingly instances turned

out to be relatively hard even for small graphs.

In all tests CBS turned out to be uncompetitive

against MDD-SAT and SMT-CBS on instances con-

To enable reproducibility of presented results we will

provide complete source codes and data on author’s web:

http://users.ﬁt.cvut.cz/surynpav/research/icaart2019.

0,001

0,01

0,1

100

2 4 6 8 10 12 14 16

Runtime (seconds)

|Agents/Tokens|

Runtime Grid 8x8 | MAPF

CBS MDD-SAT SMT-CBS

0,01

0,1

100

2 4 6 8 10 12 14 16 18

Runtime (seconds)

|Agents/Tokens|

Runtime Grid 8x8 | TSWAP

CBS MDD-SAT SMT-CBS

0,01

0,1

100

2 4 6 8 10 12 14 16 18 20 22 24 26

Runtime (seconds)

|Agents/Tokens|

Runtime Grid 8x8 | TPERM

CBS MDD-SAT SMT-CBS

0,01

0,1

100

2 4 6 8 10 12 14 16 18 20 22 24

Runtime (seconds)

|Agents/Tokens|

Runtime Grid 8x8 | TROT

CBS MDD-SAT SMT-CBS

Figure 6: Runtime comparison of CBS, MDD-SAT, and

SMT-CBS algorithms solving MAPF, TSWAP, TPERM,

and TROT on 8 × 8 grid.

brc202d

den520d

ost003d

Figure 7: Three structurally diverse Dragon-Age maps used

in the experimental evaluation. This selection includes: nar-

row corridors in brc202d, large open space in den520d, and

open space with almost isolated rooms in ost003d.

taining more agents. This is an expectable result as

it is known that performance of CBS degrades on

densely occupied instances (Surynek et al., 2016b).

In the rest of experiments we omitted MDD-SAT.

0,001

0,01

0,1

100

2 3 4 5 6 7 8 9 10 11

Runtime (seconds)

|Tokens|

Runtime Star| TROT

CBS MDD-SAT SMT-CBS

0,001

0,01

0,1

100

2 3 4 5 6 7 8 9 10 11

Runtime (seconds)

|Tokens|

Runtime Clique| TROT

CBS MDD-SAT SMT-CBS

Figure 8: Comparison of TROT solving by CBS, MDD-

SAT, and SMT-CBS on a star and clique graphs consisting

of 16 vertices.

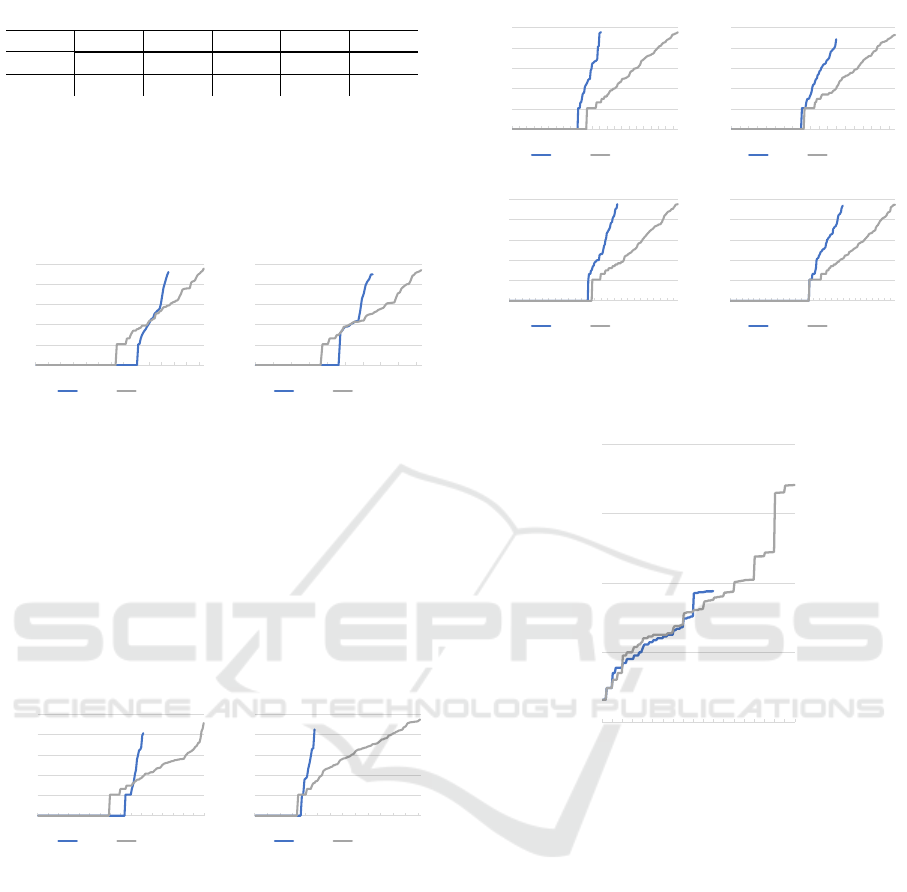
Figures 10 and 11 show sorted runtimes of CBS

and SMT-CBS solving TROT on a random graph and

a star and TSWAP on a clique, and a path all con-

sisting of 16 vertices. In all cases, CBS clearly domi-

nates in easier instances but its performance degrades

faster as instances gets harder where SMT-CBS tends

to dominate. Eventually SMT-CBS solved more out

of 160 instances per test than CBS under the given

timeout of 60 seconds. Path is particularly interesting

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

200

Number of generated clauses

|Agents|

MDD-SAT

556

56 652

1 347 469

3 087 838

2 124 941

SMT-CBS

468

31 973

598 241

1 256 757

803 671

Figure 9: Comparison of the size of encodings generated by

MDD-SAT and SMT-CBS (number of clauses is shown) on

MAPF instances.

case as the performance of CBS and SMT-CBS differs

greatly there.

0,001

0,01

0,1

100

0 20 40 60 80 100 120

Runtime (seconds)

Instance

Runtime Random (16) | TROT

CBS SMT-CBS

0,001

0,01

0,1

100

0 20 40 60 80

Runtime (seconds)

Instance

Runtime Star (16) | TROT

CBS SMT-CBS

Figure 10: Sorted runtimes of CBS and SMT-CBS solving

TROT on random and star graphs consisting of 16 vertices.

Solving of all types of relocation problems on the

same type of graph - 8 ×8 grid in this case - is shown

in Figure 12. A different pattern can be observed

in these results, SMT-CBS dominates across all dif-

ﬁculties of instances over CBS. Grids contained up

to 40 items, so having 10 random instances per num-

ber of agents, we had 400 instances in total, but only

about 250 were solved under 60 seconds in the case

of TPERM problem using SMT-CBS.

0,001

0,01

0,1

100

0 20 40 60 80 100 120 140

Runtime (seconds)

Instance

Runtime Clique (16) | TSWAP

CBS SMT-CBS

0,001

0,01

0,1

100

0 20 40 60 80 100 120

Runtime (seconds)

Instance

Runtime Path (16) | TSWAP

CBS SMT-CBS

Figure 11: Sorted runtimes of CBS and SMT-CBS solving

TSWAP on clique and path graphs consisting of 16 vertices.

SMT-CBS turned out to be fastest in performed

tests on small graphs. SMT-CBS reduces the run-

time by about 30% to 50% relatively to MDD-SAT.

More signiﬁcant beneﬁt of SMT-CBS was observed in

MAPF and TSWAP while in TROT and TPERM the

improvement was less signiﬁcant. Both MAPF and

TSWAP have more clauses in their eagerly-generated

encodings by MDD-SAT than TROT and TPERM

hence SMT-CBS has greater room for reducing the

size of encoding by constructing it lazily in these

types of relocation problems. This claim has been

experimentally veriﬁed (Figure 9); the SMT-CBS re-

duces the number of clauses to less than half of the

number generated by MDD-SAT.

0,001

0,01

0,1

100

0 20 40 60 80 100 120 140 160 180 200 220

Runtime (seconds)

Instance

Runtime Grid 8×8| TSWAP

CBS SMT-CBS

0,001

0,01

0,1

100

0 20 40 60 80 100 120 140 160 180

Runtime (seconds)

Instance

Runtime Grid 8×8| MAPF

CBS SMT-CBS

0,001

0,01

0,1

100

0 40 80 120 160 200 240

Runtime (seconds)

Instance

Runtime Grid 8×8| TROT

CBS SMT-CBS

0,001

0,01

0,1

100

0 40 80 120 160 200 240

Runtime (seconds)

Instance

Runtime Grid 8×8| TPERM

CBS SMT-CBS

Figure 12: Sorted runtimes of CBS and SMT-CBS solving

MAPF, TSWAP, TPERM, and TROT on 8 × 8 grid.

0,01

0,1

100

0 20 40 60 80 100 120 140 160 180

Runtime (seconds)

Instance

Runtime Ost003d| TSWAP

CBS SMT-CBS

Figure 13: Sorted runtimes of CBS and SMT-CBS solving

TSWAP on ost003d.

6.3 Evaluation on Large Maps

The second category of tests was focused on the per-

formance of CBS and SMT-CBS on large maps (ex-

perimenting with MDD-SAT was omitted). In the

three structurally different maps, up to 32 items were

placed randomly. Again we had 10 random instances

per each number of items.

Sorted runtimes are reported in Figures 13 and 14.

Completely different picture can be seen here. CBS

is faster than SMT-CBS across all difﬁculties of in-

stances over brc202d and den520d. In the case of

ost003d we can see CBS and SMT-CBS performing

similarly in easier instances but eventually CBS won

in hard instances containing more items.

A deeper analysis of runtimes revealed that when-

ever CBS has a chance to search for a long conﬂict

free path it can outperform SMT-CBS. On the other

hand if conﬂict handling due to intensive interaction

Conﬂict Handling Framework in Generalized Multi-agent Path ﬁnding: Advantages and Shortcomings of Satisﬁability Modulo Approach

201

0,01

0,1

100

0 20 40 60 80 100 120 140 160 180 200

Runtime (seconds)

Instance

Runtime Brc202d| TSWAP

CBS SMT-CBS

0,01

0,1

100

0 40 80 120 160 200 240

Runtime (seconds)

Instance

Runtime Den520d| TSWAP

CBS SMT-CBS

Figure 14: Sorted runtimes of CBS and SMT-CBS solving

TSWAP on brc202d and den520d.

among items prevails then SMT-CBS tends to domi-

nate which usually takes place in small graphs.

7 CONCLUSIONS

We studied a general framework for reasoning about

conﬂicts in item relocation problems in graphs based

on concepts from the CBS algorithm. In addition to

two known problems MAPF and TSWAP, we stud-

ied two derived variants TROT and TPERM. The ex-

perimental evaluation of CBS, MDD-SAT, and SMT-

CBS showed that SMT-CBS outperforms both CBS

and MDD-SAT on instances in small graphs. But we

have also shown that there is no universal winner as

CBS turned out to be faster on large maps.

The most signiﬁcant beneﬁt of SMT-CBS can be

observed on highly constrained MAPF and TSWAP

instances. The search for long paths with few con-

ﬂicts is, on the other hand, the performance bottle-

neck of SMT-CBS. For future work we plan to fur-

ther reduce the size of SAT encodings in SMT-CBS

by eliminating unnecessary time expansions in MDDs

and improve the search for long paths. We also would

like improve the performance of all implemented al-

gorithms to be able to observe their behavior on large

more densely occupied instances so far a missing case

in our experiments.

ACKNOWLEDGEMENTS

This paper has been supported by the Czech Science

Foundation (application number 19-17966S). The au-

thor would like to thank anonymous reviewers for

their effort to provide valuable comments.

REFERENCES

Audemard, G., Lagniez, J., and Simon, L. (2013). Improv-

ing glucose for incremental SAT solving with assump-

tions: Application to MUS extraction. In SAT, pages

309–317.

Audemard, G. and Simon, L. (2009). Predicting learnt

clauses quality in modern SAT solvers. In IJCAI,

pages 399–404.

Balyo, T., Heule, M. J. H., and J

arvisalo, M. (2017). SAT

competition 2016: Recent developments. In AAAI,

pages 5061–5063.

Basile, F., Chiacchio, P., and Coppola, J. (2012). A hy-

brid model of complex automated warehouse systems

- part I: modeling and simulation. IEEE Trans. Au-

tomation Science and Engineering, 9(4):640–653.

Biere, A., Biere, A., Heule, M., van Maaren, H., and Walsh,

T. (2009). Handbook of Satisﬁability. IOS Press.

Boﬁll, M., Palah

ı, M., Suy, J., and Villaret, M. (2012). Solv-

ing constraint satisfaction problems with SAT modulo

theories. Constraints, 17(3):273–303.

Bonnet,

E., Miltzow, T., and Rzazewski, P. (2017). Com-

plexity of token swapping and its variants. In STACS

2017, volume 66 of LIPIcs, pages 16:1–16:14.

Botea, A., Kishimoto, A., and Marinescu, R. (2018). On the

complexity of quantum circuit compilation. In Pro-

ceedings of SOCS 2018, pages 138–142.

Boyarski, E., Felner, A., Stern, R., Sharon, G., Tolpin,

D., Betzalel, O., and Shimony, S. (2015). ICBS:

improved conﬂict-based search algorithm for multi-

agent pathﬁnding. In IJCAI, pages 740–746.

de Wilde, B., ter Mors, A., and Witteveen, C. (2014). Push

and rotate: a complete multi-agent pathﬁnding algo-

rithm. JAIR, 51:443–492.

Dresner, K. and Stone, P. (2008). A multiagent approach to

autonomous intersection management. JAIR, 31:591–

656.

Kapadia, M., Ninomiya, K., Shoulson, A., Garcia, F. M.,

and Badler, N. I. (2013). Constraint-aware navigation

in dynamic environments. In Motion in Games, MIG

’13, pages 111–120. ACM.

Kawahara, J., Saitoh, T., and Yoshinaka, R. (2017). The

time complexity of the token swapping problem and

its parallel variants. In WALCOM 2017, volume 10167

of LNCS, pages 448–459. Springer.

Kim, D.-G., Hirayama, K., and Park, G.-K. (2014). Col-

lision avoidance in multiple-ship situations by dis-

tributed local search. Journal of Advanced Com-

putational Intelligence and Intelligent Informatics,

18:839–848.

Kornhauser, D., Miller, G. L., and Spirakis, P. G. (1984).

Coordinating pebble motion on graphs, the diameter

of permutation groups, and applications. In FOCS,

1984, pages 241–250.

Luna, R. and Bekris, K. (2011a). Efﬁcient and complete

centralized multi-robot path planning. In IROS, pages

3268–3275.

Luna, R. and Bekris, K. E. (2010). Network-guided multi-

robot path planning in discrete representations. In

IROS, pages 4596–4602.

Luna, R. and Bekris, K. E. (2011b). Push and swap: Fast co-

operative path-ﬁnding with completeness guarantees.

In IJCAI, pages 294–300.

Miltzow, T., Narins, L., Okamoto, Y., Rote, G., Thomas, A.,

and Uno, T. (2016). Approximation and hardness of

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

202

token swapping. In ESA 2016, volume 57 of LIPIcs,

pages 66:1–66:15.

Ratner, D. and Warmuth, M. K. (1986). Finding a shortest

solution for the N × N extension of the 15-puzzle is

intractable. In AAAI, pages 168–172.

Ryan, M. R. K. (2007). Graph decomposition for efﬁcient

multi-robot path planning. In IJCAI 2007, Proceed-

ings of the 20th International Joint Conference on Ar-

tiﬁcial Intelligence, pages 2003–2008.

Ryan, M. R. K. (2008). Exploiting subgraph structure in

multi-robot path planning. J. Artif. Intell. Res. (JAIR),

31:497–542.

Sharon, G., Stern, R., Felner, A., and Sturtevant, N.

(2015). Conﬂict-based search for optimal multi-agent

pathﬁnding. Artif. Intell., 219:40–66.

Sharon, G., Stern, R., Felner, A., and Sturtevant, N. R.

(2012). Conﬂict-based search for optimal multi-agent

path ﬁnding. In AAAI.

Sharon, G., Stern, R., Goldenberg, M., and Felner, A.

(2013). The increasing cost tree search for optimal

multi-agent pathﬁnding. Artif. Intell., 195:470–495.

Silver, D. (2005). Cooperative pathﬁnding. In AIIDE, pages

117–122.

Standley, T. (2010). Finding optimal solutions to coopera-

tive pathﬁnding problems. In AAAI, pages 173–178.

Sturtevant, N. R. (2012). Benchmarks for grid-based

pathﬁnding. Computational Intelligence and AI in

Games, 4(2):144–148.

Surynek, P. (2009a). An application of pebble motion on

graphs to abstract multi-robot path planning. In ICTAI

2009, pages 151–158.

Surynek, P. (2009b). A novel approach to path planning for

multiple robots in bi-connected graphs. In ICRA 2009,

pages 3613–3619.

Surynek, P. (2010). An optimization variant of multi-robot

path planning is intractable. In AAAI 2010. AAAI

Press.

Surynek, P. (2012a). On propositional encodings of coop-

erative path-ﬁnding. In ICTAI 2012, pages 524–531.

IEEE Computer Society.

Surynek, P. (2012b). Towards optimal cooperative path

planning in hard setups through satisﬁability solving.

In PRICAI 2012, pages 564–576. Springer.

Surynek, P. (2014a). Compact representations of coopera-

tive path-ﬁnding as SAT based on matchings in bipar-

tite graphs. In ICTAI, pages 875–882.

Surynek, P. (2014b). Solving abstract cooperative path-

ﬁnding in densely populated environments. Compu-

tational Intelligence, 30(2):402–450.

Surynek, P. (2017). Time-expanded graph-based proposi-

tional encodings for makespan-optimal solving of co-

operative path ﬁnding problems. Ann. Math. Artif. In-

tell., 81(3-4):329–375.

Surynek, P. (2018a). Finding optimal solutions to token

swapping by conﬂict-based search and reduction to

SAT. In Proceedings of ICTAI 2018, pages 592–599.

Surynek, P. (2018b). Lazy modeling of variants of to-

ken swapping problem and multi-agent path ﬁnding

through combination of satisﬁability modulo theories

and conﬂict-based search. CoRR, abs/1809.05959.

Surynek, P., Felner, A., Stern, R., and Boyarski, E. (2016a).

Efﬁcient SAT approach to multi-agent path ﬁnding un-

der the sum of costs objective. In ECAI, pages 810–

818.

Surynek, P., Felner, A., Stern, R., and Boyarski, E. (2016b).

An empirical comparison of the hardness of multi-

agent path ﬁnding under the makespan and the sum

of costs objectives. In SoCS 2016.

Thorup, M. (2002). Randomized sorting in o(n log log n)

time and linear space using addition, shift, and bit-

wise boolean operations. J. Algorithms, 42(2):205–

230.

Wender, S. and Watson, I. D. (2014). Combining case-based

reasoning and reinforcement learning for unit naviga-

tion in real-time strategy game AI. In ICCBR, volume

8765 of LNCS, pages 511–525. Springer.

Wilson, R. M. (1974). Graph puzzles, homotopy, and the

alternating group. Journal of Combinatorial Theory,

Series B, 16(1):86 – 96.

Yamanaka, K., Demaine, E. D., Horiyama, T., Kawamura,

A., Nakano, S., Okamoto, Y., Saitoh, T., Suzuki, A.,

Uehara, R., and Uno, T. (2017). Sequentially swap-

ping colored tokens on graphs. In WALCOM 2017,

volume 10167 of LNCS, pages 435–447. Springer.

Yamanaka, K., Demaine, E. D., Ito, T., Kawahara, J.,

Kiyomi, M., Okamoto, Y., Saitoh, T., Suzuki, A.,

Uchizawa, K., and Uno, T. (2014). Swapping labeled

tokens on graphs. In FUN 2014 Proceedings, volume

8496 of LNCS, pages 364–375. Springer.

Yamanaka, K., Demaine, E. D., Ito, T., Kawahara, J.,

Kiyomi, M., Okamoto, Y., Saitoh, T., Suzuki, A.,

Uchizawa, K., and Uno, T. (2015). Swapping labeled

tokens on graphs. Theor. Comput. Sci., 586:81–94.

Yamanaka, K., Horiyama, T., Kirkpatrick, D., Otachi, Y.,

Saitoh, T., Uehara, R., and Uno, Y. (2016). Computa-

tional complexity of colored token swapping problem.

In IPSJ SIG Technical Report, volume 156.

Yu, J. and LaValle, S. M. (2013). Planning optimal paths

for multiple robots on graphs. In ICRA 2013, pages

3612–3617.

Yu, J. and LaValle, S. M. (2015). Optimal multi-robot

path planning on graphs: Structure and computational

complexity. CoRR, abs/1507.03289.

Yu, J. and LaValle, S. M. (2016). Optimal multirobot path

planning on graphs: Complete algorithms and effec-

tive heuristics. IEEE Trans. Robotics, 32(5):1163–

1177.

Yu, J. and Rus, D. (2014). Pebble motion on graphs with

rotations: Efﬁcient feasibility tests and planning algo-

rithms. In WAFR 2014, pages 729–746.

Zhou, D. and Schwager, M. (2015). Virtual rigid bodies

for coordinated agile maneuvering of teams of micro

aerial vehicles. In ICRA 2015, pages 1737–1742.

Conﬂict Handling Framework in Generalized Multi-agent Path ﬁnding: Advantages and Shortcomings of Satisﬁability Modulo Approach

203