
Fast Nearest Neighbor Search with Narrow 16-bit Sketch
Naoya Higuchi
1
, Yasunobu Imamura
1
, Tetsuji Kuboyama
2
, Kouichi Hirata
1
and Takeshi Shinohara
1
1
Kyushu Institute of Technology, Kawazu 680-4, Iizuka 820-8502, Japan
2
Gakushuin University, Mejiro 1-5-1, Toshima, Tokyo 171-8588, Japan
Keywords:
Similarity Search, Sketch, Ball Partitioning, Hamming Distance, Dimension Reduction, Distance Lower
Bound.
Abstract:
We discuss the nearest neighbor search using sketch which is a kind of locality sensitive hash (LSH). Nearest
neighbor search using sketch is done in two stages. In the first stage, the top K candidates, which have close
sketches to a query, are selected, where K ≥ 1. In the second stage, the nearest object to the query from
K candidates is selected by performing actual distance calculations. Conventionally, higher accurate search
requires wider sketches than 32-bit. In this paper, we propose search methods using narrow 16-bit sketch,
which enables efficient data management by buckets and implement a faster first stage. To keep accuracy,
search using 16-bit sketch requires larger K than using 32-bit sketch. By sorting the data objects according to
sketch’s values, cost influence due to the increase in the number of candidates K can be reduced by improving
memory locality in the second stage search. The proposed method achieves about 10 times faster search speed
while maintaining accuracy.
1 INTRODUCTION
To implement efficient similarity search in multidi-
mensional spaces, sketches (M
¨
uller and Shinohara,
2009; Mic et al., 2016; Dong et al., 2008; Mic et al.,
2015; Wang et al., 2007) have been developed. Sketch
is a compact bit sequence representing multidimen-
sional data, which can be considered as a kind of lo-
cality sensitive hash(LSH). Ball partitioning (BP, for
short) is a method to make sketches by assigning a bit
0 or 1 to a data, such that 0 if it is in a ball and 1 other-
wise. BP is also used in vantage point tree (Yianilos,
1993).
The similarity search using sketches consists of
two stages. The first stage selects candidates depend-
ing on their Hamming distances between sketches.
The second stage selects the nearest neighbor by com-
paring the candidates with the query using distances
in the original space.
In the search using the sketch, the distance be-
tween the sketches cannot completely reflect the dis-
tance between the objects. Therefore, unlike retrieval
using a hierarchical spatial index R-tree (Guttman,
1984) or M-tree (Ciaccia et al., 1997), nearest neigh-
bor solutions cannot be accurately obtained by sketch-
based retrieval. In order to guarantee a certain level
of precision at a speed comparable to that of the hi-
erarchical spatial indexing method, the width of the
sketch has been considered to be 32 bits or 64 bits.
In this paper, we propose a method using a nar-
rower 16-bit sketch. We assume that the size of the
database is several millions. The number of 32-bit
patterns is 2
32
= about 4 billion. As long as the
database size is not huge beyond that, there are too
many empty buckets when 32-bit sketches are used as
keys. Thus, bucket method is not suitable for 32-bit
case. When sketches wider than 32 bits are used, in
the first stage search, all the sketches of the data are
prepared as they are, the distances from the sketch of
a query are calculated, and solution candidates are se-
lected by the full search.
On the other hand, the number of 16-bit pat-
terns is only 2
16
, so we can efficiently manage data
with bucket method. Then, in the first stage search,
it is enough to perform matching with sketches of
2
16
= 65,536 pieces, and it is possible to execute
at high speed at a constant cost independent of the
database size. In the first stage search, the number of
sketches close to the sketch of a query is only a few of
65,536. Therefore, if we use an algorithm to enumer-
ate sketches in the closest order without performing
matching between sketches, it is practically possible
to increase the speed so that the cost can be neglected.
Here, we will briefly explain the speeding up of
540
Higuchi, N., Imamura, Y., Kuboyama, T., Hirata, K. and Shinohara, T.
Fast Nearest Neighbor Search with Narrow 16-bit Sketch.
DOI: 10.5220/0007377705400547
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 540-547
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

the first stage search by enumerating sketches. Before
search, we prepare all 16-bit patterns sorted in ascend-
ing order of the number of ON bits. Sketches can be
enumerated in order of Hamming distance from the
sketch of a query by calculating bitwise exclusive OR
(XOR) between the sketch of the query and these bit
patterns. The second stage search is executed using
only initial part of this sequence. By this method, in
the first stage search, calculation of the Hamming dis-
tance between the sketches becomes unnecessary and
almost no search cost is required.
Here we explain sketch’s enumeration method for
the first stage speeding up using an example. Let the
sketch width be 3 bits. The distance between sketches
is assumed to be Hamming distance. Hamming dis-
tances between sketches are four types of 0, 1, 2, and
3. If sketch of a query s = 011, the sketches of respec-
tive distances are as follows.
The sketch of distance 0
One sketch that matches s, s itself, that is, 011.
The sketches of distance 1
There are three sketches that differ from s by 1 bit.
They are obtained by XOR of 3-bit strings (001,
010, 100), which have one ON bit, and s. They
are s ⊕ 001 = 010, s ⊕ 010 = 001, s ⊕ 100 = 111.
The sketches of distance 2
There are three sketches that differ from s by 2
bits. They are obtained by XOR of 3-bit strings
(011, 101, 110), which have two ON bits, and s.
They are s ⊕ 011 = 000, s ⊕ 101 = 110, s ⊕ 110
=101.
The sketch of distance 3
One sketch differs s by 3 bits, that is, 100. This is
obtained by s ⊕ 111.
In this way, in the case of 3-bit sketches, they can be
enumerated in ascending order of Hamming distance
to a query sketch, by making XOR of query sketch
with bit patterns 000, 001, 010, 100, 011, 101, 110
and 111 in ascending order of the number of ON bits.
Since the bit pattern sequence used for XOR does
not depend on the query, it is possible to prepare in
advance as arranged in ascending order of the number
of ON bits. Objects in the database can be managed
by the bucket method with the sketches themselves as
indexes, so in the first stage search, there is no need
to calculate the distance between the object and the
sketch of the query. As a result, in effect, the search
cost of the first stage can be ignored. Also, by sort-
ing objects in the database in the order of sketching,
memory locality in the second stage search can be im-
proved.
2 PRELIMINARIES
Here, we briefly introduce some necessary concepts
for our discussion.
2.1 Nearest Neighbor Search using
Sketches
We assume that data in the given database are in-
dexed by natural numbers 0 to n − 1. Thus, let db =
{x
0
, ··· , x
n−1
} ⊆ U be the given database of n data,
where U is a data space. The dissimilarity between
two data x
i
and x
j
is defined as distance D(x
i
, x
j
).
The nearest neighbor search for a query q ∈ U is to
find x ∈ db such that D(q, x) ≤ D(q, y) for all y ∈ db.
Let We can realize the nearest neighbor search using
sketches as follows, where s be a function which maps
data to its sketch, and K ≥ 1.
1. Preparation stage:
Calculate all the sketches s(x
0
), . . . ,s(x
n−1
).
2. First stage (Filtering using the Hamming dis-
tances of sketches):
Select K candidates x
i
0
, . . . , x
i
K−1
which have clos-
est sketches s(x
i
0
), . . . , s(x
i
K−1
) to the sketch s(q)
of a query q.
3. Second stage (Nearest neighbor search using ac-
tual distances):
Select the nearest neighbor data from the candi-
dates x
i
0
, . . . , x
i
K−1
.
Sketches are relatively small structures with re-
spect to their original feature data. For example, we
use 32-bit or 16-bit sketches for image feature data
of 64 bytes in our experiments. In the first stage of
searching process, we use the Hamming distances,
which can be more easily calculated using bit op-
erations than the actual distances between features.
However, sketches cannot preserve all the distance re-
lation. Therefore, we use them as a filter. The accu-
racy of search is the probability that a correct near-
est neighbor is obtained. The larger K of the number
of candidates in the first stage achieves a more accu-
rate but slower search. Thus, one of the most impor-
tant subjects on sketch is to achieve higher accuracy
with smaller K, or equivalently, to speeding up search
within acceptable error.
2.2 Sketches based on Ball Partitioning
In this paper, we use sketches based on ball partition-
ing (BP). A pair (p, r) of a point and a radius is called
a pivot. A ball partitioning BP
(p,r)
is defined as fol-
lows:
Fast Nearest Neighbor Search with Narrow 16-bit Sketch
541
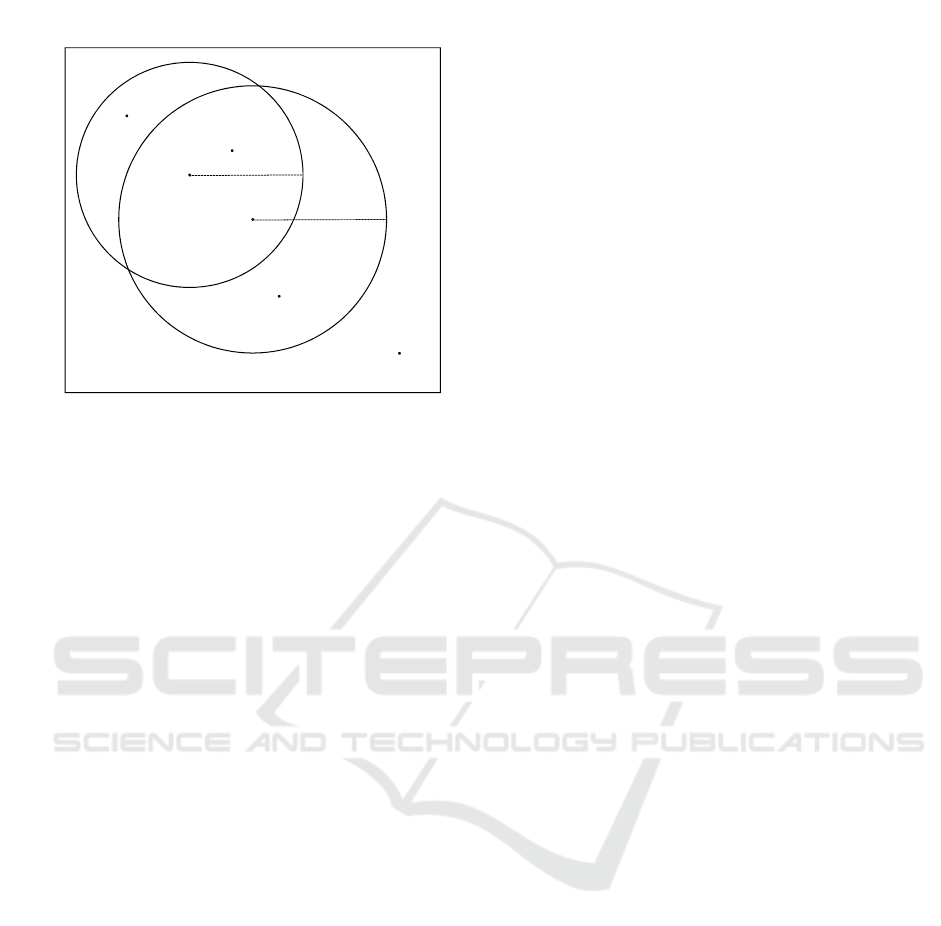
Figure 1: 2-bit sketches by two balls.
BP
(p,r)
(x) =
0 if D(p, x) ≤ r
1 otherwise
A BP based sketch function s
P
of
width w is defined by a set of w pivots
P = {(p
0
, r
0
), ..., (p
w−1
, r
w−1
)} as follows:
s
P
(x) = BP
(p
w−1
,r
w−1
)
(x)...BP
(p
0
,r
0
)
(x)
Consider 4 points A, B,C , D on a Euclidean plane
in Figure 1. Using a set of two pivots P =
{(p
0
, r
0
), (p
1
, r
1
)}, their sketches are s
P
(A) = 01,
s
P
(B) = 00, s
P
(C) = 10, s
P
(D) = 11. Let q be any
query outside of both balls. Since s
P
(q) = 11, Ham-
ming distances between sketches of q and A, B,C, D
are 1, 2, 1, 0, respectively. The order of conventional
priority in the first stage is D < A = C < B. Note that A
and C cannot be distinguished by Hamming distances
from q.
2.3 Distance Lower Bounds between
Queries and Sketches
In this paper, we use the priority based on dis-
tance lower bounds (Higuchi et al., 2018) in the first
stage, which gives accurate search than the Ham-
ming distance. This is a technique based on the fact
that sketches by ball partitioning can be regarded as
quantized images of dimensional reduction mapping
Simple-Map (Shinohara and Ishizaka, 2002). Let
P = {(p
0
, r
0
), ..., (p
w−1
, r
w−1
)} be the set of pivots.
We can get the lower bound e
i
(q, s
P
(x)) of D(q, x) as
follows.
e
i
(q, s
P
(x)) =
0 if BP
(p
i
,r
i
)
(q) = BP
(p
i
,r
i
)
(x)
|D(p
i
, q) − r
i
| otherwise
We propose priorities using the distance lower bounds
e
i
(q, s
P
(x)) as the criteria to select candidates in the
first stage. When we use as the priority
score
∞
(q, s
P
(x)) =
w−1
max
i=0
e
i
(q, s
P
(x))
which is the maximum lower bounds, we can safely
prune some of candidates because it is really a dis-
tance lower bound. We can also use their sum score
1
as the priority
score
1
(q, s
P
(x)) =
w−1
∑
i=0
e
i
(q, s
P
(x))
which is not longer a distance lower bound, but de-
rives higer accuracy than score
∞
.
2.4 Optimization of Sketches
In order to improve the accuracy of the search using
the sketch, we select the pivot set P so that the col-
lision probability becomes small. When the sketches
of different data x and
s
P
(x) = s
P
(y)
a collision is said to occur. In this paper, sketch is
optimized using QBP (Higuchi et al., 2018). If opti-
mized 16-bit sketches are used for databases of mil-
lions data, it is expected that the number of data pro-
jected on each sketch will be somewhat even.
3 FAST SEARCH USING 16-bit
SKETCHES
Since the total number of 16-bit sketches is 2
16
=
65,536, it is enough to collate with all 16-bit sketches
rather than checking with sketches of millions of in-
dividual data. The cost is independent on the database
size. In actual searching, only a small part of sketches
that approximate the sketch of the query is needed be-
cause the number of data sharing each sketch is ex-
pected to be somewhat even. So by using an algorithm
that enumerates the sketches in order of the sketch of
query, it is possible to increase the speed because the
first step search is almost negligible in cost.
3.1 Speeding Up Search using
Hamming Distances of 16-bit
Sketches
The search using 16-bit sketches, in the case of using
a Hamming distance, can be relatively easily speed
up, as explained in Introduction.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
542

A nearest neighbor search method using 16-bit
sketches is shown in Algorithm 1. It is assumed
here that the database is managed using buckets with
sketches as keys as follows.
x[0], x[1], · · · , x[n − 1]: Array of feature data,
sorted in the sketch order on the memory. (It should
not be an indirect sort via pointers)
id[i]: Data ID of feature data x[i].
f [s]: First position in the array x of the data which
sketch is s.
n[s]: Number of data which sketch is s.
In this way, data whose sketches are s become as
follows
x[ f [s]], x[ f [s] + 1], ··· , x[ f [s] + n[s] − 1]
As preparations for search by the Hamming distance,
we prepare all 16-bit patterns arranged in ascending
order of the number of ON bits.
m[0], m[1], ··· , m[2
16
− 1]
3.2 Speeding Up Search using Distance
Lower Bounds of 16-bit Sketches
In the case of using score
∞
, the distance lower bounds
are different for each query. So unlike the case using
Hamming distances, sketches cannot be enumerated
by XOR with the prepared bit pattern sequence. How-
ever, as explained below, you can enumerate sketches
in ascending order of score
∞
with sketch for queries.
First, we explain the algorithm using a concrete ex-
ample for 3-bit sketch.
Let i be the position of 2
i
when bit strings are con-
sidered as binary numbers(i = 0, 1, 2).
(p
i
, r
i
): Pivot of the ball partitioning correspond-
ing to position i.
P = {(p
0
, r
0
), (p
1
, r
1
), (p
2
, r
2
)}: Set of Pivots.
q: Query.
e
i
= |D(q, p
i
)−r
i
|: Distance lower bound between
data and query when their sketch bits are different at
the position i.
Note that, for arbitrary data x, the following in-
equality holds:
BP
(p
i
,r
i
)
(q) 6= BP
(p
i
,r
i
)
(x) → D(q, x) ≥ e
i
For simplicity, it is assumed that these distance lower
limits satisfy the following.
e
2
≥ e
1
≥ e
0
In ascending order, there are only 4 types of score
∞
between sketches, 0, e
0
, e
1
, or e
2
. Assuming that the
sketch of the query is s
P
(q) = 011, the sketch with
each score
∞
is as follows.
The sketch whose score
∞
is 0
011 itself.
The sketch whose score
∞
is e
0
It differs only the bit of position 0 of 011. That is,
010. Then, the sketch is 011. Note that s
P
(q) ⊕
001 = 010.
The sketches whose score
∞
is e
1
The bits of position 2 of 011 are the same, the bits
of position 1 are different, and the bit of position
0 is arbitrary. That is, 000 and 001. These are
XORs of s
P
(q) and 010, 011 respectively.
The sketches whose score
∞
is e
2
Bits in position 2 are different from 011, the rest
are arbitrary. That is, 100, 101, 110, 111. These
are XORs of s
P
(q) and 100, 101, 110, 111 respec-
tively.
In this way, sketches in order of score
∞
with s
P
(q)
are enumerated by XOR with s
P
(q) and the follow-
ing bit pattern sequence in ascending order of binary
numbers.
000, 001, 010, 011, 100, 101, 110, 111
Notice that score
∞
is determined by the leftmost po-
sition of the ON bit of the pattern. We can rearrange
them in order of Gray code.
000, 001, 011, 010, 110, 111, 101, 100
This is because the order of the binary value and the
order of the Gray code are both in ascending order of
the leftmost position of ON bit. The sequence of Gray
code can be generated by one bit inverting operations
as shown in Table 1.
Table 1: Gray code generation and sketch enumeration.
Gray code Sketch enumeration score
∞
000 011 0
000 ⊕ 001 = 001 011 ⊕ 001 = 010 e
0
001 ⊕ 010 = 011 010 ⊕ 010 = 000 e
1
011 ⊕ 001 = 010 000 ⊕ 001 = 001 e
1
010 ⊕ 100 = 110 001 ⊕ 100 = 101 e
2
110 ⊕ 001 = 111 101 ⊕ 001 = 100 e
2
111 ⊕ 010 = 101 100 ⊕ 010 = 110 e
2
101 ⊕ 001 = 100 110 ⊕ 001 = 111 e
2
The sequence of which bit positions are to be inverted
is like 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0. By
using this nature of Gray code, efficient enumeration
becomes possible. If the ranking of the distance lower
bounds of each bit position to the query is decided, bit
inverting operation of the relative position using it is
performed. The bit position to be inverted can be ob-
tained with bitcount(i⊕(i+1))−1. Starting from the
Fast Nearest Neighbor Search with Narrow 16-bit Sketch
543

Algorithm 1: NNSEARCHBYHAMMING.
/*x[0], x[1], · · · , x[n − 1]: Array of feature data sorted by sketches */
/*id[i]: Data ID of feature data x[i] */
/* f [s]: First position in the array x of the data which sketch is s*/
/*n[s]: Number of data which sketch is s*/
/* K : Number of candidates obtained in the first stage = number of actual distance calculations */
/*m[0], m[1], ··· , m[2
w
− 1]: All w-bit patterns in ascending order of the number of ON bits*/
/* w : the width of sketches */
function NNSEARCHBYHAMMING(query)1
(NN, nearest, checked) ← (“none”, ∞, 0);2
for i = 0 to 2
w
− 1 do3
s ← sketch(quer y) ⊕ m[i];4
(NN, nearest, checked) ←SEARCH(query, s, NN, nearest, checked);5
if checked ≥ K then6
return NN;7
end8
end9
return NN;10
end11
function SEARCH(query, s, NN, nearest, checked)12
for i = f [s] to f [s] + min(n[s], K − checked) − 1 do13
if D(query, x[i]) ≤ nearest then14
(NN, nearest) ← (id[i], D(query, x[i]));15
end16
end17
return(NN, nearest, checked + min(n[s], K − checked));18
end19
sketch s
P
(q) of the query, instead of the bit pattern of
all 0s, it is possible to enumerate sketches in ascend-
ing order of the score from the query, as shown in
Table 1. Using the nature of Gray code the algorithm
for sketch enumeration becomes very simple, since
the operation to get the next sketch in the sequence
can be achieved by just one bit inverting operation.
Here, we explain why the above method can cor-
rectly enumerate sketches. Let g(i) be the Gray code
corresponding to i (i = 0, 1, . . . ). That is, g(0) = 000,
g(1) = 001, . . . , g(7) = 100. Then, s
P
(q) ⊕ g(i) is the
i-th sketch in the enumeration to be generated. By the
nature of ⊕, the following holds.
(s
P
(q) ⊕ g(i)) ⊕ (s
P
(q) ⊕ g(i + 1)) = g(i) ⊕ g(i + 1)
Note that g(i) ⊕ g(i + 1) is a bit pattern with just one
ON bit. Thus, we have the following, where hh is the
left logical shift operation.
g(i) ⊕ g(i + 1) = (1 hh (bitcount(i ⊕ (i + 1)) − 1))
Therefore, we can enumerate desired sequence of
sketches by starting from the sketch s
P
(q) of a query
and applying the same bit inverting operations as for
the sequence of Gray codes.
Since the distance lower bounds does not neces-
sarily satisfy e
2
≥ e
1
≥ e
0
, we use the ranking of
these lower bounds. In Algorithm 2, we assume
that bidx[i], ··· , bidx[w − 1] are the rearrangement of
0, 1, · ·· , w − 1 satisfying the following.
e
bidx[w−1]
≥ ·· · ≥ e
bidx[1]
≥ e
bidx[0]
The function Search is indicated in Algorithm 1.
As a prioritization, we know that score
1
is more
accurate than score
∞
. The speeding up method for
score
∞
uses the fact that score
∞
has only w + 1 = 17
patterns. On the other hand, score
1
may have 2
w
= 2
16
patterns. Therefore, we cannot achieve the same
speeding up method by enumeration. In the experi-
ment in this paper, in search by 16-bit sketch using
score
1
, score
1
for all sketches of 2
w
= 2
16
are naively
calculated.
4 EXPERIMENTS
In this section, we report experiments using data,
which are images and music, as follows:
• Images: about 70 million 2D frequency spectrums
of 64 dimension data extracted from 2,900 videos.
• Music: about 70 million mel-frequency spectrums
of 96 dimension data extracted from 1,400 music
CD.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
544
Algorithm 2: SEARCHBYSCOREINF.
/* w : the width of sketches */
/* K : Number of candidates obtained in the first stage = number of actual distance calculations */
function SEARCHBYSCOREINF(query)1
Prepare the distance lower bounds rank order table bidx[0], . . . , bidx[w − 1] for query;2
(NN, nearest, checked) ← (“none”, ∞, 0);3
s ← sketch(quer y);4
(NN, nearest, checked) ←SEARCH(query, s, NN, nearest, checked);5
if checked ≥ K then6
return NN;7
end8
for i = 0 to 2
w
− 1 do9
s ← s ⊕ (1 hh bidx[bitcount(i ⊕ (i + 1)) − 1]);10
(NN, nearest, checked) ←SEARCH(query, s, NN, nearest, checked);11
if checked ≥ K then12
return NN;13
end14
end15
return NN;16
end17
In ICPRAM 2018 (Higuchi et al., 2018) we also used
the ICPRAM color dataset. However, there are only
about 100,000 data and it is not suitable for this re-
search, so it is not used. We adopted 32 bits and 16
bits as the width of sketches. The sets of pivots are
selected by QBP (Higuchi et al., 2018) which have
smaller collision probability. Table 2 shows the states
of buckets for 16-bit sketches, where “average” is the
average number of elements, “empty” is the number
of empty buckets, “≥ 10” is the ratio of the number
of buckets with 10 or more elements. Since many
buckets have more than 10 elements as observed in
Table 2, speeding up of the second stage by sorting
data in the order of sketch is expected. In comparative
experiments with or without sorting, about 3 times
speedup was confirmed.
Table 2: Buckets for 16-bit Sketches.
Data Image Music
average 105 108
empty 908 (1.5%) 2104 (3.1%)
≥ 10 87% 74%
Randomly generated data are not appropriate for ex-
periments of nearest neighbor search, because in
higher dimensional spaces it is rare to find near data.
Therefore, from randomly selected two data x and y,
we prepare queries by mixing x and y as noise of level
5%, 10%, . . . , 50%. For example, a query at noise
level 5% is a sum of x and y with weight 95% and 5%,
respectively. For each noise level, we prepare 1,000
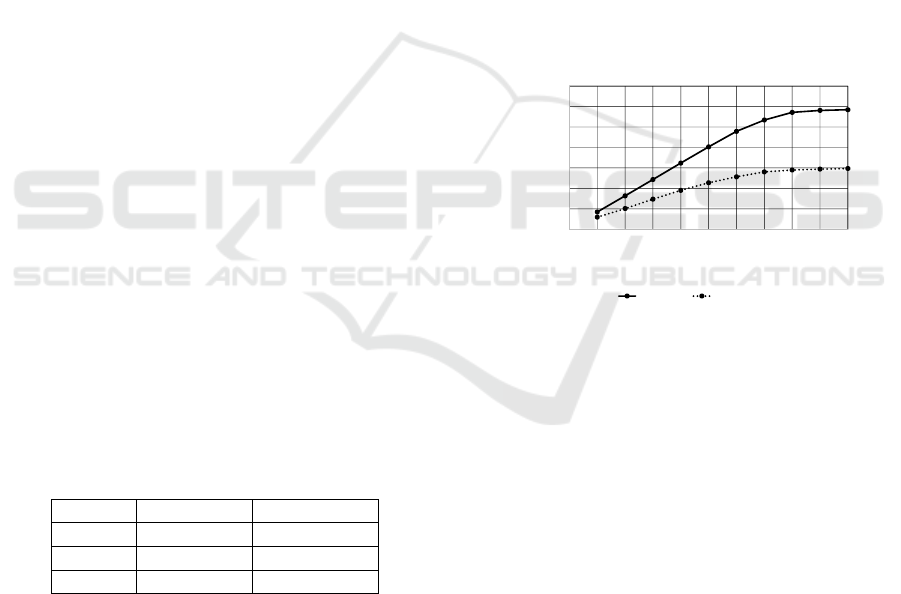
queries. The average of nearest neighbor distances for
queries are shown in Figure 2.
Figure 2: The average of nearest neighbor distances.
The PC used for the experiments was CPU Intel (R)
Xeon (R) CPU E 5 - 2640 2.5 GHz, memory 64
GBytes.
The retrieval accuracy for image data and music
data are shown in Table 3 and Table 4, respectively,
where, “score” is the search priority order, “width”
is the number of bits of sketch, “K” is the ratio of
the candidates in the first stage with respect to the
database size, “sketches” is the average number of
sketches enumerated (only for 16-bit, 100% for naive
method without enumeration), “time” is the search
time in millisecond per query (“1st st.” is the search
time for the first stage). When enumeration method is
used, the cost for the first stage cannot be separated
and omitted. For K, which is the number of actual
distance calculations in the second stage search, we
select 0.1% for 32-bit and 1.0% for 16-bit so that the
search accuracy is about the same (about 70% for im-
ages and about 65% for music). Conventional search
using 32-bit sketches with K = 0.1% achieves faster
Fast Nearest Neighbor Search with Narrow 16-bit Sketch
545

Table 3: Precisions for image search.
score Hamming score
∞
score
1
width 32 16 32 16 32 16
K 0.1% 1.0% 0.1% 1.0% 0.1% 1.0%
sketches − 100% 0.76% − 100% 0.73% − 100%
time 1st st. 28.7 4.36 − 35.6 3.23 − 32.0 4.90
(ms) total 29.8 7.16 2.85 36.9 6.06 2.68 33.2 7.76
query noise
All 70.2 73.4 73.0 74.3 79.7 79.7 80.2 85.1
5 − 10% 99.8 99.7 99.6 100 100 100 100 100
15 − 20% 96.9 94.4 94.8 99.1 99.3 99.3 100 100
25 − 30% 80.4 80.3 79.3 85.7 88.8 88.8 92.7 94.4
35 − 40% 46.0 53.9 53.3 52.4 63.5 63.5 63.7 73.2
45 − 50% 28.0 38.5 37.9 34.4 47.2 47.2 44.7 58.0
Table 4: Precisions for music search.
score Hamming score
∞
score
1
width 32 16 32 16 32 16
K 0.1% 1.0% 0.1% 1.0% 0.1% 1.0%
sketches − 100% 0.55% − 100% 0.48% − 100%
time 1st st. 30.3 4.33 − 36.3 3.23 − 34.4 4.63
(ms) total 31.7 7.89 3.58 38.0 6.82 3.38 36.0 8.30
query noise
All 65.5 66.8 66.0 63.6 75.1 73.4 72.3 77.8
5 − 10% 99.7 98.7 98.2 99.5 99.8 99.7 100 100
15 − 20% 93.3 89.1 89.3 92.2 95.3 94.8 97.2 97.2
25 − 30% 70.6 68.2 67.6 67.4 80.3 78.5 79.8 83.0
35 − 40% 40.2 44.2 43.7 36.9 55.6 53.1 51.2 61.5
45 − 50% 23.9 33.7 31.4 21.9 44.5 41.2 33.2 47.4
Table 5: Precisions over 90% for image search.
score Hamming score
∞
score
1
width 32 16 32 16 32 16
K 2.0% 6.5% 1.5% 5.0% 1.0% 2.5%
sketches − 100% 5.8% − 100% 4.1% − 100%
time(ms) 139 22.0 17.5 106 16.8 12.8 107 12.0
All 91.5 90.2 90.2 90.1 92.0 90.6 93.8 91.4
Table 6: Precisions over 90% for music search
score Hamming score
∞
score
1
width 32 16 32 16 32 16
K 3.5% 10% 3.5% 8.0% 1.5% 4.0%
sketches − 100% 7.4% − 100% 5.5% − 100%
time(ms) 227 37.4 32.7 188 30.1 25.1 160 18.7
All 90.8 90.4 90.1 90.3 92.2 90.6 92.0 90.9
retrieval than R-Tree based search, whose search time
is about 100s millisecond.
From these tables, it can be seen that as the noise
level increases, that is, as the nearest neighbor solu-
tion gets farther, the search precision becomes lower.
This may be considered to be the influence of “curse
of dimensionality” in high dimensional space. When
Hamming distance is used for prioritization, for each
database, 16-bit sketches (K = 1.0%) can achieve the
same search precision as 32-bit sketches (K = 0.1%).
Using score
∞
or score
1
for prioritization improves
search accuracy. The effectiveness of speeding up by
enumerating 16-bit sketches can also be confirmed.
There are slight differences in accuracy depending on
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
546

whether enumeration is used or not, but this is be-
cause the ones selected by the method differ when
there is one with the same priority. In addition, it can
be seen that the number of 16-bit sketches enumerated
in search time is very small. Using the speeding up
by enumeration, the retrieval speed can be increased
about 10 times as compared with using the conven-
tional 32-bit sketches. Since score
1
cannot be speed-
ing up by enumeration method, it achieves only about
4 times faster search, but the highest accuracy.
In the conventional method, it was not possible
to get higher precision by increasing K in order to
achieve faster search speed than other methods such
as R-Tree. However, we can expect that the proposed
method keeps high-speed search, even if higher ac-
curacy is required. The results compared with larger
K with precision exceeding 90% are shown in Table 5
and Table 6. Search using 16-bit sketches needs larger
K than 32-bit ones, but achieves speeding up about 8
times. Also, with score
1
you can achieve high preci-
sion without increasing K too much, and it is fastest
though not using enumeration method.
5 CONCLUDING REMARKS
Changing from 32-bit sketches to narrower 16-bit
sketches, about 10 times faster search is achieved
by efficient first stage search and data management
by the bucket method. When Hamming distance or
score
∞
are used for prioritization for 16-bit sketches,
the first stage search can be done in very short time by
enumerating sketches in order of priorities. As a fu-
ture work, we should consider enumeration algorithm
for score
1
in a similar way.
Using the 16 bit sketch, in order to maintain the
same degree of precision as in the conventional 32
bit case, the number K of first stage candidates is
required to be approximately three times as large.
By sorting data with sketch as a key, second stage
retrieval can be improved about three times faster.
Therefore, it can be expected that the superiority of
the proposed method can be preserved for data of
higher dimension than those used in the experiments.
We need to further investigate the relationship be-
tween database size n and optimal sketch width w. In
this paper we assumed n to be millions, but for larger
databases it may be better to make w greater than 16.
In the experiments in this study, we used the
heuristic method QBP (Higuchi et al., 2018) which
minimizes the collision probability as the evaluation
index for sketch optimization. By using AIR, a kind
of simulated annealing method, a pivot set of sketches
with smaller collision probability than QBP can be
obtained, but search accuracy is not improved (Ima-
mura et al., 2017). However, since the data man-
agement by the bucket method is performed in our
proposed method, as a merit of using a sketch with
smaller collision probability, there is a possibility of
improving the speed by localizing the memory access.
In any case, it seems necessary to further investigate
sketch optimization.
ACKNOWLEDGMENTS
This work was partially supported by JSPS KAK-
ENHI Grant Numbers 16H02870, 17H00762,
16H01743, 17H01788, and 18K11443.
REFERENCES
Ciaccia, P., Patella, M., and Zezula, P. (1997). M-tree: An
efficient access method for similarity search in metric
spaces. In Proc. VLBD’97, pages 426–435.
Dong, W., Charikar, M., and Li, K. (2008). Asymmetric
distance estimation with sketches for similarity search
in high-dimensional spaces. In Proc. ACM SIGIR’08,
pages 123–130.
Guttman, A. (1984). R-trees: A dynamic index structure
for spatial searching. In Yormark, B., editor, Proc.
SIGMOD’84, pages 47–57. ACM Press.
Higuchi, N., Imamura, Y., Kuboyama, T., Hirata, K., and
Shinohara, T. (2018). Nearest neighbor search using
sketches as quantized images of dimension reduction.
In Proc. ICPRAM 2018, pages 356–363.
Imamura, Y., Higuchi, N., Kuboyama, T., Hirata, K., and
Shinohara, T. (2017). Pivot selection for dimension
reduction using annealing by increasing resampling.
In Proc. LWDA 2017, pages 15–23.
Mic, V., Novak, D., and Zezula, P. (2015). Improving
sketches for similarity search. In Proc. MEMICS’15,
pages 45–57.
Mic, V., Novak, D., and Zezula, P. (2016). Speeding up
similarity search by sketches. In Proc. SISAP 2016,
pages 250–258.
M
¨
uller, A. and Shinohara, T. (2009). Efficient similarity
search by reducing i/o with compressed sketches. In
Proc. SISAP’09, pages 30–38.
Shinohara, T. and Ishizaka, H. (2002). On dimension re-
duction mappings for approximate retrieval of multi-
dimensional data. In Progress of Discovery Science,
LNCS 2281, pages 89–94.
Wang, Z., Dong, W., Josephson, W., Q. Lv, M. C., and Li,
K. (2007). Sizing sketches: A rank-based analysis
for similarity search. In Proc. ACM SIGMETRICS’07,
pages 157–168.
Yianilos, P. (1993). Data structures and algorithms for near-
est neighbor search in general metric spaces. In Proc.
SODA 1993, pages 311–321. ACM Press.
Fast Nearest Neighbor Search with Narrow 16-bit Sketch
547
