Placement-and-Proﬁt-Aware Association Rules Mining

Runyu Ma

1,∗

, Hantian Li

1,∗

, Jin Cen

and Amrinder Arora

The George Washington University, Washington D.C., U.S.A.

BizMerlinHR, Reston, Virginia, U.S.A.

Keywords:

Association Rule Mining, Data Mining, Placement-and-Proﬁt-Aware Association Rules Mining.

Abstract:

Previous approaches on association rule mining in recommendation have already achieved promising perfor-

mances. However, to the best of our knowledge, they seldom simultaneously take the proﬁt and placement

factor into consideration. In E-commerce recommendation scenario, the order of the recommendation reﬂects

as placement. In this paper, we propose a novel placement-and-proﬁt-aware association rule mining algorithm

to maximize proﬁt as well as maintaining recommendation accuracy. We also propose two metrics: Expecta-

tion of Proﬁt (EOP), which measures the overall proﬁt, and Expectation of Click rate (EOC), which measures

the user experience. Experiments on SPMF dataset show that the proposed algorithm can improve the EOP

signiﬁcantly with only slight decrease in EOC.

1 INTRODUCTION

In order to increase their net revenue and help

customers discover potentially desired items, e-

commerce service providers typically recommend ad-

ditional items to customers after they add items to

the shopping cart. For example, Figure 1 shows

an online-shopping recommendation after a customer

has added a hamper and a chair pad into the cart. In

this example, three rows of items are recommended at

the check-out page based on merchandise in the cart.

These recommended items serve two purposes: in-

crease the satisfaction of customers, and increase the

proﬁt of the merchant. Previously, researchers have

proposed Collaborate Filtering (CF) (Schafer et al.,

2007), Association Rules Mining (ARM) (Agrawal

et al., 1993) and Weighted Association Rules Min-

ing (WARM) (Cai et al., 1998) to recommend these

additional items. Although CF and ARM have shown

decent performance, they do not generally take proﬁt

into consideration. For instance, a patent about col-

laborative ﬁltering proposes a method to place ad-

vertisements automatically (Robinson, 1999). This

patent takes the users’ interests into consideration,

but ignores the proﬁt of items. So, the popular-but-

low-proﬁt item tend to be recommended. As a re-

sult, the proﬁt of E-commerce company is not guar-

anteed to be maximized. WARM is proﬁt-aware,

These authors contributed equally to this study and

share ﬁrst authorship.

but could possibly result in worse recommendation

accuracy, because it would recommend high proﬁt

but unattractive items (Cai et al., 1998). Also,

in the practice, the click-through rates of items is

highly related to their placement (McMahan et al.,

2013). However, none of these methods take the

placement into account. We propose a more com-

prehensive model that considers proﬁt maximization,

placement and recommendation accuracy. To expli-

cate this proposed model, Figure 2 shows the ab-

stract structure of the scenario in Figure 1. This

paper proposes a conﬁdence-based solution which

takes Placement, Click-through Rate Model (Chuklin

et al., 2015) and Proﬁt into account to recommend

items to maximize the proﬁts and click-through rate

which reﬂects the correlation of items. We evaluate

the proposed method on the retail dataset of Sequen-

tial Pattern Mining Framework (SPMF) (Fournier-

Viger et al., 2016) (Brijs et al., 1999) dataset, which

was downloaded from http://www.philippe-fournier-

viger.com/spmf/. Retail dataset is an anonymous re-

tail market basket data from an anonymous Belgian

retail store. Our proposed method shows a good trade-

off between proﬁt and click-through rate compared

with ARM and WARM.

Ma, R., Li, H., Cen, J. and Arora, A.

Placement-and-Proﬁt-Aware Association Rules Mining.

DOI: 10.5220/0007380606390646

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 639-646

ISBN: 978-989-758-350-6

639

Figure 1: An example of Recommendation Based on

Bought Items (Amazon.com, 2018).

1.1 Background on Association Rules

Mining

Suppose X and Y are two sets such that X ∩Y =

0. An

association rule X → Y represents an association be-

tween the presence of the item sets X and Y in trans-

actions (Nguyen et al., 2017). As far as this paper

concerned, X means the selected item set in the shop-

ping cart and Y means the item set that may be rec-

ommended.

Association rule mining has various measures to

evaluate how interesting the rules are. Two most pop-

ular measures are the support and conﬁdence. The

support of an association rule X → Y , denoted as

sup[X → Y ], is the ratio between the number of trans-

actions containing X and the number of transactions

containing X ∪Y .

Suppose T is a set of transactions, I is a set of

items. Then we deﬁne tid[X ] as a set of Transaction

IDs, which contain all items in set X. Then sup can

be deﬁned as:

sup[X → Y ] =

|tid[X ∪Y ]|

|T |

(1)

con f can be deﬁned as:

con f [X → Y ] =

|tid[X ∪Y ]|

|tid[X ]|

(2)

In past research, many methods of Association

Rules Mining have been developed, such as Apri-

ori algorithm (Agrawal and Srikant, 1994), FpGrowth

algorithm (Han et al., 2004) and ETARM (Nguyen

et al., 2017). Apriori and FpGrowth have exponential

time complexity which is not practical. ETARM pro-

poses a way to mine top-k association rules (Fournier-

Viger et al., 2012) effectively. It expands item set X

and item set Y while only reserving top-k valid associ-

ation rules with the highest support. As far as this pa-

per concerned, item set X is given and does not need

to be expanded. Item set Y contains only one item

for each placement. So this paper applies a simpliﬁed

version of ETARM to get top-k association rules.

1.2 Mining Association Rules with

Weighted Item

In 1998, Cai proposed Mining Association Rules with

Weighted Item (MARWI) (Cai et al., 1998), which

ﬁrst come up with the idea of weighted support and

weighted conﬁdence. As Cai’s deﬁnition, normal-

ized weighted support and normalized weighted con-

ﬁdence are:

w_sup(A → B) =

∑

i=1

× sup(A → B) (3)

w_con f (A → B) =

∑

i=1

× conf(A → B) (4)

where there are n items in set A ∪ B; w

means

the weight of item i; w_conf and w_sup represents

weighted conﬁdence and weighted support, respec-

tively.

MARWI is a solution for WARM problem. Let

be the proﬁt of item i, maximizing the expec-

tation of proﬁt can be achieved by maximizing the

weighted_con f idence. However, this could result

in low recommendation accuracy. To be speciﬁc, if

the proﬁt of recommended items is quite high while

their conﬁdence is very low, the weighted conﬁdence

could still be very high. In this situation, proﬁtable

but unattractive items are recommended to customers.

As a result, the shopping experience of customers is

greatly undermined. Our proposed method in Sec-

tion 3 offers an approach that increases expectation

of proﬁt while having less recommendation accuracy

loss.

1.3 Click-through Rate

Click-through Rate (CTR) (Chuklin et al., 2015) is

the ratio of users who click on a speciﬁc link to the

number of total users who view a page (Association

et al., 2014). This paper utilizes CTR as the average

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

640

Figure 2: An abstract structure of Recommendation Scenario with Click-through Rate Models 1.

prior placement click probability to predict the possi-

ble click probability of a recommended item. In the

experiment, three different CTR models are shown in

Table 1.

1.4 Structure of this Paper

This paper is structured as follows. Section 1 intro-

duces the background, the achievement and related

works. After that, section 2 introduces the deﬁnitions

and problem statement. Next, the proposed method

and algorithm is presented in Section 3. Section 4

presents experiments and empirical results. Section 5

discusses some of the challenges. Finally, the paper is

concluded in Section 6.

2 DEFINITIONS AND PROBLEM

STATEMENT

2.1 Deﬁnition

In this section, several key concepts and deﬁnitions

are introduced.

Transaction Database: Suppose there is a ﬁnite

set of items I = {i

, i

, ..., i

} which represents all

unique items or products. Transaction Database T =

, T

, ..., T

} refers to a database which stores all

paid transactions. Each transaction, with a unique

number transaction ID, is a subset of I.

Proﬁts of Items: Proﬁts of Items p indicates the prof-

its realized when an item is sold. This data is gener-

ally highly conﬁdential by its nature, and for the pur-

pose of model, we seed this data which can be down-

loaded from https://github.com/yourexpress/PPARM.

Researchers typically have access to data of the spe-

ciﬁc e-commerce providers that they are working

with, and can run the proposed method on their own

data set simply by replacing the proﬁt data ﬁle.

Set A: Set A is a set of the items in the shopping cart.

The union of set A and recommended items could be

treated as a potential transaction. That is to say, for an

item i, the higher con f (A → {i}) is, the more possi-

bility item i will be of interest to the customer.

Placement and corresponding Click-through Rate:

Placement means a location where recommended

items are displayed on the website. For example,

there are 12 placements with different items in Fig-

ure 1. Each placement s has a corresponding Click-

through Rate CT R(s) which reﬂects the average prob-

ability for that placement over all items.

Expectation of Proﬁt and Expectation of Click

Rate: The expectation of proﬁt, denoted as EOP, is

the expectation of proﬁt in the recommendation for a

single transaction. It is a measurement of how well

the recommendation algorithm is in terms of proﬁt.

The expectation of click rate, denoted as EOC, is the

expectation of click probability of all recommended

items in the recommendation for a single transaction.

Thus, EOC is the measurement of the recommenda-

tion accuracy as measured in terms of click probabil-

ity.

Recommendation Result: Recommendation result,

denoted as R, is the an arrangement of k items outputs

by the proposed method, where R = {I

, I

, ..., I

i j

means we put item i to placement j. So R is an

ordered result of k items.

Performance Score: Performance score, denoted

simply as score, is a linear weighted function of EOP

and EOC used to evaluate the recommendation result

score = EOP(R) + α EOC(R) (5)

2.2 Problem Statement

Given a transaction database T , an item proﬁt list P,

and a placement click-through rate list CT R of size k.

The problem is to maximize score by recommending

an arrangement of k items and assigning them to the

corresponding k slots in the placement.

3 PROPOSED ALGORITHM

3.1 Modeling the Problem

The problem is to ﬁnd an arrangement R =

, I

, ..., I

} of k items from items set I which can

balance EOP and EOC.

Placement-and-Proﬁt-Aware Association Rules Mining

641

Assumption 1: To calculate EOP and EOC, suppose

any two of recommended items are independent. That

is, the selection of item a is irrelevant to the selection

of item b and vice versa. For a given R we can derive:

EOC(R) =

∑

s=1

[CT R(I

, s|A)] (6)

EOP(R) =

∑

s=1

[p(i)CT R(I

, s|A)] (7)

where:

CT R(I

, s|A) = CT R(I

|s, A)CT R(s|A) (8)

CT R(I

|s, A) represents the click-through rate of item

for a speciﬁc placement s given set A; CT R(s|A)

represents the click-through rate of s given set A.

Assumption 2: The click-through rate of item i are

equal given any different placement s and the same

set A.

CT R(I

|A, s) = CT R(I

|A, s

), ∀s, s

∈ [1, k] (9)

Thus:

CT R(I

|A, s) =

CT R(I

|A). (10)

Since CT R(I

|A) is directly proportional to

con f (A → {I

}), CT R(I

|A, s) is also directly pro-

portional to con f (A → {i}):

CT R(I

|A, s) ∝ con f (A → {i}) (11)

Assumption 3: The CTR of placement s given set A

is directly proportional to the CTR of placement s:

CT R(s|A) ∝ CT R(s) (12)

Based on aforementioned assumptions, we can

simplify the EOP and EOC:

EOP(R) ∝

∑

s=1

con f (A → {I

})CT R(s)p(I

) (13)

EOC(R) ∝

∑

s=1

con f (A → {I

})CT R(s) (14)

3.2 Balancing EOP and EOC

It would be best if we can maximize EOP and EOC

simultaneously. Unfortunately, it is not always fea-

sible. To clarify this problem, we can analyze EOP

maximization problem and EOC maximization prob-

lem separately:

To maximize EOC, simply multiply top k ele-

ments in con f (A → {I

}) and CT R(s) (both sorted)

correspondingly. Thus, the problem becomes to ﬁnd

top k items with the largest conﬁdence given set A:

= arg max

i1,i2,...,ik

∑

s=1

con f (A → {I

})CT R(s) (15)

This is exactly what ARM method does.

To maximize EOP, perform the same method as

above, except conﬁdence is replaced by weighted

conﬁdence, i.e., con f (A → {I

})p(I

= arg max

i1,i2,...,ik

∑

s=1

con f (A → {I

})p(I

)CT R(s)

(16)

This is exactly what WARM method does.

However, R

is not always equal to R

. A common

case is when EOP reaches maximum, EOC is very

low and vice versa.

We introduce the performance score, denoted as

score, described in Equation 5 to evaluate the recom-

mendation result according to both EOP and EOC.

In this paper, we propose a target function to ﬁnd a

recommendation result R that gets a better score com-

pared with WARM and ARM:

= arg max

,...,i

∑

s=1

[con f (A → {I

})

∗CT R(s)p(I

)

], γ ∈ [0, 1] (17)

By varying γ, we can change the proportion of

how much we prefer the proﬁt over the conﬁdence.

Thus, WARM method becomes a special case of

our new rule where γ = 1. The ARM method becomes

another special case where γ = 0.

Our experiment shows that Equation 17 improves

the EOP signiﬁcantly while reduces the EOC slightly.

3.3 Overview of Proposed Algorithm

This section explains the proposed Placement-and-

Proﬁt-Aware Association Rules Mining (PPAARM)

algorithm to solve the problem stated in 2.2. A di-

agram of input-and-output ﬂow of the PPAARM is

illustrated in Figure 3.

In Figure 3, Item Database, Transaction History,

Proﬁts of items, γ and the Set A of items in cart are

the Input 1. These parameters can generated candi-

dates by Proﬁt-weighted Association Rules Mining

Algorithm as the Output 1. These candidates are

well balanced between proﬁt and correlation with set

A. Next, these candidates, Placements and CTR of

Placements play a role of Input 2 to generate the ﬁ-

nal results which are a group of arrangement of items

, I

, ..., I

}. Each I

indicates item i is recom-

mended to display at the location where s represents.

The notations that/ appear in Figure 3 are introduced

in section 2.1. Algorithm 1 is the pseudo-code for the

algorithm ﬂow.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

642

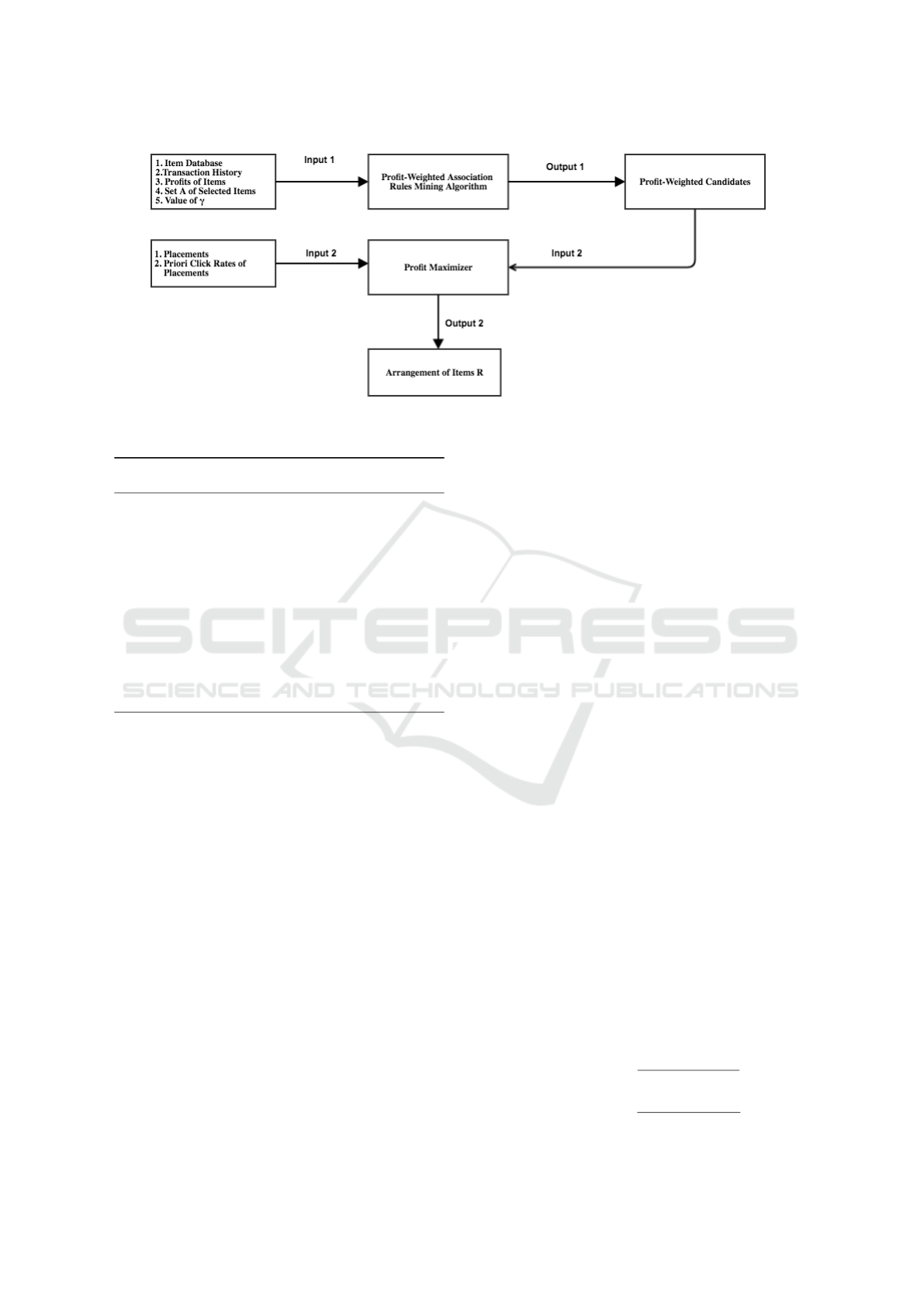
Figure 3: Input and Output Flow Diagram of PPAARM.

Algorithm 1 : Placement-and-Proﬁt-Aware Association

Rules Mining(PPAARM).

function RECOMMEND(T, I, A, p, k, γ)

Calculate con f [A → i] ∀i ∈ I − A

for all i ∈ I − A do

w_con f [A → i] ← con f [A → i] ∗ p[i]

end for

// We can get largest k elements in linear time

complexity using quick-select based algorithm

topk_w_con f ← largest_k_elements(w_con f )

sort(topk_w_con f )

return The items which each element in

topk_w_con f refers to.

end function

4 EMPIRICAL RESULTS

4.1 Basic Settings

Scenario: At the check-out page, based on the cart

and transaction history, the E-commerce website rec-

ommends 12 items to customers in 3 rows. Each row

displays 4 items.

Input data:

• Transaction History Database: The “Re-

tail” dataset in SPMF (Fournier-Viger et al.,

2016) (Brijs et al., 1999). This dataset includes

88162 transactions and 16470 unique items. Each

transaction is a sequence of items, each item is

marked with an Item ID which is an integer from

1 to 16470.

• Proﬁt Data: A dataset of proﬁt for each item. The

values of proﬁts are normalized by the maximum

proﬁt.

• Items in Cart: This data includes 100 items sets.

Each items set is a set A that is generated from

Transaction History Database. Then mark these

items sets from m = 1 to m = 100.

• Click-through Rate Models: Three click-through

rate models are presented in Table 1. Take Fig-

ure 2 as an example, the placements are marked

from s = 1 to s = 12 and customers click place-

ments are shown in CT R(s).

• Number of recommended items k: k = 12;

• γ = {0, 0.1, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0}

4.2 Set A Generator

In order to generate a group of Set A, the Set A Gen-

erator scans all items in Transaction History Database

and select unique items with top 100 highest conﬁ-

dence as the Item Pool, then select random amount of

items arbitrarily from the Item Pool as a Set A. Fi-

nally, repeat this process 100 times to get a group of

set A. The same group of set A would be used to cal-

culate all experiment results.

4.3 Evaluation Metrics

In this experiment, the total EOP is the sum of

EOP

) among all groups of set A. The total EOC

is the sum of EOP

) among all groups of set A. In

order to evaluate the experiment, total EOC and total

EOP should be normalized. Deﬁne the N as the num-

ber of A, Normalized EOP(NEOP) and Normalized

EOC(NEOC) are deﬁned respectively as

NEOP(R

) =

∑

m=1

EOP

)

(18)

NEOC(R

) =

∑

m=1

EOC

)

(19)

Placement-and-Proﬁt-Aware Association Rules Mining

643

Table 1: Click-through Rate Matrix.

Click-through Rate

CTR Model 1 CTR Model 2 CTR Model 3

Placement 1 0.1 0.1 0.1

Placement 2 0.1 0.1 0.09

Placement 3 0.1 0.1 0.08

Placement 4 0.1 0.1 0.07

Placement 5 0.05 0.01 0.01

Placement 6 0.05 0.01 0.009

Placement 7 0.05 0.01 0.008

Placement 8 0.05 0.01 0.007

Placement 9 0.01 0.001 0.001

Placement 10 0.01 0.001 0.0009

Placement 11 0.01 0.001 0.0008

Placement 12 0.01 0.001 0.0007

To evaluate the performance of the proposed al-

gorithm 1, this paper utilizes Equation 5, denoted as

score, as a metric of combined performance of EOP

and EOC. In this experiment, the score is normal-

ized. Normalized Score is the linear combination of

NEOC(R

) and NEOP(R

) as Equation 20. Further-

more, modifying α can change the preference to proﬁt

or recommendation accuracy. In this paper, α is equal

to 1, which means the performance score treats the

recommendation accuracy and the proﬁt expectation

as equally important.

NS(γ) = NEOP(R

) + αNEOC(R

) (20)

4.4 Results

4.4.1 NEOP & NEOC

In the experiment, we execute algorithm PPAARM 1

with click-through model 1. According to the re-

sults in Table 3 and Figure 4, the scatter spots of

NEOP(R

) and NEOC(R

) form a upper convex

curve. Thus the optimal point where NEOC(R

) starts

decreasing faster than NEOP(R

) exists on the curve.

To be speciﬁc, the recommended items can trade-off

proﬁt and recommendation accuracy best in this chart.

So, the proposed algorithm PPAARM can ﬁnd a better

trade-off solution between proﬁt and recommendation

accuracy.

4.4.2 Optimal Point Locating and Evaluation

According to Figure 5 and Table 3, NS(R

) achieves

the largest value when γ = 0.25. So, this point where

γ = 0.25 is the optimal point in this chart. We also set

two points where γ = 0 and γ = 1 as reference point.

Based on Equation 5, the PPAARM is equivalent

to ARM method while γ is 0; The PPAARM is equiv-

alent to MARWI method while γ is 1. By compar-

ing the evaluation metrics values of the optimal point

and reference points, we present the performance dif-

ference of PPAARM method, ETARM method and

MARWI method in Table 2.

According to Table 2, PPAARM earns much more

proﬁts than ETARM with little recommendation ac-

curacy loss, meanwhile, PPAARM achieves much

higher recommendation accuracy than MARWI with

insigniﬁcant proﬁt loss. Additionally, NS(R

) of

PPAARM is larger than ETARM and MARWI. As

NS(R

) considers both proﬁt and recommendation ac-

curacy, we can conclude that PPAARM achieves a

good balance between EOP and EOC and performs

better than ETARM method and MARWI method.

Figure 4: Trend of NEOP and NEOC when γ varies from 0

to 1 with CTR model 1.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

644

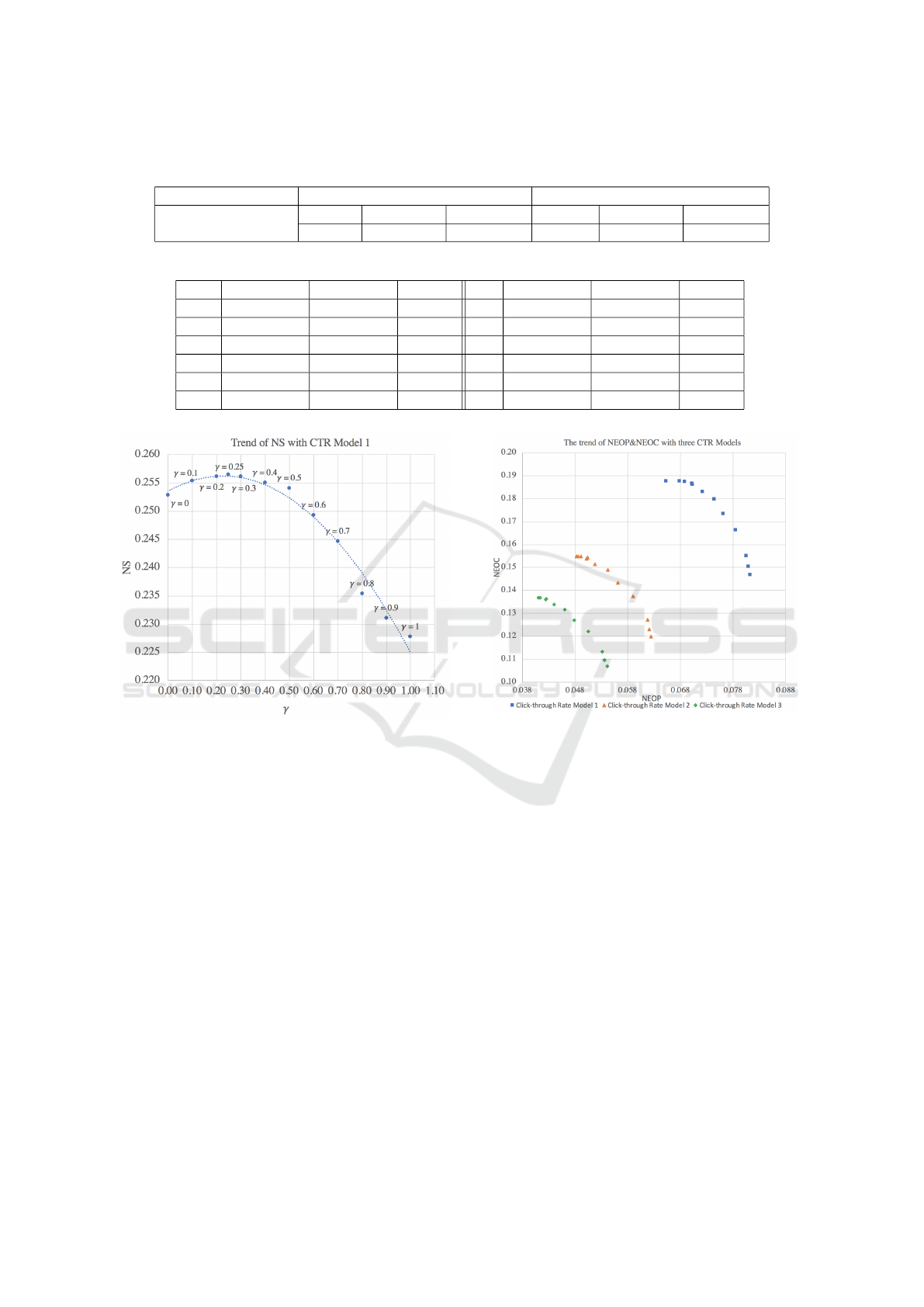
Table 2: Compare PPAARM with ETARM and MARWI. “±x%” indicates the value of PPAARM is x% larger or less than

the value of ETARM or MARWI.

ETARM(γ = 0) MARWI(γ = 1)

PPAARM(γ = 0.25)

NS(R

) NEOP(R

) NEOC(R

) NS(R

) NEOP(R

) NEOC(R

)

+1.5% +7.5% -0.6% +12.6% -13.6% +27.2%

Table 3: Experimental Results.

γ NEOP(R

) NEOC(R

) NS(R

) γ NEOP(R

) NEOC(R

) NS(R

)

0.0 0.0652 0.1876 0.2528 0.5 0.0744 0.1797 0.2541

0.1 0.0677 0.1876 0.2554 0.6 0.0761 0.1732 0.2493

0.2 0.0688 0.1874 0.2562 0.7 0.0784 0.1663 0.2446

0.25 0.0701 0.1865 0.2565 0.8 0.0804 0.1549 0.2345

0.3 0.0702 0.1860 0.2562 0.9 0.0808 0.1502 0.2311

0.4 0.0721 0.1829 0.2550 1.0 0.0811 0.1466 0.2278

Figure 5: The trend of NS when γ varies from 0 to 1 with

CTR model 1.

4.4.3 Robustness

In actual situations, CTR models are uncertain. So,

we choose three different CTR models to verify the

robustness of our proposed method. After executing

PPAARM with three different click-through models

in Table 1, we get a line chart Figure 6. Also, Figure 7

can be obtained according to Equation 20.

According to Figure 6, when γ varies from 0 to 1.

Even though these three lines are relatively far apart

on the coordinate axis, their shapes are alike. Simi-

larly, we can observe the same pattern in Figure 7.

Although Table 1 indicates the CTR models are

totally different, the conclusion in 4.4.1 and 4.4.2

remains the same. In conclusion, PPAARM is robust

wit different CTR models.

Figure 6: The trend of NEOP and NEOC when γ varies from

0 to 1 with three CTR models.

5 DISCUSSION

5.1 Data Set Limitations

In this paper, the proposed method utilizes generated

placement click-through rate and proﬁt on experiment

due to the insufﬁcient of open-source datasets that

contain placement aware data and proﬁt information

is usually very sensitive. As a result, this paper as-

sumes these two factors have little correlation and

proposes Assumption 2 and Assumption 3 in Sec-

tion 3.1. If the actual data of placement click-through

rate and proﬁt has been provided, we can use a better

model such as logistic regression (Cox, 1 01) to model

CT R(I

, s|A), thus the estimation of the click-through

rate will be more accurate.

Placement-and-Proﬁt-Aware Association Rules Mining

645

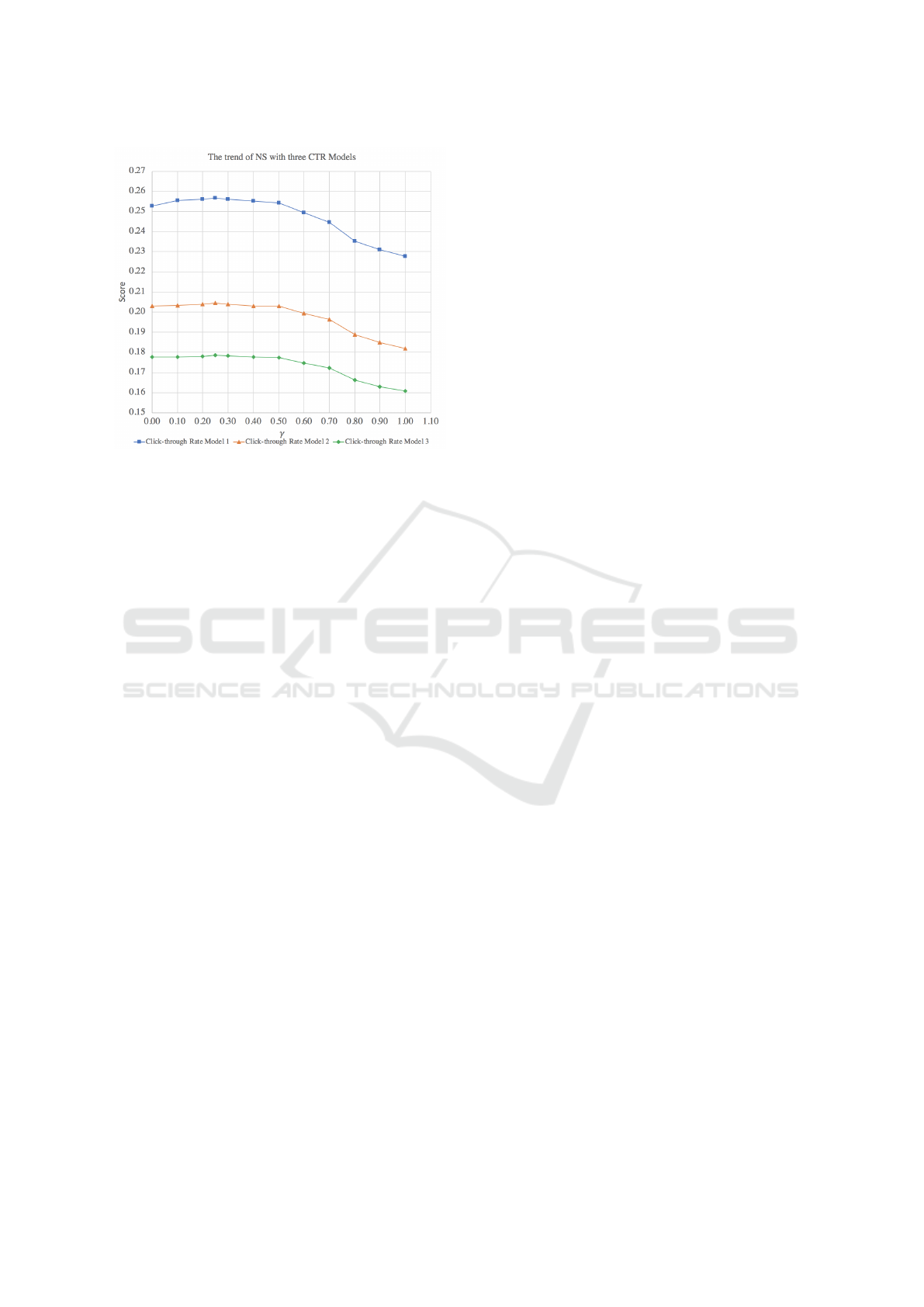
Figure 7: The trend of NS when γ varies from 0 to 1 with

three CTR models.

5.2 Adjusting γ

The parameter γ represents how much the website

prefer EOP rather than EOC. Higher EOP brings the

website more instant income while higher EOC in-

creases the recommendation accuracy, which leads to

better user experience. The larger γ is, the higher EOP

will be and the lower EOC will be.

In practical, NS(R

) is a good way to determine

the speciﬁc value of γ, since it takes both EOP and

EOC into consideration. When NS(R

) reaches a

maximum point, further increasing EOP will lead the

EOC decreasing drastically, which results in a worse

overall performance and vice versa. As a result, the

suggested value of γ should be the value that maxi-

mizes NS(R

6 CONCLUSIONS

According to the results in section 4, we can conclude

that the novel method PPAARM can ﬁnd a better so-

lution for placement-and-proﬁt-aware recommenda-

tion problem than traditional methods. This method

gets much higher EOP (Expectation of Proﬁt, a met-

ric of proﬁt) than traditional ARM method with only

little EOC (Expectation of Click Rate, a metric of re-

ommendation accuracy) losses. It can also get much

higher EOC than the traditional WARM method with

only slight decrease in EOP. Further, experiment re-

sults show that PPAARM is robust with different CTR

models.

REFERENCES

Agrawal, R., Imieli

nski, T., and Swami, A. (1993). Min-

ing association rules between sets of items in large

databases. SIGMOD Rec., 22(2):207–216.

Agrawal, R. and Srikant, R. (1994). Fast algorithms for

mining association rules in large databases. In Pro-

ceedings of the 20th International Conference on Very

Large Data Bases, VLDB ’94, pages 487–499, San

Francisco, CA, USA. Morgan Kaufmann Publishers

Inc.

Amazon.com (August, 2018). Items Related to Your Pur-

chased. http://www.amazon.com.

Association, A. M. et al. (2014). Dictionary.

Brijs, T., Swinnen, G., Vanhoof, K., and Wets, G. (1999).

Using association rules for product assortment deci-

sions: A case study. In Knowledge Discovery and

Data Mining, pages 254–260.

Cai, C. H., Fu, A. W.-C., Cheng, C., and Kwong, W. (1998).

Mining association rules with weighted items. In

Database Engineering and Applications Symposium,

1998. Proceedings. IDEAS’98. International, pages

68–77. IEEE.

Chuklin, A., Markov, I., and Rijke, M. d. (2015). Click

models for web search. Synthesis Lectures on Infor-

mation Concepts, Retrieval, and Services, 7(3):1–115.

Cox, D. (1958-01-01). The regression analysis of binary

sequences. Journal of the Royal Statistical, Society,

Series B, Methodological, 20(2):215–232.

Fournier-Viger, P., Lin, J. C.-W., Gomariz, A., Gueniche,

T., Soltani, A., Deng, Z., and Lam, H. T. (2016).

The spmf open-source data mining library version 2.

In Machine Learning and Knowledge Discovery in

Databases, volume 9853 of Lecture Notes in Com-

puter Science, pages 36–40. Springer International

Publishing, Cham.

Fournier-Viger, P., Wu, C.-W., and VS, T. (2012). Min-

ing Top-k Association Rules(MTAR). In Advances in

Artiﬁcial Intelligence, pages 61–73. Springer, Berlin,

Heidelberg.

Han, J., Pei, J., Yin, Y., and Mao, R. (2004). Min-

ing frequent patterns without candidate generation:

A frequent-pattern tree approach. Data Mining and

Knowledge Discovery, 8(1):53–87.

McMahan, H. B., Holt, G., Sculley, D., Young, M., Ebner,

D., Grady, J., Nie, L., Phillips, T., Davydov, E.,

Golovin, D., et al. (2013). Ad click prediction: a view

from the trenches. In Proceedings of the 19th ACM

SIGKDD international conference on Knowledge dis-

covery and data mining, pages 1222–1230. ACM.

Nguyen, L. T., Vo, B., Nguyen, L. T., Fournier-Viger, P.,

and Selamat, A. (2017). An Efﬁcient Top-k Aas-

sociation Rrule Mmining algorithm. applied intelli-

gence(ETARM). Applied Intelligence, 48:1148–1160.

Robinson, G. B. (1999). Automated collaborative ﬁltering

in world wide web advertising. US Patent 5,918,014.

Schafer, J. B., Frankowski, D., Herlocker, J., and Sen, S.

(2007). Collaborative Filtering Recommender Sys-

tems, pages 291–324. Springer Berlin Heidelberg,

Berlin, Heidelberg.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

646