Annealing by Increasing Resampling

in the Uniﬁed View of Simulated Annealing

Yasunobu Imamura

, Naoya Higuchi

, Takeshi Shinohara

, Kouichi Hirata

and Tetsuji Kuboyama

Kyushu Institute of Technology, Kawazu 680-4, Iizuka 820-8502, Japan

Gakushuin University, Mejiro 1-5-1, Toshima, Tokyo 171-8588, Japan

Keywords:

Annealing by Increasing Resampling, Simulated Annealing, Logit, Probit, Meta-heuristics, Optimization.

Abstract:

Annealing by Increasing Resampling (AIR) is a stochastic hill-climbing optimization by resampling with

increasing size for evaluating an objective function. In this paper, we introduce a uniﬁed view of the con-

ventional Simulated Annealing (SA) and AIR. In this view, we generalize both SA and AIR to a stochastic

hill-climbing for objective functions with stochastic ﬂuctuations, i.e., logit and probit, respectively. Since the

logit function is approximated by the probit function, we show that AIR is regarded as an approximation of

SA. The experimental results on sparse pivot selection and annealing-based clustering also support that AIR

is an approximation of SA. Moreover, when an objective function requires a large number of samples, AIR is

much faster than SA without sacriﬁcing the quality of the results.

1 INTRODUCTION

The similarity search is an important task for informa-

tion retrieval in high-dimensional data space. Dimen-

sionality reduction such as SIMPLE-MAP (Shinohara

and Ishizaka, 2002) and Sketch (Dong et al., 2008) is

known to be one of the effective approaches for efﬁ-

cient indexing and fast searching. In dimensionality

reduction, we have to select a small number of axes

with low distortion from the original space. This op-

timal selection gives rise to a hard combinatorial op-

timization problem.

Simulated annealing (SA) (Kirkpatrick and

Gelatt Jr., 1983) is known to be one of the most

successful methods for solving combinatorial op-

timization problems. It is a metaheuristic search

method to ﬁnd an approximation optimal value

of an objective function. Initially, SA starts with

high temperature, and moves in the wide range of

search space by random walk. Then, by cooling the

temperature slowly, it narrows the range of search

space so that ﬁnally it achieves the global optimum.

On the other hand, we present a method called an

annealing by increasing resampling (AIR), which is

introduced originally for the sparse pivot selection for

SIMPLE-MAP as a hill-climbing algorithm by resam-

pling with increasing the sample size and by evaluat-

ing pivots in every resampling (Imamura et al., 2017).

AIR is suitable to optimization problems that sam-

pling is used due to the computational costs, and the

value of the objective function is given by the aver-

age of evaluations for each sample. For example, in

the pivot selection problem (Bustos et al., 2001), the

objective function is given by the average of the pair-

wise distances in the pivot space for each set of sam-

ples, and pivots are selected such that they maximize

the average.

In the processes near the initial stage of the AIR,

the sample size is small and then the local optimal is

not stable and moving drastically because the AIR re-

places the previous sample with an independent sam-

ple by resampling. On the other hand, in the processes

near the ending stage of the AIR, the sample size is in-

creasing and then the local optimal is stable. This pro-

cess of AIR is similar to conventional hill-climbing

algorithms. The larger the sample size grows, the

smaller the error in the evaluation becomes. At the

ﬁnal stage, AIR works like a local search as SA. In

other words, AIR realizes behavior like SA. In addi-

tion, AIR is superior to SA on its computational costs

especially when the sample size for evaluating objec-

tive functions are very large, because AIR uses small

set of samples near the initial stage for which the eval-

uation can be done in very short time.

In the previous work (Imamura et al., 2017), we

introduce AIR for a speciﬁc problem, pivot selection.

In this paper, we show that AIR is applicable as a

more general optimization method through the uniﬁed

Imamura, Y., Higuchi, N., Shinohara, T., Hirata, K. and Kuboyama, T.

Annealing by Increasing Resampling in the Uniﬁed View of Simulated Annealing.

DOI: 10.5220/0007380701730180

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 173-180

ISBN: 978-989-758-351-3

173

view of SA and AIR. In the view, both methods are

formed as a hill-climbing algorithm using a objective

function with stochastic ﬂuctuation. The ﬂuctuation

of the evaluation in SA using acceptance rate by Hast-

ings (Hastings, 1970) can be explained by logit, and

that of AIR can be explained with probit. Since logit

can be approximated by probit, AIR can be viewed as

an approximation of SA.

The experimental results show that the global op-

timum in SA requires a large amount of computation

while cooling the temperature. On the other hand,

for AIR, increasing the size of sample for evaluating

an objective function corresponds to cooling the tem-

perature in SA. Hence, AIR can efﬁciently search the

global optimum with realizing the large number of it-

erations by increasing resampling instead of cooling

the temperature in SA without sacriﬁcing the quality

of the solution.

Furthermore, we give comparative experiments

by applying SA and AIR to two optimization prob-

lems, the sparse pivot selection for dimensional-

ity reduction using SIMPLE-MAP (Shinohara and

Ishizaka, 2002) and the annealing-based clustering

problem (Merendino and Celebi, 2013). The results

show that AIR is an approximation of SA, and AIR is

much faster than SA when the sample size for evalu-

ation is very large.

2 UNIFIED VIEW OF SA AND AIR

In this section, we give a uniﬁed view between the

simulated annealing (SA) (Kirkpatrick and Gelatt Jr.,

1983) and the annealing by increasing resampling

(AIR) (Imamura et al., 2017). The notations used are

shown in Table 1. Here, we consider the minimizing

problem of objective (energy) function E : U ×S →R,

where U is the solution space, that is, the set of all

possible solutions), and S is the sample dataset. The

goal is to ﬁnd a global minimum solution x

∗

such that

E(x

∗

,S) ≤ E(x,S) for all x ∈ U. We also use the no-

tation E(x) if the dataset S is used for evaluating ob-

jective function, i.e., E(x) = E(x,S).

2.1 Simulated Annealing

In SA, we call the procedure to allow for occasional

changes that worsen the next state an acceptance

probability (function) (Anily and Federgruen, 1987)

or acceptance criterion (Schuur, 1997). For the ac-

ceptance probability P, Algorithm 1 illustrates the

general schema for SA.

There are two acceptance probabilities com-

monly used in SA. One is a Metropolis function

Table 1: Notations.

Notation Description

t ∈ N time steps (0,1,2,. ..)

≥ 0 temperature at t

(monotonically decreasing)

S dataset for evaluating objective func-

tion E

s(t) ∈ N resampling size at t ≤ |S|

(monotonically increasing)

U solution space

x,x

∈U elements of solution space U

N(x) ⊆U neighborhood of x ∈U

E(x, S

) evaluation value for x ∈ U and dataset

⊆ S

procedure SA

// T

: the temperature at t

// S: sample data for evaluation

// rand(0,1): uniform random number

// in [0,1)

x ← initial state;

for t = 1 to ∞ do

←

randomly selected state from N(x);

∆E ← E(x

) −E(x);

ω ← rand(0,1);

if ω ≤ P(T

) then x ← x

;

Algorithm 1: Simulated annealing.

(Metropolis et al., 1953), which is a standard

and original choice in SA (Kirkpatrick and Gelatt Jr.,

1983).

(T ) = min{1,exp(−∆E/T )}.

Another is a Barker function (Barker, 1965) (or a heat

bath function (Anily and Federgruen, 1987)) P

as a

special case of a Hastings function (Hastings, 1970),

which has been introduced in the context of Boltz-

mann machine (Aarts and Korst, 1989).

(T ) =

1 + exp(∆E/T )

Consider the condition that x

is selected in N(x)

after x is selected. For the Metropolis function P

, it

holds that ω ≤ exp(−∆E/T

), which implies that

∆E + T

·log(ω) ≤ 0.

For the Barker function P

, it holds that

ω ≤

1 + exp(∆E/T

)

which implies that exp(∆E/T

) ≤

1−ω

and then

∆E + T

·logit(ω) ≤ 0, (1)

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

174

where logit(·) is the logit function deﬁned as

logit(ω) = −log



1 −ω



Now, we are to minimize the value of E(·,·). Hence,

if ∆E is less than zero, we want to transit to a “bet-

ter” state x

. The left-hand side of the acceptance con-

dition Eq. (1) is considered as ∆E with disturbance

proportional to temperature T

In SA, the temperature is gradually cooled down

to avoid getting trapped in a local minimum. On the

other hand, AIR uses the sample size of data instead

of temperature.

2.2 Annealing by Increasing

Resampling

In AIR, we consider the objective function for sam-

ple S

from dataset S , and the problem of minimizing

the average of evaluation values for samplings from

S. AIR is an optimization method taking advantage

of the nature that the smaller the sampling size is, the

larger the ﬂuctuation of evaluation is. Algorithm 2

illustrates the procedure of AIR.

procedure AIR

// T

: temperature at t

// S: sample data

x ← initial state;

for t = 1 to ∞ do

←

randomly selected state from N(x);

←

randomly selected dataset from S

such that S

⊆ S and |S

| = s(t);

if E(x

) −E(x,S

) ≤ 0 then x ← x

;

Algorithm 2: Annealing by increasing resampling (AIR).

Let N = |S|, and assume that the difference be-

tween E(x, S

) and E(x

) follows a normal distri-

bution with standard derivation σ. This assumption

is reasonable due to the central limit theory because

the objective function is obtained by the average of

evaluations for each set of independent samples.

Then, for samples S

of S such that |S

| = n, the

difference between E(x,S

) and E(x

) also fol-

lows a normal distribution with the standard error.

In other words, E(x

) − E(x,S

) is the value of

E(x

,S) −E(x, S) with ﬂuctuation of standard deriva-

tion

√

N−n

N−1

, where the term

N−n

N−1

is the ﬁnite

population correlation factor of

√

. Hence, for a uni-

formly random variable ω ranging from 0 to 1, it holds

that

E(x

) −E(x,S

) (2)

= E(x

,S) −E(x,S) +

√

N −n

N −1

·probit(ω),

where probit(·) is the inverse of the cumulative dis-

tribution function of the standard normal distribution.

Note that probit(ω) follows the normal distribution if

ω follows the uniformly random distribution between

0 and 1.

In AIR, since a subsample S

of S is selected by

resampling, the next subsample of S needs to be se-

lected independently from S

. As a similar approach,

we incrementally add a small number of samples from

S to S

without replacement. This approach allows

us a faster computation since we can reuse the previ-

ous computation for the current evaluation of sample

. However, we do not employ this approach in AIR

since the stochastic trials on the selection of state x

each time needs to be made independently. It is nec-

essary to independently select a subsample for each

trial, but to improve the efﬁciency of the process, the

current subsample may be reused, but sometimes the

subsample must be replaced.

2.3 General View of Annealing-based

Algorithms

Now we conﬁrm that the acceptance criterion of SA

based on Hasting function is

∆E + T

·logit(ω) ≤ 0, (3)

where ∆E = E(x

) − E(x), and note that E(x) =

E(x, S) if S is the dataset with maximum size to use.

In contrast, the acceptance criterion of AIR is

∆E +

√

N −n

N −1

·probit(ω) ≤ 0. (4)

Both criteria Eq. (3) and Eq. (4) are in the same

form. Also, it is known that the normal distribu-

tion is approximated by the logistic distribution; i.e.

logit(ω) ≈ σ

·probit(ω) when σ

= 1.65 as shown in

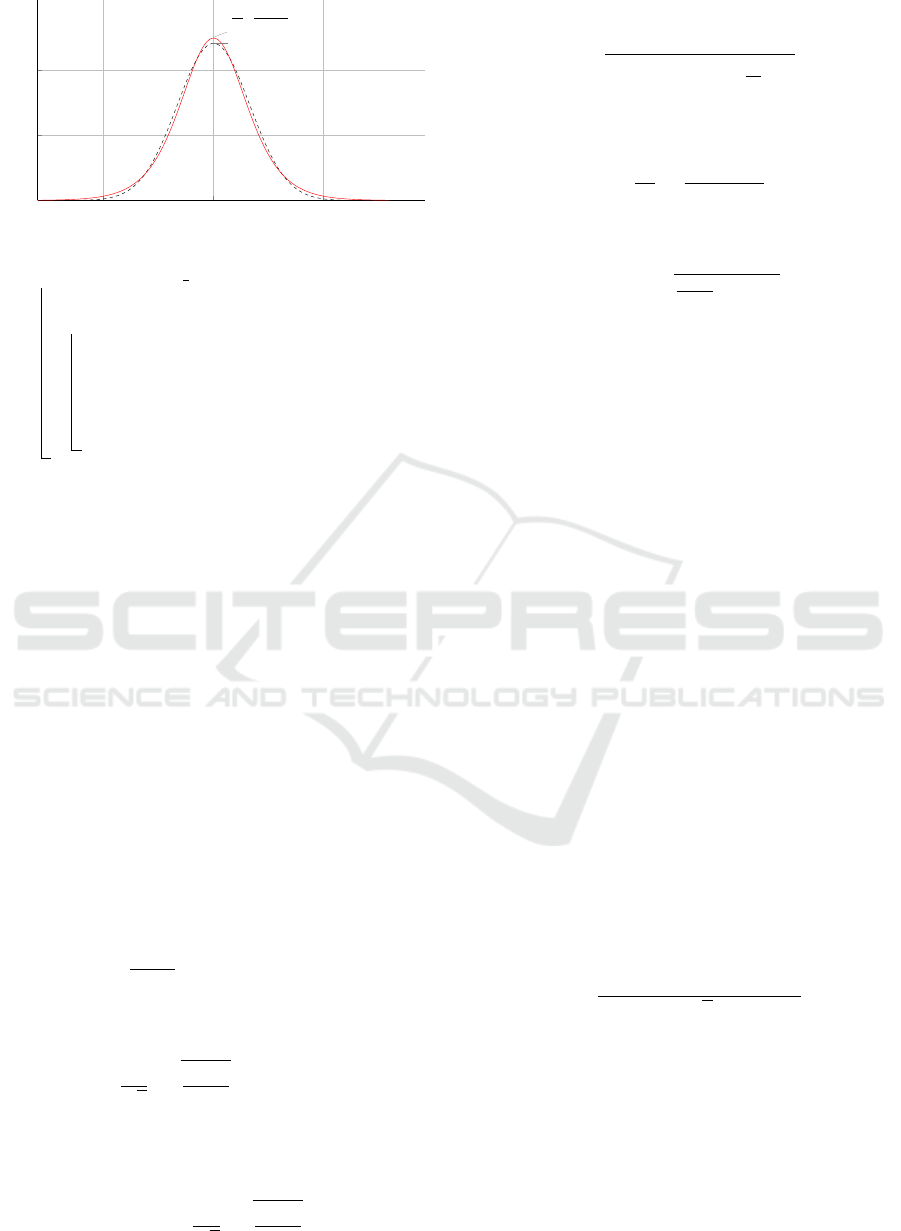
Figure 1 (Demidenko, 2013).

Therefore, we can generalize the acceptance crite-

rion of SA and AIR as follows.

∆E + α(t)·Φ

−1

(ω) ≤ 0, (5)

where α(·) is a monotonically decreasing function for

time step t (note that the dataset size n is given by

the function s(t) in AIR), and Φ

−1

(·) is the inverse of

the cumulative distribution function of a probability

distribution. Algorithm 3 shows the uniﬁed procedure

of SA and AIR.

Annealing by Increasing Resampling in the Uniﬁed View of Simulated Annealing

175

−5 0 5

0.1

0.2



1 + e

−x



N (0, 1.65)

Figure 1: Logistic distribution and normal distribution.

procedure Uniﬁed Annealing

x ← initial state;

for t = 1 to ∞ do

←

randomly selected state from N(x);

ω ← rand(0,1);

if E(x

) −E(x) +α(t) ·Φ

−1

(ω) ≤ 0

then x ← x

;

Algorithm 3: Uniﬁed procedure of SA and AIR.

2.4 Annealing Schedules of SA and AIR

The temperature cooling schedule is an important fac-

tor of SA for efﬁciency and accuracy. We consider the

corresponding sample size schedule in AIR to the ex-

ponential cooling scheme in SA. Here, we deﬁne the

schedule as follows.

T = T

·T

(0 < T

< 1),

where T

,T , and T

is the initial temperature, the cur-

rent temperature, and the ratio between T and T

, re-

spectively; Note that T

monotonically decreases as

the value of t increases. Let N, n

and n be the maxi-

mum sample size, the initial sample size, and the cur-

rent sample size, respectively. Also, let σ

be approx-

imately 1.65, and σ the standard deviation per sample.

The acceptance criterion of the next state x

in SA

is given by

∆E + T ·log



1 −ω



= ∆E + T ·logit(ω) ≤ 0. (6)

On the other hand, the acceptance criterion in AIR is

given by

∆E +

√

N −n

N −1

·probit(ω) ≤ 0. (7)

Since logit(ω) ≈ σ

·probit(ω) (Demidenko, 2013),

in order to equate formulae Eq. (6) and Eq.(7), it is

sufﬁcient to satisfy the following condition.

T ·σ

√

N −n

N −1

It follows that

n =

(N −1) ·T

·T

+ 1

By noting that T

= 1 and n = n

when T = T

, it holds

that

N −n

(N −1)n

Hence, we have

s(t) = n =

N−n

·T

+ 1

. (8)

The sample size n at time step t is given by the

function of t. Note that s(0) = n

. This for-

mula bridges the relationship between the tempera-

ture cooling scheduling T = T

·T

in SA and the sam-

ple size scheduling in AIR. By using the same ratio T

between SA and AIR, we can consider that two ap-

proaches are fairly compared in the experiments.

3 EXPERIMENTAL RESULTS

3.1 AIR Approximated by SA

In this experiment, we consider how much AIR is

approximate to SA by using MCMC (Markov chain

Monte Calro method for Metropolis-Hastings algo-

rithm), which is the basis of SA. We use MCMC in-

stead of optimization for evaluating the accuracy be-

cause it is necessary to evaluate the accuracy of distri-

bution estimation of the objective function regardless

of scheduling.

We employ the correlation coefﬁcient ρ as the ap-

proximation accuracy between the estimated distribu-

tion and the actual distribution with sampling points,

and the approximation error as 1 −ρ. A simple one-

dimensional function shown below is used as the ob-

jective function (this function itself is not essential).

y =

0.3e

−(x−1)

+ 0.7e

−(x+2)

√

This objective function is the mixture of two normal

distributions with two maxima. Experiments are con-

ducted in the following six acceptance criteria:

1. Metropolis Acceptance Criterion:

ω ≤ min{1,exp(−∆E/T

)}.

2. Hastings Acceptance Criterion:

ω ≤ min{1,exp(−∆E/T

)}.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

176

3. Φ

−1

(ω) = log(ω):

∆E + T

·log(ω) ≤ 0.

4. Φ

−1

(ω) = logit(ω):

∆E + T

·logit(ω) ≤ 0.

5. Φ

−1

(ω) = 1.60 ·probit(ω):

∆E + T

·1.60 ·probit(ω) ≤ 0.

6. Φ

−1

(ω) = 1.65 ·probit(ω):

∆E + T

·1.65 ·probit(ω) ≤ 0.

As shown in Section 2.1, the criterion (1) is equiv-

alent to the criterion (3), and the criterion (2) is to

the criterion (4) theoretically. The criteria (5) and (6)

correspond to the acceptance criteria in AIR which

approximate Hastings acceptance criterion by setting

σ = 1.60 and σ = 1.65, respectively as stated in the

condition of Eq. (4).

−5

−4

−3

−2

Number of Transitions

Estimation Error

1. Metropolis

2. Hastings

3. log(ω)

4. logit(ω)

5. 1.60 ·probit(ω)

6. 1.65 ·probit(ω)

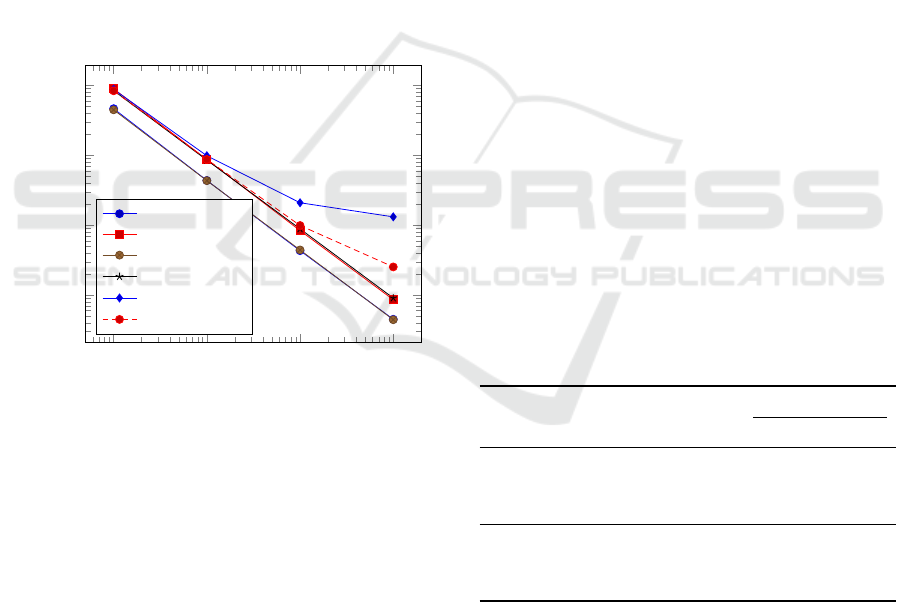
Figure 2: Estimation errors in MCMC with six acceptance

criteria.

In the experimental setting, we discard the initial

transitions as the burn-in phase. Then, we evalu-

ate the estimation errors with 1000 discrete points of

correlation coefﬁcients. Each estimation is carried out

ten times, and the average is taken as the estimation.

Figure 2 shows the estimation errors for each criteria

obtained by the experiment.

Due to the theoretical correspondences, the esti-

mation error of (1) Metropolis and (3) log(ω), and

that of (2) Heistings and (4) logit(ω) are almost

identical, respectively. As for the criteria (5) 1.60 ·

probit(ω) and (6) 1.65 ·probit(ω), up to the number

of transitions of 10

, it is observed that both are good

approximations of SA with Hastings acceptance cri-

terion. Although, beyond 10

transitions, a signif-

icant difference appears as shown in Figure 2, it is

not a concern since the number of transitions at each

temperature is less than 10

in real computations of

AIR. Also, it is not necessary to care about the op-

timal value of σ

because the temperature T absorbs

the effect of σ, and the optimal value of σ

is implic-

itly computed in practice.

3.2 Sparse Pivot Selection

We apply AIR to the sparse pivot selection for di-

mensionality reduction using SIMPLE-MAP (Shino-

hara and Ishizaka, 2002). We use real image data for

the pivot selection. In the dimension reduction, we

project data points in a high-dimensional space into a

lower dimensional space. The number of pivots in

SIMPLE-MAP corresponds to the dimensionality of

the projected space. It is required to select a small

number of pivots so that all pairwise distances be-

tween data points are preserved as much as possible

after projection. We call this problem sparse pivot se-

lection. The number of data in images is 6.8 million

extracted from 1,700 videos and dimensionality n of

data in images is 64. In this experiment, we reduce the

number of dimensions to eight using SIMPLE-MAP.

We use the average value (Ave.) and the standard de-

viation (S.D.) for distance preservation ratio (DPR)

to evaluate pivot sets using randomly selected 5,000

pairs of features. AIR ﬁnds the set of pivots with max-

imum distance preservation ratio. We set the compat-

ible annealing schedule between SA and AIR accord-

ing to Eq. (8). The experimental platform is a 64-bit

mac OS X machine with 2.53GHz Intel

Core

and 8GB RAM.

Table 2: Comparison SA with AIR in pivot selection.

DPR(%)

#transitions Time (sec) Ave. S.D.

SA 11 ×10

149.7 57.06% 0.2763

40 ×10

511.1 57.36% 0.2379

400 ×10

4864.0 57.52% 0.1485

AIR 11 ×10

28.80 57.10% 0.2260

40 ×10

70.49 57.36% 0.1333

400 ×10

592.5 57.57% 0.1547

Table 2 shows the results for each number of tran-

sitions. The best value for each performence measure

is highlighted in bold face. Note that a larger the aver-

age value for DPR implies, a better result. This exper-

iment shows that AIR achieves almost the same accu-

racy with much faster speeds (from 5.2 to 8.2 times

faster) than SA.

Annealing by Increasing Resampling in the Uniﬁed View of Simulated Annealing

177

3.3 Annealing-based Clustering

In this experiment, we focus on a clustering method

using SA. The typical objective function to minimize

is the sum of squared errors (SSE) between each point

and the closest cluster center.

Merendino and Celebi proposed an SA clustering

algorithm based on center perturbation using Gaus-

sian mutation (SAGM, for short) (Merendino and

Celebi, 2013). SAGM employs two cooling sched-

ules, the multi Markov chain (MMC) approach, and

the single Markov chain (SMC) approach. We denote

SAGM with MMC schedule by SAGM(MMC), and

SAGM with SMC schedule by SAGM(SMC). They

reported that SAGM(SMC) generally converges sig-

niﬁcantly faster than the other SA algorithms with-

out losing the quality of solutions as comparison with

the others through the experiments using ten datasets

from the UCI Machine Learning Repository (Dheeru

and Karra Taniskidou, 2017). Table 3 shows the de-

scription of the datasets used in the experiments.

Table 3: Datasets (N: #points, d: #attributes, k: #classes).

ID Data Set N d k

1 Ecoli 336 7 8

2 Glass 214 9 6

3 Ionosphere 351 34 2

4 Iris Bezdek 150 4 3

5 Landsat 6435 36 6

6 Letter Recognition 20000 16 26

7 Image Segmentation 2310 19 7

8 Vehicle Silhouettes 846 18 4

9 Wine Quality 178 13 7

10 Yeast 1484 8 10

We implement both SAGM(MMC) and

SAGM(SMC) in C++, and AIR with the corre-

sponding schedulings MMC and SMC according

to Eq. (8), denoted by AIR(MMC) and AIR(SMC),

respectively. Then, we compare the quality of

solutions and the running time for the datasets. The

experiments are conducted with an Intel

Core

i7-

7820X CPU 3.60Hz, and 64G RAM, running Ubuntu

(Windows Subsystem for Linux) on Windows 10.

The quality of the solutions is evaluated by SSE.

Then, a smaller SSE implies a better result.

Table 4 shows the quality of solutions (SSE) with

the standard deviations in parenthesis by comparing

SAGM(MMC) with AIR(MMC) in the upper table,

and by comparing SAGM(SMC) with AIR(SMC) in

the lower table. It is conﬁrmed that there is no sig-

niﬁcant differences between SAGM and AIR in the

quality of solutions.

Table 5 shows the running time for both SAGM

Table 4: Quality of solutions (Sum of squared errors).

Data ID SAGM(MMC) AIR(MMC)

1 17.55 (0.23) 17.53 (0.20)

2 18.91 (0.69) 19.05 (0.45)

3 630.9 (19.76) 638.8 (43.42)

4 6.988 (0.03) 6.986 (0.02)

5 1742 (0.01) 1742 (0.01)

6 2732 (14.17) 2720 (4.20)

7 411.9 (18.11) 395.2 (10.68)

8 225.7 (4.54) 224.6 (3.82)

9 37.83 (0.23) 37.81 (0.23)

10 58.90 (1.65) 59.08 (0.74)

Data ID SAGM(SMC) AIR(SMC)

1 17.60 (0.29) 17.56 (0.24)

2 18.98 (0.73) 19.08 (0.46)

3 630.9 (19.76) 646.8 (57.14)

4 6.988 (0.03) 6.991 (0.03)

5 1742 (0.01) 1742 (0.01)

6 2738 (17.11) 2722 (5.10)

7 413.8 (19.88) 396.2 (11.26)

8 225.8 (4.65) 224.6 (3.83)

9 37.85 (0.27) 37.82 (0.24)

10 59.36 (1.61) 59.04 (0.67)

and AIR. AIR is signiﬁcantly faster than SAGM for

all datasets except for the 9th dataset in both schedul-

ing MMC and SMC. For the 9th dataset, SAGM

slightly outperforms AIR because the size of the

dataset is very small (n = 178).

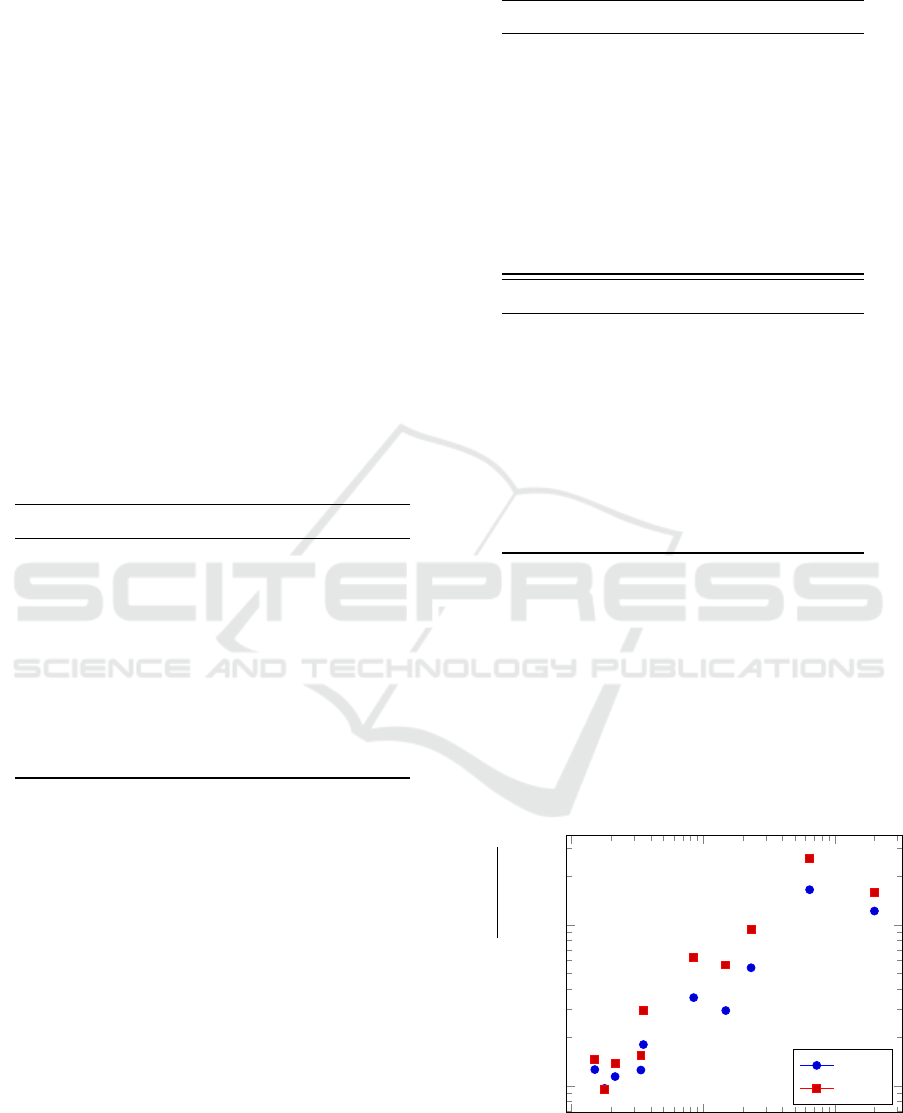
To observe the effect of the data size N on the

running time, Figure 3 show the running time ratios

of SAGM to AIR for each scheduling of MMC and

SMC. As can be seen from the ﬁgure, the larger the

data size is, basically the faster AIR is, and the sam-

pling effect of AIR appears.

Data size (N)

Running time ratios (

SAGM[sec]

AIR[sec]

)

MMC

SMC

Figure 3: Runnning time ratios of SAGM to AIR.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

178

Table 5: Average running time (sec.).

Data ID SAGM(MMC) AIR(MMC)

1 1.727 1.376

2 0.719 0.629

3 1.549 0.857

4 0.139 0.110

5 17.40 1.051

6 167.4 13.72

7 3.285 0.606

8 1.298 0.367

9 0.786 0.814

10 2.854 0.971

Data ID SAGM(SMC) AIR(SMC)

1 0.282 0.182

2 0.125 0.091

3 0.281 0.095

4 0.022 0.015

5 3.216 0.125

6 28.82 1.803

7 0.523 0.056

8 0.219 0.035

9 0.141 0.149

10 0.497 0.088

4 CONCLUSIONS

A sampling-based meta heuristics method, Annealing

by Increasing Resampling (AIR), is a stochastic hill-

climbing optimization by resampling with increasing

size for evaluating an objective function. It uses the

resampling size n instead of temperature T in the sim-

ulated annealing (SA). We showed a uniﬁed view of

SA and AIR by the approximation of logit and probit

in the hill-climbing algorithm.

We also showed the relationship between sample

size n in AIR and temperature T in SA from the the-

oretical point of view. Since the resampling size n

exponentially increases up to the total sample size N

when a common resampling size scheduling is em-

ployed. Hence, the size n is not affected by N un-

til the ﬁnal step. This is the reason why AIR is

much faster than the conventional SA especially for

the large dataset.

We also conducted experiments to support our

view, and showed that AIR achieves almost the same

quality of solutions with much faster computation

than SA by applying AIR to the sparse pivot selection

problem and the clustering problem.

The superiority of AIR over SA is that the compu-

tational cost for transitions using small sample sets,

corresponding to transisions in the high temperature

of SA, is small. For actual problems, a stable opti-

mization by SA is necessary to increase the number

of transitions at the high temperature. Even in such

cases, when using AIR, it is possible to improve the

performance of optimization without increasing the

cost much. The scheduling that takes advantage of the

beneﬁts of AIR is one of the important future works.

Another important future work is the implementa-

tion of efﬁcient similarity search in high dimensional

spaces using dimensionality reductions and sketches

highly optimized by AIR.

ACKNOWLEDGMENTS

The authors would like to thank Prof. M. Emre

Celebi who kindly provides us with the source codes

of SAGM with both SMC and MMC schedules.

This work was partially supported by JSPS

KAKENHI Grant Numbers 16H02870, 17H00762,

16H01743, 17H01788, and 18K11443.

The ﬁrst author would like to thank several pro-

gramming contests because providing the motivation

of this paper. In many problms in the contests, pa-

rameter tuning plays a crucial role for efﬁcient com-

putations and he actually has applied AIR to the au-

tomated parameter tuning in programming contests,

and remarkable achievements have been made so far

by AIR.

REFERENCES

Aarts, E. and Korst, J. (1989). Simulated annealing and

Boltzmann machines: A stochastic approach to com-

binatorial optimization and neural computing. Wiley.

Anily, S. and Federgruen, A. (1987). Simulated anneal-

ing methods with general acceptance probabilities.

J. App. Prob., 24:657–667.

Barker, A. A. (1965). Monte Carlo calculations of the radial

distribution functions for a proton-electron plasma.

Aust. J. Phys., 18:119–133.

Bustos, B., Navarro, G., and Ch

avez, E. (2001). Pivot se-

lection techniques for proximity searching in metric

spaces. In Proc. Computer Science Society. SCCC’01.

XXI Internatinal Conference of the Chilean, pages 33–

40. IEEE.

Demidenko, E. (2013). Mixed Models: Theory and Appli-

cations with R. Wiley, 2nd edition.

Dheeru, D. and Karra Taniskidou, E. (2017). UCI ma-

chine learning repository. University of California,

Irvine, School of Information and Computer Sciences,

http://archive.ics.uci.edu/ml.

Dong, W., Charikar, M., and Li, K. (2008). Asymmetric

distance estimation with sketches for similarity search

Annealing by Increasing Resampling in the Uniﬁed View of Simulated Annealing

179

in high-dimensional spaces. In Proc. 31st ACM SIGIR,

pages 123–130.

Hastings, W. K. (1970). Monte Carlo sampling methods

using Markov chains and their applications. Biome-

toroka, 57:97–109.

Imamura, Y., Higuchi, N., Kuboyama, T., Hirata, K., and

Shinohara, T. (2017). Pivot selection for dimension

reduction using annealing by increasing resampling.

In Proc. Learn. Wissen. Daten. Analysen, (LWDA’17),

pages 15–24.

Kirkpatrick, S. and Gelatt Jr., C. D. (1983). Optimization

by simulated annealing. Science, 220:671–680.

Merendino, S. and Celebi, M. E. (2013). A simulated an-

nealing clustering algorithm based on center perturba-

tion using Gaussian mutation. In Proc. FLAIRS Con-

ference, pages 456–461.

Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., and

Teller, A. H. (1953). Equation of state calculations by

fast computing machines. J. Chem. Phys., 21:1086–

1092.

Schuur, P. C. (1997). Classiﬁcation of acceptance

criteria for the simulated annealing algorithm.

Math. Oper. Res., 22:266–275.

Shinohara, T. and Ishizaka, H. (2002). On dimension re-

duction mappings for approximate retrieval of multi-

dimensional data. In Arikawa, S. and Shinohara, A.,

editors, Progress in Discovery Science, volume 2281

of LNCS, pages 224–231. Springer.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

180