
Multi-agent Planning System for Target Application of Earth Remote
Sensing Space Systems for Solving Precision Farming Tasks
Petr Skobelev, Vitaly Travin, Elena Simonova, Dmitry Mishutin, Vladimir Galuzin and
Anastasiya Galitskaya
Samara National Research University, Samara, Russia
Vladimir.Galuzin@gmail.com, An14215@Yandex.Ru
Keywords: Satellite, Ground Station, Earth Remote Sensing, Multi-agent Technology, Multi-agent System, Target
Planning, Precision Agriculture.
Abstract: The paper considers the task of constructing a schedule for target application of space remote sensing systems
for solving problems of precision farming. It also proposes a method of their solution using multi-agent
technology. Presented models and algorithms allow for solving the urgent problem of network interaction
between heterogeneous spacecraft group devices for implementation of enlarged and detailed territory
surveys, as well as adaptive planning of user requests for shooting. Results of experiments demonstrate higher
efficiency of the developed algorithms on large-scale problems in comparison with methods of traditional
centralized planning.
1 INTRODUCTION
Modern agriculture is increasingly shifting towards an
intensive type of development, one of the most
promising tools of which is precision farming.
Precision farming is a system of agricultural
production, which uses information technology,
extracting data from many different sources, and
ensuring adoption of optimal decisions in management
of an agricultural enterprise. The basis of the system is
the use of accurate maps of fields with all their
characteristics. Taking into account a large number of
factors makes it possible to get a detailed map of
individual sections of the field, assess their condition
and, if necessary, promptly adjust the production
process. To speed up the process of collecting relevant
data on the current state of farmland, it is helpful to use
space systems of Earth remote sensing (Liaghat, 2010)
which is an up-and-coming trend now.
Analysis of shooting results helps quickly and
accurately assess the area of agricultural land, the state
of crops: impurity, sparseness, death after drought,
flooding or other damaging factors, and trace stages of
their phenological development. All this information
helps respond quickly to changes in the state of crops,
and make timely decisions, which leads to an increase
in efficiency of farming in general (McCabe, et al.,
2016).
As part of implementation of this methodology, the
Samara National Research University is designing a
space system consisting of a group of AIST satellites
(two of them are in orbit, and five are planned to be
launched soon) with multispectral equipment for
receiving index characteristics of agricultural fields
and ground stations (Kirilin, 2017). Accordingly, there
appears the task of planning target application of Earth
remote sensing space systems for solving precision
farming tasks.
The first chapter of this paper discusses the need to
use data from Earth remote sensing survey for
precision farming. The second chapter describes this
problem in more detail and proposes the method for its
solution using multi-agent technology. The third
chapter provides statement of the planning problem.
The fourth chapter describes the data model used in the
planning process. The fifth chapter thoroughly
considers the planning stages. The sixth chapter proves
effectiveness of the used technologies and algorithms,
based on results of experiments. Conclusions suggest
further stages for development of the system.
Skobelev, P., Travin, V., Simonova, E., Mishutin, D., Galuzin, V. and Galitskaya, A.
Multi-agent Planning System for Target Application of Earth Remote Sensing Space Systems for Solving Precision Farming Tasks.
DOI: 10.5220/0007382706470654
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 647-654
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
647

2 PROBLEM DESCRIPTION AND
PROPOSED APPROACH TO ITS
SOLUTION
The task of constructing a schedule for target
application of space systems for conducting
operational object sounding is as follows: based on
applications from users for monitoring agricultural
fields during a specified period with the given
frequency, and taking into account restrictions on
image characteristics, the system forms a
comprehensive plan for execution of applications,
satisfying the given requirements (Darnopykh,2004).
Complexity of this task lies in heterogeneity of
technical characteristics and principles of organization
of onboard equipment of the satellite, as well as in large
dimensions: dozens of satellites and ground stations
are used, and a large number of point-type observation
objects is specified. The period for performing
shooting or data transmission operations is limited by
a non-permanent visual contact between satellites and
observation objects, as well as by the radio contact
between satellites and ground stations.
Limitations on technical characteristics of onboard
equipment and external restrictions (cloudiness,
illumination, etc.) are constraining performance of
operations. The presence of several devices increases
the number of potentially possible surveys of ground
objects, which leads to multivariance of shooting
plans. It is necessary to ensure prompt decision-making
without recalculating the entire schedule when a new
event appears in multi-criteria environment.
Traditional centralized planning is based on
mathematical methods: branch and bound method,
nonlinear programming, mathematical and dynamic
programming, discrete optimization, constraint
programming, genetic algorithms.
Disadvantages of centralized planning are the
following: determinacy and complexity of taking into
account rapidly changing conditions, lack of reliable
information about the current situation, loss of
schedule adequacy over time. It is possible to
overcome these disadvantages through the use of
distributed approach, in particular, multi-agent
approach to planning.
The Distributed Constraint Optimization Problem
(DCOP) methodology implements the use of agents in
optimization problems with constraints in distributed
systems (Meisels, 2008). The algorithms take into
account the network structure of the problem. The
general principle of such algorithms is decentralization
in decision-making, dynamic nature of emerging
decisions and gradual striving for equilibrium in
conditions when in the presence of external influences
the multi-agent system finds a new equilibrium
position. However, a disadvantage of distributed
algorithms is exponential growth either of the number
of messages exchanged by agents or of their volume
(Yokoo, 2001, Petchu, 2009). To reduce growth
various heuristics are used.
(Pinto, et al., 2018) discusses a method for
optimizing planning of interaction in a group of
satellites and ground stations, taking into account
priorities and operational constraints. In (Wörle, et al.,
2015), a system of incremental mission planning for
spacecrafts is described, in which operations are
rescheduled in the shortest possible time to meet new
restrictions and rules.
For practical solution of the planning problem for
survey schedule, it is proposed to divide the planning
process into two stages:
1. Conflict-free planning, the goal of which is to
obtain initial acceptable schedule.
2. Proactive planning that tries to improve the
resulting schedule.
When planning, it is necessary to dynamically
adjust the schedule of target application of the space
system as new applications are received, application
parameters or composition of the space system change,
or unpredictable events, related to meteorological
conditions or equipment failures, happen.
Thus, the planning system for target application of
the Earth remote sensing satellites can be attributed to
complex adaptive systems, for efficient management
of which the principle of adaptive restructuring of
decisions and action plans for real-time events is
proposed (Rzevski, 2014).
For the second planning stage, a multi-agent
approach has been chosen, since it has proven practical
effectiveness in tasks requiring operational solutions
(Wooldridge, 2009, Shoham, 2009, Skobelev, et al.,
2016).
As a result of agent interaction, the plan obtained
at the stage of conflict-free planning is adaptively
adjusted by resolving conflicts and re-planning of tasks
in order to achieve the best option for their possible
placement compared to the current one, in order to
improve the quality of the whole schedule (Skobelev,
et al., 2016).
3 DESCRIPTION OF THE
PLANNING PROBLEM
To build a schedule for target application of a swarm
of satellites, a simplified mathematical model of the
ERS space system is used.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
648

The model is defined by five sets <S,G,P,C,F>:
S = {s
i
},i= is the satellite set, in which each
satellite s
i
is characterized by orbital elements and
characteristics of onboard equipment;
G =
is the set of ground stations, where
is the set of transmitting
stations, and
is the set of
receiving stations. Each station g
k
and
is
characterized by its location, speed of receiving and
transmitting data, divergence angle, as well as the
possibility of using it to send a shooting program
and/or receive images;
P = {p
j
}, j=) is a set of observation objects,
in which each object p
j
represents an application for
survey and is a point-type object described by its
location;
C is a set of restrictions, such as the time interval
[
], in which it is necessary to perform
shooting of the object p
j
, shooting conditions
(minimum angle of Sun elevation), requirements
for characteristics of the used imaging equipment
and spatial resolution (roll and pitch angle of the
satellite during shooting);
F is the objective function.
It is required to create the shooting schedule for the
observation object by a group of satellites, compiled in
accordance with the criterion of minimizing the
interval between the possible start of shooting
and the end of transmitting the shooting results to the
ground station. The criterion is given by the objective
function F:
(1)
,
(2)
where:
is the time of receiving the image of
the j-th observation area by the ground station.
The resulting schedule must meet the following
restrictions:
1. Visibility between the satellite s
i
and the
observation object p
j
during shooting
;
2. Visibility between the satellite s
i
and the
transmitting ground station g
k
during transmitting
the shooting program
3. Visibility between the satellite s
i
and the
receiving ground station g
r
during transmitting
the shooting results
4. Availability of free space in the onboard storage
device of the satellite;
5. Consistency in the sequence of transmitting the
shooting program, the shooting itself, and
transmission and reception of the shooting
results;
6. Satellites and ground stations can simultaneously
perform no more than one operation.
4 DESCRIPTION OF THE
PLANNING PROCESS DATA
MODEL
The developed system uses an information data model.
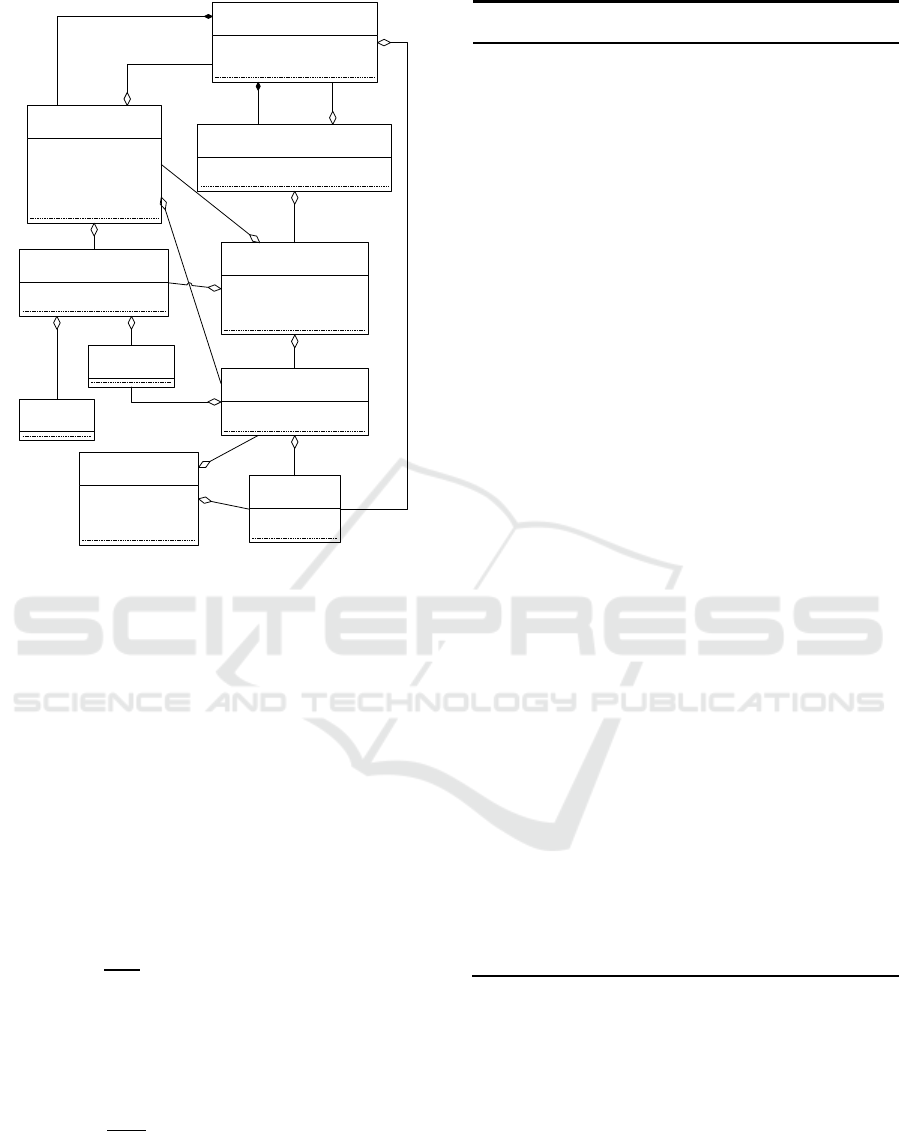
Its simplified structure is shown in Fig. 1.
The Task class is a task that needs to be scheduled.
This class has attributes that define the actual
timeframe for planning (startTime, endTime). Each
task must contain one or more operations (objects of
the Requirement class). Relations within a pair of
operations are defined through objects of the
RequirementRules class. Requirement must specify the
type of property that the resource must possess in order
to perform the operation.
The Resource class describes a resource whose
usage time needs to be scheduled. Each object of the
Resource class can be associated with one or more
objects of the Capability class, specifying the
capabilities that this resource can provide.
The Evaluation class is a possible placement of one
task operation. It shows duration of use of the resource
capability (the Capability class object) for the
operation specified by a specific time interval
(startPlanTime and endPlanTime) within the selected
allocation slot (startSlotTime and endSlotTime). The
CompoundEvaluation class represents a variant of
possible placement of a task with all its operations.
This class contains a list of objects of the Evaluation
class corresponding to each operation within the task.
The Assignment class represents the current
placement of operations for the scheduled task. The
PlacementConflict class describes placement conflicts
for operations that occurred during scheduling.The
information data model is the basis of ontology of the
planning system, which can describe the model of any
situation with the help of concepts and relations
between them. An introduction to the ontology of
description of action scenarios is also possible
(Skobelev, 2012).
Multi-agent Planning System for Target Application of Earth Remote Sensing Space Systems for Solving Precision Farming Tasks
649
CompoundEvaluation
evaluations: List<Evaluation>
task: Task
placeConflicts: List<PlaceConflict>
PlacementConflict
conflictAssignment: Assignment
placeEvaluation: CompoundEvaluation
Assignment
requirement: Requirement
capability: Capability
startTime: long
endTime: long
Evaluation
requirement: Requirement
capability: Capability
startSlotTime: long
endSlotTime: long
startPlanTime: long
endPlanTime: long
Capability
resource: Resource
capabilityType: CapabilityType
Requirement
task: Task
capabilityType: CapabilityType
RequirementRule
task: Task
reqRight:Requirement
reqLeft: Requirement
rule: String
Task
startTime: long
endTime: long
CapabilityType
Resource
Figure 1: System information data model.
5 ADAPTIVE SPACE SURVEY
SCHEDULING
There are two stages of planning a shooting schedule
for an observation object.
5.1 Stage of Conflict-free Planning
First, conflict-free planning is performed. Its purpose
is to quickly obtain an initial acceptable schedule with
any level of quality. The solution received at this stage
can show the main bottlenecks of the schedule and
becomes a reference point for further improvements.
Initially, all tasks for shooting
where M is the number of
observation objects, are placed in the queue. After that,
for each task
j
a search is performed for no more than N
options for possible placement according to the Al
Algorithm 1.
As a result of the search, a set of options is
received for possible placement of the task
j
–
C={
}, w=, where W is the number of possible
placement options found. All variants
are sorted
in descending order of the value of the objective
function Fj (2). After that, an attempt is made to
schedule task
j
in accordance with the best placement
Algorithm 1: Algorithm for finding options for possible
placement.
Input: p
j
– observation object, corresponding to task
j
, S –
set of satellites,
– set of transmitting stations,
– set
of receiving stations, C – set of placement options
Output: Set of possible placement options for task
j
1:
2:
For p
j
, the search for the earliest visibility
, corresponding to satellite s
i
,
is performed, which is limited by the time interval
[
]:
3:
if
exists then
4:
5:
Search is performed for the nearest visibility
interval
between the satellite
and the transmitting ground station g
k
within the
period [
]:
6:
if
exists then
7:
8:
Search for the nearest visibility interval between
the satellite and the receiving ground station g
r
is
performed for transmitting the shooting results
within the period
[
]:
9:
if
exists then
10:
The found intervals form a variant of possible
placement for task
j
:
11:
The newly received options for possible
placement are added to the set C: addOption(
,C)
12:
13:
go to line 8
14:
end if
15:
16:
go to line 5
17:
end if
18:
19:
go to line 2
20:
end if
option from the point of view of the objective
function, according to the Algorithm 2.
After this, the task is placed in the queue again.
The conflict-free stage is completed if, during the
next planning iteration, there are no new options for
possible placement for any tasks. After that, the stage
of proactive planning begins.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
650

Algorithm 2: Placement Algorithm.
Input: task
j
, C – set of placement options, SA –
set of assignments representing the current
schedule
Output: Set of assignments for task
j
1:
for
do
2:
In case of violation of the limitation for
simultaneous performance of operations of
satellites and ground stations, conflicts occur:
conflicts =findConflicts(
, SA )
3:
if conflicts is empty then
4:
assignments = createAssignments(
)
5:
addToSchedule( assignments, SA )
6:
markAsPlanned( task
j
)
7:
return assignments
8:
else
9:
Resolve conflicts by forming new options
of possible placement after removing conflict
intervals from the task
j
execution interval
[
]:
options = removeConflicts(task
j
, conflicts)
10:
The newly received placement options
for possible placement are added to the
set C:
addOptions(options,C)
11:
end if
12:
end for
5.2 Stage of Proactive Planning
The following list of agent classes is proposed to
improve the schedule obtained during the conflict-free
planning stage:
1. RootTaskActor – the agent exists in a single copy,
and is responsible for starting and stopping proactive
planning and managing creation of task agents.
Functions:
creation of task agents after the event of the end of
the conflict-free planning stage;
creating and deleting task agents for arising events;
creating task agents to which the message has been
sent, but they have not yet been created;
tracking the number of task agents to determine the
condition for stopping the proactivity stage.
2. TaskActor – the agent is responsible for making
permutations in the schedule. It has satisfaction
function (SF) (Mayorov, 2015), which allows it to
determine evaluation of the current satisfaction of its
demands:
,
(3)
,
(4)
where
is the current option of possible
placement of the task to shoot the observation object,
is the agent satisfaction function,
SF is the system satisfaction function.
It can also change its position at the request of
another task agent. In the absence of vacant possible
placement options, it can create nested proactivity. To
resolve conflicts, it creates the
ProactiveBroadcastWorker agent.
3. ProactiveBroadcastWorker – the agent is
responsible for polling conflict operations in order to
move them or remove them from the schedule.
Permutations of conflict operations are accompanied
by a change in the values of their satisfaction functions.
These values are summed up and on the basis of the
result obtained, it is decided whether it is necessary to
apply this permutation.
At the stage of proactive planning, task agents try to
improve their objective functions by asking conflicting
tasks to find other intervals for placement by shifting
the time or switching to another resource (satellite or
ground station). Building the chain of changes begins
from the most dissatisfied agents with the lowest
objective functions. The system organizes a special
"working group" of agents (TaskActor), which are
affected by changes (permutations and shifts in the
schedule) (see Algorithm 3). Effectiveness of each
permutation can be evaluated by changing satisfaction
functions of the agents participating in it. The resulting
version of the schedule change can be accepted or
rejected depending on the effect on the system
satisfaction function: only those changes are approved
that do not increase the system satisfaction function
(4). The function increment (4) is calculated by the
following formula:
(5)
where
is the current version of possible
placement,
is the new version of possible placement.
When constructing chains of permutations, the
following conflict situations are considered:
1. Planning a survey of the observation area by
displacing previously scheduled surveys or data
transmission sessions from the satellite schedule;
2. Approximation of the time of transmitting the
image to the ground station by displacing previously
scheduled surveys or data transmission sessions from
Multi-agent Planning System for Target Application of Earth Remote Sensing Space Systems for Solving Precision Farming Tasks
651

Algorithm 3: Proactive Plannig.
Input: task
j
, C – set of placement options, depth
of recursion, depth
max
– maximal recursion depth,
SA – set of assignments presenting the current
schedule, P – set of permutations
Output: Improved schedule
1:
if depth = 0 then
2:
The task agent views available options for
possible placement with values of objective
functions which are lower than those of the
current option: options = filterByValue( C )
3:
else if depth < depth
max
4:
The task agent only looks at placement
options that do not conflict with the current
permutation set:
options = filterByPermutations( C, P )
5:
else
6:
The task agent only looks at conflict-free
placement options that do not conflict with
the current permutation set:
options = filterByPermutations( C, P )
options = filterByConflicts ( options )
7:
end if
8:
for
do
9:
Add placement option to set of
permutations: addPermutations (
, P )
10:
if
has conflicts then
11:
Add permutations for removing conflict
operations:
addPermutations(conflicts, P)
12:
for do
13:
For each task
x
corresponding to conflict
x, recursive call of proactive planning is
carried out:
ProactivePlanning(task
x
, C, depth + 1,
depth
max
)
14:
end for
15:
end if
16:
if depth=0 and summary change of
objective function due to the received set of
permutations is less than zero, then
17:
Permutations are applied to the current
schedule: applyPermutaitons( P, SA )
18:
break;
19:
end if
20:
if summary change of objective function
due to the received set of permutations is
more than zero, then
21:
Remove own and subsidiary
permutations from the list:
removePermutations (task
j
, P)
22:
end if
23:
end for
the satellite schedule;
3. Displacement of previously scheduled data
transmission sessions from the ground station
schedule;
4 Freeing the satellite memory device from other
images in case of insufficient space in the onboard
memory device.
A task that remains unplanned is placed in the task
queue awaiting scheduling. Another attempt to plan
these tasks will be made in case of adding new
resources or changing the schedule of existing ones.
The protocol of agent interaction at the stage of
proactivity is shown in Fig. 2.
The iterative plan improvement continues until all
task agents are stopped, which would mean reaching a
consensus in negotiations and the possibility of issuing
the final solution. This state can be violated when
receiving events related to addition, deletion or change
of parameters of satellites, ground stations or
observation objects. In this case, the schedule is
reduced to an acceptable form, and then improved
according to the mechanism described above.
Figure 2: Agent negotiation protocol at the proactive
planning stage.
6 CONDUCTING
EXPERIMENTAL RESEARCH
6.1 Studying Efficiency of Proactive
Planning Algorithm
For system approbation, a model was developed
containing four satellites within a satellite group and
two ground stations within the network of ground
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
652
stations. 700 new tasks were added in the form of
applications for shooting observation objects and
transmitting the obtained images by a satellite to the
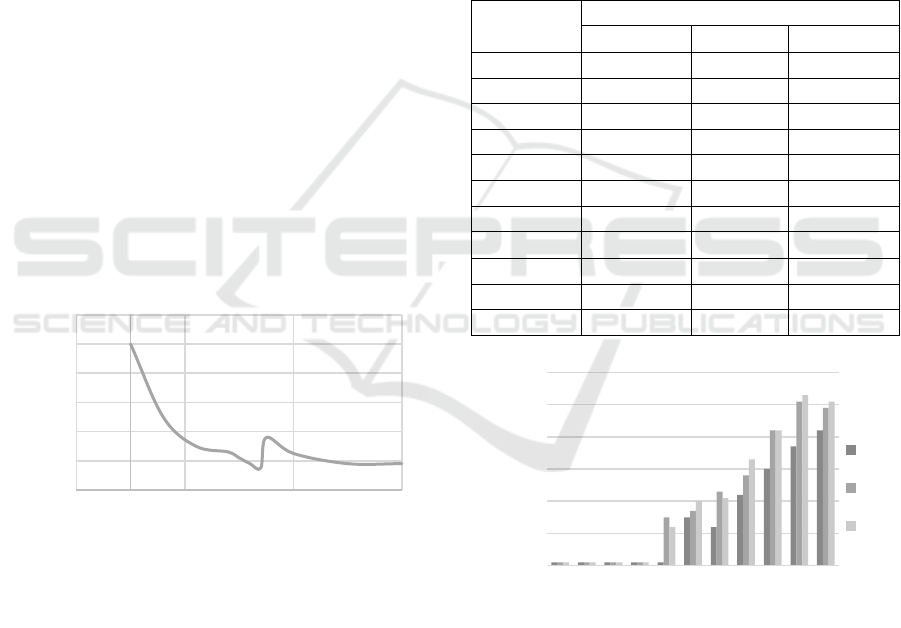
ground station. The planning period was 5 days. Fig. 3
shows the change in the system objective function
during construction of the schedule. Up to the 90th
second, conflict-free planning took place.
As a result of conflict-free planning, 521 tasks were
planned. As a result of proactive planning, the schedule
was improved, the objective function value decreased
by 0.11, and another 78 applications were planned,
which is 15% of the number of applications planned at
the conflict-free planning stage.
6.2 Studying the Ability of the System
to Adapt the Schedule
The experiment evaluated ability of the system to adapt
the schedule when group composition is changed. It
considered the time taken to restore the schedule
damaged by removal of one of the satellites. Satellite4
was removed from the schedule obtained during the
previous experiment. Removal occurred at the 120th
second and this event led to an increase in the objective
function value to 0.36 ( ). However, during
the next 80 seconds, the planning system was able to
parry the event and restructure the schedule, lowering
the value of the system objective function to 0.18
( ) (Fig. 3).
Figure 3: Change in the objective function after failure of
one of the satellites.
6.3 Comparison with Genetic
Algorithm and Branch and Bound
Method
Table 1 shows the operating time of algorithms for a
system consisting of two satellites and two ground
stations, the number of observation objects (OO) varies
from two to twelve. It is worth mentioning that in the
experimental data set there is a small number of
visibilities and a large number of conflicts on
possibilities of shooting and transmission, which
makes the search for the optimal solution even more
complicated.
Based on the data in the table, scheduling with the
help of genetic (GA) and multi-agent (MA)
algorithms took much less time compared to the
branch and bound method (BBM). However, as it is
shown in Figure 4 on the graphs of objective function
values, as a result of GA and MA, a less optimal
schedule is obtained.
Thus, BBM is slower than GA and MA, but it
guarantees optimality of the solution found. At the
same time, it cannot be used for solving large-scale
problems.
Table 1: Time Measurements in the Experiment.
Number of
OOs
Scheduling Time Interval, s
BBM
GA
MA
2
0,055
0,064
0,052
3
0,179
0,083
0,080
4
0,414
0,101
0,109
5
0,987
0,134
0,173
6
2,107
0,157
0,185
7
3,027
0,172
0,243
8
7,311
0,188
0,277
9
9,103
0,211
0,213
10
14,508
0,223
0,386
11
23,899
0,254
0,385
12
42,919
0,298
0,419
Figure 4: Values of objective function in the experiment.
6.4 Comparison with Genetic
Algorithm on Large-scale Problems
For GA and MA, a series of experiments were
conducted in which the number of OOs varied from
25 to 400, for a system of five satellites and five GSs.
According to results of the measurements made (Fig.
5), MA runs faster on tasks of higher dimensionality.
0
0,2
0,4
0,6
0,8
1
1,2
-50 50 150 250
Objective function
value
Time, sec
0
0,1
0,2
0,3
0,4
0,5
0,6
2 3 4 5 6 7 8 9 10 11 12
Objective function value
Number of OOs
BBA
GA
MA
Multi-agent Planning System for Target Application of Earth Remote Sensing Space Systems for Solving Precision Farming Tasks
653
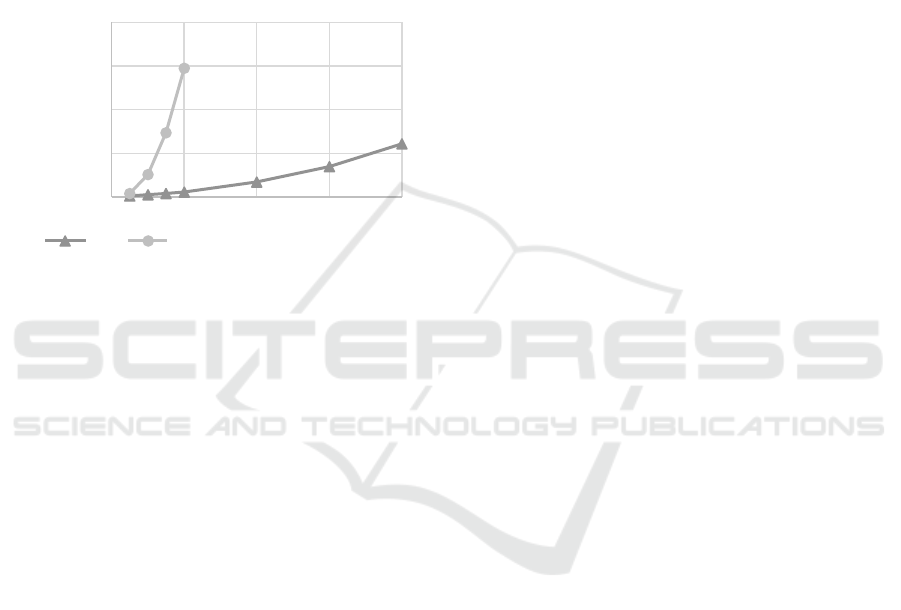
This is due to the fact that the time and quality of work
of GA depends on the population size. In this case,
both algorithms show similar results on the quality of
the schedule.
The second factor that can negatively affect the
operating time of GA is the increased number of
conflicts during crossover and mutation operations.
As a result, the objective function value of
descendants is less often better than that of ancestors.
This leads to a slowdown in the growth rate of
objective function of the best individual in the
population.
Figure 5: Values of operating time in the experiment.
7 CONCLUSIONS
The authors proposed a method for solving the
problem of scheduling space imagery for precision
agriculture by dividing the planning process into two
stages: conflict-free planning and proactive planning
based on multi-agent technology, which makes it
possible to improve the resulting schedule.
Results of experiments demonstrate higher
efficiency of the developed algorithms for large-scale
problems in comparison with methods of traditional
centralized planning.
Further research will focus on developing the
ontology of the planning system, as well as improving
the proactive planning algorithm by introducing
resource agents. This will help add new variants of
objective function for planning: uniform resource
loading; minimizing the amount of resources;
minimizing the cost of service execution with the
ability to set the cost of resource use.
ACKNOWLEDGEMENTS
This paper was prepared with financial support of the
Ministry of Education and Science of the Russian
Federation – contract №14.578.21.0230, project
unique ID is RFMEFI57817X0230.
REFERENCES
Liaghat, S., Balasundram, S. K., 2010. A Review: The Role
of Remote Sensing in Precision Agriculture. In
American Journal of Agricultural and Biological
Science, vol. 5, no. 1, pp. 50-55.
McCabe, M., Houborg, R., Lucieer, A., 2016. High-
resolution sensing for precision agriculture: from Earth-
observing satellites to unmanned aerial vehicles, In
Remote Sensing for Agriculture, Ecosystems, and
Hydrology, XVIII.
Kirilin, A., et al., 2017. AIST-2D experimental technology
small satellite. Publishing House of SSC RAS, Samara.
Darnopykh, V., 2004. Planning target application of satellites
and space systems. In Proceedings of MAI, no.16, pp. 15-
19. (In Russian)
Meisels, A., 2008. Distributed Search by Constrained
Agents. Springer.
Yokoo, M., 2001. Distributed Constraint Satisfaction:
Foundation of Cooperation in Multi-agent Systems.
Springer.
Petcu, A., 2009. A class of Algorithms For Distributed
Constraint Optimization. IOS Press.
Pinto, M., Barros, A., et al., 2018. A New Model Proposal for
Integrated Satellite Constellation Scheduling within a
Planning Horizon given Operational Constraints. In
Proceedings of ICORES 2018, pp. 312-319.
Wörle, M., Lenzen, C., et al., 2015. The Incremental Planning
System. In Space Operations: Innovations, Inventions,
and Discoveries, vol. 249, pp. 285-307.
Rzevski, G., Skobelev P., 2014. Managing complexity. WIT
Press. Boston.
Wooldridge, M., 2009. An Introduction to Multiagent
Systems, John Wiley and Sons. London.
Shoham, Y., Leyton-Brown, K., 2009. Multi-agent systems:
Algorithmic, Game Theoretic and Logical Foundations.
Cambridge University Press. Cambridge.
Skobelev, P., Simonova, E., Zhilyaev, A, 2016. Using multi-
agent technology for distributed management of cluster
of remote sensing satellites. In International Journal of
Design & Nature and Ecodynamics. vol. 11, issue 2, pp.
127-134. WIT Press.
Skobelev, P., 2012. Activity ontology for situational
management of enterprises in real-time. In Ontology of
Designing, vol. 1, issue 3, pp.6-38.
Mayorov, I., Skobelev, P., 2015.Towards thermodynamics of
real-time scheduling. In International Journal of Design
& Nature and Ecodynamics, vol. 10, issue 3, pp. 213-
223. WIT Press.
00:00
02:53
05:46
08:38
11:31
0 100 200 300 400
Operating time, min
Number of OOs
МА
ГА
GA
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
654
