Comparison between Supervised and Unsupervised Feature Selection

Methods

Lilli Haar, Katharina Anding, Konstantin Trambitckii and Gunther Notni

Institute of Mechanical Engineering, Department of Quality Assurance and Industrial Image Processing, Ilmenau,

University of Technology, Gustav-Kirchhoff-Platz 2, Ilmenau, Germany

{lilli.haar, katharina.anding, konstantin.trambitckii, gunther.notni}@tu –ilmenau.de

Keywords: Feature Selection, Dimensionality Reduction, Unsupervised Learning.

Abstract: The reduction of the feature set by selecting relevant features for the classification process is an important

step within the image processing chain, but sometimes too little attention is paid to it. Such a reduction has

many advantages. It can remove irrelevant and redundant data, improve recognition performance, reduce

storage capacity requirements, computational time of calculations and also the complexity of the model.

Within this paper supervised and unsupervised feature selection methods are compared with respect to the

achievable recognition accuracy. Supervised Methods include information of the given classes in the

selection, whereas unsupervised ones can be used for tasks without known class labels. Feature clustering is

an unsupervised method. For this type of feature reduction, mainly hierarchical methods, but also k-means

are used. Instead of this two clustering methods, the Expectation Maximization (EM) algorithm was used in

this paper. The aim is to investigate whether this type of clustering algorithm can provide a proper feature

vector using feature clustering. There is no feature reduction technique that provides equally best results for

all datasets and classifiers. However, for all datasets, it was possible to reduce the feature set to a specific

number of useful features without losses and often even with improvements in recognition performance.

1 INTRODUCTION

One of the goals of image processing is the automated

classification of objects into classes. For this purpose,

machine learning is used, which performs a grouping

based on image or object features. In order to ensure

a high accuracy, it is essential to use features that

allow an adequate separation of the classes. However,

it is difficult to assess, which features are important

and which are not. If there are only a few features,

satisfactory results could not be achieved, as the

features may be unsuitable for class separation. The

accuracy can be increased by adding more relevant

features. However, this is possible only up to a certain

number of features. When this critical number of

features is reached, the growth of accuracy stagnates

or even decreases. This behaviour is well known as

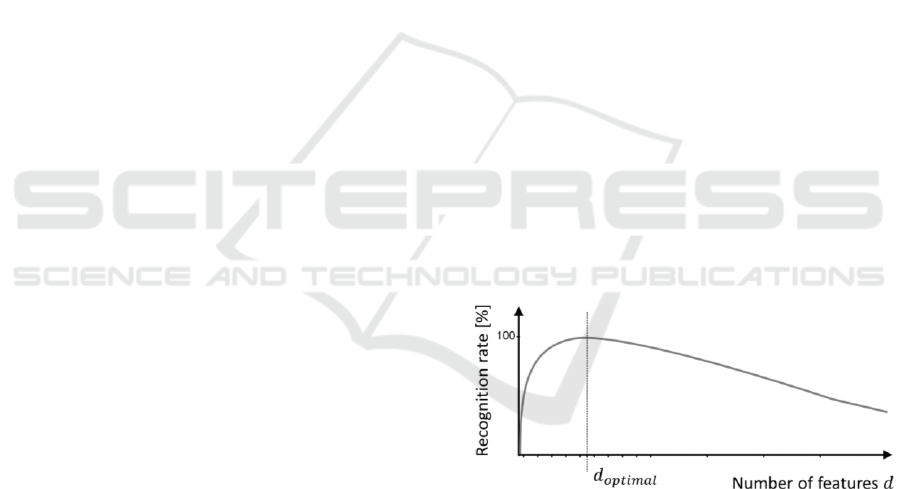
the peaking phenomenon (see Figure 1). Furthermore,

feature selection can help to avoid the curse of

dimensionality (Bellman 1961). The recognition

performance of a classifier depends on the relation

between the number of training objects and the

number of features. If the number of features

increases, the quantity of objects must increase expo-

nentially (Theodoridis and Koutroumbas 2009).

Figure 1: Illustration of the peaking phenomenon.

To counteract these two phenomena, the feature

vector should be reduced. In addition, the

computational effort and the time required for

training a classifier or for the classification process

itself can be reduced. This is especially important for

neural networks, as they require a lot of time for

training (Han et al. 2012) and also for real-time

recognition tasks, particularly in hyperspectral data.

Furthermore, a reduced number of features can avoid

overfitting. There are many different methods

available to perform this task. This paper aims to

compare different supervised and unsupervised

582

Haar, L., Anding, K., Trambitckii, K. and Notni, G.

Comparison between Supervised and Unsupervised Feature Selection Methods.

DOI: 10.5220/0007385305820589

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 582-589

ISBN: 978-989-758-351-3

methods for feature selection. Different datasets,

which are presented in section 3.1, were used for the

evaluation. The comparison was made using the

recognition rate.

2 STATE OF THE ART

The feature vector can contain redundant and/or

irrelevant features. Feature 2 in Figure 2a can separate

the given two classes alone. Instead, Feature 1 is

similar for both classes. Such a feature is considered

irrelevant. The Features, which are shown in Figure

2b, are redundant because they carry similar

information. Thus, one of the two features could be

left out without suffering any loss of information.

a) Irrelevant features b) Redundant features

Figure 2: Illustration of irrelevant and redundant features.

Three different approaches for feature selection can

be distinguished, these are filters, wrappers and

embedded methods (García et al. 2015). The filter

methods act independently of the selected classifier.

In advance, features are filtered out using heuristics

or the characteristics of the given data. This paper

uses techniques from this approach. The wrapper

methods involve the classifier to decide which

features should be removed or added. The accuracy is

determined with each new feature subset and the one

with the best results is selected. Examples of this type

of feature selection are sequential forward or

backward selection. Embedded methods use the

classifier for decision making, too. The features are

selected within the training of the classifier.

The methods for feature selection can be

categorized into supervised and unsupervised. As

with machine learning, this means that the labels of

the objects are integrated into the reduction process

or not. In the case of unsupervised methods, the

selection is done based on the attributes and their

characteristics without the inclusion of the labels.

When basically no labels are known in clustering,

only unsupervised methods can be used for feature

selection. A selection based on variance or correlation

is unsupervised. (Dy and Brodley 2000), (Mitra et al.

2002) and (Cai et al. 2010) present unsupervised

feature selection methods. Clustering can also be used

for this task.

Common supervised methods of feature selection

are, for example, InformationGain (InfoGain) (Han et

al. 2012), GainRatio (Quinlan 1993), Relief (Kira and

Rendell 1992), ReliefF (Kononenko 1994), Gini-

Index (Breiman et al. 1984).

An overview of different feature selection

methods is given in (Li et al. 2017).

2.1 Information Gain

The Information Gain score is calculated for each

feature based on entropy and indicates the level of

information about the classes to be predicted (Han et

al. 2012). Thus, it can be determined which features

are suitable for a separation of the classes. A high

value indicates a high information content. In this

way, a ranking of the features is created. This method

can distinguish irrelevant features.

2.2 ReliefF

In process of ReliefF, features are weighted, and a

ranking is created. First, an object is selected and the

nearest neighbour from the same and from the other

classes are determined (Kira and Rendell 1992),

(Kononenko 1994). The weights of the features in

which the objects of the same class match and objects

of different classes do not match are increased. On the

other hand, the weights of features in which objects

of one class differ or whose expressions are equal

between objects of different classes are reduced.

Using ReliefF allows removing irrelevant features.

2.3 Based on Variance

The characteristics of some features are almost the

same for all objects and therefore vary only slightly

(Han et al. 2012). Such features are irrelevant and add

no value to the classification, which is why they can

be removed from the feature vector.

2.4 Based on Clustering

The natural grouping tendencies of clustering can also

be used to perform a feature selection. The

Generalized Hebbian Algorithm (GHA) and the self-

organizing map (SOM) can, for example, be used to

perform a principal component analysis (RapidMiner

Inc. 2014). (Roiger 2017) proposes a wrapper

approach for feature selection using unsupervised

learning. Furthermore, it is possible to transpose the

input table and to perform the clustering on the

Comparison between Supervised and Unsupervised Feature Selection Methods

583

features instead of the objects. This process is

illustrated in Figure 3.

Figure 3: Left: Original input table, right: Transposed input

table for feature clustering.

Such feature selection methods are called feature

clustering. Similar features should be grouped in

clusters. Subsequently, only the nearest feature to the

centre of the cluster is used as the representative of

the entire cluster (Cheung and Jia 2012), (Hong et al.

2014). For this type of feature reduction, mainly

hierarchical methods, but also k-means were

investigated, the former being better suited (Jain and

Dubes 1978), (Guyon and Elisseeff 2003), (Krier et

al. 2007), (Liu and Wu, Xindong, Zhang, Shichao

2011), (Cheung and Jia 2012). However, it is

problematic to find a suitable distance measure,

especially if the features are scaled differently.

Clustering-based methods reduce the feature vector

by removing redundant features.

3 COMPARISON OF FEATURE

SELECTION ALGORITHMS

The presented feature selection methods are

compared based on the achieved recognition

accuracies of different classifiers. InfoGain and

ReliefF are classical methods, which are very

common and therefore very often used.

Instead of hierarchical clustering or k-means, the

Expectation Maximization (EM) algorithm was used

for unsupervised feature clustering (Dempster et al.

1977). Here, a mathematical model, which consists of

𝑘 probability distributions, is created. The aim of this

clustering method is to find those model parameters

of the probability distributions that represent the data

in the best way (Dempster et al. 1977) and thus to

optimize the fitting of the mathematical model to this

data (Aggarwal 2015). The EM algorithm is very

popular because of its simple implementation

(Aggarwal and Reddy 2014) and flexibility

(Aggarwal 2015). Probabilistic methods often surpass

other clustering methods (Kononenko 1994) and can

be used in many fields (Dempster et al. 1977). It is

also a stable process that is robust to outliers (Gan et

al. 2007). This paper aims to investigate whether this

type of clustering algorithm can provide a proper

feature vector using feature clustering. The features

are normalized by using Gaussian z-score

normalization before clustering.

The investigations were carried out in the data

mining program KNIME (Konstanz Information

Miner) based on the Weka plug-in and thus on Weka

implementation of these methods.

3.1 Used Datasets

Four different real datasets are used in the

investigations of this paper. The first two datasets

consist of light scattering images. These represent

reflective, industrially produced surfaces without

defects, with scratches or point defects. The

Autopetrography dataset is based on a developed

method for automatic recognition of mineral

aggregates to solve automatic analysis for all

petrography classes according to legal requirements.

Furthermore, a dataset with images of metal surfaces

with and without defects is used. In Table 1, all

datasets are listed. Figure 4 shows an example of each

dataset.

Table 1: Overview of used datasets.

Name

Number of

Objects

Number

Features

Number

Classes

Scattered_Light_1

300

182

Scattered_Light_2

900

182

Metal Surfaces

273

123

Autopetrography

15907

234

Figure 4: Example images of each dataset. From left to

right: Scattered_Light_1, Scattered_Light_2, Metal

Surfaces, Autopetrography.

3.2 Used Classification Algorithms

Three different classifiers are used. Random Forest is

insensitive to irrelevant or redundant features. Naı̈ ve

Bayes is sensitive to redundant features, whereas

𝑘 Nearest Neighbour is sensitive to irrelevant ones.

For all used classifiers the achieved results are

measured as recognition accuracy in percent. The

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

584

required computational effort is not included in the

assessment.

3.2.1 Random Forest

In some cases, a single tree classifier has an

insufficient accuracy. A combination of several trees

and randomly chosen features can improve the results

significantly. This is the keynote of Random Forest

classifier (Breiman 2001). It is based on the bagging

and random feature selection. Random Forest is a

very powerful classifier, which delivers good results

in a short time. The algorithm is understandable and

comprehensible. When building the tree, an internal

selection of the most important features is made,

which reduces the influence of irrelevant features. A

small influence remains. The number of trees in these

investigations was set to 100.

3.2.2 𝒌 Nearest Neighbour

The learning step of the 𝑘 Nearest Neighbour

algorithm is very simple, the existing training data is

just stored (Cleve and Lämmel 2014). In the

following classification step, the distances between

all training data points and the new and unknown

object are determined. Subsequently, 𝑘 objects of the

training dataset are determined, which have the

smallest distance to the new object in the feature

space. The parameter 𝑘 is a natural number specified

by the user. Assuming that these 𝑘 nearest neighbours

are most similar to the unknown object, their classes

determines the class affiliation of the unknown

object. The Ibk algorithm with 𝑘 = 15, included in

Weka, was used in this paper.

3.2.3 Naı

ve Bayes

Naı̈ve Bayes belongs to the group of statistical or

probability based classifiers (Han et al. 2012), (Cleve

and Lämmel 2014). The basic idea is to calculate the

probabilities of the class membership of an object as

a function of its specific feature vector and to select

the class with the highest result. The suffix ”naı̈ ve”

refers to the simplifying but mostly unrealistic

assumption that the features in the datasets are

independent of each other (Duda et al. 2012), (Witten

et al. 2017). This assumption is not always true,

which is why the classifier is highly sensitive to

redundant features.

4 RESULTS

A ranking of the features was created with InfoGain,

ReliefF and the statistic parameter variance.

Afterwards, one of the classifiers was trained with the

first 10 most important features of each method and

the accuracy was determined. This was done using a

10-fold cross validation for the Scattered Light

datasets and a 3-fold cross validation for the other

datasets. With each step, the number of features was

increased by adding the next 10 features with

remaining highest significance, the classifier was

trained, and the accuracy was determined. The

procedure using the clustering-based method was

similar, but the number of features was determined by

the chosen number of clusters. This value started with

10 and was increased by 10 until the full number of

features was reached.

4.1 Random Forest

Figure 5 shows the results of all four datasets by using

Random Forest. The feature selection was carried out

using the four methods described above. In any case,

a comparable accuracy can be achieved with a

significantly reduced feature vector as with a full one.

The feature clustering achieved the best results for the

Scattered_Light_1 dataset, although this method does

not involve the classes. Significantly, worse results

were provided for this dataset by using the second

unsupervised method based on variance. The two

other methods also gave worse results. Nevertheless,

the accuracy increases continuously with the number

of used features. This indicates that the Random

Forest classifier is insensitive to irrelevant features.

For the datasets, Scattered_Light_2 and

Autopetrography, the differences between the feature

selection methods are small, at most 3%. All methods

are able to create a smaller feature vector, which

nevertheless allows a similarly high accuracy as by

using the full feature number. By using the

Scattered_Light_2 dataset this comparable

recognition performance is achieved with about 30

features and with 60 features using the

Autopetrography dataset. In addition, the recognition

accuracy of the method, which is based on variance,

is at the beginning significantly worse than the other

feature selection methods, but then it increases

significantly and can obtain the same level. The

progress of the accuracy indicates that these datasets

consist of a large number of features which carry little

additional information. The Metal Surface dataset

shows a rapid increase of the accuracy, but also

greater differences between the feature selection

Comparison between Supervised and Unsupervised Feature Selection Methods

585

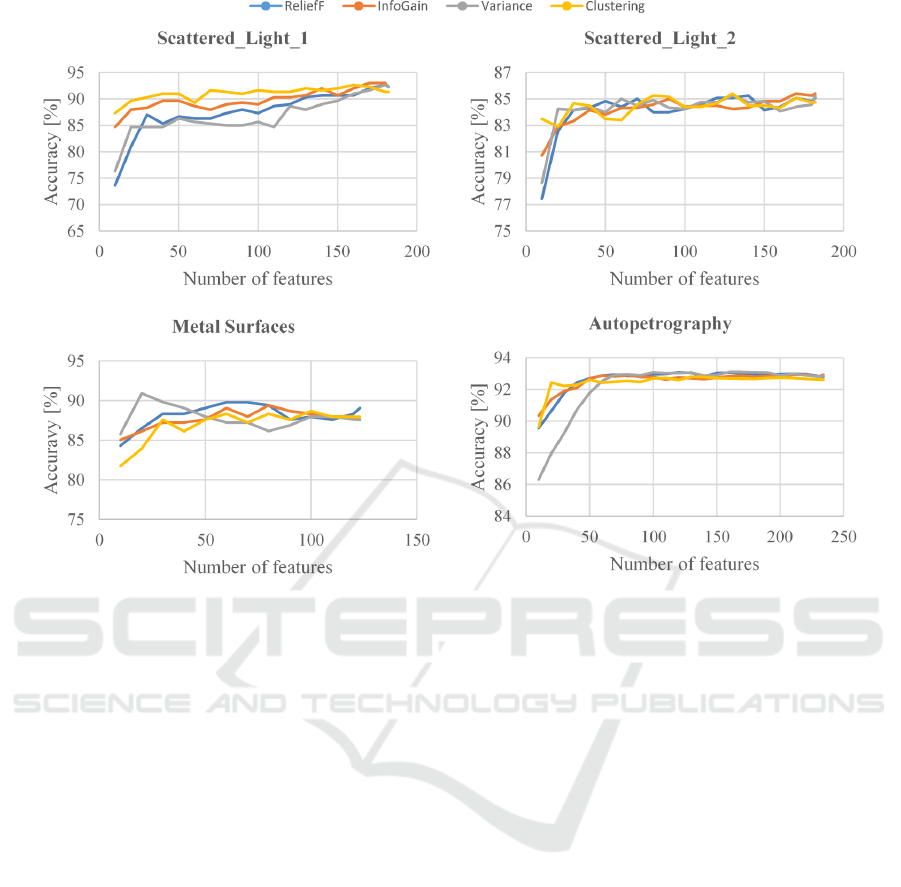
Figure 5: Recognition accuracies of different feature selection methods using Random Forest classifier.

methods and more fluctuations. Variance-based

selection achieved the best results with this dataset. A

significant improvement could be achieved with only

20 features. In addition, a comparable accuracy to the

full feature set was achieved with significantly fewer

features. The benefits are a reduction of storage

capacity requirements, of calculation time and of

computational complexity.

4.2 𝒌 Nearest Neighbour

Figure 6 shows the results by using different feature

selection methods with 𝑘 Nearest Neighbour

classifier. This classifier is sensitive to irrelevant

features. The results of the Scattered_Light_1 dataset

show, that there are many irrelevant features in this

dataset. Using the InfoGain algorithm a significantly

higher accuracy (87.7%) could be achieved with only

20 features. This value is significantly higher than

83% achievable with the full feature vector.

Thereafter, accuracy decreases until a minimum at 70

used features. This indicates an increased number of

irrelevant features. By removing these irrelevant

features, the classification process is no longer

disturbed, which is why better results are possible.

Subsequently, the accuracy increases again. The

accuracies achieved with the other feature selection

methods increases continuously. For

Scattered_Light_2 dataset, InfoGain is no longer able

to achieve such good results. ReliefF and variance

show better accuracies. A reduced number of features

(about 30) is already able to achieve similarly good

results as using full feature set. The behaviour of the

accuracy is especially interesting for the Metal

Surfaces dataset. It was possible to increase the

accuracy by about 5% - 10% with ReliefF and

InfoGain. Subsequently, the accuracies decrease until

the entire feature set is reached. This indicates that the

dataset includes many irrelevant characteristics. The

results of feature clustering are different, because this

method detects redundant instead of irrelevant

features. There is no significant increase in the

accuracy. However, the number of features can also

be reduced without lowering the recognition

performance. The variance also shows a different

trend, since it operates unsupervised. For

Autopetrography the results of ReliefF, InfoGain and

feature clustering are very similar. Variance is

initially unable to keep up. First, a continuous

increase can be seen in all procedures. Then it comes

to a stagnation. Instead of 234 features, 70 could lead

to similar results as by using the full feature set.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

586

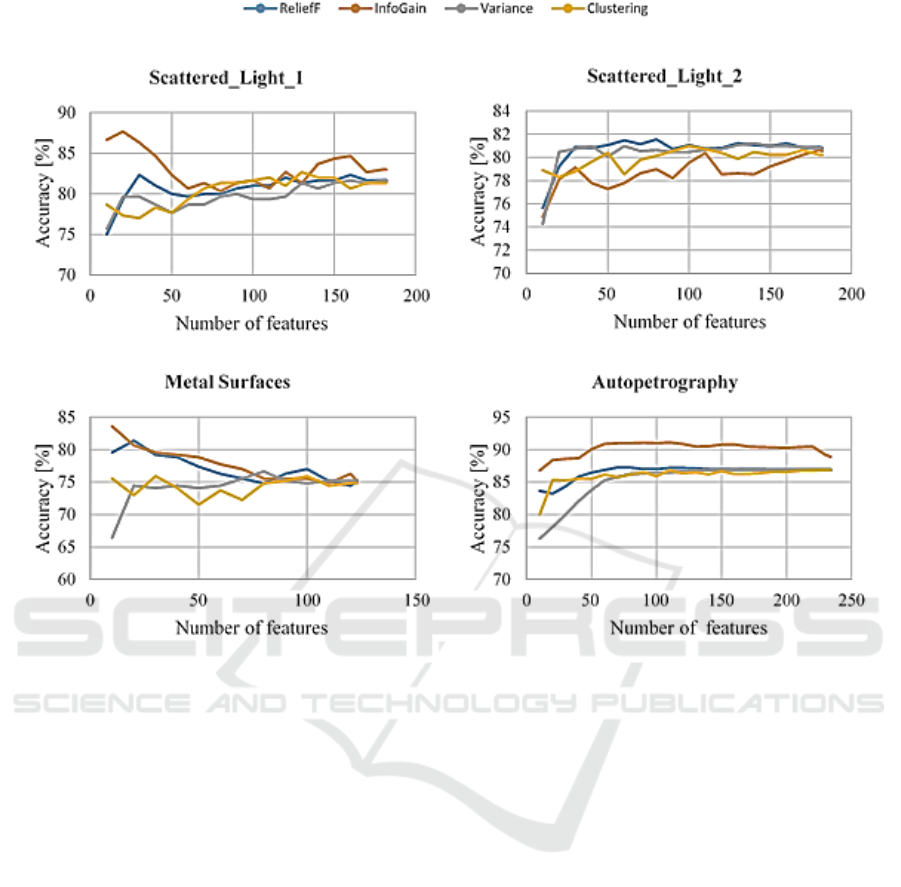
Figure 6: Recognition accuracies of different feature selection methods using IBk classifier.

4.3 Naı

Ve Bayes

This is a simple classifier, which can achieve

relatively high accuracies for simple classification

tasks. As already mentioned, this classifier is also

highly sensitive to redundant features. Figure 7

summarizes the results using Naı̈ve Bayes. Because

redundant features are removed with feature

clustering, this method is best for the

Scattered_Light_1 dataset. An accuracy, which

overcomes the result of the full feature set could be

achieved with only 40 features. After this peak, it

decreases. It can be concluded that this dataset

consists of many redundant features. A set created

with InfoGain containing a lower number of features

gained an accuracy comparable to that using the full

feature set. ReliefF could achieve such a high

accuracy with significantly more features. For the

Scattered_Light_2 dataset, the accuracies for all four

feature selection methods increase very fast, before

they stagnate and decrease again. This is typical for

the peaking phenomenon. The results of the Metal

Surfaces dataset differ more in terms of the selection

methods. Variance shows the worst results. The

gradients of ReliefF and InfoGain are similar, with

the accuracy of the latter being higher. Results

achieved with the feature subsets of feature clustering

initially show worse results, but then surpass the other

methods. Later, the accuracies of all methods are

similar. The continuous increase indicates a small

number of redundant features. For the

Autopetrography dataset, an unusual situation is

shown. InfoGain and clustering show a similar

course. Both achieve an accuracy of approximately

77% with already 10 features. Subsequently, it

decreases continuously with an increase of the

number of features, indicating an increased number of

redundant features. This also explains why the

clustering-based method performs very well in this

case. It is able to filter out redundant features. ReliefF

is significantly worse than InfoGain and the

unsupervised clustering-based method.

5 CONCLUSIONS

It has been shown that each of the four investigated

methods is suitable for creating a reduced feature set.

Comparison between Supervised and Unsupervised Feature Selection Methods

587

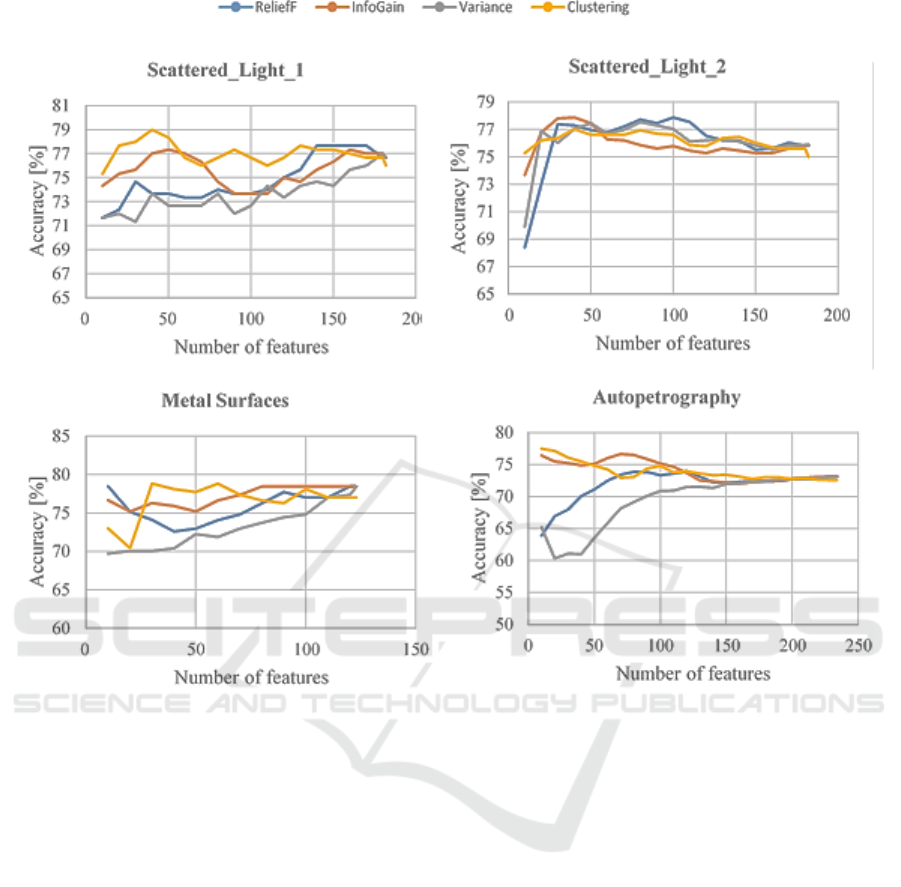
Figure 7: Recognition accuracies of different feature selection methods using Naı̈ ve Bayes classifier.

Furthermore, the results show, that EM is suitable for

feature clustering and leads to good results. The

number and constellation of optimal features are

highly dependent on the chosen machine learning

method and the given dataset. Thus, there is no

feature reduction technique that provides equally

good results for all datasets and all used classifiers.

For this reason, a suitable procedure must be selected

for each new recognition task. The unsupervised

feature clustering could often provide similarly good

results or even better than the two supervised working

feature selection methods. Because no class-labels are

included, it can also be used for datasets without

known labels and thus for feature selection in case of

unsupervised learning. Between InfoGain and

ReliefF, there were often only minor differences. In

some cases, one method was better than the other and

vice versa. For all datasets, it was possible to reduce

the feature set to a specific number of features without

losses and often even with improvements in

recognition performance. It could be shown, that a

significant improvement of the recognition

performance can be achieved by using a feature

selection carried out in advance for classifiers with

high sensitivity to irrelevant or redundant features.

Even using classifiers with low sensitivity to

redundant or irrelevant features, a reduced feature

vector can lead to higher accuracies. This reduction

allows many advantages. From the point of view of

storage capacity and computing power, it is also

absolutely necessary to keep only those data, which

provide added value for the classification task. This is

especially important in Big Data or in spectral

imaging data.

REFERENCES

Aggarwal, C. C., 2015. Data Mining: The Textbook,

Springer. Cham.

Aggarwal, C. C., Reddy, C. K., 2014. Data Clustering:

Algorithms and Applications, CRC Press. Boca Raton.

Bellman, R., 1961. Adaptive Control Processes: A Guided

Tour, Princeton University Press. Princeton, N.J.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

588

Breiman, L., 2001. Random Forests. Machine Learning

45(1), Pages 5–32.

Breiman, L., Friedman, J. H., Olshen, R. A., Stone, C. J.,

1984. Classification And Regression Trees, Wadsworth

International Group. Belmont.

Cai, D., Zhang, C., He, X., 2010. Unsupervised feature

selection for multi-cluster data. In Proceedings of the

16th ACM SIGKDD international conference on

Knowledge discovery and data mining. ACM. Pages

333–342.

Cheung, Y.-m., Jia, H., 2012. Unsupervised feature

selection with feature clustering. In Proceedings of the

The 2012 IEEE/WIC/ACM International Joint

Conferences on Web Intelligence and Intelligent Agent

Technology-Volume 01. IEEE Computer Society. Pages

9–15.

Cleve, J., Lämmel, U., 2014. Data Mining, De Gruyter

Oldenbourg. München.

Dempster, A. P., Laird, N. M., Rubin, D. B., 1977.

Maximum Likelihood from Incomplete Data via the

EM Algorithm. Journal of the royal statistical society

Series B (methodological), Pages 1–38.

Duda, R. O., Hart, P. E., Stork, D. G., 2012. Pattern

Classification, Wiley-Interscience. s.l., 2. Aufl. edition.

Dy, J., Brodley, C. E., 2000. Feature subset selection and

order identification for unsupervised learning. In

International Conference on Machine Learning. Pages

247–254.

Gan, G., Ma, C., Wu, J., 2007. Data Clustering: Theory,

Algorithms, and Applications, SIAM. Philadelphia.

García, S., Luengo, J., Herrera, F., 2015. Data

Preprocessing in Data Mining, Springer. Cham.

Guyon, I., Elisseeff, A., 2003. An introduction to variable

and feature selection. Journal of Machine Learning

Research 3(Mar), Pages 1157–1182.

Han, J., Kamber, M., Pei, J., 2012. Data mining: Concepts

and Techniques, Elsevier/Morgan Kaufmann.

Amsterdam, 3th edition.

Hong, T.-P., Liou, Y.-L., Wang, S.-L., Vo, B., 2014.

Feature selection and replacement by clustering

attributes. Vietnam Journal of Computer Science 1(1),

Pages 47–55.

Jain, A. K., Dubes, R. C., 1978. Feature definition in pattern

recognition with small sample size. Pattern recognition

10(2), Pages 85–97.

Kira, K., Rendell, L. A., 1992. A practical approach to

feature selection. In Machine Learning Proceedings.

Pages 249–256.

Kononenko, I., 1994. Estimating attributes: analysis and

extensions of RELIEF. In European conference on

machine learning. Springer, Berlin, Heidelberg. Pages

171–182.

Krier, C., François, D., Rossi, F., Verleysen, M., 2007.

Feature clustering and mutual information for the

selection of variables in spectral data. In European

Symposium on Artificial Networks, Computational

Intelligence and Machine Learning. Pages 157–162.

Li, J., Cheng, K., Wang, S., Morstatter, F., Trevino, R. P.,

Tang, J., Liu, H., 2017. Feature Selection: A Data

Perspective. ACM Computing Surveys (CSUR) 50(6),

Pages 94.

Liu, H., Wu, Xindong, Zhang, Shichao, 2011. Feature

Selection using Hierarchical Feature Clustering. In

Proceedings of the 20th ACM international conference

on Information and knowledge management. ACM.

Pages 979–984.

Mitra, P., Murthy, C. A., Pal, S. K., 2002. Unsupervised

feature selection using feature similarity. IEEE

transactions on pattern analysis and machine

intelligence 24(3), Pages 301–312.

Quinlan, J. R., 1993. C4.5: Programs for Machine

Learning, Morgan Kaufmann. San Mateo.

RapidMiner Inc., 2014. RapidMiner: Operator Reference

Manual.

Roiger, R. J., 2017. Data Mining: A Tutorial-Based Primer,

CRC Press. Boca Raton, 2nd edition.

Theodoridis, S., Koutroumbas, K., 2009. Pattern

recognition, Elsevier/Acad. Press. Amsterdam, 4th

edition.

Witten, I. H., Frank, E., Hall, M. A., Pal Christopher J.,

2017. Data mining: Practical Machine Learning Tools

and Techniques, Morgan Kaufmann. Cambridge, MA,

4th edition.

Comparison between Supervised and Unsupervised Feature Selection Methods

589