
Applications of Sparse Modelling and Principle Component Analysis
for the Virtual Metrology of Comprehensive Multi-dimensional
Quality
Sumika Arima
1
, Takuya Nagata
2
, Huizhen Bu
2
and Satsuki Shimada
2
1
Faculty of Engineering, Information, and Systems, University of Tsukuba, Tsukuba, Ibaraki Pref., Japan
2
Graduate School of Systems and Information Engineering, University of Tsukuba, Tsukuba, Ibaraki Pref., Japan
Keywords: Virtual Metrology (VM), PCA (Principal Component Analysis), LASSO (Least Absolute Shrinkage and
Selection Operator), Support Vector Machines (SVM), Multi-class Discrimination, Variable Extractions.
Abstract: This paper discussed the virtual metrology (VM) modelling of multi-class quality to describe the
relationship between the variables of a production machine's condition and the estimated/forecasted product
quality soon after finishing the machine processing. Applications of PCA and LASSO technique of the
Sparse modelling were introduced to define the multi-dimensional quality. Because the high accuracy and
quick computations are required for the VM modelling, in this study, the PCA-LASSO combination was
applied before building the VM models based on the kernel SVM (kSVM), particularly the linear kernel for
real-time use. As the result of evaluation of a CVD (Chemical vapor deposition) process in an actual
semiconductor factory, LASSO and linear-SVM could reduce the scale of the machine variable's set and
calculation time by almost 57% and 95% without deterioration of accuracy even without PCA. In addition,
as the PCA-LASSO, the multi-dimensional quality was rotated to the orthogonality space by PCA to
summarize the extracted variables responding to the primary independent hyperspace. As the result of the
PCA-LASSO combination, the scale of machine variables extracted was improved by 83%, besides the
accuracy of the linear-SVM is 98%. It is also effective as the pre-process of Partial Least Square (PLS).
1 INTRODUCTION
Semiconductor manufacturing is characterized by a
sequence of sophisticated manufacturing processes,
often exceeding several hundred production steps.
The process basically consists of main 10 or less
types of processes repeated, for example, washing,
deposition of materials on a semiconductor wafer, a
photo-lithography, an etching, a polishing, an
annealing, an intermediate test, and so on (Y.Naka,
K.Sugawa, and C. McGreavy, 2012).
Here the intermediate test is a quality check process
which occupies 30% of the whole of the production
process. Though the intermediate test aims the fast
detection of the quality defects to prevent to pile
more cost and time before the final test, the time and
the cost for the intermediate test is also serious in
100%-inspections . Virtual metrology (VM) has
become widely studied all over the world to reduce
both the defects and the cost of the test (or the test
itself) as the research area of “advanced process
control” since 2005 as in AEC/APC (Advanced
equipment control/Advanced process control)
symposium around the world.
2 QUALITY DISCRIMINATION
MODELLING FOR VIRTUAL
METROLOGY
This study has advanced in 3 phases. As the first,
Arima (2011) applies kSVM for multi-class VM
modelling mainly for high accuracy. Second is the
application of the LASSO (Least Absolute
Shrinkage and Selection Operator) for automatic
variable extractions and fast computation of kSVM
(Arima, Ishizaki, and Bu, 2015). The third phase is
for all of those; automated variable extraction, the
high accurate quality detection, and the fast
computation. This paper mainly describe the third
phase in Section 3 after explaining the results and
354
Arima S., Nagata T., Bu H. and Shimada S.
Applications of Sparse Modelling and Principle Component Analysis for the Virtual Metrology of Comprehensive Multi-dimensional Quality.
DOI: 10.5220/0007385603540361
In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 8th International Conference on Operations Research and Enterprise Systems),
pages 354-361
ISBN: 978-989-758-352-0
Copyright
c
8th International Conference on Operations Research and Enterprise Systems by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
issues of the first and the second phases in this
section.
2.1 Problem Descriptions
The target process in this study is a plasma-CVD
(Chemical vapor deposition) process. CVD is one
type of thin-film formation processes and uses the
vapor process of a target material such that the snow
falls into the ground. The thickness of the film is
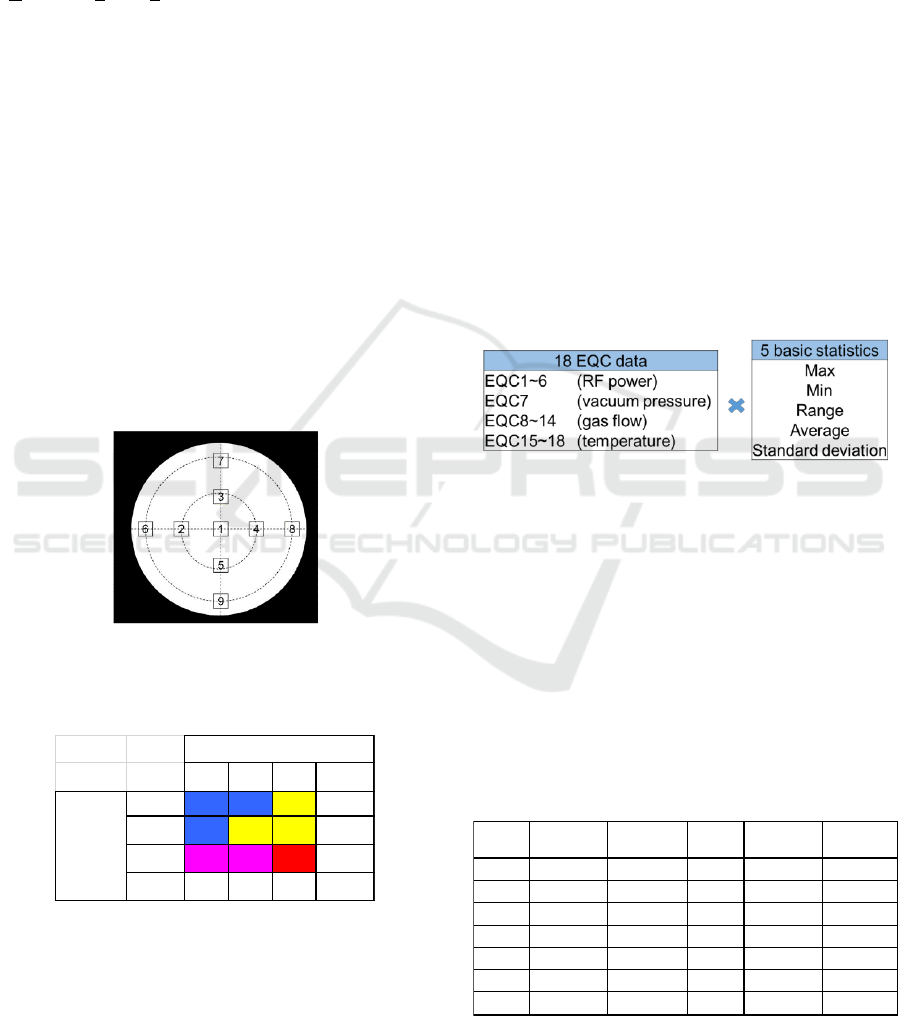
measured by nine points on a wafer after the CVD
process as the quality test for the CVD process
(Fig.2-1). Note that there are some types of layout of
the nine points. The measured data is composed into
2 factors (dimensions), “Design conformity (Dc)”
and “Uniformity (Uf)” for every wafer. Table. 2-1
shows one example of nine classes (3x3).
Not only Dc but also Uf is very important because
the larger wafer size leads the more defects besides
the higher throughput [wafers/unit time]. For
example, 30mm-size wafer is used in the target
factory, and the thickness sometimes much varies on
a wafer. The thickness influences the final quality of
the product such as the electrical resistance and the
current value.
Figure 2-1: Film thickness measured by nine points.
Table 2-1: Multi-dimensional quality class definition (nine
classes for 2-dimension).
For VM, quality was categorized by multi classes of
2 factors (dimensions), “Uniformity” and “Design
conformity” as shown in Table.2-1. Table 2-1
shows the case of nine classes as the result of 3-class
definition for each factor. The measures and
thresholds depend on the definition of the class. For
example of Table. 2-1, Dc was defined by the sum
total of square error between designed and actual
film thickness, and the boundaries of classes ‘A' and
‘B' or ‘B' and ‘C' were set as 3-quantiles between the
minimum and maximum values. Surface uniformity
(Uf) was defined by the standard deviation of the
film thickness, and the boundaries of classes ‘a' and
‘b' or ‘b' and ‘c' were set similarly as 3-quantiles.
This is only one example as the first phase
definition. The i-th wafer belongs to one of those
3x3=9 classes, and maintains the multi-dimensional
quality class expression as YC (i). Number in
Table.2-1 is the probability of the sample data. Note
that a different engineering action should be done
for the different colour in it.
On the other hand, conditions of a production
machine, used to explain the product quality, are
monitored on 18 sensors (EQC) settled in four types
of subunits of a machine (Fig.2-2). Soon after the
process end, 5 basic statistics are calculated, and 90
variables can be used for VM. Note that the original
wave data of each EQC cannot be opened for any
publications, and the statistics are used in this paper.
Figure 2-2: Machine variable set for experiment.
The challenge of VM here is to estimate/predict the
class of each product quality only by using the
machine data and the VM model that has been
learned by the set of machine data and the class data
of each product quality in a learning data set.
Table.2-2 shows the combinations of machine
variables to evaluate the VM accuracy. Note that
only the average and the standard deviation (SD) for
each EQC are used for the first phase. The choice of
the statistics is also based on engineering knowledge.
Table 2-2: 13 combinations of machine variables for the
performance evaluations ((x): # of variables).
a b c abc
A
46 18 6 70
B
14 2 8 24
C
2 0 4 6
ABC
62 20 18 100
Design
conformity
Uniformity
parameter
set No.
Avarage SD
parameter
set No.
Avarage SD
1
EQC1-18(18)
EQC1-18(18) 8 EQC8-14(7) EQC8-14(7)
2
EQC1-18(18)
- 9 EQC8-14(7) -
3 - EQC1-18(18) 10 - EQC8-14(7)
4 EQC1-6(6) EQC1-6(6) 11 EQC5-18(7) EQC5-18(7)
5 EQC1-6(6) - 12 EQC5-18(7) -
6 - EQC1-6(6) 13 - EQC5-18(7)
7 EQC7(1) EQC7(1)
Applications of Sparse Modelling and Principle Component Analysis for the Virtual Metrology of Comprehensive Multi-dimensional
Quality
355
2.2 The First Phase – SVM
Applications
As the first, S. Arima (2011) has examined VM of an
actual plasma-CVD process. Before applying the
kSVM, 2σ/3σ methods and the combination of the
Hotelling-T
2
and Q-statistics are evaluated for easier
2-class discrimination problem. The former is a
basic statistical process control (SPC), and the latter
is a representative of the multivariate statistical
process control (MSPC). The accuracy of the latter
stays low (67%) though a false error (False Positive
of confusion matrix) is much improved than the
former case. The reason why the low accuracy is
that the data is not ideally distributed along the
normal distribution, for example, subunit4:
temperatures.
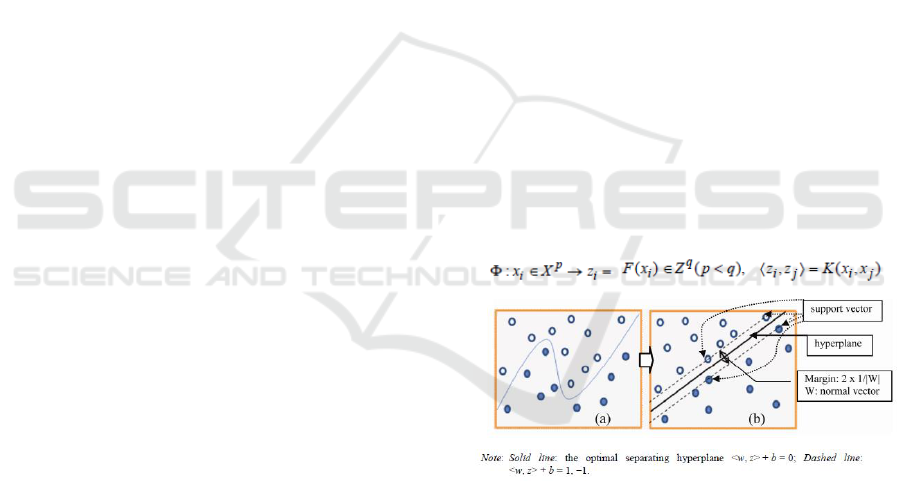
Support Vector Machines (SVM) was originally
introduced to address the Vapnik’s (1995) structural
risk minimization principle and is now famous for
high accuracy in application fields (e.g. Lee,et.al.,
2015). The basic idea of SVM is to map the data into
a higher dimensional space called feature space and
to find the optimal hyperplane in the feature space
that maximizes the margin between classes as shown
in Fig.2-3. A kernel function, such as the
Polynomial, the Gaussian (hereafter RBF: Radial
basis function), the Linear, or the Sigmoid kernel are
used to map the original data to feature space. the
simplest SVM deals with a two-class classification
problem—in which the data is separated by a
hyperplane defined by a number of support vectors.
Support vectors are a subset of the training data used
to define the boundary between the two classes.
The kernel-SVM (kSVM) is compared with the
linear discriminant analysis for the binary
classifications problem as the first. The kSVM
performs better than the linear discriminant analysis
for the 2-class model, though each of those achieves
more than 80% of accuracy. Next is the multi-class
discriminant in Table.2-1. The linear and the
nonlinear discriminant analyses are compared with
the kSVM (Fig. 2-4). Here, SVMs were originally
designed for binary classifications. However, many
real-world problems have more than two classes.
Most researchers view multi-class SVMs as an
extension of the binary SVM classification problem
as summarized by Wong and Hsu (2006). Two
approaches, one-against-all and one-against-one
methods, are commonly used. The one-against-all
method separates each class from all others and
constructs a combined classifier. The one-against-
one method separates all classes pairwise and
constructs a combined classifier using voting shemes
In this study, the former approach is used.
Independent from the combination of machine
variables, the kernel-SVM achieves the best in the
three methods. Beside that, the accuracy of the
standard linear and non-linear discriminations (5-
dimension) are less than 60% and 20%, respectively.
100% accuracy is achieved when the variables of all
machine sub-units are used for the RBF-SVM
learning (x=1, 2, or 3).
However, it also shows that when there are not
enough variables in the data set for leaning step, the
accuracy in the test step stays lower level. Since the
semiconductor manufacturing is going to be a high-
mix and low-volume production system in these
years, and the number of samples can be used in the
learning step (is limited to several tens in some
cases. Therefore, we applied LOOCV (leave-one-out
cross-validation) to the problem. LOOCV involves
using one sample as the validation data in the test
step and the remaining samples as the training data
in the learning step. This is repeated on all samples
one by one to cut the original samples on a
validation data and the training data. We confirmed
the high accuracy of SVM using LOOCV to respond
to such a case of small data set. The 9-class
discrimination can be solved by using several tens
samples in this study. However, note that the
accuracy of kSVM model depends on the variables
considered, the number of classes, and the data size.
Figure 2-3: Kernel SVM: (a) non-linear discrimination
needed and (b) mapping from original space to feature
space by a kernel function.
As the summary of the first phase, SVM was applied
to construct an accurate VM model that provided
multi-class quality prediction of the product. The
VM model predicted with 100% accuracy the quality
of the product after a CVD process. The accuracy
depends on the set of input variables, and the best
here is a case variables of all subunits are included.
We got the following issues for the practical use in
the mass production as the result of the SVM
applications of the first phase:
1) Machine variables are selected manually based on
ICORES 8th International Conference on Operations Research and Enterprise Systems - 8th International Conference on Operations
Research and Enterprise Systems
356
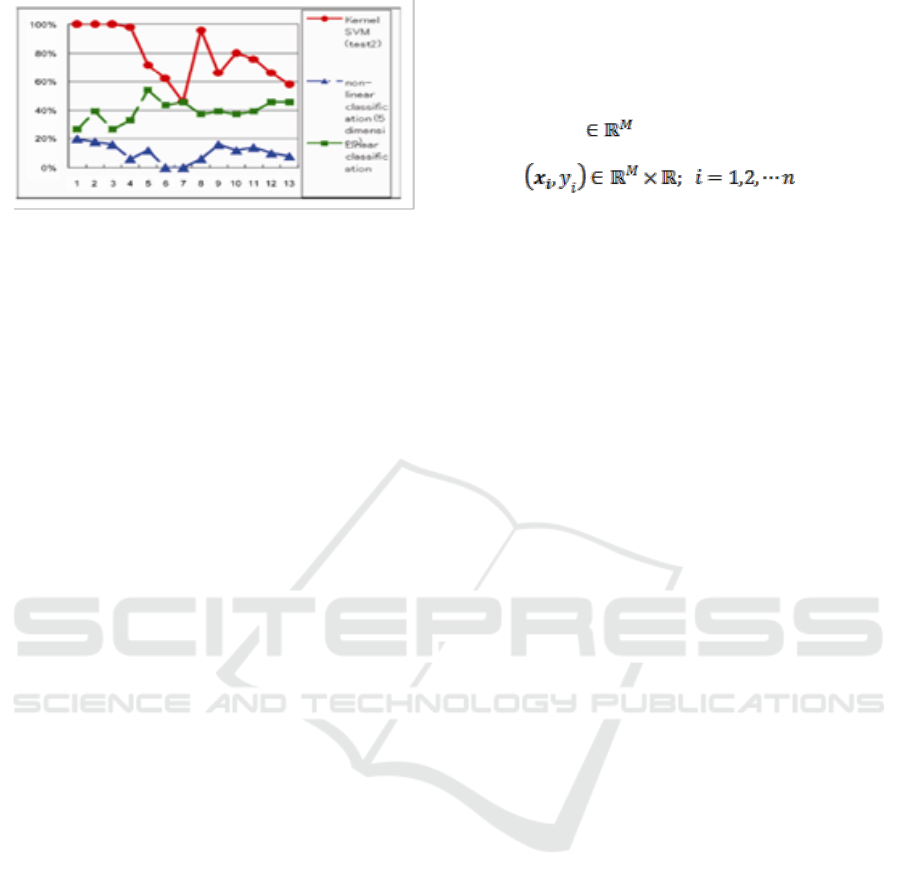
Figure 2-4: Case#2 -VM accuracy -nine classes.
(x={1,2,…13}: # EQC variables set in Table 2-2 ).
the engineering knowledge, and the best
combination of the variables are empirically
detected. The issue is to automatically extract the
variables from the wider scope.
2) SVM using the RBF kernel could achieve the
highest accuracy for the VM model as the result of
comparison of the Polynomial kernel or the Sigmoid
kernel. However, for the large model it is difficult to
build the VM model based on RBF-SVM in a
realistic time period. For example, 10 hours for
learning when RBF is used for the final test process
of an actual factory. The issue is to utilize a different
kernel function of high speed without unallowable
deterioration of the accuracy.
2.3 LASSO Applications
Second phase is for automatic variable extractions
and fast computation of SVM learning, and so
LASSO technique is applied and evaluated.
2.3.1 Problem Definition
In the first phase, much adaptive accuracy of RBF-
SVM could be evaluated by numerical experiments
of discrimination of multi-class quality by using
actual fab data. However, 13 different variable sets
are comparably evaluated to get the best accuracy in
that case. The number of the variables (M=90) are
larger than the number of samples (e.g. n=50), and
thus some of those are selected based on engineering
knowledge (Table.2-2). Here, the sparse modelling
is a rapidly progressing in recent. It is one important
research area of the compressed sensing, and it has
very wide application fields such as a medical data
processing (rapid image sensing of MRI or CT), the
earth science (data-driven modelling and
forecasting), and so on. Note that the deep learning
method also can extract meaningful variables but it
requires a big data to analyze, and so it cannot be
used in this case. This paper focuses on the
automatic variable extraction which can be used even
when M >n.
2.3.2 Methods - Lasso
Basic Least-square method is used to estimate
coefficients C to minimize the estimation error
(Eq.2) in the linear regression (Eq.1) from the data
set { }. Here, if
some variables in x may not contribute to estimate
Y, some of values in “C” should be zero to reduce
the variance of the estimation result. That responds
to “parse” case. LASSO proposed by Tibshirani
(1996) is the estimation method of the sparse
coefficient vector to reduce the variance of the
estimation result (Eq.3).
(1)
(2)
(3)
2.3.3 Numerical Results
In case of the class definition of Fig.2-1, we
empirically selected variables of 2 kinds of statistics
as the result (Table.2-2). Here, we try to
“automatically extract the variables by applying the
sparse modelling, and evaluate those accuracy as
well. The significant variables for the design
conformity (V(D)) and for the uniformity” (V(U))
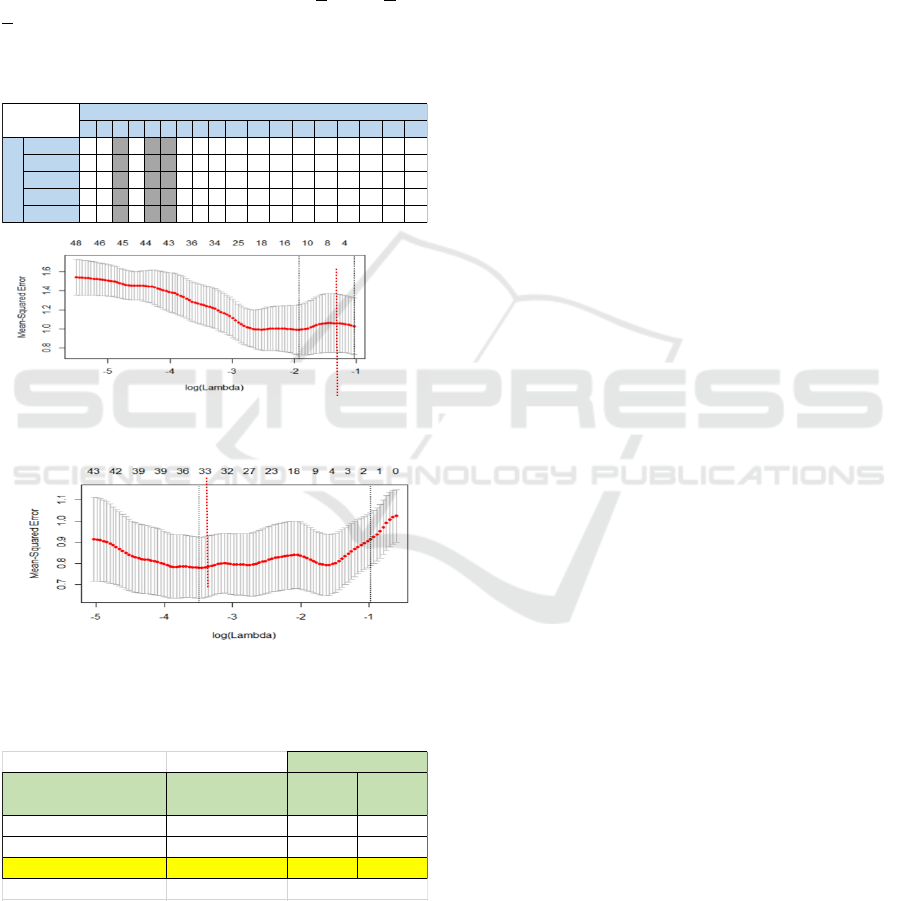
are extracted (Table.2-4). The-10-hold cross
validation is used for LASSO, and the set of
variables are selected when the lambda is minimum
as shown in Figures 2-5 and 2-6.
VM model of kSVM is built by using conjoint
form of variables (e.g. V(D)V(U)) as the first case.
Its accuracy of each kernel is evaluated for 2-
demensional quality classification by using the
LOOCV. A linear kernel is the best for the Lasso-
kSVM as shown in Table 2-5.
2.3.4 Issues for the next
We got the following issues for the practical use in
the mass production as the result of the SVM
applications of the second phase. Automated
procedure of VM modelling should be proposed.
1) LASSO regression model can achieve the
compression of the variables and computational time
Applications of Sparse Modelling and Principle Component Analysis for the Virtual Metrology of Comprehensive Multi-dimensional
Quality
357
much, however, we have to consider about the
multi-objective model. The multi-dimensional
classes of product quality may not be in the
relationship of linearly independent each other
because it has been defined by the engineering
knowledge. In that case, the join set of variables can
be redundant. The exclusion is still 7 variables as
common of Dc and Uf (Table 2-4).
2) It is required to compare with other multi-
objectives models such as PLS (Partial Least
Squares) often used in chemo-metrics research area.
Table 2-4: Variable extractions by Lasso -(Design
conformity(D) / Uniformity (U) /Both (B)).
Figure 2-5: Cross validation for Lasso parameter (λ -
[min, lse] = [ 0.1462973, 0.3540583] ) for i) D.
Figure 2-6: Cross validation for Lasso parameter ( λ -
[min, lse] = [0.03037, 0.37440] ) for ii) U.
Table 2-5: VM accuracy – Lasso-kSVM.
3 PCA AND LASSO
APPLICATIONS
3.1 Problem Definition
In this section, we will discuss an automated VM
procedure using PCA-LASSO and the kernel SVM
to solve the issues mentioned in section 2.3.4. PLS is
able to analyze the case the sample size is less than
the number of the variables.
3.2 Method - PCA and PLS
3.2.1 Basics of PCA and PLS
Principal component analysis (PCA) is a
mathematical procedure that transforms a number of
possibly correlated variables into a smaller number
of uncorrelated variables called principal
components. PCA rotates the axes of the original
variable coordinate system to new orthogonal axes,
called principal axes, such that the new axes
coincide with directions of maximum variation of
the original observations (Fig.3-1(graph)).The
regression is the modelling of relational expression
between the objective variable(s) Y and the
explanatory variables X. Coefficients are estimated
under the conditions of lowest estimation errors by
the Least-square or another method. There are some
regression models using PCA (Fig.3-1). PCR is a
representative in which PCA is applied only to X.
On the other hand, both X and Y are rotated by PCA
before regression in PLS.
3.2.2 PCA Application for Quality
Definitions
The PCA is applied for a multi-dimensional quality
definition. As the first case, PCA is used to 2-
demensional quality data (Design conformity (Dc)
and Uniformity (Uf)) to rotate to the orthogonality
space. After the PCA, the class is defined under the
threshold of 3-quantiles for each dimension. In the
second PCA application, we newly define the multi-
dimension of the quality as shown in Table.3-2 as
the result of PCA using original thickness values of
9 points. The primary principle component (PC1)
shows the level of thickness and it responds to the
“Design conformity” (Dc’). The second and the third
principle component (PC2, PC3) show the deflection
of the thickness and respond to “Uniformity” (Uf ’).
The threshold of quality class can be defined by:
i) Probability (e.g. normal distribution case)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Min U U U U U U
Max U D U D U U B U B
Range U D U U U
Average B U U B B U D U U U
Std. dev. U U B U B U U
※D:Design conformity, U: Uniformity, B:Both
Sensor No.
statistics
Variables
extracted
Quality class of VM
variables set
[# of variables]
RBF Linear
Design conformity (A,B,C) V(D) [11] 92 88
Uniformity (a,b,c) V(U) [35] 84 100
2D quality (A,B,C) X (a,b,c)
V(D)∪V(U) [39] 90 100
accuracy [%]
Kernel
↑# of variables selected.
↑# of variables selected.
ICORES 8th International Conference on Operations Research and Enterprise Systems - 8th International Conference on Operations
Research and Enterprise Systems
358

ii) Quantiles (e.g. uniform distribution case, etc.)
Based on the distribution of the principal component
scores (Fig. 3-3), only PC1’s score is statistically
adapt to the normal distribution as the result of One-
sample Kolmogorov-Smirnov test (D = 0.55944, p-
value = 2.998e-15, alternative hypothesis: two-
sided). Here, i) is selected for defining classes of Dc’
and ii) is used for defining classes of Uf ’. The
threshold here is defined as shown in Table 3-5 for i).
On the other hand, the 3-quantiles is used for ii).
Figure 3-1: Multivariate regression models.
Table 3-1: PCA result - factor loading (PC1, 2, 3).
Table 3-2: PCA result - factor loading (PC1, 2, 3).
Figure 3-3: PCA result -principal component scores.
Table 3-5: The threshold for i (yi: the score,
standard deviation).
3.3 Numerical Results
3.3.1 Automated VM Procedure
The procedure of PCA-LASSO and kSVM
STEP-1: PCA to define the multi-dimensional
quality. Select a few principal components by the
cumulative contribution ratio becomes over 80*% or
so. (*depend on the target accuracy)
STEP-2: LASSO to extract the significant machine
variables
STEP-3: Select the principal component to use in the
following step. Check the LASSO result (e.g. PC2
is excepted because of no variables selected.)
STEP-4: Select the threshold type for each PCs.
Check the distributions of principal component
scores for selected PCs (e.g. PC1 and PC3 is set to
the probability-type and to the quantiles)
STEP-5: Define the class for all samples (e.g.
product wafer here)
STEP-6: SVM learning and class discriminations.
3.3.2 PCA-LASSO (1) and Kernel SVM
As the first case, PCA is used to 2-demensional
quality data (Dc2 and Uf2) to rotate to the
orthogonality space. The threshold of quality class
can be defined by the 3-quantiles for each dimension.
Combination of LASSO and linear-SVM appear the
best accuracy again (100%) even if PCA is used. In
the same case, the accuracies of RBF-SVM and
Polynomial-SVM result 82% and 92%, respectively.
In case of PCA-LASSO (1), PC2 is excepted
because no machine variables are selected in the
LASSO regression, and only the primary principle
QC1 QC2 QC3 QC4 QC5 QC6 QC7 QC8 QC9
PC1 0.292 0.350 0.350 0.335 0.352 0.350 0.303 0.288 0.370
PC2 0.177 0.189 0.263 0.454 0.076 0.010 (0.333) (0.076) (0.731)
PC3 (0.660) 0.087 0.126 0.390 0.155 (0.030) (0.396) (0.260) 0.373
Original variables of quality measured
QC1 QC2 QC3 QC4 QC5 QC6 QC7 QC8 QC9 Average
PC1 0.292 0.350 0.350 0.335 0.352 0.350 0.303 0.288 0.370 0.332
PC2 0.177 0.189 0.263 0.454 0.076 0.010 (0.333) (0.076) (0.731) 0.003
PC3 (0.660) 0.087 0.126 0.390 0.155 (0.030) (0.396) (0.260) 0.373 (0.024)
original variables of quality
Principal
components
(PCA )
a μ-σ≦yi≦μ+σ
b μ-2σ≦yi<μ-σ, μ+σ<yi≦μ+2σ
c yi<μ-2σ, μ+2σ<yi
PC1
PC2
Applications of Sparse Modelling and Principle Component Analysis for the Virtual Metrology of Comprehensive Multi-dimensional
Quality
359
component (PC1) represents both the “Design
conformity” and “Uniformity” (PC1: Dc2 & Uf2).
Note that PLS regression cannot work well in this
case. Error is detected in calculation.
3.3.3 PCA-LASSO (2) and Kernel SVM
Here we use the result of PCA using original
thickness values of 9 points (PC1: Revised design
conformity (Dc’), PC3: Revised uniformity (Uf ’)).
2
nd
-principal component PC2 is excepted because no
machine variables are selected by LASSO.
Three principal components were obtained by PCA,
and 12 variables for PC1 and 4 variables for PC3
were chosen. Variable sets for PC1 and PC3 are
expressed as and
Since each principal
component is orthogonal, the variables chosen for
each principal component tend to be uncorrelated,
that is, they are exclusive. Thus, variables included
in the union can explain the original objective
variables without waste. The variable set used for
the SVM learning is defined as the union of the
variables extracted by LASSO:
Linear-SVM appears again the best accuracy for all
(98%) in addition to the shortest computational time.
RBF-SVM is lower accuracy (82%) though it can
keep its accuracy based on best parameters for the
gamma function. In addition, the computational time
is the largest for all. The accuracy of the
Polynomial-SVM stays about 90%.
Note that the result of the variable extraction of this
PCA-LASSO is helpful pre-process for PLS
regression though the PLS regression cannot be
solved when the original input data without the
representative object variables and extracted
explanatory variables. This is one type of cases that
PLS regression does not go well because the data set
includes an explanatory (independent) variable
irrelevant to an objective (dependent) variable. Even
though in such a case, PLS regression can succeed
by the pre-process of variable extraction of the PCA-
LASSO regression. The best number of objective
variables, that is principal components here, is the
same as the number of selected objective variables
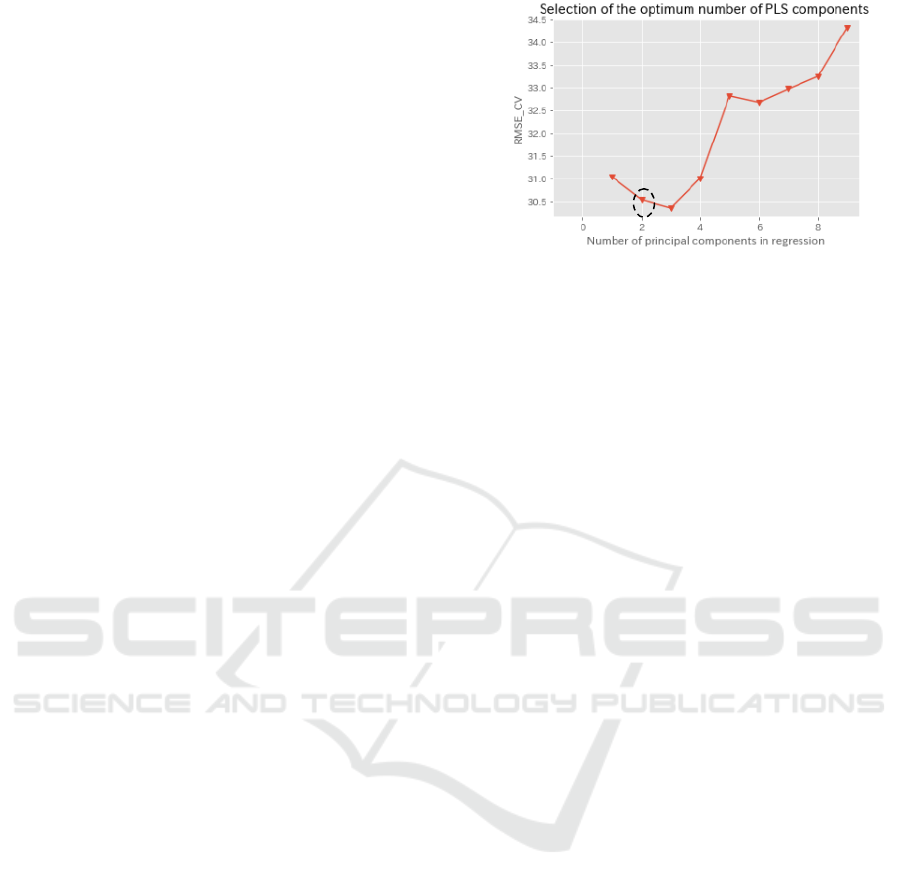
in PCA. “3” is the best of the lowest RMSE (root-
mean-square error) as shown in Fig. 3-4.
3.3.4 PCA-LASSO (3) and Kernel SVM
We can use the result of PCA to define
comprehensive index by using the contribution rate
(thus Eigen values), Eigen vectors, and so on.
However the result of LASSO for the
comprehensive index is not so effective here.
Figure 3-4: Selection of # of objective variables (principal
components here) for PLS.
3.4 Summary of Variable Extractions
PCA is combined to LASSO regressions instead of
PCR (Fig.3-1) or PLS (Fig.3-1, or as a pre-process
of PLS) to extract the optimal and smallest set of
variables for comprehensive VM modelling of
multi-dimensional quality. As the result of
comparison of PCA-LASSO (1) and (2), the
compaction rate is improved by about 66.7% and
83.3% besides the exclusion rate’ improvement
(Table 3-7). In case of PCA-LASSO (1), PC2 is
excepted because no machine variables are selected
in LASSO regression, and only the primary principle
component (PC1) represents both the design
conformity and uniformity (Dc2 & Uf 2:PC1). That
is caused the original definition of the 2 factors of
thickness is not linearly independent. In such a case,
compression rate is lower than the other case. The
exclusion rate becomes much lower in the proposed
PCA-LASSO cases (Tables 3-6, 3-8, 3-9, 3-10). See
appendix-A for the coefficients of the variables.
3.5 Conclusions of the Third Phase
In this section, automated VM procedure using
PCA-LASSO and kernel SVM is proposed and
evaluated. PCA is combined to LASSO regressions
instead of using PCR or PLS to extract the
reasonable and smallest set of variables for
comprehensive VM modelling of multi-dimensional
quality. In addition, the liner-kernel SVM using the
variables selected LASSO regressions achieves the
highest accuracy. LASSO and linear-kernel SVM
can compress the scale and computational time
much in the model learning without deterioration of
the accuracy.
ICORES 8th International Conference on Operations Research and Enterprise Systems - 8th International Conference on Operations
Research and Enterprise Systems
360

Table 3-6: The number of machine variables extracted.
Table 3-7: Compaction rate and Exclusion rate.
Table 3-8: Machine variables extracted by LASSO. (※
D: Design conformity, U: Uniformity, B:both).
Table 3-9: Variables extraction of PCA-LASSO (1). (※
PC1: Design conformity & Uniformity).
Table 3-10: Variables extraction of PCA-LASSO (2).
(PC1: Design conformity, PC3: Uniformity, B:both).
4 CONCLUSIONS
This study discussed the modelling of virtual
metrology in 3 phases. The first is the application of
SVM for multi-class virtual metrology mainly for
high accuracy. The second phase is LASSO
application for automatic variable extractions and
fast computation of Linear-SVM learning. Finally
the third phase is for all; automated extractions of
the best set of machine variables, the high accurate
quality discriminations for the multi-dimensional
classes, and the fast computation for a practical use.
ACKNOWLEDGEMENTS
We deeply appreciate the referees' advice and
comments. Also we thank ICORES secretariat for
their gentle guides.
REFERENCES
Y.Naka, K.Sugawa, C. McGreavy., 2012. Introduction to
VLSI Process Engineering, Springer.
APC Conference (USA) (Oct. 22
nd
, 2018 access)
http://www.cvent.com/events/apc-conference-xxx-
2018/event-summary-
a8d0f8ae27e84ecf97862bdc1b4c7b01.aspx.
EUROPEAN ADVANCED PROCESS CONTROL AND
MANUFACTURING CONFERENCE (Oct. 22
nd
,
2018 access): https://www.apcm-europe.eu/home/.
AEC/APC symposium Asia (Oct. 22
nd
, 2018 access):
https://www.semiconportal.com/AECAPC/index_e.ht
ml.
Literatures in “Metrology” and “Advanced process control”
sessions of IEEE Transaction on Semiconductor
Manufacturing (since 2011).
S. Arima, 2011. Virtual Metrology-based Engineering
Chain Management by Multi-classification of Quality
using Support Vector Machine for Semiconductor
Manufacturing, Int. J. Industrial and Systems
Engineering No.8 Vol.1, Inderscience pub., pp.1-18 .
S. Arima., et.al., 2015. Applications of machine learning
and data mining methods for advanced equipment
control and process control, Proceedings of AEC/APC
symposium Asia 2015, DA-O-34 (pp.1-6).
Vapnik, V.N. ,1995. The Nature of Statistical Learning
Theory, New York: Springer-Verlag.
Wong, W. and Hsu, S. ,2006. Application of SVM and
ANN for image retrieval, European Journal of
Operations Research, Vol. 173, pp.938–950.
T. Lee, C. O. Kim., 2015. Statistical Comparison of Fault
Detection Models for Semiconductor Manufacturing
Processes, IEEE Trans. on Semi. Manufacturing,
28(1), pp.80-91, IEEE.
R.Tibshirani.,1996. Regression shrinkage and selection via
the lasso, J. R. Statist. Soc. B, 58(1), pp.267-288.
R. A. Johnson, D. W. Wichern., 2007. Applied
Multivariate Statistical Analysis, Prentice Hall.
# of variables (total)
V(D+U)=V(D)⋃V(U)
# of depricated variables
V(D*U)=V(D)∩V(U)
Original 90 -
LASSO (Dc, Uf) 39 7
PCA-LASSO(1)
(pc1: Dc2 & Uf2)
30 0
PCA-LASSO(2)
(pc1: Dc', pc3:Uf')
15 1
[%]
Compaction rate
=(90-V(D+U))/90
Exclusion rate
={V(D+U)-V(D*U)}/V(D+U)
Original 0.00% -
LASSO (Dc, Uf) 56.67% 82.05%
PCA-LASSO(1)
(pc1: Dc2 & Uf2)
66.67% 100.00%
PCA-LASSO(2)
(pc1: Dc', pc3:Uf')
83.33% 93.33%
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Min U U U U U U
Max U D U D U U B U B
Range U D U U U
Average B U U B B U D U U U
Std. dev. U U B U B U U
Sensor No.
statistics
Variables
extracted
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Min PC1 PC1 PC1 PC1
Max PC1 PC1 PC1 PC1 PC1 PC1 PC1 PC1 PC1
Range PC1 PC1 PC1 PC1
Average PC1 PC1 PC1 PC1 PC1 PC1
Std. dev. PC1 PC1 PC1 PC1 PC1 PC1 PC1
Sensor No.
statistics
Variables
extracted
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Min PC1 PC3 PC1
Max PC1 PC1 PC1 PC1
Range PC1
Average PC3 PC1 B
Std. dev. PC3 PC1 PC1 PC1
Variables
extracted
Sensor No.
statistics
Applications of Sparse Modelling and Principle Component Analysis for the Virtual Metrology of Comprehensive Multi-dimensional
Quality
361
