
Probability based Proof Number Search
Zhang Song
1
, Hiroyuki Iida
1
, H. Jaap van den Herik
2
1
Japan Advanced Institute of Science and Technology, Ishikawa, Japan
2
Leiden Centre of Data Science, Leiden, The Netherlands
Keywords:
Probability, Monte-Carlo Simulations, Proof Number Search, Game Solver.
Abstract:
Probability based proof number search (PPN-search) is a game tree search algorithm improved from proof
number search (PN-search) (Allis et al., 1994), with applications in solving games or endgame positions.
PPN-search uses one indicator named “probability based proof number” (PPN) to indicate the “probability”
of proving a node. The PPN of a leaf node is derived from Monte-Carlo evaluations. The PPN of an internal
node is backpropagated from its children following AND/OR probability rules. For each iteration, PPN-search
selects the child with the maximum PPN at OR nodes and minimum PPN at AND nodes. This holds from
the root to a leaf. The resultant node is considered to be the most proving node for expansion. In this paper,
we investigate the performance of PPN-search on P-game trees (Kocsis and Szepesv
´
ari, 2006) and compare
our results with those from other game solvers such as MCPN-search (Saito et al., 2006), PN-search, the UCT
solver (Winands et al., 2008), and the pure MCTS solver (Winands et al., 2008). The experimental results
show that (1) PPN-search takes less time and fewer iterations to solve a P-game tree on average, and (2) the
error rate of selecting a correct solution decreases faster and more smoothly as the iteration number increases.
1 INTRODUCTION
Proof number search (PN-search) (Allis et al., 1994)
is a search algorithm and is one of the most successful
approaches for solving games or endgame positions.
In PN-search, each node in a search tree incorporates
two indicators called proof number and disproof num-
ber, respectively, indicating the “difficulty” of proving
and disproving a game position corresponding with
this node. For all unsolved nodes (leaf nodes), the
proof number and disproof number are 1. For a win-
ning node, the proof number and disproof number are
0 and infinity, respectively. For a non-winning node,
it is the reverse. For internal nodes, the proof num-
ber and disproof number are backpropagated from its
children following MIN/SUM rules: at OR nodes, the
proof number equals the minimum proof number of
its children, and the disproof number equals the sum-
mation of the disproof numbers of its children. It is
the reverse for AND nodes. For each iteration, go-
ing from the root to a leaf node, PN-search selects ei-
ther the child with the minimum proof number at OR
nodes, or the child with the minimum disproof num-
ber at AND nodes. Finally, it regards the leaf node
arrived at as the most proving node to expand. PN-
search is an advanced approach for proving the game-
theoretic value, especially for sudden-death games
that may abruptly end by the creation of one of a pre-
specified set of patterns such as they occur in Gomoku
and Chess. PN-search works so well because the two
games mentioned usually have an unbalanced game
tree with various branching factors. Obviously, the
proof number and disproof number are highly instru-
mental when the branching factor varies. As a result,
the proof number and disproof number can give dis-
tinguishable information to indicate the shortest path
of proving or disproving a node. For games with a
balanced tree and with an almost fixed depth and an
almost fixed branching factor such as Hex and Go, the
PN-search is quite weak, because the proof numbers
and disproof numbers are too similar to give distin-
guishable information.
To solve this obstacle, some PN-search variants
were proposed with the idea of using a parameter
to enforce a deeper search, such as Deep PN-search
(Ishitobi et al., 2015) and Deep df-pn (Zhang et al.,
2017). Another possible solution is to utilize the
heuristic information of the leaf node, such as df-pn*
(Nagai, 2002). In the last few years, the Monte-Carlo
tree search (MCTS) (Chaslot, 2010) has become quite
successful on balanced tree games such as Go. Hence,
using Monte-Carlo evaluations to obtain the proof
Song, Z., Iida, H. and van den Herik, H.
Probability based Proof Number Search.
DOI: 10.5220/0007386806610668
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 661-668
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
661

number and disproof number of the leaf nodes is a
new promising method to improve PN-search. One
pointer in this direction is the Monte-Carlo proof
number search (MCPN-search) (Saito et al., 2006).
MCPN-search has exactly the same rules as PN-
search except that the proof number and the disproof
number of unsolved nodes are derived from Monte-
Carlo simulations. This method makes MCPN-search
more efficient than PN-search especially in balanced
tree games. However, there still is a new obstacle in
MCPN-search: using the same backpropagation rules
(MIN/SUM rules) as PN-search does not work well
with Monte-Carlo evaluations, as the Monte-Carlo
evaluation leads to a convergent real number while
the MIN/SUM rules are proposed for discrete integer
numbers. Hence, it will cause an information loss of
the Monte-Carlo evaluations in the backpropagation
step.
In this paper, we propose a new application of
Monte-Carlo proof number search named probability
based proof number search (PPN-search). The idea
originates from the concept ”searching with proba-
bilities” (Palay, 1983). The core idea is that the
probability of proving a node is computed from the
probabilities of proving its children while following
the AND/OR rules of probability events. The com-
bined operation is based on the hypothesis that prov-
ing each of the children of a node is an independent
event. In Palay (1983), this idea is applied on B*
search (Berliner, 1981) without using Monte-Carlo
evaluations. In this paper, we adopt the idea together
with Monte-Carlo evaluations on PN-search and pro-
pose a new search algorithm called probability based
proof number search (PPN-search). To show the effi-
ciency of PPN-search, we conduct experiments on P-
game trees (Kocsis and Szepesv
´
ari, 2006) which are
randomly constructed game trees with a fixed depth
and a fixed branching factor, normally used to sim-
ulate balanced game trees, such as the ones occur-
ring in Hex and Go. We compare the performance
of PPN-search, MCPN-search, PN-search and other
Monte-Carlo based game solvers such as the pure
MCTS solver (Winands et al., 2008) and the UCT
solver (MCTS solver equipped with the Upper Con-
fidence Bounds applied to Trees). The experimental
results show that PPN-search outperforms other ex-
isting solvers by taking less time and fewer iterations
to converge to the correct solution on average. More-
over, the error rate of the selected moves decreases
faster and more smoothly as the number of iterations
increases.
The rest of the paper is organized as follows. In
Section 2, the formalism and the algorithm of PPN-
search are presented. In Section 3, two benchmarks
about Monte-Carlo based game solvers are introduced
and the relations between PPN-search and these game
solvers are discussed. We conduct experiments and
discuss the results in Section 4. Finally, we conclude
in Section 5.
2 PROBABILITY BASED PROOF
NUMBER SEARCH
In this section, we present the main concept (Subsec-
tion 2.1), the formalism (Subsection 2.2), and the al-
gorithm (Subsection 2.3) of probability based proof
number search (PPN-search).
2.1 Main Concept
In PPN-search, only one indicator is incorporated in
each node. The indicator is the probability. It indi-
cates the probability of proving a node. The PPN of
a leaf node is derived from Monte-Carlo simulations.
For each iteration, for all nodes from the root to a leaf
node, PPN-search selects the child with the maximum
PPN at OR nodes and the child with the minimum
PPN at AND nodes. The resultant node is regarded
as the most proving node for expansion. When new
nodes are available, PPNs are backpropagated to the
root while following the AND/OR probability rules.
Similar to the proof number, the PPN is highly rel-
evant with the branching factor because of the prob-
ability rules. So the PPN contains the information of
the tree structure above the leaf nodes. Moreover, the
Monte-Carlo simulations give the PPN more informa-
tion beneath the leaf nodes. As a result, PPN becomes
such a domain independent heuristic combining the
information above and beneath the leaf nodes.
2.2 Probability Based Proof Number
Let n. ppn be the PPN of a node n. There are three
types of nodes to be discussed below.
(1) Assume n is a terminal node
(a) If n is a winning node,
n. ppn = 1.
(b) If n is not a winning node,
n. ppn = 0.
(2) Assume n is a leaf node (not terminal), and
R is the winning rate computed by applying several
playouts from this node. Take θ as a small positive
number close to 0.
(a) If R ∈ (0, 1),
n. ppn = R.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
662

(b) If R = 1,
n. ppn = R −θ.
(c) If R = 0,
n. ppn = R + θ.
(3) Assume n is an internal node, using AND/OR
probability rules of independent events.
(a) If n is an OR node,
n. ppn = 1 −
∏
n
c
∈ children of n
1 −n
c
. ppn (1)
(b) If n is an AND node,
n. ppn =
∏
n
c
∈ children of n
n
c
. ppn (2)
2.3 Algorithm
The PPN-search includes the following four steps.
(1) Selection: for all nodes from the root to a leaf
node, do select the child with the maximum PPN at
OR nodes and the child with the minimum PPN at
AND nodes, while regarding it as the most proving
node for expansion.
(2) Expansion: expanding the most proving node.
(3) Play-out: The play-out step begins when we
enter a position that is not a part of the tree yet. Moves
are selected in a randomly self-play mode until the
end of the game. After several play-outs, the PPNs
of the expanded nodes are derived from Monte-Carlo
evaluations.
(4) Backpropagation: updating the PPNs from
the extended nodes to the root, while following the
AND/OR probability rules given above.
3 BENCHMARKS
In this section, two benchmarks of the type Monte-
Carlo based game solver are introduced (see Subsec-
tion 3.1 and Subsection 3.2). Moreover, the relations
between PPN-search and these two benchmarks are
discussed.
3.1 Monte-Carlo Proof Number Search
Monte-Carlo proof number search (MCPN-search)
(Saito et al., 2006) is an enhanced proof number
search by adding the flexible Monte-Carlo evaluation
to the leaf nodes. We discuss three differences be-
tween MCPN-search and PPN-search.
(1) MCPN-search uses two indicators: proof num-
ber (PN) and disproof number (DN). The PN (DN)
of a leaf node equals the non-winning (winning) rate
derived from Monte-Carlo simulations. In contrast,
PPN-search uses only one indicator PPN. The PPN
of a leaf node equals the winning rate derived from
Monte-Carlo simulations.
(2) MCPN-search when going from the root to
a leaf node, selects the child with the minimum PN
(DN) taking into consideration whether the current
node is an OR (AND) node, just as the original PN-
search. In contrast, PPN-search when going from the
root to a leaf node, solely selects the child with the
maximum PPN at OR nodes and the child with the
minimum PPN at AND nodes.
(3) MCPN-search backpropagates PN and DN by
following MIN/SUM rules as the original PN-search.
In contrast, PPN-search backpropagates PPN by fol-
lowing the AND/OR probability rules of independent
events.
Compared with PPN-search, an important obsta-
cle of MCPN-search is that using the same updat-
ing rules (MIN/SUM rules) as the PN-search does
not go along well with Monte-Carlo evaluations, as
the Monte-Carlo evaluation leads to a convergent real
number whereas the MIN/SUM rules are proposed
for discrete integer numbers. It will cause an infor-
mation loss in the backpropagation step. For exam-
ple, Figure 1 shows two trees ((a) and (b)) in MCPN-
search where the root is an OR node. According to the
MIN rule of MCPN-search, the PN of the root equals
the minimum PN of its children (being 0.2). How-
ever, tree (a) and tree (b) obtain the same PN for the
root, which means that both trees have the same “dif-
ficulty” to be proved. Yet, if we investigate the PN
distribution of the leaves, tree (a) is more promising to
be proved because all leaves have relatively small PNs
(0.2, 0.2, and 0.3). This is especially true if the PN of
the leaf node is derived from Monte-Carlo evaluations
which are usually slightly different. In other words,
actually all branches have an influence on the root
in a game tree even though the root is an OR node,
especially when the proof number or disproof num-
ber indicators of leaf nodes are derived from Monte-
Carlo evaluations. For PPN-search, such an obstacle
will not occur. In comparison with MCPN-search, we
simply change the PNs of the leaves in Figure 1 to
PPNs by the following operation: let PPN = 1 - PN,
which corresponds to the definitions of PPN and PN.
Then use the OR rule (Eq. (1)) to update the PPN. As
is shown in Figure 2, tree (a) has a larger PPN than
tree (b), which implies that tree (a) is more promising
to be proved than tree (b). This conclusion is fitting
to our intuition.
Figure 3 and Figure 4 show such phenomenon for
the SUM rule of MCPN-search. Here, the root is an
Probability based Proof Number Search
663

AND node and the PN of the root equals the summa-
tion of the PNs of its children. As a result, tree (a)
and tree (b) obtain the same PN which implies that
both trees have the same “difficulty” to be proved.
However, there is one leaf in tree (b) with a very big
PN 0.8 which means that this leaf is very likely to be
disproved, whereas all the leaves in tree (a) have rel-
atively smaller and more similar PNs. As is known,
for an AND node, if there exists one child that is dis-
proved, the node will be disproved. Therefore, the
SUM rule loses some information during the back-
propagation process. PPN-search is able to solve this
obstacle by changing the SUM rule to the AND rule
(Eq. (2)). As is shown in Figure 4, tree (a) obtains a
larger PPN than tree (b), which implies that tree (a)
is more promising to be proved, which corresponds to
our intuition.
Figure 1: Two examples of updating PN by MIN rule in
MCPN-search (the square represents the OR node).
3.2 Monte-Carlo Tree Search Solver
Monte-Carlo Tree Search (MCTS) (Chaslot, 2010) is
a best-first search guided by the results of Monte-
Carlo simulations. In the last few years, MCTS
has advanced the field of computer Go substantially.
Although MCTS equipped with the UCT (Upper
Confidence Bounds applied to Trees) formula which
enables the evaluations to converge to the game-
theoretic value, it is still not able to prove the game
theoretic value of the search tree. This is even more
true for sudden-death games, such as Chess. In
this case, some endgame solvers (i.e., PN-search)
are traditionally preferred above MCTS. To trans-
form MCTS to a good game solver, Winands et al.
introduced an MCTS variant called MCTS solver
Figure 2: Two examples of updating PPN by OR rule in
PPN-search (the square represents the OR node).
Figure 3: Two examples of updating PN by SUM rule in
MCPN-search (the circle represents the AND node).
(Winands et al., 2008), which has been designed to
prove the game-theoretical value of a node in a search
tree. The MCTS solver includes the following four
strategic steps.
(1) Selection: Selection picks a child to be
searched based on the previously gained information.
For pure MCTS when going from the root to a leaf
node, the child with the largest simulation value will
be selected. For UCT, an enhanced version of MCTS,
it controls the balance between exploitation and ex-
ploration by selecting the child with the largest UCT
value:
v
i
+
q
C×ln n
p
n
i
,
where v
i
is the simulation value of the node i, n
i
is the
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
664

Figure 4: Two examples of updating PPN by AND rule in
PPN-search (the circle represents the AND node).
visit count of child i, and n
p
is the visit count of cur-
rent node p. C is a coefficient parameter, which has
to be tuned experimentally. Winands et al. also con-
sider other strategies to optimize the selection based
on UCT, such as progressive bias (PB). But in this
paper, to make it easy to follow, we only apply the
UCT strategy. To transform UCT and pure MCTS to a
solver, a node is assumed to have the game-theoretical
value ∞ or −∞ that corresponds to a proved win or not
win, respectively. In this paper, we consider all the
drawn games as proved to be not win games to make
the experimental results more easy to interpret. When
a child is a proven win, the node itself is a proven win,
and no selection has to take place. But when one or
more children are proven to be not a win, it is tempted
to discard them in the selection phase. In this paper, to
make it easy to compare, i.e., we do not consider the
proved win or the proved not win node in the play-out
step, because such technique can similarly be applied
into PPN-search and MCPN-search. Moreover, for
the final selection of the winning move at the root, of-
ten, it is the child with the highest visit count, or with
the highest value, or a combination of the two. In the
UCT solver or in the pure MCTS solver, the strategy
is to select the child of the root with maximum quan-
tity v +
A
√
n
, where A is a parameter (here, set to 1), v is
the node’s simulation value, and n is the node’s visit
count.
(2) Play-out: The play-out step begins when we
enter a position that is not a part of the tree yet.
Moves are selected in self-play until the end of the
game. This task might consist of playing plain ran-
dom moves.
(3) Expansion: Expansion is the strategic task that
decides whether nodes will be added to the tree. In
this paper, we expand one node for each iteration.
(4) Backpropagation: Backpropagation is the pro-
cedure that propagates the result of a simulated game
back from the leaf node, through the previously tra-
versed node, all the way up to the root. A usual strat-
egy of UCT or pure MCTS is taking the average of
the results of all simulated games made through this
node. For the UCT solver and the pure MCTS solver
(in addition to backpropagating the values 1,0,-1) the
search also propagates the game-theoretical values ∞
or −∞. The search assigns ∞ or −∞ to a won or
lost terminal position for the player to move in the
tree, respectively. Propagating the values back in the
tree is performed similar to negamax in the context of
MIN/MAX searching in such a way that we do not
need to distinguish between MIN and MAX nodes.
More precisely, for negamax, the value of a MIN node
is the negation of the value of a MAX node. Thus, the
player on move looks for a move that maximizes the
negation of the value resulting from the move: this
successor position must by definition have been val-
ued by the opponent.
Compared with PPN-search, the main difference
between the pure MCTS solver and PPN-search is the
backpropagation strategy. For a pure MCTS solver,
the backpropagation strategy of a node is taking the
average of the simulation results of its children. In
contrast, PPN-search follows the AND/OR probabil-
ity rules presented in Eqs. (1) and (2). Actually, both
backpropagation strategies have been discussed in an
early paper of MCTS (Coulom, 2006) that points out
the weakness of AND/OR probability backpropaga-
tion rules for MCTS. Compared with taking the aver-
age, it is noted that they have to assume some degree
of independence between probability distributions for
probability backpropagation rules. This assumption
of independence is wrong in the case of Monte-Carlo
evaluation because the move with the highest value
is more likely to be overestimated than other moves.
Moreover, a refutation of a move is likely to refute si-
multaneously other moves of a node. Such statement
(Coulom, 2006) is true for MCTS when it is used to
find an approximate best move in a game AI, but is
not appropriate when MCTS is used to solve a game
or a game position. There are two reasons: (1) To
solve a game or a game position, the search algorithm
has to go deeply until to the terminal nodes to com-
pletely prove the game-theoretic value. So it is not
necessary for a search algorithm to avoid overestimat-
ing the move with the highest value. In contrast, what
really matters for a search algorithm is the speed to
approach the terminal nodes. (2) To solve a game or a
game position, we need to search on an AND/OR tree
to find the solution. Therefore, the AND/OR prob-
Probability based Proof Number Search
665
ability backpropagation rules are more suitable than
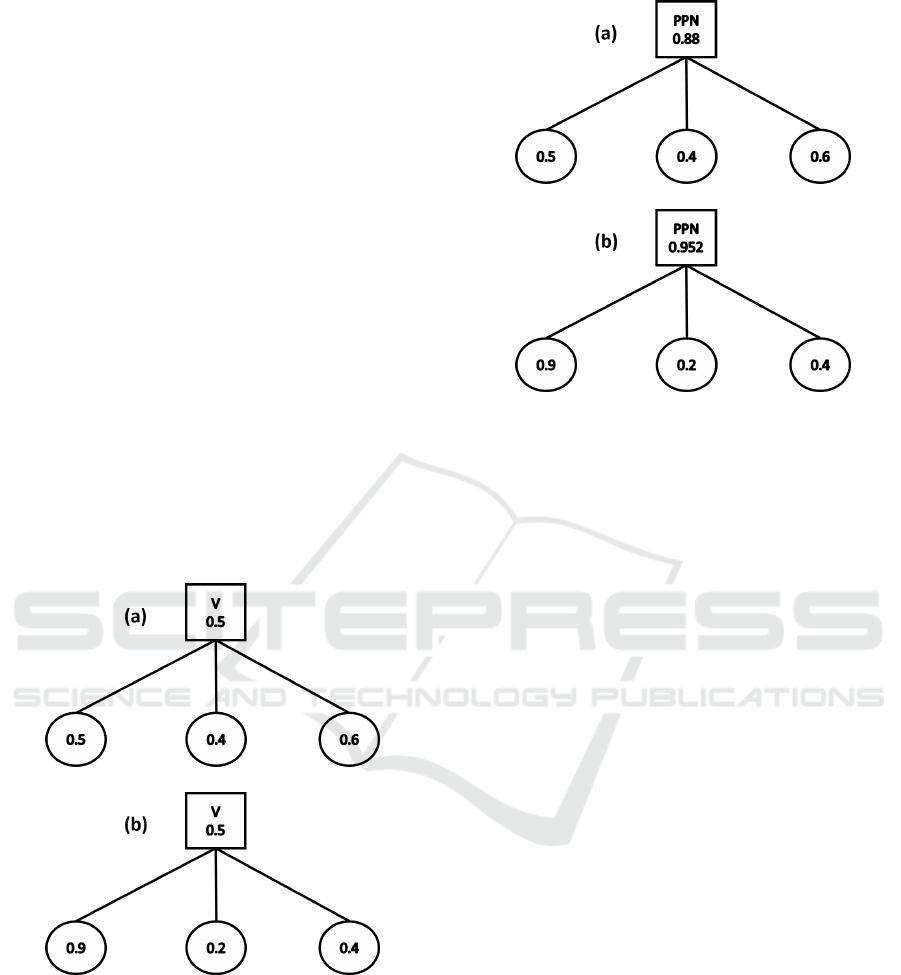
taking the average. For example, Figure 5 shows two
trees in an UCT solver or pure MCTS solver where
the root is an OR node. Assuming that all the children
have the same visit count, for updating the simulation
value of the root, we take the average of the simula-
tion value of its children. Then both trees obtain the
same simulation value, which implies that both trees
have the same possibility to win. However, to prove a
game, things are different. As the root is an OR node,
it will be proved as long as there exists one child that
can be proved. In Figure 5, tree (b) has a child with a
very large winning rate 0.9, while all children in tree
(a) have relatively small winning rate, so tree (b) is ab-
solutely more likely to be proved than tree (a). If we
use AND/OR probability rules to update these simu-
lation values, it is clear that as is shown in Figure 6
tree (b) obtains larger PPN values than tree (a), which
means that tree (b) is more likely to be proved. And
this is surely more fitting to our intuition. It is similar
for the AND rule of PPN-search. Therefore, it is dif-
ficult to prove a game-theoretic value of search tree.
In summary, PPN-search with AND/OR backpropa-
gation rules is more suitable than the UCT solver and
the pure MCTS solver.
Figure 5: Two examples of updating simulation values by
taking the average in the UCT solver or the pure MCTS
solver (the square represents the OR node).
4 EXPERIMENTS
To examine the effectiveness of PPN-Search, we con-
ducted two series of experiments on P-game trees.
The P-game tree (Kocsis and Szepesv
´
ari, 2006) is a
MIN/MAX tree where a randomly chosen value is as-
signed to each move. The value of a leaf node is given
Figure 6: Two examples of updating PPN by OR rule in
PPN-search (the square represents the OR node).
by the sum of the move values along the path. If the
sum is positive, the result is a win for MAX, if nega-
tive it is a win for MIN, and it is draw if the sum is 0.
In all experiments, for the moves of MAX the value
was chosen uniformly from the interval [0,127] and
for MIN from the interval [−127,0].
In series 1, we construct 200 P-game trees ran-
domly, with 2 branches and 20 layers, and apply
five distinct types of search: PPN-search, PN-search,
MCPN-search, the UCT solver, and the pure MCTS
solver to prove (winning) or disprove (non-winning)
these game trees. For each expanded leaf node, we
set 10 playouts to compute the winning rate for the
following four types of search PPN-search, MCPN-
search, the UCT solver, and the pure MCTS solver
(further investigation shows that the number of play-
outs does not influence the experimental results).
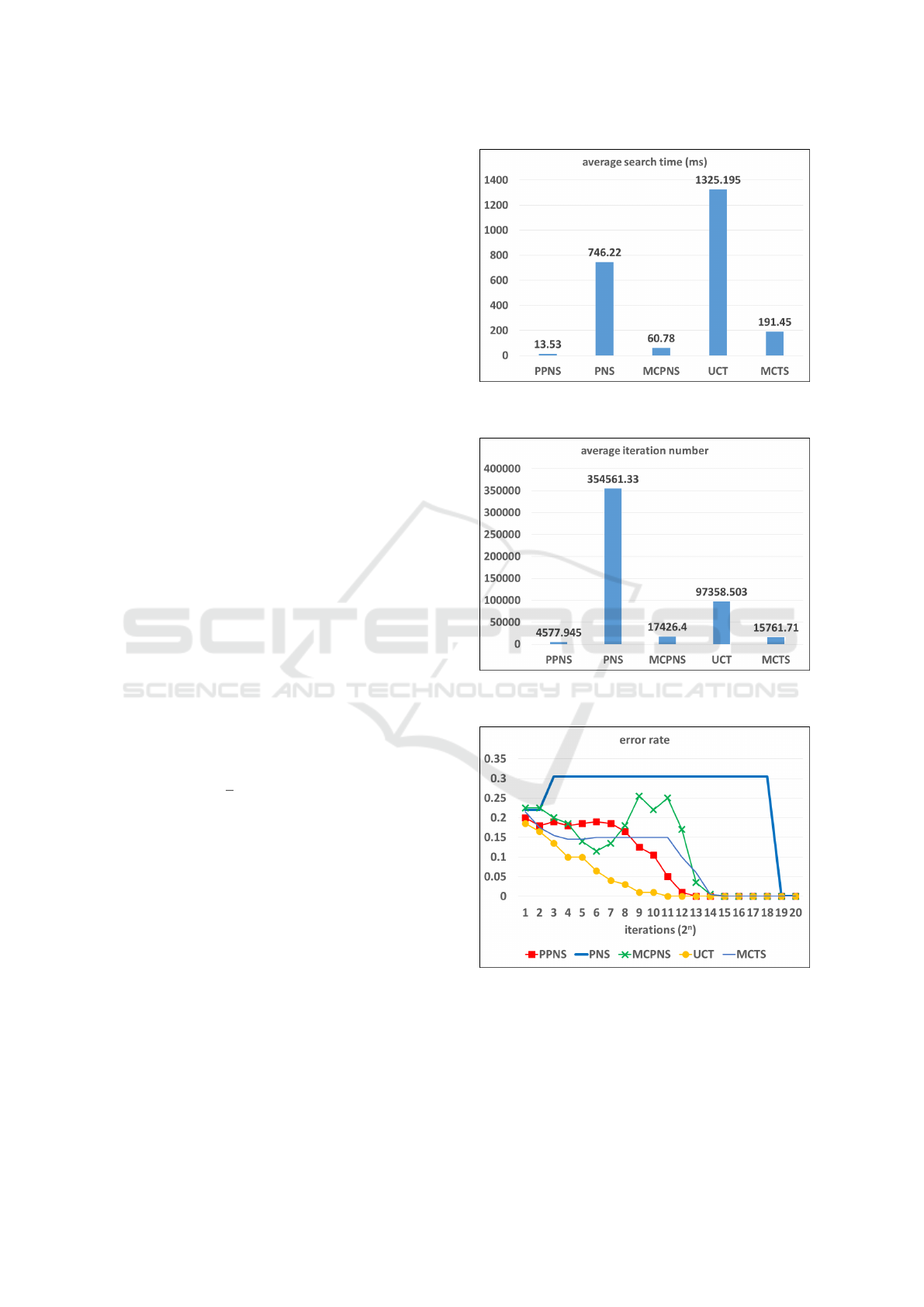
Here we report experimental results as shown in Fig-
ure 7, Figure 8, and Figure 9. Figure 7 shows the av-
erage search time for proving or disproving a P-game
tree with 2 branches and 20 layers for all five types
of search PPN-search, PN-search, MCPN-search, the
UCT solver, and the pure MCTS solver, respectively.
Figure 8 shows the average number of iterations for
proving or disproving a P-game tree with 2 branches
and 20 layers for all five types of search. Figure 9
shows the error rate of selecting a correct solution
by PPN-search, PN-search, MCPN-search, the UCT
solver, and the pure MCTS solver for each iteration
on P-game trees with 2 branches and 20 layers. More
concretely, the error rate equals the number of wrong
moves selected by the search among 200 tests di-
vided by the testing times 200. Notice that the UCT
solver or the MCTS solver expands 1 node per iter-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
666
ation while others expand 2 nodes. So, we regard 2
iterations of the UCT solver or the MCTS solver as 1
iteration, and present it in the figures.
In series 2, we construct 200 P-game trees ran-
domly, with 200 trees with 8 branches and 8 layers,
and apply five distinct types of search (the same ones
as in series 1). Figure 10, Figure 11, and Figure 12
show the analogous experimental results on P-game
trees with 8 branches and 8 layers. Notice that the
UCT solver or the MCTS solver expands 1 node per
iteration while others expand 8 nodes. So, we regard
8 iterations of the UCT solver or the MCTS solver
as 1 iteration, and present it in the figures. Accord-
ing to the figures, compared with the four types (PN-
search, MCPN-search, the UCT solver, and the pure
MCTS solver), our PPN-search outperforms the oth-
ers while averagely taking less time and fewer itera-
tions to prove or disprove a game tree. Furthermore,
compared with the three types (PN-search, MCPN-
search and the pure MCTS solver), our PPN-search
converges faster to the correct solution, and the error
rate of selected moves decreases more smoothly as the
number of iterations increases. For MCPN-search, it
takes more time and more iterations than PPN-search
to converge to the correct solution on average, and
the error rate waves as the number of iterations in-
creases, because of its inconsistent backpropagation
rules. As for the pure MCTS solver according to the
figures, the performance is better than the PN-search,
and competitive with MCPN-search, but worse than
PPN-search. The UCT solver converges faster to the
correct solution than the other types of search, but av-
eragely takes more time and more iterations to solve a
P-game tree than PPN-search, MCPN-search, and the
pure MCTS solver. Here, we tested the UCT solver
with different parameters but only show one of them
with parameter
√
2 in the figures. Actually, all these
UCT solvers averagely take more time and more itera-
tions to solve a P-game tree than PPN-search, MCPN-
search, and the pure MCTS solver. One possible rea-
son is that in P-games trees, the game trees are so
well balanced that the exploration strategy of UCT
may not be advantageous to enforce a deep search to
solve a game tree fast. In other words, UCT is a good
search algorithm to find the approximate best move
for a game AI, but the UCT solver is not a good search
algorithm to solve a game.
5 CONCLUDING REMARKS
PPN-search is a promising variant of proof number
search based on Monte-Carlo simulations and prob-
ability backpropagation rules. It only uses one in-
Figure 7: Comparison of average search time for a P-game
tree with 2 branches and 20 layers.
Figure 8: Comparison of average numbers of iterations for
a P-game tree with 2 branches and 20 layers.
Figure 9: Comparison of the error rate of selected moves
for each iteration on P-game trees with 2 branches and 20
layers.
dicator PPN to indicate the ”probability” of prov-
ing a game position, and backpropagates PPNs by
AND/OR probability rules of independent events.
Compared with PN-search, MCPN-search, the UCT
Probability based Proof Number Search
667
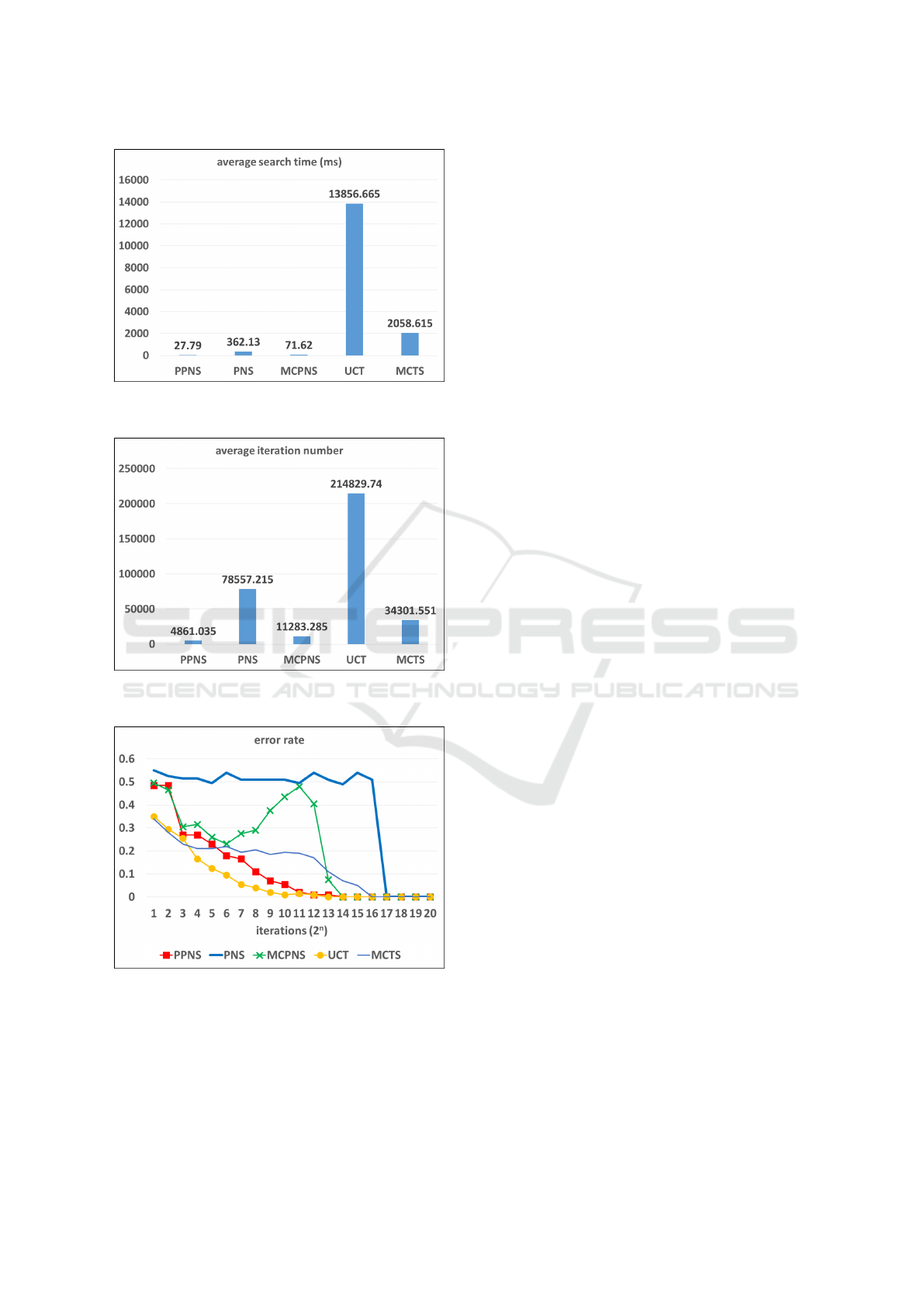
Figure 10: Comparison of average search time for a P-game
tree with 8 branches and 8 layers.
Figure 11: Comparison of average numbers of iterations for
a P-game tree with 8 branches and 8 layers.
Figure 12: Comparison of the error rate of selected moves
for each iteration on P-game trees with 8 branches and 8
layers.
solver, and the pure MCTS solver, PPN-search out-
performs them while taking less time and fewer iter-
ations to prove or disprove a game tree on average.
Moreover, the error rate of the selected moves de-
creases faster and more smoothly as the number of
iterations increases.
Further works may include (1) applying PPN-
search into real games with large-size balanced game
trees and unbalanced game trees, respectively, to fur-
ther investigate its performance; (2) proposing proba-
bility based conspiracy number search (PCN-search)
by incorporating the notion of the single conspiracy
number (Song and Iida, 2019).
REFERENCES
Allis, L. V., van der Meulen, M., and Van den Herik, H. J.
(1994). Proof-number search. Artificial Intelligence,
66(1):91–124.
Berliner, H. (1981). The B* tree search algorithm: A best-
first proof procedure. In Readings in Artificial Intelli-
gence, pages 79–87. Elsevier.
Chaslot, G. M. J.-B. C. (2010). Monte-carlo tree search.
PhD thesis, Maastricht University.
Coulom, R. (2006). Efficient selectivity and backup op-
erators in monte-carlo tree search. In International
conference on computers and games, pages 72–83.
Springer.
Ishitobi, T., Plaat, A., Iida, H., and Van den Herik, H. J.
(2015). Reducing the seesaw effect with deep proof-
number search. In Advances in Computer Games,
pages 185–197. Springer.
Kocsis, L. and Szepesv
´
ari, C. (2006). Bandit based monte-
carlo planning. In European conference on machine
learning, pages 282–293. Springer.
Nagai, A. (2002). Df-pn algorithm for searching and/or
trees and its applications. PhD thesis, Department of
Information Science, University of Tokyo.
Palay, A. J. (1983). Searching with probabilities. Technical
report, Carnegie-mellon Univ Pittsburgh Pa Dept of
Computer Science.
Saito, J.-T., Chaslot, G., Uiterwijk, J. W., and Van den
Herik, H. J. (2006). Monte-carlo proof-number search
for computer go. In International Conference on Com-
puters and Games, pages 50–61. Springer.
Song, Z. and Iida, H. (2019). Using single conspiracy num-
ber for long term position evaluation. In 10th Interna-
tional Conference on Computer and Games (in press).
Winands, M. H., Bj
¨
ornsson, Y., and Saito, J.-T. (2008).
Monte-carlo tree search solver. In International
Conference on Computers and Games, pages 25–36.
Springer.
Zhang, S., Iida, H., and Van den Herik, H. J. (2017). Deep
df-pn and its efficient implementations. In Advances
in Computer Games, pages 73–89. Springer.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
668
