Clustering Honeybees by Its Daily Activity

Edgar Acuna

, Velcy Palomino

, Jos´e Agosto

, R´emi M´egret

, Tugrul Giray

, Alberto Prado

5,6

C´edric Alaux

5,6

and Yves Le Conte

5,6

Department of Mathematical Sciences, University of Puerto Rico, Mayaguez PR 00682, U.S.A.

Program in Computing and Information Science and Engineering, University of Puerto Rico, Mayaguez PR 00682, U.S.A.

Department of Biology, University of Puerto Rico, Rio Piedras, PR 00990, U.S.A.

Department of Computer Science, University of Puerto Rico, Rio Piedras, PR 00990, U.S.A.

INRA, UR406 Abeilles & Environnement, Site Agroparc, 84914 Avignon, France

UMT PrADE, Site Agroparc, 84914 Avignon, France

alberto.prado-farias@inra.fr, cedric.alaux@inra.fr, yves.le-conte@inra.fr

Keywords:

Clustering, Honeybees Behavior, Data Wrangling, Time Series.

Abstract:

In this work, we analyze the activity of bees starting at 6 days old. The data was collected at the INRA (France)

during 2014 and 2016. The activity is counted according to whether the bees enter or leave the hive. After

data wrangling, we decided to analyze data corresponding to a period of 10 days. We use clustering method to

determine bees with similar activity and to estimate the time during the day when the bees are most active. To

achieve our objective, the data was analyzed in three different time periods in a day. One considering the daily

activity during in two periods: morning and afternoon, then looking at activities in periods of 3 hours from

8:00am to 8:00pm and, ﬁnally looking at the activities hourly from 8:00am to 8:00pm. Our study found two

clusters of bees and in one of them clearly the bees activity increased at the day 5. The smaller cluster included

the most active bees representing about 24 percent of the total bees under study. Also, the highest activity of

the bees was registered between 2:00pm until 3:00pm. A Chi-square test shows that there is a combined effect

Treatment× Colony on the clusters formation.

1 INTRODUCTION

This work is part of a larger effort to characterize and

provide tools for the analysis of individual behavior

patterns of honeybees in their natural environment,

i.e. the hives in the ﬁeld. The goal is to be able to

observe the variations in behavior of individuals in-

stead of reasoning on aggregates and averages at the

population level. In this paper, the bee activity is rep-

resented by the events entering (E) and exiting (S)

the hive. Bees were marked with individual tags and

recognized when passing an optical detector located

at the only entrance of the hive, which can associate

each event with an individual bee based on its tag.

Our hypothesis is that the individual patterns of be-

havior will form clusters of bees with similar activity,

which can inform us on the latent parameters associ-

ated to the individual bees. The categorical features

“Treatment” and “Colony” have not been taken into

account in the clustering task avoiding the use of a

similarity distance involving mixed attributes like the

Gower distance. However, the effect of both features

on the clusters formation is discussed in detail in sec-

tion 3.2. The main goal of this work is to ﬁnd out

clusters of bees with similar activity.

This paper is organizedas follows: In section 2 the

datasets used and wrangling of the times series data

are detailed. In section 3, the clustering process is

discussed. In section 4, an explanation of the ﬁnding

of the time interval with the peak activity is given. Fi-

nally, in the last section, we mention the conclusions

of this work.

2 DATA PREPARATION

2.1 Datasets

In this study, we have considered seven datasets

from experiments with bees carried out at the INRA

(France). The ﬁrst three datasets are coming from an

598

Acuna, E., Palomino, V., Agosto, J., Mégret, R., Giray, T., Prado, A., Alaux, C. and Conte, Y.

Clustering Honeybees by Its Daily Activity.

DOI: 10.5220/0007387505980604

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 598-604

ISBN: 978-989-758-351-3

 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

experiment carried out in 2014 by C. Bordier (Bor-

dier et al., 2017). In there, newly emerged bees

were infested with Nosema spores. The behavioral

recording started at age 1. The experiment was repli-

cated 3 times using 3 bee counters (colonies) each

time. All the data are pooled in the same ﬁle. In

this work, we have separated it into three datasets.

The recordings started on the following dates : 02-

04-2014(dataset 2014-I) , 14-05-2014 (dataset 2014-

II) and 18-06-2014 (dataset 2014- III). In this experi-

ment, one tag was used more than once. Thus, there

are some tags that appear in dataset 2014-I and dataset

2014-II and even in dataset 2014-III. The remaining

datasets were collected by A. Prado in 2016 (Prado

et al., 2019). Prado used 6 Treatments (5 pesticides

mixture and one control) started at 6 days old. The

experiment was replicated 6 times using 2 bee coun-

ters (colony L and colony M) each time. Recordings

for experiment April 2016 started on April 12 ,2016

and ended on May 1, 2016. In here, this dataset is

named 2016A. The ﬁrst experiment from June 2016,

included cohort1, started on 31-05-2016 , and cohort2

, started on 13-06-2016. The bees are from colony L

and theirs activity recordings end on July 4, 2016. We

have named as 2016J to the dataset including results

from this experiment. The second experiment from

June 2016 included cohort1, started on 31-05-2016,

and cohort2 , started on 13-06-2016. The bees are

from colony M and recordings end on July 4, 2016.

We have called 2016JB to the dataset containing re-

sults from this experiment. In both experiments 2016J

and 2016JB, the cohort2 has only 21 days of mea-

surements. However, we have found that bee with tag

B4359 from the 2016JB has records in days 8th,10th

and 12th of June. Bee’s activity recordings for the ex-

periment from September, 2016 started at 13-09-2016

and emded on 17-10-2016. However, there are two

bees with recordings as earlier as 08-09-2016. This

dataset is named 2016S. The ﬁrst rows of a typical

dataset (2016JB) are shown in table 1.

Table 1: First rows of the 2016JB dataset.

Id Date Time BeeID Dir. Trt. Colony

1 31-05-2016 09:42:17 B4826 S mix C M

2 31-05-2016 09:42:27 B4823 S mix C M

3 31-05-2016 09:42:27 B4823 E mix C M

4 31-05-2016 09:42:45 B4826 E mix C M

5 31-05-2016 10:49:16 B5113 S Control M

6 31-05-2016 10:54:19 B5113 E Control M

7 31-05-2016 10:54:53 B5113 S Control M

8 31-05-2016 10:56:11 B5113 E Control M

An exhaustive report of the data recollection can

be found in (Prado et al., 2019).

In this work, we are only interested in the bee

activity with respect to either entering (E) or exiting

(S) the hive. The features “Treatment” and “Colony”

have not been taken into account in the clustering task

avoiding the use of a similarity distance involving

mixed attributes like the Gower distance. However,

after the clustering task, we have used both attributes

to explain the clusters formed. Our goal is to ﬁnd out

clusters of bees with similar activity. This paper is or-

ganized as follows: In section 2 the wrangling of the

times series data is detailed, in section 3, the cluster-

ing process is discussed, in section 4 an explanation

of the ﬁnding of the time interval with the highest ac-

tivity is given, ﬁnally in the last section we mention

the conclusions of our work.

2.2 Data Wrangling

In order to have a more accurate clustering process,

we have cleanup the data by considering only bees

with more than 10 activities, somehow equivalent to

having more than 5 trips (see Table 2, column 4). All

the datasets have miss detections for direction values,

since several SS (S=Exit) or EE (E=Enter) sequences

for a given bee appear recorded. These can be ﬁxed

but up to certain amount. It is not recommended to ﬁx

more than 30 percent of missed detection since bias

will be generated (see Table 2,column 5). However,

in this paper we have not cleanup miss detection in

the collected data, since we are interestred in the bee

activity regardless if it is an entering or an exiting.

Table 2: The number of bees per experiment, number of

recording days per experiment, number of bees to be con-

sidered for the clustering processing and the number of bees

for which miss detected data can be ﬁxed.

Exp Total number

Days of

Recording

More than

5 trips

less than 30 percent of

missdetection

2014-I 300 34 219 186

2014-II 300 29 185 115

2014-III 300 28 220 174

2016J 740 35/21 544 513

2016JB 691 35/21 490 423

2016A 251 20 144 125

2016S 239 34 203 159

We have merged datasets 2016J and 2016JB since

bees’ activities included in these two datasets were

recorded by the same time calendar. In total, there

are 1431 bees, the activity recording of 786 of them

started on May 31, 2016 (ﬁrst cohort) and the record-

ing of the remaining 645 started on June 13, 2016

(second cohort) . After removing the bees with less

than 5 trips (10 activities) the number of bees is re-

duced to 1034. The Bee B4359 was discarded for

inconsistency in its recordings as mentioned in sec-

tion 2.1. Thus, only 1033 bees are considered in this

work. From these, 572 bees belong to the ﬁrst cohort

and 461 bees belong to the second cohort.

Clustering Honeybees by Its Daily Activity

599

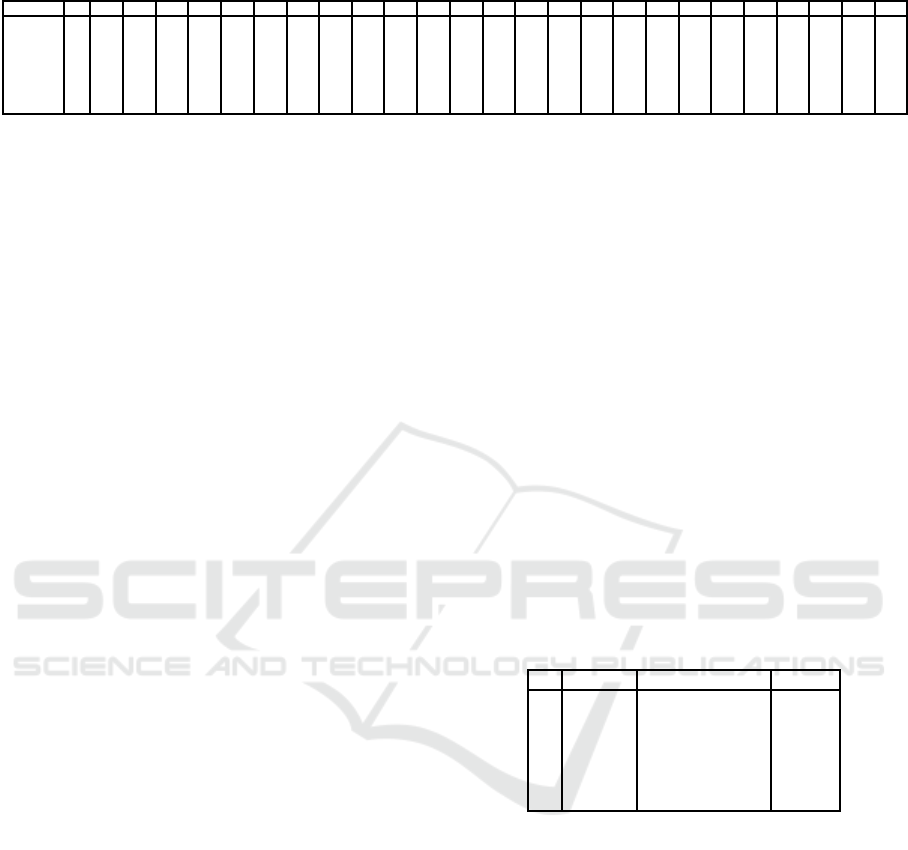
Table 3: Numbers of bees with similar time duration (given in days) for each dataset.

Exp 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

2014-I 7 4 9 9 6 6 10 5 6 11 10 8 6 3 8 12 8 12 9 5 11 11 6 9 3 4

2014-II 2 2 5 7 7 15 14 15 14 17 11 13 8 14 7 6 7 3 5 4 1 2 0 1 0 2

2014-III 2 6 7 21 15 13 7 13 13 18 16 13 13 17 12 6 8 2 5 3 0 3 1 2 2 1

2016A 1 14 10 11 13 8 5 3 12 7 7 5 5 7 10 6 11 8 0 1

2016J 2 8 11 23 31 42 32 42 34 31 42 46 22 24 19 17 30 14 10 11 13 16 3 6 5 0

2016Jb 2 9 14 22 28 16 21 33 32 31 21 32 23 27 23 19 16 17 24 10 3 10 5 11 5 8

2016S 0 7 16 4 12 13 15 19 7 11 14 10 10 11 9 6 2 1 6 8 2 3 2 3 3 2

2.3 Preparing the Data for Clustering

Our goal is to group bees according to similar ac-

tivity. Since clustering must be performed on data

tables with rows of equal length, ﬁrst, we have to

ﬁnd out bees with similar time duration of recording.

We cannot cluster bees with different time duration

of recording, say a bee with three days of record-

ing cannot be clustered along a bee with 20 days of

recording, We wrote an R script using the R package

lubridate to ﬁnd out bees with equal length time of

recordings,using days as measure of time(Grolemund

and Wickham, 2011). This does not mean that we are

looking for bees with activity recorded in the same

days. In fact, one day (24 hours) of recording can in-

volve two days-calendar. In our program, basically

we found the time duration (in hours) for the record-

ings of a bee and then this time is converted into days.

Finally, we group the bees for their time duration in

days. Table 3 shows the number of bees with simi-

lar number of days recorded for each of the datasets.

Day=0 means that less than 24 hours of bee activ-

ity was recorded, day=1 means that between 24 hours

and 47.99 hours of bee activity was recorded, and so

on. From Table 3, we can notice that there are few

activity recordings after day 25.

In this paper, due to space limitations, for cluster-

ing tasks we have only considered datasets from June

2016. Furthermore, these datasets are the ones with

less inconsistencies. In order to have a large sample

for clustering, after merging the 2016J and 2016JB

datasets, we considered all the bees with 10 or more

days of activities but considering only a time period

of length ten days. For instance, if a bee has a record-

ing of 13 days, we will only took in account its ﬁrst

10 days of activities. Using this criterion, we ended

up with 382 bees in the ﬁrst cohort and 188 bees in

cohort 2 as is showed below.

Cohort 1:

Days:Bees 0:2, 1:7 2:9 3:19 4:12 5:18 6:32 7:33

8:32 9:27 10:34 11:42 12:26 13:26 14:25 15:27 16:37

17:23 18:21 19:11 20:21 21:18 22:8 23:17 24:10 25:8

26:8 27:3 28:3 29:2 30:3 31:1 32:5 33:2

Cohort2:

Days: Bees 0:2 1:10 2:16 3:26 4:47 5:40 6:21 7:42

8:34 9:35 10:29 11:36 12:19 13:25 14:17 15:9 16:9

17:8 18:13 19:10 20:5 21 :8

3 PERFORMING THE

CLUSTERING TASK

We have carried out clustering in each June’s cohort

separately. For that, we performed subsetting of the

data ﬁle into the two cohorts and count the number of

bee’s activities per hour in each of them. The output

was saved in two csv ﬁles one for each cohort. In

the counting of the activity, we have not distinguished

the type of activity, so E and S counts as one activity

each of them. The ﬁrst six rows of the output ﬁle for

cohort1 looks like in Table 4.

Table 4: First six rows of the dataset showing counts of bee

activity per hour.

beesID hour Count

1 B4002 6/1/2016 17:00 2

2 B4002 6/3/2016 15:00 1

3 B4002 6/3/2016 16:00 1

4 B4002 6/5/2016 16:00 2

5 B4002 6/6/2016 15:00 1

6 B4002 6/7/2016 9:00 2

Then, we built a dataframe showing the 382 beees

along the number of theirs activities per day-calendar

but taking into account if the activity was either in the

morning (before 12.00) or in the afternoon (12.00 or

later) from May 31 until June 9. Thus, the dataframe

has 382 rows and 22 columns. The ﬁrst six rows of

the dataframe are shown in Table 5.

Using outlier detection techniques (Mahalanobis

distance, Local Outlier Factor(LOF) and even cluster-

ing itself), we have detected that bees with tags B4387

and B5134 are clearly outliers (Tan et al., 2005). Both

bees are from colony M. In Figure 1, we compare the

activity of a typical bee (B4013) with the activity of

the two outliers bees. Notice that the outliers bees be-

gan an unsual activity during the mornings starting at

day 5. This highly active bees may represent highly

especilized such as water foragers (Robinson et al.,

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

600

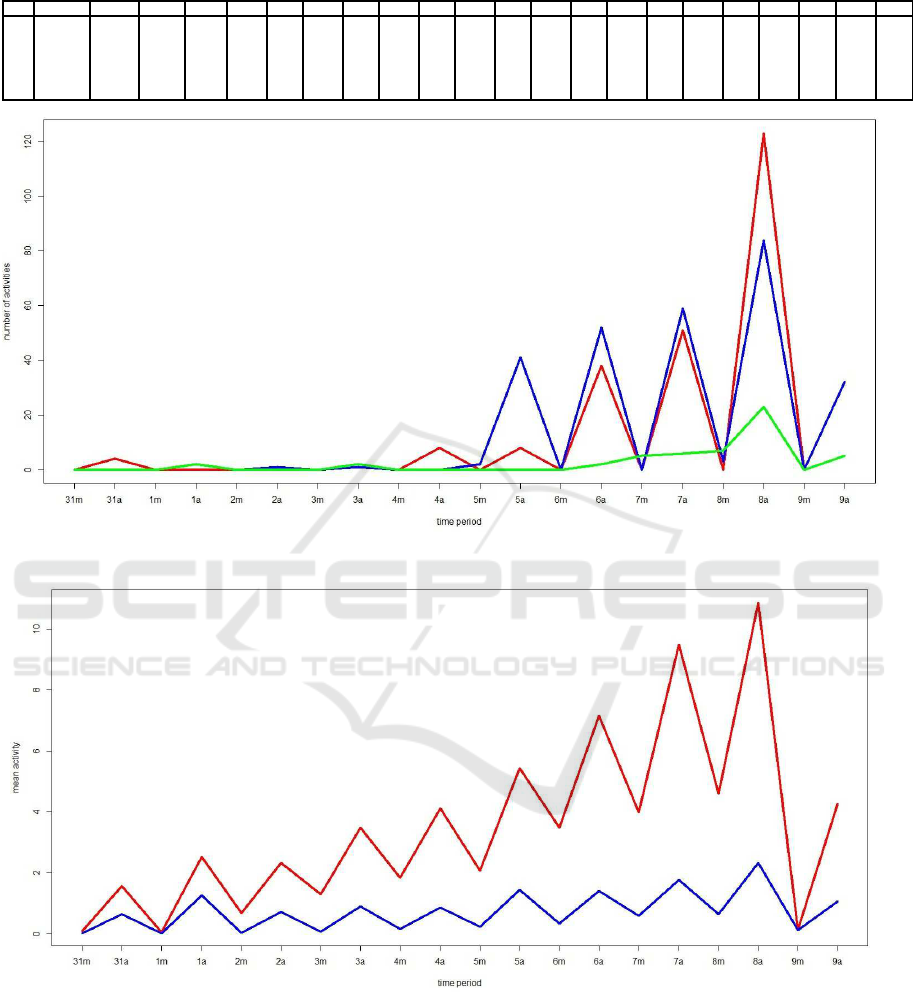
Table 5: Numbers of bees with similar time duration (given in days-calendar.

BeeID Total 31m 31a 1m 1a 2m 2a 3m 3a 4m 4a 5m 5a 6m 6a 7m 7a 8m 8a 9m 9a

1 B4002 32 0 0 0 2 0 0 0 2 0 0 0 2 0 1 2 2 1 2 0 1

2 B4005 226 0 2 0 0 0 4 0 0 0 0 0 2 0 0 0 0 0 2 0 7

3 B4006 161 0 0 0 2 0 0 0 4 0 0 0 1 0 2 0 2 2 2 0 0

4 B4010 77 0 0 0 2 0 0 0 2 0 0 0 4 0 2 1 1 0 32 0 6

5 B4011 97 0 2 0 0 0 2 0 0 0 1 0 3 0 2 0 4 0 4 0 26

6 B4012 50 0 0 0 2 0 0 0 0 0 1 0 1 0 2 2 4 0 5 1 6

Figure 1: Plot to compare the activity of a normal bee (green) with the two outliers bees (B4387 and B5134) in cohort 1.

Figure 2: Plot of bees’ activity means at each time period of the two clusters formed using kmeans.

1984). Therefore, we have excluded this two bees be-

cause it can harm the clustering process, in particular

kmeans, which requires means computation.

To ﬁnd the groups with similar activity formed

from the 380 bees in cohort 1, we apply two cluster-

ing algorithms: Kmeans, Partitioning around medoids

(PAM) and Agglomerative hierarchical(AGNES) to

the data partly shown in table 5 (Jain and Dubes,

1988). We have evaluated from two up to six clusters.

In Table 6, we show the sizes of each cluster, group-

ing the data from 2 up to 6 clusters, without taking

into consideration the two outliers

Notice that when two clusters are formed using

kmeans, the smaller cluster contains the most active

Clustering Honeybees by Its Daily Activity

601

Table 6: Cluster sizes using three algorithms, excluding the two outliers.

Algorithm K=2 K=3 K=4 K=5 K=6

Kmeans 288,92 264,8,108 7,91,238,44 27,34,234,5, 80 240, 26 ,41, 3, 5, 65

PAM 246,134 240,50,90 186,71,43,80 186,69,39,6,80 186,69,36,6,68,15

Agnes 227,143 237,13,130 227,5,8,130 237, 5,8, 100, 30 237, 4, 8,100, 30, 1

bees is about 24 percent of the total number of bees.

Similar percentaje (20 percent) was found in (Tenczar

et al., 2014). Also, when three clusters are considered,

both Kmeans and AGNES show a third cluster of very

small size compared with the other two. This suggests

the existence of more outliers.

3.1 Clustering Validation

Now, in order to determine the optimal number of

clusters, we have computed 4 internal cluster valida-

tion measures: The Silhouette, Dunn Index, Davies-

Bouldin Index, and the Calinski and Harabasz index

(Halkidi et al., 2001). A Silhouette value close to 1

indicates a good clustering. The number of clusters

with the highest Dunn index is the best one. Accord-

ing to the Davies-Bouldin index the best number of

clusters is the one with the minimum value. The opti-

mal number of clusters according to the Calinski and

Harabasz index is the one with the highest value.

Table 7 shows the results of the measures for the

kmeans algorithm. The Davies-Bouldin index was

computed using R package’s clusterSim and the re-

maining ones using the R package’s fpc.

Table 7: Internal measures for clustering validation using

kmeans, (*) indicates the best result for a clustering valida-

tion measure.

Measure K=2 K=3 K=4 K=5 K=6

Silhouette 0.4557* 0.4483 0.3813 0.3773 0.3865

Dunn 0.0571 0.0780* 0.0607 0.0607 0.0685

Davies-Bouldin 1.6793 1.3964* 1.8070 1.6652 1.6955

Calinski- Harabasz 133.97* 125.74 108.74 98.22 88.64

From Table 7, we can see that the optimal cluster

number can be either two or three. By visualization

(see Figure 4 ) three clusters are suggested, but ac-

cording to co-authors of this paper wih high domain

knowledge on bees behavior is better to consider only

two clusters.

In Table 8, we show the cluster validation mea-

sures for the clusters obtained using the PAM algo-

rithm.

Table 8: Internal measures for clustering validation using

PAM, (*) indicates the best result for a measure.

Measure K=2 K=3 K=4 K=5 K=6

Silhouette 0.4019* 0.3882 0.1971 0.1961 0.2110

Dunn 0.0395 0.0464* 0.0242 0.0255 0.0255

Davies-Bouldin 1.6773* 2.1711 2.1964 1.9573 1.8428

Calinski- Harabasz 126.69* 97.18 74.17 83.34 80.26

Using voting it seems that two clusters could be

the optimum number of clusters. In this case, there

is a concordance with the opinion of our co-authors

with domain knowledge on bees behavior.

3.2 Clusters Visualization

In this section, we will show plots for both two and

three clusters given by the kmeans algorihm and the

two clusters given by PAM.

From Figure 2, it can be seem very clearly bees

from the smaller cluster (red) have always more ac-

tivity than bees in cluster 1 (blue). Also, we can no-

tice that the bees’s activity start to increase at day 5.

This is very clear in the red cluster. On the other hand,

bees’s activity is noticeable greater in the afternoons.

The majority of the members of clusters 1 are com-

ing from colony M (168 bees out of 288, 58.33%),

whereas most of the bees in cluster 2 are from colony

L (55 bees out of 92, a 59.78%). Performing a Chi-

Square test yields a p-value of .014, hence there is

statistical signiﬁcance of dependency between clus-

ters and colonies. On the other hand, the other cate-

gorical attribute: ”Treatment” behaves in similar way

for both clusters, giving a p-value of .499. However,

most of the members of cluster 1 (23.96 percent of

bees) are coming from treatment ”Mix D”, whereas a

21.74 percent of bees in cluster 2 are comming from

treatment ”Mix E”. Finally, we analyzed the com-

bined effect of both ”Treatment” and ”Colony” on the

cluster formation, and in fact, there is an effect. In the

small cluster that includes 92 bees, the p-value for the

Chi-square test is .017, which is highly signiﬁcant. In

the large cluster including 288 bees, the p-value for

the Chi-square test is .016. A 27.27 percent of mem-

bers of cluster 1 belongs to colony L and treatment

”Mix E”. Also, in the second cluster a 25.95 percent

of bees belong to colony M and Treament ”Mix D”.

Figure 3 shows the bees grouped into two clus-

ters according to their daily activity. From Figure 4,

clearly we can notice that bees in Cluster 2(in Blue)

have more activity than bees in cluster 1 (red) and

cluster 3 (cyan), But bees in cluster 3 start to increase

theirs activity at day 7 and become the leading group.

The majority of the members of clusters 1 and 3 are

coming from colony M, but most of the bees in cluster

2 are from colony L. Finally in Figure 5, we visualize

the two clusters obtained by PAM. Figure 5 suggests

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

602

Figure 3: Plot showing activity of bees in two clusters given by kmeans.

Figure 4: Plot showing activity of bees in three clusters given by kmeans.

same result as Figure 3.

Figure 5: Plot showing activity of bees in two clusters given

by PAM.

Plotting the clusters means per hour of the two

clusters formed (see Figure 6), we can notice that one

cluster(red) shows an increasing mean activity respect

to days. Also, the highest activity is recorded between

the time interval from 2:00pm to 5:00pm. For the sec-

ond cluster (blue) the same trend is showed but bees

are less active.

4 FINDING THE TIME INTERVAL

WITH THE PEAK ACTIVITY

During the data wrangling process as well in the

clustering task, we noticed that most of bees’ ac-

tivity was between 8am and 8pm. Therefore,

ﬁrst we did an analysis for four periods of time:

8:00am-11:00am, 11:00am-2:00pm, 2:00pm-5:00pm

and 5:00pm-8:00pm, We identiﬁed that the time-

period 2:00pm-5:00pm had the largest count of activ-

Clustering Honeybees by Its Daily Activity

603

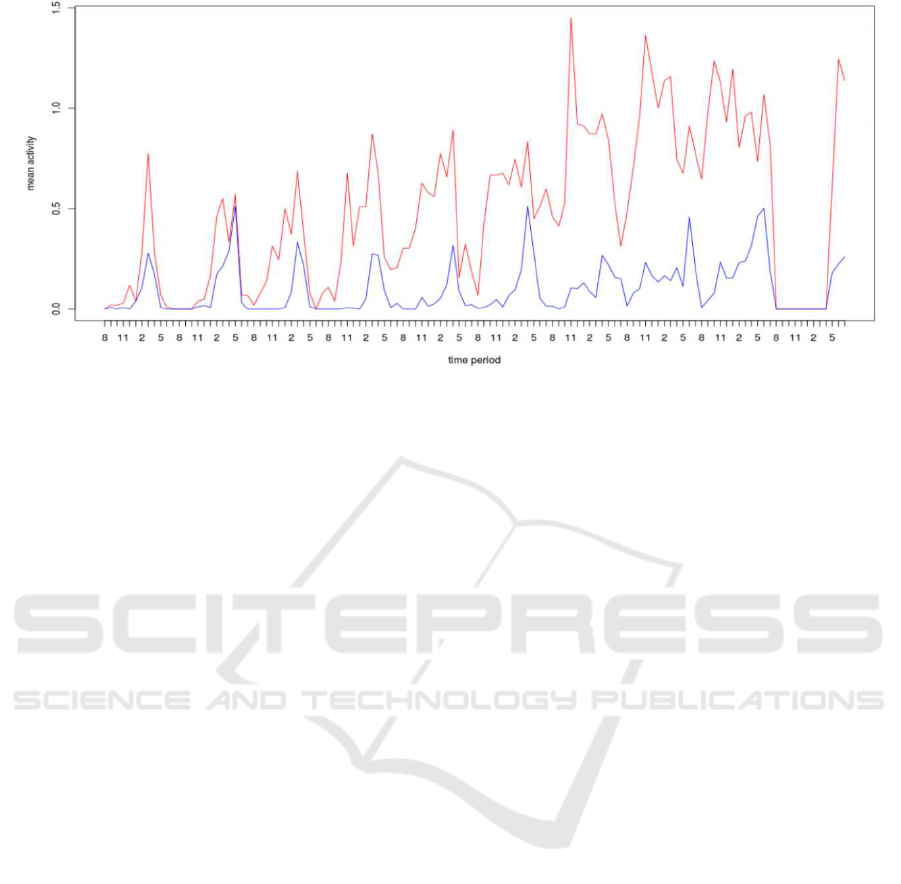
Figure 6: Plot showing means activity per hour of bees in the two clusters given by kmeans.

ity (1796) during the last four days, followed by the

time period 5:00pm-8:00pm. Finally, we carried out

an analysis by hour of the 380 bees during 8:00am-

8:00pm, and we found out that most of counting of

activity (809 counts) was from 2:00pm-3:00pm, fol-

lowed by the time period 1:00pm-2:00pm(582counts)

and in third place the time period 3:00pm-4:00pm

with 568 counts.

5 CONCLUSIONS

In this work, we have perform clustering on data

about bees’ daily activity during a time period of 10

days. According to the cluster validation measures we

decided to use two clusters as the optimum number.

Two categorial attrbutes ”Treatment” and ”Colony”

although were no used in the clustering process, they

are used in a posterior step to justyfy cluster for-

mation. Using a Chi-square test we conclude that

”treatment has no effect on the cluster formation, but

”Colony” and ”Treatment × Colony” affect indeed

the cluster formation.

Using data wrangling and visualization, we con-

clude that in one of the clusters the activity increases

with the time and remarkablly starting at the day

5. Furthermore, the highest bees’ activity occurs be-

tween 2:00pm to 3:00pm.

The R scripts and a R shiny program used in this

paper are available upon request from the ﬁrst author.

ACKNOWLEDGEMENTS

This material is based upon work supported by

the National Science Foundation under Grant No.

1707355 and 1633184. BIGDATA:Collaborative Re-

search: Large-scale multi-parameter analysis of hon-

eybee behavior in their natural habitat.

REFERENCES

Bordier, C., Suchail, S., Pioz, M., Devaud, J., Colleta,

C., Charreton, M., Conte, Y. L., and Alaux, C.

(2017). Stress response in honeybees is associated

with changes in task-related physiology and energetic

metabolism. 98:47–54.

Grolemund, G. and Wickham, H. (2011). Dates and times

made easy with lubridate. 40(3):1–25.

Halkidi, M., Batistakis, Y., and Vazirgiannis, M. (2001). On

clustering validation techniques. 17:107–145.

Jain, A. and Dubes, R. (1988). Algorithms for clustering

data. Prentice-Hall, Inc., Upper Saddle River, NJ,

USA.

Prado, A., Pioz, M., Vidau, C., Requier, F., Jury, M.,

Crauser, D., Brunet, J.-L., Conte, Y. L., and Alaux, C.

(2019). Exposure to pollen-bound pesticide mixtures

induces longer-lived but less efﬁcient honey bees.

650:1250–1260.

Robinson, G., Underwood, B., and Henderson, C. E.

(1984). A highly specialized water-collecting honey

bee. 15(3):355–358.

Tan, P., Steinbach, M., and Kumar, V. (2005). Introduction

to data mining. Addison-Wesley Longman Publishing

Co., Inc, Boston, MA, USA.

Tenczar, P., Lutz, C. C., Rao, V. D., Goldenfeld, N., and

Robinson, G. E. (2014). Automated monitoring re-

veals extreme interindividual variation and plasticity

in honeybee foraging activity levels. 95:41–48.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

604