Stochastic Phase Estimation and Unwrapping

Mara Pistellato, Filippo Bergamasco, Andrea Albarelli, Luca Cosmo, Andrea Gasparetto

and Andrea Torsello

DAIS, Ca’Foscari University of Venice, Via Torino 155, Venice, Italy

Keywords:

Phase Shift, Structured Light, 3D Reconstruction.

Abstract:

Phase-shift is one of the most effective techniques in 3D structured-light scanning for its accuracy and noise

resilience. However, the periodic nature of the signal causes a spatial ambiguity when the fringe periods are

shorter than the projector resolution. To solve this, many techniques exploit multiple combined signals to

unwrap the phases and thus recovering a unique consistent code. In this paper, we study the phase estima-

tion and unwrapping problem in a stochastic context. Assuming the acquired fringe signal to be affected by

additive white Gaussian noise, we start by modelling each estimated phase as a zero-mean Wrapped Normal

distribution with variance

. Then, our contributions are twofolds. First, we show how to recover the best

projector code given multiple phase observations by means of a ML estimation over the combined fringe dis-

tributions. Second, we exploit the Cram

er-Rao bounds to relate the phase variance

to the variance of the

observed signal, that can be easily estimated online during the fringe acquisition. An extensive set of experi-

ments demonstrate that our approach outperforms other methods in terms of code recovery accuracy and ratio

of faulty unwrappings.

1 INTRODUCTION

The recent evolution of increasingly affordable and

powerful 3D sensors and the consolidation of fast re-

construction algorithms enabled the widespread adop-

tion of 3D data in both consumer (Han et al., 2013)

and industrial (Luhmann, 2010) off-the-shelf devices.

As a consequence of the resulting increase of general

interest in the subject, 3D data capturing and process-

ing has become a trending topic in recent Computer

Vision research. The richness of information coming

from 3D data have been exploited in several ﬁelds of

application, from industrial inspection systems (Luh-

mann, 2010), robot and machine vision (Prez et al.,

2016), pipe inspection (Bergamasco et al., 2012),

medical (Cheah et al., 2003; Tikuisis et al., 2001; Pel-

lot et al., 1994) and entertainment applications (Han

et al., 2013; Winterhalter et al., 2015).

While consumer applications place more empha-

sis on speed and performance, in an industrial setup

accuracy is of greater importance. To this end, a lot of

effort has been put in reconstruction techniques trad-

ing design simplicity and speed for higher precision

in 3D recovery and robustness to surface character-

istics of captured objects. A wide range of different

techniques have been proposed over the last decades.

Different approaches can be usually categorized

on the basis of the exploited physical principle and

on the design of the adopted sensor. For instance, a

time-of-ﬂight setup combines a pulsating light emit-

ter with a sensor which measures the round-trip time

of the signal. Then, given the distance between the

sensor and the artifact, a depth map can be com-

puted and used for reconstruction (Lange and Seitz,

2001). Despite this technology have been proven re-

liable in some speciﬁc application, it suffers from

two major drawbacks. First, the sensor does not

usually provide a high resolution response. More-

over, it is particularly sensitive to signal interfer-

ences and surface response (i.e. artifact material).

For these reasons, when resolution is of greater im-

portance, triangulation-based approaches, especially

when paired with high-end hardware, proper sen-

sor calibration and advanced signal processing tech-

niques, are better suited. Among the approaches,

passive 3D sensing ones employ different cameras

which are used to capture artifact’s images at differ-

ent angles in order to triangulate the single material

points whose projection on the different images has

been matched on the basis of purely photometric in-

formation. Differently, active 3D sensing technology

exploits the projection of some structured pattern of

known spatio-temporal structure onto the object, and

recovers depth information by means of triangulation

200

Pistellato, M., Bergamasco, F., Albarelli, A., Cosmo, L., Gasparetto, A. and Torsello, A.

Stochastic Phase Estimation and Unwrapping.

DOI: 10.5220/0007389402000209

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 200-209

ISBN: 978-989-758-351-3

0 10 20 30 40 50 60

0.5

1.5

Intensity

Model

Acquired Signal

Figure 1: Left: Vertical sinusoidal pattern with a period length of 17 px. The pattern is shifted from right to left so that each

pixel observe one complete period after m samples. Center: The recovered phase for each pixel. Since the period is shorter

than the with of the projected image, we observe a phase ambiguity among the fringes. Right: Real-world example of the

acquired signal compared to the projected ideal signal for a pixel with phase 0. Note how the samples are slightly noisy

especially in the lower portion of the sine period.

between the rays emitted by the pattern projector and

the corresponding image points, matched by means

of signal decoding. Digital projector-based structured

light is an example of such approaches. The main idea

behind this technique is to decode from the image the

corresponding projector coordinates (in pixels) to es-

tablish a map between the observed scene and the pro-

jector itself (camera-projector setup) or between dif-

ferent acquisitions of the scene (multi camera setup).

In this paper we will not deal with the triangulation or

matching problems, rather we will focus on the accu-

rate recovery and decoding of the projected signal.

In literature, several different coding strategies

have been proposed, each with a speciﬁc goal in

mind. For instance, some approaches (der Jeught

and Dirckx, 2016) allow to use a reduced number of

patterns in order to increase the speed of the recon-

struction and to enable real time operations. Other

methods attain high speed by exploiting the inter-

action between the projected signal and the natu-

ral texture appearing in the scene (Vo et al., 2016).

In (Fanello et al., 2016), the authors propose to in-

fer the depth from the signal itself using a learning

technique, dropping the actual triangulation step. De-

spite the abundance of recent specialized techniques,

the most popular one is the long standing phase shift

method (Srinivasan et al., 1984). This is particularly

true in the industrial setting, since this approach al-

lows high accuracy, resilience to noise and surface

texture and great ﬂexibility. The basic idea underly-

ing phase-shift is indeed quite simple. The projected

patterns are sine wave intensity frames which are pe-

riodic along one direction of the digital projector frus-

tum. Several patterns, with different shift in the sig-

nal phase, are projected and retrieved over time, then

the initial phase (i.e. the phase at frame 0) is recon-

structed for each image pixel by means of convolu-

tion. Unfortunately, due to the periodic nature of the

pattern in space, many pixels will be characterized

by the same initial phase, thus a disambiguation step

must be employed. This step takes the name of phase

unwrapping.

The method introduced in this paper deals with

both the phase recovery and unwrapping problems at

once by casting them in a stochastic context. We as-

sume that the acquired fringe signal is affected by ad-

ditive white Gaussian noise so that we can model each

estimated phase as a zero-mean Wrapped Normal dis-

tribution with variance

. We recover the most likely

projector code, given multiple phase observations, by

means of a ML estimation over the combined fringe

distributions. Additionally, we exploit the Cram

er-

Rao bounds to relate the phase variance

to the vari-

ance of the observed signal, that can be easily esti-

mated online during the fringe acquisition. The valid-

ity of the assumptions and the effectiveness of our ap-

proach are then tested thoroughly with both real and

synthetic experiments.

2 PHASE SHIFT

Phase-shift technique consists in generating a sinu-

soidal pattern spanning either the horizontal or verti-

cal extent of the projector image plane (Fig. 1, Left).

During the acquisition, the pattern is spatially shifted

so that each projector pixel encompasses an entire pe-

riod after m subsequent shifts. Together with m, the

period length λ (measured in pixels) of the sine pat-

tern is chosen a-priori. It affects both the phase differ-

ence of two neighbouring pixels along with the spa-

tial ambiguity of all pixels in the image. Indeed, two

adjacent pixels will exhibit a phase-difference of

2π

Consequently, points which are λ pixels away will be

characterized by the same phase value.

The choice of λ is driven by two opposing needs.

On one hand, a longer period will reduce the phase

ambiguity along the image, with the extreme case of

λ larger than the projector size causing no ambiguity

at all. On the other hand, it is well known that the

phase localization of the signal is proportional to the

frequency, so we need to keep it small to increase the

Stochastic Phase Estimation and Unwrapping

201

accuracy. Usually, λ is kept in the order of dozens

of pixels (Fig. 1, Center) and an unwrapping step is

used to distinguish different fringes. The disambigua-

tion technique is based on the idea of projecting mul-

tiple different sinusoidal signals (at different periods

...λ

) that can be combined to get a unique code

for each projector’s pixel.

The problem of the aforementioned multi-phase

shift approach is that the signal acquired by the cam-

era is perturbed by different noise sources, causing an

imperfect phase estimation. Possible sources are, for

example: (I) The thermic white noise of the camera,

especially at high gains or very short exposure times;

(II) The non-linear interactions between neighbour-

ing pixels due to intrinsic properties of each mate-

rial (micro-facets and reﬂections causing a wrong sig-

nal response); (III) An imperfect mechanical and/or

electronic functioning of the projecting device (par-

ticularly true for laser projectors), (IV) External noise

sources like indoor ambient lighting subject to the os-

cillatory nature of the power outlet. Whatever the rea-

son, a noisy phase estimation affects not only the ac-

curacy of the reconstructed surface, but may cause a

completely wrong phase unwrapping. Indeed, meth-

ods not particularly tolerant to phase errors produce a

lot of erroneous codes for challenging materials, like

brushed metals or glossy plastic.

2.1 Signal Model

Before describing our method, we start by formaliz-

ing the mathematical details of the projected signal

and the corresponding noise model.

For any projector pixel P at coordinates (ξ,v), we

project over time the following sinusoidal signal, dis-

cretized as a sequence of m subsequent samples:

Z(t) = sin



2π

+ φ



, t = [0 ...m). (1)

Assuming a vertical pattern, the ideal pixel phase φ

depends both on the period λ and its horizontal po-

sition on the image plane, according to the following

simple relation:

= 2π



−





. (2)

The value of φ

cannot be measured directly, but

it can be estimated from observed samples. Such val-

ues are subject to different noise sources affecting

the acquisition process. As commonly performed in

signal theory applications (Rife and Boorstyn, 1974;

Macleod, 1998), we derive our observation model as-

suming to acquire a set of noisy samples:

z(t) = sin



2π

+ φ



+ w[t] (3)

where w[t] is a zero-mean white Gaussian noise of

variance σ

. Albeit not completely motivated by

physical considerations, the assumption we made on

the statistical nature of the noise represents a good

trade-off between the simplicity of the model and the

observed behaviour. Such convenience is supported

by our experimental evidence (see Sec. 4 for details).

Given the acquired signal z, the Maximum Likeli-

hood estimator of the phase is deﬁned as:

= argmax

p(φ

;z) (4)

where, considering our assumption on the statistical

nature of the noise, we have:

p(φ

;z) =

σ(2π)

m/2

−

2σ

∑

m−1

t=0



z(t)−sin(2π

+φ

)



(5)

Switching to the natural logarithm of the likeli-

hood and arranging the terms, we obtain the common

non-linear least-squares minimization:

(z) = argmin

m−1

∑

t=0



z(t) −sin



2π

+ φ



(6)

Since the least squares best ﬁt based of a lower

order Fourier series is exactly equivalent to the trun-

cated DFT, the phase of the acquired single-tone sig-

nal can be easily recovered as:

(z) = atan

(x,y) + π (7)

with

x =

m−1

∑

i=0

cos



2π



z(i); y =

m−1

∑

i=0

sin



2π



z(i)

and where atan

: R

→ [−π,π] evaluates the cor-

rect arctangent angle of x/y selecting the appropriate

quadrant based on the arguments signs.

2.2 Stochastic Code Estimation

After the estimation of the phase of projected signal,

our ﬁnal goal is to recover the pixel horizontal (or

vertical) coordinate ξ, usually referred as “projector

code”. To simplify the notation, let ϕ(P) =

φ(P)

2π

the fractional part inside each projected fringe. In the

typical case when λ is less than the projector’s width

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

202

max

, we observe multiple fringes along the image.

Such stripes can be sequentially enumerated follow-

ing the ordering induced by the projector’s pixel grid.

The fringe number associated to each coordinate ξ can

be simply computed as:

η(ξ) =





∈ N (8)

so that each projector coordinate can be expressed in

terms of the normalized phase and fringe number as:

ξ = (η(ξ) + ϕ(ξ))λ. (9)

Values of ϕ(ξ) are recovered as in (7), while λ is

the constant value of the chosen period length. Thus,

η(ξ) is the only element that allows us to disam-

biguate among points with the same observed phase.

Similarly to other multi-phase approaches, we use

n sinusoidal patterns with different co-prime period

lengths λ

.. .λ

to disambiguate the fringes. In this

setting, for each pixel P we estimate a sequence of n

normalized phases ˆϕ = (

.. .

) using the ML es-

timator shown in (6). Therefore, each

is a sam-

ple from a random variable which we consider dis-

tributed as a Wrapped Normal of support [0,1], un-

known mean ϕ

and variance

∼ N

(ϕ

). (10)

Note that, with a slight abuse of notation, with

,i = 1 . .. n we denote the standard deviation of the

random variable associated to the estimated phase of

period λ

(eq. 10), while with σ we express the stan-

dard deviation of w[t], which is not related to the pe-

riod length but only to the signal-to-noise ratio of the

physical device. Albeit being different, the two stan-

dard deviations are related as described in Section 3.

Since

is in general very small, we can approxi-

mate the Wrapped Normal efﬁciently with a standard

Gaussian distribution (Kurz et al., 2014).

Therefore we can express the Probability Density

Function relative to the observed phase in the i

pat-

tern as:

(

;ϕ

) =

√

2π

−

(

,ϕ

)

(11)

where d

is the signed circular distance (deﬁned in the

range [−0.5,0.5]) of two normalized phases:

(ϕ

,ϕ

) = sign(ϕ

−ϕ

)min{|ϕ

−ϕ

|,1−|ϕ

−ϕ

The PDF in (11) expresses the probability of ob-

serving a certain phase

given the true (unknown)

projected phase ϕ

and the standard deviation on the

phase observation

Since the projected phase ϕ

is uniquely identiﬁed

by the projector code ξ through equation (2), we can

rewrite (11) in the following way:

(

;ξ,

) =

√

2π

−



−





(12)

This time, p

models the probability of observing a

certain phase

at a speciﬁc projector location ξ.

When looking at all the n observed phases to-

gether, we can consider the components of vector ˆϕ

as independent samples drawn from distribution (10)

with means ϕ = (ϕ

.. .ϕ

) and ﬁxed standard devia-

tions ¯σ = (

.. .

). Similarly to what we did before

with the signal, we consider ξ as a parameter and de-

ﬁne the likelihood function describing the plausibility

of observing a projector code ξ given the estimated ˆϕ

and a pre-deﬁned ¯σ as

L (ξ; ˆϕ, ¯σ) =

∏

i=1

(ξ;

)

∏

i=1

√

2π

−



−





(13)

Given phase values estimated from the acquired

signal, we can compute the code that most likely gen-

erated such phases by maximizing the Likelihood

ξ = argmax

ξ∈[0,ξ

max

)

L (ξ; ˆϕ, ¯σ) (14)

2.3 Our Proposed Method

Following the theoretical discussion made so far, we

now summarize our proposed stochastic code recov-

ery approach. Before starting the acquisition, one

must choose how many periods to project and their

period length in pixels.

To avoid ambiguity along the projector’s codes

space, all period lengths must be co-prime and their

LCM smaller than the projector width (or height, if

we project horizontal patterns). Moreover, one must

specify the expected standard deviations of estimated

phases, i.e. the vector ¯σ.

It is worth spending a couple of words here, be-

cause ¯σ is in fact the only required parameter of our

algorithm. First, we formulated the solution assuming

a possibly different

for each projected period. This

accounts the fact that, for the microscopic character-

istics of the surface, different sine frequencies may

exhibit different signal noises. Moreover, longer peri-

ods are less localizable in space, so it is a good prac-

tice to use more samples m for long periods than for

Stochastic Phase Estimation and Unwrapping

203

the short ones. Second, this approach allows us to not

exclude a-priori any value of the estimated ˆϕ. Indeed,

the vector ¯σ is essentially a weight acting on all the

acquired patterns. One may choose to keep extremely

short or long periods, or to use very few samples, and

modify the values of the relative

accordingly.

This is an important aspect when we compare this

method with other unwrapping techniques. Indeed,

approaches like (Lilienblum and Michaelis, 2007) fail

when facing noisy observations. We prefer to accept

such values and compute the best possible code rather

than having no code at all. Our goal, in fact, is to

exploit measured phases in the best possible way.

Once ¯σ is chosen and the n sinusoidal patterns

(one for each period) are acquired, for each pixel

of the camera we estimate the phases

.. .

using

equation (7).

At this point, for each camera pixel, we search

for an initial integer estimate of the projector code

by taking the value of

ξ ∈ {0,1,...ξ

max

} for which

L (

ξ; ˆϕ, ¯σ) is maximum. Due to the different spatial

resolution between camera and projector, it is unlikely

that each camera pixel observe exactly one projector

pixel. Indeed, one of the strengths of phase-shifting is

that one can precisely recover the projector coordinate

with sub-pixel precision.

In other words, the code

ξ that maximizes the

Likelihood can assume any real value between 0 and

max

Unfortunately, due to the signed circular distance,

we cannot give a direct analytical solution for the

global maximum

ξ. However, if we restrict the search

in a small neighborhood of

ξ so that the circular dis-

tance never wraps, and take the logarithm of the Like-

lihood, L(ξ; ˆϕ, ¯σ) becomes a parabola for which we

can compute the maximum by sampling three distinct

points on it.

Therefore, once we identiﬁed the integer part of

the projector code

ξ, we recover the sub-pixel maxi-

mum

ξ with the following formula:

ξ =

L (

ξ + 1; ˆϕ, ¯σ) −L (

ξ −1; ˆϕ, ¯σ)

4L (

ξ; ˆϕ, ¯σ) −2



L (

ξ + 1; ˆϕ, ¯σ) + L (

ξ −1; ˆϕ, ¯σ)



(15)

3 ¯σ LOWER-BOUNDS

Now that we described the general algorithm, we still

need to clarify how to provide reasonable values for

the vector ¯σ.

One simple way is to empirically measure the

phase error on a set of repeated experiments and com-

pute its standard deviation.

There are two drawbacks in this approach. First,

this sort of ”calibration” must be performed every

time a new object is acquired or any other condition

changes the expected signal-to-noise ratio of acquired

sinusoids. Second, the operation cannot be performed

along with the acquisition because the exact phase of

each acquired signal is not known, as it depends on

the scene geometry.

To overcome that, the only way is to project the

same known phase for all the projector pixels (essen-

tially setting λ = 1) to collect statistics on its distri-

bution. Unfortunately, this special pattern is useless

for 3D reconstruction so it will just consume projector

time to calibrate the parameter needed for our method.

Instead of directly calibrate ¯σ, we can empirically

measure the variance of the signal noise w[t] and re-

late it to the variance of the phase estimator.

Since φ

is an unknown deterministic parameter

of some probability function via the unbiased estima-

tor

, the variance of the estimator is subject to the

Cram

er-Rao bound:

var(

) ≥

J(φ

)

(16)

where J(φ

) is the Fisher information deﬁned as:

J(φ

) = E



∂ln p(z; φ

)

∂φ





= −E



∂

ln p(z; φ

)

∂



(17)

By substituting (5) in (17) we obtain:

ln p(z;φ

) = ln



σ(2π)

m/2



−

2σ

m−1

∑

t=0



z(t) −sin



2π

+ φ



(18)

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

204

∂

ln p(z;φ

)

∂

= −2K



m−1

∑

t=0

cos



2π

+ φ



−

m−1

∑

t=0

sin



2π

+ φ



m−1

∑

t=0

sin



2π

+ φ



z(t)





∂

ln p(z;φ

)

∂



= −2K



m−1

∑

t=0

cos



2π

+ φ



−

m−1

∑

t=0

sin



2π

+ φ



m−1

∑

t=0

sin



2π

+ φ



E[z(t)]



(19)

where K = −

2σ

. Since

E[z(t)] = sin



2π

+ φ



+ E[w[t]] (20)

and E[w[t]] = 0 by deﬁnition, we obtain:



∂

ln p(z; φ

)

∂



= −2K

m−1

∑

t=0

cos



2π

+ φ



var(

) ≥

∑

m−1

t=0

cos



2π

+ φ



(21)

Equation (21) states that the variance of our phase

estimator must be greater than a value proportional

to the variance of the Gaussian white noise σ

and

inversely proportional to the number of samples m.

Indeed, since cos

(x) ≤ 1, we have:

m−1

∑

t=0

cos

(2π

+ φ

) ≤ m. (22)

This makes sense, as we expect to reduce the es-

timation error either by acquiring more samples or by

increasing the signal-to-noise ratio. With this new for-

mulation, the value of σ can be empirically estimated

online with the acquisition of the sinusoids, just by

computing the observation errors with respect to our

ideal projected pattern.

Even if we did not solved the problem completely,

we experimentally observed that the empirically esti-

mated phase standard deviation is actually very close

to the theoretical lower-bound (21). Hence, by just us-

ing a value of ¯σ equal to the lower bound, we almost

always obtain satisfactory results.

4 EXPERIMENTAL EVALUATION

We designed a set of synthetic and real-world exper-

iments to verify the correctness of the assumptions

we made in the previous sections and to compare our

method with other multi phase-shift approaches.

The real-world experiments were performed with

a structured-light scanner developed in our lab. The

device is composed by a single MatrixVision Blue-

Fox3 5Mpix camera and an LG projector with a res-

olution of 1920 ×1080 px. Camera and projector rel-

ative pose was calibrated using the ﬁducial markers

descried in (Bergamasco et al., 2011). We manu-

ally corrected the projector gamma to obtain a cam-

era signal response as linear as possible. Once cal-

ibrated, the deﬁned gamma settings remained un-

changed throughout the experiments.

4.1 Phase and Signal Standard

Deviation

We performed a ﬁrst set of experiments to assess the

validity of our statistical noise model on a real scene.

We considered three different kinds of planar sur-

faces, namely: matte white plastic, a brushed alu-

minum metal sheet and a dark coloured cardboard.

The goal is to compare the acquired signal standard

deviation σ with the standard deviation of the phase

estimator

. To do that, we generated a pattern com-

posed by a variable number of samples m with a pe-

riod equal to one. This way, each pixel P in a scene

observed exactly the same true phase φ

= 0, allow-

ing us to empirically estimate the standard deviation

of the phase error among pixels. Similarly, by know-

ing the phase, we computed the error of acquired sig-

nal with respect to the projected ideal sinusoid. In

this way we can test if our zero-mean white Gaussian

noise assumption is supported by experimental evi-

dence.

In Figure 2 we show the results of this experiment

for the three different materials. On the top row we

plotted the histogram of the error of raw acquired sig-

nal for a sinusoidal pattern composed by m = 60 sam-

ples.

In all cases, the signal was analyzed by collecting

the errors in a ROI of size 400 ×300 pixels selected

to cover the central region of the projected area. We

can see that the empirical distributions follow quite

well our supposed Gaussian model with a mean close

to zero. Especially for the cardboard material, we re-

port a little positive bias that we guess is caused by

blooming effect. In fact, blooming clearly bias the

acquired intensity by always overshooting the actual

value. Nevertheless, we think that the proposed as-

Stochastic Phase Estimation and Unwrapping

205

-0.3 -0.2 -0.1 0 0.1 0.2

Error

x 10

White Matte Plastic

-0.3 -0.2 -0.1 0 0.1 0.2

Error

x 10

Metal

-0.3 -0.2 -0.1 0 0.1 0.2

Error

x 10

Dark Cardboard

10 20 30 40 50 60

Samples

std (rad)

x 10

-3

Measured Phase std

CR Lower Bound

10 20 30 40 50 60

Samples

std (rad)

x 10

-3

Measured Phase std

CR Lower Bound

10 20 30 40 50 60

Samples

std (rad)

x 10

-3

Measured Phase std

CR Lower Bound

Figure 2: Relation between the acquired signal distribution and standard deviation σ (top row) with the theoretical lower-

bound and the empirical phase standard deviation ¯σ (bottom row) for the three different chosen materials.

sumptions are fair enough to approximate the real be-

haviour of the phenomenon. For each material, we

computed the empirical standard deviation σ (from

the m = 60 samples case) to compute the lower-bound

according to (21).

In the second row of Figure 2 we plotted both

the lower-bound and the empirically measured phase

standard deviation varying the number of samples m

for the three different materials. As expected, the em-

pirical standard deviation of the estimated phase is

proportional with the standard deviation of the sig-

nal. In fact, the white matte plastic exhibits a lower

error due to its nearly Lambertian nature. Metal sheet

is more noisy due to small reﬂections and dark card-

board is the worst since the low albedo is heavily de-

creasing the signal-to-noise ratio. In all the cases the

estimated phase standard deviation is slightly above

the theoretical lower bound computed from the sig-

nal. This validates our claim that the given bound can

be effectively used to give a good estimation of the

unknown ¯σ.

4.2 Code Estimation Comparisons

We performed a set of synthetically generated tests to

compare the code recovery accuracy of our method

with respect to a famous multi-phase shift approach

proposed by Lilienblum and Michaelis (Lilienblum

and Michaelis, 2007) and a single phase-shift ap-

proach using Graycoding to disambiguate the fringes

and just one periodic pattern to obtain the code.

In all tests we generated 3 patterns with λ

= 17,

= 23 and λ

= 27 pixels and simulated a 1920 ×

1080 pixels projector. Then we additively perturbed

the synthetic phases of each pixel with a zero-mean

Gaussian with different standard deviations. For each

experiment we recovered the projector codes with the

different methods and compute the RMS with respect

to the ground truth.

In the ﬁrst row of Fig.3 we plotted the compar-

ison as RMS and percentage of outlier codes. For

both methods, we considered a pixel as outlier if the

distance wrt. the ground-truth was greater than half

the minimum period length. From this test we can

observe how our method consistently provides lower

code RMS, less variability in the estimation and a

lower number of outliers.

In the case of single phase-shift disambiguated

with Graycoding (Fig.3, second Row), we observe

how the recovered codes are less accurate than the

multi-phase approach as we consider only a single

pattern (and hence the output coding error is almost

linearly related to the amount of phase perturbation

introduced). The outlier ratio is consistently lower

than the multi phase-shift approaches as we assumed

that the Graycoding technique never fails to disam-

biguate the correct fringe. Nevertheless, the good in-

lier ratio does not justify its adoption for the higher

overall RMS exhibited.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

206

Figure 3: Comparison of our approach with respect to (Lilienblum and Michaelis, 2007) (top row) and single phase-shift

disambiguated with Graycoding (bottom row). First and second column show respectively the coding RMS and the code

outlier percentage varying the input phase error σ.

4.3 Projector Delay Recovery

One of the key strengths of our method is the re-

silience against noisy phase estimations. To demon-

strate that, we tested the approach with the challeng-

ing task of recovery the correct code even if the pro-

jector and camera are not synchronized.

This can be useful in practice because ensuring a

proper synchronization of the camera frames with the

projected patterns usually requires a custom electron-

ics that increases the cost and complexity of the scan-

ner.

For simplicity, we assumed that the exposure time

of the camera is far lower than the display time of each

projected pattern. This way, all the acquired samples

z(t) are affected by a ﬁxed unknown integer shift but

the camera never acquires in-between two projector

frames.

We generated a synthetic 3-periods signal com-

posed by m = 60 samples (as in previous experiments)

perturbed with a variable zero-mean noise with vari-

ance σ

. Then, we shifted all the patterns by a random

shift 0 ≤ k ≤ m. Afterwards, we run our method for

each possible circular shift k of the signal collecting,

for each pixel, the value of the maximum likelihood

obtained. Pixel wise, we compared all the maximum

likelihood values to select the shift corresponding to

the higher one. The result is that each pixel votes for

the shift producing the higher maximum likelihood of

the codes.

Since the data was synthetically generated, we

marked as inliers all the pixels that actually voted

for the correct shift and plotted the inlier percentage

against the noise in Fig.5.

The experiment shows an inlier percentage greater

than 50% (sufﬁcient to correctly recover the unknown

shift) for input signal noise std. up to 0.45, which is

more than 5 times the noise levels we measured for

all the three different materials in Fig.2. Therefore,

we are conﬁdent that in the vast majority of real world

cases the synchronization may be avoided with no se-

vere consequence on the unwrapping result.

4.4 Qualitative Evaluation

Finally, we qualitatively evaluated the 3D triangu-

lated meshes obtained both with our proposed method

and the number-theoretical approach (Lilienblum and

Michaelis, 2007).

In Fig.4 we show the range-maps obtained while

reconstructing a metallic kitchen sink (top row) and

a matte chalk bas-relief (bottom). As pre-processing,

before triangulation we just ﬁltered all the codes with

a value outside the range 0. .. ξ

max

Especially in the more challenging metallic ob-

ject, our method provides a denser and less noisy re-

construction. In the optimal scenario of the Lamber-

tian white artefact, our method outperforms (Lilien-

blum and Michaelis, 2007) in high curvature regions

where self-reﬂections usually lead to higher coding

errors.

Stochastic Phase Estimation and Unwrapping

207

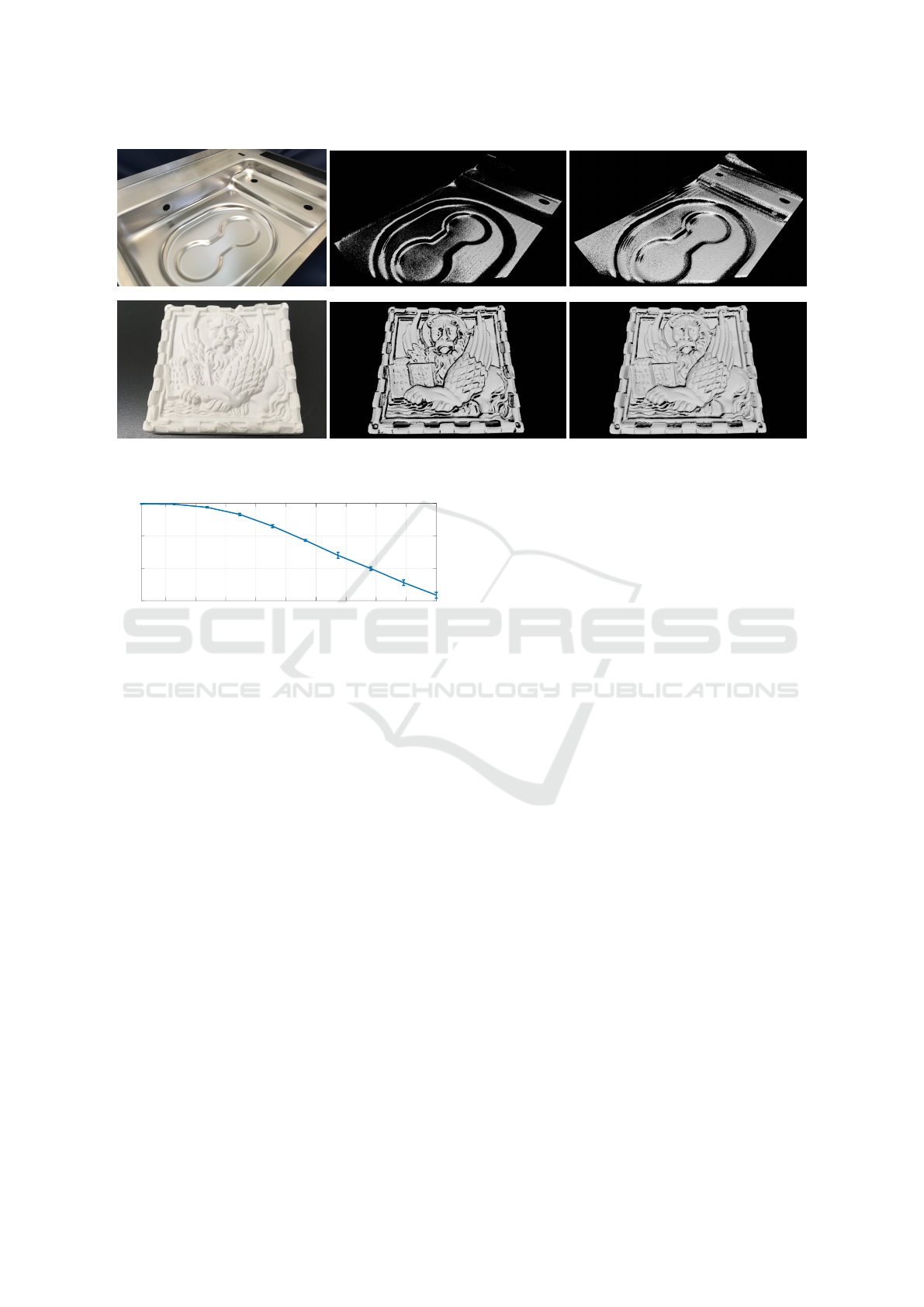
Figure 4: Examples of reconstructions for two different objects. The second column shows the triangulated mesh using

(Lilienblum and Michaelis, 2007); while the third column shows the mesh obtained applying our method.

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

Signal std

0.4

0.6

0.8

% Inliers

Figure 5: Projector delay recovery: percentage of correctly

estimated shifts (inliers) against the acquired noise standard

deviation.

5 CONCLUSIONS

In this paper we proposed a novel phase-shift tech-

nique to simultaneously disambiguate among differ-

ent phase periods and estimate the ﬁnal projector

code. Our method is based on statistical inference on

the observed phases which we assume being affected

by zero-mean Gaussian white noise. Under this as-

sumption, we derived a Maximum Likelihood estima-

tor for the ﬁnal projector code taking into account all

the observations in an optimal way.

Additionally, we exploit the Cram

er-Rao bound to

derive a lower-bound for the phase estimator variance

according to the variance of acquired signal. This

way, the estimation of the vector ¯σ (the only param-

eter required by our method) can be efﬁciently com-

puted on-line with the acquisition of the sinusoidal

patterns.

We tested our method both synthetically and with

a real camera-projector structured light setup. From

the the experiments, we observed how the empirically

estimated phase variance is close to the theoretical

lower-bound, suggesting that we can effectively use

that value for the subsequent code recovery. Compar-

isons show how our method can outperform Graycod-

ing and number theoretical multi-phase shift methods

not only in terms of accuracy but also considering the

number of correctly estimated codes. This leads to

coded images that are in general denser, even for chal-

lenging materials.

REFERENCES

Bergamasco, F., Albarelli, A., and Torsello, A. (2011).

Image-space marker detection and recognition using

projective invariants. pages 381–388.

Bergamasco, F., Cosmo, L., Albarelli, A., and Torsello, A.

(2012). A robust multi-camera 3d ellipse ﬁtting for

contactless measurements. pages 168–175.

Cheah, C.-M., Chua, C.-K., Tan, K.-H., and Teo, C.-K.

(2003). Integration of laser surface digitizing with

cad/cam techniques for developing facial prostheses.

part 1: Design and fabrication of prosthesis replicas.

International Journal of prosthodontics, 16(4).

der Jeught, S. V. and Dirckx, J. J. (2016). Real-time struc-

tured light proﬁlometry: a review. Optics and Lasers

in Engineering, 87(Supplement C):18 – 31.

Fanello, S. R., Rhemann, C., Tankovich, V., Kowdle, A.,

Escolano, S. O., Kim, D., and Izadi, S. (2016). Hy-

perdepth: Learning depth from structured light with-

out matching. pages 5441–5450.

Han, J., Shao, L., Xu, D., and Shotton, J. (2013). Enhanced

computer vision with microsoft kinect sensor: A re-

view. IEEE Transactions on Cybernetics, 43(5):1318–

1334.

Kurz, G., Gilitschenski, I., and Hanebeck, U. D. (2014). Ef-

ﬁcient evaluation of the probability density function of

a wrapped normal distribution. In 2014 Sensor Data

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

208

Fusion: Trends, Solutions, Applications (SDF), pages

1–5.

Lange, R. and Seitz, P. (2001). Solid-state time-of-ﬂight

range camera. IEEE Journal of quantum electronics,

37(3):390–397.

Lilienblum, E. and Michaelis, B. (2007). Optical 3d surface

reconstruction by a multi-period phase shift method.

JCP, 2(2):73–83.

Luhmann, T. (2010). Close range photogrammetry for in-

dustrial applications. ISPRS Journal of Photogram-

metry and Remote Sensing, 65(6):558–569.

Macleod, M. D. (1998). Fast nearly ml estimation of the

parameters of real or complex single tones or resolved

multiple tones. IEEE Transactions on Signal Process-

ing, 46(1):141–148.

Pellot, C., Herment, A., Sigelle, M., Horain, P., Ma

ıtre, H.,

and Peronneau, P. (1994). A 3d reconstruction of vas-

cular structures from two x-ray angiograms using an

adapted simulated annealing algorithm. IEEE trans-

actions on medical imaging, 13(1):48–60.

Prez, L., Rodrguez, I., Rodrguez, N., Usamentiaga, R., and

Garca, D. (2016). Robot guidance using machine vi-

sion techniques in industrial environments: A compar-

ative review. Sensors (Switzerland), 16(3).

Rife, D. and Boorstyn, R. (1974). Single tone parame-

ter estimation from discrete-time observations. IEEE

Transactions on Information Theory, 20(5):591–598.

Srinivasan, V., Liu, H. C., and Halioua, M. (1984). Au-

tomated phase-measuring proﬁlometry of 3-d diffuse

objects. Appl. Opt., 23(18):3105–3108.

Tikuisis, P., Meunier, P., and Jubenville, C. (2001). Human

body surface area: measurement and prediction using

three dimensional body scans. European journal of

applied physiology, 85(3):264–271.

Vo, M., Narasimhan, S. G., and Sheikh, Y. (2016). Tex-

ture illumination separation for single-shot structured

light reconstruction. IEEE Trans. Pattern Anal. Mach.

Intell., 38(2):390–404.

Winterhalter, W., Fleckenstein, F., Steder, B., Spinello, L.,

and Burgard, W. (2015). Accurate indoor localization

for rgb-d smartphones and tablets given 2d ﬂoor plans.

volume 2015-December, pages 3138–3143.

Stochastic Phase Estimation and Unwrapping

209