
A Heuristic Method for the Multi-skill Project Scheduling Problem with
Partial Preemption
Oliver Polo-Mej
´
ıa
1,2
, Christian Artigues
2
and Pierre Lopez
2
1
CEA, DEN, DEC, SETC, St. Paul lez Durance, France
2
LAAS-CNRS, Universit
´
e de Toulouse, CNRS, Toulouse, France
Keywords:
Project Scheduling, Multi-skill, Partial Preemption, Nuclear Research Facility.
Abstract:
In this article we consider a new scheduling problem known as the Multi-Skill Project Scheduling Problem
with Partial Preemption. The main characteristic of this problem is the way we handle the resources release
during the preemption periods: only a subset of resources are released. Since this problem is NP-hard, we
propose a greedy algorithm based on priority rules, modeling the subproblem of technicians allocation as a
Minimum-Cost Maximum-Flow problem. In order to improve the performance of the greedy algorithm, we
propose a randomized tree-based local search algorithm. Computational tests are carried out and analyzed.
1 INTRODUCTION
Scheduling activities within a research nuclear facil-
ity is a very complex task. This is due to the diver-
sity of activities to schedule, and to the big amount
of constraints we must take into account in order to
complain with the operational and legal regulations.
Because of this complexity, this research project is
carried out in order to optimize the weekly schedul-
ing within one of the research facilities of the French
Alternative Energies and Atomic Energy Commission
(CEA in short for French). After a deep analysis of
the characteristics of the studied facility, we conclude
that the problem at hand can be regarded as an exten-
sion of the Multi-Skill Project Scheduling Problem.
The Multi-Skill Project Scheduling Problem
(MSPSP) acquires great importance for scheduling
activities in very specific fields, such as pharmaceu-
tical, chemical and nuclear, where the regulation re-
quires the presence of a group of technicians having
a set of well-defined competences for the execution
of an activity. This problem shows to be more chal-
lenging than traditional scheduling problems (such as
the Resource-Constrained Project Scheduling Prob-
lem (Artigues, 2008)) due to the extra decision we
need to make: we need to decide not only which
resources will be assigned to each activity, but also
the skills with which they will contribute(Correia and
Saldanha-da Gama, 2015).
This problem consists in determining a feasible
schedule, respecting the resource constraints and the
precedence constraints between activities: a resource
cannot execute a skill it does not master, cannot be as-
signed to more than one competence requirement at a
given time, and must be assigned to the corresponding
activity during its whole processing time (Bellenguez-
Morineau, 2008).
One of the most important hypothesis of the
MSPSP is that activities are supposed to be non-
preemptive; what means that, once started, an activity
must run continuously until its completeness. How-
ever, in some practical applications as in the case of
scheduling research or engineering activities, it may
be interesting to allow the preemption of activities,
due for example to the impossibility of working con-
tinuously and other technical constraints. In order to
better represent the real situation of the nuclear lab-
oratory, we proposed in (Polo-Mej
´
ıa et al., 2018) a
more general variant of the MSPSP: the Multi-Skill
Project Scheduling Problem with Partial Preemption.
The remainder of the paper is as follows. In Sec-
tion 2, we describe the studied problem. Then, a
priority-based heuristic method is proposed in Sec-
tion 3. The computational experiments performed are
presented in Section 4. Finally, in Section 5, the main
conclusions are presented as well as some directions
for future research.
Polo-Mejía, O., Artigues, C. and Lopez, P.
A Heuristic Method for the Multi-skill Project Scheduling Problem with Partial Preemption.
DOI: 10.5220/0007390001110120
In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 111-120
ISBN: 978-989-758-352-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
111

2 PROBLEM DESCRIPTION
The main drawback of preemptive versions of vari-
ous scheduling models is that activities can be pre-
empted and continued later without any additional
cost (Ballest
´
ın et al., 2008). The possibility of re-
suming a preempted activity without any cost does
not appear realistic enough for industrial applications
(Ballest
´
ın et al., 2009; Vanhoucke, 2008), due mainly
to the cost/time of setup for resuming or simply to the
reduction in the production rate.
In real life, setup time of an activity is almost
always related to only a subset of resources, while
the others can be easily preempted with insignificant
setup time. When working with preemptive schedul-
ing problem, we commonly assume that all resources
are released during the preemption periods. What we
propose in this new variant is to handle the preemp-
tion in a different way: during the preemption periods
we will release only those resources with a low setup
time while seizing those with an important setup time.
This is what we call partial preemption (Polo-Mej
´
ıa
et al., 2018).
In our practical case, partial preemption also an-
swers to a technical requirement for the good opera-
tion of the facility. In fact, some critical activities re-
quire the presence of equipment to ensure the confine-
ment of the irradiated material or even to ensure an
inert atmosphere within this confinement. For safety
reasons, the equipment ensuring these functions must
be allocated to the activity from the beginning to the
end without interruption. The remainder resources,
however, can be preempted without problem. If we
use a traditional preemptive/non-preemptive schedul-
ing approach, these activities must be defined as “non-
preemptive” in order to respect the safety require-
ments. Using the concept of partial preemption, we
can better exploit the characteristics of these activities
while complying with all the operational constraints.
In the MSPSP with partial preemption (MSPSP-
PP), additionally to the characteristics of the classical
MSPSP, we must indicate for each activity the subset
of resources that can be released during the preemp-
tion periods. Preemption is now handled in three lev-
els according to the activities characteristics: 1) Non-
preemption, for activities where none of the resources
can be preempted; 2) Partial preemption, for activities
where a subset of resources can be preempted; and 3)
Full preemption, for activities where all resources can
be preempted.
Additional changes must be included in order to
better represent the research facility behavior:
• Resources in the MSPSP, as defined in (N
´
eron,
2002), are supposed to be disjunctive, which
Figure 1: Example of an MSPSP-PP instance.
means they can handle only one activity at a time.
In the research laboratory under consideration,
additionally to the disjunctive multi-skilled re-
sources (technicians), we must also handle some
cumulative (more than one activity at a time)
mono-skilled resources (compound machines and
equipments).
• Unlike the traditional MSPSP, in our practical
case, technicians may respond to more than one
skill requirement per activity.
• Due to operational and safety reasons, we need to
guarantee a minimum number of technicians (Nt
i
)
present during the execution of the activity.
• Due to the duration of some activities (larger
than technicians work shifts), we need to relax
the constraint stating that the same technician
must execute the activity in full (except for non-
preemptive activities, which duration is supposed
to be smaller than work shifts).
• Finally, we must include some characteristics to
our problem concerning the time windows for
scheduling. In the laboratory, the regulatory test
must be executed before a restrictive date (dead-
line, dl
i
). Moreover, some of the activities are
in collaboration with other nuclear facilities, such
activities are then restricted by a release date (r
i
)
fixed by external partners.
Summarizing, in the MSPSP with partial preemp-
tion the objective is to find a feasible schedule that
minimizes the total duration of the project (Cmax).
Finding a solution consists in determining the peri-
ods during which each activity is executed and also
which resources will execute the activity in every pe-
riod; all this, while respecting the resources capacity
and the activities characteristics. Figure 1 illustrates
an example of an MSPSP-PP instance and a possible
solution.
We must schedule these activities over renewable
resources with limited capacity; they can be cumula-
tive mono-skilled resources (machines) or disjunctive
multi-skilled resources (technicians) mastering Nb
j
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
112

skills. Multi-skilled resources are able to respond to
more than one skill requirement per activity and may
execute it partially (except for non-preemptive activi-
ties where technicians must perform the whole activ-
ity). An activity is now defined by its duration (d
i
),
its precedence relationships, its requirements of re-
source k (Br
i,k
), its requirements of skill c (Bc
i,c
), the
minimum number of technicians needed to perform
it (Nt
i
) and the subset of preemptive resources. Ac-
tivities might or not have either a deadline (dl
i
) or a
release date (r
i
).
For each instance of the MSPSP we can match
an instance of the MSPSP with partial preemption,
where none of the resources can be preempted. Since
the MSPSP has been proved to be strongly NP-hard
(Bellenguez-Morineau, 2008), we can therefore infer
that the MSPSP-PP is also strongly NP-hard. The
results presented in (Polo-Mej
´
ıa et al., 2018) show
the difficulties of Mixed Integer Linear Programming
and Constraint Programming exact methods to tackle
large instances.
In the nuclear installation under study, the
scheduling of the activities of the following week
must be constructed and validated during a meeting
of the heads of research, heads of maintenance and
engineers responsible for activities that takes place at
the end of the week. Although the planners prepare
an interim scheduling before this meeting, it is very
common that important changes must be made during
the meeting due to new information or the status of
the administrative progress of the documentation nec-
essary to carry out an activity. It is important then to
be able to have a new feasible schedule within a few
minutes. This fact forces us to develop some efficient
methods for finding good quality solutions in accept-
able computational times, such as the one proposed in
the next section.
3 PRIORITY LIST-BASED
HEURISTIC
3.1 Flow Problem for Technicians
Allocation
The MSPSP-PP can be seen as a problem consisting
of two coupled sub-problems: an activity scheduling
problem combined with an allocation problem of the
technicians performing each activity. In a heuristic
approach, even when the periods in which an activity
will be executed are defined, we still have the problem
of choosing the technicians who will perform it. To
achieve this allocation in the best way, we must first
Figure 2: Flow graph for the MSPSP.
allocate the technicians with the least chances of be-
ing necessary to the activities not yet scheduled, that
is to say, the less critical technicians.
According to the work of Bellenguez-Morineau
(Bellenguez-Morineau, 2008) for the MSPSP, the al-
location problem of technicians with the lowest criti-
cality can be treated as a Minimum-Cost Maximum-
Flow (MCMF) problem (Ahuja, 2017) on a graph
G
i
= (X, F), X = S ∪ P, where S represents the set
of skills required by activity A
i
and P is the subset
of available technicians and who master at least one
of the skills required by activity A
i
(Figure 2). The
MCMF problem is a way of minimizing the cost re-
quired to deliver maximum amount of flow possible
in the network.
In this graph, there is an edge between the source
vertex and each vertex S
k
∈ S whose maximum capac-
ity is equal to b
i,k
(need of the skill k for executing the
activity A
i
). There is also an edge between a vertex S
k
and a vertex P
j
∈ P, iff the technician P
j
masters the
skill S
k
. The maximum capacity of this arc is fixed to
1 because, in the MSPSP as defined in (N
´
eron, 2002),
a technician can only respond to one unit of need per
skill. Similarly, there is an edge between each vertex
P
j
and the sink of the graph, with a maximum capac-
ity equal to 1 (a technician can only answer one skill
per activity). We associate a cost (CP
j
) related to the
criticality of the technician P
j
to these last arcs.
Using one of the existing polynomial algorithms
such as the Edmonds-Karp Algorithm (Edmonds and
Karp, 1972), one can solve the problem of maximum
flow at minimum cost for the proposed graph. To de-
termine the technicians to allocate, we just look at the
vertices P
j
∈ P through which the flow passes. If the
maximum flow going throw the graph is less than the
sum of the skill needs, we can conclude that there is
no possible assignment for this activity.
The graph presented in Figure 2 was designed un-
der the set that each technician can only respond to
one skill requirement per activity. However, this con-
straint has been relaxed for the MSPSP-PP and tech-
nicians can respond to several skills per activity. We
must then redefine the graph to take this change into
account. More precisely, the maximum capacities of
A Heuristic Method for the Multi-skill Project Scheduling Problem with Partial Preemption
113
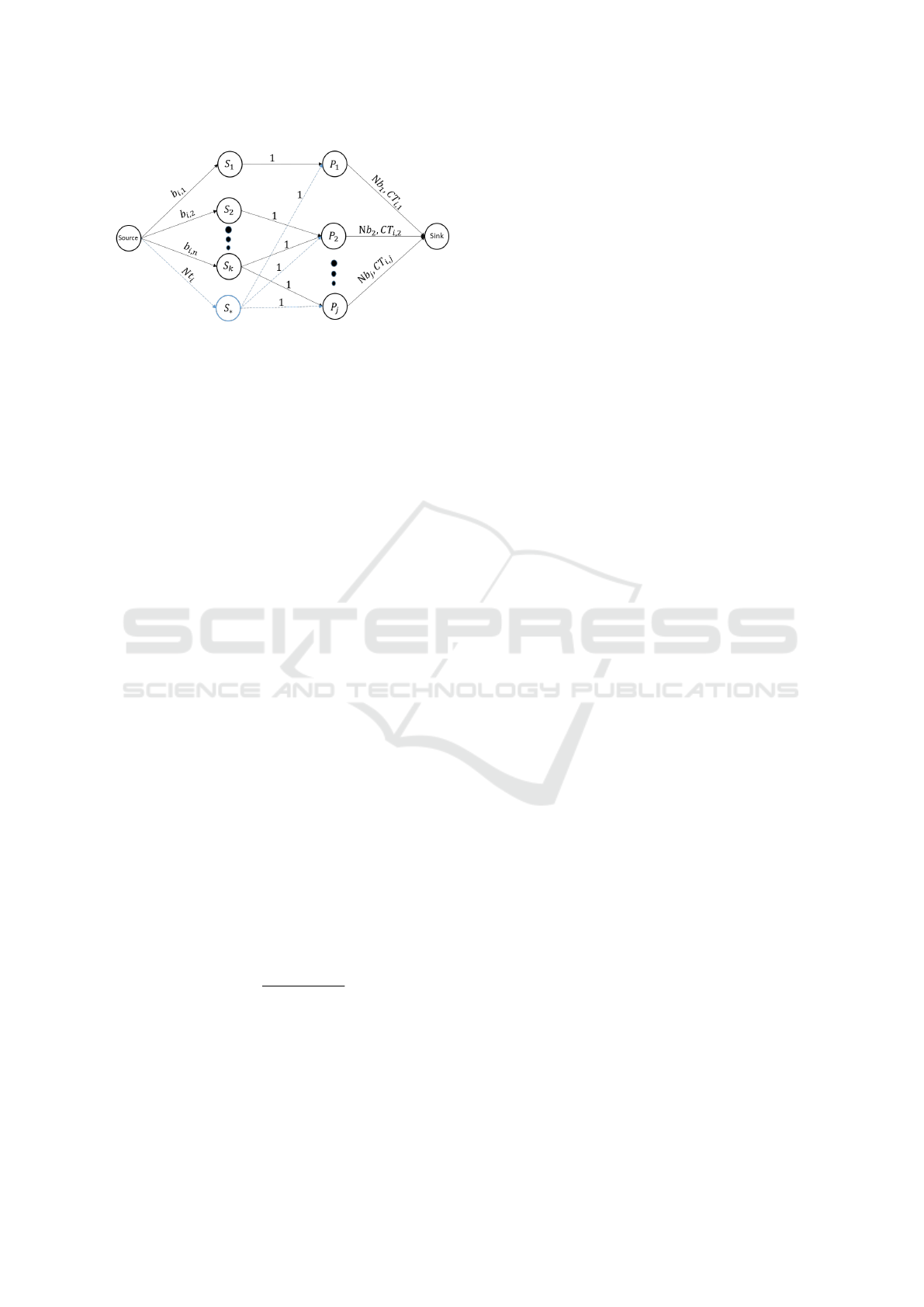
Figure 3: Flow graph for the MSPSP-PP.
the arcs connecting all vertices P
j
and the sink are
now equal to the number of skills mastered by the
technician P
j
(Nb
j
). As indicated in Section 2, in our
industrial problem we must allocate a minimal num-
ber of technicians (Nt
i
) for the activity execution. In
order to take into account this constraint, we must add
an additional S
k
vertex (S
∗
) linked to the source vertex
with a capacity equal to Nt
i
and connected to all ver-
tices P
j
∈ P with a capacity of 1. Concerning the unit
cost of the arcs connecting technicians vertices to the
sink, we use a cost function CT
i, j
(Definition 2) which
varies according to the technician P
j
and the activity
A
i
analyzed. The new graph is shown in Figure 3.
Definition 1. The correlation indicator Cr
i, j
ex-
presses the correlation of the technician P
j
and the
activity A
i
. It indicates the degree to which the activ-
ity A
i
might require the technician P
j
for its execution.
Let us define ST
j
as the skill set that a technician P
j
masters, and let SA
i
be the skill set needed to execute
the activity A
i
. The correlation indicator is calculated
as follows:
Cr
i, j
= Cardinality(ST
j
∩ SA
i
) (1)
Definition 2. The criticality cost CT
i, j
of a technician
P
j
is an indicator of the degree to which a technician
could be requested by the set of not yet scheduled ac-
tivities (set L). It is directly proportional to the sum
of duration (d
l
) of every activity A
l
∈ L multiplied by
the correlation indicator between the activity A
l
and
the technician P
j
. This cost is inversely proportional
to the correlation with the studied activity. This indi-
cator is calculated as follows:
CT
i, j
=
∑
L
(d
l
∗Cr
l, j
)
Cr
i, j
(2)
In case of equality of such a cost for different tech-
nicians, we break the ties in order to ensure that the
flow algorithm always minimizes the number of tech-
nicians allocated to each activity.
3.2 Greedy Algorithm: Serial
Generation Scheme
For this heuristic method, we propose to use a serial
scheduling scheme with priority rules. Given a set J
containing the activities to be scheduled and sorted
according to a priority rule, we take one by one the
activities in J and perform their scheduling and tech-
nicians allocation (using the proposed method in Sec-
tion 3.1) sequentially as early as possible. For every
activity A
i
∈ J, we check each time t, beginning with
t = r
i
e
(earliest start time, see Definition 3 below), the
ability to schedule the activity during period t depend-
ing on the type of preemption it has:
• For non-preemptive activities, we check the possi-
bility of continuous execution from t to t + d
i
− 1
(taking into account the availability of resources
and technicians), where d
i
is the duration of the
activity. If the answer is positive, we schedule
the whole activity and move on to the next one.
If continuous execution is not possible, we check
for the next t (a period where an event happens:
end of an activity, new availability of technicians,
etc.) until the activity can be scheduled.
• For partially preemptive activities, we will first
determine the minimum end date (starting from
the analyzed t period) depending on the avail-
ability of preemptive resources and technicians.
We will then check the continuous availability of
non-preemptive resources. If non-preemptive re-
sources are available without interruption, we al-
locate them to the activity from t until the end
date. Preemptive resources are allocated for pe-
riods t
0
∈ t..end date where all preemptive re-
sources are available. If continuity is not verified,
we go to the next t and repeat until getting an af-
firmative answer.
• For preemptive activities, the availability of
resources and technicians during period t is
checked. If they are available, we allocate them
for the period t; then increase t and repeat the pro-
cess until the duration of the activity is complete.
Definition 3. “Earliest start time” (r
i
e
) indicates the
date before which activity A
i
can not begin. It is cal-
culated using the precedence constraints and is equal
to the longest path from the source vertex (A
0
) to the
activity vertex (A
i
) in the precedence graph (taking
into account the release date and the possible end date
of the predecessors).
The steps of the serial generation schema are
presented in Algorithm 1.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
114

Algorithm 1: Greedy Serial Scheme Generation.
The presence of deadlines is one of the criti-
cal constraints for generating feasible solutions using
heuristic methods. In order to maximize the chance of
finding feasible solutions, we propose to use a 2-step
approach to generate the schedule. As a first step, ac-
tivities with a deadline and its previous activities (set
DL) are scheduled following a slack time-based pri-
ority list. Then, the rest of the activities (set L) are
scheduled using the other priority rules.
3.2.1 Scheduling Activities with Deadline
For this first part of the heuristic, we use a serial
scheduling generation scheme using a priority list
based on the “slack time” of activities with a deadline
(dl
i
). Giving priority to activities with the smallest
slack time.
Definition 4. “Slack time” (Slack
i
) refers to the mar-
gin that an activity A
i
has in its planning window. It is
a function of the deadline (dl
i
), the earliest start time
(r
i
e
), and the activity duration (d
i
). We calculate it as
follows:
Slack
i
= dl
i
− r
i
e
− d
i
(3)
We define the set Prec
i
as the set containing all the
predecessors of activity A
i
and which is sorted accord-
ing to the number of precedences of each element in
the subset. Items with the lowest number of predeces-
sors will be at the beginning. The set DL is thus con-
stituted as follows: DL = {Prec
1
, Prec
2
, ..., Prec
n
}
where Slack
1
≤ Slack
2
≤ ... ≤ Slack
n
.
We perform the serial scheduling of the activi-
ties contained in DL. Once these activities have been
scheduled, we must proceed to schedule the activities
without a deadline (set L) according to one of the pri-
ority rules.
3.2.2 Scheduling Other Activities
Once planned activities with deadline and its prede-
cessors, we must perform the scheduling of the re-
maining activities (L). To choose the order in which
activities will be scheduled, we propose to use the
most common priority rules in the scheduling liter-
ature:
• Longest Duration (LD): prioritizes the activity A
i
with the greatest duration (d
i
).
• Most Successors (MS): prioritizes the activity A
i
with the highest number of successors.
• Earliest Start Time (EST): prioritizes the activity
A
i
with the lowest earliest start date (r
i
e
).
• Earliest Finish Time (EFT): prioritizes the activity
A
i
with the smallest “earliest finish time”. This
date is calculated by adding the duration of the
activity (d
i
) to the earliest start date (r
i
e
), ie: r
i
e
+d
i
.
• Greatest Rank (GR): prioritizes the activity A
i
for
which the sum of the durations of its successors is
the largest.
• Greatest Resource Demand (GRD): prioritizes the
activity A
i
with the highest resource consumption.
In order to increase the chances of finding a fea-
sible solution from the beginning, and even improve
the solution we get, we propose to build the set of ac-
tivities to schedule L as follows: L = {NPA, SPA, PA}
where NPA is the subset of non-preemptive activities,
SPA is the subset of partially preemptive activities and
PA is the subset of preemptive activities. NPA, SPA
and PA are sorted according to the priority rule. With
this approach, we exploit the ability of preemptive and
partially preemptive activities to fill the unused spaces
left after scheduling the non-preemptive activities.
The heuristic presented before is a single-pass
heuristic because only one priority rule is used to se-
lect the activities to be scheduled. In order to im-
prove the results we get, we can execute the procedure
using all the activity priority rules presented before
and keeping the minimum makespan, as proposed by
Almeida et al. (Almeida et al., 2016). This process
originates a so-called multi-pass heuristic.
3.3 Tree-based Local Search Algorithm
Greedy construction algorithms, as the one proposed
in Section 3.2, may accept some myopic choices that
lead us to local optimum, needing an additional phase
were changes can be performed to ameliorate the cur-
rent solution (Voß et al., 2005). In order to im-
prove our results, we propose to use a tree-based lo-
cal search algorithm partially inspired by the Limited
Discrepancy Search (Harvey and Ginsberg, 1995) and
Branch-and-Greed (Sourd, 2001) methods.
For each sequence (priority rule), there is a big
amount of possible schedules that are defined by the
A Heuristic Method for the Multi-skill Project Scheduling Problem with Partial Preemption
115

Figure 4: Binary tree.
technician allocations we made. In fact, for each pe-
riod we choose to schedule an activity, there could
be a large number of possible technicians allocation.
Because of the combinatorial explosion, enumerate
all possible solutions for a same priority rule can be
prohibitive. An incomplete binary search tree maybe
then interesting.
For generating this tree, we use the same approach
than in the greedy algorithm (Algorithm 1). But now,
every time we must realize the technician allocation
(Step 3 in Algorithm 1), we will generate a node hav-
ing in the left-hand branch the best allocation we get
solving the MCMF with the method in Section 3.1,
while in the right-hand branch we have the second
best solution (this solution should not change the start
time of the activity), if such solution exists. Again, for
non-preemptive activities only one node will be gen-
erated (since the flow problem must be solved only
once to ensure that the same technicians execute the
whole activity), while for preemptive and partially
preemptive activities we must generate as much nodes
as time units of duration the activity has.
Visiting the whole binary search tree can be still
prohibitive for industrial instances (specially for in-
stances having a big amount of preemptive and par-
tially preemptive activities). We must limit even more
the number of visited branches. From the way the
solution is constructed in our greedy algorithm, we
can infer that heuristic’s probability of making mis-
takes decreases as we add more activities to the par-
tial schedule (going deep in the search tree); if there
are less activities to be scheduled the criticality cost of
a technician (Definition 2) is more accurate. We can
then decrease the number of branches examined by
giving each node a probability, decreasing according
to the depth in the tree, to examine the right branch
(second best answer for the MCMF). In this first ver-
sion of the algorithm, we propose to use a constant
gradual decrease (∆), calculated as follows:
∆ =
Prob
max
Depth
max
(4)
In Equation 4, Prob
max
represents the maximum
probability of analyzing the right branch at the top of
the search tree. Depth
max
is the maximum depth of
the tree.
For exploring the search tree, we use a depth-
first search approach, going from the left side to the
right side (exploring first the answer we get using the
greedy algorithm). In order to accelerate the search
process, we cut all solutions (or partial solutions) that
do not improve the Cmax. Every time a better Cmax
is found, the upper bound is updated. The tree-based
local search procedure is presented in Algorithm 2.
Algorithm 2: Tree-based Local Search Algorithm.
Select first activity from the list
while Node 6= root do
Select time periods for scheduling the activy
if Time perids exist then
if Left branch visited(Node) = false then
Solve MCMF
Allocate best solution
Go to next node
else
p ← random(0, 1)
if Right branch visited(Node) = false and
p ≤ P(Node) and Second best solution exist
then
Solve MCMF
Allocate second best solution
Go to next node
else
Backtrack
end if
end if
if Currect Cmax ≥ Best Cmax then
Backtrack
end if
if Node is a leaf and Current Cmax ≥ Best
Cmax then
Update Best Cmax
end if
else
Backtrack
end if
end while
Again, the proposed algorithm can be seen as
a single-pass. To improve the results, we can de-
velop its multi-pass version executing the algorithm
for all the priority rules proposed in Section 3.2.2.
To get faster results, we propose first to determinate
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
116

Table 1: Distribution of preemption type.
Set A Set B Set C Set D
Non-preemptive 10% 10% 80% 33.3%
Partially preemptive 10% 80% 10% 33.3%
Preemptive 80% 10% 10% 33.3%
the Cmax for every priority list using the greedy al-
gorithm; and after to execute the local search algo-
rithm starting from the list with the lowest Cmax to
the list having the biggest Cmax, keeping always the
best Cmax as upper bound for cutting branches.
4 COMPUTATIONAL
EXPERIMENTS
4.1 Greedy Algorithm
We generated a set of instances using a basic instance
generation algorithm that allows the control of certain
aspects such as: proportions of preemption type, per-
centage of activities with deadline and release date,
number of precedence relationships, skill number per
technician, etc. All the parameters settings are set to
reflect the characteristics of the actual installation. To
test this heuristic, we have generated 4 sets (A, B, C
and D) of 40 instances. For each instance in a set,
there is a similar instance in the other sets having as
only difference the distribution of the preemption type
of activities (this distribution is presented in Table 1).
These instances have an average makespan of 23 time
units, 10 activities with duration between 1 to 10 time
units, 15 skills, 8 cumulative resources, 8 technicians
(multi-skilled resources), 20% of activities with re-
lease date and deadline, all other characteristics are
random.
The proposed heuristic has been coded in C++. To
solve the flow problems, we used the adapted C++
version of the Edmonds-Karp algorithm proposed in
Ababei (Ababei, 2009). To obtain the optimal solu-
tions we use the mixed-integer linear programming
(MILP) model proposed in (Polo-Mej
´
ıa et al., 2018),
which was solved using CPLEX 12.7.1. All compu-
tational tests have been carried out using a Intel Xeon
E5-2695 processor running at 2.3 GHz and limiting
the number of thread used by Cplex at 8.
Table 2 shows average gap values (percentage er-
ror) between the solution we get with the heuristic
and the optimal one. We observe that the heuristics
using the priority rule Most Successors (MS) seems
to give in average smaller gaps than the other lists,
followed by the Greatest Rank (GR) and Longest Du-
ration (LD) priority rules. However, p-values of the
Table 2: Gap for the greedy serial scheme algorithm.
Gap
All A B C D
LD 11.85% 12.08% 12.29% 10.87% 12.14%
MS 11.49% 12.04% 12.14% 9.41% 12.36%
EST 13.73% 14.81% 13.42% 11.76% 14,91%
EFT 15.21% 15.75% 13.01% 18.16% 13.93%
GR 11.93% 12.04% 12.14% 11.18% 12.36%
GRD 12.23% 13.62% 12.24% 11.84% 11.20%
Multi-pass 7.45% 7.99% 9.00% 4.78% 8.03%
Table 3: p-values for t-test of average gap of priority rules.
MS EST EFT GR GRD
LD 0.6901 0.0178 0.0031 0.9262 0.6515
MS - 0.0045 0.00004 0.2362 0.4081
EST - - 0.0831 0.0372 0.0926
EFT - - - 0.0001 0.0024
GR - - - - 0.7620
t-test for paired samples (test used to determine if the
average time were statistically equal or not; for more
details we recommend (Derrick et al., 2017)), pre-
sented in Table 3, show us that there is not enough sta-
tistically evidence to affirm that MS rule outperforms
the GR and LD rules. From Table 2 we can also con-
clude that the Earliest Finish Time (EFT) rule gives us
the worst results, followed by the Earliest Start Time
(EST) rule. This is confirmed by the p-values in Ta-
ble 3, where we can appreciate that these two rules
are always outperformed by the other rules.
If we analyze the results in Table 2 according to
the distribution of the preemption type, we can see
that 4 out of 6 priority rules give better results when
the proportion of non-preemptive activities is high
(Set C). This is corroborated by the results of the t-
test for the multi-pass heuristic in Table 4. In the other
hand, there is not enough statistical evidence to con-
clude about the impact of a high proportion of pre-
emptive and/or partially preemptive activities within
the instances.
We also wanted to know how the heuristic behaves
for bigger instances. We generate 4 new sets (A1, B1,
C1, D1) of 50 instances having similar characteristics
to the 4 first sets (A, B, C, D) except for the number
of activities within the instances (30 activities now),
Table 4: p-values for t-test of average gap multi-pass heuris-
tic according to preemption type.
B C D
A 0.5821 0.0271 0.6269
B - 0.0265 0.3813
C - - 0.0262
A Heuristic Method for the Multi-skill Project Scheduling Problem with Partial Preemption
117
Table 5: Gap for the greedy serial scheme algorithm (larger
instances).
Gap
All A1 B1 C1 D1
(119 ins) (46 ins) (44 ins) (1 ins) (28 ins)
LD 7.15% 6.62% 7.45% 1.33% 7.76%
MS 7.59% 7.18% 7.94% 4.00% 7.81%
EST 8.37% 8.65% 8.07% 12.00% 8.26%
EFT 9.09% 9.06% 8.95% 5.33% 9.48%
GR 7.52% 6.98% 7.87% 4.00% 7.96%
GRD 7.67% 7.19% 7.60% 4.00% 8.68%
Multi-pass 4.98% 4.58% 5.25% 1.33% 5.32%
activities duration (from 5 up to 10 time units) and the
average makespan (from 60 up to 90 time units). We
try again to solve the instances using the MILP model
with CPLEX (configured with default settings). After
a computation time limited to 30 minutes, only 73 out
of 200 instances have been solved to optimality with
an average solving time of 544.39 seconds (standard
deviation of 407.82 seconds).
Using a relaxed version of the MILP model (based
on the preemptive MSPSP), we were able to deter-
mine the optimal solution of 46 more instances and
improve the lower bounds for the remainders. How-
ever, there are still 57 instances for which we could
not find an initial solution (testing other configuration
parameters for primal heuristics or search strategies
within CPLEX, should be done in the future to im-
prove the MILP results). These results confirm the
interest of heuristic methods for solving the MSPSP-
PP in acceptable times; especially for instances with
a high percentage of non-preemptive activities, for
which the MILP model seems to be more difficult to
solve (for 45 instances out of 50 within set C1 we
could not find an initial solution within the time limit).
Table 5 shows the average gap (percentage differ-
ence between the optimal solution and the obtained
value with the heuristic method) for each list and the
multi-pass version of the heuristic for those instances
solved to optimality with MILP methods. Results
show again that the priority rules based on Most Suc-
cessors, Longest Duration and Greatest Rank give the
best results; while Earliest Finish Time rule gives the
worst. In general, the average gap for the heuristic
seems to be statistically the same for small and big
instances.
For the instances for which optimality was not
proved by the MILP methods, we used the best lower
bound as reference for calculating the gap. Results
in Table 6 show that the average gap increases at
the same time as the proportion of non-preemptive
activities within the instances (set C1). This result
should not be seen as a contradiction to our previous
Table 6: Average gap to lower bound for the greedy serial
scheme algorithm (larger instances).
Average gap to lower bound
All A1 B1 C1 D1
(81 ins) (4 ins) (6 ins) (49 ins) (22 ins)
LD 19.62% 9.37% 7.84% 26.45% 9.46%
MS 22.02% 9.07% 11.63% 30.14% 9.12%
EST 23.92% 9.91% 11.20% 32.28% 11.30%
EFT 24.68% 8.65% 9.99% 34.22% 10.36%
GR 22.01% 9.07% 11.63% 30.03% 9.32%
GRD 22.30% 8.52% 8.67% 30.98% 9.17%
Multi-pass 17.25% 6.01% 6.14% 24.10% 7.07%
conclusion from results in Table 2 (the greedy algo-
rithm gives better results for highly non-preemptive
instances), this behavior can be explained by the qual-
ity of the lower bounds: it is harder to find good lower
bounds for highly non-preemptive activities. We must
remember that solving the MILP model we could not
find any initial solution for 45 instances within set C1.
If we analyze only those instances for which a so-
lution was found (24 instances) we have an average
gap of 3.69% for the MILP methods and 6.66% for
the greedy algorithm. Even if the MILP methods give
us better values, they required bigger amount of time
(30 minutes) compared against the time required by
greedy algorithm (less than 1 second).
4.2 Tree-based Local Search Algorithm
The probability of visiting the right-hand branch
(Prob
max
) is the main parameter of the proposed algo-
rithm. It plays an important role in the quality of the
obtained solution and also in the time required to visit
all the search tree. Further research may be necessary
in order to identify the right way to set this parame-
ter having a compromise between quality of solution
and time required to get it (especially for industrial
instances).
In order to test the feasibility of the algorithm we
decided to set this value arbitrarily to 75% for execut-
ing preliminary tests with small instances. We solved
again the sets of instances A, B, C and D using the
tree-based local search algorithm. Table 7 shows the
new values for the gap and the average percentage
of improvement with respect to the greedy algorithm.
As expected, we observe than the priority rules Earli-
est Finish Time (EFT) and Earliest Start Time (EST),
which gave the worst results for the greedy algorithm,
show the bigger average improvement; while the pri-
ority rules Most Successors (MS) and Greatest Rank
(GR), those with the best results for the greedy algo-
rithm, show the lower average improvement. LD, MS
and GR priority rules keep giving the best results for
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
118

Figure 5: Time and gap evolution chart.
average gap.
If we analyze the results for the multi-pass ver-
sion, we observe a reduction of the average gap go-
ing from 7.45% to 5.89%. Again, the algorithm
seems to give better results when the proportion of
non-preemptive activities is high (Set C). There is
not enough statistical evidence to conclude about the
other instances sets.
For small instances (sets A, B, C and D), run-
ning time seems not to be a problem (even when we
use a high value for Prob
max
). However, for bigger
instances (sets A1, B1, C1 and D1), running time
may become prohibitive for high values of Prob
max
.
We wanted to study the behavior of the solving time
and the average gap when we increase the value of
Prob
max
. Using the multi-pass version of the local
search algorithm, we measure average time and gap
for different values of Prob
max
(5%, 10%, 15% and
20%) for those instances solved to optimality; these
values are presented in Figure 5. Results for Set C1
are not presented in Figure 5 since only 1 instance
was solved to optimality. However, for highly non-
preemptive activities solving time remains reasonable
(less than 15 sec) even when Prob
max
goes to 75%.
The curves in Figure 5 show similar behaviors for
highly preemptive (Set A1) and partially preemptive
(Set B1) instances. This was expected, since for these
two types of activities, we may re-evaluate the tech-
nicians allocations for every unit time of the activ-
ity duration (what increases significantly the number
of nodes in the search tree). We observed an ex-
ponential increase on the average solving time when
Prob
max
= 20% for all sets of instances; this while the
average gap presents an exponential decrease. Also
as expected, the average time for solving instances
within Set D1, is lower than for instances within
sets A1 and B1; this is due to the presence of more
non-preemptive activities. If we take the results for
Prob
max
= 15% (the best compromise solving time
and average gap) as reference point, we observe an
important reduction of the general average gap de-
creasing from 4.98% (for the multi-pass version of the
greedy algorithm) to 2.88%.
5 CONCLUSIONS AND FUTURE
RESEARCH
In this article we consider a new variant of the Multi-
Skill Project Scheduling Problem including partial
preemption (MSPSP-PP). The main characteristics of
this variant is the innovative way we handle the re-
lease of resources during preemption periods. Instead
of releasing of resources, as we do in classical pre-
emptive scheduling, we will release only those hav-
ing a smal setup time/cost. The proposed problem can
be easily adapted to other field, specially those where
setup times/costs are important or hard to estimate.
The MSPSP-PP is NP-hard, we then propose a
greedy algorithm based on priority rules and using
a serial schedule generation scheme. To solve the
subproblem of technicians allocation, we proposed to
model it as a Minimum-Cost Maximum-Flow prob-
lem. The proposed algorithm gives us encouraging
results that are improved when we used it as a multi-
pass heuristic, obtaining an average gap of 7.45%.
In order to improve the solution obtained with the
greedy algorithm, we proposed a randomized tree-
based local search algorithm that allows us to reduce
the average gap from 4.98% to 2.88%. Both algo-
rithms seem to give better results when the proportion
of non-preemptive activities is high.
As future work, we must study the way to choose
the right value for the probability of visiting the right-
hand branch in the search tree, in order to have a com-
promise between the solutions quality and the time
required to get them. A different approach for gener-
ating the tree search node is also necessary in order to
A Heuristic Method for the Multi-skill Project Scheduling Problem with Partial Preemption
119

Table 7: Gap for the tree-based local search algorithm.
Gap
All A B C D
Gap Improv. Gap Improv. Gap Improv. Gap Improv.t Gap Improv.
LD 8.86% 2.78% 10.18% 1.73% 8.91% 3.02% 6.66% 4.12% 9.70% 2.23%
MS 9.29% 2.02% 9.46% 2.40% 9.28% 2.59% 8.33% 1.01% 10.08% 2.08%
EST 9.92% 3.33% 9.92% 4.52% 10.71% 2.43% 9.11% 2.52% 10.68% 3.83%
EFT 10.11% 3.77% 10.11% 5.15% 10.53% 2.38% 13.76% 4.12% 10.13% 3.44%
GR 9.46% 2.48% 9.46% 2.40% 9.28% 2.59% 8.18% 2.85% 10.08% 2.08%
GRD 9.47% 3.01% 9.47% 3.81% 9.00% 2.83% 8.06% 3.60% 9.19% 1.81%
Multi-pass 5.89% 1.88% 5.89% 1.99% 6.10% 2.67% 4.14% 0.62% 5.69% 2.24%
improve the solving times.
Experimental tests show that the proposed heuris-
tic is very sensitive to the sequence (priority rule) we
use. We must then identify the structure of the opti-
mal sequences in order to improve our results.
REFERENCES
Ababei, C. (2009). C++ adapted version of the
Edmonds-Karp relabelling MCMF algorithm.
https://github.com/eigenpi/MCMF4. Online; ac-
cessed 01 September 2018.
Ahuja, R. K. (2017). Network Flows: Theory, Algorithms,
and Applications. Pearson Education, 1st edition.
Almeida, B. F., Correia, I., and Saldanha-da Gama, F.
(2016). Priority-based heuristics for the multi-skill re-
source constrained project scheduling problem. Ex-
pert Systems with Applications, 57:91–103.
Artigues, C. (2008). The resource-constrained project
scheduling problem. In Resource-constrained project
scheduling: models, algorithms, extensions and appli-
cations, pages 21–36. John Wiley & Sons.
Ballest
´
ın, F., Valls, V., and Quintanilla, S. (2008).
Pre-emption in resource-constrained project schedul-
ing. European Journal of Operational Research,
189(3):1136–1152.
Ballest
´
ın, F., Valls, V., and Quintanilla, S. (2009). Schedul-
ing projects with limited number of preemptions.
Computers & Operations Research, 36(11):2913–
2925.
Bellenguez-Morineau, O. (2008). Methods to solve multi-
skill project scheduling problem. 4OR, 6(1):85–88.
Correia, I. and Saldanha-da Gama, F. (2015). A modeling
framework for project staffing and scheduling prob-
lems. In Schwindt, C. and Zimmermann, J., editors,
Handbook on Project Management and Scheduling
Vol.1, International Handbooks on Information Sys-
tems, pages 547–564. Springer International Publish-
ing, Cham.
Derrick, B., Toher, D., and White, P. (2017). How to com-
pare the means of two samples that include paired
observations and independent observations: A com-
panion to Derrick, Russ, Toher and White (2017).
Tutorials in Quantitative Methods for Psychology,
13(2):120.
Edmonds, J. and Karp, R. M. (1972). Theoretical improve-
ments in algorithmic efficiency for network flow prob-
lems. Journal of the ACM (JACM), 19(2):248–264.
Harvey, W. D. and Ginsberg, M. L. (1995). Limited dis-
crepancy search. In International Joint Conferences
on Artificial Intelligence, pages 607–615.
N
´
eron, E. (2002). Lower bounds for the multi-skill project
scheduling problem. In Proceedings of the Eighth
International Workshop on Project Management and
Scheduling, Valencia, Spain.
Polo-Mej
´
ıa, O., Anselmet, M.-C., Artigues, C., and Lopez,
P. (2018). Mixed-integer and constraint programming
formulations for a multi-skill project scheduling prob-
lem with partial preemption. In 12th International
Conference on Modelling, Optimization and Simula-
tion (MOSIM 2018), 8 pages, Toulouse, France.
Sourd, F. (2001). Scheduling tasks on unrelated machines:
Large neighborhood improvement procedures. Jour-
nal of Heuristics, 7(6):519–531.
Vanhoucke, M. (2008). Setup times and fast tracking in
resource-constrained project scheduling. Computers
& Industrial Engineering, 54(4):1062–1070.
Voß, S., Fink, A., and Duin, C. (2005). Looking Ahead with
the Pilot Method. Annals of Operations Research,
136(1):285–302.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
120
