Modeling of Goal-oriented Human Motion Evolution using Hidden

Markov Models

Eman Ahmed

1,2

, Reda A El-Khoribi

, Alexandre Muzy

, Gilles Bernot

and Gamal Darwish

Faculty of Computers and Information, Cairo University, Giza, Egypt

Laboratoire d’ Informatique, Signaux et Systèmes de Sophia-Antipolis (I3S) UNS CNRS, Université Côte d’Azur, France

{eman.ahmed.sayed.ahmed, gilles.bernot}@i3s.unice.fr

Keywords:

Fetus Human, Movement, Goal, Sensory-motor Loop.

Abstract:

Humans have the ability to make many complex movements at the same time with full coordination through

the whole body. This requires control of all body muscles. The body muscles are controlled by the Central

Nervous System (CNS) which consists of the brain and the spinal cord through a group of neurons called the

motor neurons. Each muscle is controlled by lower-level motor neurons called the motor neurons. A motor

neuron controls a group of muscle ﬁbers of the muscle such that when it is activated, this group contracts.

Hence, a muscle movement occurs. Currently, many questions remain unanswered: How this system evolves

to generate the complex movements? How to control the muscles to achieve a certain goal such as reaching

a target position? and how a human becomes able to deﬁne goals in the ﬁrst place? It is believed that the

development of motion begins prenatally with spontaneous fetal movements. In this paper, we are trying to

answer these questions by proposing a theoretical model of human learning of motion starting from being a

fetus. Simulation is provided using computational intelligence and statistical methods.

1 INTRODUCTION

Human motion evolve during different stages starting

from being a fetus till being an infant and then be-

ing an adult (Adolph, 2008). Most of the literature

is focused on modeling the adult sensory-motor sys-

tem such as how the human arm is able to reach a

certain target and grab an object. Modeling of motor

control using forward and inverse models have been

studied extensively in the previous year (D.M.Wolpert

and M.Kawatob, 1998).

However, working on adult models pre-assumes

the adult being able to identify a goal and focus on

how he will be able to achieve it. The question of how

can a human identify a goal in the ﬁrst place is not

answered yet. To answer this, we believe we should

go back to the fetus stage and model the evolution of

the human motion.

The fetal human possesses an active central ner-

vous system from at least the eighth week of develop-

ment (Flower, 1985). Until then, his nervous system

grows gradually. With his rapidly maturing nervous

system, his nerves are connecting his brain to the rest

of his body traveling from the the brainstem down to

the spine ﬁnally extending to his torso and limbs. Us-

ing his developing muscles and reﬂexes, the fetus is

able to move his limbs. The soft cartilage hardens

into bones starting with arms and legs. The sensory

system develops such that the brain dedicates special

areas for smell, taste, hearing, vision and touch. At

this stage, he may be able to hear mother’s heart beat

and voice, sucking his thumb. He starts feeling move-

ments and his ﬂexing arms and legs are soft and be-

coming stronger. After that, he may make movements

in response to presses on the mother’s belly as ex-

plained in (Viola Marx, 2015). He can feel his own

face and anything within his reach, he will be experi-

menting and reﬁning his sense of touch and grasp by

touching the womb surrounding him and grasping his

cord. Until this stage, eyelids may open as a reﬂex but

he cannot see yet.

Accordingly, the fetus is able to make all these ac-

tions without his vision, he depends on other senses

only, mainly the senses of touch and hearing.

The question now is how he becomes able to ex-

plore his body and his surrounding? how he is able

to control his hand to touch and grasp? This brings

us back to how a movement occurs through the brain

and the muscular body.

For a movement to occur, this involves a muscle

Ahmed, E., El-Khoribi, R., Muzy, A., Bernot, G. and Darwish, G.

Modeling of Goal-oriented Human Motion Evolution using Hidden Markov Models.

DOI: 10.5220/0007391906050612

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 605-612

ISBN: 978-989-758-351-3

605

contraction which is achieved by sending a command

signal from the brain to the motor neurons controlling

this muscle ﬁbers to be activated causing contraction

of the muscle. In response, a group of sensory neu-

rons inform the brain with the changes that have oc-

curred. This is done through a sensory-motor loop.

Whether the sensory neurons feedback are sufﬁcient

to learn goals or not is another question that arises.

In this paper, we are trying to answer all the men-

tioned questions: how can a human identify a goal?

how he becomes able to explore his body and his sur-

rounding?. In other words, we are interested in un-

derstanding how a goal-oriented movement is devel-

oped and we believe this starts from the fetus stage by

learning how to deﬁne different tasks and control his

muscles to achieve them. With the help of a computa-

tional model, we provide a simulation at a high level

of abstraction of how the movements may evolve dur-

ing the fetus stage. The model is built upon the de-

velopment of one muscle moving upward in a vertical

direction.

In the next section, we provide a simpliﬁed bio-

logical explanation of how muscles work for achiev-

ing a movement. Section 3 gives a brief explanation

on Hidden Markov Models. In section 4, a theoretical

framework is demonstrated. The implementation of

the framework is illustrated in section 5 using cluster-

ing and a hidden markov model. Simulation results

are presented in section 6. The paper is concluded in

section 7.

2 THE SENSORY-MOTOR

SYSTEM

Muscles exist in pairs called antagonist muscles. One

muscle performing an action is called the agonist and

the other muscle performs the opposite action and is

referred to as antagonist. Each antagonist muscle has

a set of sensory neurons called proprioceptors that

signal sensory information to the brain. The brain

uses the sensory information to gain his awareness of

the positions of the different limbs among the body

(Heuer and Keele, 1996).

The brain can control any muscle contraction by

activating the corresponding motor neurons. The pair

of antagonist muscles are connected through tendons

attaching them to the bones. One antagonist muscle

contraction causes the extension of the other antago-

nist muscle in the pair.

To make a movement, the contraction of one mus-

cle is required. A command signal is sent to activate

the motor neurons controlling the muscle ﬁbers of this

muscle causing their contraction. Reference (Perru-

choud et al., 2014) provides an abstract architecture

for the sensory-motor loop with biological illustra-

tion.

There exist another class of receptors providing

information about mechanical forces arising from the

body itself, the musculoskeletal system in particular.

These are called proprioceptors, roughly meaning “re-

ceptors for self.” The purpose of proprioceptors is pri-

marily to give detailed and continuous information

about the position of the limbs and other body parts

in space. Among the proprioceptors is the Golgi Ten-

don Organ that signals the tension of the tendon and

muscle spindle which provides the brain with muscle

length information (Purves D and et al., 2001).

Muscle contraction causes an increase in tension

at the tendon and decrease in the muscle length. Con-

sequently, it causes increase in the length of its antag-

onist muscle. The tension at the tendon is signaled

by a proprioceptor referred to as Golgi Tendon Organ

and it is activated as soon as there is tension. Tension

is relaxed due to reﬂexes unless contraction occurs.

The muscle spindle activates when the muscle

is stretched indicating the rate of change of muscle

length and signals the new length after the stretch is

ﬁnished (Byrne and Dafny, 1997). Unfortunately, the

proprioceptions are usually noisy and the brain is usu-

ally unable to perceive the precise proprioceptive val-

ues. However, the brain learns through the imperfect

perceptions (Bays PM, 2007)(Prinz and Bridgeman,

1995).

3 HIDDEN MARKOV MODEL

(HMM)

One of our main hypotheses is that humans learn

from the most frequent actions at all stages. HMM

is suitable for our problem in the sense that our brain

learns through sequences of actions generated over

time. Since the sensory neurons produce feedbacks

to the brain in response to commands, the senses are

observed. On the other hand, the commands are hid-

den as there are no sensory neurons that can describe

the issued commands. Repetition of an action makes

it a habit. Following the same concept, we hypoth-

esize that the brain learns motion generation through

the most frequently used commands.

An HMM model λ = (Q, A, O, B, π), is character-

ized by the following components:

• Q = q

, q

, ..., q

a hidden sequence of T states,

each one is drawn from a set of states Z =

, z

, ..., z

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

606

• A =







·· · a







a transition proba-

bility matrix A, each a

i j

representing the probabil-

ity of moving from state i to state j, s.t.

∑

j=1

i j

1∀i.

• O = o

, o

, ..., o

a sequence of T observations,

each one is drawn from a set of observations X =

, x

, ..., x

• B = b

) a sequence of observation likelihoods,

called emission probabilities, each representing

the probability of an observation o

being gener-

ated from a state i.

• π is the initial probabilities of all the states.

Generally, HMM is used to solve one of the following

problems:

1. Problem 1 (Likelihood): Given an HMM λ =

(π, A, B) and an observation sequence O, deter-

mine the likelihood P(O|λ).

2. Problem 2 (Decoding): Given an observation se-

quence O and an HMM λ = (π, A, B), discover the

best hidden state sequence Q. We will use the

Viterbi algorithm for solving this problem.

3. Problem 3 (Learning): Given an observation se-

quence O and the set of states in the HMM Q,

learn the HMM parameters A and B. We will

use Baum-Walsh Expectation Maximization algo-

rithm for this problem.

More details about HMM can be found in (L, 1989).

4 THEORETICAL FRAMEWORK

4.1 Abstractions

Two abstractions have been used:

1. The pair of antagonist muscle is abstracted to be

one muscle.

2. When a tension is generated by one muscle, the

muscle spindle of the antagonist will be activated

due to its stretching. In our abstract model, an

increase in tension of one muscle will cause the

increase in length of the antagonist muscle by the

same amount. We will abstract both propriocep-

tors and treat them as being proprioceptors of one

muscle due to the dependency relation between

the length and the tension.

According to the above abstractions, our goal of

reaching a target is reduced to getting a certain muscle

length which is a function of muscle tension. Hence,

our problem becomes a fetus who learns how to reach

different tension levels of one muscle. We are go-

ing to use the term tension and proprioception inter-

changeably in the rest of the paper.

4.2 The Proposed Framework

The framework consists of three main blocks:

1. The Sensory-Motor Map Memory

It is a memory recording all the commands that

are issued and the corresponding sensory feed-

backs referred to as proprioceptors.

2. The Cognitive Map

In literature, the cognitive map is deﬁned as a

person’s spatial memory that store knowledge of

the world and its events and processes (Breed and

Moore, 2012)(Fortin, 2008). We see that moving

from one position to another can be seen as a task

in a broader sense. Hence, we will use it to repre-

sent the cognition ability of the fetus of his body

in the ﬁrst place. From our point of view, the cog-

nitive map comprises three main units:

(a) Tasks Perception

It is processing the input data from the sensory-

motor map and getting perceptions. Tasks are

then deﬁned out of these perceptions.

(b) Tasks Learning

Each perceived task is to be learned in this unit

using an HMM model. EM algorithm is re-

sponsible for getting the parameters that repre-

sent this task. The task parameters are saved in

the cognitive memory.

After learning a task, the fetus is able to per-

form it whenever he likes. Initially, the task

may not be learned well so the fetus will try

to enhance his ability of doing it. The measure

of performance will be measured in this unit.

3. The Internal Model

When a fetus intends to accomplish a task, he

will need to issue the corresponding command se-

quence. He will exploit the learned task param-

eters and apply HMM decoding problem using

the Viterbi algorithm to estimate the command se-

quence. The internal model is responsible for ap-

plying the decoding (inverse model).

Figure 1 depicts the proposed system framework.

Our hypothesis is that the fetus passes through

three phases to learn:

1. Phase I: Build the training set of commands and

perceptions. We assume that the fetus makes

Modeling of Goal-oriented Human Motion Evolution using Hidden Markov Models

607

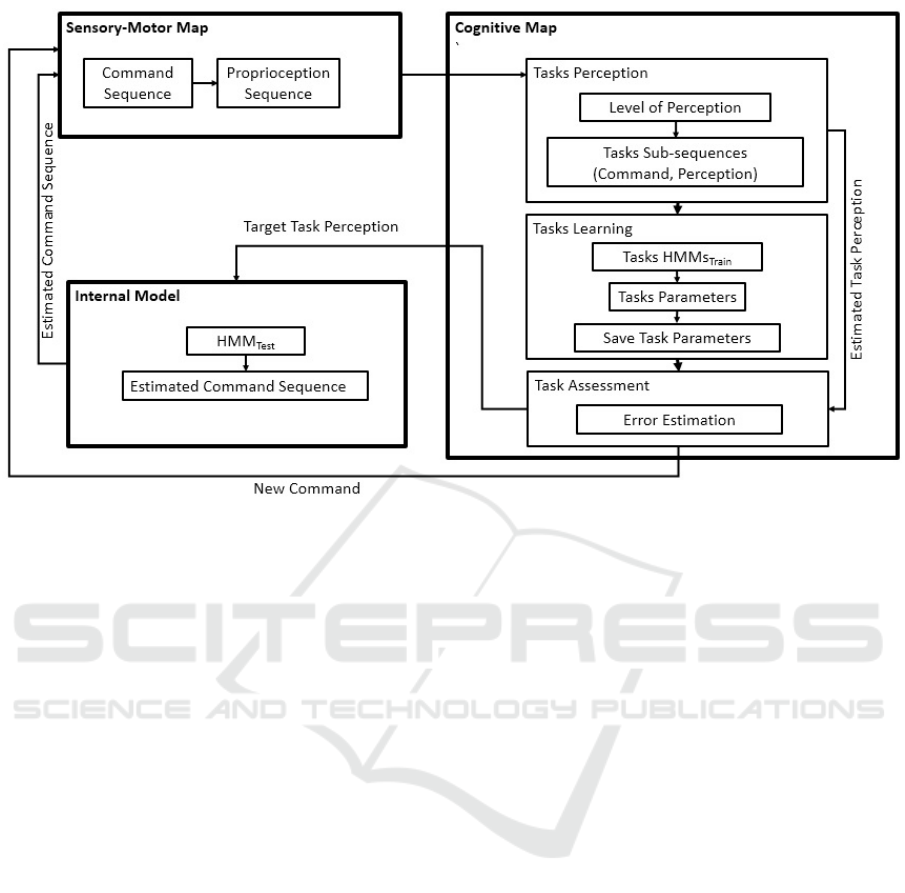
Figure 1: The proposed system framework. The sensory-motor map is responsible for building the training set of commands

and perceptions, the cognitive map trains his cognition abilities using the recorded training set and the internal model helps

the cognitive map to learn how to retrieve the commands to make intended movements.

movements that gets all the possible tensions in

this phase.

• Generate random motor command that results

in muscle contractions.

• Proprioception (tendon tension) is produced.

• Recording in sensory-motor map memory the

association “this command sequence = these

proprioceptions”.

2. Phase II: Train his cognition abilities using the

recorded training set.

• Learn the relationship between the recorded

commands and the recorded proprioceptions

according to the level of perception of the fe-

tus.

• Get parameters that represent this relationship.

• Record the parameters in memory.

3. Phase III: Try retrieving the commands to make

intended movements.

• Given a target perception, guess the estimated

target command according to the parameters

and issue it.

• Get the corresponding estimated perception.

• Compare the target perception to the estimated

perception.

• A new command is issued. It will increase the

training sequence and will result in better esti-

mation and may help in exploring greater pro-

prioception values.

It is important to notice that one perception value

can be achieved by different command sequences.

Our model is based on two hypotheses: the ﬁrst hy-

pothesis is that the fetus will usually apply the com-

mand sequence that is most probable and the second

hypothesis is that despite the noise, the original rela-

tionship between the commands and the accurate per-

ceptions will be approximated.

We are going to use HMM for modeling the re-

lationship between the command sequence and per-

ceptions for one muscle such that phase II represents

learning the relation between O and Q and get the

mapping parameters as in HMM problem 3. Then,

after the brain develops by learning and obtaining

its mapping parameters, it starts gaining the ability

of decoding (HMM problem 2) by choosing a target

observation sequence and discover which commands

should be issued to obtain it.

The details of implementation is presented in the

next section.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

608

5 IMPLEMENTATION

5.1 The Command Sequence

Motor neurons ﬁre when they receive a command so

that the corresponding muscle ﬁbers contract. Hence,

there will be a spike coming out from the ﬁring neuron

when there is a command. Accordingly, the command

sequence represents the hidden state sequence Q such

that any command q

at time t represents whether

there is a spike (1) or not (0). In other words, a com-

mand state sequence is represented by a binary se-

quence such that 1 implies contraction and 0 implies

no contraction.

Initially, the time between consecutive command

signals is large and it decreases gradually as the fetus

gets older as he gains more energy and becomes able

to get stronger contraction.

The command state sequence Q is generated from

a Bernoulli distribution given by:

= p

(1 − p)

1−t

(1)

such that q

= 1 refers to issuing a command with

probability p and q

= 0 implies the absence of com-

mand with probability (1 − p).

5.2 The Proprioception

It dictates the sensory values are achieved using a

given command sequence. As explained above, the

proprioception represents the tension in our problem.

When a command is given to a muscle, a force is

generated causing increase in its ﬁbers tension. Mus-

cles differ in terms of the number of ﬁbers and size

such that increasing them means the ability to get

more force. Each muscle is represented by a Gaus-

sian function with large variance for large muscles

and small variance for small muscles.

Muscle = exp

−

(x − mean)

(2)

such that x represents the ﬁber sizes.

The proprioception is given by a convolution func-

tion between the muscle and the command sequence:

tension = MuscleΘQ (3)

such that Θ denotes the convolution operator and

Q is the state sequence.

Figure 2: Proprioception Values for each Sequence.

5.3 The Perceptions

Initially, the fetus is not able to distinguish precise

proprioceptive (tension) values. Accordingly, cluster-

ing of similar proprioception values is performed us-

ing K-Means clustering. The clustering is applied to

the proptioceptive values with small number of levels

at ﬁrst, then, the number of levels increases gradually

as the fetus gains more abilities for distinguishing dif-

ferent tension levels. The perceptions are the cluster

centers.

The perceptions represent the sequence of obser-

vations O such that o

∈ X and X = T where T is a

vector of the clustered tendon tensions.

By recording all this information, the fetus brain

builds his training dataset. After that, it starts to learn

the relation between O and Q and gets the mapping

parameters as in problem 3.

The fetus brain then learns different tasks where

each task represents moving to a new proprioceptive

value from the current proprioceptive value.

5.4 The Task

It is a notion that describes what a muscle can do in

terms of changing its tension from one perceived val-

ues to another. All tasks are deﬁned from the percep-

tions of the training set. The perceptions are divided

into a combination of each two pairs of perceptive val-

ues in increasing order and all subsequences of mov-

ing between these pairs are collected to be the training

set of this task.

A Hidden Markov Model is built for each task and

is trained using these sequences using Baum Walsh

Expectation Maximization algorithm to get the tran-

sition and emission matrices from the collected se-

quences.

After the brain develops by learning the tasks and

obtaining its mapping parameters, its starts gaining

the ability of decoding (problem 2) by choosing a

target observation sequence and discover which com-

mands should be issued to obtain it.

Given a target perception sequence, the most prob-

able command state sequence is obtained using the

Viterbi algorithm.

Modeling of Goal-oriented Human Motion Evolution using Hidden Markov Models

609

(a) Two Clusters

(b) Four Clusters

Figure 3: The estimated sequences versus the original sequences of a HMM of 100 observation sequence for different number

of clusters.

6 SIMULATION

Results show that the fetus is able to approximate the

correct proprioceptive values over time by retrieving

the required command sequence and by improving his

perceptions to be able to identify more proprioceptive

values.

Our simulation is based upon three stages, each

stage is of duration 50 time units. Within each stage,

we simulate the sequences that can be generated by

the fetus according to his energy and the level of per-

ception that should be increasing with time. We hy-

pothesize that the energy is initially low and increase

with time from the fact that the fetus can not do strong

activities such as kicking in his early stage.

We apply our simulation on one muscle due to the

fact that the abilities of the fetus changes over time,

we built our simulation on a sequence that is grow-

ing with time. First, the simulation has a command

sequence of 50 observations generated by Equation 1

with probability of ﬁring equals 0.2 which is a small

probability that mimic the low energy the fetus has at

his early age. Despite that the resulted proprioceptive

values are very low and the cognition will not be able

to recognize any task to be learned, these are recorded

in memory.

Next, another 50 observations are added with

probability of ﬁring equals to 0.8 where there is an

increase in energy that makes the fetus more capa-

ble of doing stronger actions and hence, issues more

commands. The corresponding proprioceptive values

were calculated as in Equation 3.

Initially, the fetus can either sense a tension or not.

This is simulated by clustering the proprioception into

two large levels of perception as illustrated in Figure

3a. In this case, the fetus recognizes only one task

moving between zero and a perceived tension value.

We are only interested in learning moving from one

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

610

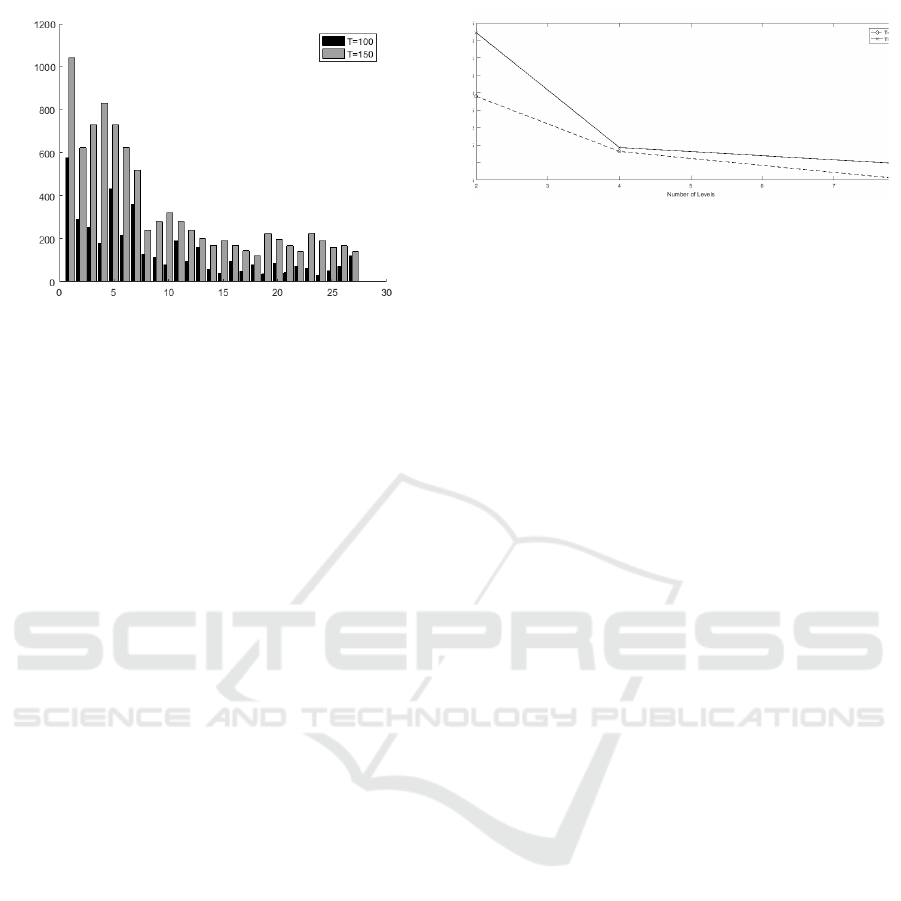
Figure 4: Number of sequences per task for 100 observa-

tions and 150 observations.

tension to another higher tension which involves issu-

ing one or more commands. This is because moving

from one tension to another lower tension is a triv-

ial task as no command will be issued and it can be

learned easily.

Second, fetus capability becomes stronger and he

is able to issue more commands and reach greater ten-

sion values. Figure 2 shows the range of tension val-

ues that exist in sequences of duration 100 and 150,

respectively.

Also, the fetus capabilities evolve by being able

to distinguish different tension values. We simulated

this by repeating the experiment with smaller step to

get 4-clusters as depicted in Figure 3b. Hence, there

are six tasks the fetus should learn.

The experiment is also repeated for 8-clusters.

The fetus will continue to experiment the tasks

and more 50 observations with probability 0.9 are

added which enhances the learning of the previous

tasks.

Increasing the sequence length means increasing

the proprioceptive values that are obtained. Accord-

ingly, the perceptions will approximate more propri-

oceptive values. This make it necessary for the fetus

to increase his level of perception to cover all the new

values.

Figure 4 depicts the number of sequences avail-

able for each task during 100 observations and 150

observations.

Results show that the fetus is able to approximate

the correct proprioceptive values over time by retriev-

ing the required command sequence and by improv-

ing his perceptions to be able to identify more propri-

oceptive values as shown in Figure 5.

Figure 5: Mean Squared Error of all tasks for each quan-

tization level for both sequences of T=100 and T=150 for

unnoisy proprioceptions.

7 CONCLUSION

We have tackled the problem of understanding how

human movements evolve since the age of the fetus.

We proposed the ﬁrst model that describes how a fe-

tus learns to control one muscle to get an intended

perception by giving it the essential command. The

model passes through random stage where all com-

mands issued are random and demonstrates how this

converges to learning the appropriate relationship be-

tween commands and perceptions. We have proposed

our model of applying k-means clustering to simu-

late perception development over time and we have

shed light on the idea of how the human builds his

own abilities of identifying goals which represented

here reaching one perceived tension value from an-

other. The simulation was done using Hidden Markov

Model since its basics matches with our hypothesis

that we learn from the most frequent actions which

are represented as sequences. The model presented

in this paper is a simple abstract model to illustrate

the whole process. Further improvements are being

done on this model to include more details. This work

would beneﬁt biologists to gain better understanding

of the fetus stage and how the human movements de-

velop, further, it may help them discover some early

impairments in case of monitoring the fetus actions

and responses over time. Moreover, it can be used

in the robotics and humanoids ﬁeld to explore more

varieties.

ACKNOWLEDGEMENTS

The authors thank the NeuroMod insti-

tute (http://univ-cotedazur.fr/en/idex/projet-

structurant/cauca) in Nice-Sophia Antipolis that

funded this research.

Modeling of Goal-oriented Human Motion Evolution using Hidden Markov Models

611

REFERENCES

Adolph, K. (2008). Motor and Physical Development: Lo-

comotion. Encyclopedia of Infant and Early Child-

hood Development.

Bays PM, W. D. (2007). Computational principles of sen-

sorimotor control that minimize uncertainty and vari-

ability. The Journal of Physiology., 578(Pt 2):387–

396.

Breed, M. D. and Moore, J. (2012). Chapter 8 - move-

ment: Search, navigation, migration, and dispersal. In

Breed, M. D. and Moore, J., editors, Animal Behavior,

pages 219 – 252. Academic Press, San Diego.

Byrne, J. H. and Dafny, N. e. (1997). Neuroscience On-

line: An Electronic Textbook for the Neurosciences

http://nba.uth.tmc.edu/neuroscience/, chapter Chapter

1: Motor Units and Muscle Receptors, page Sec-

tion 3. Department of Neurobiology and Anatomy,

The University of Texas Medical School at Houston

(UTHealth).

D.M.Wolpert and M.Kawatob (1998). Multiple paired for-

ward and inverse models for motor control. El Sevier,

Neural Networks, 11:1317–1329.

Flower, M. J. (1985). Neuromaturation of the human fetus.

The Journal of Medicine and Philosophy, 10(3):237–

251.

Fortin, N. (2008). Navigation and episodic-like memory

in mammals. In Byrne, J. H., editor, Learning and

Memory: A Comprehensive Reference, pages 385 –

417. Academic Press, Oxford.

Heuer, H. and Keele, S. W. (1996). Handbook of Perception

and Action Volume 2: Motor skills, volume 2. ACA-

DEMIC PRESS.

L, R., editor (1989). A Tutorial on Hidden Markov Mod-

els and Selected Applications in Speech Recognition

Proceedings of the IEEE, volume 77 of 2.

Perruchoud, D., Murray, M. M., Lefebvre, J., and Ionta, S.

(2014). Focal dystonia and the sensory-motor inte-

grative loop for enacting (smile). Frontiers in Human

Neuroscience, 8:458.

Prinz, W. and Bridgeman, B. (1995). Handbook of Per-

ception and Action Volume 1: Perception, volume 1.

ACADEMIC PRESS.

Purves D, Augustine GJ, F. D. and et al., e., editors

(2001). Mechanoreceptors Specialized for Proprio-

ception. Neuroscience, Sunderland (MA): Sinauer

Associates, 2 edition.

Viola Marx, E. N. (2015). Fetal behavioural responses to

maternal voice and touch.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

612