
Periodic Vehicle Routing Problem in a Health Unit
F. Alves
1,2
, F. Alvelos
3
, A. M. A. C. Rocha
3
, Ana I. Pereira
1,2
and Paulo Leit
˜
ao
1
1
Research Centre in Digitalization and Intelligent Robotics (CeDRI), Instituto Polit
´
ecnico de Braganc¸a,
Campus de Santa Apol
´
onia, 5300-253 Braganc¸a, Portugal
2
Algoritmi R&D Centre, University of Minho, Braga, Portugal
3
Department of Production and Systems, Algoritmi Research Centre, University of Minho, Braga, Portugal
Keywords:
Home Health Care, Operations Research, Periodic Vehicle Routing.
Abstract:
In logistics of home health care services in the Health Units, the managers and nurses need to carry out the
schedule and the vehicles routes for the provision of care at the patients’ homes. Currently, in Portugal, these
services are increasingly used but the problem is still, usually, solved manually and without computational
resources. The increased demand for home health care due to the boost of the elderly people number entails
a high associated cost which, sometimes, does not guarantee the quality of the service. In this sense, the
periodic vehicle routing problem is a generalization of the classical vehicle routing problem in which routes
are determined for a time horizon of several days. In this work, it is provided a periodic vehicle routing
problem applied in the Health Unit in Braganc¸a. An integer linear programming formulation for the real
database, allowed to solve the problem in an efficient and optimized way using the CPLEX
R
software.
1 INTRODUCTION
Home Health Care (HHC) is a growing medical ser-
vice in many countries (Benzarti et al., 2013). One of
the tasks of the HHC involves the management deci-
sions, that is, it is necessary to create the planning and
the routing of vehicles or nurses/doctors in the domi-
ciliary services. In Portugal, there is a large number
of elderly people who need support in their homes,
therefore the operational management problems re-
lated to home care visits are very important.
The HHC service in a health care unit has a fleet
of vehicles used by nurses/doctors to travel to the pa-
tients locations. A periodic aspect is also involved,
since the jobs need to be performed, repeatedly, du-
ring a specific visits schedule. Usually, the HHC
management is solved manually by a senior nurse or
manager, who often spends a huge amount of time
to create next week’s schedule (Fikar and Hirsch,
2017). However, the scheduling and routing problems
in this area are complex procedures (Nickel et al.,
2012) due to the mathematical modeling complex-
ity and, more importantly, the absence of computa-
tional resources in the Health Unit. From a mathe-
matical point of view, this problem has special inter-
est, because it is an NP-hard problem, such as peri-
odic vehicle routing problem (PVRP). In this sense,
the PVRP is a generalization of the classical vehicle
routing problem (VRP) where routes are determined
for a planning horizon of multiple periods with some
customers demanding multiple visits (Angelelli and
Speranza, 2002; Beltrami and Bodin, 1974; Cordeau
et al., 1997). This approach is different from route
planning, in the sense that route planning performs
the scheduling for one day and this approach per-
forms for a certain period of time (Campbell and Wil-
son, 2014). Many real-world applications in trans-
portation systems require finding, for a fleet of ve-
hicles, a set of minimum cost routes that satisfy or-
ders or services requested by customers/patients, over
a given planning horizon (e.g. one week). This prob-
lem is very important in real-world applications such
as the distribution for bakery companies (Pacheco
et al., 2012) and also in blood product distribution
(Hemmelmayr et al., 2009), among other services.
Some authors address and describe the HHC prob-
lem through a hybridization of constraint program-
ming and meta-heuristics including simulated anneal-
ing and tabu search (Bertels and Fahle, 2006) or ge-
netic algorithm (Alves et al., 2018). Other approaches
in the HHC problem can be found in Trautsamwieser
et al. (Trautsamwieser et al., 2011) and Nickel et
al. (Nickel et al., 2012). Thus and although there
is already an extensive operational research in HHC,
many focus only on the daily scheduling of the pro-
blem of home visits. However, in these types of health
384
Alves, F., Alvelos, F., Rocha, A., Pereira, A. and Leitão, P.
Periodic Vehicle Routing Problem in a Health Unit.
DOI: 10.5220/0007392803840389
In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 384-389
ISBN: 978-989-758-352-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
services, the scheduling and routing may be periodic
in order to group periods of home visits and to respect
regularities imposed by patients (becoming a PVRP).
Typically, the PVRP has a time horizon of T days, and
there is a demand and regularity of delivery for each
client or patient indicating how many times within the
period of T days the customer should be visited. The
solution to the PVRP is to find the T sets of routes that
together satisfy the constraints of the requested quan-
tity and regularity and also minimize travel distances.
The applicability and versatility of the problem
has led to extensive research addressing both new
applications and solution methods. It has become a
topic with extensive studies in operational research
with extension in diverse services. However, only
limited research has been conducted into the HHC
problem.
The paper is organized as follows: the next sec-
tion, briefly reviews the main definitions and the pro-
blem approach. Section 3 presents the integer linear
programming model for the PVRP. The case study,
based on real data from a Braganc¸a Health Unit, is de-
scribed in Section 4. In Section 5 the results are ana-
lyzed and discussed. Finally, some conclusions and
future work are drawn in Section 6.
2 PVRP DEFINITION
The problem addressed in this article is related to the
schedule and routes of home care visits outside the
Health Unit of Braganc¸a in a certain time horizon.
The home care service can be provided by nursing
teams of a Health Unit, which involves the scheduling
of nurses and the definition of transportation routes
to the patients’ homes. Currently, home visits are
planned manually and without computational support,
which can lead to not obtaining the optimal solution,
especially when certain constraints must be met (dis-
tances and costs involved, time windows, among o-
thers). Thus, it is necessary to develop approaches
that are able to overcome the difficulties that may o-
ccur in these services, such as the accumulation of
delays on routes, the definition of routes that are too
long, the planning without feasible options for repla-
cing nurses, and the difficulties in managing periodic
visits.
Therefore, the first approach is to define the ge-
neral characteristics of the problem, such as the num-
ber and characterization of health professionals, the
number of available vehicles (m), the number of pa-
tients (n) and treatments they need, locations that can
be traveled and their distances, among others. These
data allow us to formulate and model the problem, in
an attempt to minimize the time spent on visits, re-
duce costs and provide support for decision making.
In this paper, an approach for the optimization of
the PVRP, which deals with home care visits in or-
der to perform treatments for patients belonging to a
Health Unit is presented. For this problem the number
of vehicles involved in the home care and the patients
requesting this type of health services is considered.
The problem in establishing periodic routes pro-
duces a schedule within a time horizon of T days,
where each patient i, in addition to the number of
visits, may have a minimum and/or maximum time
period between successive visits, e
i
, i.e. the num-
ber of visits combined with the time period, leads to
the set of patterns p
i
that corresponds to the possi-
ble patterns of visits in the time horizon T . For ex-
ample, if the planning is executed for a time horizon
of 5 days (T = 5), with a time period between visits
of at least two days (e
i
≥ 2), the set of patterns will
be p
i
=
{{
1, 4
}
,
{
1, 5
}
,
{
2, 5
}}
. This corresponds to
visiting the patient twice during the 5 days of the pla-
nning period and should be done on days 1 and 4, or
on days 1 and 5 or alternatively on days 2 and 5, and
no other pattern of visits is possible. The problem is to
simultaneously select the pattern of each patient and
establish the routes for each day of the time horizon.
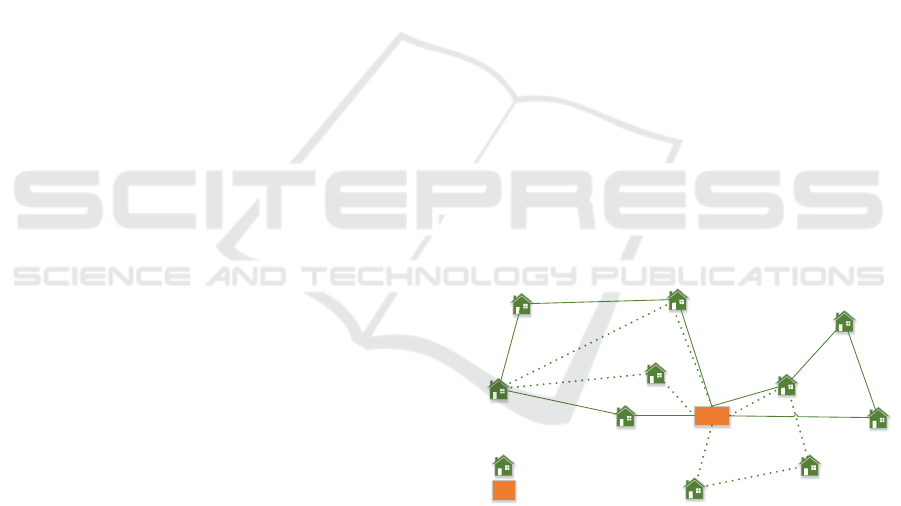
The Figure 1 shows an example of PVRP in which
routes 1 and 2 will have to occur at different times
(because they have points in common).
Depot - Health Unit
Patients
route 1
route 2
route 3
route 4
Figure 1: Illustration of the PVRP.
Similarly, routes 3 and 4 will also have to occur in
different periods. In the PVRP, the cost of visiting
patients is independent of the vehicles that carry it,
not considering restrictions that include incompati-
bilities between vehicles and patients. The matrix
cost = (c
i j
), with rank n, reflects the time spent on
the route between patient i and patient j.
The PVRP consists of establishing r routes of
lower cost in order to satisfy the time horizon and cer-
tain assumptions, such that:
• Each patient belongs to exactly one route.
Periodic Vehicle Routing Problem in a Health Unit
385

• Each route starts and ends at the depot (Health
Unit of Braganc¸a)
3 FORMULATION OF THE
INTEGER LINEAR
PROGRAMMING MODEL
The PVRP can be considered as an integer linear opti-
mization problem where it is not only established the
scheduling of patients visits, but also the design of
the routes for the different days of the time horizon
in order to minimize the costs associated with all the
routes of the time period under study. Consider the
following input:
• L = {1, . . . , T } is the set of days in the planning
horizon;
• N = {1, . . . , n} is the set of patients;
• The index of a route starting or ending at the depot
has the value {0};
• M = {1, . . . , m} is the set of vehicles;
• p
i
is the set of patterns of patient i;
• u
kl
i
is an integer corresponding to the place in the
sequence of visits of vehicle k on day l for the
patient i;
• a
sl
i
is a variable to represent the s pattern that in-
cludes the patient i on day l.
The optimization problem is to find the optimal
values for the binary decision variables such as x
kl
i j
and y
s
i
. Thus, the formulation of PVRP is defined as
follows, where the binary variables take the form:
y
s
i
=
1, if patient i is visited according to
the s pattern belonging to p
i
;
0, otherwise.
x
kl
i j
=
1, if the vehicle k visits patient j
immediately after patient i on day l;
0, otherwise.
The integer programming model is given by:
minimize
n
∑
i=0
n
∑
j=0
c
i j
m
∑
k=1
t
∑
l=1
x
kl
i j
!
(1)
subject to:
∑
s∈p
i
y
s
i
= 1, ∀i ∈ N (2)
n
∑
j=0
m
∑
k=1
x
kl
i j
−
∑
s∈p
i
a
sl
i
y
s
i
= 0, ∀i ∈ N; ∀l ∈ L; i 6= j (3)
n
∑
j=0
x
kl
ji
−
n
∑
j=0
x
kl
i j
= 0,
∀i ∈ N;∀k ∈ M;∀l ∈ L; i 6= j
(4)
n
∑
j=1
x
kl
0 j
≤ 1, ∀k ∈ M; ∀l ∈ L (5)
u
kl
j
≥ u
kl
i
−C(1 − x
kl
i j
) + 1,
∀i, j ∈ N; ∀k ∈ M;∀l ∈ L; i 6= j
(6)
x
kl
i j
∈
{
0, 1
}
, ∀i, j ∈ N; ∀k ∈ M; ∀l ∈ L (7)
y
s
i
∈
{
0, 1
}
, ∀i ∈ N;∀s ∈ p
i
(8)
The objective function (1) represents the minimiza-
tion of total cost, in this case the distance.
Constraints (2) ensure that each client will be
assigned to one of the admissible visit patterns,
while constraints (3) ensure that each client is visited
exactly on the days of the pattern that is assigned. In
turn, constraints (4) guarantee continuity of the route,
i.e, a vehicle entering a vertex will have to leave it.
Constraints (5) ensure that the number of available ve-
hicles is not exceeded. Finally, the sub-circuit elimi-
nation restrictions can be expressed by constraints (6).
In the presented formulation, the cost of visiting the
patients is independent of the vehicles that do it, not
considering restrictions that include incompatibilities
between vehicles and patients. Thus, in the follow-
ing section will be presented the real case study based
on the Health Unit in Braganc¸a, where the proposed
formulation will be applied.
4 CASE STUDY
In this section a real case study of a Braganc¸a Health
Unit for a time horizon of T = 5 days (one week of
home visits) is presented. In that same week, the
Braganc¸a Health Unit has five vehicles available for
home care visits (m = 5), in which they visit fifteen
patients (n = 15) with the need for treatments, where
they are dispersed by their locations. Table 1 summa-
rizes the data for the problem in question.
Table 1: Problem Data Information.
Vehicles Patients Locations Time Horizon
5 15 15 5 days
According to the problem database, there are 5 ve-
hicles available for home visits at the Health Unit of
Braganc¸a, which are homogeneous in terms of capa-
cities and/or visits to patients. The number of patients
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
386

Table 2: Distances between patient locations.
HU 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
HU 0,0 15,2 18,0 22,4 25,0 20,6 11,2 21,2 26,2 32,0 25,5 33,5 15,0 11,2 32,0 30,4
1 15,2 0,0 32,6 14,6 32,2 32,2 24,8 21,0 31,6 17,8 15,6 26,4 16,6 26,4 46,9 45,4
2 18,0 32,6 0,0 34,4 20,2 23,9 16,4 36,2 36,1 47,4 43,3 50,3 23,4 9,4 21,2 13,0
3 22,4 14,6 34,4 0,0 25,0 42,7 33,5 35,4 45,0 15,0 29,2 40,3 11,2 32,0 53,2 47,2
4 25,0 32,2 20,2 25,0 0,0 41,2 31,6 46,1 50,5 40,0 47,2 57,0 15,8 25,5 41,2 29,2
5 20,6 32,2 23,9 42,7 41,2 0,0 10,0 20,6 13,9 50,0 33,5 35,4 35,4 15,8 20,0 29,2
6 11,2 24,8 16,4 33,5 31,6 10,0 0,0 20,6 19,8 42,4 30,4 35,4 25,5 7,1 22,4 25,5
7 21,2 21,0 36,2 35,4 46,1 20,6 20,6 0,0 12,2 36,4 14,1 15,0 33,5 26,9 40,3 46,1
8 26,2 31,6 36,1 45,0 50,5 13,9 19,8 12,2 0,0 48,1 26,2 24,2 40,8 26,9 33,4 42,9
9 32,0 17,8 47,4 15,0 40,0 50,0 42,4 36,4 48,1 0,0 25,0 35,4 25,5 43,0 64,0 60,4
10 25,5 15,6 43,3 29,2 47,2 33,5 30,4 14,1 26,2 25,0 0,0 11,2 32,0 35,0 52,2 55,0
11 33,5 26,4 50,3 40,3 57,0 35,4 35,4 15,0 24,2 35,4 11,2 0,0 42,4 41,2 55,2 60,8
12 15,0 16,6 23,4 11,2 15,8 35,4 25,5 33,5 40,8 25,5 32,0 42,4 0,0 22,4 43,0 36,1
13 11,2 26,4 9,4 32,0 25,5 15,8 7,1 26,9 26,9 43,0 35,0 41,2 22,4 0,0 21,2 20,0
14 32,0 46,9 21,2 53,2 41,2 20,0 22,4 40,3 33,4 64,0 52,2 55,2 43,0 21,2 0,0 15,8
15 30,4 45,4 13,0 47,2 29,2 29,2 25,5 46,1 42,9 60,4 55,0 60,8 36,1 20,0 15,8 0,0
is 15 that require and need treatments in their respec-
tive locations. Regarding the locations, it is necessary
to know the different locations/cities of each patient
belonging to the Health Unit and the respective tem-
poral distance (minutes) between each one of them.
In this way, Table 2 presents the distances (in kilo-
meters) between locations. The patients seek and
need home visits with a certain regularity in the pe-
riod of the visits (T = 5 days). Thus, Table 3 shows
the number of times each patient should be visited.
Table 3: Regularity of visits required by each patient in the
time horizon.
Period of visits they require for T = 5
Patient 1 1
Patient 2 1
Patient 3 2
Patient 4 3
Patient 5 1
Patient 6 2
Patient 7 1
Patient 8 1
Patient 9 2
Patient 10 3
Patient 11 1
Patient 12 1
Patient 13 1
Patient 14 2
Patient 15 1
According to these data, it is also possible to iden-
tify some patterns about the number of visits required
by each patient for the T period, knowing in advance
that between two or more visits a day of interval is
required. Thus, in this way it is possible to illustrate
the different patterns according to Table 4:
Based on all the data, the main objective is to ob-
tain vehicle routing/scheduling, finding the T sets of
routes that satisfy the constraints and minimizing the
Table 4: Patterns of visits according to the period T .
Possible Pattern for visits to T = 5 days
1 Visit 1, 2, 3, 4 or 5
2 Visit 1-3, 1-4, 1-5, 2-4, 2-5, 3-5
3 Visit 1-3-5
total time required to carry out the trips, treatments
and return to the starting point (Depot - Health Unit).
5 ANALYSIS AND DISCUSSION
OF RESULTS
In this section the computational results of the model
developed and proposed for the resolution of PVRP
will be presented and analyzed.
The model was coded and implemented in
the IBM
R
ILOG
R
CPLEX
R
Optimization Studio
that supports Optimization Programming Language
(OPL). The data of the real case under study was im-
plemented according to the periodic home care visits
approach and the results were obtained on an Intel (R)
Core i7 CPU 2.2GHz PC with 6.0 GB of RAM.
The CPLEX
R
took about 11 hours to reach the so-
lution. The obtained solution had the objective value
of 473 and besides the regularity and periodicity of
visits imposed by the patients in the time horizon, the
model established the route patterns according to the
objective reached. This solution indicates the mini-
mum distance to be traveled (cost) for the vehicles to
make the home visits routes, according to the defined
time horizon and the regularity needed by the patients
and nurses of the Health Unit of Braganc¸a.
From Table 5, it is possible to get some statisti-
cal details, such as the number of variables used, the
average value of the target solution, among other pa-
Periodic Vehicle Routing Problem in a Health Unit
387

7
8
5
11
10
14
1
6
12
4
9
3
2
15
13
Depot – Health
Unit
Patients
Route 1 -
Monday
Route 2 -
Wednesday
Route 3 -
Friday
Vehicle 1
Vehicle 3
Vehicle 3
Frequency
of 3 visits
Frequency
of 2 visits
Figure 2: Representation of the PVRP solution.
rameters that allow to summarize the objective solu-
tion.
Table 5: Statistical values obtained by CPLEX
R
.
Statistic Value
Constraints 5874
Variables 6955
Objective 473
Nodes 4724907
Mean Objective 547
Figure 2, in turn, illustrates the solution obtained,
which includes the scheduling and the set of routes
for the periodicity of home visits in question.
In this sense, two of the five vehicles available
were used, where only one was used on two different
days. Another thing to mention, is that from the de-
fined time horizon only 3 days were subjected to the
service of home care visits. These days allow to com-
ply with all requirements according to the periodicity
imposed. Certain patients require a higher frequency
of visits, however it is possible to check those that be-
long to more than one route and day of visits, as can
be seen in Figure 2. It is possible to conclude with the
solution provided, that all patients are visited and all
routes meet the time period between successive visits
leading to admissible patterns.
The analysis showed that the problem can be
solved by CPLEX
R
and provided the optimal solution
of the single problem.
6 CONCLUSIONS AND FUTURE
WORK
The PVRP are an extension of the classic vehicle
routing problems. They are more difficult to solve
when compared to the problems of classic routes,
since they do not only aim to find a set of routes,
but also the definition of a schedule of visits of the
patients that minimizes the operational costs of the
system/service within a time horizon. Since the route
problem addressed is a periodic approach that covers
a time horizon with several days, an integer linear pro-
gramming model was developed using OPL/CPLEX
R
implementation for its resolution and optimization.
The developed model allows to solve problems
of routes with time period between successive vi-
sits, meeting the demand and regularity of visits by
the patients. In this way it was possible to estab-
lish the home visits in a Health Unit in Braganc¸a,
optimizing the routes in the service. In this work, a
small real case of 15 patients is solved, allowing the
Health Unit to plan routes and visits using computa-
tional support. However, replicating the problem with
larger instances and/or increasing difficulty, may not
be feasible due to the rather long computational time
required.
The developed approach allows the planning of
a set of routes that, with the existing resources, and
guarantees the visit to all the locations with the time
period defined by the managers, without incurring
additional costs or deficiencies in the service. In this
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
388

way, obtaining the solutions allows reducing and opti-
mizing costs and routes, improving the health service
provided and serving as a decision support system,
which does not exist today.
For future work, it is intended to use meta-
heuristics, to test this integer linear programming
model in larger instances and/or instances from the
literature, in an attempt to overcome other logistical
difficulties in the home health care services.
ACKNOWLEDGEMENTS
This work has been supported by COMPETE:
POCI-01-0145-FEDER-007043 and FCT - Fundac¸
˜
ao
para a Ci
ˆ
encia e Tecnologia within the project
UID/CEC/00319/2013.
REFERENCES
Alves, F., Pereira, A. I., Fernandes, A., and Leit
˜
ao, P.
(2018). Optimization of home care visits schedule
by genetic algorithm. In International Conference on
Bioinspired Methods and Their Applications, pages 1–
12. Springer.
Angelelli, E. and Speranza, M. G. (2002). The periodic ve-
hicle routing problem with intermediate facilities. Eu-
ropean journal of Operational research, 137(2):233–
247.
Beltrami, E. J. and Bodin, L. D. (1974). Networks and vehi-
cle routing for municipal waste collection. Networks,
4(1):65–94.
Benzarti, E., Sahin, E., and Dallery, Y. (2013). Operations
management applied to home care services: Analysis
of the districting problem. Decision Support Systems,
55(2):587–598.
Bertels, S. and Fahle, T. (2006). A hybrid setup for a hybrid
scenario: combining heuristics for the home health
care problem. Computers & Operations Research,
33(10):2866–2890.
Campbell, A. M. and Wilson, J. H. (2014). Forty years of
periodic vehicle routing. Networks, 63(1):2–15.
Cordeau, J.-F., Gendreau, M., and Laporte, G. (1997). A
tabu search heuristic for periodic and multi-depot ve-
hicle routing problems. Networks: An International
Journal, 30(2):105–119.
Fikar, C. and Hirsch, P. (2017). Home health care routing
and scheduling: A review. Computers & Operations
Research, 77:86–95.
Hemmelmayr, V., Doerner, K. F., Hartl, R. F., and Savels-
bergh, M. W. (2009). Delivery strategies for blood
products supplies. OR spectrum, 31(4):707–725.
Nickel, S., Schr
¨
oder, M., and Steeg, J. (2012). Mid-term
and short-term planning support for home health care
services. European Journal of Operational Research,
219(3):574–587.
Pacheco, J., Alvarez, A., Garc
´
ıa, I., and Angel-Bello, F.
(2012). Optimizing vehicle routes in a bakery com-
pany allowing flexibility in delivery dates. Journal of
the Operational Research Society, 63(5):569–581.
Trautsamwieser, A., Gronalt, M., and Hirsch, P. (2011). Se-
curing home health care in times of natural disasters.
OR spectrum, 33(3):787–813.
Periodic Vehicle Routing Problem in a Health Unit
389
