SIMSEA: A Multiagent Architecture for Fishing Activity in a Simulated

Environment

Jos´e Cascalho

1,2,3

, Paulo Trigo

1,4

, Maria Jo˜ao Cruz

, Armando Mendes

2,3,5

, Eva Giacomello

6,7

Adriana Ressurreic¸˜ao

6,7,9

, Tom´as Dentinho

and Telmo Morato

6,7

BioISI - Biosystems and Integrative Sciences Institute, FCUL -Universidade de Lisboa, Lisboa, Portugal

NIDeS - N´ucleo de Desenvolvimento em e-Sa´ude, Universidade dos Ac¸ores, Ponta Delgada, Portugal

FCT - Universidade dos Ac¸ores, Ponta Delgada, Portugal

ISEL - Instituto Superior de Engenharia de Lisboa, Lisboa, Portugal

Algoritmi, Universidade do Minho, Portugal

MARE – Marine and Environmental Sciences Centre, Horta, Portugal

OKEANOS Centre, Universidade dos Ac¸ores, Horta, Portugal

FCAA - Universidade dos Ac¸ores, Angra do Hero´ısmo, Portugal

CCMAR Centre of Marine Sciences, Faro, Portugal

Keywords:

Multiagents, Finite-state Machines, Muti-criteria Decision-making.

Abstract:

Understanding ﬁshermen decision-making proccess, plays a key role i n predicting the impacts of the ﬁshing

activity in the marine ecosystems. Simulating ﬁshing activity using multiagent based approaches provides

tools that assist decision-makers in order to pursuit sustainable ﬁshing activity. In this paper we present a

multiagent architecture for the ﬁshing activity where geo-referenced resources and ﬁshing agents with different

proﬁles are used to model and simulate the complexity of human ﬁshing activity. A ﬁrst implementation of

the model (via NetLogo), along with gathered results, provides insights into t he capability to build a research

tool for ﬁsheries management.

1 INTRODUCTION

Fishing activity has been under scrutiny mainly be-

cause of the over-ﬁshing and its impact in marine

ecosystems as well as in the economy of ﬁshing com-

munities. Different research tools have been used to

understand the exploitation of the marine ecosystems,

including trophic web and biogeochemical simulation

models, despite the consid erable problems in tuning

and validating complex numerical models with ﬁeld

data (Pitcher et al., 2007; Morato et al., 2016). M ulti-

agent systems have been increasingly used in the con-

text of what is being deﬁned as a coupled human and

natural systems o r CHANS systems (An, 2012). In

these systems it is usually aggregated a GI S r epresen-

tation, making interaction m ore representative of the

real world and socio -econom ic mo dels, re- focusing

attention in e cosystem analysis from the ecology of

’nature’ to the important inﬂuence of people (An,

2012). With regard to the scenario being studied, dif-

ferent levels of complexity mu st be considered and all

of them must be somehow inco rporated in the model

(Pitcher et al., 2010).

In this paper we presen t the SIM SE A , a multi-

agent architecture for simulating ﬁshing activity in

a geo-referenced scenario where simulated human

decision-making agents with different proﬁles are

used to explore the complexity of human decision-

making. Proﬁles contribute to increase the diversity of

behaviours of these agents, tuning their decision s by

using a multi-criteria decision-mak ing process. In this

paper we resport on the ﬁrst implementation of a m o-

del in NetLogo (Tisue and Wilensky, 2004) applied to

the scenario of dem ersal ﬁshing activity in Azores ar-

chipelago (NE Atlantic). Agents have different roles

in the mo del, they are either static or dynamic, re-

presenting different entities such as vessels, ports and

ﬁshing grounds (are a s where ﬁshing activity occurs).

The model uses a multi-criteria decision-making me-

chanism applied on the top of a ﬁnite-state mach ine

to model agents’ behaviour which simulate human

decision-making. Moreover, the concept of risk aver-

202

Cascalho, J., Trigo, P., Cruz, M., Mendes, A., Giacomello, E., Ressurreição, A., Dentinho, T. and Morato, T.

SIMSEA: A Multiagent Architecture for Fishing Activity in a Simulated Environment.

DOI: 10.5220/0007393502020209

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 202-209

ISBN: 978-989-758-350-6

sion is used to create behaviour diversity among these

agents. A set of agents with different proﬁles descri-

bed as optimistic, pessimistic or middle are used to

tune the behaviour of these agents. To the best of our

knowledge, this is the ﬁrst study focused on the simu-

lation of ﬁshing activities in the Azores using Agent-

Based Systems.

The paper is organized as follows: In section 2

a background and related work is presented. Then,

in section 3, a description is mad e of the a rchitecture

proposed. In sections 4 and 5, the imp lementation and

the running experiment using NetLogo are d iscussed.

Finally, in section 6, the conclusions are presented.

2 BACKGROUND AND RELATED

WORK

Previous work on multiagent based simulation de-

monstrated the utility of these tools applied to dif-

ferent areas (Abar et al., 2017) . DISPLACE (Bas-

tardie et al., 201 5; Bastardie et al., 2013) is a n agent

based simulation tool applied to the ﬁshin g activity,

calculating the income and evaluating the best ves-

sels’ trajectory under spatial co nstraints. It includes

a geo-referenced dyna mic m odel of the resources (i.e.

ﬁshing stocks) and the vessels have a simple decision-

making process based on a ﬁnite-state machine ar-

chitecture. This model is used essentially to evalu-

ate the costs/beneﬁts of agents’ decisions predicting

also what are ﬁshing captures in different scenarios.

Souli´e an d Th´ebaud (2006), also developed a multi-

agent bio-e conomic mode l to analyze the consequen-

ces of regu la tory measures, such as temporary ﬁshing

bans on the allocation of ﬁshing effort between target

species and areas, and the potential e conomic impacts

of th ese measures.

The models produced in the con text of the

CHANS systems are often based on pro duction rule

systems i.e. systems that use rules if-then-else, and

some deliberative capabilities to fulﬁl goals however

without explicit de liberation or cognitive processes.

One of the reasons pointed out by som e authors is th e

fact that simpler models are better suited if the ob-

jective is to predict the behaviour of an organization

as a whole instead of predicting with accuracy a be-

haviour at the individual or small group level ( Balke

and Gilbert, 2014). Alth ough SIMSEA is intended to

analyse the global behaviour of a set of entities, it also

has the goal to address a small group of agents follo-

wing speciﬁc constraints related to th e location and

availability of resources. So, it is expe cted to provide

decision-making methods that increase the capability

of the simulation to address the diversity of behavi-

ours related to the ﬁshing activity.

Usually when human decision-making is part of

the simulated model of an agent, the concept of

being rational (Kennedy, 2012) is addressed. A ra-

tional agent has consistent an d well-deﬁned preferen-

ces across all available decisions options and cho oses

the option that meets its preferences best, taking into

account all relevant information. U sually, th e boun-

ded rationality, a concept of rationality more close

to human decision-making, is adopted. If an agent

has a bounded rationality, h e takes a decision ba-

sed on his limited information and cognitive capabili-

ties in his limited processing time (Groeneveld et al.,

2017). A rational decision-making is often associa-

ted to maximizing expected utility. So, bounded rati-

onal agents are the ones that provide answers to pro-

blems maximizing the utility measured in that spe c iﬁc

contexts and within their own limitations. Maximi-

zation utility is usually addressed as a multi- criteria

decision problem, where enric hed methodologies are

used, implying the selec tion of the best compromise

solution that usually depends on the preferenc e s of

the decision-maker (Tomic et a l., 2011) . In SIM-

SEA, agents modelling human behaviour use a multi-

criteria decision-making mechan ism. Moreover, to

increase the diversity of behaviours, it was decided

to adopt the concept of risk aversion/ risk seeking

as a way to express agents with different behaviours

and characterize their proﬁles as optimistic v s. pes-

simistic. Several authors have been considering these

same concepts as a way to d escribe how agents’ be-

liefs have consequences in their behaviour. In particu-

lar, in a ﬁnancial crisis scenario, an optimistic behavi-

our corresponds to an agent that overestimates their

informa tion and capacities (Said et al., 2018). Ot-

her authors use the risk aversion perspective to create

agents with different behaviours (Magessi and Antu-

nes, 2013). In this case, they may have a high pre-

disposition for risk, called a r isk-demander, or a low

predisposition for risk, a risk-fearful.

3 MODELS ARCHITECTURE

SIMSEA is intended to simulate ﬁshing activity. The

architecture is organized in thre e layers where each

one is associated to different entities with speciﬁc pur-

poses. The rationale behind the cre ation of the three

layers is the following:

• The bottom layer ref ers to the geo-physical en-

vironm ent with information gather e d from geo-

graphic information systems (GIS). This data is

ﬁxed along the simulation.

SIMSEA: A Multiagent Architecture for Fishing Activity in a Simulated Environment

203

Figure 1: Different layers in SIMSEA architecture: The bottom layer corresponds to physical features (e.g. bathymetry, water

temperature, etc); the mid layer includes the bio-dynamic features (eg. ﬁsh biomass index) and identiﬁes ﬁshing areas; the

top layer includes ﬁxed (i.e. ﬁshing grounds and ports) and moving agents (e.g. vessels).

• The mid layer corresponds to ﬁshery resources,

attributing a value of available ﬁsh biomass for

each ﬁshing ground. This data can be obtained

from the biology and behaviour of the species

considered in the model or from other type of ex-

perts’ data related to the amount of resources in

the different ﬁshing areas of the scenario.

• The top layer includes the static and moving

agents (e.g. ﬁshing grounds, ports and vessels)

and their (economic and social) interactio n.

Agents in the model have different levels of com -

plexity. For example, vessels movements are the re-

sult of ﬁshermen decision-making and, so, it must

be added decision-making c apabilities to these agen ts

whereas ﬁshing gr ounds are just reac tive agents to-

ward constraints imposed to the model i.e. closin g

a ﬁshing ground to the ﬁshing activity. As depicted

in ﬁgur e 1, c onstraints to the agents’ behaviours with

respect to the bio-dynamics (e.g. stock more or less

abundant) and the interaction between agents (e. g. a

port closes w ith adverse weather conditions) are also

part of the model.

3.1 Simulated Environment

The simula te d environment corresponds to the bottom

and mid layers in the model. At the bottom layer it is

deﬁned the geo-referenced physical area for the sce-

nario where data on bathymetry, mean temperature,

etc, may be allocated. The mid layer adds biological

informa tion related to the ﬁsher y resources, e.g. ﬁs-

hing stock for different species and the variation of

recruitment f or the species captured (Bastardie et al.,

2013).

Table 1: High l evel description of agents using Backus-

Naur Form.

Agent ::=

< agentType,agentFeatureSpace,agentDecisionSpace >

agentType ::=

V ESSEL|F ISHGROUND|PORT

agentFeatureSpace ::=

V ESSEL

FeatureSpace

|FISH GROU ND

FeatureSpace

PORT

FeatureSpace

agentDecisionSpace ::=

V ESSEL

DecisionSpace

|FISHGROU ND

DecisionSpace

PORT

DecisionSpace

V ESSEL

FeatureSpace

::=

< geoRe f Local , velocity,workingPeriodMax,workingPeriodMin,

restingPeriod,catchRate, f ishingDistanceMax, f ishingDistanceMin

f ishingPr iceMax, f ishingPriceM in, f ishingCostMax, f ishingCostMin,

size,registeredPort, portOrigin, portDestination

vector,

f ishingGround

vector, pro f ile vector >

V ESSEL

DecisionSpace

::=

< DECISION

portDestination

,DECISION

f ishingGround

PORT

FeatureSpace

::=

< geoRe f Local , state,constraintDestination, destination

vector >

PORT

DecisionSpace

::=

< DECISION

portState

,DECISION

constraintDestination

DECISION

constraintQuota

,DECISION

constraintFishing

FISHINGGROU ND

FeatureSpace

::=

< geoRe f Local , state,biomassIndex >

FISHGROU ND

DecisionSpace

::=

< DECISION

FishGroundState

3.2 Agency Model

Agents main properties are summarized as follow (ta-

ble 1):

• Agents make decisions supported by a set of fea-

tures, some related to their own properties, others

as a resu lt of environment perception.

• Each agent ca n be of the type VESSEL,

FISHGROUND or PORT:

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

204

(a) VESS EL and PORT types model human beha-

viours.

(b) FISH G ROUND type is used to model the d yn-

amics associated to ﬁshing on a spec iﬁc ﬁshing

ground.

• Feature space contains the set of featur e s for each

agent type in the model.

• Decision space has a set of higher level functions

deﬁned in the decision-making context as multi-

criteria decision-making mec hanism or as con-

straint decisions based on rules applied to some

scenario.

Table 2 describes the details of the features as-

sociated to each agent. Agents are implemented

through ﬁnite-state machines (Adam et al., 2017) and

the decision-making functions are called in speciﬁc

agents’ states. In the exam ple discussed in section 4,

only the decision-making func tion related to getting

to the ﬁshing ground is implemented. The oth er ty-

pes are the ones that r e sult from rules imposed to the

scenario. These rules model decisions concerning the

management of r e sources by local government autho-

rities

FISHGROUND and PORT types can be on a o pen

or closed state. The de cision to open or close a port

can be autonomou s (e.g. weather conditio ns) while

the decision to close or o pen a ﬁshin g area may occur

from co nstraints deﬁned in the scenario to be studied.

Destination constraints are imposed by rules (e.g. De-

mersal ﬁshing ac tivity restricted 3 nm from shore).

FISHGROUND type uses an index of relative abun-

dance of ﬁsh (biomass index) which determines the

catch f or each vessel in that speciﬁc area.

Table 2: Lower level description of agents using Backus-

Naur Form.

velocity ::= nm/h

workingPeriod ::= #hours-at-ﬁshing

restingPeriod ::= #hours-at-port

f ishingMaxDistance ::= max-distance

f ishingMinDistance ::= min-distance

size ::= size A|size B

portDestination vector ::= [] |[portDestination

, portDestination

,...]

f ishingGround vector ::= [] |[ f ishingGround

, f ishingGround

,...]

catchRate ::= kg/h

DECISION

portDestination

::=

multi

criteria decision f unction(portDestination vector)

DECISION

f ishingGround

::=

multi

criteria decision f unction()

DECISION

portState

::= multi criteria decision

unction()

DECISION

constraintDestination

::=

constraint

decision f unction( f ishingGround vector)

In future models, these rules can be modelled as part of

governance agents.

3.3 Decision-making

Two main concerns guided the implementation of

decision-making. First w e needed to use a decision

mechanism with enough complexity to tackle a simu-

lation where agents model human decision-making.

Secondly, we were looking for a way to identify dif-

ferent proﬁles among agents that took decisions, ex-

pecting that these agents’ behaviours could be biased

to a m ore o r less aversion to risk behaviour. Based

on these two concerns, we decided to follow a multi-

criteria approach with the following components:

• A set o a

...a

alternatives (options) for ea c h

agent’s decision.

• A set of criteria, c

,... c

, deﬁned for each alter-

native;

• A set of weights w

...w

which represents the re-

lative importance each criterion has for the agents;

• A set of f

,... f

evaluation criteria.

Naturally, each criterion has a possible different

domain from the other criteria and c are should be ta-

ken in eliminating the scaling-effects of the used cri-

teria.

More formally, we deﬁne a multi-criteria problem

as:

decision = argmax

∈A

{ f

),... f

)|a

∈ A}

(1)

where A is a ﬁnite set of alternative actions, c

, i =

1,..., n are n criteria, w

, i = 1.... ,n are the associa-

ted weights denoting the relative importance of eac h

criterion and f

,. . . , f

are the evaluation criteria for

each a

. This means that as an output of the decision,

the option based on the evaluation of multiple criteria

applied to each alternative in A must be the best op-

tion th at maximizes the result.

Each f

) is calculated as follows:

• V

) is calculated for each criterion c

, i ∈

{1,...,n }

• f

) = sgn (c

) ∗V

), sg n(c

) ∈ {−1,1}

To make the ﬁnal decision, an utility function is

calculated for each a

, x ∈ {1,...,k} as depicted in

equation 2.

U(a

) =< w

,...,w

> ∗

< f (c

), f (c

),..., f (c

) >

(2)

The option a

with highest utility is, then, selected.

Note that sgn(c

) expresses the signal of the criteria,

maximizing or minimizing the contribution of c

the utility.

As mentioned before, the output of the function

must be a universal compa rable value. One p ossi-

bility is to consider the value of a cost/gain for each

SIMSEA: A Multiagent Architecture for Fishing Activity in a Simulated Environment

205

e.g. the cost in euros/km of a vessel’s tr ip. This

was the solution tha t was tested in the simulation (see

section 4). However th ere are other options like the

ones that use preference functions that sum up the

contribution of the option a

that represents the inten-

sity of a prefe rence when co mpared to the o ther opti-

ons (Tom ic et al., 2011 ). In this case the c ontribution

to utility is the result of compariso n with other options

instead of having an universal comparable value. This

option is expected to be tested in future experiments.

Finally, selecting from a set of options a

can also

be constrained by rules specifying which set of opti-

ons can be considered . So, for each decision, a co n-

straint shou ld be taken into account following the ru-

les which are applied to the original set of option s a

returnin g a sub-set of options (equation 3).

New

A = constraints(A), New A ⊂ A (3)

4 IMPLEMENTATION OF

SIMSEA IN NetLogo

NetLogo (Tisue and Wilensky, 2004) is a free soft-

ware platform founded in multiagent programming

languag e and modelling environment for simulating

complex natural and social phenomena. With Net-

Logo the modeller can give instructions to hund-

reds or thousands of independent agents specifying

how they should b ehave and inter act with one anot-

her. NetLogo is being used to build an endless vari-

ety of simulations, allowing to explore the behaviour

of individuals under various conditions and the pat-

terns th at emerge from their interactions. The mo-

ving agents are called turtles and move over a two-

dimensional grid of patches which may also execute

instructions and interact w ith turtles and other pat-

ches. The execution cycle of instructions in NetLogo

is made b y calling all the age nts in the model by a su-

pervisor agent called the observer. NetLogo includes

a tool for running the simulation experiments, dubbed

Behaviour Space, that a llows parameter sweeping i.e.

systematically testing the behaviour of a model across

a range of parameter settings.

Netlogo have been considered as one of the tools

that supports simulation at a medium-scale of scalabi-

lity (Abar et al., 2017). T he fact that the development

effort is easy and that the high level language used

to model the agents facilitates the interaction betwe en

researchers with different b a ckgrou nds, led us to im-

plement a ﬁrst prototype in NetLogo. T he following

features were used in the model tested:

• The scenario o f the exp e riment is the archipelago

of Azores, NE Atlantic;

• A multi-criteria decision-making mechanism is

used to select a ﬁshing ground for vessels of a spe -

ciﬁc size, located at ports in one of the archipelago

islands;

• Two criteria for selecting a ﬁshing ground are ap-

plied: the distance from the port of orig in and the

ﬁsh biomass index;

• A proﬁle is deﬁned by weighting the two criteria

differently.

A description of the e nvironment and how the

vessels make decisions is explained in the following

sections.

4.1 Environment

The environment is deﬁned by th e combination of a

geo-referenced physical area, the bathymetry and a

biomass index. Depth was obtained as bathymetric

data composite using multiple sources: GEBCO

08,

grid (MOMARGIS v2, DOPUAz), multi-beam su r-

veys (GMRT grids), point and contour data digitized

from na utical charts in the vicinity of the island s.

In the SIMSEA model geo-r eferenced physical

area of the scenario represents the archipelago of the

Azores and respective ﬁshing areas within the Exclu-

sive Economic Zone (EEZ) . A value of bathymetry

is added to each cell of the grid (corresponding to an

area 0 .14km

) used in the scenario.

The biomass index is a measure of relative bio-

mass of ﬁsh , a nd the model use it to represent the

biomass of ﬁsh in the different ﬁshing areas. I n the

present model it is assumed that the value is static for

each simulation. A range of values from 1 to 9 was

arbitrarily attributed to the index, and randomly asso-

ciated to each ﬁshing area.

Vessels moving in th e environment know both the

bathymetry of each patch and the location of the dif-

ferent ﬁshing grounds. In the simulation, it was consi-

dered the ﬁshing of the mo st valuable com mercial ﬁsh

species in the Azores, the blackspot seabream Pagel-

lus bogaraveo (Menezes et al., 2013).

4.2 Agent’s Decisions

The decision-making mechanisms were modelled

only for agents of the VESS EL type when they select

a speciﬁc ﬁshing ground.

U(a

f g

) = w

∗ f (c

f g

) + w

∗ f (c

f g

)

(4)

Two criteria c

and c

, are used to calculate the

utility for each ﬁshing ground option (see equation 4).

The ﬁrst corresponds to th e distance from port origin

to the ﬁshing ground , mea sured as a mean distance

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

206

between the closest patch and the most distant patch

of a speciﬁc ﬁshing ground area from the port. It has

a negative contribution to the ﬁnal result as depicted

in equatio n 5. The second criterion is the index of

biomass of the ﬁshing ground area and has a positive

contribution as de picted in equation 6. The maximum

value corresponds to the patches where it is expected

to capture more ﬁsh.

f (c

f g

) =

−V

f g

) = − f uel price ∗ distance(a

f g

)

(5)

f (c

f g

) =

f g

) = + f ish

price/kg ∗ biomass index(a

f g

)

(6)

With the help of the equation 4, three different

proﬁles are identiﬁed, based on the risk aversion con-

cept (Mandrik and Bao, 2005). The ﬁrst one, optimis-

tic, assumes tha t it will always be rewarding to select

the spot with the hig hest biomass index discarding the

distance from the po rt. In this case, the weight w

1, meaning that it takes into account only the index

of biomass criterion. The second one, pe ssimistic, se-

lects the closest spot, because it assumes that it will

be never captured e nough ﬁsh to compensate the trip

cost. In this case, the weight w

= 1. Finally, the

middle p roﬁle corresponds to the ﬁsherman that weig-

hts equ ally the two criteria evaluating the cost of long

distances versus the gains of ﬁsh catches.

5 RUNNING THE EXPERIMENT

To test SIMSEA model, two experiments were run

with different ﬁshing price i.e. the Exp. 1 with lower

price and the Exp. 2 with a higher price. An expe-

riment comprised four simulations, each one with a

random distribution of bioma ss index and with a set

of proﬁles covering all the possible types of ﬁshermen

behaviour. Moreover, each simulation was run for dif-

ferent sets of optimistic vessels, pessimistic vessels,

middle vessels and for a set of half of vessels optimis-

tic and a half pessimistic (mixed).

The experiment intended to test the capabilities of

the model. The values used for the different parame-

ters are no t yet validated and some of them are only

referenc e values.

5.1 Input Variables

Table 3 describes the input variables tested in the sim-

ulation. Each experiment had four simulations, each

one setting a random distribution of biomass index.

A simulation run for a time limit of 240 ho urs, cor-

respond ing to 10 days and was repeated 25 times for

each proﬁle. The moving agents representing vessels

were divided in two c ategories according to vessel

length, namely size A to simulate vessels with 0-9 m

in length and size B to simulate vessels with size su-

perior to 9 m. The variables fuel price and working

and resting pe riod, had d ifferent values according to

the vessel type.

The two categories of boats were proscribed to

ﬁsh within 3 nau tical miles from shore and size A bo-

ats were also prohibited to travel beyond 30 nautical

miles.

The vessels move along a grid of patches and cap-

ture quantities of ﬁsh propo rtional to the ﬁsh biomass

present in a given area.

Table 3: Input variables tested in the SIMSEA.

Experiment

Exp. 1 Exp. 2

simulations

4 4

N. runs

by proﬁle

Optimistic 25 25

Pessimistic 25 25

Mixed 25 25

Middle 25 25

Working P eriod (h)

A (6-12)

B (12-120)

A (6-12)

B (12-120)

Resting Period (h)

A (10)

B (8)

A (10)

B (8)

Fuel price (euros/nm)

A (4)

B (7)

A (4)

B (7)

Fish price (euros/kg)

8 15

Biomass index

Random Random

The proﬁle is related to the choices made by ﬁs-

hermen to select a speciﬁc ﬁshing area. The proﬁ-

les optimistic, pessimistic and middle were present in

both experiences. The choice of ﬁshing grounds was

dependent on the eva luation ma de within each proﬁle.

The simulation run for the cases where all vessels

A and B w e re optimistic (w

=1), pessimistic (w

=1),

middle (w

=0.5 an d w

=0.5) or mixed (half of the

vessels pessimistic, the other half optimistic). Suc h

behavioural diversity was expected to represent the

different behaviours of ﬁshermen.

Fuel price per n autical mile (nm) was determined

for each vessel type according to the vessels charac-

teristics. Fuel price was calculated by multiplying the

vessel spee d by the vessel consu mption per mile and

this value b y the current f uel price for ﬁsheries in the

region (0.58 Euros). The price of the ﬁsh was esta-

blished according to the annual average value in the

auction for blackspot seabream.

SIMSEA: A Multiagent Architecture for Fishing Activity in a Simulated Environment

207

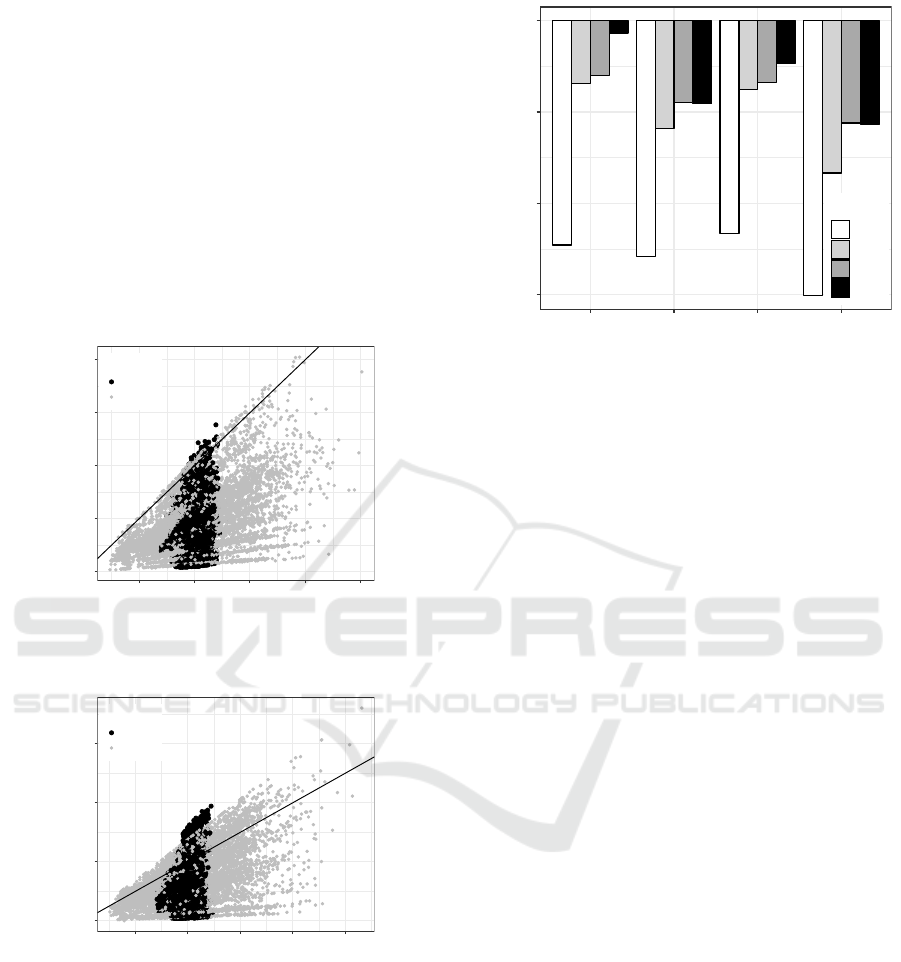
5.2 Experimental Results

Figure 2 and 3 shows cost vs. gain of ﬁshing resulting

from the simulation, for both Vessel A a nd B types.

In both ﬁgures it is possible to observe that Vessel A

has the points restricted to a speciﬁc range cost. This

result may be related to the fact that A are prohibi-

ted to travel beyond 30 nautical miles. Nevertheless,

vessels of both types re a ch the break even in the two

experiments, showing that restrictions do not rule out

the possibility of vessels having proﬁt. It is also worth

of notice the higher gain variability from experiment

2, with higher ﬁsh p rices when c ompared with expe-

riment 1, as expected.

10000

20000

30000

40000

10000 20000 30000 40000 50000

Cost

Gain

vessel_size

Figure 2: Cost vs gain for Vessel A (black dot) and Vessel

B (grey dots) types. Gains are calculated from the sale of

the captured ﬁsh using t he lowest ﬁsh sale price.

20000

40000

60000

10000 20000 30000 40000 50000

Cost

Gain

vessel_size

Figure 3: Cost vs gain for Vessel A (black dot) and Vessel

B (grey dots) types. Gains are calculated from the sale of

the captured ﬁsh using t he highest ﬁsh sale price.

The estimation of mean proﬁt for th e types of

agent proﬁle and ﬁsh biomass distribution index led to

major differences in values, as demonstrated in ﬁgur e

4. This ﬁgure shows the importance of distribution

of biomass for the ﬁnal results of the experiments. It

also shows tha t the different proﬁles have signiﬁcant

differences in revenue outcomes, providing an insight

of the sensitivity of the model towards these two pa-

rameters

−15000

−10000

−5000

middle mixed optimistic pessimistic

Profile

Profit mean (value)

biomass

bio1

bio2

bio3

bio4

Figure 4: Mean proﬁt per agents proﬁle on experiment 2.

The four colors distinguish the biomass scenarios.

These experiments conﬁrm the complexity of the

simulation model and the high inﬂuence of results for

the contr olled factors as agent’s proﬁle, vessel type

and ﬁsh biomass distribution.

6 CONCLUSION

In this paper we pr esent SIMSEA, a multiagent simu-

lation system to support decision management related

to ﬁshing activity. A three layer architecture aggre-

gates the data from GIS and the data from ﬁshing re-

sources to feed the agents, representing the entities in

the simulate d con text.

The NetLogo implementation provid e d insights

on how the mo del reacts to the diversity of data. The

experiment used proﬁles and a randomized set of ini-

tial parameters to study the output patterns. These

features and data w e re responsible for a diversity of

outputs for each category of vessel’s size and for the

different proﬁles. As a ﬁrst approach testing the mo-

del, it is possible to identify that ﬁshing pro ﬁt m ay be

inﬂuenced by agent proﬁle and the variability associ-

ated to the distribution of biomass index. As expected

the proﬁles that target ﬁshing areas with higher bi-

omass index are those that obtain a higher revenue,

even when they ignore the cost associated to the dis-

tance.

Further work must be done to improve the de-

cision model. Improvements can be obtained by

adding a dynamic ﬁshing stock model, by increa-

sing the space of decision in the VESSEL and PORT

agents’ types a nd, at the same time, testing other

multi-criteria decision-m a king mechanisms, such as

the ones based on comparing preferences.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

208

ACKNOWLEDGEMENTS

This work was funded by FEDER (85%) and by the

Azorean Regional Funds (15%), trough the Operati-

onal Program Azores 2020, in the scope of the pro-

ject ACORES-01-0145- FE D ER-000049. We thank

Luis Ro drigues and Hugo Diogo for sharing the

data u sed in this study, and the anonymous re-

viewers for their valuable comments and suggesti-

ons. AR acknowledges Fundac¸˜ao para a Ciˆenc ia

e Tecnologia (FCT), through postdoctoral grant

(SFRH/BPD/102494/2014) and the strategic pro je c t

UID/MAR/0429 2/2013 granted to MARE.

REFERENCES

Abar, S., Theodoropoulos, G. K., Lemarinier, P., and

O’Hare, G. M. (2017). Agent based modelling and si -

mulation tools: A review of the state-of-art software.

Computer Science Review, 24:13 – 33.

Adam, C., Taillandier, P., and Dugdale, J. (2017). Compa-

ring Agent Architectures in Social Simulation: BDI

Agents versus Finite-state Machines. In 50th Hawaii

International Conference on System Sciences , page

7p., Waikoloa, United States.

An, L. (2012). Modeling human decisions in coupled hu-

man and natural systems: Review of agent-based mo-

dels. Ecological Modelling, 229:25 – 36. Modeling

Human Decisions.

Balke, T. and Gilbert, N. (2014). How do agents make de-

cisions? a survey. Journal of Artiﬁcial Societies and

Social Simulation, 17(4):13.

Bastardie, F., Nielsen, J. R., Eigaard, O. R., Fock, H. O.,

Jonsson, P., and Bartoli no, V. (2015). Competition for

marine space: modelling the baltic sea ﬁsheries and

effort displacement under spatial restrictions. ICES

Journal of Marine Science, 72(3):824–840.

Bastardie, F., Nielsen, J. R., and Miethe, T. (2013). Dis-

place: A dynamic, individual-based model for spatial

ﬁshing planning and effort displacement - integrating

underlying ﬁsh population models. 71:366–386.

Groeneveld, J., M¨uller, B., Buchmann, C., Dressler, G.,

Guo, C., Hase, N., Hoffmann, F., John, F., Klas-

sert, C., Lauf, T., Liebelt, V., Nolzen, H., Pannicke,

N., Schulze, J., Weise, H., and Schwarz, N. (2017).

Theoretical foundations of human decision-making in

agent-based land use models – a review. Environmen-

tal Modelling & Software, 87:39 – 48.

Kennedy, W. G. (2012). Modelling Human Behaviour in

Agent-Based Models, pages 167–179. Springer Net-

herlands, Dordrecht.

Magessi, N. T. and Antunes, L. (2013). Modelling agents’

risk perception. In Omatu, S., Neves, J., Rodriguez,

J. M. C., Paz Santana, J. F., and Gonzalez, S. R.,

editors, Distributed Computing and Artiﬁcial Intelli-

gence, pages 275–282, Cham. Springer International

Publishing.

Mandrik, C. and Bao, Y. (2005). Exploring the concept and

measurement of general risk aversion. 32:531–539.

Menezes, G., Diogo, H., and Giacomello, E. (2013). Re-

construction of demersal ﬁsheries history on the con-

dor seamount, azores archipelago (northeast atlantic).

Deep Sea Research Part II: Topical Studies in Ocea-

nography, 98:190–203.

Morato, T., Lemey, E., Menezes, G., Pham, C. K., Brito,

J., Soszynski, A., Pitcher, T. J., and Heymans, J. J.

(2016). Food-web and ecosystem structure of the

open-ocean and deep-sea environments of the azores,

ne atlantic. Frontiers in Marine Science, 3:245.

Pitcher, T. J., Clark, M. R., Morato, T., and Watson, R.

(2007). Seamounts: ecology,ﬁsheries and conserva-

tion., volume 12.

Pitcher, T. J., Clark, M. R., Morato, T., and Watson, R.

(2010). Seamount ﬁsheries: Do they have a f uture?

Oceanography (Special Issue on Mountains in the

Sea), 23(1):134 – 144.

Said, Y. B., Kanzari, D., and Bezzine, M. (2018). A Be-

havioral and Rational Investor Modeling to Explain

Subprime Crisis: Multi Agent Systems Simulation in

Artiﬁcial Financial Markets, pages 131–147. Sprin-

ger International Publishing, Cham.

Tisue, S. and Wilensky, U. (2004). Netlogo: A simple envi-

ronment for modeling complexity.

Tomic, V., Marinkovic, Z., and Janosevic, D. (2011). Pro-

methee method implementation with multi-criteria de-

cisions. 9:193–202.

SIMSEA: A Multiagent Architecture for Fishing Activity in a Simulated Environment

209