Lifetime and Buffer-Size Optimization for RF Powered Wireless
Sensor Networks
Bikrant Koirala and Keshav Dahal
University of the West of Scotland, School of Computing, Engineering and Physical Sciences, Paisley, U.K.
Keywords: Energy Harvesting, RF Energy, Wireless Sensors, Lifetime, Buffer Capacity.
Abstract: Radio Frequency-Energy Harvesting (RF-EH) system usually incorporates ‘harvest-store-use’ mechanism,
i.e. the harvested RF energy is first stored in an energy buffer and when the stored energy level is sufficient
enough to power an application it is then supplied to the device. To improve the network’s performance in
terms of lifetime and buffer capacity, it is crucial to develop a model for RF powered Wireless Sensor
Networks (WSNs), which considers source-load relations, buffer size and ambient conditions within the
context of Energy Neutral Operation (ENO) and minimum energy wastage. In this paper, we propose a model
for RF powered WSNs that makes use of available RF energy with variations in maximum and minimum
energy levels for two different worst case scenarios encompassing ENO and buffer requirements. We develop
an algorithm based on the proposed model to find the optimum energy consumption rate of each sensor nodes
that would ensure maximum lifetime of the WSN with minimum buffer capacity. We verified our approach
by comparing the results with all other possible consumption rates. We also performed a comparative analysis
to find the effect of available RF energy fluctuation in the individual sensor nodes’ lifetime.
1 INTRODUCTION
Radio Frequency Energy Harvesting (RF-EH)
technique is a promising technique to sustainably
power Wireless Sensor Networks (WSNs) by
harvesting energy from ambient RF signals. This
technique has added benefits of being wireless,
energy is available in the form of transmitted energy
from RF sources, small size and low cost when
compared to energy harvesting systems from other
sources (Lu et al., 2015a). However, RF energy
harvesting as a new element in WSNs also introduces
challenges for developing efficient energy
management system along with other design issues
like data delivery scheme, topology, connectivity and
energy storage technology (Lu et al., 2015b, Zahid
Kausar et al., 2014).
For any EH system, to optimize energy utility and
to minimize waste, the system needs to operate in
accordance with the energy profile of the source and
also its design should consider load and harvester
properties (Pimentel and Musilek, 2010) . Energy
neutrality is a condition for an EH system to operate
perpetually, i.e., for Energy Neutral Operation
(ENO), the energy used by a system should always be
less than the energy harvested, which can be ensured
by incorporating an energy management system
between the harvester and the load to satisfy the
energy generation profile from the energy
consumption profile (Zahid Kausar et al., 2014, Morsi
et al., 2015).
Figure 1: Block diagram of a RF-EH System.
The energy management system can adopt two
methods to control the incoming energy flow, i.e.,
harvest-use or harvest-store-use. In harvest-use
method, the harvested energy is immediately used to
power the application, for this, the converted
electricity has to constantly exceed the minimum
energy required by the application. In the harvest-
store-use method, the network node has an energy
storage buffer, a rechargeable battery or a capacitor,
to store the converted electricity. Whenever the
harvested energy is more than load’s consumption,
102
Koirala, B. and Dahal, K.
Lifetime and Buffer-Size Optimization for RF Powered Wireless Sensor Networks.
DOI: 10.5220/0007393901020107
In Proceedings of the 8th International Conference on Sensor Networks (SENSORNETS 2019), pages 102-107
ISBN: 978-989-758-355-1
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

the excess energy is stored in the buffer for future use
(Lu et al., 2015b).
To determine the load energy consumption rate
for various associated source energy levels, it is
necessary to develop a model for RF powered WSNs,
which would ensure continuous work of applications
with minimal energy wastage even in worst case
scenarios and it should also be applicable for diverse
ambient conditions. In addition, the relation between
harvested energy, consumed energy and energy
buffer size defined by the model, should be able to
represent the network’s optimal performance
scenario (Kansal et al., 2007).
Network lifetime is one of the crucial
performance matrices for a WSN, which can be
prolonged by improving its energy efficiency.
Moreover, the location and orientation of sensor
nodes affect their energy harvesting rates, which
eventually determines the lifetime of each individual
node. Understanding the relation between the node’s
energy harvesting rate and lifetime, within the
periphery of energy neutrality and zero energy
wastage, is important for designing any energy-aware
routing algorithm (Cammarano et al., 2016,
Mansourkiaie et al., 2017).
In this paper, we present a system model for RF
powered WSN based on harvest-store-use method
that takes into consideration the worst case scenarios.
The model provides optimum values of load energy
consumption rate and buffer size for a given energy
harvesting rate, increasing the WSN’s lifetime. In
particular, we make the following contributions:
 We propose a model for RF powered WSN
incorporating harvester’s efficiency and
ambient conditions, which ensures energy
neutrality and minimal energy wastage.
 We develop an algorithm based on the
proposed model that selects the optimum
value for load energy consumption rate and
buffer capacity from all valid set of values.
 We analyse the lifetime and buffer capacity
of the WSN for optimum load energy
consumption rate along with all other non-
optimum values.
 We also analyse and compare the maximum
and minimum lifetimes of sensor nodes with
optimal energy consumption rate exposed to
various RF energy fluctuation levels.
The rest of the paper is organized as follows.
Section 2 presents related works in the area of EH
systems and energy management. In Section 3, we
have described the proposed system model and
algorithm to estimate optimum energy consumption
rate. Section 4 deals with the simulation results and
related discussions. Section 5 details conclusion and
possible future work. Finally, the paper ends with
acknowledgements and references.
2 RELATED WORKS
The authors in (Moser et al., 2010) propose a model
for optimizing the energy management of sensor
nodes powered from solar energy. The authors opted
for an offline multi-parametric programming to
compute the application parameters and have also
presented a software design comprising a worst-case
prediction of the incoming energy. The authors
evaluated the designed framework for upper control
layer that prevents the sensor nodes from running out
of energy as well as for the lower layer, which ensures
minimal energy loss.
Another energy management framework based on
solar energy harvesting has been proposed in
(Castagnetti et al., 2012). The framework is used to
simulate an energy harvesting sensor node based on
power consumption and energy harvesting, taking
into account energy-neutral and negative-energy
conditions. The framework describes a generic
energy harvesting system comprising charge
consumption rate and energy availability as its
parameters along with two energy management
architectures, namely - online duty-cycle adaptation
and closed-loop power manager.
The definition of WSN lifetime differs depending
on the type of application, main function and
topology of network (Mansourkiaie et al., 2017). In
some works (Chen et al., 2013, Najimi et al., 2014),
network lifetime is specified as the instant at which
certain number of nodes run out of their stored
energy, in (Salarian et al., 2014) the lifetime of the
node consuming highest energy is considered as the
network’s lifetime, while the duration for which the
first node in a network is depleted of energy is taken
as the network’s lifetime in (Jung and Weitnauer,
2013).
The work in (Mansourkiaie et al., 2017) presents
a framework to maximize the lifetime of WSNs for
structural health monitoring with and without energy
harvesting. F. Mansourkiaie et al proposed an
optimization technique for transmission power level
and route selection for each sensor node based on
Branch-and-Bound and Genetic Algorithms. The
authors also compared their algorithm with the
existing routing algorithms.
In (Akbas et al., 2016) the authors describe a joint
optimization framework for transmission power level
and packet size to maximize WSN lifetime. The work
Lifetime and Buffer-Size Optimization for RF Powered Wireless Sensor Networks
103

highlights the joint impact of the packet size and
transmission power levels on the network lifetime and
also suggests an optimal packet size for each specific
scenario where the network lifetime is higher than
other packet sizes.
A. Kansal et al in (Kansal et al., 2007) present an
EH system model based on ENO. The authors also
incorporated energy storage parameters in the model
and evaluated the experimental results with the
theoretical optimal values. Solar powered systems
utilizing conservative duty cycle were used to
compare the performance of the designed system with
other approaches.
3 SYSTEM MODEL
Based on the EH system model described in (Kansal
et al., 2007), we propose a system model for RF
powered WSNs encompassing ENO and buffer
requirements. The model assumes average source
energy emission and load energy consumption rate to
be P
S
and P
L
respectively. We further assume that the
energy rates vary between two extremities: P
Smax
and
P
Smin
for source emission, likewise P
Lmax
and P
Lmin
for
load consumption, where max and min represent
maximum and minimum rates respectively, such that
P
Smax
= P
S
+ σ P
S
and P
Smin
= P
S
- σ P
S
(1)
P
Lmax
= P
L
+ ρ P
L
and P
Lmin
= P
L
- ρ P
L
(2)
where, σ and ρ is the variation factors defined in
the interval 0 ≤ σ ≤ 1 and 0 ≤ ρ ≤ 1.
So, assuming an ideal buffer with zero leakage
loss and capacity B, the two worst case conditions for
a given time interval T can be states as:
B
0
+ ɳ
int
A(d,f,x)P
Smin
T- P
Lmax
T ≥ 0 (3)
B
0
+ ɳ
int
A(d,f,x)P
Smax
T- P
Lmin
T ≤ B (4)
where B
0
is the initial energy stored in the buffer,
ɳ
int
is the overall harvester efficiency and A(d,f,x)
represents the path-loss dependent on source-
harvester separation (d), source frequency (f) and
ambient condition (x).For the above stated conditions,
former ensures energy neutrality while the later
accommodates the additional constraint to be
satisfied for the energy buffer size.
Considering the limiting conditions and setting T
so as to ensure ENO for worst case scenarios, we get,
ɳ



,,







ɳ



,,



=


(5)
Equation (5) gives the optimum load consumption
rate for any given P
S ,
considering the buffer capacity
is always greater or at worst equal to the initial stored
energy, i.e. B ≥ B
0
. This leads to,
R
=


≥ 0 (6)
where R can be defined as buffer ratio, which
gives the measure of buffer capacity.
Algorithm 1: Optimum Values for P
Lmax
and P
Lmin
.
For given parameters, the optimum values of
P
Lmax
and P
Lmin
can be calculated as shown in
Algorithm 1. The algorithm opts for the values from
a possible set of energy consumption rates so as to
best satisfy both conditions stated in equations (3) and
(4). The optimum average energy consumption rate
and buffer ratio can be further deduced using the
algorithm outputs.
Input: P
Smax
, P
Smin
, ɳ
int,
A(d,f,x)
Output: Optimum values for P
Lmax
and P
Lmin
1: P
Lmax
= 0
2: k = 0
3: while P
Lmax
≤ ɳ
int
A(d,f,x)P
Smax
4: for P
Lmin
= 0 to P
Lmax
5: if
ɳ



,,







ɳ



,,



≥ 0
6: P
L
_minimum(k) = P
Lmin
7: P
L
_maximum(k) = P
Lmax
8: increment k
9: end if
10: end for
11: increment P
Lmax
12: end while
13: P
L
_small = smallest element among
P
L
_maximum(k)
14: P
L
_large = largest element among
P
L
_minimum(k)
15: for i = 0 to k
16: D_max(i) = P
L
_maximum(i) - P
L
_small
17: D_min(i) = P
L
_minimum(i) - P
L
_large
18: D_sum(i) = D_max(i) + D_min(i)
19: end for
20: ind = index of smallest element among
D_sum(i)
21: P
Lmax
_opt = P
L
_maximum(ind)
22: P
Lmin
_opt = P
L
_minimum(ind)
SENSORNETS 2019 - 8th International Conference on Sensor Networks
104

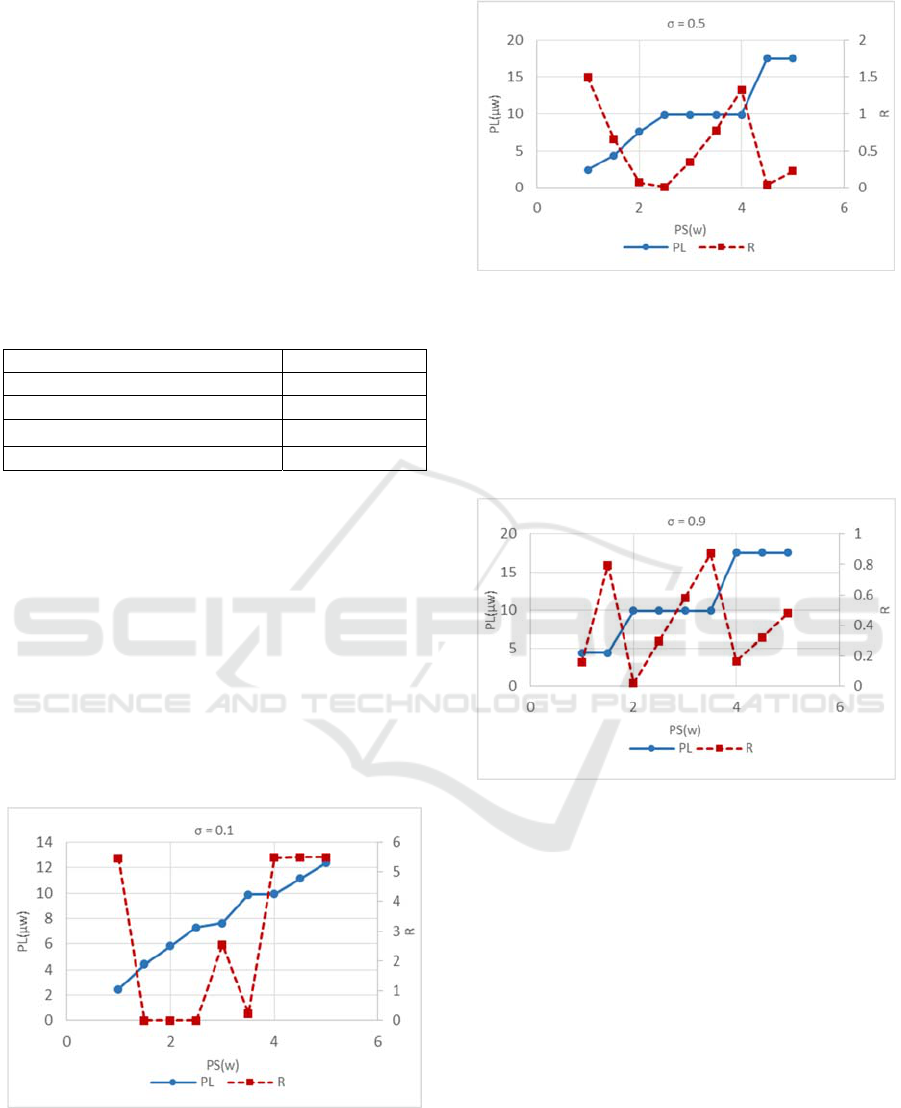
4 SIMULATION RESULTS AND
DISCUSSIONS
In this section, we analyse the optimum values of load
energy consumption rate for various source energy
rates along with corresponding buffer ratios through
simulations in MATLAB. The simulation parameters
are listed in Table 1.
The harvester efficiency does not vary
significantly for a small variation in the associated
energy levels (Chaour et al., 2017, Visser and Vullers,
2013).
Table 1: MATLAB Simulation Parameters.
Parameter Value
Source to RF-EH distance 5
m
Source frequency 2.45 GHz
Overall harvester efficiency 0.7
Ambient condition Free space
For simulations the harvester efficiency is
considered to be constant within the range of
parameters used. Fig. 2-3 shows the variation of
average energy consumption rate (
P
L
and buffer ratio
(
R ) with available source power ( P
S
) for different
values of variation factor (σ). The simulations show
that for a constant value of σ,
P
L
increases with the
increase in
P
S
 and as σ is increased, P
L
tends to
increase for same
P
S
values.
It is also evident from the results that the
maximum value of R decreases for higher values of σ,
suggesting a need for lower buffer capacity for high
variations in source energy rate.
Figure 2: Optimal energy consumption rate and buffer ratio
against average source energy rate with variation of 0.1.
Figure 3: Optimal energy consumption rate and buffer ratio
against average source energy rate with variation of 0.5.
The observations also shows that as P
s
increases,
R decreases, increases or remains unchanged for
different rates of change of P
L
with P
S
. We found that
R decreased for higher rates while it remained
unchanged for intermediate values and increased for
relatively lower rates.
Figure 4: Optimal energy consumption rate and buffer ratio
against average source energy rate with variation of 0.9.
The other objective of this work is to evaluate the
WSN’s lifetime (t
N
) for the optimum energy
consumption rate obtained from the MATLAB
simulations. The measure for t
N
is evaluated for a time
window T during which the average source energy
rate is assumed to be
P
S
with σ as associated variation
factor. To show that the obtained optimum
consumption rate provides maximum network’s
lifetime with minimal buffer capacity, we compare
the network lifetimes and buffer capacities for other
consumption rates considering energy neutral
conditions as described by system model in Section
3. For this, we assume network’s lifetime as the
duration for which the first node of a WSN depletes
its energy. We consider a multi-hop WSN scenario in
NS-2.35 with parameters as shown in Table 2 and
Lifetime and Buffer-Size Optimization for RF Powered Wireless Sensor Networks
105

analyse the network’s lifetime for different values of
energy consumption rates.
Table 2: NS-2.35 Simulation Parameters.
Parameter Value
Channel T
y
pe Wireless
Propa
g
ation Model Two-Ra
y
Groun
d
MAC Type 802.11
Antenna T
y
pe Omnidirectional
Routin
g
Protocol DSDV
Traffic TCP (FTP)
Simulation Time 100s
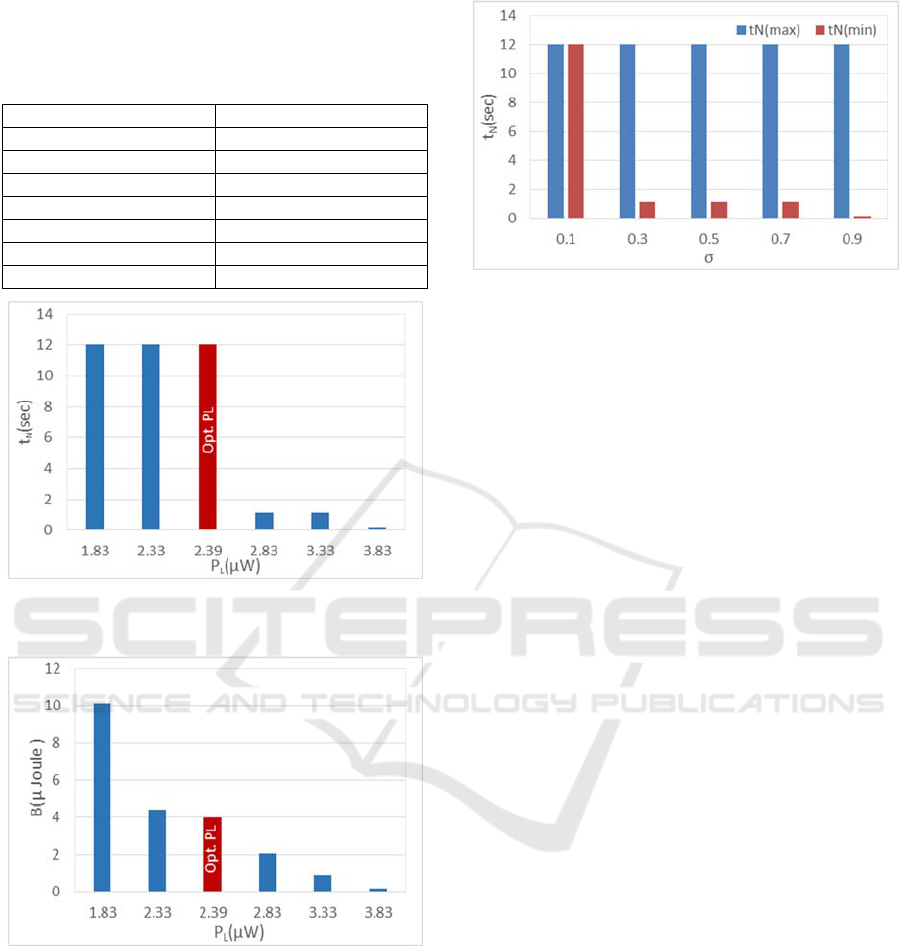
Figure 5: Network lifetime for different values of energy
consumption rates (optimal rate marked as Opt. PL).
Figure 6: Buffer capacity for different values of energy
consumption rates (optimal rate marked as Opt. PL).
Figure 5 and 6 depict the network lifetime and
buffer capacity respectively for different values of
load energy consumption rate. It is evident from the
figure that the WSN lifetime, as compared to the
optimum rate, is almost same for lower consumption
rates while dramatically shorter for higher rates. From
the simulations we also found that for the lower
values of consumption rate the increase in lifetime
was minimal but the corresponding buffer sizes were
Figure 7: Maximum and minimum lifetimes of sensor nodes
with optimal energy consumption rate exposed to different
source energy variation levels.
much larger, up to 180%, than the buffer size for the
optimum energy consumption rate. On the other hand,
though the buffer sizes for consumption rates higher
than the optimum rate are lower by 50% to 90%, the
network lifetime is reduced greatly by 95%. Hence,
the observation indicates that for optimum energy
consumption rate a higher WSN lifetime can be
achieved for a relatively lower value of buffer
capacity.
We also analysed the lifetimes of individual
sensor nodes with optimum energy consumption rate
for different values of average source energy
variation factor. Figure 7 illustrates that for minimum
variation of 0.1, the maximum and minimum
lifetimes are same, however for higher variations, the
difference between maximum and minimum lifetimes
tends to increase.
5 CONCLUSION AND FUTURE
WORK
In this paper, we have presented a model for RF
powered WSN considering energy neutrality and
minimum energy wastage. Based on the model, we
developed an algorithm that opts for the optimal
energy consumption rate and buffer capacity based on
worst cases scenarios. Further, we analysed the
simultaneous changes in consumption rate and buffer
capacity due to change in source energy rate, ensuring
continuous energy supply to the load and minimizing
energy wastage. We also evaluated the lifetime and
buffer capacity of the WSN for optimum load energy
consumption rate. The results showed that for the
obtained optimum energy consumption rate the
network’s lifetime is relatively higher for a smaller
buffer size as compared to other non-optimal rates.
SENSORNETS 2019 - 8th International Conference on Sensor Networks
106

Finally, we performed a comparative analysis to find
the effect of source energy fluctuation in the
individual sensor nodes’ lifetime.
One of the possible avenues of future work
includes designing of energy management system for
RF powered WSNs. As for a given energy harvesting
rate a corresponding optimal energy consumption rate
can be obtained, which can be implemented in a
power management module to dynamically adjust
individual node’s energy consumption rate.
ACKNOWLEDGEMENTS
The first author would like to acknowledge the
support provided by EU Erasmus Mundus project,
SmartLink (552077-EM-1-2014-1-UK-ERA), to
carry out this research at the University of the West
of Scotland, UK.
REFERENCES
Akbas, A., Yildiz, H. U., Tavli, B. & Uludag, S. 2016. Joint
optimization of transmission power level and packet
size for WSN lifetime maximization. IEEE Sensors
Journal, 16, 5084-5094.
Cammarano, A., Petrioli, C. & Spenza, D. 2016. Online
energy harvesting prediction in environmentally
powered wireless sensor networks. IEEE Sensors
Journal, 16, 6793-6804.
Castagnetti, A., Pegatoquet, A., Belleudy, C. & Auguin, M.
2012. A framework for modeling and simulating energy
harvesting WSN nodes with efficient power
management policies. EURASIP Journal on Embedded
Systems, 2012, 8.
Chaour, I., Fakhfakh, A. & Kanoun, O. 2017. Enhanced
Passive RF-DC Converter Circuit Efficiency for Low
RF Energy Harvesting. MDPI Sensors, 17, 546.
Chen, J., Li, J. & Lai, T. H. 2013. Trapping Mobile Targets
in Wireless Sensor Networks: An Energy-Efficient
Perspective. IEEE Trans. Vehicular Technology, 62,
3287-3300.
Jung, J. W. & Weitnauer, M. A. 2013. On using cooperative
routing for lifetime optimization of multi-hop wireless
sensor networks: Analysis and guidelines. IEEE
Transactions on Communications, 61, 3413-3423.
Kansal, A., Hsu, J., Zahedi, S. & Srivastava, M. B. 2007.
Power management in energy harvesting sensor
networks. ACM Trans. Embed. Comput. Syst., 6, 32.
Lu, X., Wang, P., Niyato, D. & Han, Z. 2015b. Resource
allocation in wireless networks with RF energy
harvesting and transfer. IEEE Network, 29, 68-75.
Lu, X., Wang, P., Niyato, D., Kim, D. I. & Han, Z. 2015a.
Wireless Networks With RF Energy Harvesting: A
Contemporary Survey. IEEE Communications Surveys
& Tutorials, 17, 757-789.
Mansourkiaie, F., Ismail, L. S., Elfouly, T. M. & Ahmed,
M. H. 2017. Maximizing Lifetime in Wireless Sensor
Network for Structural Health Monitoring With and
Without Energy Harvesting. IEEE Access, 5, 2383-
2395.
Morsi, R., Michalopoulos, D. S. & Schober, R.
Performance analysis of wireless powered
communication with finite/infinite energy storage.
2015 IEEE International Conference on
Communications (ICC), 8-12 June 2015 2015. 2469-
2475.
Moser, C., Thiele, L., Brunelli, D. & Benini, L. 2010.
Adaptive Power Management for Environmentally
Powered Systems. IEEE Transactions on Computers,
59, 478-491.
Najimi, M., Ebrahimzadeh, A., Andargoli, S. M. H. &
Fallahi, A. 2014. Lifetime maximization in cognitive
sensor networks based on the node selection. IEEE
Sensors Journal, 14, 2376-2383.
Pimentel, D. & Musilek, P. Power management with energy
harvesting devices. CCECE 2010, 2-5 May 2010 2010.
1-4.
Salarian, H., Chin, K.-W. & Naghdy, F. 2014. An energy-
efficient mobile-sink path selection strategy for
wireless sensor networks. IEEE Transactions on
vehicular technology, 63, 2407-2419.
Visser, H. J. & Vullers, R. J. M. 2013. RF Energy
Harvesting and Transport for Wireless Sensor Network
Applications: Principles and Requirements.
Proceedings of the IEEE, 101, 1410-1423.
Zahid Kausar, A. S. M., Reza, A. W., Saleh, M. U. &
Ramiah, H. 2014. Energizing wireless sensor networks
by energy harvesting systems: Scopes, challenges and
approaches. Renewable and Sustainable Energy
Reviews, 38, 973-989.
Lifetime and Buffer-Size Optimization for RF Powered Wireless Sensor Networks
107