
Towards Adaptive Deep Reinforcement Game Balancing
*
Ashey Noblega, Aline Paes and Esteban Clua
Department of Computer Science, Institute of Computing, Niter
´
oi, RJ, Brazil
Keywords:
Game Balancing, Reinforcement Learning, Deep Learning, Dynamic Balancing, Playability.
Abstract:
The experience of a player regarding the difficulty of a video game is one of the main reasons for he/she decide
to keep playing the game or abandon it. Effectively, player retention is one of the primary concerns related to
the game development process. However, the experience of a player with a game is unique, making impractical
to anticipate how they will face the gameplay. This work leverages the recent advances in Reinforcement
Learning (RL) and Deep Learning (DL) to create intelligent agents that are able to adapt to the abilities of
distinct players. We focus on balancing the difficulty of the game based on the information that the agent
observes from the 3D environment as well as the current state of the game. In order to design an agent that
learns how to act while still maintaining the balancing, we propose a reward function based on a balancing
constant. We require that the agent remains inside a range around this constant during the training. Our
experimental results show that by using such a reward function and combining information from different
types of players it is possible to have adaptable agents that fit the player.
1 INTRODUCTION
In video game, the gameplay portrays an important
role to the success of a game. Thus, arguably, even
if a game has the most realistic audiovisual features
or the most fanciful story, but it contains challenges
unsuitable to the player’s ability, this may affect his
experience, making him abandon the game.
Thus, issues related to the gameplay refer to how
the game interacts with the player, such as, the game’s
challenges, objectives, rules, and so on (Southey
et al., 2005). Many efforts have been made to yield
adjustable games such that the player does not get
frustrated by a very difficult game, or bored, when the
game is too easy. Commonly, this problem is tackled
by creating a finite number of difficulty levels (Olesen
et al., 2008) that the players must select according to
their beliefs on which one better fits. Nevertheless,
this is possibly an ineffective solution as the player
may have intermediate skills between these classes or
because he is constantly learning (or forgetting) skills,
or still because the player may have a wrong vision of
its own abilities (Missura and G
¨
artner, 2009).
Thus, terms such as difficulty adjustment (Hu-
nicke, 2005; Missura and G
¨
artner, 2009), adaptive
*
The authors would like to thank NVidia and the Brazi-
lian research agencies CAPES and CNPq for funding this
research.
game (Spronck et al., 2006) and dynamic game bal-
ancing (Andrade et al., 2006) are receiving a great at-
tention in the games’ industry. Particularly, the topic
of dynamic game balancing refers to the process of
automatically changing behaviors, parameters, and/or
elements of the scenarios in a video game in real-time,
to match the game to the ability of a specific player
(Andrade et al., 2005). For a long time, most of the
effort to yield balanced games were based on creating
specific heuristics and/or probabilistic methods that
would hardly adapt to different games or players with
diverse abilities (Silva et al., 2015; Hunicke, 2005).
Based on this motivation, we propose a strategy
where the non-player characters, which can certainly
influence the gameplay, have the ability to learn how
to act and leverage the game balancing. By going in
this direction, we expect that they can match the hu-
man player performance, whatever the game is, and
consequently make the player has more fun and stick
to the game.
To achieve similar game-based goals, previous
works have taken advantage of Machine Learning
methods, focusing on providing artificial agents with
the ability of learning from experience without be-
ing explicitly programmed (Mitchell, 1997; Michal-
ski et al., 2013). Other approaches follow a semi-
automatic analysis of the playability of a game
(Southey et al., 2005), recognizing the level of knowl-
edge the player has to configure opponents (Bakkes
Noblega, A., Paes, A. and Clua, E.
Towards Adaptive Deep Reinforcement Game Balancing.
DOI: 10.5220/0007395406930700
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 693-700
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
693

et al., 2009) and new environments according to the
player’s progress(Lopes et al., 2018).
Other researchers have attacked the same problem
by recognizing the type of player, followed by a com-
parison to groups of similar players and, finally, con-
figuring the game according to the mapped character-
istics (Missura and G
¨
artner, 2009). However, it may
be difficult to fit the player to a group of other players,
as human behavior presents quite singular and unique
traits (Charles et al., 2005).
There are still other approaches that focus on
creating adaptable agents that directly interacts with
the environment, taking advantage of Reinforcement
Learning techniques (Sutton et al., 1998). In this case,
the agent receives the current state of the environment
and a reward value aiming at learning the policy it
should follow. Previous work(Andrade et al., 2005)
has followed this approach by using the classical Q-
learning algorithm (Watkins and Dayan, 1992). Nev-
ertheless, value-based methods such as Q-learning
may face difficulties to deal with continuous space
and may converge slowly, as they are not directly op-
timizing the policy function.
In this work we propose a NPC-agent that does
not need a representative model of the player to
adapt to him, and whose policy is directly in-
duced from how the agent observes the game. To
achieve that, we designed a reward function that is
based on a game-balancing constant and introduce it
into the Proximal-Policy-Opmitization (PPO) (Schul-
man et al., 2017) algorithm, a reinforcement learn-
ing method that directly optimizes the policy using
gradient-based learning. In order to tackle the com-
plexity of the environment, the PPO implementation
we selected follows a Deep Reinforcement Learning
approach (Mnih et al., 2015). In this way, we can also
benefit from the remarkable results that other game-
based problems have recently achieved (Mnih et al.,
2013; Silver et al., 2016; Lample and Chaplot, 2017).
We take advantage of the Unity ML-Agents Toolkit
(Juliani et al., 2018) to implement the graphical envi-
ronments and to run the PPO algorithm. Experimen-
tal results show that we are able to devise adaptable
agents, at least when facing other non-human players.
2 RELATED WORK
The challenge of balancing the game refers to the abil-
ity of a game to modify or adjust its level of difficulty
according to the level of the user so that he can be con-
tent with the game. This includes avoiding that the
player get stressed or bored when playing the game
due to very difficult or easy situations (Csikszentmi-
halyi and Csikszentmihalyi, 1992). In fact, (Andrade
et al., 2006) has showed that satisfaction and balance
are quite related, by asking some players to answer a
series of questions after experiencing a fighting game.
To achieve game balancing, previous work has fo-
cused on trying to add new content (environments,
elements, obstacles, etc., ) regarding the abilities of
the player while others has sought to create intelli-
gent agents capable of facing the player but without
hindering their possible success (Bakkes et al., 2012).
Examples of the first group includes (Bakkes et al.,
2014) and (Hunicke, 2005), which tries to modify
the environment or adding new elements, but know-
ing beforehand how to represent the behavior of the
player within the game.
Regarding the second group, in (Missura and
G
¨
artner, 2009), the authors tried to create an auto-
matic adjustment by first identifying the level of the
player and then fitting him into a specific group (Easy,
Medium or Difficult). The goal is to include a new
player inside one of these groups so that their oppo-
nents are easier or more difficult to confront. That
work sees the identification of the type of player as
a fundamental issue to have balanced games. Our
work aims to avoid creating abstractions and repre-
sentations of the player, as this is sometimes difficult
to observe beforehand. Instead, we focus on repre-
senting the current state of the game to determine the
decision-making policy of the agent against his oppo-
nent.
Meanwhile, (Silva et al., 2015) uses a heuristic
function to determine the performance of the player
when facing his enemies during the game and, accord-
ing to it, the difficulty of the game is increased or de-
creased. Regarding the use of Reinforcement Learn-
ing (RL), which is the Machine Learning technique
most used to game-based issues, (Andrade et al.,
2006) adopted RL to teach a virtual agent to imitate
the player. After that, the agent is further trained to
balance the difficulty of the game. The work pre-
sented in (Andrade et al., 2005), unlike to the previous
one, only used RL to teach the agent to fight and the
balancing is achieved by a heuristic function tuned ac-
cording to the abilities of the player. We do not intend
to teach the agent to imitate a player, but, instead, we
aim at devising an agent that learns altogether how to
play the game and how to adapt to the player.
3 REINFORCEMENT LEARNING
In this work we rely on Reinforcement Learning (Sut-
ton et al., 1998) to make the agent learn how to act to
achieve game balancing. We benefit from the Unity
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
694

ML-agents (Juliani et al., 2018) to implement the
game environment coupled with the RL algorithms’
implementation. In this section we overview both
these components of our work.
Reinforcement Learning aims at teaching the
agent to make decisions when facing a certain situa-
tion through trial and error. When learning, the agent
receives an stimuli in the form of a reward so that it
can evaluate if the chosen action was good for the de-
cision making or not.
A RL task can be formally described as a Markov
Decision Process (MDP) (White III and White, 1989).
Thus, at each time step t of the decision making
process, the environment is represented by a state
s ∈ S (the set of states), and the agent may choose
an action a ∈ A(the set of actions) that is available
in the state s. A transition function (possibly non-
determinisic) T ∇ defines indicates the state s
0
that
the agent will land on in the instant t + 1, given it
has taken action a in t when it was in the state s. Af-
ter going from the state s to the state s
0
because of
the action a, the agent receives an immediate reward
R
a
(s, s
0
). A discount factor γ indicates how the future
rewards matters compared to the current one.
The overall goal is to find a policy π
∗
=
argmax
a
E[R|π] that maps from states to actions in or-
der to maximize the accumulated reward R (obtained
from the environment in every rollout of a policy) of
all states(Sutton et al., 1998).
Proximal Policy Optimization. As the RL method,
in this work we follow the Proximal Policy Opti-
mization algorithm due to its recent success on han-
dling a number of game problems (Schulman et al.,
2017). It is a policy search-based method largely in-
spired on the Advantage Actor Critic (A2C) frame-
work (Mnih et al., 2016). The Advantage Actor
critic method relies on a gradient estimator coupled
with an advantage function
ˆ
A
t
= −V (s
t
)+r
t
+γr
t+1
+
··· + γ
T −t+1
r
T −1
+ γ
T −t
V (s
T
) such that ˆgL
PG(θ)
=
ˆ
E [∇
θ
logπ
θ
(a
t
|s
t
)A
t
]. The estimator of the advantage
function runs the policy for T timesteps instead of
waiting to the end of the episode to collect the reward,
and uses those collected samples to update the policy.
Here is where the Critic comes, to estimate the
advantage function value. Within Deep Reinforce-
ment Learning, we have a neural network to estimate
π(s, a, θ) (the actor) and another one to estimate the
advantage function (the critic), where they possibly
have shared parameters.
Algorithm 1 reproduces the PPO algorithm
from (Schulman et al., 2017). Note that L represents
either a clipped version or a KL-penalized version of
the objective function differentiated through the esti-
mator ˆg.
Algorithm 1: PPO top-level algorithm, Actor-Critic style,
as presented in (Schulman et al., 2017).
for iteration = 1, 2, ... do
for actor = 1 to N do
Run policy π
θ
old
in environments for T
timesteps;
Compute advantage estimates
ˆ
A
1
, ...,
ˆ
A
T
;
end
Optimize surrogate L wrt θ, with K epochs
and minibatch size M ≤ NT ;
θ
old
← θ
end
4 BALANCING GAMES WITH
DEEP RL AND A BALANCING
CONSTANT
This work aims at creating a game agent with two im-
plicit goals that should be targeted at the same time:
learning how to play a game and, at the same time,
learning how to go keep up with the player to main-
tain the game balanced. To that, we build a reinforce-
ment learning task and use the PPO algorithm to solve
it due to one main reason: our task contemplates a
continuous space and policy search is more appro-
priate to tackle this kind of environment. Moreover,
PPO has succeeded in a number of other game-based
tasks (Schulman et al., 2017). In this section we bring
the details of our contributions.
Reward Function. A key component of an RL task
is how we reward or penalize the learner according to
his actions in the environment. To tackle the balanc-
ing game problem, the reward function must envision
the behavior of the agent in the game environment
(for example, how to move, or how to fight) along
with the balancing itself (how to not bw much worse
or much better than the player). Thus, we propose a
game-based reward function that includes a balancing
constant aiming at pointing out how the agent can be
a fair opponent to the player. In this way, he will have
some implicit knowledge on how far (or near) he is
from the desired balanced state and, if he is within it,
how he should behave in such a state.
Balancing Constant (BC). The balancing state
refers to the moments of the game that a skill dif-
ference remains in a certain range(1). The intuition
behind this is that in such a state, the agent is not
Towards Adaptive Deep Reinforcement Game Balancing
695
that easy to confront or that difficult to overcome by
the player. Consequently, the balancing constant is a
value that helps our function to achieve the desired
behaviour. In other words, this constant means the
maximum skill difference between the agent and the
player.
0 ≤ ∆Skill ≤ BC (1)
BC-Based Reward Function (BCR). Neverthe-
less, by using the BC in our reward function it is pos-
sible to distinguish two additional situations when the
agent is not in a balanced state, i.e., the BCR can iden-
tify in which situation the agent is and, according to
it, to provide a reward value to stimulate the desired
learning (equation 2). The three reward situations are
as follows:
Subjugated Punishment (SP), defined as
∆Skill < 0: In this case, the reward value is di-
rectly proportional to the inability of the agent to
represent an obstacle to the player, i.e., the more
docile the agent is the more it will be punished.
Conservation Reward (CR), defined as , 0 ≤
∆Skill ≤ BC: In this case, the reward value represents
a compensation for maintaining the degree of com-
petition within the desired range of the BC, which in
turn encourages the agent to reach the limit of equi-
librium.
Rebellious Punishment (RP), defined as BC <
∆Skill. This is an inverse retaliation to the Subju-
gated Punishment case, obtained by overcoming the
BC limit that the agent can have with respect to his
opponent.
BCR(∆Skill) =
∆Skill
Skill
max
, i f ∆Skill < 0
∆Skill
BC
, i f 0 ≤ ∆Skill ≤ BC
−
∆Skill−BC
Skill
max
−BC
, i f BC < ∆Skill
(2)
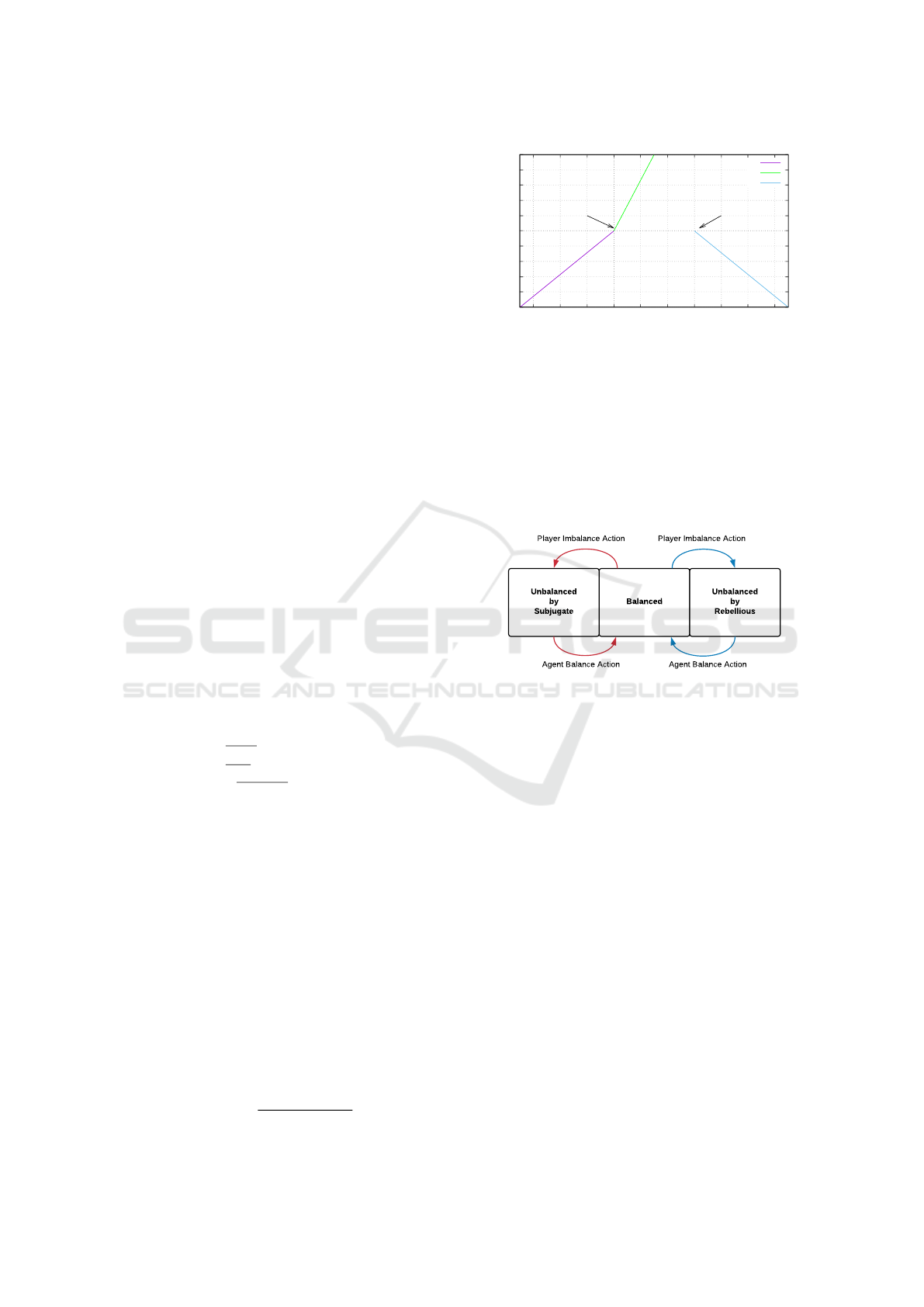
We can see in the figure 1 that BCR(∆Skill) is a
piece-wise function that reflects our idea of the three
possible major cases that the agent may attained dur-
ing training. Thus, if the agent is very distant from
the range of balancing, consequently, it will receive
an even greater punishment; on the other hand, if it
gets to be within the balancing state, it is stimulated
to reach the limit of the range.
BC-Based Balancing Metric (BCM). The BCM
(equation 3) is a measure that allows for evaluating
the percentage of times that an agent is in one of the
states reflecting the three situations mentioned above:
Unbalanced by Subjugate, Balanced, or Unbalanced
by Rebellious.
BCM =
T
B
T
US
+ T
B
+ T
UR
(3)
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
-30 -20 -10 0 10 20 30 40 50 60
Minimum difference Maximum difference
Reward
ΔSkill
SP
CR
RP
Figure 1: The BC-Based Reward Function with BC = 30
and Skill
max
= 100.
Our hypothesis is that as a base case of balanc-
ing, the player can perform different actions that may
cause the agent to receive a punishment for not keep-
ing the game within the BC interval, so the agent
must perform an action to control this situation. Con-
versely, an unbalanced state will make the agent to ex-
ecute an action to move the game to a balanced state,
as shown in figure 2.
Agent Balance ActionAgent Balance Action
Player Imbalance ActionPlayer Imbalance Action
Balanced
Unbalanced
by
Rebellious
Unbalanced
by
Subjugate
Figure 2: Minimal Agent Balancing Interaction.
5 EVALUATION
In this section we present our test scenario and show
the results we have obtained with the game balancing
method we proposed here.
5.1 Unity ML-Agents Toolkit
To produce the game environment scenarios and run
the RL algorithm, we rely on The Unity ML-Agents
Toolkit (Juliani et al., 2018). It is a free-source toolkit
that allows the development of virtual environments
to serve as training scenarios for intelligent agents,
using machine learning algorithms based on Ten-
sorFlow (Abadi et al., 2016). The toolkit contains
three high-level key components: (1) the Learning
Environment, containing all the elements of the
game that are part of the Unity, (2) the Python API,
composed of the training algorithms, and (3) the
External Communicator, connecting the Python API
to the Unity.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
696

The toolkit has a component called Brain which
contains three elements of the RL task: (1) the Ob-
servation, which is the information provided by the
agent about the environment, either in a numerical
format (floating-point number vector) or visual (im-
ages taken by the cameras linked to the agent); (2)
the Action, represented as a vector of continuous or
discrete actions; and (3) the Reward.
Furthermore, a set of extensible examples using
different RL algorithms are available in the toolkit.
The Proximal Policy Optimization (PPO) (Schulman
et al., 2017) implemented in the toolkit has the pos-
sibility of propagating its performance with the In-
trinsic Curiosity Module (ICM) or even with a Long-
Short-Term Memory model (LSTM). As we previ-
ously mentioned, we focus on creating an intelligent
agent based on the PPO algorithm.
5.2 Test Game Scenario
We evaluate our game balancing method in an en-
vironment similar to the commercial game Capcom
Street Fighter, inspired by (Andrade et al., 2006). The
game consists of the confrontation of two entities (the
agent and the player), whose objective is to defeat the
opponent through physical attacks. The game ends
when one of them makes the other to be lifeless or
when the time of 100 seconds has passed. In this last
case, the winner is the player that has more life points
in the end of the game. This game is based on a 3D
environment, like most of the current video games
5.3 Player Simulation
To simulate the behavior of players with distinctive
nature, we created two types of enemies with different
abilities that are going to confront our learner agent,
as follows:
• Defensive Simulation: This programmed enemy
emulates the behavior of a player whose goal is
to win by a minimum difference. Thus, he adopts
a defensive posture to avoid taking any damage
while still maintaining his advantage.
• Aggressive Simulation: The behavior of this
other type of emulated player differs from the pre-
vious one because this one tries to win with the
maximum possible difference, i.e., it will try to at-
tack all the possible times to generate the greatest
damage in our learner agent.
5.4 Skill Study
Naturally, as we work with a fighting game, we con-
sider adequate to measure the balance of the game by
computing the difference in the life health score of the
agent and the player (Equation 4). Therefore, the bal-
ancing state is assumed as long as the agent maintains
a difference within the BC interval (Equation 5).
∆H = H
Agent
− H
Player
(4)
0 ≤ ∆H ≤ BC (5)
In this way, our objective is advising the agent
to maintain a life difference not bigger than the BC
along the game time, as shown in Figure 3.
(a) Balancing State at the time t
i
(b) Balancing State at the time t
i+1
Figure 3: Persistence of the BC throughout the game with
BC = 30.
5.5 Observation Parameters (State) and
Actions
The reinforcement learning task requires that we ab-
stract the environment into the state representation so
that the agent can make a decision regarding their ac-
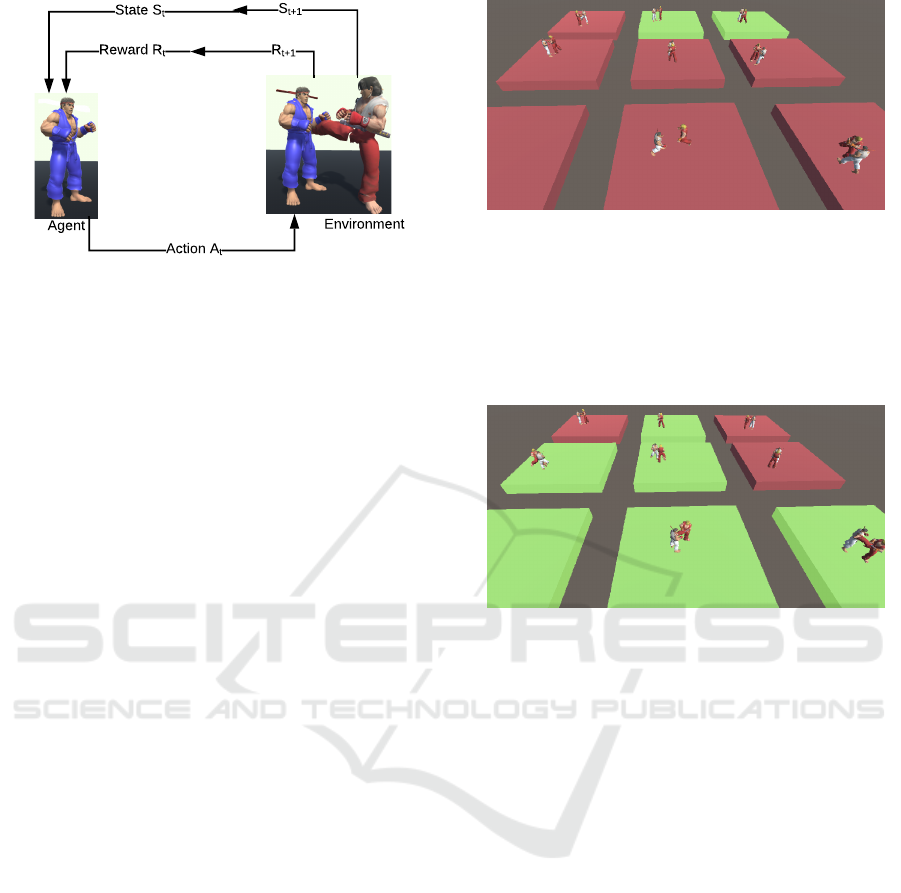
tions. Figure 4 illustrates the learning loop of our
study game. Thus, as we tackle a fighting game, we
represent the observation of the current state of the
game using the following information:
• Information related to the physical space: distance
between the learner agent and the player.
• Information related to the balancing constant: the
value of the difference between the health of the
agent and the health of the player and the type of
reward the agent receive (subjugated or rebellious
punishment, or conservative reward.
• Information related to the actions: the last action
of the agent and the player, as well as a discrete
value that tells us if the player has changed action
since the last observation.
All of these values are normalized between -1 and
1, as a recommendation of the Unity plugin for better
performance.
Concerning the actions, both agents can Move
(Walk forward, Walk Backward), Duck and Attack
(Kick, Punch).
Towards Adaptive Deep Reinforcement Game Balancing
697
Agent
Action A
t
Reward R
t
State S
t
S
t+1
R
t+1
Environment
Figure 4: RL process focused on games.
5.6 Experimentation
The experimentation process was carried out using
three values of BC (20,30 and 40), which the agent
uses as a limit of their ability. As we described ear-
lier, we created two different types of emulated play-
ers to face our agent and allows him to train, aiming
at obtaining:
• Two different types of agents, namely an aggres-
sive and a defensive one, which fight and behave
within the boundary of the BC when confronted
with their same type of emulated agent.
• A third type of agent (Mixed Agent) that is trained
with the two different types of emulated players.
Thus, we would like to demonstrate that given the
experience of facing different types of players, the
agent can adapt to them when it is necessary.
We change some default parameters of the PPO
implementation to improve the training. The first one
is the β parameter, responsible for defining how the
agent explores its actions. The greater is this value,
the more at random the agent chooses its actions and,
therefore, the more it will explore the action space
during its training. This variable is directly related
to the strength of the entropy regularization. We set
this variable as (1e − 5) so that our agent experiences
new possibilities and applies the learned model to
reach the goal. During the experiments, smaller val-
ues make the agent learn only a certain number of ac-
tions that, while helped him reach part of his goals,
were very repetitive. The learning rate parameter was
also adjusted with the same intent as the β parame-
ter. We set this variable to be (5e − 4) so that the
agent maintains an equilibrium between not learning
too fast or delaying too much by exploring new ac-
tions. The other parameters were kept with the default
values of the plugin.
We created 9 independent copies of the scene to
accelerate the training by working together to find a
better policy. All of them have the emulation of one
type of the player’s behavior, except for the mixed
Figure 5: Initial stage of the training process with 9 scenes
in parallel.
agent training that had 4 passive and 5 aggressive em-
ulations. The figure 5 shows us how each of them is
independent from each other: some of them are in a
balanced state (green platforms) while others have not
reached the best policy.
Figure 6: Intermediate stage of the training process with 9
scenes at the same time.
5.7 Results
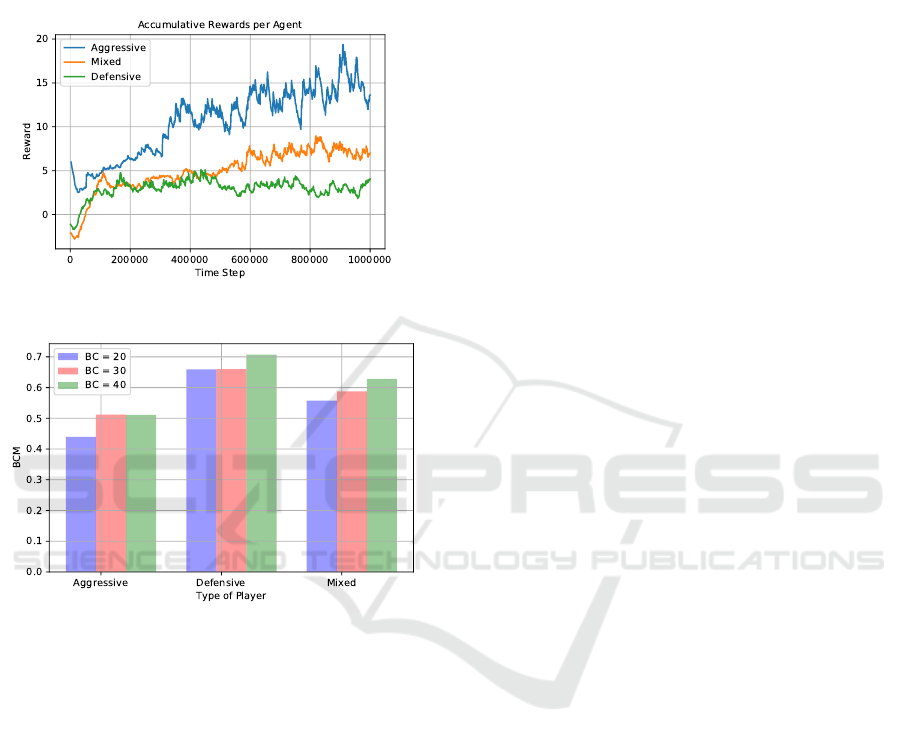
Based on our experiments, we start by indicating that
after 500k steps the agent tends to continuously im-
prove its policy, generating a greater reward, as shown
in Figure 7 and many of the 9 scenarios manage to
balance the game (Figure 6). Hence, in the case of
the agents that learn from only one type of player,
we observed that the agent who faces aggressive em-
ulation did not take long to learn the (defensive) pol-
icy and then maintain it until the number of iterations
is finished. Because the emulation is so aggressive,
the agent learned that it is better to defend itself and
maintain a minimum difference than trying to reach
a ∆Skill = BC or higher (be more aggressive). Un-
like the other, he tries to be more aggressive and his
training goes more slowly since the agent must also
learn how to attack (to reach the balancing state) and
defend himself (to stay within the balancing state).
Figure 7 shows how the agent that learns with the
mixed simulated types of players has an intermedi-
ate reward gain between the other two cases. This is
likely due to the fact that he must learn how to behave
when facing two different strategies of its opponents,
consequently, he has more things to learn. Regarding
the balancing constant values, the results show that
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
698
when the BC is higher, the agent is able to maintain
his skill difference with respect to the player into the
interval of balancing. He is also able to remain in the
balanced state even when he suffers some damage by
the opponent because there is still some life difference
between them.
Figure 7: Accumulated Reward throughout the training.
Figure 8: Evaluation on BC-Metric.
Conversely, it is quite hard to preserve the equilib-
rium when the BC is small because any wrong action
by the agent could take it to any of the unbalanced
states. For example, we can observe in Figure 8 when
the agent has a BC = 20 and he needs to fight against
an aggressive player, the former spends a little less
than 50% of the time in our target balanced state.
Finally, our BC-Metric showed 3 interesting
points. First, the agent remains at least 50% of time in
the state of balancing in all cases, except when BC =
20 as we described before. Second, we see some evi-
dence to confirm the hypothesis about a small value of
BC, showing that in this case, it is difficult to stay in
the balanced state with a narrow range. Third, the re-
sults show that by offering new experiences through
the mixed agent, it is able to achieve a better deci-
sions because he learns a new type of behavior that
one style alone cannot offer, In this case, the results
exceed 50% of BC-Metric, even with a BC = 20, as
exhibited in the Figure 8.
6 CONCLUSIONS
Game balancing faces the complex challenge of
adapting the virtual characters to the same (or a
higher) level as the player. In this work, we con-
tributed with a deep reinforcement learning strategy
that aims at reaching such a balancing through the re-
ward function. To that, we designed a function that
makes use of a balancing constant to limit and mea-
sure the behavior of the agent. By training the agent
with such a function, we were able to not only limit-
ing the agent to behave like the player (when the BC
is zero), but we also gave him the possibility of stim-
ulating himself to learn the games’ actions, so that it
is still a good adversary to the player. With the exper-
imental results, we could observe that the agent stays
as long as possible in a balanced state (at least 50%
of the game). Furthermore, we could see that it can
learn new ways of acting when confronting different
styles of players.
As future work, we intend to deeply explore the
adaptability of the agent, by composing rewards that
point out to more granular aspects such as resistance
and stamina, and gathering the results when it con-
fronts real players.
REFERENCES
Abadi, M. et al. (2016). Tensorflow: A system for large-
scale machine learning. In 12th USENIX Sympo-
sium on Operating Systems Design and Implementa-
tion (OSDI 16), pages 265–283.
Andrade, G., Ramalho, G., Gomes, A. S., and Corruble, V.
(2006). Dynamic game balancing: An evaluation of
user satisfaction. AIIDE, 6:3–8.
Andrade, G., Ramalho, G., Santana, H., and Corruble, V.
(2005). Extending reinforcement learning to provide
dynamic game balancing. In Proc. of the Workshop
on Reasoning, Representation, and Learning in Com-
puter Games, 19th Int. Joint Conference on Artificial
Intelligence (IJCAI), pages 7–12.
Bakkes, S., Tan, C. T., and Pisan, Y. (2012). Personalised
gaming: a motivation and overview of literature. In
Proc. of The 8th Australasian Conference on Interac-
tive Entertainment: Playing the System, page 4. ACM.
Bakkes, S., Whiteson, S., Li, G., Viniuc, G. V., Charitos, E.,
Heijne, N., and Swellengrebel, A. (2014). Challenge
balancing for personalised game spaces. In 2014 IEEE
Games Media Entertainment, pages 1–8.
Bakkes, S. C., Spronck, P. H., and Van Den Herik, H. J.
(2009). Opponent modelling for case-based adaptive
game AI. Entertainment Computing, 1(1):27–37.
Charles, D., Kerr, A., McNeill, M., McAlister, M., Black,
M., Kcklich, J., Moore, A., and Stringer, K. (2005).
Player-centred game design: Player modelling and
adaptive digital games. In Proc. of the digital games
research conference, volume 285, page 00100.
Towards Adaptive Deep Reinforcement Game Balancing
699

Csikszentmihalyi, M. and Csikszentmihalyi, I. S. (1992).
Optimal experience: Psychological studies of flow in
consciousness. Cambridge university press.
Hunicke, R. (2005). The case for dynamic difficulty adjust-
ment in games. In Proc. of the 2005 ACM SIGCHI In-
ternational Conference on Advances in computer en-
tertainment technology, pages 429–433. ACM.
Juliani, A., Berges, V.-P., Vckay, E., Gao, Y., Henry, H.,
Mattar, M., and Lange, D. (2018). Unity: A General
Platform for Intelligent Agents. ArXiv e-prints.
Lample, G. and Chaplot, D. S. (2017). Playing fps games
with deep reinforcement learning. In AAAI, pages
2140–2146.
Lopes, R., Eisemann, E., and Bidarra, R. (2018). Authoring
adaptive game world generation. IEEE Transactions
on Games, 10(1):42–55.
Michalski, R. S., Carbonell, J. G., and Mitchell, T. M.
(2013). Machine learning: An artificial intelligence
approach. Springer.
Missura, O. and G
¨
artner, T. (2009). Player modeling for
intelligent difficulty adjustment. In Int. Conference
on Discovery Science, pages 197–211. Springer.
Mitchell, T. (1997). Machine learning. McGraw-Hill
Boston, MA:.
Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T.,
Harley, T., Silver, D., and Kavukcuoglu, K. (2016).
Asynchronous methods for deep reinforcement learn-
ing. In Int. Conference on Machine Learning, pages
1928–1937.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,
Antonoglou, I., Wierstra, D., and Riedmiller, M.
(2013). Playing atari with deep reinforcement learn-
ing. arXiv preprint arXiv:1312.5602.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness,
J., Bellemare, M. G., Graves, A., Riedmiller, M., Fid-
jeland, A. K., Ostrovski, G., et al. (2015). Human-
level control through deep reinforcement learning.
Nature, 518(7540):529.
Olesen, J. K., Yannakakis, G. N., and Hallam, J. (2008).
Real-time challenge balance in an rts game using rt-
neat. 2008 IEEE Symposium On Computational Intel-
ligence and Games, pages 87–94.
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and
Klimov, O. (2017). Proximal policy optimization al-
gorithms. arXiv preprint arXiv:1707.06347.
Silva, M. P., do Nascimento Silva, V., and Chaimowicz,
L. (2015). Dynamic difficulty adjustment through an
adaptive AI. In Computer Games and Digital Enter-
tainment (SBGames), 2015 14th Brazilian Symposium
on, pages 173–182. IEEE.
Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L.,
Van Den Driessche, G., Schrittwieser, J., Antonoglou,
I., Panneershelvam, V., Lanctot, M., et al. (2016).
Mastering the game of go with deep neural networks
and tree search. nature, 529(7587):484.
Southey, F., Xiao, G., Holte, R. C., Trommelen, M., and
Buchanan, J. W. (2005). Semi-automated gameplay
analysis by machine learning. In AIIDE, pages 123–
128.
Spronck, P., Ponsen, M., Sprinkhuizen-Kuyper, I., and
Postma, E. (2006). Adaptive game AI with dynamic
scripting. Machine Learning, 63(3):217–248.
Sutton, R. S., Barto, A. G., Bach, F., et al. (1998). Rein-
forcement learning: An introduction. MIT press.
Watkins, C. J. and Dayan, P. (1992). Q-learning. Machine
learning, 8(3-4):279–292.
White III, C. C. and White, D. J. (1989). Markov deci-
sion processes. European Journal of Operational Re-
search, 39(1):1–16.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
700
