Liquidity Stress Detection in the European Banking Sector
Richard Heuver
1
and Ron Triepels
1,2
1
De Nederlandsche Bank, Amsterdam, The Netherlands
2
Tilburg University, Tilburg, The Netherlands
Keywords:
Liquidity Stress, Risk Monitoring, Financial Market Infrastructures, Large-value Payment Systems.
Abstract:
Liquidity stress constitutes an ongoing threat to financial stability in the banking sector. A bank that manages
its liquidity inadequately might find itself unable to meet its payment obligations. These liquidity issues, in
turn, can negatively impact the liquidity position of many other banks due to contagion effects. For this reason,
central banks carefully monitor the payment activities of banks in financial market infrastructures and try to
detect early-warning signs of liquidity stress. In this paper, we investigate whether this monitoring task can be
performed by supervised machine learning. We construct probabilistic classifiers that estimate the probability
that a bank faces liquidity stress. The classifiers are trained on a dataset consisting of various payment features
of European banks and which spans several known stress events. Our experimental results show that the
classifiers detect the periods in which the banks faced liquidity stress reasonably well.
1 INTRODUCTION
It is the nature of banks to attract deposits and pro-
vide loans. The maturity mismatch of short-term de-
posits versus long-term loans makes banks vulnerable
to liquidity risk. Liquidity risk is ”the risk that a firm
will not be able to meet efficiently both expected and
unexpected current and future cash flow and collat-
eral needs” (BIS, 2008). When a bank does not man-
age its liquidity adequately, it might find itself unable
to fulfill its short-term payment obligations and face
bankruptcy. These liquidity issues, in turn, can spread
across a payment system and affect the liquidity po-
sition of many other banks. For this reason, central
banks closely monitor the payment activities of banks
and try to anticipate early signs of liquidity stress.
In recent years, the payment data generated by Fi-
nancial Market Infrastructures (FMIs) has become an
important new source to detect liquidity risks. FMIs
are often called the financial backbone of our modern
society. Their main purpose is to facilitate the clear-
ing, settlement, and recording of monetary and other
financial transactions. The most important FMIs are
the Large-Value Payment Systems (LVPSs) which are
developed and maintained by central banks to process
high-value payments and administer monetary policy.
The transaction log generated by such systems pro-
vides detailed insight into the payment behavior of
banks and can be analyzed to detect cases were banks
manage their liquidity in an unsafe manner.
Several unsupervised methods have been pro-
posed for this purpose based on traditional statistics,
see e.g. (Heijmans and Heuver, 2014), and unsu-
pervised machine learning, see e.g. (Triepels et al.,
2018). The idea behind these methods is to derive the
patterns by which banks usually manage their liquid-
ity from the transaction log of an LVPS and search for
cases where the current payment behavior of banks
deviates from their expected patterns. Such anoma-
lies can be due to a bank facing liquidity stress which
forces it to change its payment behavior.
However, a drawback of these unsupervised meth-
ods is that it can be difficult to determine what kind
of patterns are learned about the payment behavior of
banks. In addition, when there is a significant devi-
ation between the expected and current payment be-
havior of a bank, it is often not clear whether this de-
viation is due to the bank facing liquidity stress or
whether the bank needs to pay some unusual one-time
payments that do not pose a real threat to its liquidity
position on the long-term.
This paper aims to investigate whether liquidity
stress at banks can also be detected by supervised
machine learning. In supervised machine learning, a
model is trained from a labeled training set contain-
ing explicit examples of the output to be predicted. A
supervised machine learning model can be trained to
detect whether a bank is likely facing liquidity stress
by learning the patterns that are characteristic for a
266
Heuver, R. and Triepels, R.
Liquidity Stress Detection in the European Banking Sector.
DOI: 10.5220/0007395602660274
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 266-274
ISBN: 978-989-758-350-6
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

stressed and non-stressed bank. These patterns can be
derived from historical labeled payment data of a pre-
selected set of banks that faced known stress events
such as a takeover or bank run.
There are two main challenges to make this super-
vised method work in practice. First, stress events at
banks are quite rare and typically last for only a few
days which makes it difficult to learn the patterns of
a stressed bank. Second, there is currently not much
data recorded about stress events at banks, and such
data is difficult to obtain.
In this paper, we show how these challenges can
be addressed. We construct several probabilistic clas-
sifiers that estimate the probability that a bank faces
liquidity stress. The classifiers are trained on a dataset
that describes the payment behavior of several Euro-
pean banks over the past ten years. We elaborate on
how to deal with the imbalance between stress and
non-stress examples by training the classifiers based
on a weighted loss function. Furthermore, we dis-
cuss how we labeled the dataset by searching online
for news articles about stress events at the banks. Al-
though the quality of the stress classes is not ideal,
we will show that the classifiers detect liquidity stress
reasonably well.
2 RELATED RESEARCH
Many papers have studied the problem of predicting
the emergence of a financial crisis in a country. Fi-
nancial crises are predicted from historical panel data
consisting of macroeconomic variables such as the
GDP growth rate of a country. Traditionally, this has
been done by a logit model (Demirg-Kunt and Detra-
giache, 1998) or by the signal extraction method of
(Kaminsky and Reinhart, 1999). An extensive com-
parison of these two methods can be found in (Davis
and Karim, 2008). More recent papers have also ex-
plored how machine learning can be applied to predict
financial crises. For example, (Chamon et al., 2007)
applied a random forest to predict the emergence of
a capital account crisis based on a wide range of
macroeconomic features categorized by four sectors
(external, fiscal, financial, and corporate). Moreover,
(Fioramanti, 2008) constructed a multi-layer percep-
tron network to predict the emergence of a sovereign
debt crisis based on a large set of internal, external,
and debt related features of a country.
There are also many papers that have studied the
problem of predicting how well a bank performs. This
problem is called bank performance prediction. Typi-
cally, the performance of a bank is predicted from fi-
nancial ratios that are derived from the financial state-
ments of banks such as their balance sheets. Early
papers on this topic predict bank performance based
on statistical methods such as discriminant analysis,
see (Beaver, 1966; Altman, 1968). In recent years,
machine learning is also becoming increasingly pop-
ular in this research area. Several machine learning
techniques have been applied to perform bank per-
formance prediction including neural networks (Tam,
1991) and support-vector machines (Min and Lee,
2005). An extensive overview of these techniques can
be found in (Kumar and Ravi, 2007).
The problem studied in this paper is similar to
bank performance prediction. However, we predict
stress at banks based on features derived from the pay-
ment data generated by FMIs. We call this problem
liquidity stress detection. The use of payment data
has some advantages over financial statements. Un-
like financial statements, payment data can be made
available in near real-time, provides detailed insight
into the liquidity management of banks, and cannot
be easily manipulated (e.g. by window dressing).
3 LIQUIDITY STRESS
DETECTION
In this section, we formalize the problem of liquidity
stress detection (section 3.1 until 3.3). Furthermore,
we discuss how this problem can be solved by a lo-
gistic regression model (section 3.4) and multi-layer
perceptron network (section 3.5).
3.1 Notation
Let B = {b
1
, . . . , b
n
} be a set of n banks and T =
{t
1
, . . . ,t
l
} a set of l time intervals. The time intervals
are consecutive, equally spaced, and collectively span
the operating time of the financial system (e.g. by
days or hours). Furthermore, let:
x
(k)
i
= [x
(k)
i1
, . . . , x
(k)
im
]
T
(1)
be a column vector of m payment features of bank b
k
at time interval t
i
. Each feature vector describes the
payment behavior of a bank at a particular time in-
terval and includes features related to the bank’s liq-
uidity position, payment flows, and collateral. We de-
note the set of all feature vectors by X . Finally, let
y
(k)
i
∈ {0, 1} be the stress class that indicates whether
bank b
k
faces liquidity stress at time interval t
i
.
3.2 Classification Problem
Our goal is to construct a probabilistic classifier that
classifies a feature vector by whether or not the cor-
Liquidity Stress Detection in the European Banking Sector
267

responding bank faces liquidity stress. We can define
this classifier as a probability function:
f : X → [0, 1] (2)
where:
f (x
(k)
i
) = P(y
(k)
i
= 1|x
(k)
i
) (3)
is the conditional probability that bank b
k
faces liq-
uidity stress given that we observe feature vector x
(k)
i
at time interval t
i
. A bank is classified as facing liq-
uidity stress if f (x
(k)
i
) is high, i.e.:
φ(x
(k)
i
, ζ) =
(
1, if f (x
(k)
i
) ≥ ζ
0, otherwise
(4)
Here, ζ ∈ [0, 1] is a threshold close to one that deter-
mines how confident the classifier needs to be to clas-
sify a feature vector as belonging to a stressed bank.
3.3 Model Assumptions
Throughout this paper, we consider the case of esti-
mating f under the following two assumptions:
1. Payment features and stress classes are indepen-
dent of each bank, i.e. (x
(a)
i
, y
(a)
i
) is independent
of (x
(b)
i
, y
(b)
i
) for each time interval t
i
∈ T and
a 6= b.
2. Payment features and stress classes are time
invariant, i.e. (x
(k)
a
, y
(k)
a
) is independent of
(x
(k)
b
, y
(k)
b
) for each bank b
k
∈ B and a 6= b.
These assumptions do not hold in practice but greatly
simplify the detection of liquidity stress. It is well
known that liquidity issues can spread across banks
by contagion effects. Moreover, a bank that is cur-
rently facing liquidity stress has a higher probability
to be also stressed in the next time intervals since liq-
uidity issues can take quite some time before they are
resolved. We will show that, even by making these
strong simplifications, we can detect liquidity stress
quite well.
Not every classifier is suitable to estimate f . We
want a classifier that produces well-calibrated prob-
abilities and can deal with severely imbalanced data.
In our experiments, the probability of a feature vec-
tor belonging to a stressed bank was less than 0.1
percent. Such severely imbalanced data harms the
performance of many classifiers. A logistic regres-
sion model or multi-layer perception network is par-
ticularly suited to estimate f . Both types of mod-
els are probabilistic and have found to produce well-
calibrated probabilities in practice (Niculescu-Mizil
and Caruana, 2005). Moreover, they can be easily
adapted to deal with unbalanced data.
3.4 Logistic Regression
Logistic Regression (LR) is a simple probabilistic bi-
nary classifier. It is an extension of multiple linear
regression to the case where the response variable of
the regression model is a binary variable.
We consider the following LR model to detect liq-
uidity stress:
ˆy
(k)
i
= σ(wx
(k)
i
+ b) (5)
where, w is a m-dimensional row vector of weights, b
is a bias term, and σ is the sigmoid function:
σ(x) =
1
1 + e
−x
(6)
The sigmoid function in equation 5 rescales the linear
combination to the range (0, 1). The output ˆy
(k)
i
is an
estimate of f (x
(k)
i
).
3.5 Multi-Layer Perceptron
A Multi-Layer Perceptron (MLP) network is a type
of feed-forward neural network. It is similar to an
LR model with the exception that it processes input
features through one or more hidden layers consisting
of non-linear computational units. These additional
hidden layers enable the MLP network to learn a non-
linear mapping from its inputs to its outputs.
We focus on an MLP network consisting of mul-
tiple hidden layers and a single sigmoid output. Let δ
be the number of layers or depth of the network and s
i
the size of the i-th layer. We denote the output of the
i-th layer by h
i
. The first layer of the network is the
input layer, and the output of this layer is the feature
vector that is presented to the network:
h
1
= x
(k)
i
(7)
The input is processed through the hidden layers. The
output of the i-th layer is:
h
i
= ψ
(s
i
)
(W
i
h
i−1
+ b
i
) for 1 < i < δ (8)
where, W
i
is a s
i
by s
i−1
matrix of weights, b
i
is a s
i
-
dimensional column vector of bias terms, and ψ
(s
i
)
(x)
is a set of s
i
non-linear activation functions that are
applied to each element of x. Usually, ψ is taken to be
the hyperbolic tanh function (LeCun et al., 1998) or
rectified linear function (Glorot et al., 2011). Finally,
the output of the last hidden layer h
δ−1
is processed
through a single sigmoid unit:
ˆy = h
δ
= σ(w
δ
h
δ−1
+ b
δ
) (9)
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
268

where w
δ
is a s
δ
-dimensional row vector of weights
and b is a bias term. The output h
δ
of the final layer
is an estimate of f (x
(k)
i
).
3.6 Model Estimation
The parameters of the LR model and MLP network
can be estimated from a historical dataset of features
vectors with known stress classes. Let Θ be the set
of parameters to be optimized. Moreover, let D =
{d
1
, d
2
, . . . } be a dataset of tuples where each tuple:
d
j
= (x
(k)
i
, y
(k)
i
) (10)
consists of a feature vector x
(k)
i
and corresponding
stress class y
(k)
i
. We find optimal values for the pa-
rameters by minimizing the mean cross entropy. The
cross entropy of a single feature vector is:
J (x
(k)
i
, y
(k)
i
) = −y
(k)
i
log ˆy
(k)
i
(11)
− (1 − y
(k)
i
)log(1 − ˆy
(k)
i
) (12)
The cross entropy averaged over all feature vectors in
D is:
J (D) =
1
|D|
∑
d∈D
J (x
(k)
i
, y
(k)
i
) (13)
The optimal values of the parameters are found by
solving the following optimization problem:
Θ
∗
= arg min
Θ
J (D) (14)
Usually, such a problem is solved by gradient-based
optimization in conjunction with back-propagation
(Werbos, 1982; Bottou, 2004).
However, an issue in our application is that the
stress classes are highly imbalanced which makes it
difficult to solve equation 14 by gradient-based opti-
mization. One way to deal with this issue is to opti-
mize a weighted version of cross entropy which also
takes into account the probability of a feature vector
belonging to a stressed bank. The weighted cross en-
tropy of a single feature vector is:
J
0
(x
(k)
i
, y
(k)
i
) = −ay
(k)
i
log ˆy
(k)
i
(15)
− (1 − a)(1 − y
(k)
i
)log(1 − ˆy
(k)
i
) (16)
where a ∈ (0, 1) is the importance that we assign to
predicting the stress class correct. We set a equal to
the probability that a feature vector does not belong
to a stressed bank. In this way, when there are fewer
stress examples in the dataset, there is a higher incen-
tive for the classifiers to assign a high probability to
the stress examples.
4 EXPERIMENTAL SETUP
In this section, we elaborate on a series of experi-
ments that were conducted to determine how well the
LR model and MLP network detect liquidity stress in
real-world data. We discuss the characteristics of the
data (section 4.1 until 4.4), the implementation of the
classifiers (section 4.5), and the performance evalua-
tion procedure (section 4.6).
4.1 Data Sources and Features
We created a dataset of feature vectors which de-
scribes the payment behavior of all European banks
on a daily basis over the last ten years. It is compiled
from data generated by three important FMIs of the
Eurosystem: its large-value payment system called
TARGET2
1
, collateral management system, and min-
imum reserve system.
The majority of features were derived from TAR-
GET2. Based on the transaction log of this payment
system, we calculated for each bank its:
• Daily net value of payments (i.e. total inflow mi-
nus total outflow)
• Daily net number of transactions (i.e. total num-
ber of incoming payments minus total number of
outgoing payments)
• Daily net payment time within the day weighted
by value (i.e. the weighted payment time of in-
coming payments minus the weighted payment
time of outgoing payments)
• Daily net payment time within the day weighted
by the number of transactions (i.e. the weighted
payment time of incoming payments minus the
weighted payment time of outgoing payments)
These payment features were calculated for each pay-
ment type separately. Each payment settled in TAR-
GET2 has an associated type that describes the nature
of the payment, e.g. a customer payment, inter-bank
payment, or administrative payment. Furthermore,
we calculated for each bank its:
• Daily end-of-day account balance
• Daily minimum account balance (i.e. the lowest
value within the day)
We also derived features that describe the activities
of the banks on the interbank money market. To de-
rive these features, we applied the Furfine algorithm
(Furfine, 1999) on the transaction log of TARGET2
to classify each transaction as a regular transaction or
1
More information about TARGET2 can be found in
(ECB, 2018).
Liquidity Stress Detection in the European Banking Sector
269

money market transaction
2
. Accordingly, based on
the subset of money market transactions, we calcu-
lated for each bank its:
• Daily number of money market counterparties
• Daily HHI-index (Hirschman, 1945) of money
market counterparties weighted by the value of
the money market loans
• Daily spread of the weighted borrowing rate to
EONIA (i.e. the difference between the money
market rate of the bank and the EONIA)
These money-market features were calculated for the
case in which a bank is the lender as well as the bor-
rower in a money-market transaction.
Besides the payment features and money-market
features, we also derived features from the European
collateral management system. This system records
the amount of collateral European banks have de-
posited at the Eurosystem and how much of this col-
lateral is available for banks to make payments during
the day. From collateral data of this system, we cal-
culated for each bank its:
• Daily average haircut on all collateral
• Daily value of collateral before the haircut
• Daily value of collateral after the haircut
Banks cannot use collateral within the Eurosystem at
the market value. Instead, the value of collateral is de-
creased by a certain percentage to account for poten-
tial credit risk that the European Central Bank could
face should a bank default and its collateral needs to
be sold. This percentage is called the haircut.
Finally, we derived data about the minimum re-
serve requirement of each bank from the Europen
minimum reserve system. The minimum reserve re-
quirement is the average amount of liquidity that a
bank must keep on its settlement accounts during the
maintenance period. Based on this data and the trans-
action data of TARGET2, we calculated for each bank
the relative difference between its end-of-day balance
and its minimum reserve requirement.
4.2 Data Normalization
However, a problem with the features is that they each
are on a different scale. In addition, the range of each
feature depends on the type of bank (e.g. small or
large) for which it is calculated. Hence, we cannot
easily compare the feature vectors of one bank with
the feature vectors of another bank.
2
See (Arciero et al., 2016) for more information on how
the Furfine algorithm can be applied to identify money mar-
ket transactions in the transaction log of TARGET2.
To address this issue, we re-scaled the feature vec-
tors of each bank separately by z-normalization. The
normalized value of a feature was calculated by:
˜x
(k)
i j
=
x
(k)
i j
− ¯x
(k)
j
s
(k)
j
(17)
where, ¯x
(k)
j
and s
(k)
j
are respectively the sample mean
and standard deviation of the j-th feature in a feature
vector estimated for bank b
k
. Normalized feature ˜x
(k)
i j
represents the number of standard deviations x
(k)
i j
de-
viates from the mean s
(k)
j
of bank b
k
. Notice that, af-
ter performing this normalization, the features of each
bank have zero mean and unit variance.
4.3 Stress Classes
Obtaining data about the periods in which banks faced
liquidity stress is difficult. A good indicator of liquid-
ity stress is when a bank requests emergency liquidity
assistance. When a bank faces liquidity stress, it can
turn to the central bank that acts as a lender of last re-
sort and request liquidity in exchange for collateral of
lesser quality. Although data about the use of emer-
gency liquidity by European banks is recorded, we
were not able to obtain it because such data is highly
confidential and could not be made available for re-
search purposes.
Instead, we obtained the stress classes by perform-
ing an online news analysis. We asked payment ex-
perts in the Eurosystem which banks suffered from
severe liquidity stress recently. The experts provided
us with a short-list of seven banks
3
. For each bank on
this list, we searched for evidence of liquidity stress
on Wikipedia and in online news articles of several
national and international financial newspapers (e.g.
the Financial Times). All noteworthy events that we
found about the banks that could indicate possible liq-
uidity stress were organized in a detailed timeline.
Based on the timeline, we assigned the feature
vector of each bank at each day in the analysis period
to one of the following stress codes:
1. No stress - if we could not find any evidence of
liquidity stress at the bank at the given day
2. Possibly stress - if we could find some evidence
of liquidity stress at the bank at the given day but
which was not that severe (e.g. shares of the bank
dropped or a staff member had been fired)
3
Because of confidentiality reasons, we cannot disclose
the names of these banks. Instead, we will refer to the banks
by letter, i.e. bank A, bank B, and so on.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
270

Bank A Bank B
. . .
Bank F
Bank G
Experiment 1
Test
Train / Fold 1
. . .
Train / Fold 5 Train / Fold 6
Experiment 2
Train / Fold 1
Test
. . .
Train / Fold 5 Train / Fold 6
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Experiment 6
Train / Fold 1 Train / Fold 2
. . .
Test
Train / Fold 6
Experiment 7
Train / Fold 1 Train / Fold 2
. . .
Train / Fold 6
Test
Figure 1: The partitioning of the dataset during the experiments. In each experiment, the dataset was partitioned in a training
set and test set. Accordingly, the training set was further partitioned in six cross-validation folds. The test set and the cross-
validation folds each contained only the feature vectors of a particular bank. The experiments were repeated such that the
feature vectors of each bank are used exactly once for testing.
3. Stress - if we could find clear evidence of liquidity
stress at the bank at the given day (e.g. the start of
a bank run or rumors of a takeover)
4. Bankrupt - if the bank is no longer operating and
only participates in the financial system for ad-
ministrative reasons
In most cases, the stress codes of the banks started at
1 (no stress) and incrementally increased over time to
stress code 4 (bankrupt).
Finally, the feature vectors were labeled based on
the stress codes. Feature vectors with stress code 1
(no stress) were assigned the no stress class and fea-
ture vectors with stress code 3 (stress) were assigned
the stress class. No stress class was assigned to the
feature vectors with stress code 2 (possibly stress) and
stress code 4 (bankrupt). These unlabeled feature vec-
tors were not used for model training but only for out-
of-sample prediction.
4.4 Data Partitioning
We performed a series of experiments to determine
how well liquidity stress at the banks can be detected
out-of-sample. During each experiment, the dataset
was partitioned into a separate training set and test
set. A classifier was trained on the training set which
contained the feature vectors of all banks except for
one bank. The feature vectors of this holdout bank
were put in the test set and used to evaluate how well
the classifier performs. We repeated this experiment
seven times such that the feature vectors of each bank
were used exactly once for testing. Accordingly, we
measured the average performance of the classifier
over the experiments. Figure 1 provides a schematic
overview of the experiments.
4.5 Model Implementation
We trained the LR model described in section 3.4 and
two variations of the MLP network described in sec-
tion 3.5 on each training set. The MLP networks have
one hidden layer with either a hyperbolic tangent ac-
tivation or rectifier linear activation. We will refer to
these networks as MLP1 and MLP2 respectively. All
classifiers were optimized by stochastic gradient de-
scent with momentum and mini-batches. This proce-
dure was performed for a fixed number of epochs with
a constant learning rate. To avoid over-fitting, we ap-
plied L2 weight decay (Krogh and Hertz, 1992) on all
weights of the MLP networks.
The MLP networks have some hyper-parameters
that needed to be tuned. These parameters include the
number of units in the hidden layer and the amount
of weight decay. We optimized these parameters by
a variation of k-fold cross-validation using R package
caret (Kuhn, 2008). During the validation procedure,
the training set was partitioned in six folds that each
contained the feature vectors of a particular bank. An
MLP network was trained on five of the folds having
a particular configuration of hidden units and weight
decay. Accordingly, the loss function of the network
was evaluated on the holdout fold. This process was
repeated until each configuration of parameters was
evaluated once on each fold. Finally, we choose the
configuration for which the network achieved the low-
est loss averaged over all holdout folds.
4.6 Evaluation Metrics
The performance of each classifier was evaluated by
calculating its precision, recall and F
1
-score on each
Liquidity Stress Detection in the European Banking Sector
271

Table 1: The precision, recall, and F
1
-score of the classifiers in case they are trained based on regular cross entropy. In all
experiments, a threshold of ζ = 0.9 was used to generate alarms for liquidity stress.
Precision Recall F
1
ζ = 0.9 LR MLP1 MLP2 LR MLP1 MLP2 LR MLP1 MLP2
Bank A 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
Bank B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
Bank C 1.00 0.00 0.00 0.25 0.00 0.00 0.40 0.00 0.00
Bank D 1.00 1.00 1.00 0.20 0.20 0.20 0.33 0.33 0.33
Bank E 0.80 0.00 1.00 0.09 0.00 0.09 0.16 0.00 0.16
Bank F 1.00 1.00 1.00 0.40 0.10 0.30 0.57 0.18 0.46
Bank G 0.80 0.83 1.00 0.40 0.50 0.40 0.53 0.63 0.57
Average 0.66 0.40 0.57 0.19 0.11 0.14 0.28 0.16 0.22
Table 2: The precision, recall, and F
1
-score of the classifiers in case they are trained based on weighted cross entropy. In all
experiments, a threshold of ζ = 0.9 was used to generate alarms for liquidity stress.
Precision Recall F
1
ζ = 0.9 LR MLP1 MLP2 LR MLP1 MLP2 LR MLP1 MLP2
Bank A 0.02 0.00 0.00 0.17 0.00 0.00 0.04 0.00 0.00
Bank B 0.67 1.00 1.00 0.40 0.40 0.20 0.50 0.57 0.33
Bank C 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
Bank D 0.33 0.50 1.00 0.20 0.20 0.20 0.25 0.29 0.33
Bank E 1.00 1.00 1.00 0.96 0.48 0.89 0.98 0.65 0.94
Bank F 0.40 0.17 1.00 0.40 0.50 0.40 0.40 0.26 0.57
Bank G 0.86 1.00 0.88 0.60 0.60 0.70 0.71 0.75 0.78
Average 0.47 0.52 0.70 0.39 0.31 0.34 0.41 0.36 0.42
test set. For a given threshold ζ, precision is the prob-
ability that a feature vector belongs to a stressed bank
given that a classifier predicted liquidity stress:
Precision(ζ) = P(y
(k)
i
= 1| ˆy
(k)
i
≥ ζ) (18)
In contrast, recall is the probability that a classifier
predicts liquidity stress given that a feature vector be-
longs to a stressed bank:
Recall(ζ) = P( ˆy
(k)
i
≥ ζ|y
(k)
i
= 1) (19)
The F
1
-score is the harmonic mean of precision and
recall:
F
1
(ζ) = 2 ·
Precision(ζ) · Recall(ζ)
Precision(ζ) + Recall(ζ)
(20)
It constitutes an overall measure to compare the per-
formance of a set of competing classifiers. We deter-
mined the classifier that achieved the highest F
1
-score
averaged over all test sets.
5 RESULTS
Table 1 shows the performance evaluation of the clas-
sifiers in case they are trained by regular cross en-
tropy. The results for weighted cross entropy are
shown in Table 2. A threshold of ζ = 0.9 was used in
all experiments. This means that the classifiers raised
an alarm when they were at least 90% sure that a bank
was facing liquidity stress.
A few things stand out in these tables. We see
that the classifiers detect liquidity stress much better
when they are trained by weighted cross entropy. The
average F
1
-score of the models increases when they
are trained by weighted cross entropy instead of cross
entropy. This increase can be attributed to the fact that
weighted cross entropy incentives the models more to
assign a high probability to the stress cases.
Moreover, we see that MLP2 detects liquidity
stress overall the best. The network achieves an av-
erage F
1
-score of 0.42 with an average precision of
70% and average recall of 34%. These measures im-
ply that more than two-thirds of all alarms generated
by the network were correct and the network detected
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
272

0
25
50
75
100
Time
Stress Probability (%)
Stress Codes
1 − No Stress 2 − Possibly Stress 3 − Stress
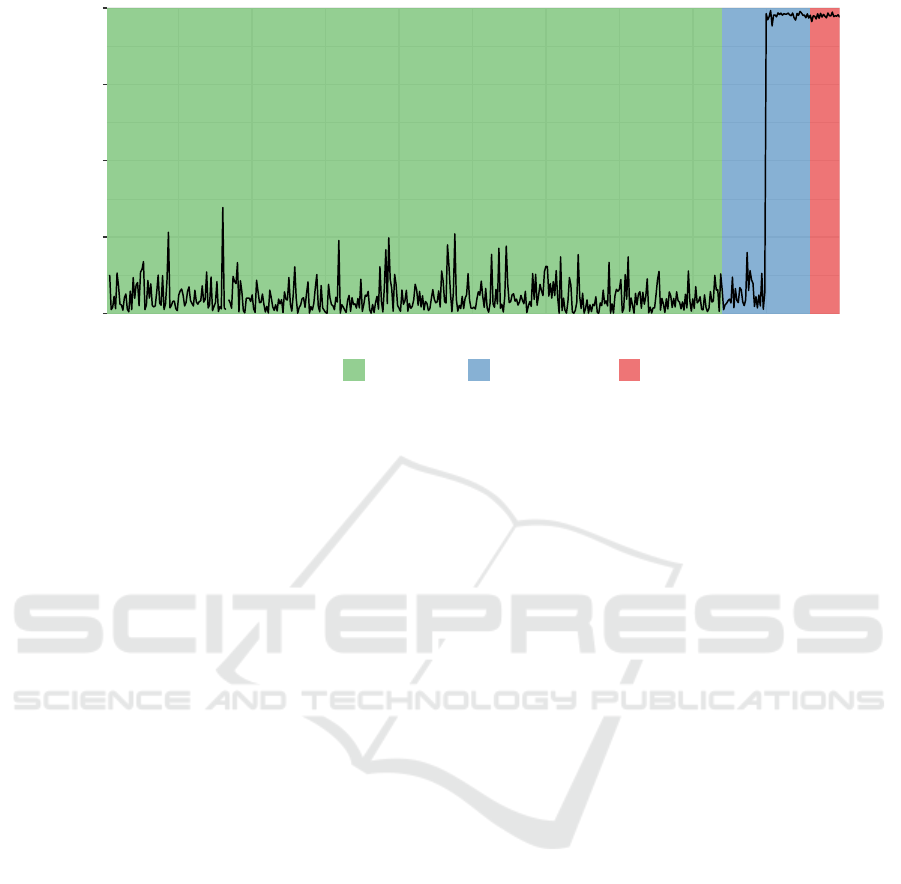
Figure 2: The out-of-sample predictions of MLP2 for bank E. The background colors highlight the stress codes that were
assigned to the feature vectors of the bank by our news analysis. The classifier picks up an early-warning sign of liquidity
stress in the ’Possibly Stress’ period, quite some time before newspapers reported the stress in the ’Stress’ period. Note that,
because of confidentiality reasons, we were not allowed to include the original figure in this paper. This figure is artificially
generated and closely resembles the original figure.
more than one-third of all stress cases. The LR model
achieved a similar F
1
-score but generated alarms for
liquidity stress with much lower precision.
The break-down of the performance metrics by
bank in Table 1 and 2 also shows that the classifiers
do not perform well on every bank. In particular, they
have difficulties detecting liquidity stress at bank A
and C. We suspect that the classifiers do not perform
well on these banks because the stress classes of these
banks are of poor quality. Our news analysis provides
only a rough approximation of the level of stress that
banks experience. News items can be incorrect, im-
precise, or incomplete. Also, many stress events do
not become known to the general public or cannot
be observed in payment data. All these factors could
have caused the wrong stress class being assigned to
the feature vectors of these banks.
Another factor that negatively impacts the perfor-
mance of the classifiers is the relatively small train-
ing sets on which they were trained. There are many
forms of liquidity stress that a bank can face. For ex-
ample, a bank can face liquidity problems for only a
few days which results in a bank-run or face long-
term solvency issues that eventually lead to a state
takeover. It is unlikely that the classifiers were able
to learn to recognize all these different forms of stress
from data of only seven stressed banks.
We also determined whether the classifiers detect
liquidity stress before the stress became known to the
general public. This was done, similarly as in the
performance evaluation, by classifying out-of-sample
the feature vectors of a holdout bank. However, this
time, we also classified the features vectors that are
assigned stress code 2 (possibly stress) by our news
analysis. If the classifiers assign these feature vectors
to the stress class, then they likely pick up an early-
warning sign of liquidity stress.
Figure 2 depicts the out-of-sample predictions of a
bank. It shows that the classifier detects an early sign
of liquidity stress in the ’possibly stress’ period, quite
some time before the stress became publicly known in
the ’stress’ period. We checked whether we could find
the same stress sign by the method of (Heijmans and
Heuver, 2014), i.e. by studying simple plots of the
features one-at-a-time, but were unable to spot any
irregularities. Hence, the classifier must have found
that a combination of features that is characteristic for
a bank that is facing liquidity stress.
6 CONCLUSIONS
We conclude that liquidity stress at banks can be rea-
sonably well detected by supervised machine learn-
ing. Our best classifier generated alarms for liquidity
stress with a precision of 70% and a recall of 34%. In
some cases, the classifier identified signs of liquidity
stress well before the stress was reported by finan-
cial newspapers. Most of these signs remained un-
detectable when studying simple plots of the features
one-at-a-time. Although our method needs some fur-
ther improvements to be used in practice, we believe
Liquidity Stress Detection in the European Banking Sector
273

that it is a promising new tool for central banks to
monitor the financial activities of banks.
There are several ways in which our method can
be improved. Our classifiers were trained on data of
only seven banks. It is to be expected that the classi-
fiers perform much better when they are trained on a
larger dataset containing a more diverse set of stress
events. Moreover, the generation of the stress classes
by our news analysis still involved a lot of manual
work. Future research could investigate whether this
step can be automated by applying techniques of nat-
ural language processing or sentiment analysis.
REFERENCES
Altman, E. I. (1968). Financial ratios, discriminant anal-
ysis and the prediction of corporate bankruptcy. The
Journal of Finance, 23(4):589–609.
Arciero, L., Heijmans, R., Heuver, R., Massarenti, M., Pi-
cillo, C., and Vacirca, F. (2016). How to measure
the unsecured money market: the Eurosystem’s im-
plementation and validation using TARGET2 data. In-
ternational Journal of Central Banking.
Beaver, W. H. (1966). Financial ratios as predictors of fail-
ure. Journal of Accounting Research, pages 71–111.
BIS (2008). Principles for sound liquidity risk management
and supervision. Bank for International Settlements.
Bottou, L. (2004). Stochastic learning. In Advanced Lec-
tures on Machine Learning, pages 146–168.
Chamon, M., Manasse, P., and Prati, A. (2007). Can we pre-
dict the next capital account crisis? IMF Staff Papers,
54(2):270–305.
Davis, E. P. and Karim, D. (2008). Comparing early warn-
ing systems for banking crises. Journal of Financial
stability, 4(2):89–120.
Demirg-Kunt, A. and Detragiache, E. (1998). The deter-
minants of banking crises in developing and devel-
oped countries. Staff Papers (International Monetary
Fund), 45(1):81–109.
ECB (2018). TARGET2 user information guide v12.0. ECB
Website.
Fioramanti, M. (2008). Predicting sovereign debt crises
using artificial neural networks: a comparative ap-
proach. Journal of Financial Stability, 4(2):149–164.
Furfine, C. H. (1999). The microstructure of the federal
funds market. Financial Markets, Institutions & In-
struments, 8(5):24–44.
Glorot, X., Bordes, A., and Bengio, Y. (2011). Deep sparse
rectifier neural networks. In Proceedings of the Four-
teenth International Conference on Artificial Intelli-
gence and Statistics, pages 315–323.
Heijmans, R. and Heuver, R. (2014). Is this bank ill? the
diagnosis of doctor TARGET2. The Journal of Finan-
cial Market Infrastructures, 2 nr 3:3–36.
Hirschman, A. O. (1945). National power and the structure
of foreign trade. University of California Press.
Kaminsky, G. L. and Reinhart, C. M. (1999). The
twin crises: the causes of banking and balance-of-
payments problems. The American Economic Review,
89(3):473–500.
Krogh, A. and Hertz, J. A. (1992). A simple weight decay
can improve generalization. In Advances in Neural
Information Processing Systems 4, pages 950–957.
Kuhn, M. (2008). Building predictive models in R using the
caret package. Journal of Statistical Software, 28.
Kumar, P. R. and Ravi, V. (2007). Bankruptcy predic-
tion in banks and firms via statistical and intelligent
techniques–a review. European Journal of Opera-
tional Research, 180(1):1–28.
LeCun, Y., Bottou, L., Orr, G. B., and M
¨
uller, K. R. (1998).
Efficient BackProp, pages 9–50. Springer Berlin Hei-
delberg.
Min, J. H. and Lee, Y.-C. (2005). Bankruptcy prediction
using support vector machine with optimal choice of
kernel function parameters. Expert Systems with Ap-
plications, 28(4):603–614.
Niculescu-Mizil, A. and Caruana, R. (2005). Predicting
good probabilities with supervised learning. In Pro-
ceedings of the 22nd International Conference on Ma-
chine Learning, pages 625–632.
Tam, K. Y. (1991). Neural network models and the predic-
tion of bank bankruptcy. Omega, 19(5):429–445.
Triepels, R., Daniels, H., and Heijmans, R. (2018). De-
tection and explanation of anomalous payment behav-
ior in real-time gross settlement systems. In Lec-
ture Notes in Business Information Processing, vol-
ume 321, pages 145–161.
Werbos, P. J. (1982). Applications of advances in nonlin-
ear sensitivity analysis. In System Modeling and Op-
timization, pages 762–770.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
274