Virtual Network Functions Placement for Defense Against Distributed
Denial of Service Attacks
Sonia Haddad-Vanier
1
, Celine Gicquel
2
, Lila Boukhatem
2
, Kahina Lazri
3
and Paul Chaignon
3
1
SAMM Universit
´
e Paris I Panth
´
eon Sorbonne, France
2
LRI, CNRS - Universit
´
e Paris Saclay, Universit
´
e Paris-Sud, France
3
Orange Labs Products & Services, France
Keywords:
Network Optimization, Distributed Denial of Service (DDos) Attacks, Network Function Virtualizing (NFV),
Mathematical Programming, Mixed Integer Linear Program (MILP), Bilevel Programming.
Abstract:
In this paper, we are interested in the problem of Virtual Network Function (NFV) placement to counter Dis-
tributed Denial of Service (DDoS) attacks. A DDoS attack is one of the most common and damaging types
of cyberattacks. In Network Function Virtualization (NFV) technology network functions, more specifically
security mechanisms, are implemented as software. Such approach significantly reduces the cost of the in-
frastructure and simplifies the deployment of new services. We propose two new models for this critical and
complex problem. The first model is a mixed-integer linear program aiming at eliminating all DDos attacks
before they reach their target. As its size grows exponentially with the network size, we propose a constraint
generation algorithm to solve it. The numerical results obtained for different realistic network instances show
the effectiveness of our approach. The second model is a bilevel programming problem that achieves a trade-
off between NFVs placement costs and security levels requirements. Our results show that this mechanisms
overcomes DDos attacks by effectively filtering attacks while minimizing the total cost of deployed NFV.
1 INTRODUCTION
The present work investigates new mathematical pro-
gramming models for the defense against Distributed
Denial of Service attacks (DDoS) in communication
networks. A distributed denial of service is a type of
security attacks in which multiple compromised com-
puter systems attack a target, such as a server, a web-
site or another network resource, and cause a denial of
service for users of the targeted resource. The flood
of incoming messages, connection requests or mal-
formed packets to the target system forces it to slow
down or even crash and shut down, thereby denying
service to legitimate users.
DDoS attacks are one of the most common and
damaging types of cyberattacks. In recent years, the
number, scope and diversity of DDoS attacks have in-
creased dramatically. Recent statistics showed that
in 2014 the number of daily DDoS attacks reached
20,000 attacks, with peak volumes of up to 0.5 Tbp
(Arbor Networks, 2014) (Arbor Networks, 2014a)
(Czyz et al., 2014). In 2013, the attack against
Spamhaus, a spam-fighting group based in London
and Geneva, generated a 300 Gbps illigitimate traf-
fic (Gilbert, 2014). More recently in 2016, the BBC
website was targeted by a DDoS attack of more than
600 Gbps (Khandelwal, 2016). In 2018, the num-
ber of DDoS attacks against companies like Insta-
gram or Github has reached 600 attacks per day with
peak speeds of 1.7 terabits. In addition, we ob-
serve a continuous appearance of new types of attacks
(Rossow, 2014) as well as new variations of known
attacks. Damage caused by DDoS attacks to com-
panies include loss of customer trust and monetary
losses which were evaluated at an average of $40000
per hour by (Incapsula, 2014).
Today, DDoS defense is mostly implemented us-
ing expensive hardware components that are fixed in
terms of strength, functionality and capacity. This
means in particular that the location and capacity (in
terms of the volume of malicious traffic it can process)
of the defense appliances are determined in advance,
before the DDoS attacks actually take place. Com-
panies are thus forced to over provision by deploy-
ing appliances capable of handling a high but prede-
fined volume of attack at several points in the network
142
Haddad-Vanier, S., Gicquel, C., Boukhatem, L., Lazri, K. and Chaignon, P.
Virtual Network Functions Placement for Defense Against Distributed Denial of Service Attacks.
DOI: 10.5220/0007397601420150
In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 142-150
ISBN: 978-989-758-352-0
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(Seyed et al, 2015). With the emergence of new and
larger DDoS attacks, this strategy entails high costs
for companies as it requires to frequently invest in
more efficient and specialized hardware components.
The cost of deploying and maintaining a physical fire-
wall is estimated at 116.000 $ for the first year and an
annual cost of 108.200 $ for a medium-sized US com-
pany with 5Mbps of Internet connectivity. The de-
velopment of Software-Defined Networks (SND) and
virtualized network functions offers opportunities to
reduce security costs and also to provide flexible and
scalable solutions.
Network Function Virtualization (NFV) is a recent
network architecture concept in which network func-
tions (e.g. network address translation, firewalling,
domain name service, etc.) are implemented as soft-
ware and deployed as virtual machines running on
general purpose commodity hardware like x86- or
ARM-based servers (Jakaria et al, 2016). Virtualiza-
tion increases manageability, reliability and perfor-
mance of the network and allows a flexible and dy-
namic implementation of the network services, which
significantly reduces the cost of the infrastructure and
simplifies the deployment of new services. These nu-
merous benefits have convinced operators to largely
embrace virtualization of network functions (Dono-
van, 2014).
NFV offers new possibilities to counter DDoS at-
tacks. In particular, its flexibility and reactivity allows
to postpone the determination of the DDoS defense
architecture to be used after the attack is detected, its
target identified and its volume estimated. This allows
to place adapted defense mechanisms where they are
needed and to launch them depending on the scale of
the attack (Seyed et al, 2015).
The use of virtual network functions (NFV) for
protection against DDoS attacks was investigated in
several recent works. (Seyed et al, 2015) devel-
oped the Bohatei system based on NFV and SDN
(software-defined networking). Their system includes
a resource manager which determines the type, num-
ber and location of virtual machines to be instantiated
based on the available information of the on-going at-
tack so as to minimize the costs related to the ma-
licious flow traffic. They formulate the underlying
optimization problem as a mixed-integer linear pro-
gram and solve it using a two-step heuristic. Note that
their problem modeling assume that the flow of the at-
tack, once detected, can be flexibly routed towards the
launched virtual machines. (Jakaria et al, 2016) also
proposed a DDoS defense architecture based on the
dynamic allocation of filtering NFVs. In their frame-
work, the external traffic to the targeted server is di-
rected by a central dispatcher to one of the activated
NFVs which will stop the malicious traffic and for-
ward the clean one to its destination. The authors
mention that the decision to add or remove filtering
NFVs to/from the active architecture should be based
on a real-time analysis of the inflow traffic but the
question of devising a mechanism to optimally deploy
the NFVs is left for future work.
In the previous works (Seyed et al, 2015) (Jakaria
et al, 2016) using NFV technologies to eliminate sus-
picious packets, the authors considered that the rout-
ing of attacks was known and they assumed the ability
to redirect attacks to filtering agents.
Today, in the context of networks that evolve dy-
namically, these assumptions are no longer realistic.
Indeed, with the advent of 5G networks, ISPs are
preparing to lend “slices” of their physical networks
to service providers. Service providers are likely to
rely on their own, proprietary algorithms to route traf-
fic on their slice of the network.
Therefore, in order to propose a satisfying secu-
rity solutions to operators, it is necessary to develop
approaches that optimize the NFV deployment
without knowing the routing attacks. This is the
purpose of our study.
In the present work, we focus on the deployment
of an architecture based on the NFV technology to
secure networks against DDoS attacks. We assume
that the on-going attack has been detected and that
its ingress points, its volume and its target have been
identified. Based on this information, we seek to de-
termine the optimal number and location of NFVs in
order to remove all the illegitimate traffic while trying
to minimize the total cost of the activated NFVs. An
important feature of our problem is that it tackles sit-
uations where network routing is very dynamic mak-
ing it difficult to know how the illegitimate traffic will
be routed in the network and cannot decide to route
it to one of the instantiated filtering NFVs. This im-
plies that our NFV placement decisions should take
into account all the possible routes that the illegiti-
mate traffic could use between the ingress points and
the target so as to ensure that the attack is stopped in
all cases. Another important aspect of the problem is
that the capacity of the NFVs activated at a given node
of the network might not be enough to filter all the at-
tacking traffic going through it. Therefore, we need a
cumulative elimination process which on each of the
potential paths of the illegitimate traffic, the necessary
NFVs are placed on multiple nodes of the paths to re-
move the entire malicious traffic. These two aspects
greatly increase the hardness of the problem.
We propose in what follows to tackle this opti-
mization problem using mathematical programming
Virtual Network Functions Placement for Defense Against Distributed Denial of Service Attacks
143

based approaches. Our contributions are threefolds.
First, we present a simple mixed-integer linear pro-
gramming (MILP) model for this problem. This
model is based on a conservative (pessimistic) esti-
mation of the malicious flow on each potential path
it can use between its source point and its target. It
thus provides a defense architecture which will stop
all the attacking flows but whose cost might be higher
than actually needed. Second, as this MILP model in-
volves an exponential number of constraints, we de-
velop a solution approach based on a constraint gen-
eration scheme to solve medium-size instances of the
problem. Third, we discuss a more evolved bi-level
programming model for this problem in which the
amount of malicious traffic on each potential path is
estimated more realistically. This model could enable
us to provide solutions reaching a better tradeoff be-
tween the security criteria and the placement costs of
NFVs.
The paper is organized as follows. Section 1 de-
scribes the problem and introduces the adopted model
notations. Section 2 describes the mixed-integer lin-
ear program we developed for high security case. The
high security requirements dictate that all the DDoS
attacks should be removed before reaching the des-
tinations. We then present in Section 3 a solution
approach based on a constraint generation scheme.
Some preliminary numerical results carried out on
public data released by large European SPs are given
in Section 4. Finally, we present in Section 5 a bi-
level programming model (Lodi, 2011)(Fischetti et
al., 2017) leading to find deine a right trade-off be-
tween NFV deployment cost and DDoS mitigation ef-
ficiency. In this last model, the assignments of NFVs
is decided in the context of the worst case of attacks
routing. By this way, we reduce the NFVs costs while
keeping a satisfying security level for operators.
2 PROBLEM DESCRIPTION AND
NOTATION
We aim at determining the optimal placement of a
set of virtual network functions in order to secure a
telecommunication network against DDoS attacks.
The network topology is modeled by a graph G =
(V, E) in which V , the set of nodes, represents specific
equipments in the network (routers, switches, data
centers, etc.) and E, the set of arcs, corresponds to
the links that can be used to route the traffic. /
The illegitimate traffic corresponding to the DDoS
attack is represented as a set D of source-target nodes:
(s,t) ∈ D if there is some malicious flow between
node s ∈ V and t ∈ V to be stopped. The amount of
illegitimate traffic between s to t is denoted ψ
st
.
NFVs are used to stop the illegitimate traffic be-
fore it reaches its target. A NFV will be instantiated
on a node v ∈ V of the network and will filter the ma-
licious flow. There are N types of NFVs available. A
NFV of type n is characterized by its filtering capac-
ity φ
n
, i.e. the amount of malicious flow it can stop,
its cost K
n
and its computing resources consumption.
We consider R types of computing resources
(CPU, memory, etc.). The amount of computing re-
source r required by the instantiation of one NFV of
type n is denoted γ
rn
, the amount of computing re-
source r available at node v is denoted Cap
r
v
.
The main difficulty to determine the optimal NFV
placement to counter the attack is that we do not know
how the malicious flow will be routed in the network.
Hence, in order to make sure that all the illegitimate
traffic will be stopped before reaching its target, we
have to consider all the potential paths that can be
used by the malicious flow between its source point
and its target and place enough NFVs on each of these
paths to filter the flow if routed through it.
3 MODEL 1: AN MILP MODEL
FOR HIGH LEVEL SECURITY
REQUIREMENTS
We present in this section a first mixed-integer linear
programming (MILP) model for this problem. This
model is based on a conservative (pessimistic) esti-
mation of the malicious flow on each potential path
it can use between its source point and its target. It
thus provides a defense architecture which will stop
all the attacking flow but whose cost might be higher
than actually needed.
We denote ℘
st
the set of all paths between nodes
s and t. As no information about the malicious traffic
routing is available, we focus on the worst-case situ-
ation and we consider that we have to place enough
NFVs on each path p to be able to filter the whole
amount of the malicious flow, ψ
st
.
We introduce the following decision variables:
• x
n
v
: number of NFVs of type n placed at node v
• ϕ
st
v
: filtering capacity installed at the node v dedi-
cated to filtering the attack (s,t)
This leads to the following MILP model.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
144


























minz =
∑
v∈V
∑
n∈N
K
n
v
x
n
v
(1.0)
∑
n∈N
γ
rn
x
n
v
− cap
r
v
≤ 0 ∀v ∈ V, ∀r ∈
¯
R (1.1)
∑
st∈D
ϕ
st
v
≤
∑
n∈N
φ
n
x
n
v
∀v ∈ V (1.2)
∑
v∈p
ϕ
st
v
≥ ψ
st
∀p ∈℘
st
, ∀st ∈ D (1.3)
x
n
v
∈ Z
+
∀v ∈ V, ∀n ∈ [1..N] (1.4)
ϕ
st
v
≥ 0 ∀st ∈ D, ∀v ∈ p (1.5)
(1)
The objective function (1.0) aims at minimizing
the total costs associated with the NFV instantiation.
Constraints (1.1) ensure that for each resource of
type r available at node v, the NFVs placed at this
node consume no more than the available amount of
resource r.
Constraints (1.2) are the filtering capacity con-
straints. They guarantee that, on each node, the sum
of the filtering capacities assigned to the different at-
tacks is less than the total filtering capacity placed on
this node. Note that we assume in constraints (1.2)
that the filtering capacity placed in v to counter the
attack (s,t) is not dedicated to a single path p ∈ ℘
st
but rather that it can be reused to filter the same attack
(s,t) on all paths p ∈℘
st
. This assumption is justified
by the fact that we consider the ’worst’ value of the
flow on each path and that the real traffic on each path
will not be simultaneously equal to its worst value.
Constraints (1.3) require that, for each path p of
each (s,t) attack, the total filtering capacities installed
on the nodes of p be greater than ψ
st
, the ’worst’ pos-
sible value for the malicious flow on this path.
4 SOLUTION APPROACH
Problem (1) is a mixed-integer linear program which
can theoretically be solved directly by a mathemat-
ical programming solver such as CPLEX. However,
its size grows exponentially fast with the size of the
network due to constraints (1.3). Even for medium
size instances, the explicit enumeration of all possible
paths between the source and the target of an attack
requires a prohibitive computation time.
We thus propose in what follows a constraint gen-
eration approach in which only a small subset of con-
straints (1.3) are added to the formulation during the
course of the Branch & Bound algorithm.
Initialization For each attack (s, t), we look for
the shortest path (in terms of the number of hops)
between s and t and add the constraint of type (1.3)
corresponding to this shortest path in the formulation.
Iteration During the course of the Branch &
Bound algorithm, each time an integer solution (x, ϕ)
complying with the set of filtering constraints (1.3)
currently added to the formulation is found, we carry
out the following procedure:
1. We build an oriented weighted graph G
0
=
(V, E, w) in which the weight on arc u, w
u
, is equal
to the filtering capacity currently installed at its
ending node v, i.e. to the value of the decision
variable φ
st
v
in the current solution.
2. We look for the shortest path ˜p between s and t in
G
0
. ˜p is the path in ℘
st
on which the total installed
filtering capacity is the smallest.
3. If
∑
v∈ ˜p
ϕ
st
v
≥ ψ
st
, it means that the filtering capac-
ity installed on all paths in ℘
st
is greater than the
flow of the attack, i.e. that all constraints of type
(1.3) are satisfied by the current integer solution.
In this case, no constraints of type (1.3) are added
to the formulation.
4. If
∑
v∈ ˜p
ϕ
st
v
< ψ
st
, we add constraint
∑
v∈ ˜p
ϕ
st
v
≥
ψ
st
.
In our numerical experiments, this solution ap-
proach was implemented using the LazyConstraint-
Callback routines of CPLEX solver.
5 PRELIMINARY
COMPUTATIONAL RESULTS
We report in this section the results of some experi-
ments carried out to assess the numerical efficiency of
the constraint generation approach discussed in Sec-
tion 4.
5.1 Instances
We randomly generated a set of medium-size in-
stances of the problem following the indications pro-
vided by public data released by different cloud and
telecom providers. More precisely:
• We used 4 internet network topologies: 3 topolo-
gies from the Internet Topology Zoo library (see
(Zoo Topology)): BICS (V = 32, E = 48), Intel-
liFiber (V = 73, E = 96) and Cogentco (V = 197,
E = 245) and one topology corresponding to the
network of the French company Free (V = 120,
E = 167).
• R = 2 types of computing resources were taken
into account at each node: the number of CPUs
and the memory. More precisely, we considered
three types of nodes: small nodes with Cap =
(4, 32), medium nodes with Cap = (40, 160) and
large nodes with Cap = (400, 1600). For each of
Virtual Network Functions Placement for Defense Against Distributed Denial of Service Attacks
145

the 4 topologies mentioned above, we randomly
assigned each node to one of these 3 types.
• A single type of NFV was considered requiring
γ
1,1
= 4 CPUs and γ
1,2
= 16 units of memory, pro-
viding a filtering capacity of φ
n
= 16 Mbps, with
a unit cost of K
1
= 130.
• The number of source-target pairs was set to A =
5. In each instance, we considered 5 different
sources and a single targeted node, which were
randomly selected. The intensity of each attack
was randomly generated following a uniform dis-
tribution in the interval [32; 1200] Mbps.
For each considered topology, we randomly gen-
erated 10 instances, corresponding to 10 attack con-
figurations, leading to a set of 40 medium-size in-
stances.
5.2 Results
Each generated instance was solved with the mixed-
integer linear programming solver CPLEX 12.8.9
using formulation (1) where constraints (1.3) were
either all added a priori to the formulation or were
dynamically generated as lazy constraints during the
Branch & Bound search. The first solution approach
is referred to as EXP (explicit formulation), the
second as LCG (lazy constraint generation) in what
follows.
For each solution approach and each topology, we
report in Table 1:
• Cost: the average cost of the NFV placement,
• #FC: the average number of filtering constraints
(1) added to the formulation,
• #Nodes: the average number of nodes explored
by the Branch & Bound algorithm embedded in
CPLEX solver before a guaranteed optimal solu-
tion is found or the computation limit of 20 min-
utes is reached,
• Time: the average time in seconds needed to ob-
tain a guaranteed optimal solution (in case no op-
timal solution was found within 20 minutes of
computation, the value 1200s was used to com-
pute the average).
All tests were run on a an Intel Core i5 (1.9GHz)
with 16 GB of RAM, running under Windows 10.
Results from Table 1 show the overall usefulness
of the LCG solution approach. Namely, for the In-
telliFiber topology, LCG was capable of providing
the optimal solution of the problem in a significantly
reduced computation time as compared to the one
needed by EXP. As for the larger Free and Cogentco
topologies, EXP was not able to provide a feasible so-
lution for the problem within 20min of computation
due to the fact that the complete enumeration of all
the paths to be considered for each attack could not
terminate within this time limit. In contrast, LCG was
capable of providing the optimal solution for 18 out of
the 20 corresponding instances, with a MIP gap less
than 0.5% for the two remaining instances.
6 MODEL2: A BILEVEL MODEL
FOR OPTIMIZED
SECURITY-COST TRADEOFF
SOLUTIONS
The defense architecture provided by the resolution of
problem (1) satisfies the security requirements of the
operators. However, these solutions are based on a
pessimistic estimation of the malicious flow that will
be routed on each path p so that more NFVs than ac-
tually needed will be implemented, leading to over
expensive solutions.
Namely, even if we do not know the exact rout-
ing of the flow between s and t, we can exploit the
fact that the amount of malicious flow routed on each
path p will be limited by the forwarding capacity
of the nodes and by the bandwidth of the links on
the path. Moreover, these routing capacities will be
shared among several (s, t) pairs, which will further
limit the flow to be considered on each path.
It is thus interesting to develop approaches where
this knowledge is exploited to refine the estimation of
the malicious flow on each potential path in order to
offer a better tradeoff between the security criteria and
the investment costs of NFVs.
In order to achieve this, we propose a bilevel pro-
gramming model. In the bilevel model we developed,
the objective function seeks a compromise between
the installation costs of the NFVs and the penalizing
costs of the illegitimate flow not stopped. Bilevel op-
timization is a special kind of optimization where one
problem is embedded (nested) within another. The
outer optimization task is commonly referred to as the
upper-level optimization task, and the inner optimiza-
tion task is commonly referred to as the lower-level
optimization task. These problems involve two kinds
of variables, referred to as the upper-level variables
and the lower-level variables.
At the first level, the Leader problem computes
the optimal placement of the NFVs by minimizing
the sum of two costs: the installation costs of these
NVFs and a penalty cost. Penality cost is proportional
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
146

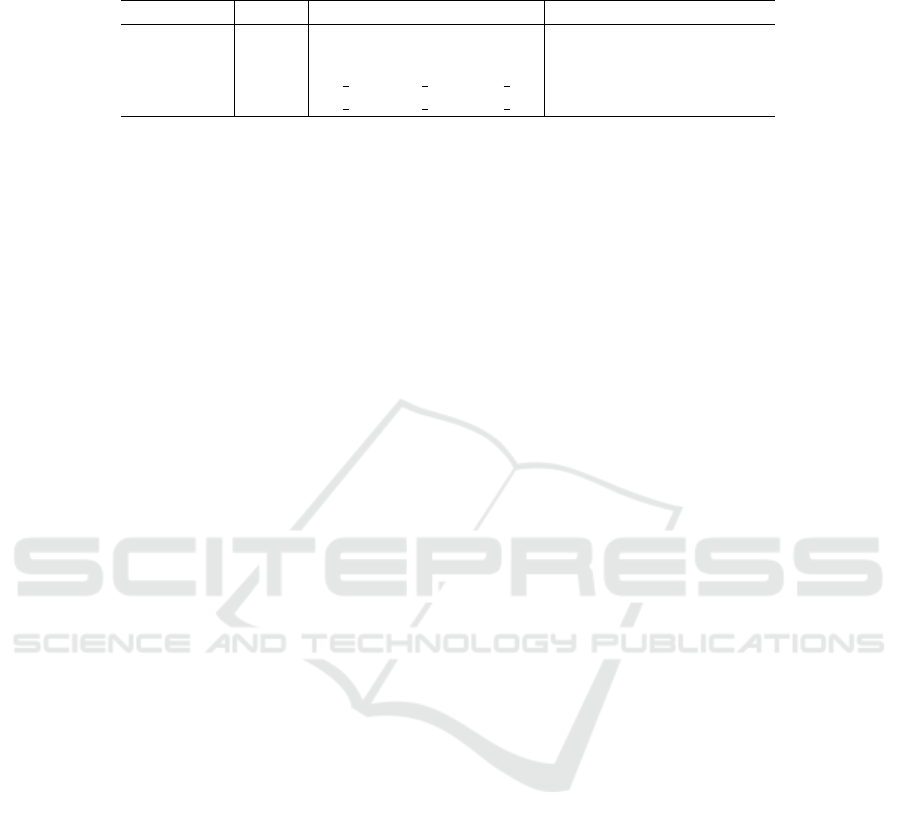
Table 1: Numerical results.
EXP LCG
Topology Cost #FC #Nodes Time #FC #Nodes Time
BICS 19526 3796 0 0.2s 9 7 0.1s
IntelliFiber 27742 51709 360 103.2s 20 12234 1.3s
Free 21255 20 0 0.1s
Cogentco 27599 26 1464328 246.6s
to the value of the illegitimate flow which can not be
stopped by the installed NFV.
Due to the unknown routing of attacks, we com-
pute at the second level the ”worst” illegitimate flow
routing. Thus at the second level, for a given fixed
placement of NFV (Leader solution), the follower
problem considered that each attack (s,t) would route
as much illegitimate traffic as possible between s and
t . Intuitively, for a given assignment, this considered
amount is the worst routing of the attacks for this
placement, which allows as much illegitimate flow as
possible to reach its target.
We present in the following section two alterna-
tive formulations of the ”Virtual Network Functions
Placement to Defense Against Distributed Denial of
Service Attacks” problem. The first one is based on
the arc-path formulation of a multi-commodity flow
problem. This formulation uses flow on paths deci-
sion variables. The second one is based on a node-arc
model of a multi-commodity flow problem using arc
flow decision variables. The benefits of each formu-
lation are described in the next sections.
6.1 Bilevel Problem: Arc-Path
Formulation
6.1.1 The Leader Problem: Arc-Path
Formulation
At the first level, the Leader optimization problem
assigns filtering NFVs on the network nodes for
defense against different attacks.
In this first sub-section, we will use an arc-path
formulation for the attack flow. We thus define
℘
st
, (s,t) ∈ D, the set of all the paths p connecting
the attack source vertex s to its destination vertex t
with (s,t) ∈ D. Let H(x, ϕ) be the penalties costs for
illegitimate traffic.
We define two families of decision variables:
• x
n
v
: number of NFVs of type n placed at node v,
• δ
st
p,v
: the filtering capacity installed at the node v
dedicated to the flow on the path p ∈ ℘
st
of the
attack (s,t).
The Integer Linear Problem that we define to
model the Leader problem is the following:



















minz =
∑
v∈V
∑
n∈N
K
n
v
x
n
v
+ πH(x, δ)(2.0)
Subject to
∑
n∈N
γ
rn
x
n
v
− cap
r
v
≤ 0∀v ∈ V∀r ∈
¯
R(2.1)
∑
st∈D
∑
p∈℘
st
δ
st
p,v
≤
∑
n∈N
φ
n
x
n
v
∀v ∈ V (2.2)
x
n
v
∈ Z
+
∀v ∈ V, ∀n ∈ [1..N](2.3)
(2)
The objective function of this model, expressed in
(2.0) is to minimize the sum of two costs: the total
costs of the NFV installation added to the penalties
costs induced by the non stopped illegitimate traffic.
Constraints (2.1) ensure that for each resource of type
r available at node v, the NFV installed at this node
v consume no more than the amount of the total re-
source r available at v. The constraints (2.2) are fil-
tring capacity constraints, they express that, on each
node, the sum of the filtering capacities assigned to
the different attacks is less than the total filtering ca-
pacity installed on this node.
6.1.2 The Follower Problem: Arc-Path
Formulation
Since the routing of illegitimate traffic is unknown,
our solution approach is based on the worst case. The
worst routing is that the Follower routing problem al-
lows attacks to avoid as much as possible the NFVs
(defense) installed by the Leader problem.
We evaluate each of the NFV placement solutions
according to the ”worst routing” of illegitimate flows,
which is, the routing that allows the largest part of
the illegal flows to reach their destination.
The routing of the traffic in the network is limited
by the forwarding capacity of each node v, denoted
For
v
, and by the bandwidth of each link u, denoted
b
u
.
We propose an arc-path multicommodity flow for-
mulation for the Follower routing problem.
Virtual Network Functions Placement for Defense Against Distributed Denial of Service Attacks
147

For that, we define two families of decision variables:
• f
st
p
: the amount of the illegitimate st flow routed
on the path p ∈ ℘
st
, p is the path linking s to t in
the graph G.
• q
st
p
: The amount of the illegitimate flow on the
path p ∈ ℘
st
stopped before reaching its destina-
tion t.
The obtained mathematical model for the Fol-
lower problem is:



































H(x, ϕ) = max
∑
st∈D
(ψ
st
−
∑
p∈℘
st
q
st
p
)(3.0)
Subject to
∑
st∈D
∑
p∈℘
st
,u∈p
f
st
p
− b
u
≤ 0∀u ∈ E(3.1)
∑
st∈D
∑
p∈℘
st
,v∈p
f
st
p
− For
v
≤ 0∀v ∈ V (3.2)
∑
p∈℘
st
f
st
p
= ψ
st
∀st ∈ D(3.3)
q
st
p
= min[
∑
v∈p
δ
st
v,p
, f
st
p
]∀p ∈℘
st
, ∀st ∈ D(3.4)
f
st
p
, q
st
p
≥ 0∀st ∈ D, ∀p ∈ ℘
st
and u ∈ E(3.5)
(3)
The objective function (3.0) of the follower prob-
lem is to maximize the total amount of attack flow
that will reach its destination (worst case). For each
attack, the amount of flow reaching its destination
is computed by substruction between the flow of the
source s minus the total flow filtered through all pos-
sible paths for that attack. The capacity constraints
(3.1) express that for each link u in the network, the
total flow through u does not exceed the residual capc-
ity of u. The constraints (3.2) ensure that the forward-
ing capacity of the node v is respected: the total flow
through node v must be less than the value of For
v
.
For each attack (s, t), the constraints (3.3) are the
demand constraints. They insure that the illegitimate
(s,t) flow should be routed over all possible paths in
the set ℘
st
. Constraints (3.4) computes the value of
the illegitimate (s,t) filtered through a path p. This
value should be equal to the minimum value between
the flow f
st
p
routed on p and the total filtering capacity
dedicated to this path.
The previous Follower problem formulation is not
linear because of the constraints (3.4). It can be lin-
earzed by introducing additional binary variables as
follows:
y
st
p
=





1 if
∑
v∈p
δ
st
v,p
≤ f
st
p
0 if
∑
v∈p
δ
st
v,p
≥ f
st
p





































H(x, ϕ) = max
∑
st∈D
(ψ
st
−
∑
p∈℘
st
q
st
p
)(4.0)
Subject to
∑
st∈D
∑
p∈℘
st
,u∈p
f
st
p
− b
u
≤ 0∀u ∈ E(4.1)
∑
st∈D
∑
p∈℘
st
,v∈p
f
st
p
− For
v
≤ 0∀v ∈ V (4.2)
∑
p∈℘
st
f
st
p
= ψ
st
∀st ∈ D(4.3)
q
st
p
≥
∑
v∈p
δ
st
v,p
− ψ
st
(1 − y
st
p
)∀p ∈ ℘
st
, ∀st ∈ D(4.4)
q
st
p
≥ f
st
p
− ψ
st
y
st
p
∀p ∈ ℘
st
, ∀st ∈ D(4.5)
y
st
p
∈ {0, 1}, f
st
p
, q
st
p
≥ 0∀st ∈ D, ∀p ∈ ℘
st
and u ∈ E(4.5)
(4)
Constraints (4.4) and (4.5) link together variables
y
st
p
, f
st
p
and δ
st
v,p
. They can be explained in the follow-
ing way: If y
st
v
= 0, so the constraints (4.4) are inac-
tive because they only require that q
st
p
be greater than
a negative value. On the other hand, the constraints
(4.5) impose that q
st
p
is greater than f
st
p
: as the ob-
jective function tends to choose the smallest possible
values for q
st
p
, we will have q
st
p
= f
st
p
in any optimal so-
lution. Conversely, if y
st
v
= 1, the constraints (4.5) are
inactive and the constraints (4.4) impose q
st
p
≥
∑
v∈p
δ
st
v,p
.
6.2 Bilevel Problem: Node-Arc
Formulation
6.2.1 The Leader Problem: Node-Arc
Formulation
At the first level, the Leader optimization problem
take decisions on the NFV defense placement and the
distribution of filtering capacities.
The first formulation we have proposed for the
Leader problem uses flow on paths decision variables.
We present here another formulation based on flow on
arcs decision variable.
Thus, we define two families of decision vari-
ables:
• x
n
v
: number of NFVs n placed at node v
• ϕ
st
vb
: filtering capacity installed at node v dedi-
cated to attack (s,t)
We propose the following multi-commodity node-
arc formulation of the Leader problem:



















minz =
∑
v∈V
∑
n∈N
K
n
v
x
n
v
+ πH(x, ϕ)(5.0)
Subject to
∑
n∈N
γ
rn
x
n
v
− cap
r
v
≤ 0∀v ∈ V ∀r ∈
¯
R(5.1)
∑
st∈D
ϕ
st
v
≤
∑
n∈N
φ
n
x
n
v
∀v ∈ V (5.2)
x
n
v
∈ Z
+
∀v ∈ V, ∀n ∈ [1..N](5.3)
(5)
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
148

The objective function (5.0) is to minimize the
installation costs of NFVs added to the penalization
costs related to the unstopped traffic, noted H(x, ϕ).
Constraints (5.1) are capacity constraints. They
ensure that for each resource type r available at
node v, NFVs installed at v consume no more than
the amount of this resource available at v. The
constraints (5.2) ensure that, at each node, the total
filtering capacities assigned to the different attacks is
less than the total filtering capacity installed at this
node.
6.2.2 The Follower Problem: Node-Arc
Formulation
In order to model the ’worst’ possible routing accord-
ing to a given NFV placement, we use here node arc
multicommodity flow formulation.
We introduce the arc- flow decision variables,
θ
st
u
, representing the amount of illegitimate flow (s,t)
routed on the arc u.
Moreover, we define E
+
v
(resp. E
−
v
) the set of arcs
arriving at (respectively from) node v.
The Follower problem is expressed as follows:





























H(x, ϕ) = max
∑
st∈D
∑
u∈E
−
t
θ
st
u
(6.0)
∑
st∈D
θ
st
u
− b
u
≤ 0∀u ∈ E(6.1)
∑
st∈D
∑
u∈E
−
v
θ
st
u
− For
v
≤ 0∀v ∈ V (6.2)
∑
u∈E
+
s
θ
st
u
= ψ
st
∀st ∈ D(6.3)
∑
u∈E
+
v
θ
st
u
= max

∑
u∈E
−
v
θ
st
u
− ϕ
st
v
;0

∀st ∈ D, ∀v ∈ V(6.4)
θ
st
u
≥ 0∀st ∈ D, ∀u ∈ E(6.5)
(6)
The objective function (6.0) of the follower
problem is to maximize the amount of unfiltered
illegitimate flow. This is computed as the total
amount of illegitimate flow arriving at its destination
t over all attacks (s, t). The constraints (6.1) ensure
that capacity transmission of link u is not exceeded.
The constraints (6.2) ensure that the forwarding
capacity of the node v is respected: the total incoming
flow at v must be less than its forwarding capacity
For
v
. The demand constraints (6.3) express that
the illegitimate flow coming from the source s is
all routed in the network. The constraints (6.4)
correspond to the equilibrium of the routing in each
node v of the network while taking into account the
NFV assignment. Thus, the amount of illegitimate
flow out of v,
∑
u∈E
+
v
θ
st
u
, is equal to 0 if the incoming
flow is zero or it is less than the installed filtering
capacities. This is equal to the incoming flow minus
the installed NFVs in the case where this quantity
is positive, that is to say in the case where all the
illegitimate flows entering in v could not be filtered.
The formulation of the Follower problem is not
linear because of the max term in the constraints (6.3).
It can be linearized by introducing y
st
v
binary variables
defined by:
z
st
v
=
(
1 if
∑
u∈E
−
v
θ
st
u
− ϕ
st
v
≥ 0
0 if
∑
u∈E
−
v
θ
st
u
− ϕ
st
v
≤ 0















































H(x, ϕ) = max
∑
st∈D
∑
u∈E
−
t
θ
st
u
(7.0)
∑
st∈D
θ
st
u
− b
u
≤ 0∀u ∈ E(7.1)
∑
st∈D
∑
u∈E
−
v
θ
st
u
− For
v
≤ 0∀v ∈ V (7.2)
∑
u∈E
+
s
θ
st
u
= ψ
st
∀st ∈ D(7.3)
∑
u∈E
+
v
θ
st
u
≤ 0 + ψ
st
z
st
v
∀st ∈ D, ∀v ∈ V (7.4)
∑
u∈E
+
v
θ
st
u
≤
∑
u∈E
−
v
θ
st
u
− ϕ
st
v
+ ψ
st
(1 − z
st
v
)
∀st ∈ D, ∀v ∈ V (7.5)
θ
st
u
≥ 0∀st ∈ D, ∀u ∈ E(7.6)
z
st
v
∈ {0, 1}∀st ∈ D, ∀v ∈ V (7.7)
(7)
The constraints (7.4) and (7.5) link together
variables z
st
v
, ϕ
st
v
and θ
st
u
. They can be understood
in the following way: If z
st
v
= 1, the constraints
(7.4) are inactive because they only impose that the
illegitimate flow coming out of v is smaller than the
total flow of the attack. The constraint (7.5) requires
that the illegitimate flow coming out of v be equal to
the incoming flow from which the part of the flow
filtered in v has been removed. Conversely, if z
st
v
= 0,
the constraint (7.5) is inactive and the constraint (7.4)
imposes that the outgoing flow is null.
This bilevel model meets the expectations of op-
erators, as it allows a compromise between the costs
of NFVs and the security requirements. However,
bilevel optimization problems are very challenging
optimization models as they are not obvious to im-
plement and may require significant computing time
(Lodi et al. , 2011), (Lodi, 2011), (Fischetti et al.,
2017), (Fischetti et al., 2018). Extensive research is
needed to develop relevant and effective resolution al-
gorithms for our bilevel model. This constitutes our
undergoing research developments on the topic.
Virtual Network Functions Placement for Defense Against Distributed Denial of Service Attacks
149

7 CONCLUSION
In this article, we studied the defense mechanisms
for DDoS attacks using NFV technology. This prob-
lem is of major importance for operators as DDoS
attacks may cause serious damages including mon-
etary losses and loss of customer confidence. Tra-
ditional defense methods require specialized and ex-
pensive hardware components. These methods fixing
the defense mechanisms in the equipments lack the
flexibility and adaptability that are needed to counter
DDoS attacks.
In this paper, we propose a security mechanism
that uses the flexibility and advantages of NFV tech-
nology. Our approach is based on mathematical pro-
gramming techniques. These methods lead to the de-
velopment of models that represent several technical
constraints while optimizing the NFVs deployment
costs. Our resolution algorithms give optimal solu-
tions or solutions with high quality (bounds to opti-
mality).
To make telecom operators benefit from recent ad-
vances in softwarization of networks, we proposed
models offering variable levels of security and NVF
installation costs. The first model we developed
achieved the highest level of security requirements at
the expense of the cost. Therefore, we addressed the
issue of the tradeoff between security requirements
and costs by proposing a bilevel model leading lower
costs but also lower security.
The first model we proposed try to filter all ille-
gitimate traffic while the second model offers a better
distribution of filtering capacities. The obtained nu-
merical results show the effectiveness and relevance
of our approach. The third model is a bilevel prob-
lem that reduces the costs of NFVs as the NFV place-
ment decision is made according to the worst attack
flow. In this last model, we offer a reasonable tradeoff
between the achieved security level and the induced
costs. Our solution allows to reduce the costs while
guaranteeing a satisfactory level of security. This
bilevel model opens an important research topic on
the resolution of bilevel programming models for se-
curity.
In the future, first we aim at implementing ef-
ficient solving algorithms for our bilevel problem.
Then we will deepen our investigation about bilevel
and robust optimization approaches for security issues
against DDoS attacks.
REFERENCES
Arbor Networks. ATLAS Summary Report: Global Denial
of Service. www.atlas.arbor.net/summary/dos.
Arbor Networks. NTP attacks: Welcome to the hockey stick
era, 2014. www.bit.ly/1ROlwQe.
J. Czyz, M. Kallitsis, M. Gharaibeh, C. Papadopoulos, M.
Bailey, and M. Karir. Taming the 800 pound gorilla:
The rise and decline of ntp ddos attacks. Proceed-
ings of the 2014 Conference on Internet Measurement
Conference, pp435-448, 2014.
J. Donovan, How SDN enabled innovations will im-
pact AT&T’s plans to transform it’s infrastruc-
ture. Open Networking Summit ONS2014, 2014,
www.bit.ly/1RQFMko.
M. Fischetti, I. Ljubic, M. Monaci, M. Sinnl: A new
general-purpose algorithm for mixed-integer bilevel
linear programs, Operations Research 65(6): 1615-
1637, 2017.
M. Fischetti, I. Ljubic, M. Monaci, M. Sinnl: On the Use
of Intersection Cuts for Bilevel Optimization, Mathe-
matical Programming, to appear, 2018.
D. Gilbert. Biggest internet attack in history threatens
critical system, 2014. www.ibtimes.co.uk/biggest-
internet-attack-history-threatenscritical-
infrastructure-450969.
Incapsula Survey. What DDoS Attacks Really Cost Busi-
nesses, 2014. https://www.imperva.com/resources/re
source-library/infographics/what-ddos-attacks-really-
cost-your-business/
A. H. M. Jakaria, Wei Yang, Bahman Rashidi, Carol Fung,
and M. Ashiqur Rahman, VFence: A Defense against
Distributed Denial of Service Attacks using Network
Function Virtualization, IEEE 40th Annual Computer
Software and Applications Conference, 2016.
S. Khandelwal. 602 gbps! this may have been the largest
ddos attack in history. www.thehackernews.com/
2016/ 01/biggest-ddos-attack.html.
Lodi A. (2011) On Bilevel Programming and Its Impact in
Branching, Cutting and Complexity. In: Achterberg
T., Beck J.C. (eds) Integration of AI and OR Tech-
niques in Constraint Programming for Combinatorial
Optimization Problems. CPAIOR 2011. Lecture Notes
in Computer Science, vol 6697. Springer, Berlin, Hei-
delberg.
Lodi, A., Ralphs, T. K., Woeginger, G.: Bilevel Pro-
gramming and Maximally Violated Valid Inequali-
ties. Technical Report OR/11/3, DEIS - Universit
`
a di
Bologna.
C. Rossow. Amplification hell: Revisiting network proto-
cols for ddos abuse. in USENIX Security Symposium,
2014.
Seyed K. Fayaz, Yoshiaki Tobioka, Vyas Sekar, and
Michael Bailey. Bohatei: Flexible and elastic ddos de-
fense. In 24th USENIX Security Symposium, pages
817–832. USENIX, 2015.
Topology Zoo. www.topology-zoo.org.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
150