
Determining Capacity of Shunting Yards by Combining Graph
Classification with Local Search
Arno van de Ven
1
, Yingqian Zhang
1
, Wan-Jui Lee
2
, Rik Eshuis
1
and Anna Wilbik
1
1
Eindhoven University of Technology, Eindhoven, The Netherlands
2
Maintenance Development, NS (Dutch Railways), Utrecht, The Netherlands
Keywords:
Planning and Scheduling, Machine Learning, Convolutional Neural Networks, Classification, Local Search.
Abstract:
Dutch Railways (NS) uses a shunt plan simulator to determine capacities of shunting yards. Central to this
simulator is a local search heuristic. Solving this capacity determination problem is very time consuming, as it
requires to solve an NP-hard shunting planning problem, and furthermore, the capacity has to determined for
a large number of possible scenarios at over 30 shunting yards in The Netherlands. In this paper, we propose
to combine machine learning with local search in order to speed up finding shunting plans in the capacity
determination problem. The local search heuristic models the activities that take place on the shunting yard as
nodes in an activity graph with precedence relations. Consequently, we apply the Deep Graph Convolutional
Neural Network, which is a graph classification method, to predict whether local search will find a feasible
shunt plan given an initial solution. Our experimental results show our approach can significantly reduce the
simulation time in determining the capacity of a given shunting yard. This study demonstrates how machine
learning can be used to boost optimization algorithms in an industrial application.
1 INTRODUCTION
The Dutch Railways (NS) operates a daily amount of
4,800 domestic trains serving more than 1.2 million
passengers each day. When trains are temporarily not
needed to operate a given timetable they are main-
tained and cleaned at dedicated shunting yards. Here,
NS is dealing with the so-called shunting activities
(Boysen et al., 2012). An example of a shunting yard
is shown in Figure 1.
Figure 1: Shunting yard with specific tracks for inspection
and cleaning activities. Source: www.sporenplan.nl.
NS is expanding their fleet of train units by 37% in
the next five years. The management team questions
if the capacity of existing shunting yards is sufficient
to handle the expansion. A shunt plan simulator has
been developed to help solve this capacity determina-
tion problem. The simulator is used to both determine
the capacity of shunting yards as well as analyze dif-
ferent scenarios on each shunting yard. Central to the
simulator is a local search heuristic (or LS) (van den
Broek, 2016; van den Broek et al., 2018). LS requires
an initial solution as a starting point, which is created
by a simple sequential algorithm that contains all im-
portant features to be able to apply search operators.
After a predefined running time, LS either returns a
feasible plan, or cannot find any feasible plan.
LS is much more computationally efficient than
the previously formulated mathematical optimization
model (Kroon et al., 2008). However, given that there
are over 30 shunting yards in The Netherlands, and
more than 50 possible scenarios to be evaluated for
each shunting yard, NS has been looking for solutions
to speeding up capacity determination. In this paper,
we propose to use machine learning to approximate
the local search heuristic, that is, we learn the rela-
tion between the input instances and the correspond-
ing outputs of LS. Given any initial solution, a con-
structed classification model predicts whether LS can
find a feasible solution before actually applying LS. In
this way, LS does not have to evaluate every generated
initial solution, and hence its computation time on de-
termining the maximum capacity of a given shunting
yard is greatly reduced.
van de Ven, A., Zhang, Y., Lee, W., Eshuis, R. and Wilbik, A.
Determining Capacity of Shunting Yards by Combining Graph Classification with Local Search.
DOI: 10.5220/0007398502850293
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 285-293
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
285

Essential to any local search algorithm is a solu-
tion representation that properly captures all impor-
tant aspects of the solution. The local search heuris-
tic by (van den Broek, 2016; van den Broek et al.,
2018) models the activities that take place on the
shunting yards as nodes in an activity graph. Repre-
senting shunt plans as activity graphs enables us to
use graph classification. Recent research on graph
classification has proven to achieve high accuracy in
predicting the class labels of an arbitrary graph, see
e.g., (Zhang et al., 2018), (Niepert et al., 2016) and
(Kipf and Welling, 2016). Therefore, in this paper,
we use a Deep Graph Convolutional Neural Network
(DGCNN) (Zhang et al., 2018) to train a model that
predicts the class label, i.e., feasible or infeasible, of
each graph in the dataset. To assess the effectiveness
of our approach, we measure the decrease in compu-
tation time in our experiments. We demonstrate how
machine learning methods can be used to boost opti-
mization algorithms in an industrial application.
The rest of our paper is organized as follows. In
Section 2, we describe background information, re-
lated work and clarify the position of our work within
the simulation process. Section 3 shows how we use
DGCNN to approximate LS. Section 4 describes the
experiment setup and results in terms of prediction ac-
curacy and decreased computation time.
2 BACKGROUND AND RELATED
WORKS
2.1 Shunt Plan Simulator
The shunt plan simulator at NS consists of three se-
quential stages: (1) generating an instance of a given
shunting yard, (2) generating an initial solution, and
(3) finding a feasible solution using a local search
heuristic. The maximum capacity of a given shunt-
ing yard is then determined by repeatedly running the
local search heuristic with different instances of dif-
ferent scenarios. After a sufficient number of runs,
the simulation converges towards a number of train
units for which the heuristic can solve at least 95% of
the instances. This number is used to determine the
capacity of the given shunting yard. The capacity is
defined as the number of train units a shunting yard
can serve during a 24-hour time period.
Figure 2 shows a diagram explaining the software
structure of the simulator. The instance generator is
a parameterizable program, developed by NS, which
derives instances for the Train Unit Shunting Problem
automatically. Instances can be generated for each
shunting yard individually with parameters specifi-
cally based on a day-to-day schedule at that shunt-
ing yard. Examples of parameters are number of train
units, arrival/departure distribution and the set of ser-
vice tasks that can be performed. Parameters can be
changed to test different scenarios.
Instance
Generator
Local Search
Heuristic
Storage and Retrieval
Capacity
Analyzer
Initial Solution
Generator
DGCNN
Feasibility
prediction
Figure 2: Diagram software structure simulator.
The output of the instance generator is a set of ar-
riving trains (AT), a set of departing trains (DT) and
a set of service tasks for each train unit that has to be
performed. For both (AT) and (DT), train composi-
tion, train units and arrival/departure time are speci-
fied. The set of service tasks contains a list of ser-
vice tasks for each train unit that has to be done in the
time that the train unit is present on the service site.
Trains can be composed of one or more train units of
the same type, which are a set of carriages that form
a self-propelling vehicle that can drive in both direc-
tions. Of the same train unit type, there exist multi-
ple subtypes, where the subtype indicates how many
carriages the train unit consists of. Figure 3 shows
a train unit type and corresponding subtypes. Train
composition, train units and arrival/departure time are
specified for both AT and DT. The set of service tasks
contains a list of service tasks for each train unit that
has to be done in the time that the train unit is present
on the shunting yard.
Figure 3: Train unit type VIRM with 6 and 4 carriages.
The output of the instance generator serves as in-
put for the initial solution generator. The algorithm
of Hopcroft-Karp (Hopcroft and Karp, 1973) is used
to produce a matching between arriving and depart-
ing train units. Next, a service task schedule is con-
structed in a greedy way, which forms an initial solu-
tion of the given instance. Note that generally initial
solutions are not feasible, that is, an initial solution
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
286

may violate the temporal or routing constraints. The
purpose of an initial solution is that it contains all im-
portant features to serve as a starting point for the lo-
cal search heuristic to find a feasible solution. In ear-
lier work (van den Broek, 2016; van den Broek et al.,
2018), 11 operators in LS have been defined to move
through the search space. LS ends when a feasible so-
lutions has been found or when the predefined maxi-
mum runtime has been reached. In the latter case, no
feasible solutions are found. Experiments in (van den
Broek, 2016) show that LS is capable to find feasible
shunt plans in both artificial and real-world scenar-
ios. The performance of LS has been compared to
a mathematical optimization model developed at NS
that tries to find the optimal solution, and LS is capa-
ble of planning more train units in most experiments.
As it is computationally expensive to use LS to eval-
uate every instance, in this work, we approximate LS
using a machine learning model.
2.2 Optimization Methods with
Machine Learning
In recent years, many studies have investigated boost-
ing optimization using machine learning, see e.g.
(Meisel and Mattfeld, 2010; Lombardi and Milano,
2018). For instance, in (Verwer et al., 2017), the au-
thors use regression models and decision trees to pre-
dict outcomes of auctions, and such predictive mod-
els are consequently used to evaluate and design op-
timal auction parameters. In (Defourny et al., 2012),
the authors combine the estimation of statistical mod-
els to return a decision rule given a state with sce-
nario tree techniques from multi-stage stochastic pro-
gramming. In the context of planning and schedul-
ing, (Peer et al., 2018) develop a Deep Reinforcement
Learning (DRL) solution to decide the best strategy
of parking trains. In their work, the existing opti-
mization model is completely replaced by a machine
learning model.
In our work, we use machine learning techniques
to learn the relation between the input instances and
the corresponding outcomes of local search. Our
work is also similar to the research line of simula-
tion optimization. The idea of simulation optimiza-
tion is to combine meta-heuristic search algorithms
with function approximation models for fitness ap-
proximation in order to reduce the time on determin-
ing the capacity (Carson and Maria, 1997; Amaran
et al., 2016).
The position of our work in the shunt plan sim-
ulator is between the initial solution generation and
applying initial solutions to local search (Figure 2).
After generating an initial solution, a trained classifi-
cation model (DGCNN) predicts whether LS can find
a feasible solution. If the outcome is positive, LS is
applied to find a feasible solution. Otherwise, the neg-
ative outcome leads to discarding the initial solution
and drawing a new instance from the instance genera-
tor. Therefore, accurately predicting feasibility leads
to a decrease in computation time since less time is
wasted on instances that may turn out to be infeasible
(see Section 4).
3 APPROXIMATING LS USING
DGCNN
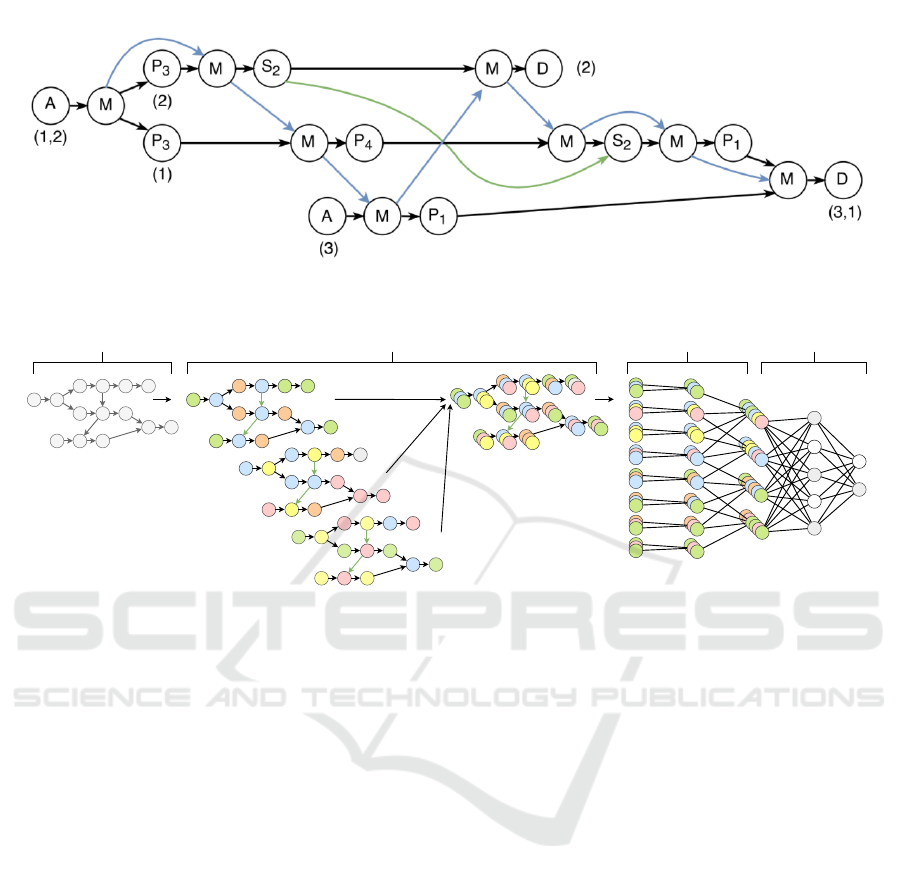
A shunt plan can be modelled as an activity graph.
Figure 4 shows an example of an activity graph. The
activities nodes, including arrival (A), service (S),
parking (P), movement (M) and departure (D), are
connected by edges indicating the precedence rela-
tions. The solid, black arcs represent the order of op-
erations of one or more train units. The corresponding
train units of the nodes are between parentheses. The
blue edges determine the order of the movements, and
the green edge indicates which service task is com-
pleted first. The assigned track for each parking node
is shown in subscript. The specific service task for
each service node is shown in subscript.
In this paper, we aim to predict whether an initial
solution that is represented by a given activity graph
can lead to a feasible solution. To this end, we treat
the prediction problem as a graph classification prob-
lem. Given a graph G = (V, E) where V is a finite set
of nodes and E is a finite set of edges. Node features
encode information about tracks, train units, duration
and activities. Each graph G
i
∈ G has a corresponding
class y
i
∈ C where C is the set of class labels given as
C = 0 (infeasible), 1 (feasible). The accuracy of the
derived model is assessed by comparing the predicted
label y
0
i
with the actual label y
i
.
There are many successful machine learning al-
gorithms that could be used to predict feasibility of
initial solutions. However, most algorithms involve
heavy feature engineering on problem instances. Re-
cently, a Deep Graph Convolutional Neural Network
(DGCNN) has been proposed in (Zhang et al., 2018)
for graph classification, which accepts graphs of arbi-
trary structure. The proposed architecture addresses
two main challenges: (1) how to extract useful fea-
tures characterizing the rich information encoded in
graph classification and (2) how to sequentially read
a graph in a meaningful and consistent order.
To tackle the first challenge, graph convolution
layers are used to extract local substructure features
from nodes and define a consistent node ordering.
Determining Capacity of Shunting Yards by Combining Graph Classification with Local Search
287
12.00h
12.30h
13.00h
12.45h
12.07h
-
12.41h
Figure 4: The activity graph of a shunt plan. The activity nodes in an shunt graph are encoded with starting and/or ending
times. For clarity, only a few starting and ending times are visualized.
1 3
6
6
2 5
1
8
2
2 7
7
4 8
1 3
6
6
2 5
1
8
2
2 7
7
4 8
1 3
6
6
2 5
1
8
2
2 7
7
4 8
1 3
6
6
2 5
1
8
2
2 7
7
4 8
1 3
6
6
2 5
1
8
2
2 7
7
4 8
1 3
6
6
2 5
1
8
2
2 7
7
4 8
1 3
6
6
2 5
1
8
2
2 7
7
4 8
1
1
1
2
2
2
3
3
3
4
4
4
5
5
5
6
6
6
7
7
7
8
8
8
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8
8
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8
8
Input graph Graph convolution layers 1-D convolution Dense layers
Figure 5: The overall structure of DGCNN used in our problem. An input graph of arbitrary structure is first passed through
multiple graph convolution layers where node labels are propagated between neighbors, visualized as different colors. Then
the node features are passed to traditional CNN structures to learn a predictive model. The figure is slightly modified from
(Zhang et al., 2018).
Their graph convolution model effectively mimics
two popular kernels, the Weisfeiler-Lehman Subtree
Kernel (Shervashidze et al., 2011b) and the Propa-
gation Kernel (Neumann et al., 2016), explaining its
graph-level classification performance. To address the
second challenge, a SortPooling layer is introduced,
which sorts the node features under the previously
defined order and unifies input sizes. This is done
because in contrast to images graphs lack a tensor
representation with fixed ordering, which limits the
applicability of neural networks on graphs. Finally,
traditional convolutional and dense layers are added
to read the sort graph representations and make pre-
dictions. The authors of (Zhang et al., 2018) show
DGCNN can achieve good performance on several
graphs such as social networks. In this paper, we ap-
ply a modified DGCNN, which is described as fol-
lows.
The second localized graph convolution step in-
volves appending node labels of neighbouring nodes
to original node labels. The variety of original node
labels defines how many new node labels will be cre-
ated after appending neighbouring node labels. Lo-
cal search specifies eight different activities in shunt
graphs. This original representation can be modi-
fied to include more information in the graphs. The
amount of original node labels can be increased by
including specific types of activities to effectively ex-
ploit the graph structure for a classification task.
In our problem, shunt graphs contain, among oth-
ers, Parking (P) and Service (S) activity nodes. In-
stead of just using P and S as original node labels,
both can be encoded with more information. The spe-
cific parking track can be appended to get P
i
, where
i = 1, ..., T and T is the number of parking tracks
on a shunting yard. The specific service task can be
appended to get S
i
, where i = 1, ..., ST and ST is
the number of service tasks that can be performed on
a shunting yard. Experiments showed that including
both P
i
and S
i
is beneficial.
As the train unit shunting problem is a scheduling
problem, the activity nodes in an shunt graph are en-
coded with starting and ending times. Therefore, the
nodes in an activity graph are implicitly sorted based
on the starting time. Thus, the sorting function of
Sortpooling in DGCNN is redundant, and therefore is
removed from our model. Figure 5 shows the network
structure that we use in our problem. It is slightly
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
288

modified from DGCNN in (Zhang et al., 2018).
4 EXPERIMENTS
We evaluate how much running time can be reduced
in determining capacity in shunting yards with our ap-
proach. To this end, we first generate and analyze data
from the simulator. Then we report the performance
of the DGCNN model on predicting whether initial
plans would lead to feasible plans. From the perfor-
mance of DGCNN, we can finally estimate the differ-
ence of running time with or without using DGCNN
feasibility prediction in the simulator (illustrated in
Figure 2).
4.1 Data Generation
In order to evaluate our method, we generate data in-
stances from the instance generator in the shunt plan
simulator. The instance generator can be specified ac-
cording to a set of input parameters based on the day-
to-day schedule at the given service site. The most
important parameters include: (1) number of train
units, (2) different train unit types and subtypes, (3)
probability distributions of arrivals per train unit type,
and (4) set of service tasks including duration.
We generated 10,000 instances with 21 train units
based on one of the service sites operated by NS. The
amount of 21 train units has been purposely chosen.
An increasing number of train unit increases the dif-
ficulty in finding feasible solutions. The preliminary
experiments have shown that the instances with fewer
train units are rather easy for the local search algo-
rithm to find feasible solutions and hence, less insight-
ful and valuable to the business. For the shunting yard
that we used in the experiments, the instances with 20
to 22 train units are most interesting for NS, as they
are neither easy nor too difficult for LS. Among them,
initial solutions generated for 21 train units are the
hardest to be correctly classified, and therefore they
are considered the most suitable data to explore the
usefulness of our approach to NS.
Initial solutions were created for all instances and
LS was applied to solve them. The maximum running
time for LS to solve each instance is set to 300 sec-
onds. Among 10,000 instances, LS was not able to
find feasible solutions for 2,750 instances. The out-
comes (feasible, infeasible) were recorded as classifi-
cation labels, where feasible instances (class 1) are
initial solutions leading to feasible plans using LS
within 300 seconds, while infeasible ones (class 0)
are those LS could not find feasible plans within the
time limit.
Figure 6: Distribution of iterations for feasible and infeasi-
ble solutions.
Figure 7: Scatter plot of iterations versus runtime.
Figure 8: Histogram of the runtime (in seconds) for feasible
solutions.
Figure 9: T-SNE visualization on the data instances.
Figure 6 visualizes the distribution of iterations
for both feasible and infeasible instances. Regarding
feasible solutions, the minimum and maximum num-
bers of iterations in local search are 108 and 2599
respectively with an average of 733 iterations. The
minimum and maximum number of iterations for in-
feasible solutions are 1057 and 2939 with an average
Determining Capacity of Shunting Yards by Combining Graph Classification with Local Search
289
of 1962 iterations. Clearly, the number of iterations
for infeasible solutions are much higher because lo-
cal search ran for the maximum time of 300 seconds
and was not able to find a feasible solution. Figure
7 shows a scatterplot with the number of iterations
on the x-axis and runtime on the y-axis. The runtime
of feasible instances increases as the number of itera-
tions increases. The spread in the beginning is small,
meaning that the time per iteration is quite similar. As
the runtime increases, the spread becomes larger. Fig-
ure 8 shows a histogram of the runtime for all feasible
instances. Infeasible instances are omitted for clarity
because their runtime is always around 300 seconds.
Considering feasible instances, the minimum runtime
is 1 second, while the maximum runtime is 300 sec-
onds. The average runtime is 96 seconds. ±80% of
all feasible instances has been found within 150 sec-
onds.
In addition, we use T-distributed Stochastic
Neighbor Embedding (t-SNE) (van der Maaten and
Hinton, 2008) visualize the generated data instances.
It models each high-dimensional object by a two-
dimensional point in such a way that similar objects
are modeled by nearby points and dissimilar objects
are modeled by distant points with high probability.
t-SNE can be useful in visualizing patterns in data as
well as the separability of classes. Clearly separable
clusters indicate good classification can be achieved,
while mixed clusters indicate the opposite. Figure 9
shows a visualization of the node feature data after
passing graphs through multiple convolution layers.
The figure indicates these two classes of graphs are
highly overlapped and thus form a difficult classifica-
tion problem.
4.2 Predicting Feasibility by DGCNN
The PyTorch (0.4.0) implementation of DGCNN is
used with Python (3.6.4) for the experiments. Train-
ing was done on an 1.7 GHz Intel Core i7 MacBook
Air. The DGCNN implementation is not parallelized,
thus only 1 CPU core is used. Every time a new epoch
begins, training data is randomly shuffled and pro-
cessed in batches of several graphs to enable faster
learning.
When applying DGCNN, we need to determine
the level of details, or node representation, on the
node labels in the graph. We apply the Weisfeiler-
Lehman subtree kernel (Shervashidze et al., 2011a) to
append node labels of the neighbouring nodes to the
original node labels. The appended labels are sorted
alphabetically and compressed into new, shorter la-
bels. At the end of an iteration, the counts of the
original node labels and the counts of the compressed
node labels are represented as a feature vector. Neu-
ral networks are trained on these feature vectors. The
original node labels define how many new node labels
will be created after appending neighbouring node la-
bels. The length of the feature vector depends on the
amount of different node labels in the initial solution.
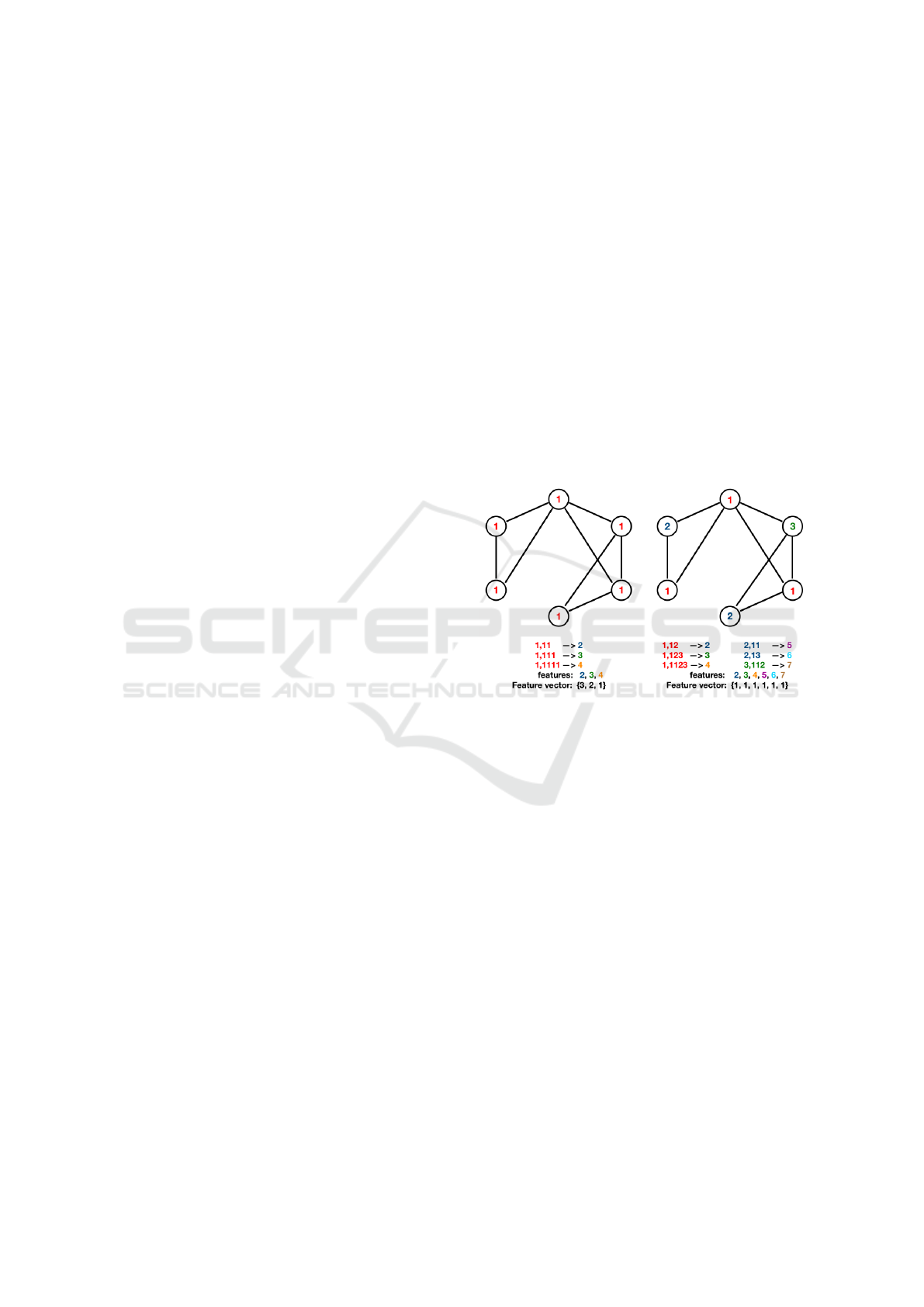
Figure 10 visualizes how the length of the feature vec-
tor changes if node labels differ for the same graphs.
In the left graph, originally, all nodes have the same
node label. The right graph originally contains three
different node labels. The appended and compressed
labels after one iteration of the Weisfeiler-Lehman
subtree kernel are visualized below both graphs. The
feature vectors of both graphs contain the counts of
the compressed node labels after one iteration. As
can be seen, the length of the feature vector gets big-
ger when the level of detail (variety of node labels in
the original graph) increases.
Figure 10: Different feature vectors for different amounts
of node labels.
Too many node labels may result in very dissim-
ilar feature vectors. In both cases, neural networks
may not be able to distinguish between feasible and
infeasible instances. Hence it is important to select
the best amount of the original node labels. Based on
the data associated to the nodes (Figure 4) the level of
detail can be determined in the following three ways:
(1) regular labels, (2) regular labels and service tasks,
(3) regular labels, service tasks, and parking loca-
tions. Regular labels are the labels of the 8 node types
(7 illustrated in Figure 4 and one additional activity
called “Saw Move”). This level of detail would result
in the smallest feature vectors. One step further is to
specify the service task as a node type. On the cho-
sen service site, five different service tasks are avail-
able: internal cleaning, soap external cleaning, oxalic
external cleaning, technical checkup A, and techni-
cal checkup B. Either one would replace the regular
service task node (S) resulting in 12 different node la-
bels. The most detailed representation specifies both
parking locations and service tasks, which results in
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
290

24 different node labels given 13 different tracks in
the service site.
4.2.1 Sampling
The generated instances are not balanced, with 7205
samples in class 1, and 2795 in class 0. Under-
sampling and oversampling are two commonly used
methods dealing with class imbalance problems. The
risk of undersampling is loss of information due to
removing potentially important instances. Whereas
oversampling increases the possibility of overfitting.
We create three datasets with different balancing
strategies: (1) only undersampling, with 2795 sam-
ples for both classes, (2) only oversampling, with
7205 samples for both classes, (3) both under- and
oversampling, with 5000 samples for both classes.
Together with the three different node representa-
tion strategies, we end up with nine datasets. DGCNN
is applied on all nine datasets to find the best combi-
nation of methods dealing with class imbalance and
the level of detail of node labels. We use 5-fold cross
validation. Table 1 shows the classification perfor-
mance. It shows that the performance increases as we
add more detailed information about the planning in-
stances on the nodes in the graph. The three datasets
with the highest level of detail are highlighted in the
table. In addition, the results show that using under-
sampling is the best of the methods dealing with class
imbalance. The runtime for undersampled datasets
is also significantly lower than when (a combination
with) oversampling is used, which is logical as the
undersampled dataset is smaller.
4.2.2 Hyperparameter Tuning
We use the best performing dataset to tune the hyper-
parameters of DGCNN using grid search. The follow-
ing combination of parameter values has achieved the
best performance and is used to generate the final pre-
diction model: (1) unifying nodes in graph: 0.7; (2)
learning rate: 1 × 10
−5
; (3) number of convolution
layers: 3; (4) number of nodes in convolution layers:
64; (5) number of training epochs: 120; (6) batch size:
100.
Table 2 shows the confusion matrix of the final
classification model. Each column of the matrix rep-
resents the instances in a predicted class while each
row represents the instances in an actual class. Each
cell counts the number of instances that corresponds
to the row and column value. Correctly predicted
classes are true negatives (TN; top left cell) and true
positives (TP; bottom right cell). Incorrectly pre-
dicted classes are false negatives (FN; bottom left
cell) and false positives (FP; top right cell). The fi-
nal classification model of DGCNN is able to predict
feasibility of an initial solution with 65.1% accuracy.
It has been shown to be a difficult classification prob-
lem. A previous study (Dai, 2018) applied heavy fea-
ture engineering and tested various classifiers for this
classification task, which resulted in a highest accu-
racy of 66.3%. However, to derive features, that ap-
proach assumes extensive domain knowledge on the
shunting services planning problem. In comparison,
DGCNN takes initial solutions directly as inputs.
Despite the difficulty of the classification problem,
in the next section, We show the value of our approach
in speeding up finding feasible solutions for capacity
determination.
4.3 Accelerating Simulations to
Determine Capacities
Being able to predict feasibility of an initial solution
before applying local search may lead to a decrease
in computation time when determining the maximum
capacity of a service site. We measure the effect of
our approach by calculating the expected difference
in running time with and without using DGCNN. As
every instance was solved by the local search heuristic
and its running time was recorded, we derive in Table
3 the running time of LS without DGCNN for all four
types of instances (TN, FP, FN, and TP), as well as
the average running time of feasible and infeasible in-
stances.
The total running time on the testing data with-
out applying DGCNN in Table 3 is 221,710 seconds,
roughly 62 hours. This is the existing situation, where
the local search algorithm has to evaluate every gen-
erated instance. We call our approach where DGCNN
is applied to predict the feasibility of instances before
applying LS “the new situation”.
We use the following process to estimate the run-
ning time in the new situation. For each instance in
the test set, DGCNN is used to predict whether it
is feasible or infeasible. If feasible, the local search
heuristic is applied to find a feasible solution (or ter-
minate if it turns out to be infeasible given the prede-
fined time limit). If, however, the predicted outcome
is infeasible, this instance is discarded immediately
and a new instance is drawn from the instance gener-
ator. This new instance is again fed to DGCNN, and
the prediction of feasibility leads to either applying
LS, or discarding this instance. This process contin-
ues until all instances have been classified as feasible.
Figure 11 shows a Markov Transition Diagram to vi-
sualize this process, where the probabilities of transi-
tions are obtained from Table 2.
Determining Capacity of Shunting Yards by Combining Graph Classification with Local Search
291
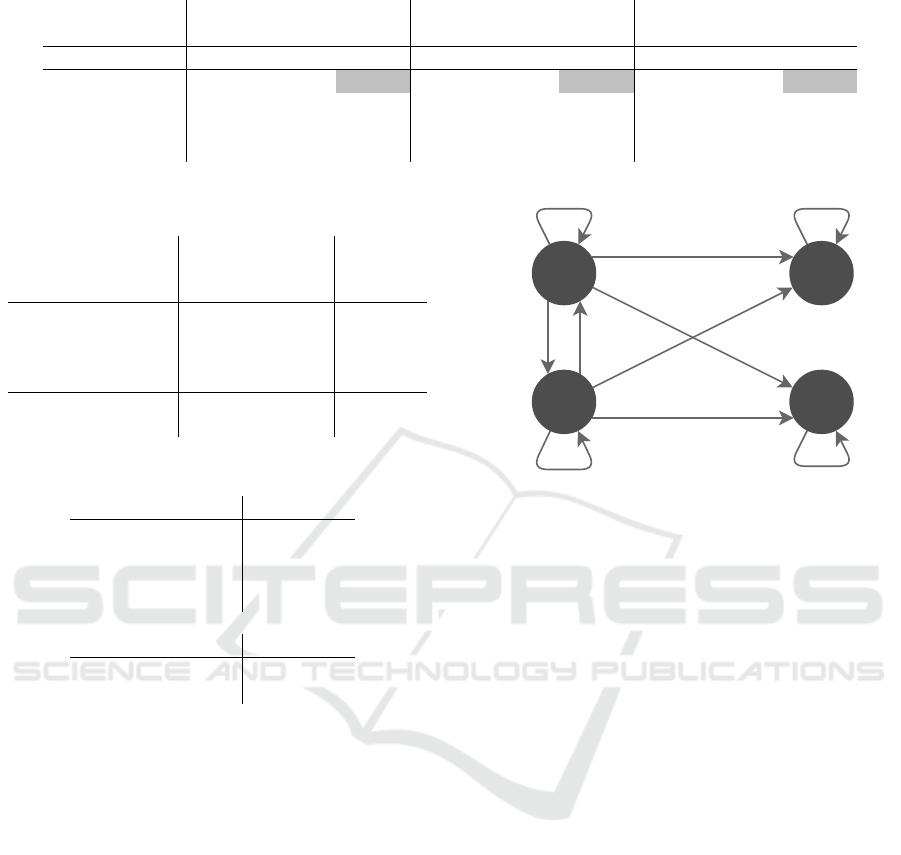
Table 1: Accuracy, standard deviation and runtime DGCNN on test sets of 9 datasets.
DGCNN
RESULTS
Undersampling Oversampling
Undersampling and
Oversampling
# node labels 8 12 24 8 12 24 8 12 24
Accuracy (%) 59.89 60.80 62.10 60.15 60.85 61.28 60.15 60.19 60.89
Standard
deviation (%)
±1.28 ±0.92 ±0.88 ±0.47 ±0.74 ±0.16 ±0.56 ±1.06 ±0.50
runtime (h) 3.6 3.6 3.6 13.1 13.1 13.1 10.4 10.4 10.4
Table 2: Confusion matrix of the final classification model
DGCNN.
Predicted labels
0 1
Correct
Incorrect
0
372
33.3%
185
16.5%
67%
33%
Actual
labels 1
205
18.3%
356
31.9%
63%
37%
Correct
Incorrect
64%
36%
66%
34%
65.1%
34.9%
Table 3: Runtime per quadrant and average runtimes.
Quadrant Time (sec)
True negatives 110,877
False positives 56,037
False negatives 24,362
True positives 30,434
Averages Time (sec)
Average feasible 97.7
Average infeasible 299.7
Figure 11 shows that if an instance is classified
as feasible, it will never leave that state. Note that
being classified as feasible can either be correct (true)
or incorrect (false). Since no new instances will be
generated for instances classified as FP or TP, those
runtimes remain the same in the new situation. If an
instance is classified as infeasible, a new instance is
drawn. This new instance can be transferred to any
other state based on the probabilities. The runtime for
TN and FN will change in the new situation.
The total runtime for the TN instances without
DGCNN is 110,877 seconds. The total runtime de-
creases to 62,123 seconds when using DGCNN. A
decrease of 44.0%. The runtime for FN without
DGCNN is 24,362 seconds. The total runtime in-
creases to 34,259 seconds when using DGCNN. This
is because the instances are actually feasible, but in-
correctly classified as infeasible. Therefore, new in-
stances will be generated and some of those will turn
out to be infeasible, causing a longer running time.
While the runtime for FN instances increased with
40.6%, the total runtime of all instances decreased
TN
FN TP
FP
0.183
0.333
0.319
0.165
0.319
0.165
0.333
1
1
0.183
Figure 11: Markov Transition Diagram transfer probabili-
ties.
with 38,857 seconds to a total of 182,853 seconds.
This decrease in runtime will save 17.5% when deter-
mining the capacity of a service site.
We have shown that using our approach, roughly
51 hours can be saved in determining whether one
given shunting yard has sufficient capacity in han-
dling 21 train units with one particular scenario. Such
tests have to be done for more than 50 scenarios.
Hence, our approach will save about 100 days on de-
termining whether 21 train units can be handled in the
testing yard. Furthermore, if it is concluded that the
site has sufficient capacity for 21 trains units, the sce-
narios with 22 or more train units will be generated
and tested in order to find out the maximum number
of the units that the given shunting yard can deal with.
With 35 service sites in the Netherlands, the time re-
duction using our approach has a great impact.
5 CONCLUSION
In this work we have shown that combining a
Deep Graph Convolutional Neural Network with lo-
cal search leads to a decrease in computation time in
determining capacities in shunting yards. The compu-
tation time was decreased by 17.5% determining the
capacity of one shunting yard if DGCNN is used to
predict whether an initial solution will become feasi-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
292

ble after applying local search.
Our results demonstrate how existing research in
graph classification can be used to boost optimization
algorithms in an industrial application. It shows the
value of using machine learning models as approxi-
mation functions of optimization algorithms in find-
ing solutions. As future work, we may increase the
performance of our approach by collecting data in a
more robust way. Since there are a lot of randomness
in creating initial solutions and in the process of find-
ing feasible solutions, it could be beneficial to apply
local search multiple times on one initial solution.
ACKNOWLEDGEMENTS
The work is partially supported by the NWO funded
project Real-time data-driven maintenance logistics
(project number: 628.009.012).
REFERENCES
Amaran, S., Sahinidis, N. V., Sharda, B., and Bury, S. J.
(2016). Simulation optimization: a review of algo-
rithms and applications. Annals of Operations Re-
search, 240(1):351–380.
Boysen, N., Fliedner, M., Jaehn, F., and Pesch, E. (2012).
Shunting yard operations: Theoretical aspects and
applications. European Journal of Operational Re-
search, 220(1):1–14.
Carson, Y. and Maria, A. (1997). Simulation optimization:
Methods and applications. In Winter Simulation Con-
ference Proceedings, pages 118–126.
Dai, L. (2018). A machine learning approach for optimiza-
tion in railway planning. Master’s thesis, Delft Uni-
versity of Technology.
Defourny, B., Ernst, D., and Wehenkel, L. (2012). Sce-
nario trees and policy selection for multistage stochas-
tic programming using machine learning. Journal on
Computing. Published online before print.
Hopcroft, J. and Karp, R. (1973). An algorithm for max-
imum matchings in bipartite graphs. Annual Sympo-
sium on Switching and Automata Theory, 2(4):225–
231.
Kipf, T. and Welling, M. (2016). Semi-supervised classi-
fication with graph convolutional networks. CoRR,
abs/1609.02907.
Kroon, L. G., Lentink, R. M., and Schrijver, A. (2008).
Shunting of passenger train units: an integrated ap-
proach. Transportation Science, 42(4):436–449.
Lombardi, M. and Milano, M. (2018). Boosting com-
binatorial problem modeling with machine learning.
In Proceedings of the Twenty-Seventh International
Joint Conference on Artificial Intelligence (IJCAI-18),
pages 5472–5478.
Meisel, S. and Mattfeld, D. (2010). Synergies of operations
research and data mining. European Journal of Oper-
ational Research, 206(1):1–10.
Neumann, M., Garnett, R., Bauckhage, C., and Kersting,
K. (2016). Propagation kernels: efficient graph ker-
nels from propagated information. Machine Learning,
102(2):209–245.
Niepert, M., Ahmed, M., and Kutzkov, K. (2016). Learn-
ing convolutional neural networks for graphs. CoRR,
abs/1605.05273.
Peer, E., Menkovski, V., Zhang, Y., and Lee, W.-J. (2018).
Shunting trains with deep reinforcement learning. In
Proceeding of 2018 IEEE International Conference
on Systems, Man, and Cybernetics. ieee.
Shervashidze, N., Schweitzer, P., Leeuwen, E. J. v.,
Mehlhorn, K., and Borgwardt, K. M. (2011a).
Weisfeiler-lehman graph kernels. Journal of Machine
Learning Research, 12(Sep):2539–2561.
Shervashidze, N., Schweitzer, P., van Leeuwen, E.,
Mehlhorn, K., and Borgwardt, K. (2011b). Weisfeiler-
lehman graph kernels. Journal of Machine Learning
Research, 12:2539–2561.
van den Broek, R. (2016). Train shunting and service
scheduling: an integrated local search approach. Mas-
ter’s thesis, Utrecht University.
van den Broek, R., Hoogeveen, H., van den Akker, M., and
Huisman, B. (2018). A local search algorithm for train
unit shunting with service scheduling. Transportation
Science, submitted.
van der Maaten, L. and Hinton, G. (2008). Visualizing data
using t-SNE. Journal of Machine Learning Research,
2579-2605:671–680.
Verwer, S., Zhang, Y., and Ye, Q. C. (2017). Auction opti-
mization using regression trees and linear models as
integer programs. Artificial Intelligence, 244:368–
395.
Zhang, M., Cui, Z., Neumann, M., and Chen, Y. (2018). An
end-to-end deep learning architecture for graph clas-
sification. In AAAI, pages 4438–4445.
Determining Capacity of Shunting Yards by Combining Graph Classification with Local Search
293
