4-valued Logic for Agent Communication with Private/Public

Information Passing

Song Yang, Masaya Taniguchi and Satoshi Tojo

Japan Advanced Institute of Science and Technology, Japan

Keywords:

Agent Communication, Rational Agent, Dynamic Epistemic Logic, Modal Logic, 4-valued Logic.

Abstract:

Thus far, the agent communication has often been modeled in dynamic epistemic logic, where each agent

changes his/ her belief, restricting the accessibility to possible worlds in Kripke semantics. Prior to the mes-

sage passing, in general, the sender should be required to believe the contents of the message. In some

occasions, however, the recipient may not believe what he/ she has heard since he/ she may not have enough

background knowledge to understand it or the information may be encrypted and he/ she may not know how

to decipher it. In this paper, we generalize those messages that require special knowledge as private informa-

tion and formalize that the recipient does not change his/ her belief receiving such private messages. Then,

we distinguish the validity of the information from the belief change of the recipient; that is, even though

the communication itself is held and the information is logically contradictory to his/ her original belief, the

recipient may not change his/ her belief. For this purpose, we employ 4-valued logic where each proposition

is given 2 (usual true and false) times 2 (private or public information or not) truth value.

1 INTRODUCTION

In van Ditmarsch et al. (2008), there have been dis-

tinguished the following difference in agent commu-

nication.

• public announcement: every agent receives the

same information.

• whisper: other agents notice there happens an in-

formation transmission among others but the con-

tents cannot be seen.

• channel: one to one communication: other agents

cannot notice there has been an information trans-

mission.

In addition, in this work we would distinguish the

public/ private message passing, that is, the recipi-

ent cannot read nor understand what is written. The

most probable case is that the information is mean-

ingless for the recipient because he/she does not have

enough background knowledge to understand it, e.g.,

the message might be written in an unknown foreign

language. The second most probable case is that the

message is encrypted and the recipient cannot deci-

pher it; in the latter case a simple tip or a password

may sufﬁce to read it. In either way, we can general-

ize these cases into a category, that is, private infor-

mation. Here, we distinguish the following two cate-

gories.

• the contents of the message is only privately un-

derstood.

• the contents of the message is publicly under-

stood.

In this paper, we distinguish these two, introduc-

ing 4-valued logic; that is, we distinguish if the mes-

sage passing is successful and the recipient surely has

received the message (T/F), and if his/her belief is af-

fected even though the message might contradict to

the belief of the recipient, since the agent could not

decipher the contents. Here, the communication may

fail in three cases shown in Figure 1.

In the following Section 2, we summarize the fun-

damental mechanism of belief change by dynamic

epistemic logic (DEL), that is by the accessibility re-

striction in Kripke semantics. In Section 3, we survey

the history and application of 4-valued logic. In Sec-

tion 4, we revise the belief change by private/ public

information passing, and show the recursion axiom to

the ordinary DEL, that is sound and complete. Finally

in Section 5, we summarize our contribution.

Yang, S., Taniguchi, M. and Tojo, S.

4-valued Logic for Agent Communication with Private/Public Information Passing.

DOI: 10.5220/0007400000540061

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 54-61

ISBN: 978-989-758-350-6

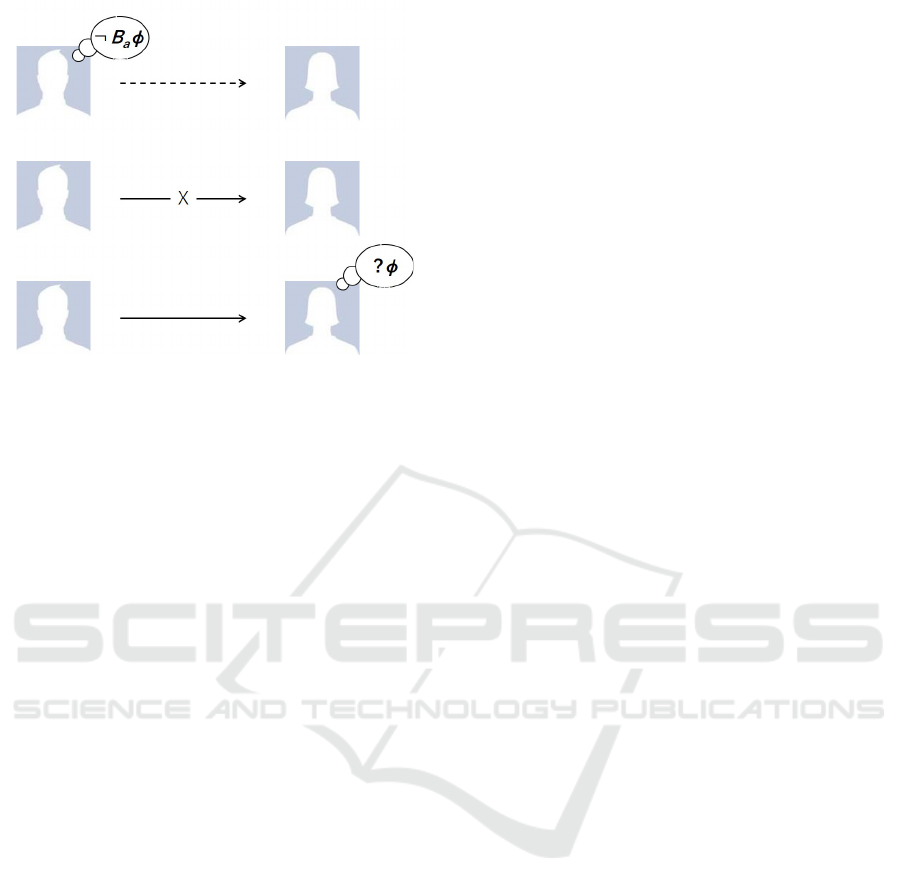
Figure 1: Three different miscommunication; top: the

sender does not believe the contents of the information,

middle: there is no channel between two agents, bottom:

the recipient cannot decipher the contents.

2 SEMI-PRIVATE

ANNOUNCEMENT IN DEL

Hatano et al. (2015) showed a modal epistemic lan-

guage which has formalized agents’ belief and chan-

nels.

2.1 Syntax

Let PROP = { p, q,.. .} be a ﬁnite set of propositional

variables and G = {a,b,. . .} a ﬁnite set of agents. The

language is generated by the following Backus-Naur

form:

α ::= p | ¬α | α ∨ α | c

ϕ ::= α | B

α | [α↓

]ϕ | ¬ϕ | ϕ ∨ ϕ

where p ∈ PROP,a ∈ G, b ∈ G and α is an objective

(non-modal) formula.

Here, c

means “There is a channel from agent a

to agent b”, B

ϕ means “agent a believes ϕ”. [α↓

]ϕ

will be deﬁned in section 2.3.

2.2 Semantics

A Kripke model M is a tuple:

M = (W,R

,V )

where W is a non-empty set of worlds, G is a non-

empty set of agents, R

= {R

| a ∈ G} and R

⊂ W ×

W is an accessibility of agent a on W, C

= {C

| a ∈

G,b ∈ G} and C

⊆ W is a channel relation, and V :

Prop → P(W ) is a valuation function. Here, C

= W

for all a ∈ G because each agent must have a channel

to itself.

Given any model M, any world w ∈ W and any

formula ϕ, we deﬁne the satisfaction relation induc-

tively as follows:

M,w |= p iff w ∈ V (p)

M,w |= c

iff w ∈ C

M,w |= ¬ϕ iff M,w 6|= ϕ

M,w |= ϕ ∨ ψ iff M,w |= ϕ or M, w |= ψ

M,w |= B

ϕ iff ∀u ∈ W ((w,u) ∈ R →

M,u |= ϕ)

Here, we say ϕ is valid on M if M,w |= ϕ for any

w ∈ W, and ϕ is valid in a class of Kripke models if ϕ

is valid on any M in the class. Then, it is clear that in

Table 1, all of the axioms are valid and all of the rules

preserve validity on M.

Table 1: Hilbert-style Axiomatization K

of Static Logic.

(Taut) ϕ, ϕ is a tautology.

) B

(ϕ → ψ) → (B

ϕ → B

ψ) (a ∈ G)

(Selfchn) c

(a ∈ G)

(MP) From ϕ and ϕ → ψ, infer ψ

Nec

From ϕ, infer B

ϕ (a ∈ G)

2.3 Semi-private Announcement

We often use public announcement to express the

communication between agents. However, in general,

most of the announcements are made between a group

of agents, so that only the agent in the group can get

the message, while others cannot know what they are

talking. This kind of announcement is called semi-

private announcement (Sano and Tojo (2013)).

Here, we use the dynamic operator [ϕ↓

], which

means “after the agent a sent a message ϕ to the

agent b via a channel”, to express the semi-private

announcement. Then, [ϕ↓

]ψ stands for ‘after the

agent a sent a message ϕ to the agent b via a chan-

nel, ψ holds”. We provide the semantic of [ϕ↓

]ψ on

a Kripke model M = (W,R

,V ) as follows:

M,w |= [ϕ↓

]ψ iff M

ϕ↓

,w |= ψ

where M

ϕ↓

= (W,R

,V ) and R

∈ R

is deﬁned

as:

• If i = b, for all x ∈ W ,

(x) :=

(

(x) ∩ JϕK

if M,x |= c

∧ B

(x) otherwise.

• Otherwise, R

:= R

Here, JϕK

is called the truth set of ϕ in M, which

is deﬁned as follows:

JϕK

= {w ∈ W | M,w |= ϕ}

4-valued Logic for Agent Communication with Private/Public Information Passing

Semantically speaking, [ϕ↓

] revises agent b’s be-

lief when agent a believes ϕ, and there is a channel

from a to b. Otherwise, agent b’s belief will not be

restricted (Barwise and Seligman (1997)). And it is

easy to see that others than b will not revise their be-

lief while they don’t get the message ϕ. Here, all of

the agents are considered as believable and receivable,

while they can only tell the truth and they receive any

message made by others (Seligman et al. (2011)).

In the syntax including [ϕ↓

]ψ, ψ is valid on the

class of all ﬁnite Kripke models iff ψ is a theorem in

[ ·↓

] of Table 2 as follows:

Table 2: Hilbert-style Axiomatization K

[ ·↓

In addition to all the axioms and rules of K

, we add:

[ϕ↓

]p ↔ p

[ϕ↓

↔ c

[ϕ↓

]¬ψ ↔ ¬[ϕ↓

]ψ

[ϕ↓

]ψ ∧ χ ↔ [ϕ↓

]ψ ∧ [ϕ↓

]χ

[ϕ↓

ψ ↔ B

ψ(c 6= b)

[ϕ↓

ψ ↔ (c

∧ B

ϕ → B

(ϕ → ψ))∧

(¬(c

∧ B

ϕ) → B

ψ)

(Nec

[ϕ↓

]

) From ψ, infer [ϕ↓

]ψ

The prove is shown in Hatano et al. (2015).

3 4-VALUED MODAL LOGIC

In classical logic, a proposition has only two possi-

ble truth values, which are usually called true and

false. In other words, if a proposition is not true, it

is false, and vice versa. However, sometimes a propo-

sition is not true, while it is not false. For example,

we cannot say that the sentence “There is no alien in

the universe” is true, while we cannot say it is false.

So we can see sometimes two possible values are not

enough.

To resolve this problem, many-valued logic whose

proposition has more than two truth values has been

studied. The sum of possible truth values can be

three, four, any natural number more than three, and

even inﬁnite. Malinowski (2014) added a new possi-

ble truth value Undeﬁned, to mark indeterminacy of

some proposition. Bo

cvar(Ciucci and Dubois (2013))

added a truth degree 0.5, whose reading as “mean-

ingless” or “senseless”. Cattaneo and Nistic

o (1989)

use a structure hΣ, 0, ≤,

∼

i to express the third

value. Łukasiewicz provided an inﬁnite-valued logic

that considered the truth value as a real number be-

tween 0 and 1. In Łukasiewicz logic, the number

of truth value shows the probability that the formula

is false (Giles (1976)). In this paper, we consider

4-valued logic with Belnapian truth values(Odintsov

and Wansing (2010)).

In 4-valued logic, the four values are usually

called true, false, neither and both. Belnap considered

the valued as follows:

• the value of p is True(T) means that the computer

is told that p is true.

• the value of p is False(F) means that the computer

is told that p is false.

• the value of p is Neither(N) means that the com-

puter is not told anything about p.

• the value of p is Both(B) means that the computer

is told that p is both true and false(perhaps from

different sources, or so on).

Odintsov and Wansing (2017) shows that 4-valued

logic can also be used in modal logic, whose oper-

ators includes  and ♦.(Blackburn et al. (2002))

3.1 Language and Truth-table

To deﬁne the language of Belnap-Dunn Modal Logic



, ﬁrst we consider the language L



where



:= {∧,∨, →,⊥,∼,}

where ∼ stands for “strong negation” and other oper-

ators are deﬁned as follows:

¬ϕ := ϕ → ⊥, ϕ ↔ ψ := (ϕ → ψ) ∧ (ψ → ϕ)

♦ϕ :=∼  ∼ ϕ, ϕ ⇔ ψ := (ϕ ↔ ψ) ∧ (∼ ϕ ↔∼ ψ)

Then, we can deﬁne the language BK



as the least



-logic containing the following three groups of ax-

ioms:

• Axioms of classical propositional logic in the lan-

guage ∨,∧, →,⊥.

• Strong negation axioms:

∼ (p ∧ q) ↔ (∼ p∨ ∼ q)

¬(p → q) ↔ (p∧ ∼ q)

∼ (p ∨ q) ↔ (∼ p∧ ∼ q)

∼∼ p ↔ p, and ∼ ⊥

• Modal axioms:

(p → q) → (p → q) ¬ ∼ p ↔ ¬ ∼ p

The truth-tables are shown in Table 3,4,5.

Table 3: Truth-table of “∼”.

ϕ ∼ ϕ

T F

F T

B B

N N

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

Table 4: Truth-table of “∧”.

∧ T F B N

T T F B N

F F F F F

B B F B F

N N F F N

Table 5: Truth-table of “∨”.

∨ T F B N

T T T T T

F T F B N

B T B B T

N T N T N

We can represent the elements of T,F,B, N as

pairs (a,b), where a,b ∈ {0,1}, then T,F, B, N can be

written as follows: (Odintsov and Wansing (2010))

T = (1, 0),F = (0, 1), N = (0, 0),B = (1, 1).

Under the presentation above, we can get the form

of twist-operators following:

(a,b) ∨ (c,d) = (a ∨ c, b ∧ d)

(a,b) ∧ (c,d) = (a ∧ c, b ∨ d)

∼ (a,b) = (b, a),(a,b) → (c, d) = (a → c, a ∧ d)

3.2 Semantics

A BK-model is a tuple M = (W,R,V ) where W is a

non-empty set of worlds, R ⊂ W ×W is an accessibil-

ity relation on W , and V : Prop ×W → T, F, B,N} is

a valuation function. It will be convenient to have an-

other deﬁnition closed to the standard Kripke model,

so we assign functions v

−

: Prop → 2

deﬁned as

follows instead of V : (Odintsov and Wansing (2017))

(p) = {w|V (p,w) ∈ {T,B}}

−

(p) = {w|V (p,w) ∈ {F,B}}

For a BK-model M = (W,R, v

−

), we deﬁne

and |=

−

between the worlds of M and formulas

as follows: (Odintsov and Wansing (2017), Odintsov

and Wansing (2010))

M,w |=

p ⇔ w ∈ v

(p)

M,w |=

−

p ⇔ w ∈ v

−

(p)

M,w |=

ϕ ∧ ψ ⇔ M,w |=

ϕ and

M,w |=

−

ϕ ∧ ψ ⇔ M,w |=

−

ϕ or

M,w |=

−

M,w |=

ϕ ∨ ψ ⇔ M,w |=

ϕ or

M,w |=

−

ϕ ∨ ψ ⇔ M,w |=

−

ϕ and

M,w |=

−

M,w |=

ϕ → ψ ⇔ M, w |=

ϕ ⇒

M,w |=

−

ϕ → ψ ⇔ M, w |=

ϕ and

M,w |=

−

M,w 6|=

⊥ always

M,w |=

−

⊥ always

M,w |=

∼ ϕ ⇔ M,w |=

−

M,w |=

−

∼ ϕ ⇔ M,w |=

M,w |=

ϕ ⇔ ∀u ∈ W ((w,u) ∈ R ⇒

M,u |=

ϕ)

M,w |=

−

ϕ ⇔ ∃u ∈ W ((w,u) ∈ R and

M,u |=

−

ϕ)

M,w |=

♦ϕ ⇔ ∃u ∈ W ((w,u) ∈ R and

M,u |=

ϕ)

M,w |=

−

♦ϕ ⇔ ∀u ∈ W ((w,u) ∈ R ⇒

M,u |=

−

ϕ)

If we use a pair (a,b) to express the value of for-

mula “ϕ” in world w according to the previous sub-

chapter, the basis deﬁnition of |=

and |=

−

can also

be written as follows:

M,w |=

ϕ ⇔ a = 1

M,w |=

−

ϕ ⇔ b = 1

4 4-VALUED LOGIC FOR

MULTI-AGENT

COMMUNICATION

Consider two people Ann and Bill, who are chatting

on the Internet. Ann learned a new dance and she

believes that her dance is very good, so she wants to

tell Bill it. Then she sends a video of her dance to

Bill. However, Bill doesn’t get the message that Ann’s

dance is good. The possible reasons are as follows:

• The Internet is not connected.

• Bill’s computer is too old to watch the video.

so he cannot get the message to revise his belief. Also,

it can be explained in other ways. For another exam-

ple, let agents a and b be two companies. p means

that “a is faced with bankruptcy”. Obviously, if a and

b are opponents, they won’t tell it to each other if they

believe p or the negation of p. Such p can be seen as

a private proposition.

Hatano et al. (2015) can express the disconnection

by channels, but it cannot show the other situation.

Here, we use a pair (a,b) to express the value of a

proposition ϕ. (a ∈ {T,F},b ∈ {0, 1})

• ϕ : (T,1) means “ϕ is true and public.”

• ϕ : (T,0) means “ϕ is true and private.”

• ϕ : (F, 1) means “ϕ is false and public.”

• ϕ : (F, 0) means “ϕ is false and private.”

4-valued Logic for Agent Communication with Private/Public Information Passing

If ϕ is public, other agents can get this message, and if

ϕ is private, others cannot revise their beliefs by this

message.

4.1 Syntax

In this paper, we deﬁne a new kind of 4-valued logic

different from BK-model.

Let PROP = { p,q,. ..} be a ﬁnite set of propo-

sitional variables and G = { a, b,... } a ﬁnite set of

agents. The language is generated by the following

Backus-Naur form:

α ::= p | ¬α | α ∧ α | c

ϕ ::= α | B

α |

pub

α | [α↓

]ϕ | ¬ϕ | ϕ ∧ ϕ

where p ∈ PROP,a ∈ G, b ∈ G and α is an objective

(non-modal) formula.

Here, c

means “There is a channel from agent

a to agent b”.

pub

α means “α is public”. And B

means “agent a believes α.”

The truth-table of ¬ is as follows:

Table 6: Truth-table of ¬.

ϕ ¬ϕ

(T,1) (F,1)

(T,0) (F,0)

(F, 1) (T, 1)

(F, 0) (T, 0)

The truth-table of ¬ is as follows. Here, we let

pub

ϕ be always public.

Table 7: Truth-table of

pub

(T,1) (T,1)

(T,0) (F,1)

(F, 1) (T, 1)

(F, 0) (F,1)

For the 4-valued logic, we deﬁne ∧. Let ϕ and ψ

be two proposition. Then the proposition ϕ∧ψ is true

if and only if ϕ is true and ψ is true. And ϕ ∧ ψ is

public if and only if ϕ is public and ψ is public. Table

8 shows the truth-table of ∧.

Table 8: Truth-table of ∧.

∧ (T,1) (T,0) (F,1) (F, 0)

(T,1) (T,1) (T, 0) (F,1) (F, 0)

(T,0) (T,0) (T, 0) (F,0) (F, 0)

(F, 1) (F,1) (F,0) (F, 1) (F,0)

(F, 0) (F,0) (F,0) (F, 0) (F,0)

We deﬁne the function ∨ as follows:

ϕ ∨ ψ := ¬(¬ϕ ∧ ¬ψ)

Table 9: Truth-table of ∨.

∨ (T,1) (T,0) (F,1) (F,0)

(T,1) (T,1) (T, 0) (T, 1) (T, 0)

(T,0) (T,0) (T, 0) (T, 0) (T, 0)

(F, 1) (T, 1) (T, 0) (F,1) (F,0)

(F, 0) (T, 0) (T, 0) (F,0) (F,0)

The truth-table of ∨ is shown in Table 9.

Here, we should take notice of the truth-table of ∨.

In this paper, we deﬁne that if ϕ ∨ ψ is public if and

only if ϕ is public and ψ is public. In other words, if

ϕ is private, ϕ ∧ψ and ϕ ∨ψ are all private even if ψ is

public. It is because that if we cannot tell ϕ to others,

anything related to ϕ like ϕ ∧ ψ or ϕ ∨ ψ also cannot

be told to others.

Finally, we deﬁne the “→” as follows:

ϕ → ψ := ¬ϕ ∨ ψ

The truth-table of → is shown in Table 10.

Table 10: Truth-table of →.

→ (T,1) (T,0) (F,1) (F,0)

(T,1) (T,1) (T, 0) (F,1) (F,0)

(T,0) (T,0) (T, 0) (F,0) (F,0)

(F, 1) (T, 1) (T, 0) (T, 1) (T,0)

(F, 0) (T, 0) (T, 0) (T, 0) (T, 0)

Notice that ϕ → ψ is public only if ϕ is public and

ψ is public, which is similar to the operator ∨.

4.2 Semantics

Here, we use Kripke semantics with our syntax. A

Kripke model M is a tuple:

M = (W,R

,V )

where W is a non-empty set of worlds, G is a non-

empty set of agents, R

= {R

| a ∈ G} and R

⊂

W × W is an accessibility of agent a on W , C

| a ∈ G,b ∈ G} and C

⊆ W is a channel rela-

tion, and V : Prop×W → {(T,1),(T,0),(F, 1),(F,0)}

is the valuation function. In many cases it is conve-

nient to replace the four-valued V by two function,

so we assign functions v

: Prop → 2

deﬁned as

follows to express V :

(p) = {w|V (p,w) ∈ {(T,1),(T,0)}}

(p) = {w|V (p,w) ∈ {(T,1),(F, 1)}}

Given any model M, any world w ∈ W , any agent

a,b ∈ G, and any formula ϕ, we deﬁne the satisfaction

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

relation M,w |=

ϕ and M,w |=

ϕ as follows:

M,w |=

p iff w ∈ v

(p)

M,w |=

ϕ ∧ ψ iff M,w |=

ϕ and M, w |=

M,w |=

ϕ ∨ ψ iff M,w |=

ϕ or M, w |=

M,w |=

ϕ → ψ iff M,w 6|=

ϕ or M, w |=

M,w |=

¬ϕ iff M,w 6|=

M,w |=

t pub

ϕ iff M,w |=

M,w |=

ϕ iff ∀u ∈ W ((w,u) ∈ R

→

M,u |=

ϕ)

M,w |=

iff w ∈ C

M,w |=

p iff w ∈ v

(p)

M,w |=

ϕ ∧ ψ iff M,w |=

ϕ and M, w |=

M,w |=

ϕ ∨ ψ iff M,w |=

ϕ and M, w |=

M,w |=

ϕ → ψ iff M,w |=

ϕ and M, w |=

M,w |=

¬ϕ iff M,w |=

M,w |=

p pub

ϕ always

M,w |=

ϕ iff M,w |=

M,w |=

always

Here, M, w |=

ϕ iff M,w |=

ϕ means that if

ϕ is public, the message that agent a believes ϕ is also

public and vice versa.

Also, let the value of ϕ in world w be (a,b), we

can deﬁne |=

and |=

in the other way as follows:

M,w |=

ϕ iff a := T

M,w |=

ϕ iff b := 1

Semantically speaking, in a model M, M,w |=

means ϕ is true in world w, and M,w |=

ϕ means ϕ

is public in world w.

4.3 Multi-agent Communication

In this paper, we use the same dynamic operator [ϕ↓

]

as Hatano et al. (2015), which means “after agent a

sends a message ϕ to agent b via a channel”, and

[ϕ↓

]ψ means “after agent a sends a message ϕ to

agent b via a channel, ψ holds”. Here, the commu-

nication [ϕ↓

] will success only if the following hold:

• There is a channel from agent a to agent b.

• Agent a believes the content of the message ϕ.

• The message ϕ is public.

In Hatano et al. (2015), all of the message is

regarded as public message, which can be told to

others. Here, we use 4-valued logic which can

express whether a formula is public or not, so even if

agent a believe ϕ and there is a channel from a to b,

the communication will fail if ϕ is private, which is

different from Hatano et al. (2015).

The semantics of [ϕ↓

]ψ on a Kripke model M =

(W,R

−

) is given as follows:

M,w |=

[ϕ↓

]ψ iff M

ϕ↓

,w |=

M,w |=

[ϕ↓

]ψ iff M

ϕ↓

,w |=

where M

ϕ↓

= (W,R

) and R

∈ R

is de-

ﬁned as:

• If i = b, for all x ∈ W ,

(x) :=











(x) ∩ JϕK

if M,x |=

∧ B

and M, x |=

(x) otherwise.

• Otherwise, R

:= R

The truth set JϕK

is deﬁned by:

JϕK

= {w ∈ W | M,w |=

ϕ}.

Semantically speaking, after [ϕ↓

], agent b will re-

vise his/ her belief if there is a channel from agent a to

b, agent a believes the content of the message ϕ, and

ϕ is public. Otherwise, agent b will not revise his/

her belief. Other agents than b will not change beliefs

because they get no message.

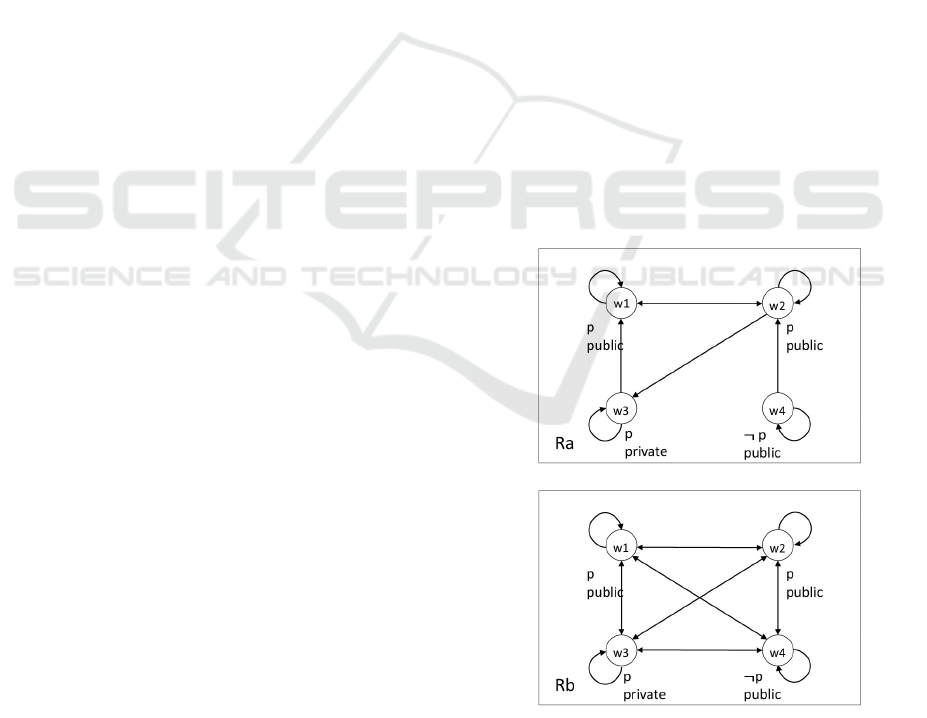
Example : Here, we give an example to show the

belief change after a semi-announcement. Consider a

Kripke model M = (W,R

). (see Figure 2)

Figure 2: Accessibility relations of agents a and b.

Let G = {a,b}, W = {w

}, R

{(w

),(w

)}, R

= W × W ,

4-valued Logic for Agent Communication with Private/Public Information Passing

= {w

}, C

0, C

= C

= W , v

(p) =

} and v

(p) = {w

As the conﬁguration above, p is true in w

and is false in w

. p is public in w

and is pri-

vate in w

. According to the deﬁnition of B

ϕ, we

can see that agent a believe p in world w

and

, while not believing anything in world w

. Agent

b doesn’t believe anything in any world. There are

channels from agent a to b in w

, while no

channel exists in w

Now, consider the model M

ϕ↓

which shows the

new accessibility relation after the action agent a

sends the message ϕ to agent b.

• In world w

, agent a believes p so a can send the

message, there is a channel from agent a to b so

the message can be sent to b, and as p is public so

b can understand the message p. As the result, b

will revise his/ her belief to believe p.

• In world w

, agent a believes p so a can send the

message, and as p is public so b can understand

the message p. However, there isn’t a channel

from agent a to b so the message cannot be sent to

b. So as the result, b won’t revise his/ her belief.

• In world w

, agent a believes p so a can send the

message, and there is a channel from agent a to b

so the message can be sent to b. However, as p is

private so b cannot understand the message p. As

the result, b won’t revise his/ her belief.

• In world w

, there is a channel from agent a to b so

the message can be sent to b, and as p is public so

b can understand the message p. However, agent

a doesn’t believe p so a cannot send the message.

As the result, b won’t revise his/ her belief.

We can see that after the action [ϕ↓

] which means

that agent a tells b the message p, agent b becomes

to believe p only in world w

. In other worlds,

agent b doesn’t change his/ her belief. So in the

new model M

ϕ↓

= (W,R

), R

:= W ×

W /{(w

),(w

)} shown in Figure 3.

Figure 3: Accessibility relation of agent b after the an-

nouncement.

4.4 Hilbert-style Axiomatization

Here, we say ϕ is t-valid on M if M,w |=

ϕ for any

w ∈ W , and ϕ is t-valid in a class of Kripke models if ϕ

is valid on any M in the class. If we disregard whether

a formula is public or private, the deﬁnition of t-valid

is just the same as the deﬁnition of valid in chapter

2. So it is clear that in Table 11, all of the axioms

are t-valid and all of the rules preserve validity on M.

However, the concept p-valid deﬁned in the same way

has no meaning, for there isn’t a tautology about the

concept of public and private.

Table 11: Hilbert-style Axiomatization K

of 4-valued

logic.

(Taut) `

ϕ, ϕ is a tautology.

) `

(ϕ → ψ) → (B

ϕ → B

ψ)

(Selfchn) `

(MP) From `

ϕ and `

ϕ → ψ, infer `

Nec

From `

ϕ, infer `

Here, a ∈ G.

In our 4-valued logic, the following equivalence

relations hold.

Table 12: Hilbert-style Axiomatization K

[ ·↓

] of 4-valued

logic.

In addition to all the axioms and rules of K

, we add:

[α↓

]p ↔ p

[α↓

↔ c

[α↓

]¬ϕ ↔ ¬[α↓

]ϕ

[α↓

]

pub

ϕ ↔

pub

[α↓

]ϕ ∧ ψ ↔ [α↓

]ϕ ∧ [α↓

]ψ

[α↓

ϕ ↔ B

ϕ(c 6= b)

[α↓

ϕ ↔ ((c

∧ B

α ∧

pub

α) → B

(α → ϕ))

∧(¬(c

∧ B

α ∧

pub

α) → B

ϕ)

(Nec

[α↓

]

) From `

ϕ, infer `

[α↓

]ϕ

Prove: It is clear that equivalence relation of the ﬁrst

value of the pairwise truth hold except [ϕ↓

ψ, ac-

cording to the prove in Hatano et al. (2015). The sec-

ond value of the pairwise truth shows whether a for-

mula is public or private, so the equivalence relations

also hold with the second value of the pairwise truth.

Therefore, it is easy to see that the value of left and

right are the same except the line [ϕ↓

ψ.

Then, consider [ϕ↓

ψ, which means “after the

announcement ϕ from agent a, agent b believes ψ”.

According to the deﬁnition, the communication suc-

cesses for three conditions. First, c

is true, which

means that there is a channel from a to b. Second, B

is true, which means that agent a believes ϕ. Third,

ϕ is public, which is the same as

pub

ϕ is true. So if

the formula (c

∧ B

ϕ ∧

pub

ϕ) is true, the commu-

nication will succeed, and if the formula is false, the

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

communication will fail. Therefore, the relation about

[ϕ↓

ψ is also an equivalence relation.

In our 4-valued logic, if we just look at the ﬁrst

value of the pairwise truth, which shows whether a

formula is true or false, and ignore the operator “

pub

”

in the syntax, furthermore if we change “|=

” into

“|=” and disregard the “|=

” in the semantic, this

logic will be the same with the logic in Hatano et al.

(2015), which has been proved to be complete and

sound, So if we disregard whether a formula is public

or private, the logic in this paper is also complete and

sound.

5 CONCLUSION

We have shown a 4-valued logic which distinguishes

the ordinary truth value of each proposition as well

as the information is private or public. By private

information transmission, since the recipient cannot

read the contents he/ she does not change his/ her be-

lief. This unsuccessful message passing corresponds

to such practical situations that the information needs

other background knowledge, password, deciphering

protocol, and so on.

We have reconstructed the dynamic epistemic

logic including the 4-valued logic, and have intro-

duced the two kinds of negations, the truth tables

for the logical connectives, their semantics, and its

Hilbert-style axiomatization. Since the recursion ax-

ioms can reduce the formulae with dynamic operators

to those without them, we can ensure the complete-

ness and soundness if we disregard the second value

of the pairwise truth.

In the current stage, our formalization may still

have redundancy; in the case we need a password for

the private information, the password itself would be

formalized in the very similar way to the channel vari-

ables. However, our objective is to formalize the un-

successful communication in general. Thus, we will

further develop the distinction between miscommuni-

cation by lack of necessary information and that by

unsuccessful message transmission in future.

ACKNOWLEDGEMENTS

This work is supported by JSPS kaken 17H02258.

REFERENCES

Barwise, J. and Seligman, J. (1997). Information ﬂow: the

logic of distributed systems, volume 44. Cambridge

University Press.

Blackburn, P., De Rijke, M., and Venema, Y. (2002). Modal

logic: graph. Darst, volume 53. Cambridge Univer-

sity Press.

Cattaneo, G. and Nistic

o, G. (1989). Brouwer-zadeh posets

and three-valued łukasiewicz posets. Fuzzy sets and

Systems, 33(2):165–190.

Ciucci, D. and Dubois, D. (2013). A map of dependen-

cies among three-valued logics. Information Sciences,

250:162–177.

Giles, R. (1976). Łukasiewicz logic and fuzzy set the-

ory. International Journal of Man-Machine Studies,

8(3):313–327.

Hatano, R., Sano, K., and Tojo, S. (2015). Linear algebraic

semantics for multi-agent communication. In Pro-

ceedings of the International Conference on Agents

and Artiﬁcial Intelligence-Volume 1, pages 174–181.

SCITEPRESS-Science and Technology Publications,

Lda.

Malinowski, G. (2014). Kleene logic and inference. Bul-

letin of the Section of Logic, 43(1/2):43–52.

Odintsov, S. P. and Wansing, H. (2010). Modal logics

with belnapian truth values. Journal of Applied Non-

Classical Logics, 20(3):279–301.

Odintsov, S. P. and Wansing, H. (2017). Disentangling

fde-based paraconsistent modal logics. Studia Logica,

105(6):1221–1254.

Sano, K. and Tojo, S. (2013). Dynamic epistemic logic for

channel-based agent communication. In Indian Con-

ference on Logic and Its Applications, pages 109–120.

Springer.

Seligman, J., Liu, F., and Girard, P. (2011). Logic in the

community. In Indian Conference on Logic and Its

Applications, pages 178–188. Springer.

van Ditmarsch, H., van der Hoek, W., and Kooi, B. (2008).

Dynamic Epistemic Logic. Springer.

4-valued Logic for Agent Communication with Private/Public Information Passing