
A Simulation-based Optimisation Approach
for Inventory Management of Highly Perishable Food
Ning Xue
1
, Dario Landa-Silva
1
, Grazziela P. Figueredo
2
and Isaac Triguero
1
1
ASAP Research Group, School of Computer Science, University of Nottingham, U.K.
2
IMA Research Group, School of Computer Science, University of Nottingham, U.K.
Keywords:
Highly Perishable Food Inventory, Discrete Event Simulation, Particle Swarm Optimisation.
Abstract:
The taste and freshness of perishable foods decrease dramatically with time. Effective inventory management
requires understanding of market demand as well as balancing customers needs and preferences with prod-
ucts’ shelf life. The objective is to avoid food overproduction as this leads to waste and value loss. In addition,
product depletion has to be minimised, as it can result in customers reneging. This study tackles the produc-
tion planning of highly perishable foods (such as freshly prepared dishes, sandwiches and desserts with shelf
life varying from 6 to 12 hours), in an environment with highly variable customers demand. In the scenario
considered here, the planning horizon is longer than the products’ shelf life. Therefore, food needs to be re-
plenished several times at different intervals. Furthermore, customers demand varies significantly during the
planning period. We tackle the problem by combining discrete-event simulation and particle swarm optimisa-
tion (PSO). The simulation model focuses on the behaviour of the system as parameters (i.e. replenishment
time and quantity) change. PSO is employed to determine the best combination of parameter values for the
simulations. The effectiveness of the proposed approach is applied to some real-world scenario correspond-
ing to a local food shop. Experimental results show that the proposed methodology combining discrete event
simulation and particle swarm optimisation is effective for inventory management of highly perishable foods
with variable customers demand.
1 INTRODUCTION
Effective planning is important in production systems
that aim at effective management and coordination
of related activities and resources for an organisation
(Makui et al., 2016). A common aim in such sys-
tems is to achieve optimal production planning and
inventory management to meet (often variable) prod-
ucts demand over the planning horizon (Ramezanian
et al., 2012). Within the food production sector, pro-
ducers aim at delivering optimal planning to manage
supply/demand effectively. Perishability is a key at-
tribute that cannot be ignored in food supply chain
management. Critical decisions must be made regard-
ing the replenishment of food items in the right time
and quantity with the goal of maximising profit while
minimising complete stock depletion and waste.
This paper tackles inventory management of
highly perishable food with a very limited shelf life
and with variable customers demand. We focus on a
scenario in the hospitality sector, that of shops selling
foods such as freshly prepared dishes, sandwiches and
desserts. The production planning period is longer
than the shelf life of the products. This means that
products need to be replenished frequently during
the planning period. In addition, customers demand
for the foods varies greatly over time. A particular
strain is put into production, when rare and/or extreme
external events occur. For instance, when demand
changes dramatically due to weather conditions, spe-
cial events (e.g. holiday season, football matches) and
promotions. Production planning and inventory man-
agement under such conditions is difficult and subject
to high uncertainty.
Planning problems involving such complexity of-
ten require the use of simulation models to understand
the behaviour of the system as parameters change.
The abstracted simulation model is capable of encom-
passing the stochasticity and the variabitity found in
the real-world, therefore assisting in addressing the
problem’s complexity. Also, detailed reports regard-
ing the dynamic of the system and the simulation out-
puts can be extracted for further analysis and to be
employed as inputs to future optimisation exercises
406
Xue, N., Landa-Silva, D., Figueredo, G. and Triguero, I.
A Simulation-based Optimisation Approach for Inventory Management of Highly Perishable Food.
DOI: 10.5220/0007401304060413
In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 406-413
ISBN: 978-989-758-352-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(Duong and Wood, 2018). We apply discrete event
simulation (DES) to understand the behaviour of the
system as parameters (i.e. replenishment time and
quantity) change. Discrete events at particular times
such as sales and food expiring are simulated as the
changes of state in the system. A Particle Swarm Op-
timisation (PSO) algorithm (Shi and Eberhart, 1998)
is implemented to determine the best combination of
parameter values that leads to an optimal solution.
We investigate the optimisation of replenishment time
and quantities in the tackled scenario. Experimental
results using real-world data from a food shop demon-
strate the effectiveness of the proposed method for
tackling inventory management of highly perishable
foods with variable customers demand.
Problems related to the planning of perishable in-
ventories and ordering policies arise in different sec-
tors including food, chemicals, drugs and blood banks
(Vila-Parrish et al., 2008). Regarding modelling tech-
niques and mathematical methods, linear program-
ming, integer or mixed integer programming are the
most dominant methods, please refer to (Soto-Silva
et al., 2016) for model details. Literature reviews on
perishable inventory systems can be found in (Fergu-
son et al., 2007), (Bakker et al., 2012), (Yu et al.,
2012) ,(Bushuev et al., 2015). Perishable inventory
research to date has made a lot of progress on food
sectors of grocery retailers context, where the shelf
life usually ranges from several days to months. To
the best of our knowledge, this is the first attempt to
address the problem of inventory planning of perish-
able food with shelf life of just a few hours.
The remainder of this paper is organised as fol-
lows: the problem is described in detail in Section
2; the solution method is presented in Section 3; the
computational experiments follow in Section 4; fi-
nally conclusions are drawn in the last section.
2 PROBLEM DESCRIPTION
We model the food production of a food shop that
produces and sells fresh prepared dishes, sandwiches
and desserts. The shop usually opens at 7:00AM sell-
ing items produced early that morning and leftover
items produced the night before. It is expected that
the number of leftover items from the night before is
enough to cover demand until around 10:00AM. Af-
ter that, food items produced after the shop opens are
served to customers. Depending on the demand, prod-
uct shelves will be replenished several times in a day.
To aim for freshness, food items are marked as ex-
pired after 6 to 12 hours (exact time depends on the
product type) on the shelf. The expired product is
subsequently thrown away. If food items are prepared
and placed in the shelves too early and not sold out be-
fore they have perished then waste may occur. How-
ever, items not prepared on time to supply demand
may result in customers reneging (i.e. customers leav-
ing because the preferred item is out of stock). Due
to this dynamic complexity, the store manager faces a
challenging problem of both preparing enough items
and reducing waste. The goal is to determine the re-
plenishment time and replenishment quantity for each
item that needs to be prepared in advance, in order to
minimise food wastage and running out of inventory
(i.e., ‘a stock out’).
The items demand may change dramatically in a
day or week as shown in Figures 1 and 2, respectively.
In this paper we only predict the next day hourly de-
mand. Prediction beyond that is out of the scope of
this paper because of the sensitivity to the effect of
store promotions, weather, traffic conditions and spe-
cial events (e.g. holiday, football match) which is not
yet considered here.
Figure 1: Demand fluctuates considerably in a day.
Figure 2: Demand fluctuates considerably in a week.
A Simulation-based Optimisation Approach for Inventory Management of Highly Perishable Food
407

2.1 Discrete Event Simulation Model
The following notation is used in the DES model:
• e: the number of items expiring.
• r: the number of customers reneging.
• w
e
: the weight of e in the objective function .
• w
r
: the weight of r in the objective function .
• t
i
: the ith replenishment time, t
i
< t
i+1
and t
i
∈ T .
• q
i
: the replenishment quantity at t
i
, q
i
∈ Q.
• (t
l
i
,t
u
i
): the lower bound and the upper bound of t
i
respectively, in minutes.
• (q
l
i
, q
u
i
): the lower bound and the upper bound of
q
i
respectively, in units.
• l: the shelf life of an item, in minutes.
• (r
l
, r
u
): the lower bound and the upper bound for
calculating (t
l
i
,t
u
i
), in minutes.
A solution to the inventory manage-
ment problem is encoded by two n-tuples
s =
{
t
0
,t
1
,t
2
, ..., t
n
}
,
{
q
0
, q
1
, q
2
, ..., q
n
}
, representing
replenishment times and replenishment quantities,
respectively.
The problem can be formally defined as follows:
minw
e
e + w
r
r (1)
subject to
t
l
i
≤ t
i
≤ t
u
i
∀i ∈ I (2)
q
l
i
≤ q
i
≤ q
u
i
∀i ∈ I (3)
3 SOLUTION METHOD
We use the solution framework illustrated in Figure
3 to explore optimal replenishment time and quantity
for each item. The framework has 2 phases: 1) gener-
ate data for the simulation and 2) execute simulation-
based optimisation. The first phase for generating
data, denoted DG, generates a set of traces for the
simulation according to predicted demand. For this, 5
replications are performed in this work, hence gener-
ating 5 traces. The aim of performing multiple repli-
cations is to produce multiple samples in order to ob-
tain a better estimate of mean performance. The sec-
ond phase, applies discrete event simulation to simu-
late each generated trace and the best combination of
parameters values (i.e. replenishment time and quan-
tity) for the simulation is determined by the PSO.
DG
Demand
DES PSO
Output
Figure 3: Solution framework. The first layer (green circle)
represents the demand; the second layer is the data genera-
tion, followed by the discrete event simulation phase (DES)
coupled with the particle swarm optimisation (PSO).
3.1 Data Generation
We generate trace data based on predicted hourly
sales. Each trace contains transaction time and the
number of units sold at that time. We first analyse his-
torical customer arrival intervals for an item within a
recent month, as an example shown in Figure 4.
Figure 4: Frequency of customer arrival intervals for a given
item in a recent month.
The upper part of the graph shows the distribution
box plot. In the lower part, the horizontal axis shows
the interval in minutes of customer arrivals while the
vertical axis shows the frequency. The figure shows
that the inter-arrival times distribution is right skewed
with fat tails (with mean=3.67, median=2). In fact,
the shape of the distribution is similar to an expo-
nential distribution, namely Erlang distribution when
K = 1. Further exploration suggested that Erlang dis-
tribution (mean=3.67, and K=0.85) fits well with the
historical data. We use a QQ (quantile quantile) plot
of inter-arrival distribution with the Erlang distribu-
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
408
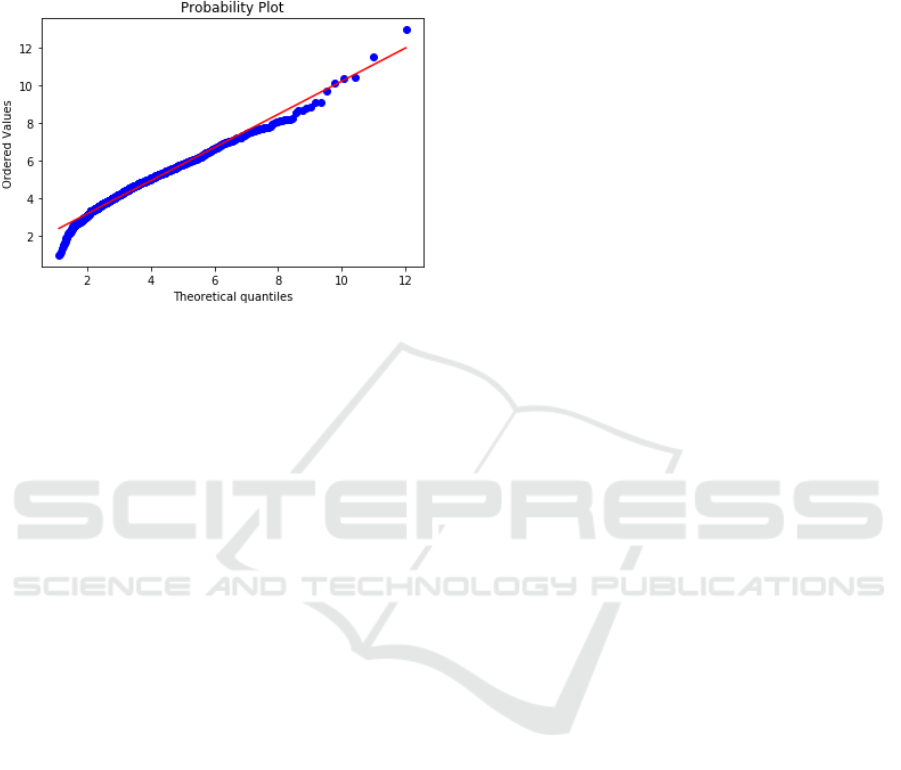
tion to do a more thorough check for the distribution.
It can be seen that most dots fit the line, suggesting the
shape of the data matches the shape of the probability
density function of Erlang.
Figure 5: QQ (quantile quantile) plot of historical data and
simulated Erlang data.
Next, we generate the number of units that would
be sold in each transaction. This number is ran-
domly drawn with some probability from historical
data. Note that not all numbers are randomly gener-
ated as we have to ensure the total units in each hour
matches predicted values. Therefore, it is necessary to
fix some values instead of generating them randomly.
3.2 Simulation-based Optimisation
At this stage, DES is applied to simulate each gener-
ated trace (Section 3.1). For each simulation with cer-
tain parameters values (i.e. replenishment time and
quantity), we calculate the objective function value
(Section 2.1), which is the solution fitness in the PSO,
and update parameters values. Finding the best com-
bination of parameters values (i.e. replenishment time
and quantity) for the simulation is guided by the PSO.
The reason to use simulation to obtain the solution
fitness is twofold: firstly, simulation can generate ran-
dom samples; secondly, due to the stochastic and dy-
namic complexity nature, the objective function is not
easy to be mathematically expressed and computed
directly.
3.2.1 Discrete Event Simulation
DES has been widely applied in production planning
due to its capability for modelling uncertainties that
lie in a planning process. A DES models the operation
of a system as a discrete sequence of events in time.
Each event, such as a customer consuming a product,
occurs at a particular time and changes the state of the
system. In the context of inventory management, the
optimisation procedure can be used to find the most
suitable parameters for the simulation in order to find
the best possible solutions to a problem. Optimisa-
tion techniques that have been applied to inventory
management can be widely classified into mathemat-
ical programming (e.g. linear/non-linear program-
ming) and direct search methods (e.g. gradient based,
statistical models, (meta)-heuristics). Please refer to
the review papers by (Arisha and Abo-Hamad, 2010)
(De Meyer et al., 2014) for more details.
3.2.2 Particle Swarm Optimisation
We implemented PSO to determine the best combi-
nation of parameters values for the simulation model
(Section 2.1. The reasons to adopt PSO as optimiser
for this problem are threefold: PSO is simple in im-
plementation; PSO uses simple fast to execute mathe-
matical operators and is efficient in memory require-
ment, both essential for simulation based optimisa-
tion; and PSO is a general parameter value optimisa-
tion method which requires no assumptions about the
problem being optimised.
PSO is a population-based meta-heuristic intro-
duced by Eberhart and Kennedy (Kennedy, 1995)
that has been successfully applied to several inven-
tory management applications (Tsai and Yeh, 2008)
(Xu et al., 2013) (Park and Kyung, 2014). PSO is in-
spired on the social behaviour patterns of a biological
group such as a flock of birds or a school of fish. In
the PSO method, a decision variable is regarded as
a particle, and the population of decision variables is
considered as a swarm. PSO was initially proposed
for continuous function optimisation. In this work
we truncate continuous values to integers when im-
plementing PSO as the number of units and time are
both expressed by integer values. Our experiments
here indicate that this truncation does not affect sig-
nificantly the performance of the method, as it was
also found in other works (Laskari et al., 2002).
PSO is initialised with a group of random parti-
cles (solutions) and then the algorithm searches for
optima by updating generations of particles. In each
iteration of PSO, each particle is updated within its
given bounds by following two “best” values. The
first one is the best solution that the particle and its
neighbours have achieved so far (local best). The
other one is the best solution found so far by any par-
ticle in the whole population (global best). Based on
these two best values, a particle updates its velocity
and positions. More details of how PSO works can
be found in (Kennedy, 1995) and (Shi and Eberhart,
1998). There are many variants (Rini et al., 2011) of
PSO, but in this paper we implemented the standard
A Simulation-based Optimisation Approach for Inventory Management of Highly Perishable Food
409

one (Kennedy, 1995). The fitness of a particle is com-
puted by means of the simulation as mentioned pre-
viously, hence the approach being a simulation-based
optimisation technique.
4 EXPERIMENTS
The proposed solution method was implemented in
Python and run on a PC with Intel i7 2.40GHZ pro-
cessor and 4GB RAM, similar computing equipment
available in a typical food shop in the scenario con-
sidered here.
4.1 Problem Instance Data
A set of problem instances reflecting characteristics of
the real-world scenarios considered was generated by
a prediction model. Each instance contains predicted
hourly sales of an item in a day. Five instances of each
item are generated. The instances groups are called I6
and I12, where the number corresponds to shelf life.
For example, I6 are the instances where the shelf life
of the item is 6 hours.
4.2 Parameters Tuning
Considering the two objectives of minimising waste
and minimising the number of customers reneging,
we can think of trade-off solutions exhibiting a com-
promise between these two objectives. This is be-
cause arguably minimising waste (producing less)
could be in conflict with minimising reneging (pro-
ducing more). However, the desirable overall optimal
solution for our case will obviously have zero waste
and zero customers reneging.
Since the desired optimal solution will have 0
as the value for waste and customers reneging, the
goal is to find the parameter values that quick-
est converge to 0 in the objective function. The
Irace package (L
´
opez-Ib
´
anez et al., 2011) is ap-
plied for parameter tuning using 4 selected instances
(I6 1, I6 2, I12 1, I12 2).
A standard implementation of the PSO algorithm
requires 4 parameters:
• Swarm size (n): Number of particles in the popu-
lation.
• Inertia (ω): Inertia weight in a particle’s move-
ment.
• Personal best attraction (phi
p
): Weight for parti-
cle’s pull towards its own best solution achieved
so far.
• Neighbour best attraction (phi
g
): Weight for pull
towards the global best solution.
The parameters, their range considered in the tun-
ing (based on some preliminary runs) and the best val-
ues found are given in Table 1. The maximum number
of experiments is set to 1000 and other parameters for
Irace are set to default values.
Table 1: Parameter Tuning for the PSO Using Irace.
Parameters Type Range Best
n C (5, 10, 20, 50
30, 40, 50,
60, 70, 80,
90, 100, 120,
140, 160, 180,
200, 240, 280,
, 320)
ω R (-2, 2) 0.637
phi
p
C (-4, -3.5, -3, 0.5
-2.5, -2, -1.5,
-1, -0.5, 0,
0.5, 1, 1.5,
2, 2.5, 3,
3.5, 4)
phi
g
C (-4, -3.5, -3, 1.5
-2.5, -2, -1.5,
-1, -0.5, 0,
0.5, 1, 1.5,
2, 2.5, 3,
3.5, 4)
C: Categorical
R: Real
4.3 Algorithm Performance
In order to analyse the performance of the proposed
solution method, we test the algorithm on 10 prob-
lem instances using the best-suited parameter values
given in Table 1. In order to obtain statistically sound
results, all experiments are conducted with 10 inde-
pendent runs (mean values were recorded) over all
10 problem instances. To obtain a better estimate of
mean performance, each experiment run is based on
the mean values of 5 simulations. Each simulation
is terminated after reaching an optimal solution (i.e.
with objective function value equal to 0 representing
the best fitness). For each instance, all 10 runs start
with the same initial solution created at random.
The computation time for each problem instance
is given in Table 2. It can be seen that all instances
were solved well under 2 minutes. Solving the group
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
410
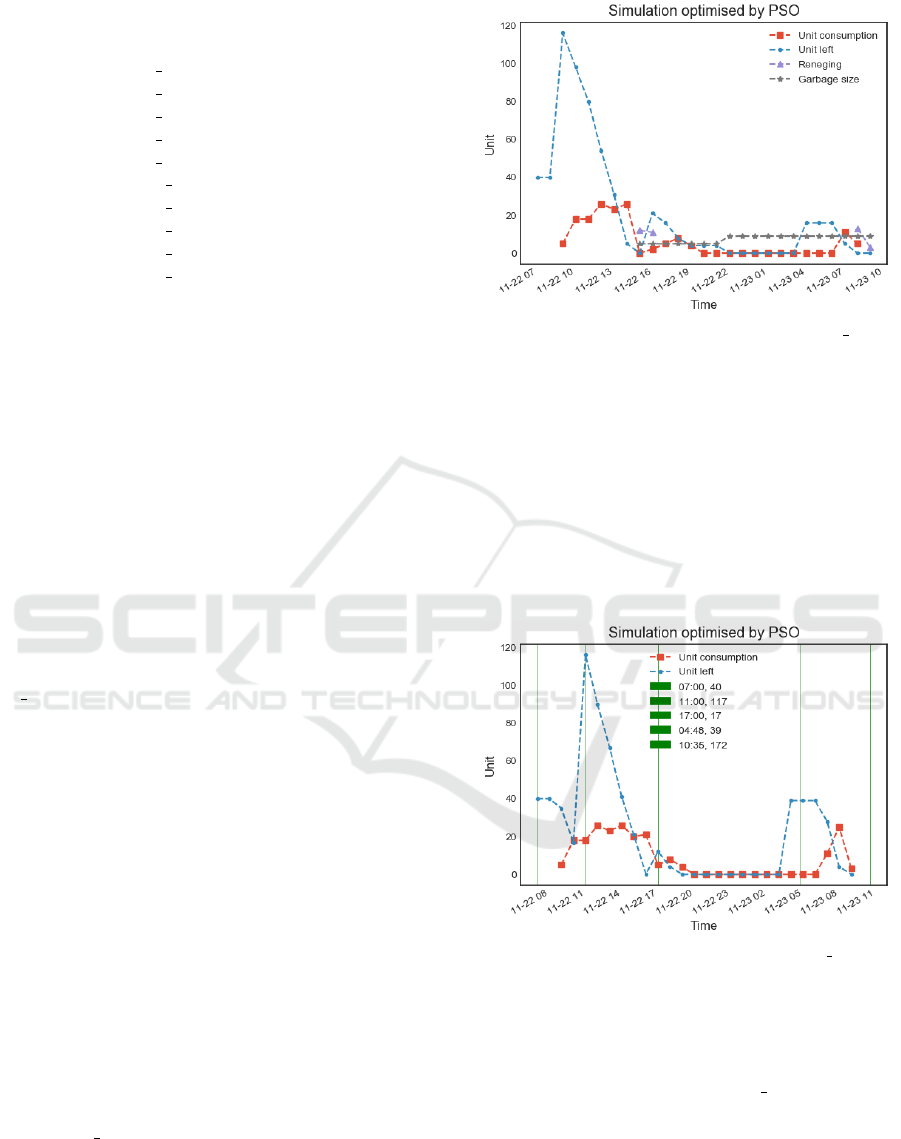
Table 2: Computation Times.
Instance Time(s)
I6 1 92.4
I6 2 81.6
I6 3 70.8
I6 4 60
I6 5 65
I12 1 31.2
I12 2 42
I12 3 34.8
I12 4 49.2
I12 5 34
of instances I6 requires more decision variables (be-
cause of more frequent replenishment), hence taking
longer computation time compared to instances I12.
We now describe some examples of replenishing
plans. Figure 6), is an example of such plan for an
instance with 6 hours shelf life. The horizontal axis
shows the length of the planning period (i.e. 1 day),
while the vertical axis shows the number of units of
an item. The Unit consumption line corresponds to
the total number of units sold during the day. The
Unit left line corresponds to the units available on the
shelf. The Reneging line is for the number of cus-
tomers reneging at different times during the day. The
Garbage size line is the cumulative sum of items that
have been thrown away due to expiration.
Figure 6 shows a non-optimal solution for instance
I6 1 found during the algorithm execution and before
reaching an optimal solution. This figure captures the
simulation scenario in which a large number of items
were replenished (unit left line) at around 10 am. This
large replenishment was sufficient to cover the high
demand (unit consumption line) from 11 am to around
3 pm. Due to the faltering demand from 3pm onward,
the number of units left is higher that the consumption
by 4pm. However, because of the 6 hours shelf life of
the item, those leftovers have to be thrown away at
4pm. Since there was no fresh items produced and
placed timely on the shelf at 4pm, some customers
left because the item they wanted was out of stock.
A similar situation occurred later at night. It can be
seen that this is a non-optimal solution or inventory
management plan because the replenishment time and
quantity have led to both item wastage and customer
reneging.
Figure 7 shows an optimal solution for the same
instance I6 1 discussed above, in which there is no
item wastage and no customers reneging. The re-
plenishment times are represented by the vertical bars
and the corresponding replenishment time and quan-
tity are given in the legend. In this optimal solution,
it can be seen that although the unit left line is well
Figure 6: Non-optimal solution for instance I6 1.
above the unit consumption line, there is no wastage
or reneging because replenishment has been done ef-
fectively to supply demand. A typical convergence
rate of one simulation (i.e. simulation based on 1
trace) of this solution is given in Figure 8. The hori-
zontal axis corresponds to number of iterations while
the vertical axis corresponds to fitness values. It can
be seen in the figure that convergence is very fast in
the first 250 iterations and it slows down after that. Fi-
nally, an optimal solution was found just before 600
iterations.
Figure 7: Optimal solution for instance I6 1.
Another example of a replenishment plan, this
time for an instance for an item with 12 hours shelf
life, is shown in Figure 9. This plan is a non-
optimal solution obtained before an optimal solution
was found for problem instance I12 1. Similar to the
previous example, this figure captures the simulation
of a scenario in which a large number of items are re-
plenished at around 10am. Items have not been sold
out by 10pm and hence they are thrown away after the
12 hours shelf life passes. A number of items were
produced around 11pm. Demand increased from 7am
in the next day and customers consumed all items by
A Simulation-based Optimisation Approach for Inventory Management of Highly Perishable Food
411
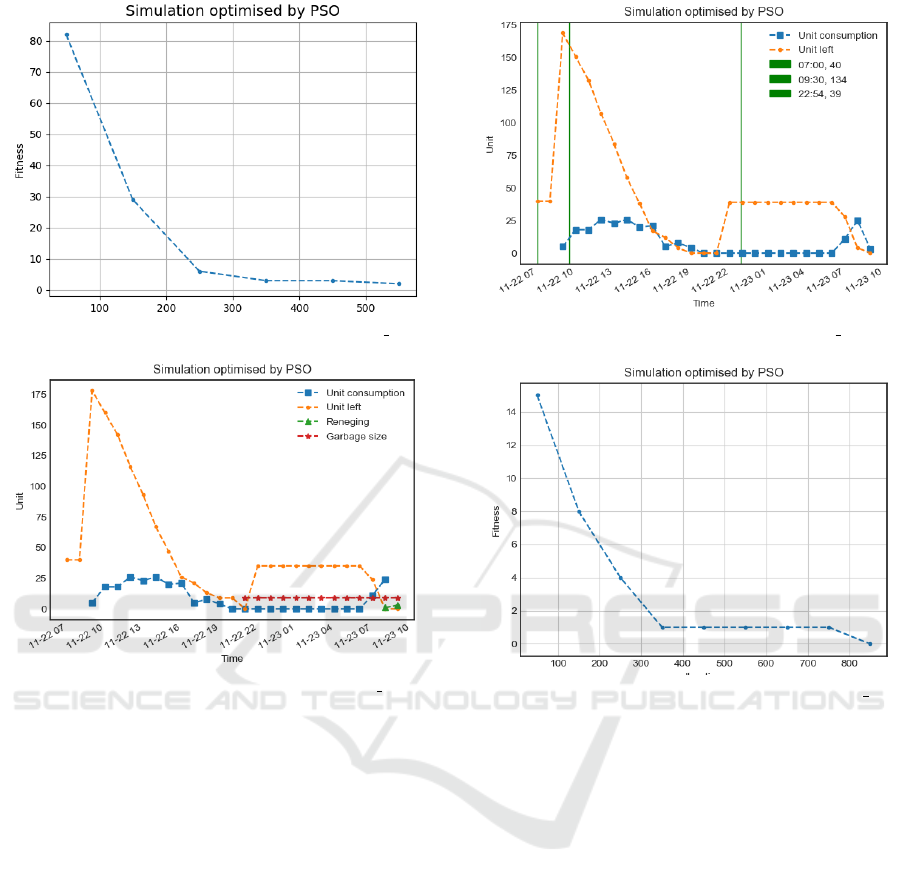
Figure 8: Convergence rate of solving instance I6 1.
Figure 9: Non-optimal solution for instance I12 1.
around 9am. As no replenishing takes place since
then, customers that arrived after 9am left after not
being able to supply their demand.
Figure 10 shows an optimal replenishment plan
with no item wastage or customers reneging. The
convergence rate of one simulation for this solution
is shown in Figure 11. This figure shows that conver-
gence is very fast within the first 350 iterations and an
optimal solution is found before 900 iterations.
5 CONCLUSIONS
In this paper, we addressed an inventory management
problem considering a scenario in which food items
have very short shelf life and they need to be replen-
ished several times during the day in order to satisfy
demand, avoid wastage and avoid customers reneg-
ing. This problem arises in many restaurants and
other places in the hospitality sector. In the scenario
tackled here, the planning horizon is longer than the
shelf life of the food items. In addition, demand varies
considerably within the planning horizon. A replen-
Figure 10: Optimal solution for instance I12 1.
Figure 11: Convergence rate of solving instance I12 1.
ishment plan consists of determining the times dur-
ing the planning horizon in which food items should
be replenished and the corresponding quantities in or-
der to minimise waste and the number of customers
reneging.
We model this inventory problem using Discrete
Event Simulation (DES) to understand the dynam-
ics of the system as parameters change. Then, Par-
ticle Swarm Optimisation (PSO) is employed to de-
termine the best combination of parameter values for
the simulations. Experimental results on 10 prob-
lem instances have demonstrated the effectiveness of
the proposed simulation-based optimisation approach
for solving different problem instances. This solu-
tion framework could be easily adapted to other sim-
ilar inventory replenishment scenarios. For instance,
to minimise perishable wastage in restaurants, super-
markets and hospitals. Particular benefit could also
be obtained when venues need to comply with more
strict regulations due to the nature of the clientele,
such as pregnant women, immunocompromised indi-
viduals, and transplant patients.
Although the solution quality and computation
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
412

time in this work are acceptable by the typical store
manager, the abstract model created for simulation
still does not yet reflect the entire complexity of the
shop production dynamics. Further work will be un-
dertaken to improve the current model to enable even
better decision support. One aspect to be considered
is the inclusion of the food preparation process and
defrosting times, rather than just focusing on deter-
mining replenishment times and quantity. Also, an in-
depth study comparing the PSO to other optimisation
methods could also be an interesting future research
direction.
ACKNOWLEDGEMENTS
This research was supported by and PXtech Limited
and Innovate UK.
REFERENCES
Arisha, A. and Abo-Hamad, W. (2010). Simulation optimi-
sation methods in supply chain applications: a review.
Bakker, M., Riezebos, J., and Teunter, R. H. (2012). Re-
view of inventory systems with deterioration since
2001. European Journal of Operational Research,
221(2):275–284.
Bushuev, M. A., Guiffrida, A., Jaber, M., and Khan, M.
(2015). A review of inventory lot sizing review papers.
Management Research Review, 38(3):283–298.
De Meyer, A., Cattrysse, D., Rasinm
¨
aki, J., and Van Or-
shoven, J. (2014). Methods to optimise the design and
management of biomass-for-bioenergy supply chains:
A review. Renewable and sustainable energy reviews,
31:657–670.
Duong, L. N. K. and Wood, L. C. (2018). Discrete event
simulation in inventory management. In Encyclopedia
of Information Science and Technology, Fourth Edi-
tion, pages 5335–5344. IGI Global.
Ferguson, M., Jayaraman, V., and Souza, G. C. (2007).
Note: An application of the eoq model with nonlin-
ear holding cost to inventory management of perish-
ables. European Journal of Operational Research,
180(1):485–490.
Kennedy, R. (1995). J. and eberhart, particle swarm opti-
mization. In Proceedings of IEEE International Con-
ference on Neural Networks IV, pages, volume 1000.
Laskari, E. C., Parsopoulos, K. E., and Vrahatis, M. N.
(2002). Particle swarm optimization for integer pro-
gramming. In Evolutionary Computation, 2002.
CEC’02. Proceedings of the 2002 Congress on, vol-
ume 2, pages 1582–1587. IEEE.
L
´
opez-Ib
´
anez, M., Dubois-Lacoste, J., St
¨
utzle, T., and
Birattari, M. (2011). The irace package, iterated
race for automatic algorithm configuration. Tech-
nical report, Technical Report TR/IRIDIA/2011-004,
IRIDIA, Universit
´
e Libre de Bruxelles, Belgium.
Makui, A., Heydari, M., Aazami, A., and Dehghani, E.
(2016). Accelerating benders decomposition approach
for robust aggregate production planning of products
with a very limited expiration date. Computers & In-
dustrial Engineering, 100:34–51.
Park, K. and Kyung, G. (2014). Optimization of total in-
ventory cost and order fill rate in a supply chain using
pso. The International Journal of Advanced Manufac-
turing Technology, 70(9-12):1533–1541.
Ramezanian, R., Rahmani, D., and Barzinpour, F. (2012).
An aggregate production planning model for two
phase production systems: Solving with genetic algo-
rithm and tabu search. Expert Systems with Applica-
tions, 39(1):1256–1263.
Rini, D. P., Shamsuddin, S. M., and Yuhaniz, S. S. (2011).
Particle swarm optimization: technique, system and
challenges. International journal of computer appli-
cations, 14(1):19–26.
Shi, Y. and Eberhart, R. (1998). A modified particle swarm
optimizer. In Evolutionary Computation Proceedings,
1998. IEEE World Congress on Computational Intel-
ligence., The 1998 IEEE International Conference on,
pages 69–73. IEEE.
Soto-Silva, W. E., Nadal-Roig, E., Gonz
´
alez-Araya, M. C.,
and Pla-Aragones, L. M. (2016). Operational research
models applied to the fresh fruit supply chain. Euro-
pean Journal of Operational Research, 251(2):345–
355.
Tsai, C.-Y. and Yeh, S.-W. (2008). A multiple objective par-
ticle swarm optimization approach for inventory clas-
sification. International journal of production Eco-
nomics, 114(2):656–666.
Vila-Parrish, A. R., Ivy, J. S., and King, R. E. (2008).
A simulation-based approach for inventory modeling
of perishable pharmaceuticals. In Simulation Con-
ference, 2008. WSC 2008. Winter, pages 1532–1538.
IEEE.
Xu, J., Zeng, Z., Han, B., and Lei, X. (2013). A dynamic
programming-based particle swarm optimization al-
gorithm for an inventory management problem under
uncertainty. Engineering Optimization, 45(7):851–
880.
Yu, Y., Wang, Z., and Liang, L. (2012). A vendor managed
inventory supply chain with deteriorating raw materi-
als and products. International Journal of Production
Economics, 136(2):266–274.
A Simulation-based Optimisation Approach for Inventory Management of Highly Perishable Food
413
