
Robust Cylinder Estimation in Point Clouds
from Pairwise Axes Similarities
Mara Pistellato, Filippo Bergamasco, Andrea Albarelli and Andrea Torsello
DAIS, Ca’Foscari University of Venice, Via Torino 155, Venice, Italy
Keywords:
Cylinder Fitting, Point Clouds, Industrial Reconstruction, Game Theory, Dual-quaternions, Model Fitting.
Abstract:
The ubiquitous presence of cylindrical shapes in both natural and man-made environments makes their auto-
mated extraction a pivotal task for a broad range of applications such as robot manipulation, reverse engineer-
ing and automated industrial inspection. Albeit conceptually simple, the task of fitting cylinders from 3D data
can quickly become challenging if performed "in-the-wild", when no prior is given to the number of primitives
to find or when the point cloud is noisy and not oriented. In this paper we introduce a new robust approach
to iteratively extract cylindrical primitives from a 3D point cloud by exploiting mutual consensus of different
cylinder candidates. First, a set of possible axes is generated by slicing the point cloud with multiple random
planes. Then, a game-theoretic inlier selection process is performed to extract a subset of axes maximizing the
fitness against a payoff function based on the shortest geodesic path in SE(3) between pairs of corresponding
3D lines. Finally, the probability distribution resulting from the previous selection step is used to weight the
input candidates and robustly obtain the final cylinder coefficients. Compared to other methods, our approach
does not require point normals, offers superior resilience to noise and does not depend on delicate tuning of
multiple parameters.
1 INTRODUCTION
Cylinders, and other quadrics in general, represent
more than 85% of the objects that can be found in in-
dustrial and human made scenes (Hakala et al., 1980).
Their automated segmentation and extraction is an
important task in a broad range of applications, rang-
ing from industrial automation (Rahayem and Kjel-
lander, 2011) to natural landscapes analysis (Pfeifer
et al., 2004). Popular applications in this context in-
clude robot manipulation (Specian et al., 2018), auto-
mated pipe-run reconstruction (Qiu et al., 2014), in-
take measurements (Bergamasco et al., 2012) and Ge-
ometric Reverse Engineering (Lukács et al., 1997).
All the aforementioned applications operate on 3D
spatial information that must be acquired from a
scene. Notwithstanding the recent advances in 3D
reconstruction techniques, the availability of a high-
quality oriented point cloud is not always affordable
in practice. For example, shiny metal surfaces still
represent a challenge situation that may lead to in-
complete or noisy 3D surfaces (Amir and Thörnberg,
2017). For this reason, any robust quadrics fitting
technique must rely to some sort of outlier detection
to be used in practice. In the specific case of cylin-
ders, various methods have been proposed in the lit-
erature that operate directly on 3D point clouds. As a
general taxonomy, we can distinguish between fitting
algorithms and extraction algorithms. The formers
require pre-segmented point clouds, where each point
must be associated a-priori to each different cylindri-
cal object. They are typically based on a non-linear
least-squares minimization of the point distances to
the cylindrical surface (Lukács et al., 1998). How-
ever, given the well known sensitivity of least squares
to outliers, they tend to suffer to the poor quality of
such mandatory cylinder segmentation. Methods be-
longing to the latter category use statistically robust
techniques to extract cylinder shapes out of a noisy
point cloud. They are usually less accurate than the
former but exhibit a clear advantage when point data
include clutter, spurious points and incomplete areas.
This category can be further split among methods that
require oriented point clouds (where a normal vec-
tor is associated to each 3D point) and the ones that
only rely on the reciprocal position of points. The for-
mer makes heavy use of surface normals to reduce the
search space of cylinder parameters by means of sam-
ple consensus techniques (Torr and Zisserman, 2000)
or specially designed voting spaces (Rabbani and den
640
Pistellato, M., Bergamasco, F., Albarelli, A. and Torsello, A.
Robust Cylinder Estimation in Point Clouds from Pairwise Axes Similarities.
DOI: 10.5220/0007401706400647
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 640-647
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
Heuvel, 2005). Unfortunately, reliable surface normal
is in general more difficult to obtain than the point
cloud itself. Hence, the quality of normal vectors di-
rectly affects the reliability of the cylinder extraction
technique. If the point cloud is not oriented, param-
eter search space quickly grows to a dimensionality
where voting or consensus techniques become less ef-
fective in practice. Recently, (Rahayem et al., 2012)
proposed a method that just requires point clouds (ac-
quired from laser scanner) to extract and fit cylindri-
cal shapes. Albeit being robust to noisy data, it can
operate on a scene composed by a single cylinder at
a time. In this paper we propose a novel cylinder ex-
traction technique also belonging to this latter cate-
gory. We build our method on the same basic idea
of (Rahayem et al., 2012) expanding the technique to
work with a simultaneous presence of multiple cylin-
ders and extreme noise conditions. Compared to ex-
isting methods, our approach offers three main advan-
tages. First, it is almost parameter free. There are no
requirements about prior knowledge on the geometry
of the point cloud or the characteristics of the cylin-
ders involved in the scene. This is mostly due to the
game-theoretical process that is able to reliably per-
form inlier selection based on mutual consensus of
multiple candidates. Second, it offers accurate results
since multiple hypotheses are averaged on the basis
of their relative fitting score to a common cylindri-
cal model. Third, it can work reliably even if most
of the cylindrical shape is not available due to self-
occlusion. In practice, primitives can be fit out from a
single scanner range image. An extensive evaluation
presented in Section 3 demonstrates all these features
on both synthetic and real-world cases.
2 THE PROPOSED METHOD
We restrict our application to cylindrical shapes de-
fined by the locus of points lying at a distance r to a
3D line in space, called axis
1
.
We over-parametrize a cylinder ζ with the triplet
(p,~v,r) where p ∈ R
3
and~v ∈ R
3
define axis point and
direction respectively. We pose the additional con-
straints of kvk = 1 and hp,~vi = 0 resulting in only 5
degrees of freedom out of the 7 parameters used for
the parametrization. The intersection between ζ and
a plane P (whose normal ~n is not orthogonal with ~v)
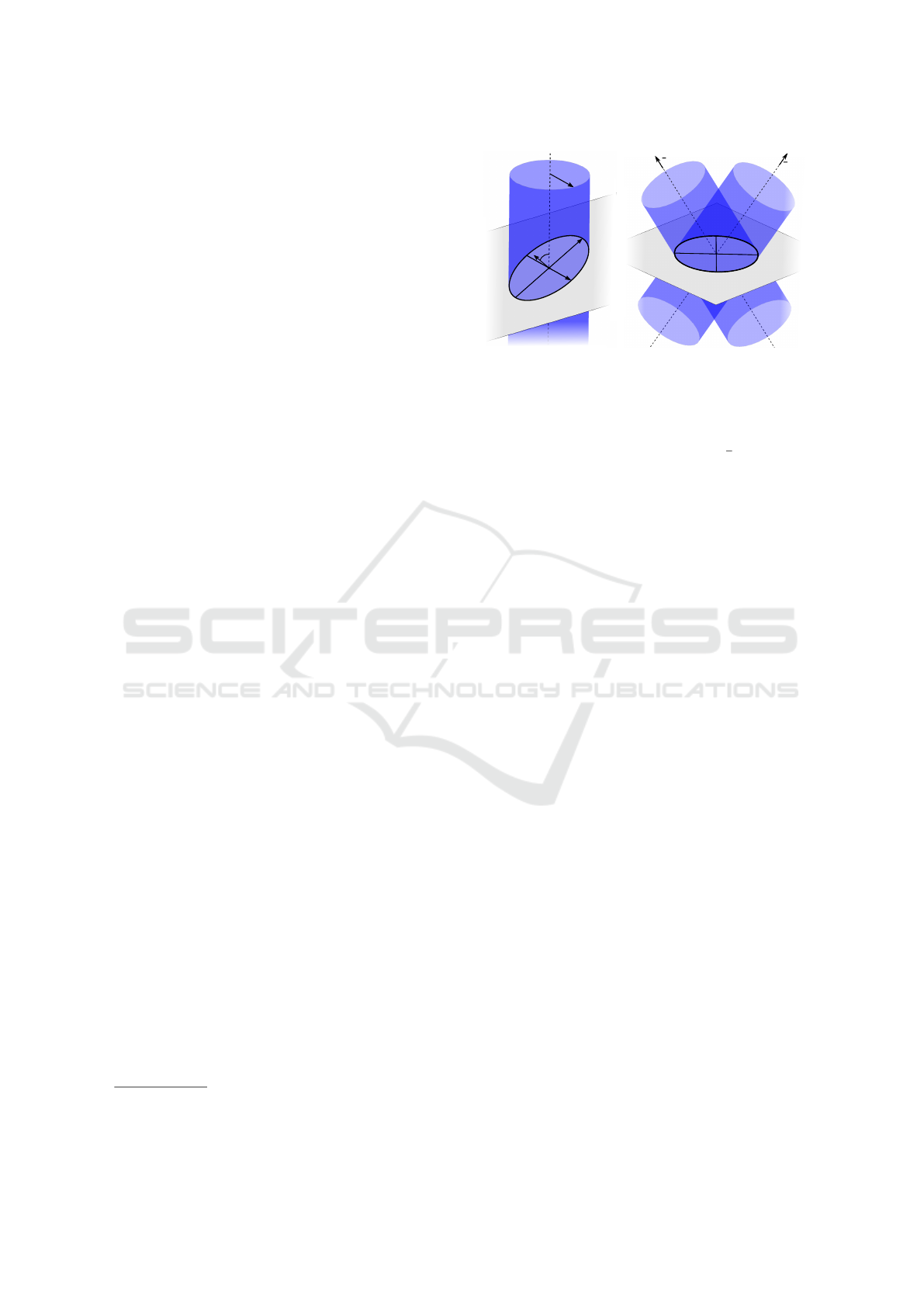
results in an ellipse E with the following properties
(See Fig. 1, Left): (i) the minor semi-axis b is equal
to the cylinder’s radius r; (ii) the ellipse center c lies
1
This implies that the considered cylinders extends in-
finitely along their axes
P
r
a
b
c
N
ζ
α
v
1
v
2
a
b
Figure 1: Left: plane-cylinder intersection. Right: two pos-
sible cylinders deriving from an ellipse in 3D space.
on the cylinder axis; (iii) The ratio between the semi-
major axes a and b is related to the angle α between~v
and~n according to the formula cosα =
b
a
.
These properties can be used to extract cylinders
from planar slices of a 3D point cloud. For simplic-
ity, let’s assume to have acquired a scene containing
one single cylindrical shape and many other points re-
sulting from other objects or noise. If 3D data is suf-
ficiently dense, a subset S of points can be extracted
comprising all the samples lying close to a plane P,
that we suppose not being parallel to the cylinder axis.
According to what said before, some of the points
will lie on the ellipse generated by the cylinder in the
scene, some others will be distributed with no par-
ticular pattern (ie. they are outliers with respect to
the elliptical shape). Therefore, any sufficiently ro-
bust fitting operation that extracts the elliptical shape
E out of S will give clues on the unknown cylinder
present in the scene.
In particular, the minor axis of E will define the
radius of the cylinder and the center c the position of
the axis. Similarly to what happens with camera poses
(Bergamasco et al., 2014), the ratio between a and b
determines the direction ~v up to two equally-possible
configurations (See Fig.1, Right). Due to this intrinsic
ambiguity, at least two plane slices are needed to fully
recover the coefficients of a cylinder.
In their paper, (Rahayem et al., 2012) propose to
use multiple slices to collect the centers (c
1
... c
n
) and
minor axes (b
1
... b
n
) of each fitted ellipses. This
way, the cylinder radius is recovered averaging each
b
1
... b
n
and the axis (p,~v) by fitting a 3D line to
c
1
... c
n
in a least-squares sense. The approach has
three drawbacks. First, it totally discards information
given by each ellipse regarding the possible orienta-
tion of cylinder axis (due to the mentioned ambigu-
ity). Second, it can only handle a single cylinder in
the data. Third, can badly suffer from possible wrong
estimations since all the values are averaged without
weighting their reliability. This aspect is partially rel-
Robust Cylinder Estimation in Point Clouds from Pairwise Axes Similarities
641

evant though since the following non-linear optimiza-
tion may still be able to recover the correct shape.
Our approach follows a similar strategy. We slice
the scene with n different random planes. From the
2D scattered point set obtained in each section i =
1.. .n, we robustly extract all the j = 1...N
i
possible
ellipses using RANSAC and the ellipse model estima-
tion method described in (Halır and Flusser, 1998).
When considered in 3D space, each extracted ellipse
E
i, j
is defined by its major and minor semi-axes vec-
tors ~a
i, j
∈ R
3
and
~
b
i, j
∈ R
3
and its center c
i, j
∈ R
3
.
By construction, ~a
i, j
and
~
b
i, j
are both defined up to a
sign and orthogonal to the normal~n
i
of the i
th
plane.
From each E
i, j
, we compute the two possi-
ble cylinder candidates as the tuples (r,c,~v
1
)
i, j
and
(r,c,~v
2
)
i, j
, where:
r = k
~
b
i, j
k
c = c
i, j
~v
1
= R ~n
i
~v
2
= R
T
~n
i
R = I +
s
1 −
k
~
b
i, j
k
2
k ~a
i, j
k
2
~
b
i, j
k
~
b
i, j
k
×
+
+(1−
k
~
b
i, j
k
k ~a
i, j
k
)
~
b
i, j
k
~
b
i, j
k
2
×
. (1)
In the tuples, r and c denote the cylinder radius
and axis point shared by the two candidates.
2
. Con-
versely, ~v
1
and ~v
2
are the two possible axis orienta-
tions obtained by rotating the plane normal~n
i
around
the minor-axis of the ellipse E
i, j
with an angle of
±arccos
k
~
b
i, j
k
k ~a
i, j
k
.
2.1 Cylinder Similarity Function
Extracting the most probable cylinder out of all the
generated tuples can be seen as a clustering problem.
Indeed, we aim to extract the largest group of candi-
dates that are all consistent with respect to one spe-
cific cylinder model in the scene. To do so, we must
first define a similarity function between any two can-
didates to measure their consistency against a com-
mon model. The non-trivial aspect is that, a part from
the relative radii, to have a well-defined function both
the combined axes positions and orientations must be
considered .
We start by defining a distance between two 3D
axes in space. Let l
1
= (c
1
,~v
1
) and l
2
= (c
2
,~v
2
) be
2
Matrix R is obtained by Rodrigues’ formula. The sym-
bol [.]
×
denotes the skew-symmetric matrix of the cross-
product.
two 3D lines defined respectively by a point c and a
unitary-norm vector~v. Following (Bergamasco et al.,
2015) , we construct a rigid motion (
¯
R,
¯
T ) mapping
line l
1
to l
2
or, more formally, the roto-translation
such that ∀p ∈ l
1
,∃ k ∈ R.
¯
Rp+
¯
T = c
2
+k~v
2
. Among
all the possible motions, we can easily express the one
exhibiting the shortest translation length and smaller
rotation angle taking advantage of the kinematic no-
tion of a screw. That is, every rigid-motion can be
modeled as a rotation with a certain angle about an
axis (not necessarily passing through the origin) fol-
lowed by a translation along that axis (Chen, 1991).
In our case, let m
1
= c
1
+t
1
~v
1
(for some scalar t
1
) be
the point of line l
1
closest to the line l
2
. Similarly, let
m
2
= c
2
+t
2
~v
2
be the point of l
2
closest to line l
1
. By
construction, the vector T = m
2
− m
1
is orthogonal to
both l
1
and l
2
and its length is the minimum distance
between all the points of the two lines. This implies
that T has the same direction (but possibly different
length and orientation) of the vector~v
⊥
=~v
1
×~v
2
. So,
the rotation with angle β = arcsin(k~v
⊥
k) around the
axis defined by point m
1
and vector
~
s =~v
⊥
/k~v
⊥
k will
let l
1
be parallel to l
2
. Since m
1
lies on the rotation
axis, its position will not change after the transforma-
tion, hence the distance between the two lines will re-
main equal to kT k. Trivially, a final translation along
T will let l
1
coincide with l
2
.
Such modelling is convenient because the param-
eters of the screw motion can be related to the scalar
and vector part of a unit dual quaternion
ˆ
q (Eq.2):
ˆ
q = cos
ˆ
θ
2
+
ˆ
ssin
ˆ
θ
2
ˆ
θ = 2β + ε2kT k
ˆ
s = i
~
s + εi(m
1
×
~
s) (2)
In the expression, i = (i, j,k) is the row vector of
quaternions imaginary bases,
ˆ
s is a dual quaternion
(with zero scalar part) describing the rotation axis and
ˆ
θ is the dual angle expressing the angle of rotation and
the amount of translation.
The set of unit dual quaternions is a 6-dimensional
manifold embedded an 8-dimensional Euclidean
space (McCarthy, 1990) for which the corresponding
log map can be defined in closed form as in (3)
log(
ˆ
q) =
ˆ
s
ˆ
θ
2
. (3)
The existence of such log map allow us to define a
distance function between l
1
and l
2
induced by the
length of the geodesic path in SE(3) from the origin
(ie. the identity motion) to
ˆ
q:
d(l
1
,l
2
) = min(k log(
ˆ
q)k,klog(−
ˆ
q)k) (4)
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
642

Note that in (4) the minimum is necessary due to the
antipodal property of dual quaternions (i.e.
ˆ
q and
−
ˆ
q represent the same transformation but with two
different trajectories). For more informations about
dual numbers and dual quaternion algebra for geomet-
ric applications we suggest (Daniilidis, 1999; Kavan
et al., 2008). With the defined distance between two
cylinder axes, we can finally formulate a similarity
function between two candidates ξ
1
= (r
1
,c
1
,~v
k
1
)
i
1
, j
1
and ξ
2
= (r
2
,c
2
,~v
h
2
)
i
2
, j
2
as:
π(ξ
1
,ξ
2
) =
1 if ξ
1
= ξ
2
e
−
d
(c
1
,v
1
),(c
2
,v
2
)
λ
if i
1
6= i
2
∧
Ad(ξ
1
,ξ
2
) < r
1
+ r
2
0 otherwise
(5)
where λ is a free parameter
3
and Ad(ξ
1
,ξ
2
) is the
minimum distance (kT k) between the two candidate
axes (c
1
,v
1
) and (c
2
,v
2
) as defined previously. Eq.(5)
is simple if we reason in terms of compatibility be-
tween candidates. The function assumes values be-
tween 0 (not compatible with the same cylindrical
model) and 1 (fully compatible): any candidate has
maximum similarity with itself and 0 similarity with
any other candidate either generated by the same
plane or with its axis further than the sum of the re-
spective radii. The former may happen in two cases:
(i) the candidate results from a distinct coplanar el-
lipse or (ii) has been generated by the same ellipse
but with different ~v. In the final case of "close" can-
didates from different planes, the similarity is made
inversely proportional to the axis distance defined in
(4) thanks to the negative exponential with factor λ.
2.2 The Inlier Selection Process
We cast the selection of a subset of candidates in
the context of Evolutionary Game Theory (Weibull,
1995). In such scenario we have that pairs of individ-
uals, belonging to a certain population, play a game
one versus the other on the basis of pre-programmed
strategies. A selection process brings some individu-
als matching well together to thrive, while driving the
"unfitting" ones to extinction.
In our specific case, all the M =
∑
n
i=1
N
i
cylin-
der candidates ξ
1
... ξ
M
are the individuals that we
call hypotheses. We express how well two hypothe-
ses play together by defining a fitness through the
payoff-function, formulated as in (5) that can be con-
veniently represented as an M × M symmetric matrix
3
In all our tests we fixed λ = 5.
Π in which an element at row i and column j is equal
to π(ξ
i
,ξ
j
). We consider a discrete probability distri-
bution x = (x
1
,x
2
,.. . ,x
M
) over the set of hypotheses.
The problem of finding a coherent set of candidates
can be described formally in finding a particular dis-
tribution x ∈ ∆
n
maximizing the average payoff x
T
Πx.
One possible solution to the problem employs an evo-
lutionary process starting from a uniform distribution
x
(0)
and evolving through the common discrete-time
replicator dynamic (Taylor and JONKER, 1978)
x
(t+1)
i
= x
(t)
i
(Πx
(t)
)
i
x
(t)
T
Πx
(t)
(6)
Equation (6) belongs to a class of evolutionary
dynamics called Payoff-Monotonic Dynamics that are
guaranteed to converge to a solution
ˆ
x in which the
set of hypotheses with associated probability greater
than 0 (namely the support of a population) cannot in-
clude any strategy with mutual payoff equal to 0. In
other words, the candidates with associated non-zero
probability in
ˆ
x will be the ones generated from differ-
ent planes and with the distance between the two axes
greater than the sum of the two radii. After the inlier
selection process, the final cylinder axis is computed
by fitting a line through the centres of the winning
candidates in a least-squares sense.
2.3 Extracting Multiple Cylinders
To extract multiple cylinders, the inlier selection is
simply repeated by ensuring that the winning candi-
dates resulting from the previous extraction cannot be
selected anymore. Specifically, after the extraction of
each cylinder, we modify the payoff matrix Π accord-
ing to the current population support.
Let k
1
,k
2
,.. . k
h
be the set of indices of non-zero
elements of
ˆ
x (ie. ˆx
K
= 0 ∀K ∈ k
1
... k
h
). Π is modi-
fied so that all the rows and columns at indices k
1
... k
h
are set to zero. After that, the initial population x
0
is
reset to the uniform distribution and the inlier selec-
tion process (6) is run again until convergence. Since
we are using a payoff-monotonic dynamic, all the pre-
vious candidates indexed by k
1
... k
h
cannot be in-
cluded in the next set of winning candidates. Such
process is repeated until all the cylinders are extracted
from the scene.
3 EXPERIMENTAL EVALUATION
To assess the effectiveness of our approach, we de-
vised a set of tests in synthetical and real-world envi-
ronments. The former allows us to control several fac-
tors (noise, outliers, data sampling) and it is designed
Robust Cylinder Estimation in Point Clouds from Pairwise Axes Similarities
643
10 20 30 40 50 60 70 80 90
Number of Planes
0
5
10
15
Angle Error (deg)
Axis Angle Error
θ = 50°
θ = 90°
θ = 135°
θ = 180°
θ = 360°
10 20 30 40 50 60 70 80 90
Number of Planes
0
0.05
0.1
0.15
0.2
Error (%)
Radius Error
θ = 50°
θ = 90°
θ = 135°
θ = 180°
θ = 360°
10 20 30 40 50 60 70 80 90
Number of Planes
0
0.05
0.1
0.15
0.2
0.25
0.3
Distance Error
Axis center error
θ = 50°
θ = 90°
θ = 135°
θ = 180°
θ = 360°
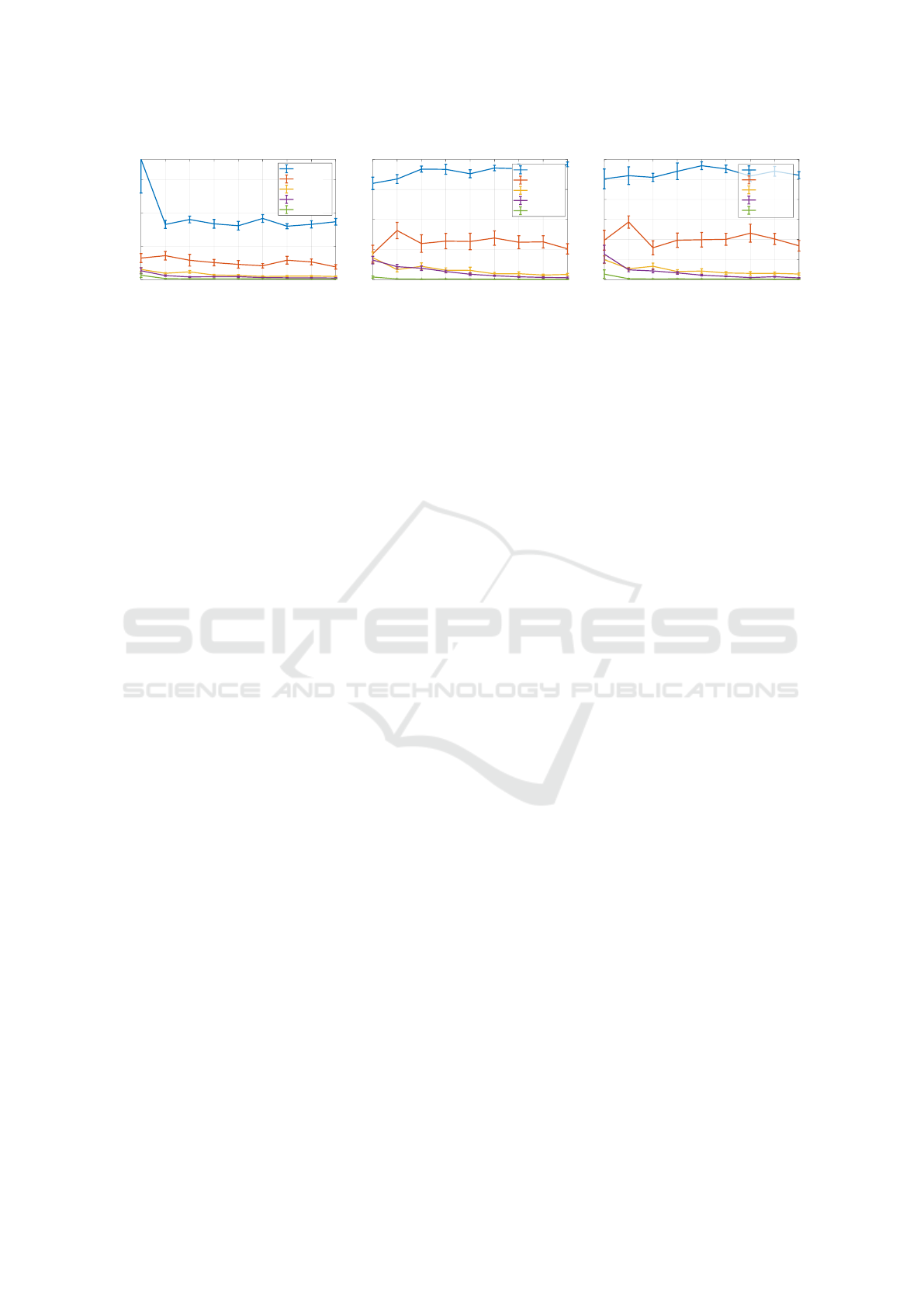
Figure 2: Angle, radius and center errors varying the number of randomly generated planes. Each curve denotes a different
cylinder surface coverage (corresponding to the angle θ).
to capture the potentials of our approach. Since our
method is addressed to real-world applications, a set
of qualitative experiments performed on real scans
will be presented as well.
Synthetic Setup. We generated a cylinder centered
at origin, aligned to the z-axis and with unitary radius.
All its points were perturbed with a zero-mean addi-
tive Gaussian noise of standard deviation σ. Addition-
ally, some outlier points were perturbed with a salt
and pepper noise, with a different standard deviation
denoted as σ
o
(with σ
o
> σ). The amount of outliers
is controlled by a parameter p, that is the probability
for a point to be an outlier. Since most of the time
range data does not cover all the cylinder’s surface,
we also introduced a parameter θ, that is the angle
underlying the covered cylinder’s surface. In the case
θ = 360
◦
, the object is complete. For each experiment
we measured the fitting precision through three differ-
ent quantities, namely the radius relative error (in %
with respect to the actual value), the axis rotation and
translation errors.
3.1 Sensitivity Analysis
As discussed, the number of slicing planes is the
only parameter required by our method. The num-
ber of planes affects the robustness of the proposed
algorithm, and should be adjusted depending on the
features of the acquired scene. For this reason we
started by analysing how important is this parame-
ter for the stability of our approach. Specifically, we
tested our algorithm varying the number of random
planes (ranging from 10 to 90) and their inclination
with respect to the real cylinder’s axis.
In the first experiment, we tested the goodness of
the cylinder fitting for different surface coverages (de-
termined by the angle θ) for a synthetically generated
a cylinder with σ = 0.005 and σ
o
= 0.01 with p = 0.1.
Figure 2 shows the results in three plots that are angle,
radius and translation error. Each configuration was
tested 10 times and the error bars display the stan-
dard error of the mean. As expected, plots show an
improved accuracy as the angle θ increases, due to
a better ellipse fitting. In particular, for the angles
higher than 135
◦
we can observe minor changes in
terms of precision, since the curves shrink in the lower
part of each plot. The curves exhibit the same general
behaviour, that is an overall improvement and stabil-
ity as the number of slicing planes increases. Despite
this, we noticed that the number of planes is not as
critical as one could expect: in cases or medium levels
of noise, 30 to 50 planes could be a suitable number
to obtain a reasonably good result. Of course, if the
scene to be processed contains more than one primi-
tive to be extracted, the number of planes should be
kept high to capture all the relevant elements.
3.2 Comparisons
In this section we compare the performances of the
proposed technique with two different methods. We
employed the previously described synthetic setup,
working with a single cylinder scenario. This allows
us to separate the precision of the fitting algorithm
from the primitive extraction ability. We compared
our technique with (Rahayem et al., 2012) and (Torr
and Zisserman, 2000). The first computes the cylin-
der’s axis fitting a line through the centers of the el-
lipses, and computes the radius as the mean value of
all the radii, then refines the fitting through a non-
linear optimization. In the following comparisons we
used the same ellipses as input. The second approach
consists in a sample consensus technique which ex-
ploits points normals to compute the best cylinder es-
timate in a point cloud. We run this algorithm setting
the maximum inlier distance at 0.03, with 5000 max-
imum iterations.
In the first experiment we tested the reconstruc-
tion ability in presence of escalating Gaussian noise
levels. We fixed the outlier parameters σ
o
= 0.04 and
p = 0.3, while increasing the standard deviation of
the additive noise from 0.001 to 0.05. For each ex-
periment we extracted 20 random planes and repeated
each test 20 times. Figure 3 shows the resulting error
plots, where the bars denote the standard error val-
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
644
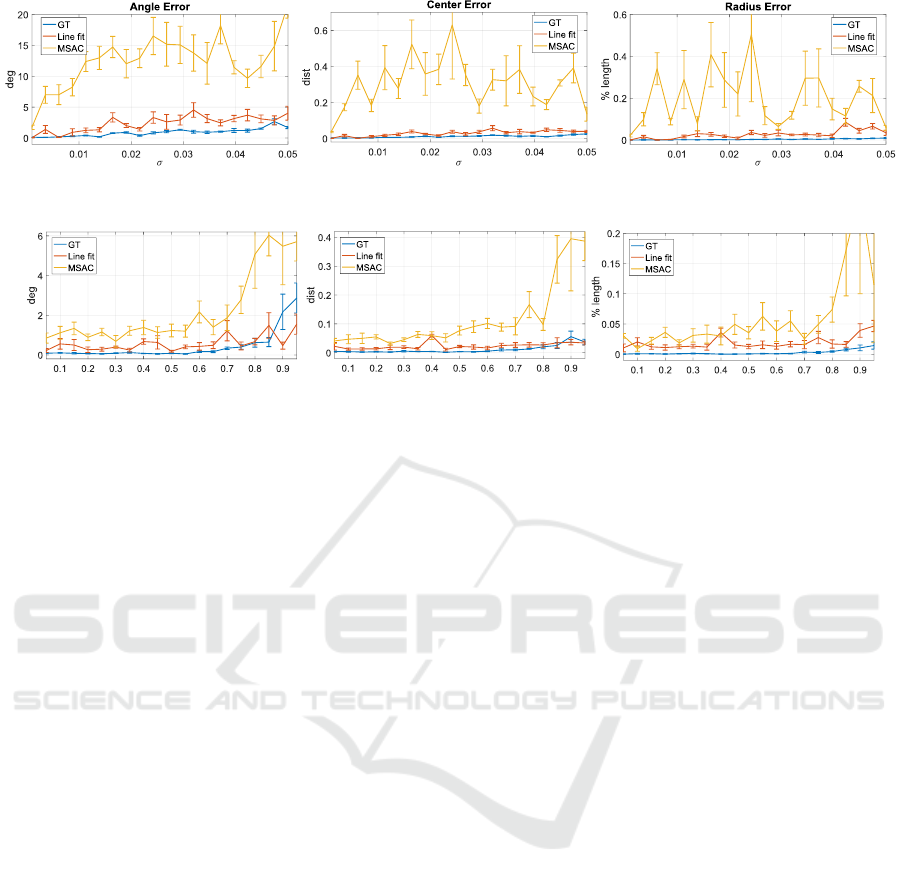
Figure 3: Angle, center and radius error means increasing the standard deviation of additive, zero-mean Gaussian noise. We
tested three different cylinder fitting technique, each one denoted by a curve.
o
o
o
p
p
p
Figure 4: Angle, center and radius error means varying the salt and pepper noise parameters. We increased the outlier
probability p and keep σ
o
= 0.1;. Each curve denotes a different cylinder fitting technique.
ues. In the case of center dislocation and radius er-
rors, our algorithm and the line fitting method offer
similar results. Nevertheless, our approach is able to
provide a more stable and accurate result. In the case
of axis rotation error, our technique results in a more
precise assessment, thanks to the intrinsic outlier se-
lection performed by the game theoretical approach.
The second group of experiments is designed to
compare the performances of the three methods with
different amounts of outliers. Figure 4 shows the be-
haviour of the techniques varying the outliers’ fre-
quency: we fixed σ
o
= 0.1 and increased the value
of p. In all tests we set σ = 0.001 and extracted the
ellipses from 20 random planes. All tests were re-
peated 10 times for each configuration. The proposed
approach outperforms the other methods, in particular
it offered a high level of robustness when the outlier
component is significant.
Finally, we compared the accuracy achievable
when the scene is partially occluded. In the last com-
parison experiment (Fig.5) we performed the fitting
for different values of θ, which is the angle that ex-
presses the amount of covered cylinder’s surface. The
MSAC approach was not accounted since its error
values were too high to be included in the visualisa-
tion. We set the additive Gaussian noise standard de-
viation σ = 0.005; while the outlier parameters were
σ
o
= 0.01 and p = 0.1. We also increased the number
of random planes to 40 (with any inclination angle) to
have a more stable result. The performances of our
approach and the line fitting method are similar look-
ing at the recovered center dislocation and radius rela-
tive error (center and right plots); in particular the line
fitting algorithm performed slightly better with angles
smaller than 90
◦
. As the other experiments had al-
ready pointed out, the critical factor in cylinder fitting
is the correct axis angle. The leftmost plot of Figure 5
shows the improvements of our approach with respect
to the other method, increasing the axis precision up
to 4 degrees.
In general the proposed game theoretical algo-
rithm provides more stable results if compared to
other techniques. It sometimes offers slightly better
results with respect to the fitting line technique, but
the accuracy in many cases is superior, especially with
many outliers. Also, the axes angle is a critical ele-
ment to be recovered, and our algorithm ensures the
best candidate selection.
3.3 Real-world Experiments
We employed actual scans to test the capabilities of
our approach in real-world applications. We used the
point cloud dataset presented in (Calli et al., 2017),
that contains scans of the Yale-CMU-Berkeley Object
and Model Set (Calli et al., 2015). The dataset con-
tains coloured point data of several objects with no
surface normals. We selected a subset of them to cre-
ate a number of scenes in which some cylinders are to
be extracted. Moreover, we aim to evaluate the good-
ness of our algorithm in presence of multiple cylindri-
cal shapes of unknown location.
The first test was designed to measure the repeata-
bility of the extraction algorithm, along with its ca-
pability in locating primitives given real-world data.
We generated a scene containing two instances of the
object "tomato soup" (radius = 33 mm, height = 101
mm) arranged at a known random translation.. The
corresponding point cloud contains 373,205 vertices
Robust Cylinder Estimation in Point Clouds from Pairwise Axes Similarities
645
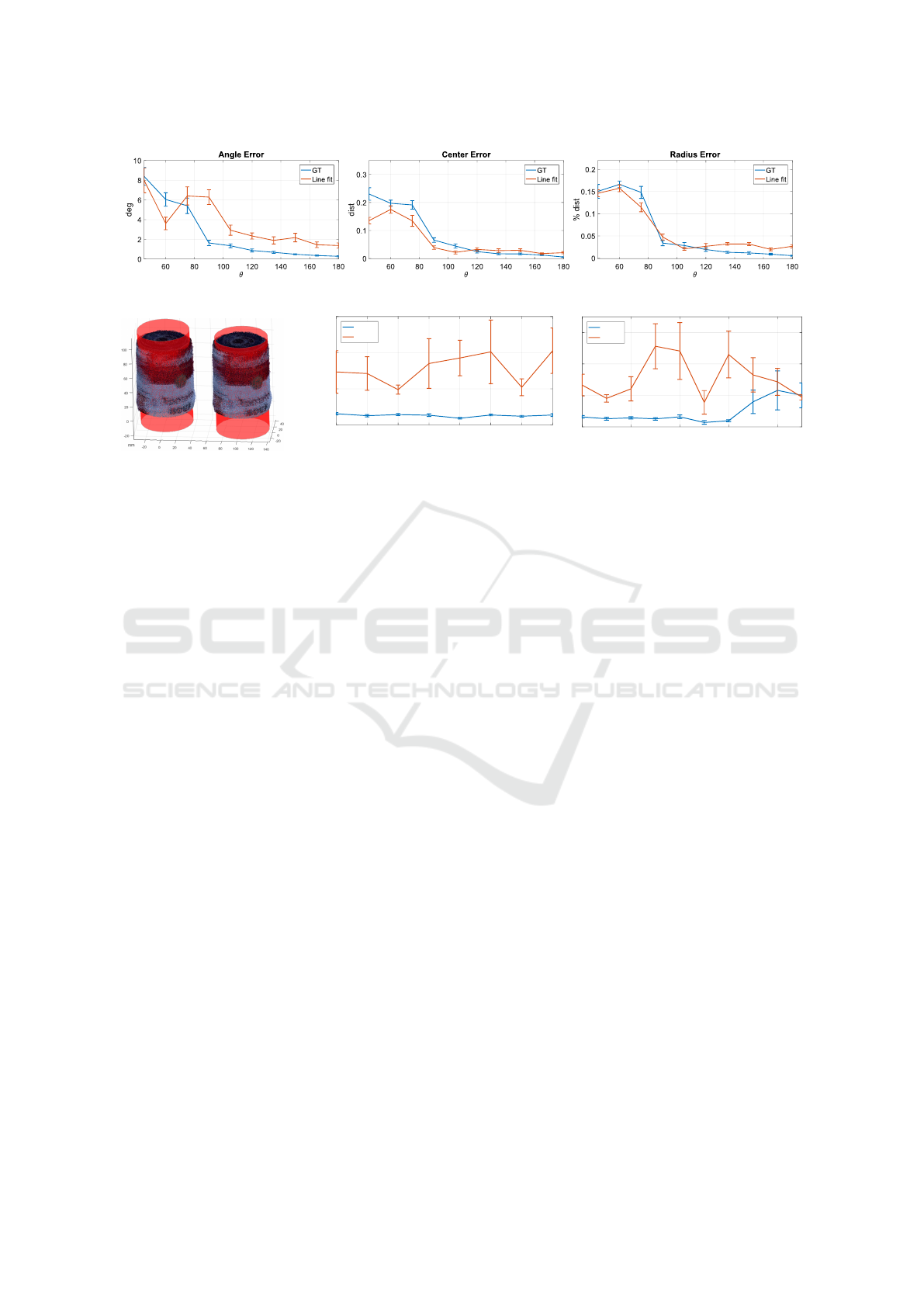
Figure 5: Angle, center and radius error means increasing the cylinder coverage angle θ.
0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Sampling %
0
10
20
30
deg
GT
MSAC
0 20 40 60 80
Min Angle
0
10
20
30
deg
GT
MSAC
Figure 6: Left: an example of the generated scene with two scans of tomato soup object. In red, the cylinders fitted by our
method. Center and right: relative angle means of the two fitted axes from the scene. The bars represent the standard error.
and appears quite thick, with no outliers. Figure 6
(left) shows an example of generated scene, together
with the cylinders extracted by our method (in red).
We exploited this setting to compare our algorithm
with MSAC approach. The line fitting method (Ra-
hayem and Kjellander, 2011) was excluded because
it can not be applied in a scene for multiple cylin-
der extraction. To extract multiple primitives with
MSAC, we iteratively removed the points belonging
to a cylinder if their distance from the fitted axis is be-
tween ±5% of the radius. The surface normals (used
in MSAC) have been computed by fitting a plane on
80 neighbour points that we empirically determined
giving good results. The ellipses extraction from the
slicing planes is performed just once, then the game
theoretical approach selects a group of inliers using a
different payoff matrix, as explained in 2.3. Since the
exact center and axes of the objects is unknown, we
evaluated the repeatability and accuracy of the extrac-
tions measuring the relative angle between the couple
of fitted axes. Ideally, these values should be as clos-
est to zero as possible. In the central plot of Figure
6 we show the relative angle between the pairs of fit-
ted axes, varying the proportion of randomly sampled
data from the original point cloud. We run our algo-
rithm generating 40 planes and MSAC setting 3000
iterations and minimum inlier distance equal to 2mm.
In the rightmost plot of Figure 6 we computed the
same quantity filtering out the points for which the
angle between their normal and a predefined direction
is above a threshold (specified on the x-axis). In this
way we simulated an incomplete acquisition, as we
had a range-map (note that min angle = 0 corresponds
to the whole point cloud). We used (0, 1,0) as "ob-
serving" direction and run the tests by randomly sam-
pling the 80% of the points. We used 50 planes and in-
creased the number of MSAC iterations to 5000. Each
test was performed 20 times. In all the experiments
our algorithm gave an angle between 2 and 5 degrees,
except for the final part of the rightmost plot, where
the error reaches 10 degrees. In all cases, MSAC ap-
proach exhibited an unstable behaviour and a higher
standard error, likely due to an inaccurate normal es-
timation. We additionally tested the extraction algo-
rithm "in the wild", generating random scenes with
various features and using 60 slicing planes. In Fig-
ure 7 a selection of qualitative results is shown. In the
leftmost example we used objects of different radius
and height: "tomato soup" (radius 33 mm), "Master
Chef" (radius 51 mm) and "c cup" (radius 32.5 mm).
Each computed radius is displayed next to the corre-
sponding cylinder. The central picture shows a con-
figuration of nine "tomato soup" items, for which we
run 9 times the inlier selection process to extract all
the cylinders. Finally, the rightmost image shows an
example of a generic scene with various items. Such
results show the capability of our technique to cor-
rectly extract cylinder primitives in an heterogeneous
scene, intrinsically excluding all non-cylindrical 3d
data.
4 CONCLUSIONS
We proposed a novel technique to extract multiple
cylindrical objects from generic point clouds. The
game theoretic process combined with a specially de-
signed payoff-function among cylinder candidates al-
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
646

Figure 7: Qualitative examples obtained in different kinds of scenes, generated using real scans data.
low the method to be general enough to be used with-
out prior knowledge of the scene. Our approach ex-
hibits a high robustness with respect to outliers, that
makes it perfect to be applied in scenarios where a
noisy point cloud is acquired without normal vectors.
Qualitative experiments show that the proposed ex-
traction method offers high flexibility in very hetero-
geneous and complex scenes.
REFERENCES
Amir, Y. M. and Thörnberg, B. (2017). High precision laser
scanning of metallic surfaces.
Bergamasco, F., Albarelli, A., Cosmo, L., Torsello, A.,
Rodolà, E., and Cremers, D. (2015). Adopting an
unconstrained ray model in light-field cameras for 3d
shape reconstruction. volume 07-12-June-2015, pages
3003–3012. cited By 6.
Bergamasco, F., Cosmo, L., Albarelli, A., and Torsello, A.
(2012). A robust multi-camera 3d ellipse fitting for
contactless measurements. pages 168–175.
Bergamasco, F., Cosmo, L., Albarelli, A., and Torsello,
A. (2014). Camera calibration from coplanar circles.
pages 2137–2142.
Calli, B., Singh, A., Bruce, J., Walsman, A., Konolige, K.,
Srinivasa, S., Abbeel, P., and Dollar, A. M. (2017).
Yale-cmu-berkeley dataset for robotic manipulation
research. The International Journal of Robotics Re-
search, 36(3):261–268.
Calli, B., Singh, A., Walsman, A., Srinivasa, S., Abbeel, P.,
and Dollar, A. M. (2015). The ycb object and model
set: Towards common benchmarks for manipulation
research. In Advanced Robotics (ICAR), 2015 Inter-
national Conference on, pages 510–517. IEEE.
Chen, H. H. (1991). A screw motion approach to unique-
ness analysis of head-eye geometry. In Proceedings.
CVPR 1991, pages 145–151.
Daniilidis, K. (1999). Hand-eye calibration using dual
quaternions. The International Journal of Robotics
Research, 18(3):286–298.
Hakala, D., Hillyard, R., and Malraison, P. J. (1980). Natu-
ral quadrics in mechanical design. In CAD/CAM VIII
part of Autofact West Anaheim, California.
Halır, R. and Flusser, J. (1998). Numerically stable direct
least squares fitting of ellipses. In Proc. 6th Inter-
national Conference in Central Europe on Computer
Graphics and Visualization. WSCG, volume 98, pages
125–132. Citeseer.
Kavan, L., Collins, S., Žára, J., and O’Sullivan, C. (2008).
Geometric skinning with approximate dual quaternion
blending. ACM Trans. Graph., 27(4):105:1–105:23.
Lukács, G., Marshall, A. D., and Martin, R. R. (1997). Ge-
ometric least-squares fitting of spheres , cylinders ,
cones and tori.
Lukács, G., Martin, R., and Marshall, D. (1998). Faithful
least-squares fitting of spheres, cylinders, cones and
tori for reliable segmentation. In Computer Vision -
ECCV’98, pages 671–686.
McCarthy, J. M. (1990). Introduction to Theoretical Kine-
matics. MIT Press, Cambridge, MA, USA.
Pfeifer, N., Gorte, B., and Winterhalder, D. (2004). Au-
tomatic reconstruction of single trees from terrestrial
laser scanner data.
Qiu, R., Zhou, Q.-Y., and Neumann, U. (2014). Pipe-run
extraction and reconstruction from point clouds. In
Computer Vision – ECCV 2014, pages 17–30.
Rabbani, T. and den Heuvel, F. A. V. (2005). Efficient
hough transform for automatic detection of cylinders
in point clouds.
Rahayem, M., Werghi, N., and Kjellander, J. (2012). Best
ellipse and cylinder parameters estimation from laser
profile scan sections. Optics and Lasers in Engineer-
ing, 50(9):1242 – 1259.
Rahayem, M. R. and Kjellander, J. A. P. (2011). Quadric
segmentation and fitting of data captured by a laser
profile scanner mounted on an industrial robot. The In-
ternational Journal of Advanced Manufacturing Tech-
nology, 52(1):155–169.
Specian, A., Mucchiani, C., Yim, M., and Seo, J. (2018).
Robotic edge-rolling manipulation: A grasp planning
approach. IEEE Robotics and Automation Letters,
3(4):3137–3144.
Taylor, P. D. and JONKER, L. B. (1978). Evolutionarily
stable strategies and game dynamics.
Torr, P. H. S. and Zisserman, A. (2000). MLESAC: A new
robust estimator with application to estimating image
geometry. CVIU, 78:138–156.
Weibull, J. (1995). Evolutionary game theory. MIT Press,
Cambridge, Mass. [u.a.].
Robust Cylinder Estimation in Point Clouds from Pairwise Axes Similarities
647
