Pareto-based Soft Arc Consistency for Multi-objective Valued CSPs

Limeme Ben Ali

, Maher Helaoui

and Wady Naanaa

Faculty of Economics and Management of Sfax, University of Sfax, Tunisia

Higher Institute of Business Administration, University of Gafsa, Tunisia

National Engineering School of Tunis, University Tunis El Manar, Tunisia

Keywords:

Multi-objective Optimization, Multi-objective Valued Constraint Satisfaction Problems MO-VCSP, Soft

Local Arc Consistency, Lower Bound Set, Pareto Dominance.

Abstract:

A valued constraint satisfaction problem (VCSP) is a soft constraint framework that can formalize a wide

range of applications related to Combinatorial Optimization and Artiﬁcial Intelligence. Most researchers have

focused on the development of algorithms for solving mono-objective problems. However, many real-world

satisfaction/optimization problems involve multiple objectives that should be considered separately and sat-

isﬁed/optimized simultaneously. Solving a Multi-Objective Optimization Problem (MOP) consists of ﬁnding

the set of all non-dominated solutions, known as the Pareto Front. In this paper, we introduce multi-objective

valued constraint satisfaction problem (MO-VCSP), that is a VCSP involving multiple objectives, and we ex-

tend soft local arc consistency methods, which are widely used in solving Mono-Objective VCSP, in order to

deal with the multi-objective case. Also, we present multi-objective enforcing algorithms of such soft local

arc consistencies taking into account the Pareto principle. The new Pareto-based soft arc consistency (P-SAC)

algorithms compute a Lower Bound Set of the efﬁcient frontier. As a consequence, P-SAC can be integrated

into a Multi-Objective Branch and Bound (MO-BnB) algorithm in order to ensure its pruning efﬁciency.

1 INTRODUCTION

Solving a Single-Objective Optimization Problem

amounts to determining the best solutions that satisfy

a set of constraints and optimize an objective function

deﬁned by the user. The best solution, also known

as the optimal solution, is the solution with the high-

est assessment against the deﬁned objective. Such

a problem can be formulated in terms of a Valued

Constraint Satisfaction Problem (VCSP). However,

when dealing with real-world problems such as Sup-

ply Chain Problem, Production Management Prob-

lems, Communication Problems, Time-cost trade-off

problem (Afruzi et al., 2013), Scheduling Problems

(Hazır et al., 2010) and many others, a single objec-

tive function may be insufﬁcient. In fact, most of the

real-world applications require the integration of mul-

tiple simultaneous objective functions, often conﬂict-

ing. When considering multiple objectives functions,

the notion of optimal solution from single-objective

optimization does not apply anymore, and instead one

must rely on the notion of Pareto Dominance. A so-

lution s is better, in the Pareto sense, than another so-

lution s

if s is better than s

for at least one objective

and not worse for any of the remaining ones. If none

of the two solutions is better than the other, they rep-

resent two different trade-offs of the objectives func-

tion that, without knowledge of the decision maker’s

preferences, are considered to be equally valuable. A

very important task of interest in a multi-objective op-

timization problem (MOP) is to compute its efﬁcient

frontier E (and, possibly, one or all efﬁcient solutions

for each of its elements). In order to present a more

powerful modeling to these real problems, we propose

a generalization of VCSPs to Multi-Objective Valued

Constraint Satisfaction Problems (MOVCSPs).

The classical Constraint Satisfaction Problem

(CSP) model considers only the feasibility of sat-

isfying a collection of simultaneous requirements

(van Beek and Manchak, 1996; Jeavons and Cooper,

1995). Various extensions have been proposed to this

model, to allow it to deal with different kinds of op-

timization criteria, or preferences between different

feasible solutions. Two very general extended frame-

works that have been proposed are the semi-ring CSP

(Bistarelli et al., 1999) and the valued CSP (VCSP)

(Schiex et al., 1995). The semi-ring framework is

slightly more general, but the VCSP framework is

294

Ben Ali, L., Helaoui, M. and Naanaa, W.

Pareto-based Soft Arc Consistency for Multi-objective Valued CSPs.

DOI: 10.5220/0007401802940305

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 294-305

ISBN: 978-989-758-350-6

simpler, and sufﬁciently powerful to describe many

important classes of problems (Cohen et al., 2008).

In this framework every constraint has an associated

cost function which assigns a cost to every tuple of

values for the variables in the scope of the constraint.

In the literature, many local consistency algorithms

have been proposed for soft CSPs. Soft Consistency

algorithms work by making explicit the inconsistency

level originally implicit in the problem. The general

idea is to safely move costs (i.e., without changing the

level of consistency of the solution) from high arity

constraint to smaller arity ones.

In this paper we address combinatorial problems

that can be expressed as MOVCSPs. We introduce

a generic formalization of multi-objective problems

in terms of Valued CSP framework. Several models

using the soft CSP framework have been presented in

the literature (Emma and Javier, 2006; Bistarelli et al.,

2008; Bistarelli et al., 2012; Wilson et al., 2015).

Our new MOVCSP model is important for two rea-

sons; ﬁrst we pick up an understanding of the nature

of multi-objective optimization problems, and we ac-

cede to some theoretical results from the Valued CSP.

Given a MO-VCSP, we deﬁne the Lower Cost Vec-

tor (LCV) operator on cost. Furthermore, we present

its generalization to be applicable over sets of k-ary

cost functions. Also, we show how to use the LCV

value (i.e., the value returned by LCV) inside the soft

arc consistency techniques in order to deal with the

multi-objective case. Thereafter, we introduce new

deﬁnitions for the support notion based on LCV. As

consequence, the LCV value corresponds to the trans-

ferred cost vector in the new Pareto-based soft arc

consistency operations commonly known as Equiva-

lence Preserving Transformation (EPT).

The rest of the paper is organized as follows.

Section 2 summarizes the background notions about

valued constraint satisfaction problems and multi-

objective optimization. Section 3 shows how to ex-

tend the VCSP formalism to model multi-objective

optimization problems. Section 3 also, presents basic

operations over costs and their extension to costs sets.

In Section 4, we introduce soft local consistencies

based on the Pareto principle and the main differences

while considering multiple objective functions. Fur-

thermore in the same section, we describe the multi-

objective extension of Soft Arc Consistencies main-

taining algorithms (Maintain P-SAC). In Section 5,

we give a description of the extension of depth-ﬁrst

branch-and-bound, to solve MOVCSP problems, that

maintain Pareto soft local consistencies during search.

Section 5 also presents the related work and a discus-

sion of potential extensions. At last, Section 6 wraps

up the paper, presenting our conclusions.

2 BACKGROUND

In this section, we point out the speciﬁc features of

the multi-objective problems and recall the main def-

initions of the VCSP framework.

2.1 Multi-objective Optimization

Multi-objective Optimization Problems deal with

multiple objectives, which should be simultaneously

optimized (Deb and Kalyanmoy, 2001; Le Thi et al.,

2008; Chiandussi et al., 2012).

Example 1. Π PROJECT MODELED AS A BI-

OBJECTIVES DISCRETE TIME COST TRADE-OFF

PROBLEM (VANHOUCKE AND DEBELS, 2007). Let

Π be a project deﬁned as follows:

Π is a project comprised of 6 tasks: A, B, C, D,

E and F. The predecessors of each task are deﬁned

in column 2 (Preds) of Table 1. The various options

of the executions times and the relative costs of each

tasks (option 1, option 2, option 3) are deﬁned in

columns 3, 4 and 5.

Solving the problem is equivalent to ﬁnding one

option for each task such that:

1. The precedence constraints are satisﬁed.

2. Both global costs and global makespan are opti-

mized.

Table 1: Π project.

Tasks Preds option 1 option 2 option 3

A – (5,100) (3,250) (1,500)

B A (5,100) (4,300) (2,900)

C A (5,100) (3,350) (2,600)

D A (10,200) (8,500) (7,800)

E B,C (5,100) (3,300) (1,600)

F D,E (5,100) (4,580) (2,2500)

The project network G = (V,A) of the project Π is

depicted in Fig.1 where V = {A,B,C,D, E,F} is the

set of Tasks and A is the set of arcs representing the

precedence constraints. Each task can be executed in

three options (modes). Each node V

of G is labeled

by a set of pairs (time,cost) representing time, cost

values of each option of the task V

Optimizing simultaneously two functions can be

contradictory, since reducing the cost, φ

, often in-

creases the project execution period, φ

, and con-

versely.

The concept of looking for an optimal solution be-

comes more difﬁcult to deﬁne. In this case, and in ac-

cordance with the Pareto optimal, the desired optimal

solution is no longer a single point, but a set of non-

dominated solutions. Otherwise, solving a problem

with several objective functions, commonly referred

Pareto-based Soft Arc Consistency for Multi-objective Valued CSPs

295

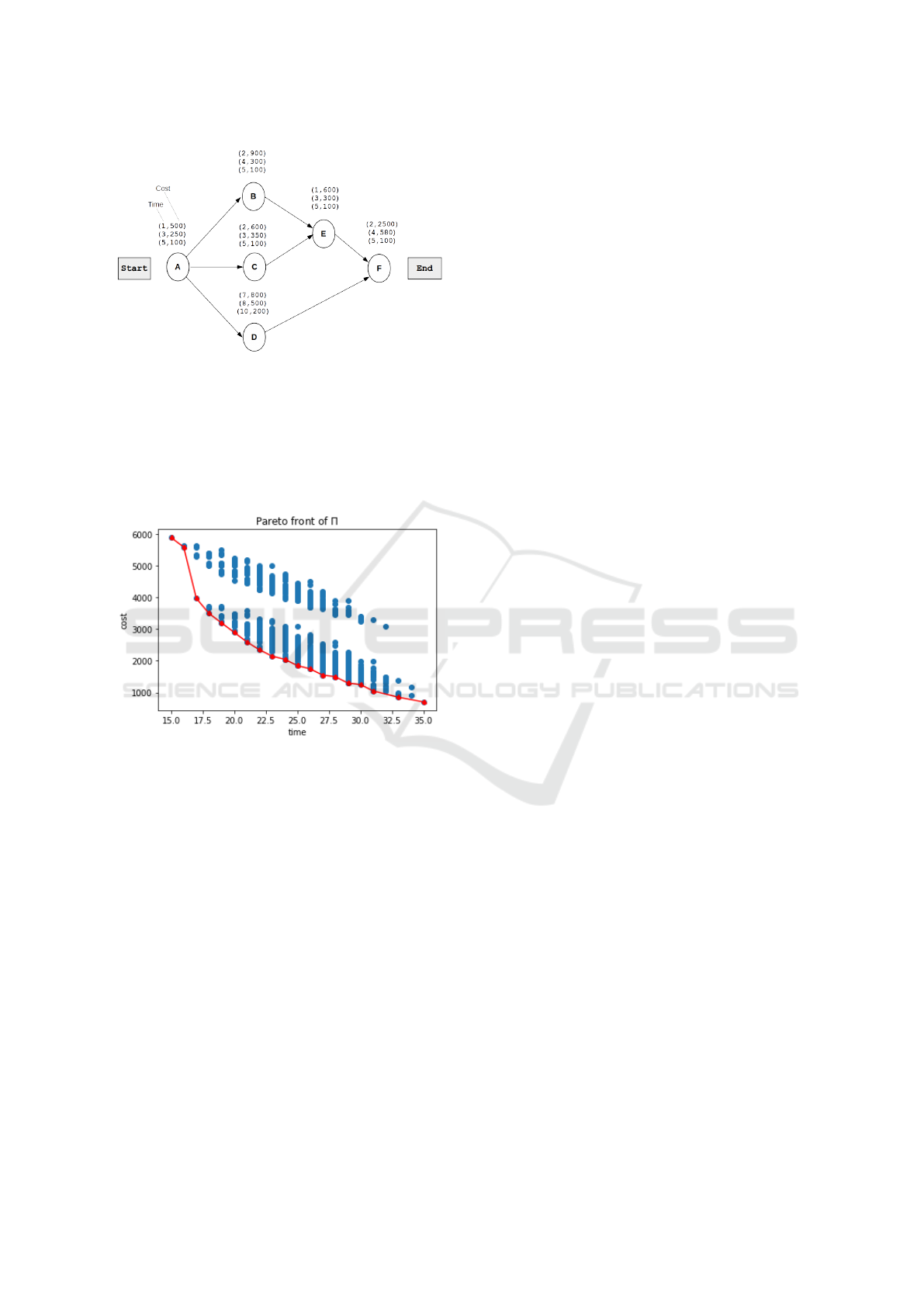
Figure 1: Project network of Π.

to a multi-objective problem, is to compute the best

set of trade-off solutions called the Pareto Front.

The Pareto front E

of the Project Π is shown in

Fig.2. The set of non-dominated solutions after re-

moving redundant solutions is composed of 19 solu-

tions marked with red points in Fig.2.

Figure 2: The Pareto front of Π.

A multi-objective problem can be deﬁned as a

problem where one seeks action that satisﬁes a con-

straint set and optimizes a set of objective functions.

A very important task of interest in a multi-objective

problem is to compute its efﬁcient frontier E.

2.2 Valued Constraint Satisfaction

Problem and Soft Local Consistency

The Valued CSP (VCSP) framework is a generic op-

timization framework with a wide range of applica-

tions. Soft arc consistency operations transform a

VCSP into an equivalent problem by shifting weights

between cost functions. The principal aim is to pro-

duce a good lower bound on the cost of solutions, an

essential ingredient of a branch-and-bound search.

Valued Constraint Satisfaction Problem. The

Constraint Satisfaction Problem (CSP) consists of

ﬁnding an assignment to n ﬁnite-domain variables

such that a set of constraints are satisﬁed. Crisp con-

straints in the CSP are replaced by cost functions in

the Valued Constraint Satisfaction Problem (VCSP)

(Schiex et al., 1995). A cost function returns a val-

uation (a cost, a weight or penalty) for each combi-

nation of values for the variables in the scope of the

function. Crisp constraints can still be expressed by,

for example, assigning an inﬁnite cost to inconsistent

tuples. In the most general deﬁnition of a VCSP, costs

lie in a valuation structure (a positive totally-ordered

monoid) (E,⊕, 4), where E is the set of valuations

which are totally ordered by 4 and combined using

the aggregation operator ⊕ (Schiex et al., 1995) and

> and ⊥ denotes maximum and minimum elements

of E given by 4. In this paper we only consider inte-

ger or rational costs.

A Valued Constraint Satisfaction Problem can be

seen as a set of valued constraints, which are simply

cost functions placed on particular variables. One can

propose this deﬁnition.

Deﬁnition 1 ((Schiex et al., 1995)). A Valued

Constraint Satisfaction Problem (VCSP) is a tuple

(X, D,C,S), where X is a set of n variables, each vari-

able x ∈ X has a domain of possible values D

∈ D,

C is a set of cost functions and S = (E,⊕,4) is a val-

uation structure. Each cost function hσ, φ

i ∈ C is

deﬁned over a tuple of variables σ ⊆ X (its scope) as

a function φ

from the Cartesian product of the do-

mains Π

x∈σ

to E.

As we search for assignments with minimal val-

uation computed by combining violated constraints

by ⊕, one may see that the element > corresponds

to unacceptable violation and is used to express hard

constraints while ⊥ element corresponds to complete

satisfaction.

EPTs and Soft Arc Consistency. The soft local

consistency, we study below, has an important role

in the efﬁcient resolution of VCSPs (Allouche et al.,

2016; Larrosa and Schiex, 2004; Bistarelli et al.,

2008). By deﬁnition, local consistency is a family

of increasingly harder properties about a Soft Con-

straint Satisfaction Problem. The control parameter is

the size of the sub-network (i.e., the number of vari-

able tuples) involved. The larger the tuples, the harder

the property is. The simplest form of local consis-

tency is node consistency, which only takes into ac-

count unary constraint. The next one is arc consis-

tency, which takes into account binary constraint. In

general, k-consistency takes into account constraints

with k variables in their scope (Cooper, 2005).

Various consistency notions have been proposed

for Valued CSP. Examples include NC

∗

(Larrosa and

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

296

Schiex, 2004), AC

∗

(Lee and Leung, 2012), FDAC

∗

(Larrosa and Schiex, 2004; Lee and Leung, 2012),

EDAC

∗

(de Givry et al., 2005), VAC (Cooper et al.,

2008) and OSAC (Cooper et al., 2010). Existential

Directional Arc Consistency EDAC* is the strongest

known polynomial-time achievable form of soft arc

consistency. Note, however, that EDAC* has only

been deﬁned in the special case of binary (de Givry

et al., 2005) and ternary (Lee and Leung, 2012) VC-

SPs.

Enforcing such local consistencies requires apply-

ing equivalence preserving transformations (EPTs)

that shift costs between different scopes (Cooper and

Schiex, 2004). EPT is based on three cost trans-

fers operations which are also called SAC operations

(de Givry et al., 2005). Project operation which

projects costs from a cost function (on two or more

variables) to a unary cost function. Extend performs

the inverse operation, sending costs from a unary cost

function to a higher-order cost function. Finally, Pro-

jectUnary projects costs from a unary cost function to

the nullary cost function φ

∅

which is a lower bound

on the value of any solution.

Deﬁnition 2. For a VCSP (X,D,C,S), an equivalence

preserving transformation (EPT) on F ⊆ C is an op-

eration which transforms the sub-problem VCSP(F)

into an equivalent VCSP. When F contains, at

most, one non unary constraint, such an equivalence-

preserving transformation is called a Soft Arc Con-

sistency (SAC) operation.

For simplicity, we restrict ourselves to binary

VCSP. A binary VCSP is AC

∗

, DAC

∗

, FDAC

∗

, EAC

∗

EDAC

∗

if it is NC and respectively AC, DAC, FDAC,

EAC, EDAC (Larrosa, 2002).

Local consistency properties are used to transform

problems into equivalent simpler ones. From a prac-

tical point of view, the effect of applying local consis-

tencies at each node of the search tree of a branch and

bound algorithm is to prune values and to compute

good lower bounds.

3 MULTI-OBJECTIVE VALUED

CONSTRAINT SATISFACTION

PROBLEM

Compared to Integer Linear Programming (ILP)

(Le Thi et al., 2008; Teghem, 2009), the VCSP ap-

proach is an interesting alternative way to treat com-

plex (multi-objective) optimization problems. VC-

SPs are a pragmatic extension of the CSP dedicated

to optimization which authorizes an important efﬁ-

ciency gains with regard to the usual approach in con-

straint programming. The latter approach consists

in encapsulating the objective function into a vari-

able. In this section, we formalize a Multi-Objective

Valued Constraint Satisfaction Problem (MO-VCSP).

Furthermore, we introduce operations over costs and

their extension to deal with MO-VCSP.

3.1 Model

In a Multi-Objectives Valued Constraint Satisfaction

Problem (MO-VCSP), as for a VCSP (Schiex et al.,

1995), for each objective j = 1,2,. .., k, we assume

that E

, the set of possible valuations for objective j,

is a totally ordered set with ⊥

as minimal element

and >

as maximal element. We also need a mono-

tone and binary operator ⊕

to aggregate valuations

for objective j. These components can be gathered

in k valuation structures each one can be speciﬁed as

follows:

Deﬁnition 3 (Valuation Structure). Each valuation

structure S

of a MO-VCSP is the triple (E

,⊕

)

such as:

• E

is a set of valuations for objective function j;

• 4

is a total order on E

;

• ⊕

is commutative, associative and monotone.

Proposition 1. Let {S

= (E

,⊕

,⊥

)}

j=1

be a family of valuations structures. Then, the

structure S = (E, ⊕,4,⊥, >), where E = E

... × E

,⊕ =



⊕

,..., ⊕



,4=



,..., 4



,⊥ =

(⊥

,..., ⊥

) and > = (>

,..., >

), is a valuation

structure. The relation between valuations vectors

4 is based on Pareto dominance relation (Teghem,

2009). For distinction, S will be called a multi-

valuation structure.

Once the valuation structure S is speciﬁed, the

multi-objective valued constraint satisfaction problem

(MO-VCSP) can be deﬁned as follows:

Deﬁnition 4 (MO-VCSP). A multi-objective valued

constraint satisfaction problem (MO-VCSP) is de-

ﬁned by the tuple (X, D,C,S) such as:

• X is a ﬁnite set of variables;

• D is a ﬁnite set of domains, such that D

∈ D de-

notes the domain of x ∈ X.

• S =(E

×.. .×E

,(⊕

,..., ⊕

),(4

,..., 4

)) is a

multi-valuation structure.

• C is a set of multi-valued constraints. Each con-

straint is an ordered pair (σ,Φ

) where σ ⊆ X

is the scope of the constraint and Φ

is a func-

tion from Π

x∈σ

to Π

j=1

, such that Φ

(t) =

(φ

(t),...,φ

(t)).

Pareto-based Soft Arc Consistency for Multi-objective Valued CSPs

297

For a variable x, we can only assign a value of

its domain. The valuation V of an assignment t to a

subset of variables V ⊆ X is obtained by

V (t) =

(σ,Φ)∈C,σ⊆V

Φ(t ↓ σ)

which can be written as

V (t) =





(σ,Φ)∈C,σ⊆V

(t ↓ σ),. ..,

(σ,Φ)∈C,σ⊆V

(t ↓ σ)





where φ

= Φ[ j] and t ↓ σ denotes the projection of

t on variables σ.

The arity of a multi-valued constraint is the size

of its scope. The arity of the problem is the maxi-

mum arity over all its constraints. In this work, we

are concerned with binary MO-VCSPs. These are

MO-VCSPs whose constraints are exclusively unary

or binary. Moreover, we suppose that all constraints

have distinct scopes. This allows us to identify every

constraint (σ, Φ) of C with its scope-indexed vector

. We write Φ

as a shorthand for Φ

and Φ

as a shorthand for Φ

x,y

. Without loss of generality,

we assume that C contains a unary multi-valued con-

straint Φ

for every variable x ∈ X as well as a zero-

arity multi-valued constraint Φ

∅

Finding an assignment that optimizes all objec-

tives simultaneously is not always possible. Indeed,

in general, such an ideal assignment does not exist or

cannot be reached, because of the trade-off between

the objectives. Thus, the (optimal) solution of MO-

VCSP can be characterized by using the concept of

Pareto Optimality.

Example 2. We return again to the DTCT project Π

presented in Example 1. This project Π can be mod-

eled as a bi-objectives VCSP P

deﬁned as follows:

1. X

is a ﬁnite set of variables such that i = {Tasks};

2. D is a set of ﬁnite domains, where D

∈ D denotes

the set of options that can be taken by task i; we

therefore have D

= {v

3. S = (E

× E

⊕

,⊕



,

) is a multi-

valuation structure, where ⊕

and ⊕

is the sum

operator over time and cost values respectively.

4. C is a set of valued constraints. Each valued con-

straint C

is an ordered pair (σ,Φ

) where σ ⊆ X

is the scope of C

and Φ

(v) = (φ

(v),φ

(v)).

The predecessors of each task are deﬁned in col-

umn 2 (Preds) of Table 2 which can be expressed by

crisp constraint C

taking bi-value (⊥

,⊥

) if prece-

dence is satisﬁed and (>

) otherwise.

We get

= (X , D,S,C ∪C

)

Table 2: Bi-objectives VCSP P

= Π.

Preds Φ

) Φ

)

– (5,100) (3,250) (1,500)

(5,100) (4,300) (2,900)

(5,100) (3,350) (2,600)

(10,200) (8,500) (7,800)

(5,100) (3,300) (1,600)

(5,100) (4,580) (2,2500)

The Dominance relation among valuation vectors

is deﬁned as follows:

Deﬁnition 5 (Dominance). Let V and V

be two k-

sized valuation vectors, and let V [ j] (V

[ j]) be the j

component of V (resp. V

). We say that V dominates

, denoted by V ≺

, iff (i) V [ j] 4

[ j] holds

true for all objective j ∈ 1..k. And (ii) there exist at

least one objective j ∈ 1..k such that V [ j] ≺

[ j].

A solution t is a complete assignment. It is said to

be efﬁcient or Pareto optimal if it respects the deﬁni-

tion 6 below.

Deﬁnition 6 (Pareto Optimal Solution). For a MO-

VCSP and a complete assignment t, we say t is a

Pareto optimal solution (resp. a non-dominated so-

lution) iff there does not exist another assignment t

such that V (t

) ≺

V (t).

Solving MO-VCSP is to ﬁnd all Pareto Optimal

solutions representing the Pareto front corresponding

to the set off all non-dominated solutions called NDS.

Deﬁnition 7 (Pareto Front). For a MO-VCSP, a set

of cost vector obtained by Pareto optimal solution is

called Pareto Front. Solving a MO-VCSP is to ﬁnd the

Pareto front.

3.2 Operations over Costs and their

Extensions

The following deﬁnitions require that assumed valu-

ation structures for the MO-VCSP are fair (Cooper

and Schiex, 2004). A valuation structure S

is fair if

for any valuation pair α, β ∈ E

, if α 

β, there is a

maximum difference between β and α. The only max-

imum difference between β and α is noted by β 

α.

Another requirement for the purpose of this paper, is

that the valuation structures must be a lattice which

mean that any pairs of valuation (costs) must have a

lower bound, denoted LC. In order to generalize, we

will stretch this notion of LC on costs sets.

In the multi-objective case, operations overs costs

will be extended to costs vectors. Let us consider

problems with k objectives. The only difference is

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

298

that cost are now k-vectors and cost functions are now

k-functions. > = (>

,..., >

) is a k-vector, where

each >

∈ E

is the maximum acceptable cost for the

objective j. ⊥ = (⊥

,..., ⊥

) is a k-vector, where

each ⊥

∈ E

is the lowest acceptable cost for the ob-

jective j.

A k-vector u = (u

,..., u

) is a vector of k-

components, where each u

∈ E

and u

. Let u

and v be two distinct k-vectors.

• The aggregation of two costs values for an objec-

tive j is deﬁned as:

⊕

def

(

⊕

, if u

⊕

≺ >

, otherwise.

• The aggregation of two k-ary cost vectors is de-

ﬁned as:

u⊕v

def

(

>, if ∃ j,u

⊕

= >

⊕

,..., u

⊕

), otherwise.

• For two cost values u

∈ E

, such that u



the subtraction of v

from u

for an objective j is

given by:



def

(



, if u

≺

, otherwise.

• The subtraction of a cost vector v from a cost vec-

tor u, such that, ∀ j ∈ {1, ...,k}, u

∈ u, and v

∈ v

we have u



is deﬁned as:

uv

def

(

>, if ∃ j,u



= >



,..., u



), otherwise.

Let V be a set of k-ary cost vectors. We deﬁne its

non-domination closure as

∗

= {u ∈ V | ∀v ∈ V, v ⊀

u}.

Let V

and V

be two sets closed under non-

domination. We say that V

dominate V

(noted

≺

) if ∀v ∈ V

,∃u ∈ V

s.t u ≺

Theorem 1. Let S a multi-valuation structure. If each

is a fair valuation structure, then so is S.

The result above ensures that the equivalence pre-

serving transformation applied during soft arc consis-

tency operations for mono-objective VCSP can still

be applied for multi-objective VCSP.

Deﬁnition 8. Lower Cost (LC

) Let F

be a subset

of E

, an element c ∈ F

is minimal in F

iff: c 

x,∀x ∈ F

. The set of all minimal elements of F

will

be denoted by LC

The (LC) operator can be applied over cost vectors

as follows:

Deﬁnition 9. Lower Cost Vector (LCV) Let L =

,..., L

} be a set of k-cost vectors, where L

,..., L

). The Lower Cost Vector of L denoted by

LCV(L) is deﬁned as follow:

LCV(L) =



,..., L

),...,LC

,..., L

)



Similarly, we deﬁne the Upper Cost Vector (UCV)

of set of m k-cost vector U = {U

,...,U

} as be-

ing the k-vector UCV(U) corresponding to the upper

value, for each objective j ∈ 1..k, of the j

compo-

nents of U

,...,U

Note that, if k = 1, all previous deﬁnitions reduces

to the classical ones.

4 PARETO-BASED SOFT LOCAL

ARC CONSISTENCY (P-SAC)

The Pareto-based soft local arc consistency, presented

below, has an important role in the efﬁcient resolu-

tion of MO-VCSPs. We propose to extend and adapt

soft arc consistency techniques for MO-VCSPs. P-

SAC, computing a lower bound set of the cost of the

Pareto optimal solutions set, avoids unnecessary ex-

plored branches and accelerates the convergence to

the Pareto front (see Deﬁnition 7).

4.1 Pareto-based Equivalence

Preserving Transformation (P-EPT)

Enforcing local arc consistencies requires applying

equivalence preserving transformations (EPTs) that

shift costs between different scopes. As for mono-

objective case, equivalence preserving transforma-

tion in the multi-objective case is based on three basic

operations (project, extend and project-unary). The

main difference is that the transferred data between

constraints is now a k-ary cost vector.

The main Pareto-based EPT (P-EPT) is deﬁned

below and described in Algorithm 1. This is an exten-

sion of the standard EPT version deﬁned in (Cooper,

2005) for the multi-objective case.

Deﬁnition 10. Two MO-VCSP P = (X , D,C, S), P

) are equivalent if for all complete as-

signment t, we have: V

(t) = V

(t).

Deﬁnition 11. The sub-problem of a MO-VCSP

(X, D,C,S) induced by F ⊆ C is the MO-VCSP(F) =

,F,S ), where X

∈F

σ and D

= {D

i ∈ X

For a MO-VCSPs (X, D,C,S), a Pareto-based

equivalence preserving transformation (P-EPT) on

Pareto-based Soft Arc Consistency for Multi-objective Valued CSPs

299

F ⊆ C is an operation which transforms the multi-

objective sub-problem MO-VCSP(F) into an equiv-

alent MO-VCSP. When F contains at most one k-ary

cost functions Φ

such that |σ| ≥ 2, such a P-EPT is

called a Pareto Soft Arc Consistency (P-SAC) opera-

tion.

The Pareto projection operation is deﬁned as fol-

lows:

Deﬁnition 12. Let α be the Lower Cost Vector of u ∈

with respect to Φ

α = LCV{Φ

(u,v)}

v∈D

The Pareto Projection (P-Project) consists of adding

α to Φ

(u) as follows:

(u) ⊕ α, ∀u ∈ D

and subtracting α from Φ

(u,v) as follows:

(u,v)  α, ∀v ∈ D

, ∀u ∈ D

the inverse operation is Pareto extend operation

deﬁned as follows:

Deﬁnition 13. Let β be a cost k-vector such that β is

the Lower Cost Vector of u ∈ D

with respect to Φ

β = LCV{Φ

(u)}

u∈D

The Pareto Extension (P-Extend) consists of adding β

to Φ

(u,v), as follows:

(u,v) ⊕ β, ∀v ∈ D

and subtracting β from Φ

(u),

(u)  β, ∀u ∈ D

Theorem 2. Given any fair binary MO-VCSP P =

(X, D,C,S), for any Φ

∈ C,x ∈ σ and u ∈ D

, the

application of P-Project or P-Extend on P yields an

equivalent MO-VCSP.

Algorithm 1 gives three basic P-EPT which are

also P-SAC operations (Cooper and Schiex, 2004). P-

Project projects cost vectors from a set of cost func-

tions (on two or more variables) on a set of unary cost

functions. P-Extend performs the inverse operation,

sending cost vectors from a set of unary costs func-

tions to a set of higher arity cost functions. Each cost

vector contains k-ary cost function for each objective

j ∈ {1..k}. Finally P-ProjectUnary projects cost vec-

tors from a set of unary cost functions to the nullary

k-ary cost function Φ

∅

. Observe that Φ

∅

is a k lower

bound vector on the value of any solution. For each of

the P-SAC operations given in Algorithm 1, a precon-

dition is given which guarantees that cost values, for

each objective, remain non-negative after the Pareto-

EPT has been applied.

Algorithm 1: The basic equivalence-preserving transforma-

tions required to establish different forms of soft arc consis-

tency.

Precondition: (α ≺ LCV{Φ

(u,v)}

v∈D

)

1: procedure P-PROJECT(x,u,y, α)

2: Φ

(u) ← Φ

(u) ⊕ α

3: for each v ∈ D

4: Φ

(u,v) ← Φ

(u,v)  α

Precondition: (α ≺ LCV{Φ

(u)}

u∈D

)

5: procedure P-EXTEND(x,u, y,α)

6: for each v ∈ D

7: Φ

(u,v) ← Φ

(u,v) ⊕ α

8: Φ

(u) ← Φ

(u)  α

Precondition: (α ≺ LCV{Φ

(u)}

u∈D

)

9: procedure P-PROJECTUNARY(x,α)

10: for each (u ∈ D

) do

11: Φ

(u) ← Φ

(u)  α

12: Φ

∅

← Φ

∅

⊕ α

Example 3 (MO-VCSP). Consider the problem de-

picted in Figure 3(a). It has two variables x, y

with two values a,b in their domains. Unary multi-

objective costs are depicted within small circles. Bi-

nary multi-objective costs are represented by edges

connecting the corresponding values. The label of

each edges, which is a pair of integers, represents

the corresponding cost for each objective. If two val-

ues are not connected, the binary pair of cost between

them is (0, 0). In this problem, there are two Pareto

optimal solutions. The cost of solution 1 is the pair

(1,300) and it is attained by the assignment (a, a).

The cost of solution 2 is the pair (2, 200) and it is at-

tained by the assignment (a,b).

4.2 P-SAC Techniques

In this section we extend previously-deﬁned notions

of soft arc consistency to deal with the multi-objective

case. To describe our P-SAC, we need to introduce

some new concepts related to the support notion. The

main idea in our extension is to take advantage of the

LCV operator in the deﬁnition of Pareto support.

Deﬁnition 14. (Maximal Subset) Let (hxi, Φ

) be a

unary multi-objective constraint and (hx,yi, Φ

) a bi-

nary multi-objective constraint. We deﬁne a maximal

subset as follows:

• D

is a maximal subset of D

if D

⊆ D

and ∀c

∈

, ∃ j ∈ 1..k; φ

) = ⊥

• D

is a simple maximal subset of D

, for a value

u ∈ D

, if D

⊆ D

and ∀ c

∈ D

, ∃ j ∈ 1..k;

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

300

Figure 3: Three equivalent MO-VCSP instances (> = (4, 400)).

(u,c

) = ⊥

• D

is a full maximal subset of D

, for a value

u ∈ D

, if D

⊆ D

and ∀ c

∈ D

, ∃ j ∈ 1..k;

(u,c

) ⊕ φ

) = ⊥

Deﬁnition 15. Let (hxi,Φ

) be a unary multi-

objective constraint. A subset of values D

⊆ D

a Pareto Support for x if D

⊆ D

is maximal subset

of D

and LCV(D

) = LCV{Φ

(u)}

u∈D

= ⊥. Equiva-

lently,

P S(x)

def

(

a ∈ P S (x), if ∃ j, φ

(a) = ⊥

a /∈ P S (x), ∀ j, φ

(a)  ⊥

We will denote the Pareto Support Set by P S .

The ﬁrst level of Pareto local consistency is Pareto

node consistency. It is deﬁned as follows:

Deﬁnition 16 (Pareto Soft Node Consistency). A

variable x is Pareto soft node consistent (P-NC

∗

) if

each value u ∈ D

satisﬁes Φ

∅

⊕ Φ

(u) ≺ > and

P S(x) 6= ∅. (i.e,. Φ

∅

⊕ LCV{Φ

(u)}

u∈D

= Φ

∅

). A

MO-VCSP is P-NC

∗

iff all variables are P-NC

∗

Pareto soft node consistency can be established by

repeated calls to P-ProjectUnary until convergence.

Example 4. The variable x presented in the

Figure 4-a is not Pareto soft node consistent.

LCV{Φ

(a)}

a∈D

= (1, 2) 6= ⊥ = (0,0). After ap-

plying Pro jectUnary operation, variable x (see

Figure 4-b) become Pareto soft node consistent.

LCV{Φ

(a)}

a∈D

= (0, 0) = ⊥ and P S (x) = {u,v}.

Following (Cooper and Schiex, 2004), Pareto soft

arc consistency is based on the notion of Pareto Sim-

ple Support.

Deﬁnition 17. Let (hx, yi,Φ

) a binary multi-

objective constraint. A subset of values D

⊆ D

a Pareto Simple Support for a value u ∈ D

, if D

is a simple maximal subset of D

and LCV(D

) =

Figure 4: Example of enforcing Pareto Soft NC* property

(⊥ = (0,0), > = (4,400)).

LCV{Φ

(u,v)}

v∈D

= ⊥. We will denote the Pareto

Simple Support Set by P SS .

A Pareto soft arc consistent problem is deﬁned as

follows:

Deﬁnition 18 (Pareto Soft Arc Consistency). A

variable x is Pareto soft arc consistent if for ev-

ery u ∈ D

has a non empty Pareto Simple Sup-

port set (P S S (x(u)) 6=

0), equivalently, Φ

(u) ⊕

LCV{Φ

(u,v)}

v∈D

= Φ

(u).

A MO-VCSP is Pareto Soft arc-consistency (P-

∗

) if all variables are Pareto soft node consistent

and Pareto soft arc-consistent.

Stronger Pareto local arc consistency levels rely

on the notion of Pareto Full Support.

Deﬁnition 19. Let (hx,yi,Φ

) be a binary multi-

objective constraint. A set of values D

⊆ D

is a Pareto Full Support for a value u ∈ D

is full maximal subset of D

and LCV(D

) =

LCV{Φ

(u,v)

(v)}

v∈D

= ⊥. We will denote the

Pareto Full Support set by P F S

Pareto Directional Arc Consistency consists in

combining the binary costs and unary cost in the cal-

culation of the minimum valuation to be projected.

Pareto-based Soft Arc Consistency for Multi-objective Valued CSPs

301

This consistency level requires a total order on the

variables.

Deﬁnition 20 (Pareto Directional Arc Consistency).

A variable x is Pareto directional arc consistent (P-

DAC*) if ∀u ∈ D

, ∀y, y > x, P F S (x(u)) 6=

Equivalently,

(u) ⊕ LCV{Φ

(u,v) ⊕ Φ

(b)}

v∈D

= Φ

(u)

A MO-VCSP is Pareto Soft directional arc-

consistency (P-DAC

∗

) if all variables are P-DAC

∗

and P-NC

∗

Inspired by the work of (de Givry et al., 2005), P-

FDAC

∗

is an improvement of P-AC

∗

and P-DAC

∗

Deﬁnition 21 (Pareto Full Directional Arc-consis-

tency). A MO-VCSP is Pareto FDAC (P-FDAC*)

with respect to an order < on the variables if it is

P-AC∗ and P-DAC∗ with respect to <.

Pareto full supports can be established in two di-

rections if this can produce an increase in the lower

bound set. This is a local natural consistency property,

called Pareto soft existential arc-consistency (P-EAC

∗

inspired by the work of (de Givry et al., 2005)). Pareto

Existential arc consistency (P-EAC) is independent of

a variable order. For each variable x in turn, P-EAC

shifts costs to Φ

if this can lead to an immediate in-

crease in Φ

∅

via P-ProjectUnary.

Deﬁnition 22 (Pareto Soft Existential Arc-consis-

tency). A variable x is Pareto soft existential arc-

consistent (P-EAC

∗

) if P S(x) 6= ∅, and ∀Φ

∈

C, ∃a ∈ D

,P F S ((x,a)) 6= ∅.

A MO-VCSP is Pareto soft existential arc-

consistency (P-EAC

∗

) if all variables are Pareto

soft node consistent and Pareto soft existential arc-

consistent. A MO-VCSP is P-EDAC

∗

if it is P-FDAC

∗

and P-EAC

∗

4.3 Enforcing Pareto Soft Arc

Consistencies

Enforcement of such a Pareto local consistency prop-

erty previously deﬁned requires applying P-EPT. Any

Multi-objective Valued CSP can be transformed into

an equivalent instance having the P-NC

∗

property by

projecting any unary multi-valued constraint towards

the zero-arity multi-objective constraint Φ

∅

and sub-

sequently pruning every unfeasible value.

Enforcing P-NC

∗

is described in Algorithm 2.

Procedure Enforce P-NC

∗

(see Algorithm 2) en-

force Pareto NC

∗

, where ProjectUnary() applies

EPTs that move unary costs towards Φ

∅

while keep-

ing the solution unchanged, and PruneVar() remove

unfeasible values.

Algorithm 2: Enforce P-NC*.

1: procedure ENFORCE P-NC

∗

(X )

2: for each x ∈ X do

3: Pro jectUnary(x)

4: for each x ∈ X do

5: PruneVar(x)

6: procedure PROJECTUNARY((x))

7: α ← LCV

u∈D

(Φ

(u))

8: for each u ∈ D

9: Φ

(u) ← Φ

(u)  α

10: Φ

∅

← Φ

∅

⊕ α

11: procedure PRUNEVAR(x)

12: for each u ∈ D

, s.t.,Φ

(u) ⊕ Φ

∅

≺

{s ∈

NDS} do

13: D

← D

\ {u}

Theorem 3. Given a set of non-dominated solu-

tions NDS found during the exploration of the search

space: The value a ∈ D

deleted by the function

PRUNEVAR may only participate in solutions domi-

nated by some solutions in NDS.

Likely, P-AC

∗

can be enforced by projecting bi-

nary multi-valued constraints towards unary multi-

valued constraints and thereafter enforcing P-NC

∗

Since enforcing P-NC

∗

may prune some domain val-

ues, some variables may have become Pareto soft arc

inconsistent. Therefore, the entire process is repeated

until no changes are performed. Algorithm 3 allows

enforcing various levels of previously deﬁned Pareto-

based soft local arc consistencies.

Property 1. The complexity of P-EDAC

∗

= |NDS| ∗

O(ed

max{nd,max{|E

j=1

}), where n, e, k, E

and

d are the number of variables, the number of con-

straints, the number of objectives, the set of possible

valuations for the objective j and larger domain size

(de Givry et al., 2005).

Property 2. On a problem with a single objective

function (i.e., k=1), the enforcement algorithms of P-

AC*, P-DAC*, P-FDAC* and P-EAC*, are equiva-

lent to classical soft arc consistency algorithms AC*,

DAC*, FDAC* and EAC*.

5 DISCUSSION AND FUTURE

WORKS

Multi-Objective Branch-and-Bound (MO-BB) is a

general search scheme for multi-objective constraint

optimization problems. The search space is repre-

sented as a tree. The algorithm searches in a depth-

ﬁrst manner the tree deﬁned by the problem. Its out-

puts are the set of Non Dominated Solutions (NDS).

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

302

Algorithm 3: Enforcement algorithms of P-AC*, P-DAC*,

P-FDAC*, P-EAC*.

1: procedure ENFORCE P-AC

∗

(x,y)

2: for each u ∈ D

3: α ← LCV{Φ

(u,v)}

v∈D

4: if Φ

(u) ⊕ α 6= Φ

(u) then

5: Pro ject(x,u,y,α)

6: Pro jectUnary(x)

7: PruneVar(x)

8: procedure ENFORCE P-DAC

∗

(x,y)

9: for each u ∈ D

10: P[u] ← LCV{Φ

(u,v) ⊕ Φ

(v)}

v∈D

11: for each v ∈ D

12: Extend(y,u,x, P[u]

Φ

(u,v))

13: Pro ject(x,u,y,P[u])

14: Pro jectUnary(x)

15: PruneVar(x)

16: procedure ENFORCE P-FDAC

∗

(x,y)

17: if x < y then

18: Enforce P-DAC(x,y)

19: Enforce P-AC(y,x)

20: procedure ENFORCE P-EAC

∗

(x)

21:

α ← LCV{Φ

(u)

∈C s.t. y<x

LCV{Φ

(u,v) ⊕ Φ

(v)}

v∈D

}

u∈D

22: if Φ

∅

⊕ α 6= Φ

∅

then

23: Enforce P-FDAC(x,y)

24: procedure ENFORCE P-EDAC

∗

(x,y)

25: if x < y then

26: Enforce P-EAC(x,y)

27: Enforce P-FDAC(x,y)

The efﬁciency of the algorithm greatly depends on its

pruning ability which, in turns, depends on the com-

putation of a good lower bound set at each visited

node.

Algorithms that compute lower bound such as

mini-bucket elimination MBE (Emma and Javier,

2006; Larrosa and Schiex, 2004) or Existential Direc-

tional Arc consistency EDAC* (de Givry et al., 2005)

are a fundamental component of mono-objective

Branch and Bound because they can be executed at

every search node in order to detect infeasible nodes

(Larrosa and Schiex, 2003; de Givry et al., 2005).

The elementary operations made during applying P-

SAC on MO-VCSPs are deleting values, the projec-

tion and extension of costs vector. All these opera-

tions cannot add to the problem of binary constraints

on which the ﬁltering technique P-SAC

∗

is applied.

So the problem remains binary. In addition, generally

the ﬁltering algorithms are incremental. This means,

if a consistency is established in the search tree node

then determining the local consistency in a son node

can be done by considering only the changes between

it and the parent node. This property is very useful

since the ﬁltering is performed at each node of the

search tree. Another key property is that the ﬁltering

technique P-SAC

∗

computes a lower bound set for

the cost of the optimal solution. For the resolution of

MO-VCSP, Pareto SAC

∗

can be used to obtain good

quality lower bounds set (LB) or it can be integrated

into multi-objective branch and bound in order to in-

crease its pruning efﬁciency to generate the set of all

non-dominated solutions.

In practice, this set of solutions can be important

(risk of memory explosion) and it is going to slow

down Pareto-NC

∗

. In order to reduce this set we can

calculate a lower bound and/or an upper bound for

every objective on the set of non-dominated solutions

then, we compare to an under/over-approximation of

several solutions at once.

Alternatively, we can proceed for a decomposi-

tion scheme of an initial problem in order to solve

small instances of MO-VCSP. As a ﬁrst step, we want

to identify some new tractable classes of MO-VCSP.

Where, we can solve instances of MO-VCSP in poly-

nomial time with MO-BnB+P-SAC by restrictions of

objectives functions to be in a speciﬁc class C (such

as; modular objective functions (Helaoui and Naanaa,

2013), sub-modular objective functions (Helaoui and

Naanaa, 2012) or even Directional Substitutable Val-

uation Functions (Naanaa, 2008)). As a natural exten-

sion of this work, we will propose a problem decom-

position scheme for MO-VCSPs that takes advantage

of restricted objective Functions even when the stud-

ied problem is not limited to these Functions. This

decomposition scheme can work within a backtrack-

based search and consists in decomposing the orig-

inal problem into a set of

|NDS|

i=1

∈ C , and then

tractable sub-problems. This decomposition scheme

can be distinguished by the possibility of instantiat-

ing variables by assigning to them subsets of values

instead of single values for the

|NDS|

i=1

, where each

one is in C . On a more practical side, we plan to im-

plement our algorithms and to integrate them into an

existing VCSP solver.

6 CONCLUSION

The Valued Constraint Satisfaction Problem (VCSP)

is a generic optimization problem consisting in a net-

work of local cost functions deﬁned over discrete

variables. It has applications in Artiﬁcial Intelli-

Pareto-based Soft Arc Consistency for Multi-objective Valued CSPs

303

gence, Operations Research, Bio-informatics and has

been used to tackle optimization problems in other

graphical models (including discrete Markov Random

Fields and Bayesian Networks).

In this paper, we introduce a Multi-Objective

VCSP (MO-VCSP), that is a VCSP involving mul-

tiple objectives. We propose a new extension of lo-

cal arc consistency to the MO-VCSP. The incremental

lower bounds set produced by Pareto-based soft local

arc consistency can be used for pruning inside Branch

and Bound search. The latter algorithm enables the

calculation of the set of all Pareto Optimal (PO) so-

lutions, an algorithm that enforces a Pareto soft local

arc consistency property takes into account the Pareto

principle by updating the set of Non-Dominated So-

lutions during a Branch and Bound search.

REFERENCES

Afruzi, E. N., Roghanian, E., Najaﬁ, A., and Mazinani, M.

(2013). A multi-mode resource-constrained discrete

time–cost tradeoff problem solving using an adjusted

fuzzy dominance genetic algorithm. Scientia Iranica,

20(3):931 – 944.

Allouche, D., Bessiere, C., Boizumault, P., de Givry, S.,

Gutierrez, P., Lee, J. H., Leung, K. L., Loudni,

S., M

etivier, J.-P., Schiex, T., and Wu, Y. (2016).

Tractability-preserving transformations of global cost

functions. Artif. Intell., 238(C):166–189.

Bistarelli, S., Gadducci, F., Larrosa, J., and Rollon, E.

(2008). A soft approach to multi-objective optimiza-

tion. In Proceedings of the 24th International Confer-

ence on Logic Programming, ICLP ’08, pages 764–

768, Berlin, Heidelberg. Springer-Verlag.

Bistarelli, S., Gadducci, F., Larrosa, J., Rollon, E.,

and Santini, F. (2012). Local arc consistency

for non-invertible semirings, with an application to

multi-objective optimization. Expert Syst. Appl.,

39(2):1708–1717.

Bistarelli, S., Montanari, U., Rossi, F., Schiex, T., Verfail-

lie, G., and Fargier, H. (1999). Semiring-based csps

and valued csps: Frameworks, properties, and com-

parison. Constraints, 4(3):199–240.

Chiandussi, G., Codegone, M., Ferrero, S., and Varesio, F.

(2012). Comparison of multi-objective optimization

methodologies for engineering applications. Comput-

ers and Mathematics with Applications, 63(5):912 –

942.

Cohen, D., Jeavons, P., and Zivny, S. (2008). The expres-

sive power of valued constraints: Hierarchies and col-

lapses. Theoretical Computer Science TCS, 409:137–

153.

Cooper, M., De Givry, S., Sanchez, M., Schiex, T., and Zyt-

nicki, M. (2008). Virtual arc consistency for weighted

csp. In Proceedings of the 23rd National Conference

on Artiﬁcial Intelligence - Volume 1, AAAI’08, pages

253–258. AAAI Press.

Cooper, M., de Givry, S., Sanchez, M., Schiex, T., Zytnicki,

M., and Werner, T. (2010). Soft arc consistency revis-

ited. Artiﬁcial Intelligence, 174(7):449 – 478.

Cooper, M. and Schiex, T. (2004). Arc consistency for soft

constraints. Artif. Intell., 154(1-2):199–227.

Cooper, M. C. (2005). High-order consistency in valued

constraint satisfaction. Constraints, 10(3):283–305.

de Givry, S., Zytnicki, M., Heras, F., and Larrosa, J. (2005).

Existential arc consistency: Getting closer to full arc

consistency in weighted csps. In Proceedings of the

19th International Joint Conference on Artiﬁcial Intel-

ligence, IJCAI’05, pages 84–89, San Francisco, CA,

USA. Morgan Kaufmann Publishers Inc.

Deb, K. and Kalyanmoy, D. (2001). Multi-Objective Opti-

mization Using Evolutionary Algorithms. John Wiley

& Sons, Inc., New York, NY, USA.

Emma, R. and Javier, L. (2006). Bucket elimination for

multiobjective optimization problems. J. Heuristics.

Hazır, O., Haouari, M., and Erel, E. (2010). Robust schedul-

ing and robustness measures for the discrete time/cost

trade-off problem. European Journal of Operational

Research, 207(2):633 – 643.

Helaoui, M. and Naanaa, W. (2012). A submodular-

based decomposition strategy for valued csps. The

Sixth ”Starting Artiﬁcial Intelligence Research” Sym-

posium. Montpellier, France.

Helaoui, M. and Naanaa, W. (2013). Modularity-based de-

compositions for valued csp. Annals of Mathematics

and Artiﬁcial Intelligence.

Jeavons, P. G. and Cooper, M. C. (1995). Tractable con-

straints on ordered domains. Artiﬁcial Intelligence,

79(2):327 – 339.

Larrosa, J. (2002). Node and arc consistency in weighted

csp. In Eighteenth National Conference on Artiﬁ-

cial Intelligence, pages 48–53, Menlo Park, CA, USA.

American Association for Artiﬁcial Intelligence.

Larrosa, J. and Schiex, T. (2003). In the quest of the best

form of local consistency for weighted CSP. In IJCAI-

03, Proceedings of the Eighteenth International Joint

Conference on Artiﬁcial Intelligence, Acapulco, Mex-

ico, August 9-15, 2003, pages 239–244.

Larrosa, J. and Schiex, T. (2004). Solving weighted CSP by

maintaining arc consistency. Artif. Intell., 159(1-2):1–

26.

Le Thi, H. A., Bouvry, P., and Pham Dinh, T., editors

(2008). Solving the Multiple Objective Integer Linear

Programming Problem, Berlin, Heidelberg. Springer

Berlin Heidelberg.

Lee, J. and Leung, K. (2012). Consistency techniques

for ﬂow-based projection-safe global cost functions in

weighted constraint satisfaction. J. Artif. Intell. Res.

(JAIR), 43:257–292.

Naanaa, W. (2008). Substitutability based domain decom-

position for constraint satisfaction. CP.

Schiex, T., Fargier, H., and Verfaillie, G. (1995). Valued

constraint satisfaction problems: Hard and easy prob-

lems. In Proceedings of the 14th International Joint

Conference on Artiﬁcial Intelligence - Volume 1, IJ-

CAI’95, pages 631–637, San Francisco, CA, USA.

Morgan Kaufmann Publishers Inc.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

304

Teghem, J. (2009). Multi-objective integer linear program-

ming. Springer US, Boston, MA.

van Beek, P. and Manchak, D. W. (1996). The design and

experimental analysis of algorithms for temporal rea-

soning. J. Artif. Intell. Res., 4:1–18.

Vanhoucke, M. and Debels, D. (2007). The discrete

time/cost trade-off problem: extensions and heuristic

procedures. Journal of Scheduling, 10(4):311–326.

Wilson, N., Razak, A., and Marinescu, R. (2015). Com-

puting possibly optimal solutions for multi-objective

constraint optimisation with tradeoffs. In Proceedings

of the 24th International Conference on Artiﬁcial In-

telligence, IJCAI’15, pages 815–821. AAAI Press.

APPENDIX

Proof of Theorem 1

Proof. We have for all j ∈ 1..k, S

is fair then for any

valuation pair α,β ∈ E

, if α 

β, there is a max-

imum difference between β and α, denoted β 

α.

For each pair of multi-valuation u, v ∈ Π

j=1

, if

∀ j, u



which implies by deﬁnition that u ≺

(u dominates v), there is a maximum difference be-

tween v and u which is equal to (u



,..., u



). Where k denotes the number of objectives.

Proof of Theorem 2

Proof. Following (Cooper and Schiex, 2004), and un-

der assumption that every valuation structure S

fair, to demonstrate equivalence, it is sufﬁcient to

prove that the cost vector Φ

(u,v) ⊕ Φ

(u) is an in-

variant of P-Project(x,u,y,α) and P-Extend(y,u, x,α).

For any v ∈ D

, let γ be the initial k-cost value of

(u,v) and δ the initial k-cost value of Φ

(u). Af-

ter the execution of P-Project , we have Φ

(a,b) ⊕

(a) = (γ  α) ⊕ (δ ⊕ α) = γ ⊕ δ. After the ex-

ecution of P-Extend, we have Φ

(a,b) ⊕ Φ

(a) =

(γ ⊕ α) ⊕ (δ  α) = γ ⊕ δ. This proves the invari-

ance.

Proof of Theorem 3

Proof. Given a set of non-dominated solutions NDS

found during the exploration of the search space:

Denote by SP

u∈D

the set of solutions of a MO-

VCSP to which a value u ∈ D

may participate.

The function PRUNEVAR

∗

deletes a value u ∈ D

if and only if for each objective i it ∃ a non dominated

solution s ∈ NDS such that Φ

(u) ⊕ Φ

∅

= >

Since s ∈ NDS then >

is an element of the solu-

tion s ∈ NDS, so if Φ

(u) ⊕ Φ

∅

= >

(element of the

solution s ∈ NDS) then unary cost of the value u ∈ D

denoted by Φ

(u) combined with the total of the min-

imum unary costs of other variables denoted by Φ

∅

is dominated by at least one solution s ∈ NDS:

for each objective j ∃ s ∈ NDS such that

v∈(y∈s)

(v)  φ

(u) ⊕

∅

⇒ ∃ s ∈ NDS ≺

(u) ⊕ Φ

∅

Secondly, any solution where u ∈ D

denoted by s

∈

u∈D

is dominated by unary cost of value u ∈ D

(u) combined with the total of the minimum unary

costs of other variables denoted by Φ

∅

(u) ⊕ Φ

∅

≺

∀ s

∈ SP

u∈D

And since the unary cost combined with the unary

total minimum cost of the other variables is domi-

nated by a solution s ∈ NDS we have:

∃ s ∈ NDS ≺

(u) ⊕ Φ

∅

∧

(u) ⊕ Φ

∅

≺

∀ s

∈ SP

u∈D

We can therefore conclude, as there is a partial or-

der between dominated solution.

∃ s ∈ NDS ≺

∀ s

∈ SP

u∈D

And thereafter the value u ∈ D

may only partici-

pate in solutions dominated by at least one of the so-

lutions s ∈ NDS.

Pareto-based Soft Arc Consistency for Multi-objective Valued CSPs

305