
Using Synchronizing Heuristics to Construct Homing Sequences
Berk Çiri¸sci
1
, M. Yu¸sa Emek
1
, Ege Sorguç
2
, Kamer Kaya
1
and Husnu Yenigun
1
1
Computer Science and Engineering, Sabanci University, Istanbul, Turkey
2
Computer Engineering, Middle East Technical University, Ankara, Turkey
Keywords:
Finite State Machines, Homing Sequences, Synchronizing Sequences.
Abstract:
Computing a shortest synchronizing sequence of an automaton is an NP-Hard problem. There are well-known
heuristics to find short synchronizing sequences. Finding a shortest homing sequence is also an NP-Hard prob-
lem. Unlike existing heuristics to find synchronizing sequences, homing heuristics are not widely studied. In
this paper, we discover a relation between synchronizing and homing sequences by creating an automaton
called homing automaton. By applying synchronizing heuristics on this automaton we get short homing se-
quences. Furthermore, we adapt some of the synchronizing heuristics to construct homing sequences.
1 INTRODUCTION
In model based testing (Broy et al., 2005) and in par-
ticular, for finite state machine based testing (Lee and
Yannakakis, 1996), test sequences are designed to be
applied at a designated state. For the test sequence
to be applied, the implementation under test must be
brought to this particular state, which is accomplished
by using a final state recognition sequence, such as a
synchronizing sequence or a homing sequence (Ko-
havi, 1978; Lee and Yannakakis, 1996).
A synchronizing sequence is an input sequence
such that when this input sequence is applied, the sys-
tem moves to a particular state, regardless of the ini-
tial state of the system. On the other hand, a hom-
ing sequence is an input sequence such that when this
sequence is applied to the system, the response ob-
served from the system makes it possible to identify
the final state reached. Note that, using homing se-
quences requires one to observe the reaction of the
system under test to the sequence applied. However
when a synchronizing sequence is used, no such ob-
servation is required. Therefore, one may prefer to
use a synchronizing sequence for final state identifi-
cation. Unfortunately, a synchronizing sequence may
not exist for a finite state machine, whereas a homing
sequence always exists for a minimal, deterministic,
and completely specified FSMs (Kohavi, 1978; Broy
et al., 2005; Lee and Yannakakis, 1996).
Whether one uses a synchronizing sequence or a
homing sequence, it is obviously preferable to use
a sequence as short as possible. Unfortunately, the
problem of finding a shortest synchronizing sequence
and finding a shortest homing sequence is known to
be NP–hard (Eppstein, 1990; Broy et al., 2005).
There exist heuristic algorithms, known as syn-
chronizing heuristics, for constructing short syn-
chronizing sequences. Among such heuristics are
Greedy (Eppstein, 1990), Cycle (Trahtman, 2004),
SynchroP (Roman, 2009), SynchroPL(Roman, 2009),
FastSynchro (Kudlacik et al., 2012), and forward
and backward synchronization heuristics (Roman and
Szykula, 2015).
Although synchronizing heuristics are widely
studied in the literature, to the best of our knowledge,
there does not exist many (if not any) heuristic algo-
rithm to construct short homing sequences, apart from
a variant of the algorithm given as Fast–HS in Sec-
tion 5 (see e.g. (Broy et al., 2005)), which originally
appeared in (Ginsburg, 1958; Moore, 1956).
In this paper, we suggest several homing heuristics
to construct short homing sequences. We first define
an automaton called a homing automaton (see e.g.
Figure 3) of a given finite state machine (see e.g. Fig-
ure 2). We show that a synchronizing sequence of the
homing automaton is a homing sequence of the given
finite state machine (for example, aa is a homing se-
quence for the finite state machine in Figure 2 and it
is also a synchronizing sequence for the automaton in
Figure 3.
This allows us to use the existing synchronizing
heuristics as heuristic algorithms to construct short
homing sequences for the given finite state machine.
We then show how the existing synchronizing heuris-
362
Çiri¸sci, B., Emek, M., Sorguç, E., Kaya, K. and Yenigun, H.
Using Synchronizing Heuristics to Construct Homing Sequences.
DOI: 10.5220/0007403503620369
In Proceedings of the 7th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2019), pages 362-369
ISBN: 978-989-758-358-2
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
tics can be modified to work directly on the given
finite state machine to construct homing sequences.
We present an experimental study to assess the per-
formance of these approaches as well.
In (Güniçen et al., 2014), a similar relation was
studied between distinguishing sequences of a finite
state machine and the synchronizing sequences of an
automaton derived from the given finite state ma-
chines. Our work has been inspired from (Güniçen
et al., 2014). However, we define the automaton from
the given finite state machine differently compared
to (Güniçen et al., 2014), so that the synchronizing
sequences of the automaton corresponds to the hom-
ing sequences (not to the distingushing sequences) of
the given finite state machine. In addition, we suggest
modifications of the existing synchronizing heuristics
that allows us to use these heuristics directly on the
finite state machine.
A similar work also appeared in (Kushik and
Yevtushenko, 2015). However, (Kushik and Yev-
tushenko, 2015) considers nondeterministic finite
state machines, whereas in our work we consider de-
terministic finite state machines. When the approach
is considered as restricted to the deterministic case,
it becomes possible to use efficient synchronizing
heuristics developed for deterministic automata for
computing homing sequences.
The rest of the paper is organized as follows. Sec-
tion 2 introduces the notation and gives the back-
ground. Section 3 shows how we form the relation
between the synchronizing sequences and the homing
sequences. We introduce two synchronizing heuris-
tics existing in the literature that one can use to derive
homing sequences in Section 4. We then show in Sec-
tion 5 how the synchronizing heuristics introduced in
Section 4 can be modified to be applied on the finite
state machines directly. The experimental study that
we have performed together with concluding remarks
are given in Section 6.
2 PRELIMINARIES
A Deterministic Finite Automaton (DFA) (or simply
an automaton) is a triple A = (S,X,δ) where S is a
finite set of states, X is a finite set of alphabet (or
input) symbols, and δ : S ×X → S is a transition func-
tion. When δ is a total (resp. partial) function, A is
called complete (resp. partial). In this work we only
consider complete DFAs unless stated otherwise.
A Deterministic Finite State Machine (FSM) is
a tuple M = (S,X,Y,δ,λ) where S is a finite set of
states, X is a finite set of alphabet (or input) symbols,
Y is a finite set of output symbols, δ : S × X → S is
0
1
2
b
b
a
b
a
a
Figure 1: An automaton A
0
.
0
1
2
b/1
b/0
a/0
b/1
a/1
a/0
Figure 2: An FSM M
0
.
a transition function, and λ : S × X → Y is an output
function. In this work, we always consider complete
FSMs, which means the functions δ and λ are total
functions.
An automaton and an FSM can be visualized as a
graph, where the states correspond to the nodes and
the transitions correspond to the edges of the graph.
For an automaton the edges of the graph are labeled
by input symbols, whereas for an FSM the edges are
labeled by an input and an output symbol. In Figure 1
and Figure 2, an example automaton and an example
FSM are given.
An input sequence ¯x ∈ X
is a concatenation of
zero or more input symbols. More formally, an input
sequence ¯x is a sequence of input symbols x
1
x
2
...x
k
for some k ≥ 0 where x
1
,x
2
,...,x
k
∈ Σ. As can be
seen from the definition, an input sequence may have
no symbols; in this case it is called the empty se-
quence and denoted by ε.
For both automata and FSMs, the transition func-
tion δ is extended to input sequences as follows.
For a state s ∈ S, an input sequence ¯x ∈ X
and an
input symbol x ∈ X, we let
¯
δ(s,ε) = s,
¯
δ(s,x ¯x) =
¯
δ(δ(s,x), ¯x). Similarly, the output function of FSMs
is extended to input sequences as follows:
¯
λ(s,ε) = ε,
¯
λ(s,x ¯x) = λ(s,x)
¯
λ(δ(s,x), ¯x). By abusing the notation
we will continue using the symbols δ and λ for
¯
δ and
Using Synchronizing Heuristics to Construct Homing Sequences
363

¯
λ, respectively.
Finally for both automata and FSMs, the transition
function δ is extended to a set of states as follows. For
a set of states S
0
⊆ S and an input sequence ¯x ∈ X
,
δ(S
0
, ¯x) = {δ(s, ¯x) | s ∈ S
0
}.
An FSM M = (S,X,Y,δ,λ) is said to be minimal
if for any two different states s
i
,s
j
∈ S, there exists an
input sequence ¯x ∈ Σ
such that λ(s
i
, ¯x) 6= λ(s
j
, ¯x).
Definition 1. For an FSM M = (S, X,Y,δ,λ), a
Homing Sequence (HS) of M is an input sequence
¯
H ∈ X
such that for all states s
i
,s
j
∈ S, λ(s
i
,
¯
H) =
λ(s
j
,
¯
H) =⇒ δ(s
i
,
¯
H) = δ(s
j
,
¯
H).
Intuitively, an HS
¯
H is an input sequence such that
for all states output sequence to
¯
H uniquely identifies
the final state. In other words, if the current state of
an FSM is not known, then a homing sequence can
be applied to the FSM and the output sequence pro-
duced by the FSM will tell us the final state reached.
A homing sequence is also called a homing word in
the literature.
For FSM M
0
given in Figure 2 aa is an HS. If M is
minimal, then there certainly exists an HS for M (Ko-
havi, 1978). If M is not minimal, there may also be
an HS for M. Furthermore, when M is not minimal, it
is always possible to find an equivalent minimal FSM
M
0
such that M
0
is minimal (Kohavi, 1978).
Definition 2. For an automaton A = (S,X,δ), a Syn-
chronizing Sequence (SS) of A is an input sequence
¯
R ∈ X
such that |δ(S,
¯
R)| = 1.
A synchronizing sequence is also called a reset se-
quence in the literature. An automaton does not nec-
essarily have an SS. It is known that the existence of
an SS for an automaton can be checked in polynomial
time (Eppstein, 1990).
For a set of states C ⊆ S we use the notation C
2
=
{{s
i
,s
j
}|s
i
,s
j
∈ C} to denote the set of multisets with
cardinality 2 with elements from C, i.e C
2
is the set
of all subsets of C with cardinality 2, where repetition
is allowed. An element {s
i
,s
j
} ∈ C
2
is called a pair.
Furthermore it is called a singleton pair (or an s–pair)
if s
i
= s
j
, otherwise it is called a different pair (or a d–
pair). The set of s–pairs and d–pairs in C
2
is denoted
by C
2
s
and C
2
d
respectively. A sequence (word) w is
said to be a merging sequence for a pair {s
i
,s
j
} ∈ S
2
if δ({s
i
,s
j
},w) is a singleton. Note that for an s–pair,
every sequence (including ε) is a merging sequence.
3 THE RELATION BETWEEN
HOMING SEQUENCES AND
SYNCHRONIZING SEQUENCES
In this section, we will derive an automaton A
M
from
a given FSM M. We call A
M
the the homing automa-
ton of M. The construction of A
M
from M is similar
to the construction of product automaton (as exists in
the literature) from a given automaton to analyse the
existence of and to find synchronizing sequences.
Definition 3. Let M = (S, X ,Y,δ,λ) be an FSM. The
homing automaton (HA) A
M
of M is an automaton
A
M
= (S
A
,X,δ
A
) which is constructed as follows:
- The set S
A
consists of all 2-element subsets
of S and an extra state q
. Formally we have
S
A
= {{s
i
,s
j
} | s
i
,s
j
∈ S ∧ s
i
6= s
j
} ∪ {q
}.
- The transition function δ
A
is defined as follows:
• For an input symbol x ∈ X, δ
A
(q
,x) = q
.
• For q = {s
i
,s
j
} ∈ S
A
and an input symbol x ∈ X,
– If δ(s
i
,x) = δ(s
j
,x)), then δ
A
(q,x) = q
.
– If λ(s
i
,x) 6= λ(s
j
,x)), then δ
A
(q,x) = q
.
– Otherwise, δ
A
(q,x) = {δ(s
i
,x),δ(s
j
,x)}.
As an example, the HA for FSM M
0
given in Fig-
ure 2 is depicted in Figure 3.
Lemma 1. Let M = (S,X,Y, δ, λ) be an FSM, A
M
=
(S
A
,X,δ
A
) be the HA of M. For an input sequence
¯x ∈ X
, (λ(s
i
, ¯x) 6= λ(s
j
, ¯x))∨(δ(s
i
, ¯x) = δ(s
j
, ¯x)) ⇐⇒
δ
A
({s
i
,s
j
}, ¯x) = q
.
Proof. Let ¯x = ¯x
0
x ¯x
00
where ¯x
0
, ¯x
00
∈ X
and x ∈
X such that (δ(s
i
, ¯x
0
) 6= δ(s
j
, ¯x
0
)) ∧ (λ(s
i
, ¯x
0
) =
λ(s
j
, ¯x
0
)). So the new state according to δ
A
is
q
0
= {δ(s
i
, ¯x
0
),δ(s
j
, ¯x
0
)}. If λ(s
i
, ¯x
0
x) 6= λ(s
j
, ¯x
0
x) then
δ
A
(q
0
,x) = q
and δ
A
(q
, ¯x
00
) = q
. If λ(s
i
, ¯x
0
x) =
λ(s
j
, ¯x
0
x) but δ(s
i
, ¯x
0
x) = δ(s
j
, ¯x
0
x) then δ
A
(q
0
,x) = q
and δ
A
(q
, ¯x
00
) = q
.
For the reverse direction, again writing ¯x = ¯x
0
x ¯x
00
where ¯x
0
, ¯x
00
∈ X
and x ∈ X such that δ
A
({s
i
,s
j
}, ¯x
0
) =
{s
0
i
,s
0
j
} for some states s
0
i
,s
0
j
and δ
A
({s
i
,s
j
}, ¯x
0
x) = q
.
This means that λ(s
i
, ¯x
0
) = λ(s
j
, ¯x
0
) and δ(s
i
, ¯x
0
) 6=
δ(s
j
, ¯x
0
) but after consuming input x, λ(s
i
, ¯x
0
x) 6=
λ(s
j
, ¯x
0
x) where x is the first input which forces FSM
to produce different outputs. Or δ(s
i
, ¯x
0
x) = δ(s
j
, ¯x
0
x),
in this case x is the merging input. This proves that
(λ(s
i
, ¯x) 6= λ(s
j
, ¯x)) ∨ (δ(s
i
, ¯x) = δ(s
j
, ¯x)).
We can now give the following theorem that states
the relation between HSs of M and SSs of A
M
.
Theorem 1. Let M = (S,X,Y,δ,λ) be an FSM and
A
M
= (S
A
,X,δ
A
) be the HA of M. An input sequence
¯x ∈ X
is an HS for M iff ¯x is an SS for A
M
.
MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development
364
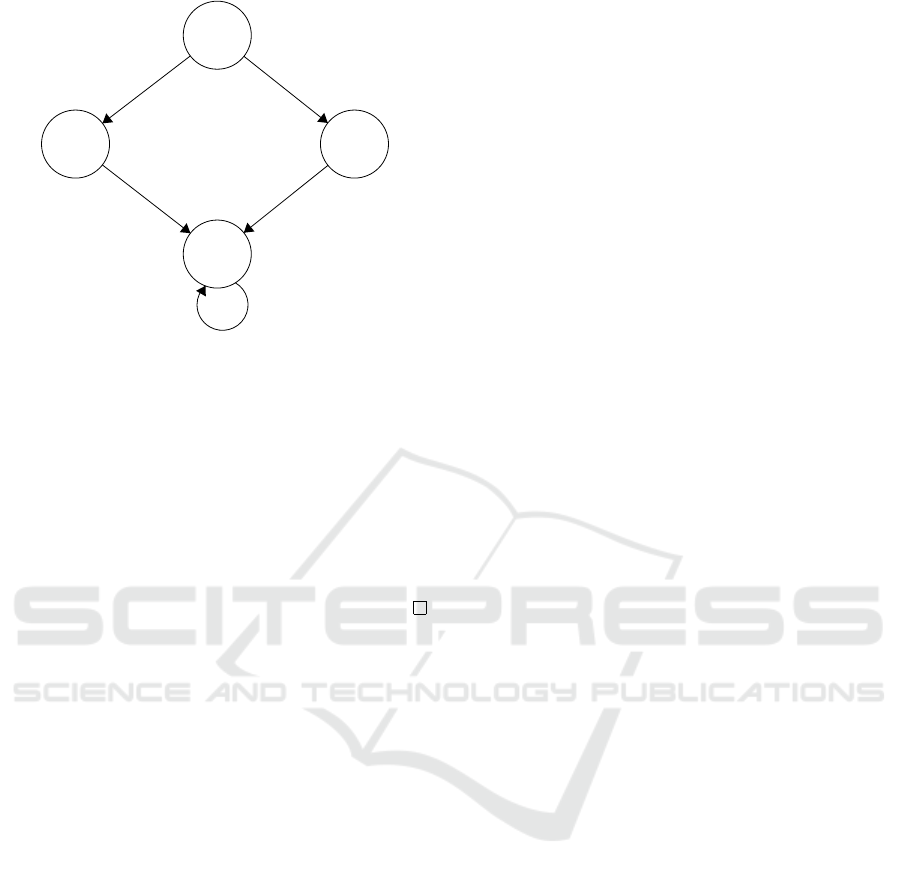
{0,1}
{0,2} {1,2}
q
b
a
a,b
a,b
a,b
Figure 3: A
M
of M
0
in Figure 2.
Proof. If ¯x is an HS of M, for any two states s
i
and s
j
in M, λ(s
i
, ¯x) 6= λ(s
j
, ¯x) or δ(s
i
, ¯x) = δ(s
j
, ¯x). Lemma
1 states that δ
A
({s
i
,s
j
}, ¯x) = q
for any {s
i
,s
j
} ∈ S
A
.
For q
, δ
A
(q
, ¯x) = q
. Hence ¯x is an SS for A
M
.
If ¯x is an SS for A
M
, first note that δ
A
(q
, ¯x) = q
.
For any state of A
M
of the form {s
i
,s
j
}, we must also
have δ
A
({s
i
,s
j
}, ¯x) = q
. From the other direction of
Lemma 1, we have for any pair of states λ(s
i
, ¯x) 6=
λ(s
j
, ¯x) or δ(s
i
, ¯x) = δ(s
j
, ¯x).
For example, consider the Homing Automaton A
M
given in Figure 3 of the FSM M
0
given in Figure 2.
One can see that aa is an HS for M
0
and it is also an
SS for A
M
.
4 SYNCHRONIZING
HEURISTICS FOR HOMING
AUTOMATON
Although finding a shortest SS is known to be an NP-
Hard problem, finding a short SS by applying heuris-
tics is studied widely. As shown in Theorem 1, find-
ing an HS for an FSM M is equivalent to finding an SS
for its corresponding homing automaton A
M
. Based
on Theorem 1, we can apply widely known SS heuris-
tics to A
M
in order to find a possibly short HS for FSM
M. Please recall that an SS may not exist for an au-
tomaton in general. However, for a homing automa-
ton of a minimal FSM, an SS will always exist due to
Theorem 1.
Among such SS heuristics, Greedy is one of the
fastest and the earliest that appeared in the litera-
ture (Eppstein, 1990). Other than Greedy heuristic,
SynchroP is one of the best known heuristics in terms
of finding short SSs (Roman, 2005). Although, Syn-
chroP is good in terms of length, it is slow compared
to Greedy since it performs a deeper analysis on the
automaton.
Both Greedy and SynchroP heuristics have two
phases. Phase 1 is common in these heuristics. The
purpose of Phase 1 is to compute a shortest merging
word τ
{i, j}
for each {s
i
,s
j
} ∈ S
2
. This computation
is performed by using a backward breadth first search
(see e.g. Figure 4 in (Cirisci et al., 2018)), rooted at
s-pairs {s
i
,s
i
} ∈ S
s
2
, where these s-pair nodes are the
nodes at level 0 of the BFS forest. A d-pair {s
i
,s
j
} ap-
pears at level k of the BFS forest if |τ
{i, j}
| = k. When
the automaton has a synchronizing sequence, each d-
pair should have a merging word since it is a nec-
essary condition for synchronizing automata (Epp-
stein, 1990). Phase 1 requires Ω(n
2
) time since each
{s
i
,s
j
} ∈ S
2
is considered exactly once.
Even though Phase 2 of Greedy and Phase 2 of
SynchroP (e.g. see Figure 5 and Figure 6 in (Cirisci
et al., 2018)) are different, they are quite similar. For
both algorithms, Phase 2 keeps track of a set of ac-
tive states C and iteratively reduces the cardinality of
C. In each iteration, a d-pair {s
i
,s
j
} ∈ C
2
d
in the ac-
tive states is selected to be merged. After selecting
{s
i
,s
j
}, the current (active) state set C is updated by
applying τ
{i, j}
, i.e. C is updated as δ(C, τ
{i, j}
). Ap-
plying τ
{i, j}
will definitely merge {s
i
,s
j
}, and it may
merge some more states in C as well. This process
will iterate until all states are merged so that C be-
comes singleton.
Phase 2 of Greedy and Phase 2 of SynchroP only
differ in the way they select the d-pair {s
i
,s
j
} ∈ C
2
d
to be used in an iteration. While Greedy simply con-
siders a d-pair {s
i
,s
j
} ∈ C
2
d
having a shortest merg-
ing word τ
{i, j}
, SynchroP selects a d-pair {s
i
,s
j
} ∈ C
2
d
such that ϕ(δ(C,τ
{i, j}
)) is minimized, where ϕ(S
0
) for
a set of states S
0
⊆ S is defined as:
ϕ(S
0
) =
∑
s
i
,s
j
∈S
0
|τ
{i, j}
|
ϕ(S
0
) is a heuristic indication of how hard is to
bring set S
0
to a singleton. The intuition here is that,
the larger the cost ϕ(S
0
) is, the longer a synchroniz-
ing sequence would be required to bring S
0
to a sin-
gleton set. For an automaton with p input symbols
and n states, the common first phase of Greedy and
SynchroP needs O(pn
2
) time (Eppstein, 1990). The
second phase of Greedy can be implemented to run
in O(n
3
) time (Eppstein, 1990), whereas the second
phase of SynchroP runs in O(n
5
) time (Roman, 2005).
Therefore, the overall time complexity for Greedy is
O(pn
2
+ n
3
) and for SynchroP it is O(pn
2
+ n
5
).
As suggested by Theorem 1, in order to construct
a homing sequence for an FSM M, one can first con-
Using Synchronizing Heuristics to Construct Homing Sequences
365

struct the homing automaton A
M
of M, and then use
Greedy or SynchroP heuristics to find a synchronizing
sequence for A
M
, which will be a homing sequence
for M. Constructing the homing automaton A
M
of
M = (S,X,Y, δ, λ) would require O(pn
2
) time where
p = |X| and n = |S|. Note that the number of states of
A
M
is 1 +n(n−1)/2, and A
M
still has p input symbols
(see Definition 3). Therefore, applying Greedy to A
M
requires O(pn
4
+ n
6
) time, and applying SynchroP to
A
M
requires O(pn
4
+ n
10
). These complexities would
allow one to use synchronizing heuristics on homing
automaton only for FSMs with small number of states
in practice.
In the next section, we consider adapt-
ing/modifying the synchronizing heuristics to
construct a homing sequence directly from the FSM,
without constructing a homing automaton.
5 ADAPTING SYNCHRONIZING
HEURISTICS FOR HOMING
SEQUENCE CONSTRUCTION
The high computational complexity of applying syn-
chronizing heuristics on homing automata results
from the fact that, the homing automata already have
the number of states squared compared to the number
of states of the corresponding FSM. In this section,
we present heuristic algorithms that work directly on
the FSM.
Inspired by the synchronizing heuristics that are
given in Section 4, we implemented three differ-
ent homing heuristics, Fast–HS, Greedy–HS and
SynchroP–HS, for constructing a homing sequence of
an FSM. These homing heuristics consist of two sepa-
rate phases, as in the case of synchronizing heuristics.
Phase 1 is common in all these heuristics and
given as Algorithm 4. In Phase 1, a shortest homing
word τ
{i, j}
for each {s
i
,s
j
} ∈ S
2
is computed by using
a breadth first search. Generation of the BFS forest is
very similar to what is done in synchronizing heuris-
tics, except that a d-pair {s
i
,s
j
} that gives different
outputs for its states, i.e. when λ(s
i
,x) 6= λ(s
j
,x) for
an input symbol x ∈ Σ, is located at level 1 of the for-
est by setting τ
{i, j}
= x.
Similar to the synchronizing heuristics, Phase 2
of homing heuristics iteratively builds a homing se-
quence. In each iteration, again a pair {s
i
,s
j
} is
picked (how this pair is picked depends on the heuris-
tic used), and the corresponding homing word τ
{i, j}
is
appended to the homing sequence Γ accumulated so
far. However, instead of tracking the set of states yet
to be merged, the set D of state pairs yet to be homed
Algorithm 1: Phase 1 of Homing Heuristics.
Input : An FSM M = (S,Σ,O,δ,λ)
Output : A homing word for all {s
i
,s
j
} ∈ S
2
1: Q ← an empty queue Q: BFS frontier
2: P ←
/
0 P: nodes of BFS forest constructed
3: for {s
i
,s
i
} ∈ S
2
s
do
4: push {s
i
,s
i
} onto Q
5: insert {s
i
,s
i
} into P
6: set τ
{i,i}
← ε
7: end for
8: for ({s
i
,s
j
} ∈ S
2
) ∧ ({s
i
,s
j
} 6∈ P) do
9: for x ∈ Σ do
10: if λ(s
i
,x) 6= λ(s
j
,x) then
11: push {s
i
,s
j
} onto Q
12: insert {s
i
,s
j
} into P
13: set τ
{i, j}
← x
14: end if
15: end for
16: end for
17: while P 6= S
2
do
18: {s
i
,s
j
} ← pop next item from Q
19: for x ∈ Σ do
20: for {s
k
,s
l
} ∈ δ
−1
({s
i
,s
j
},x) do
21: if {s
k
,s
l
} 6∈ P then
22: τ
{k,l}
← xτ
{i, j}
23: push {s
k
,s
l
} onto Q
24: P ← P ∪ {{s
k
,s
l
}}
25: end if
26: end for
27: end for
28: end while
are tracked. Initially, S is set to S
2
d
, i.e. all d–pairs.
When the set of d–pairs yet to be merged becomes
the empty set, the iterations stop.
Phase 2 of Fast–HS (Algorithm 2) does not per-
form a search in the set of d–pairs but it randomly
selects a d–pair from the current d–pair set to home.
Unlike Fast–HS, in Phase 2 of Greedy–HS (Algo-
rithm 3) the d-pair to be selected is searched among
all d–pairs yet to be homed in D, and the d-pair that
has a shortest homing word is selected.
Phase 2 of SynchroP–HS (Algorithm 4) performs
a deeper analysis. Similar to synhronizing heuristic
SynchroP, the homing heuristic SynchroP–HS iterates
through the all the d–pairs in D and determines the d–
pair to be homed according to the Φ cost given below,
where D is a set of d–pairs and τ
{i, j}
is the homing
word for the d–pair {s
i
,s
j
}.
Φ(D) =
∑
{s
i
,s
j
}∈D
|τ
{i, j}
|
MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development
366

Algorithm 2: Phase 2 of Fast–HS.
Input : An FSM M = (S,Σ,O,δ,λ),τ
{i, j}
for
all {s
i
,s
j
} ∈ S
2
Output : Homing sequence Γ for M
1: D ← S
2
d
D: current set of d–pairs
2: Γ ← ε HS to be constructed, initially empty
3: while D 6=
/
0 do There are pairs to be homed
4: Let {s
i
,s
j
} be a random pair from D
5: Γ ← Γτ
{i, j}
6: D
0
←
/
0
7: for {s
k
,s
l
} ∈ D do
8: if δ(s
k
,τ
{s
i
,s
j
}
) 6= δ(s
l
,τ
{s
i
,s
j
}
) and
λ(s
k
,τ
{s
i
,s
j
}
) = λ(s
l
,τ
{s
i
,s
j
}
) then
9: insert δ({s
k
,s
l
},τ
{i, j}
) into D
0
10: end if
11: end for
12: D ← D
0
13: end while
Algorithm 3: Phase 2 of Greedy–HS.
Input : An FSM M = (S,Σ,O,δ,λ),τ
{i, j}
for
all {i, j} ∈ S
2
Output : Homing sequence Γ for M
1: D ← S
2
d
D: current set of d–pairs
2: Γ ← ε HS to be constructed, initially empty
3: while D 6=
/
0 do There are pairs to be homed
4: {s
i
,s
j
} ← argmin
{s
k
,s
l
}∈D
|τ
{k,l}
|
5: Γ ← Γτ
{i, j}
6: D
0
←
/
0
7: for {s
k
,s
l
} ∈ D do
8: if δ(s
k
,τ
{i, j}
) 6= δ(s
l
,τ
{i, j}
) and
λ(s
k
,τ
{i, j}
) = λ(s
l
,τ
{i, j}
) then
9: insert δ({s
k
,s
l
},τ
{i, j}
) into D
0
10: end if
11: end for
12: D ← D
0
13: end while
6 EXPERIMENTS AND
CONCLUSION
In this section, we explain the experimental study
we have conducted to assess the performance of the
heuristics suggested in this paper. Similar to the other
works in the literature, we used randomly generated
FSMs in our experiments, where for each state s
i
∈ S
and for each input symbol x ∈ X, the next state δ(s
i
,x)
is randomly set to a state s
j
∈ S, and the output λ(s
i
,x)
is randomly set to an output symbol y ∈ Y .
We experimented with FSMs with number of
Algorithm 4: Phase 2 of SynchroP–HS.
Input : An FSM M = (S,Σ,O,δ,λ),τ
{i, j}
for
all {i, j} ∈ S
2
Output : Homing sequence Γ for M
1: D ← S
2
d
D: current set of d–pairs
2: Γ ← ε HS to be constructed, initially empty
3: while D 6=
/
0 do There are pairs to be homed
4: for {s
i
,s
j
} ∈ D do
5: D
{i, j}
←
/
0
6: for {s
k
,s
l
} ∈ D do
7: if δ(s
k
,τ
{i, j}
) 6= δ(s
l
,τ
{i, j}
) and
λ(s
k
,τ
{i, j}
) = λ(s
l
,τ
{i, j}
) then
8: insert δ({s
k
,s
l
},τ
{i, j}
) into D
{i, j}
9: end if
10: end for
11: end for
12: {s
i
,s
j
} ← argmin
{s
k
,s
l
}∈D
Φ(D
{k,l}
)
13: D ← D
{i, j}
14: end while
states n ∈ {32,64}, the number of input symbols
p ∈ {2,4,8}, and the number of output symbols q ∈
{2,4,8}. For each combination of n, p,q values, we
generated 100 random FSMs. Hence a total of 1800
FSMs are used in the experiments. All algorithms are
implemented in C++ and the times elapsed are mea-
sured in terms of microseconds.
We implemented 2 synchronizing heuristics
which find synchronizing sequences (corresponding
to a homing sequence on the FSM) on homing au-
tomata. These are Greedy and SynchroP heuristics
given in Section 4. After creating the HA A
M
ex-
plained in Section 3, we applied the implemented syn-
chronizing heuristics on the A
M
. The time required
for constructing the homing automaton can be seen
in the column HA Time in Table 1. Compared to the
rest of the algorithm, the time required for the con-
struction of A
M
is negligible. Greedy and SynchroP
share the first phase. The column P1 Time in Table 1
gives the time for this common phase 1. As known
from the literature, Phase 1 time dominates Phase 2
time for Greedy, whereas the Phase 2 time dominates
Phase 1 time for SynchroP. Hence, the running time
for Greedy is faster compared to SynchroP. Also as
expected, SynchroP constructs sequences with shorter
lengths compared to Greedy.
We have also implemented a brute–force exponen-
tial time algorithm to construct the shortest homing
sequences. For small states sizes like 32 and 64, it is
possible to compute the shortest homing sequences.
The columns under the Shortest in Table 1 give the
time required to compute and length of the shortest
homing sequences. The experiments show that, at
Using Synchronizing Heuristics to Construct Homing Sequences
367

Table 1: Experiments for using synchronizing heuristics on homing automata.
States Inputs Outputs
Shortest SS based
Length Time HA Time P1 Time
Greedy SynchroP
Length P2 time Length P2 time
32 2 2 6.1 2410 46 11480 7.59 10 6.69 1925547
32 2 4 4.02 320 27 7372 4.79 5 4.32 1134028
32 2 8 3.04 96 16 5493 3.54 3 3.21 465578
32 4 2 5.2 10253 54 10298 7.15 7 6.21 2341436
32 4 4 3.7 580 53 10158 4.69 5 4.07 1306012
32 4 8 3 154 33 7649 3.56 3 3.05 516154
32 8 2 5 41776 127 16875 7.07 7 5.62 2922721
32 8 4 3.19 1590 80 11880 4.67 4 3.92 1328281
32 8 8 2.97 394 69 11249 3.56 3 3.1 561097
64 2 2 7.65 24051 185 240952 9.46 24 8.45 559041289
64 2 4 4.93 2281 161 203926 5.81 22 5.13 359077761
64 2 8 3.73 695 123 202362 4.28 21 3.98 145568201
64 4 2 6.95 278938 447 365706 9.18 24 7.75 795062568
64 4 4 4.25 10815 298 280419 5.69 16 5 428513432
64 4 8 3.12 1052 237 367358 4.24 12 3.81 154977902
64 8 2 6.24 6746717 806 525592 9.04 23 7.33 1000322128
64 8 4 4 19652 628 400603 5.65 16 4.9 456867018
64 8 8 3 1222 459 411719 4.24 13 3.78 154973825
Table 2: Experiments with homing heuristics on FSMs.
States Inputs Outputs
HS based
P1 Time
Fast–HS Greedy–HS SynchroP–HS
Length P2 time Length P2 time Length P2 time
32 2 2 81 7.69 181 7.71 149 7.22 3019
32 2 4 52 4.8 120 4.8 104 4.65 2127
32 2 8 33 3.58 86 3.57 55 3.41 1594
32 4 2 56 7.2 117 7.14 85 6.76 1850
32 4 4 49 4.7 126 4.7 88 4.59 2272
32 4 8 16 3.59 89 3.59 56 3.49 1784
32 8 2 66 7.1 132 7.09 99 6.7 2167
32 8 4 28 4.7 98 4.7 67 4.54 1823
32 8 8 18 3.58 95 3.58 63 3.52 2004
64 2 2 278 9.53 313 9.66 302 9.14 25852
64 2 4 278 5.68 282 5.84 253 5.64 27990
64 2 8 231 4.27 231 4.27 194 4.24 26139
64 4 2 424 9.24 385 9.24 351 8.59 30794
64 4 4 292 5.69 270 5.73 243 5.57 26754
64 4 8 222 4.29 217 4.29 193 4.27 25266
64 8 2 474 9.15 356 9.14 320 8.72 27811
64 8 4 328 5.69 298 5.69 260 5.54 27936
64 8 8 164 4.29 217 4.29 182 4.24 24772
Table 3: Experiments on larger state sizes.
States Inputs Outputs
Fast HS Greedy HS
Length P2 Time Length P2 Time
2048 2 2 19.46 14816 19.57 18509
4096 2 2 21.62 52520 21.47 63327
8192 2 2 23.79 168106 23.76 224572
MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development
368

least for the small state sizes used in these experi-
ments, the heuristics find homing sequences which
are not too long compared to the shortest possible.
On the other hand, the time used by these heuris-
tics indicate that the methods based on using syn-
chronizing heuristics on homing automata will not
scale well. As noted before, the main reason is the
fact homing automata requires squaring the number
of states in the computation.
In order to enhance the time performance, we have
adapted the approach used in synchronizing heuristics
to compute homing sequences directly on FSMs. We
implemented 3 homing heuristics introduced in Sec-
tion 5, namely Fast–HS, Greedy–HS, and SyncrhoP–
HS. We experimented with these heuristics using the
same set of randomly generated FSMs.
Note that the three homing heuristics share their
first phase given as Algorithm 4. In all experiments
we measured the time for the Phase 1 of these heuris-
tics (given in P1 Time in Table 2) and the time to home
all d–pairs, which is Phase 2 of heuristics (given in
columns P2 time in Table 2), separately. The time
performance of homing heuristics in Table 2 are much
better compared to the time performance of the syn-
chronizing heuristics given in Table 1. Note that, the
time it takes for these heuristics is much faster (es-
pecially for Greedy–HS and Fast–HS) compared to
the time needed to find the shortest homing sequence
given in Table 1. As expected, however, the perfor-
mance on the length of the homing sequences de-
grades slightly, when we use the homing heuristics.
Note that Fast–HS picks the d–pair to be used ran-
domly, whereas Greedy–HS selects the d–pair with
the shortest homing word. Therefore, one would ex-
pect Fast–HS to have faster Phase 2 time compared to
Greedy–HS. Although this doesn’t seem to be the case
for the results given in Table 2, one can see that as the
state size increases (especially when the number of
inputs is small), the speed of Fast–HS becomes ap-
parent. Table 3 shows the experiment that reveals the
difference between speeds of Fast–HS and Greedy–
HS. We also see that as state size grows the gap be-
tween the Phase 1 and Phase 2 time increases such
that Phase 1 of Greedy–HS and Fast–HS is up to 10
times slower than the Phase 2 of these heuristics.
In this work, we have used an idea taken from
(Güniçen et al., 2014) which allows us to use synchro-
nizing heuristics for computing homing sequences.
Similar to the results obtained in (Güniçen et al.,
2014), this work shows how the existing synchroniz-
ing heuristics can be used to compute short homing
sequences. As a future work, the same idea can be
adapted to compute Unique Input Output (UIO) se-
quences as well. Since this problem is known to be
hard (Lee and Yannakakis, 1996), there are heuris-
tics to compute short UIO sequences. From a given
FSM, one can construct an automaton such that a syn-
chronizing sequence (for a subset of states) on this au-
tomaton corresponds to a UIO sequence of the orig-
inal FSM. This would similarly allow us to use ex-
isting synchronizing heuristics to compute UIO se-
quences.
REFERENCES
Broy, M., Jonsson, B., Katoen, J., Leucker, M., and
Pretschner, A., editors (2005). Model-Based Testing
of Reactive Systems, Advanced Lectures, volume 3472
of Lecture Notes in Computer Science. Springer.
Cirisci, B., Kahraman, M. K., Yildirimoglu, C. U., Kaya,
K., and Yenigün, H. (2018). Using structure of au-
tomata for faster synchronizing heuristics. In Proc. of
MODELSWARD’18, pages 544–551.
Eppstein, D. (1990). Reset sequences for monotonic au-
tomata. SIAM J. Comput., 19(3):500–510.
Ginsburg, S. (1958). On the length of the smallest uniform
experiment which distinguishes the terminal states of
a machine. J. ACM, 5(3):266–280.
Güniçen, C.,
˙
Inan, K., Türker, U. C., and Yenigün, H.
(2014). The relation between preset distinguishing
sequences and synchronizing sequences. Formal As-
pects of Computing, 26(6):1153–1167.
Kohavi, Z. (1978). Switching and Finite Automata Theory.
McGraw–Hill, New York.
Kudlacik, R., Roman, A., and Wagner, H. (2012). Effective
synchronizing algorithms. Expert Systems with Appli-
cations, 39(14):11746–11757.
Kushik, N. and Yevtushenko, N. (2015). Describing hom-
ing and distinguishing sequences for nondeterminis-
tic finite state machines via synchronizing automata.
In Drewes, F., editor, Implementation and Application
of Automata, pages 188–198, Cham. Springer Interna-
tional Publishing.
Lee, D. and Yannakakis, M. (1996). Principles and methods
of testing finite state machines-a survey. Proceedings
of the IEEE, 84(8):1090–1123.
Moore, M. E. (1956). Gedanken-experiments on sequential
machines. Automata studies, pages 129–153.
Roman, A. (2005). New algorithms for finding short re-
set sequences in synchronizing automata. In IEC
(Prague), pages 13–17.
Roman, A. (2009). Synchronizing finite automata with
short reset words. Applied Mathematics and Compu-
tation, 209(1):125–136.
Roman, A. and Szykula, M. (2015). Forward and backward
synchronizing algorithms. Expert Systems with Appli-
cations, 42(24):9512–9527.
Trahtman, A. N. (2004). Some results of implemented al-
gorithms of synchronization. In 10th Journees Mon-
toises d’Inform.
Using Synchronizing Heuristics to Construct Homing Sequences
369
