
Spectral Algorithm for Line Graphs to Find Overlapping Communities
in Social Networks
Camila P. S. Tautenhain and Mariá C. V. Nascimento
Instituto de Ciência e Tecnologia, Universidade Federal de São Paulo,
Keywords:
Overlapping Community Detection, Modularity Maximization, Spectral Method, Social Network Analysis.
Abstract:
A great deal of community detection communities is based on the maximization of the measure known as
modularity. There is a dearth of literature on overlapping community detection algorithms, in spite of the im-
portance of the applications and the overwhelming number of community detection algorithms yet proposed.
To this end, one of the suggestions in the literature consists of partitioning the set of edges into communities,
also known as link partitions, by applying community detection algorithms to line graphs. In line with this,
in this paper, overlapping vertex communities are obtained from link partitions by a method that selects the
communities of the edges that represent the highest modularity gain. We also introduce a spectral algorithm to
find link partitions from line graphs. We show that the modularity of communities in line graphs is equivalent
to the adaptation of modularity of communities in the original graphs, when considering the non-backtracking
matrix instead of the adjacency matrix in its formula. The results of the experiments carried out with over-
lapping community detection algorithms showed that the proposed method is competitive with state-of-the-art
algorithms.
1 INTRODUCTION
Complex networks can model real systems such as
social, metabolic and citation networks. These net-
works can be partitioned into communities of densely
connected vertices for a better understanding of the
characteristics of the system. In the context of social
networks, the identification of communities is of great
interest in applications such as targeting market cam-
paigns, prediction of interactions amongst users and
detecting non-human users.
The traditional approach to detect communities in
networks is to find the best vertex partition according
to a given measure that assesses its quality. Examples
of measures are the modularity (Newman and Girvan,
2004), the statistical significance (Lancichinetti et al.,
2011) and the map equation (Rosvall and Bergstrom,
2007).
The number of edges within the groups minus the
number of edges expected in a random graph with the
same degrees as the graph under the consideration is
virtually the definition of modularity. The higher the
modularity of a partition, the better the partition ac-
cording to this measure.
Because the modularity maximization problem is
NP-Hard (Brandes et al., 2008), its exact optimization
is unrealistic in scenarios where the networks have a
large number of vertices. Therefore, the literature has
been virtually focused on developing approximation
methods and heuristics. Spectral decomposition met-
hods in particular have presented good results in (Nas-
cimento and De Carvalho, 2011) and in (Newman,
2013b). Krzakala et al. (2013) introduced the non-
backtracking matrix which indicates whether or not
a pair of edges is adjacent. Based on computational
experiments, the authors suggested that the spectrum
of such matrix is more meaningful than the spectrum
of the adjacency matrix to detect communities in net-
works.
A characteristic of social networks is the existence
of overlapping communities meaning that vertices be-
long to more than one community (Xie et al., 2013).
A user of Facebook, for example, might join diffe-
rent groups. Nonetheless, many works are strict on
selecting only one community for each vertex, i.e.,
disjoint communities (Xie et al., 2013). Among the
methods capable of finding either disjoint or overlap-
ping communities, the ones presented in (Lancichi-
netti et al., 2011) and in (Xie et al., 2011) are worth
mentioning.
306
Tautenhain, C. and Nascimento, M.
Spectral Algorithm for Line Graphs to Find Overlapping Communities in Social Networks.
DOI: 10.5220/0007403803060317
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 306-317
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

The partitioning of edges into communities to de-
fine link partitions has also been studied in the lite-
rature as an approach to identify overlapping vertex
communities (Evans and Lambiotte, 2009). Evans
and Lambiotte (2009) suggested that link partitions
can be obtained by (vertex) community detection al-
gorithms applied to their respective line graphs. Zhou
et al. (2017), however, observed that the resulting par-
titions may present communities with an undesirable
large number of overlappings.
In this paper, we adapted the modularity mea-
sure to assess the adjacency relations between edges
instead of vertices. Moreover, we demonstrated that
this adaptation is equivalent to the classical modula-
rity in line graphs. As another contribution, we in-
troduce a strategy to identify disjoint and overlapping
vertex communities from link partitions and a spectral
divisive community detection algorithm, here called
SpecDiv. SpecDiv is a hybridization of the Leading
Eigenvalue algorithm proposed by Newman (2006)
with a local search heuristic. The proposed strategy
constructs the vertex communities according to the
link partitions found by SpecDiv and based on the
gain of modularity.
The computational experiments showed that this
strategy was competitive with state-of-the-art over-
lapping community detection algorithms. Further-
more, we obtain link partitions by applying classical
community detection algorithms to line graphs. The
experiments carried out with real and sparse LFR ar-
tificial networks showed that disjoint partitions obtai-
ned by the proposed strategy using line graphs are
closer to the expected partitions than those found by
traditional community detection methods. In both ca-
ses, SpecDiv is competitive with the reference algo-
rithms. These results suggest that link partitions can
also be advantageous for existing vertex community
detection algorithms. As part of the experiments, we
also illustrate a practical application of the overlap-
ping community detection in a Twitter network from
the literature.
2 RELATED WORKS
This section presents the community detection met-
hods related to the introduced algorithm. First, we
briefly discuss the disjoint community detection met-
hods. After, we examine the overlapping community
detection methods and, in special, link community
methods.
2.1 Disjoint Community Detection in
Networks
This section briefly describes disjoint community de-
tection methods used as reference in the experiments
performed and presented in this paper. They are: the
Louvain method (Blondel et al., 2008), Infomap (Ros-
vall and Bergstrom, 2007), Label Propagation Algo-
rithm (Raghavan et al., 2007) and Walktrap (Pons and
Latapy, 2005). We also discuss the Leading Eigenva-
lue method of Newman (2006) since our algorithm is
based on it and highlight a few other spectral-based
methods. As an extensive literature review on this
subject is out of the scope of this paper, we refer
the reader to the recent survey of Fortunato and Hric
(2016). We chose these methods due to their good
results to a wide variety of networks and consolida-
ted use as reference algorithms in the literature (Yang
et al., 2016).
There are two overlapping community detection
methods discussed in the next section which are also
capable of finding disjoint communities: the Or-
der Statistics Local Optimization Method (OSLOM)
(Lancichinetti et al., 2011) and the Speak Listener
Propagation Algorithm (SLPA) (Xie et al., 2011).
To find the vertex partitions, the Louvain and the
Leading Eigenvalue methods aim at maximizing the
modularity measure. The Louvain method is a greedy
strategy that merges communities of vertices that in-
crease the modularity value. The Leading Eigenvalue
method is based on the observation that the signs of
components of the eigenvector associated with the lar-
gest eigenvalue of the modularity matrix can be used
to partition the set of vertices into two communities.
The method then hierarchically divides each commu-
nity into two new communities.
Infomap aims at optimizing the map equation
measure, which is inspired by the duality between
the community detection problem and random walks
paths in digraphs. Walktrap also relies on random
walks to form vertex partitions by inferring the proba-
bility of random walkers leaving communities to re-
ach vertices from other communities. The Label Pro-
pagation Algorithm (LP) is a strategy which propaga-
tes labels through the network to define the label of
a vertex based on the communities to which its neig-
hbors belong to.
Several other spectral-based methods for finding
disjoint communities in networks exists besides the
Leading Eigenvalue method. Zhang and Newman
(2015), for example, designed a heuristic based on the
spectral decomposition of the modularity maximiza-
tion matrix. As previously mentioned, Krzakala et al.
(2013) introduced the spectral decomposition of the
Spectral Algorithm for Line Graphs to Find Overlapping Communities in Social Networks
307

non-backtracking matrix. Both Newman (2013a) and
Singh and Humphries (2015) studied variations of the
non-backtracking matrix to improve its representati-
veness regarding networks.
Closely related to the spectral decomposition met-
hods are the methods based on statistical inference
(Newman, 2013b; Ali and Couillet, 2017), which
Newman (2013b) showed to be equivalent to modula-
rity maximization decomposition methods under spe-
cific parameter settings. These methods detect com-
munities by fitting the stochastic block models to the
networks using maximum likelihood methods.
2.2 Overlapping Community Detection
in Networks
As mentioned earlier, a reduced number of algorithms
to detect overlapping communities can be found in the
literature. Among them, OSLOM and SLPA perform
such task with satisfactory outcomes when applied to
LFR networks as pointed out in the literature review
presented by Xie et al. (2013).
SLPA is an extension of LP to detect overlapping
communities in networks. SLPA keeps the informa-
tion about the community labels propagated to each
vertex along the iterations. A post-processing strategy
is responsible for defining the most frequent commu-
nity labels of the vertices as their communities, ba-
sed on a threshold parameter. OSLOM is a heuristic
method that employs a fitness function to assess the
statistical significance of the communities compared
to a null model, i.e., a network with no community
structure.
Evans and Lambiotte (2009) and Ahn et al. (2010)
suggested detecting communities of links instead of
vertices to deal with overlapping communities. In this
strategy, each vertex belongs to the communities of its
incident edges. Evans and Lambiotte (2009) recom-
mended the detection of link partitions through the
partitioning of the vertices of the line graphs. Ahn
et al. (2010), on the other hand, studied the hierarchi-
cal partitioning of links in graphs by measuring the
similarity of edges using a measure known as Jaccard
index.
Although Xie et al. (2013) have shown through ex-
periments that OSLOM and SLPA outperformed the
link partitioning method of Ahn et al. (2010), appro-
aching the problem by line graphs enables the use
of any vertex community detection algorithm to find
overlapping communities. In this sense, methods that
aim at finding communities of links have been incre-
asingly studied in the last years. Some examples of
algorithms that find overlapping communities based
on line graphs are the genetic algorithms proposed
by Pizzuti (2009), Shi et al. (2013) and Li and Liu
(2018).
Spectral methods have also been used to detect
overlapping communities from link partitions. The
pioneer spectral method for this task was the one in-
troduced by Zhang et al. (2007). The algorithm pro-
posed by the authors is based on the spectral decom-
position of an adaptation of the modularity measure
to deal with the soft assignment of vertices to com-
munities. The overlapping communities are achieved
by analyzing how much each vertex belongs to each
community. Jiang and McQuay (2012) also explored
the soft assignment of nodes to communities through
a spectral decomposition method.
Gui et al. (2018) designed a spectral method that
used the eigenvectors associated with the two largest
eigenvalues of the Laplacian matrix of a line graph to
project the graph into points in a plane. These points
were then used to calculate the similarity between the
vertices in order to hierarchically merge them into
communities.
As opposed to disjoint community detection, for
which several spectral clustering methods have been
studied (Nascimento and De Carvalho, 2011), the li-
terature still lacks spectral heuristics that maximize
the modularity measure in order to find overlapping
communities. Even though Nicosia et al. (2009), for
example, introduced an adaptation of the modularity
measure to assess overlapping vertex communities,
they used a genetic algorithm to maximize it rather
than a spectral-based method.
3 MODULARITY
MAXIMIZATION
Let G = (V, E) be an undirected and simple graph
such that V and E are its set of vertices and edges,
respectively.
The set of vertices is represented by integer sca-
lars, such that V = {1, 2,. . . , |V|}. An edge is an unor-
dered tuple (i, j) that has end points in two vertices
i, j ∈ V . The adjacency matrix A = [a
i j
] ∈ R
|V |×|V |
re-
presents the pairwise relation between vertices of G.
An element a
i j
is 1 if edge (i, j) ∈ E, and 0, other-
wise. The total number of the edges is denoted by
m =
∑
i∈V
∑
j∈V
a
i j
2
. The degree of vertex i is given by
d
i
=
∑
j∈V
a
i j
.
Let the communities of a graph be defined by
integer scalars called community labels. A ver-
tex partition into communities is defined as P =
{c
1
, c
2
, ..., c
|V |
}, where c
i
is the label of the commu-
nity that vertex i belong to. Two vertices are in the
same community when they share the same label.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
308

Considering the community labels of vertices i
and j, i.e. c
i
and c
j
, let δ
c
i
c
j
be 1 if c
i
= c
j
and
0, otherwise. The modularity matrix is given by
B = [b
i j
] ∈ R
|V |×|V |
, where each element is calcula-
ted according to Equation (1).
b
i j
= a
i j
−
d
i
d
j
2m
(1)
The modularity of a partition P is given Q(P ) ac-
cording to Equation (2).
Q(P ) =
1
2m
∑
i∈V
∑
j∈V
b
i j
δ
c
i
c
j
(2)
According to Equation (2), higher values of modu-
larity are obtained when the number of edges within
the communities is greater than the expected number
of edges of a random graph with the same degree se-
quence as V .
3.1 Non-backtracking Matrix
An edge e
1
= (i, j) is said to be adjacent to anot-
her edge e
2
= (k, r) if and only if they share ex-
actly one end point. The set of edges adjacent to
e
1
= (i, j) is thereby given by N (i, j) = {(k, r) ∈
E such that (i, j) and (k, r) are adjacent in G}. More-
over, the degree of an edge e
1
= (i, j) is the number
of its adjacent edges and is given by d
0
(i, j)
= |N (i, j)|.
Because we only deal with undirected graphs, we
adapted the non-backtracking matrix introduced by
Krzakala et al. (2013) to ignore edge directions. Let
O = [o
(i, j),(k,r)
] ∈ R
|E|×|E|
be the non-backtracking
matrix, where (i, j), (k, r) ∈ E and each element is gi-
ven by Equation (3).
o
(i, j),(k,r)
=
1, if (i, j) is adjacent to (k, r)
0, otherwise
(3)
Therefore, o
(i, j),(k,r)
is 1 if edges (i, j) and (k, r)
share exactly one end vertex, i.e., they are adja-
cent. The non-backtracking matrix can be under-
stood as an adjacency matrix between edges. The
analogous definition of m to the non-backtracking
matrix is y =
∑
(i, j)∈E
∑
(k,r)∈E
o
(i, j),(k,r)
2
. Furthermore,
the non-backtracking modularity matrix is given by
H = [h
(i, j),(k,r)
] ∈ R
|E|×|E|
, where each element is cal-
culated according to Equation (4).
h
(i, j),(k,r)
= o
(i, j),(k,r)
−
d
0
(i, j)
d
0
(k,r)
2y
(4)
We introduce an adaptation of the modularity me-
asure to consider the non-backtracking matrix instead
of the adjacency matrix in Equation (5).
Qo(P ) =
1
2y
∑
(i, j)∈E
∑
(k,r)∈E
h
(i, j),(k,r)
δ
c
i
c
j
δ
c
k
c
r
(5)
By replacing the adjacency matrix by the non-
backtracking matrix, Equation (5) evaluates the mo-
dularity over the edges of G, instead of E: it calcu-
lates the number of edges within communities minus
the expected number edges in a random graph whose
edges have the same degree sequence as E.
3.2 Line Graphs
Let G
0
= (V
0
, E
0
) be the line graph of G. Its set of
vertices is V
0
= E, i.e., each edge of G is a vertex of
G
0
. The set of edges of G
0
is given by E
0
= {(e
1
, e
2
),
such that e
1
∈ E and e
2
∈ E are adjacent in G}. The
number of edges of G
0
is denoted by m
0
and coincides
with y, i.e., m
0
= y.
The adjacency matrix of G
0
is A
0
= [a
0
(i, j),(k,r)
] ∈
R
|E|×|E|
where a
0
(i, j),(k,r)
receives value 1 if and only
if edges (i, j), (k, r) ∈ E are adjacent in G. Thereby,
a
0
(i, j),(k,r)
= o
(i, j),(k,r)
and, consequently, A
0
= O. The
degree of a vertex e
0
1
= (i, j) ∈ V
0
is defined by d
0
e
0
1
=
∑
e
0
2
∈V
0
a
0
e
0
1
e
0
2
= d
0
(i, j)
.
A vertex partition of G
0
represents a link parti-
tion of G. A link partition is here denoted by P
0
=
{c
0
1
, c
0
2
, ..., c
0
|E|
}, where c
0
e
is the label of the commu-
nity to which e ∈ E belongs to.
Let the modularity of a partition P
0
of line graph
G
0
be defined by Equation (6).
Q
0
(P
0
) =
1
2m
0
∑
e
1
∈V
0
∑
e
2
∈V
0
a
0
e
1
e
2
−
d
0
e
1
d
0
e
2
2m
0
δ
c
0
e
1
c
0
e
2
= Q
0
(P
0
) =
1
2y
∑
(i, j)∈E
∑
(k,r)∈E
h
(i, j),(k,r)
δ
c
0
(i, j)
c
0
(k,r)
(6)
On the one hand, Qo(P ) (Equation (5)) assesses
a vertex partition and, on the other, Q
0
(P
0
) (Equation
(6)) evaluates a link partition.
Consider a pair of edges (i, j) ∈ E and (k, r) ∈ E.
The product δ
c
i
c
j
δ
c
k
c
r
is equal to 1 if and only if i, j, k
and r are in the same community in vertex partition P
of G. In these cases, edges (i, j) and (k, r) will be in
the same community in the related link partition P
0
.
Consequently, Qo(P ) reduces to Q
0
(P
0
).
Nevertheless, Q
0
(P
0
) does not reduce directly into
Qo(P ). Two edges (i, j), (k, r) ∈ E might be in the
same community in a link partition P
0
. However, one
or more of their end points might be end point of ot-
her edges that belong to different communities in P
0
.
A vertex can be in any of the communities of its in-
cident edges in a vertex partition P . This observation
induces a natural overlapping of communities in P .
Spectral Algorithm for Line Graphs to Find Overlapping Communities in Social Networks
309

Therefore, maximizing the non-backtracking mo-
dularity in a graph G is equivalent to maximize the
classical modularity in its line graph G
0
, provided that
the former accounts for overlapping communities.
4 SPECTRAL DECOMPOSITION
This section presents the spectral decomposition of
the modularity measure of a partition P
F
in an arbi-
trary graph F = (V
F
, E
F
) that can be either G or G
0
.
If F is a line graph, then the modularity is equivalent
to the non-backtracking modularity in G. The decom-
position of the modularity is based on the study per-
formed by Newman (2006). Assume that m
F
∈ R and
B
F
= [b f
i j
] ∈ R
|V
F
|×|V
F
|
are the number of edges and
the modularity matrix of G
F
, respectively.
First, consider a bipartition of the vertices of F.
Let s = [s
i
] ∈ R
|V
F
|
be a vector where each element
s
i
is either 1 or −1, depending on which of the com-
munities vertex i belongs to. The modularity can be
expressed in a matricial form in function of s, as pre-
sented in Equation (7).
Q(s) =
1
2m
F
s
T
B
F
s (7)
Let λ
1
, λ
2
, . . . , λ
|V
F
|
be the eigenvalues of B
F
de-
creasingly sorted by value, i.e., λ
1
≥ λ
2
≥ ··· ≥ λ
|V
F
|
.
Moreover, let Λ ∈ R
|V
F
|×|V
F
|
be a diagonal matrix
such that the diagonal element in row j and column
j is given by the j − th largest eigenvalue, λ
j
. The
eigenvectors of B
F
are arranged in matrix U = [u
i j
] ∈
R
|V
F
|×|V
F
|
such that each column j is the eigenvector
u
j
associated with the eigenvalue λ
j
.
Matrix B
F
is symmetric because F is undirected
and thus admits an eigen-decomposition. The vector
s can be written as a linear combination of the eigen-
vectors: s =
∑
i∈V
F
α
i
u
i
, where α
i
= u
T
i
s ∈ R. Equa-
tion (7) can then be rewritten as shown in Equation
(8).
Q(s) =
1
2m
F
∑
i∈V
F
α
i
u
T
i
B
F
∑
j∈V
F
α
j
u
j
=
1
2m
F
∑
i∈V
F
(u
T
i
s)
2
λ
i
(8)
Newman (2006) suggested approximating Equa-
tion (8) using the largest eigenvalue λ
1
. The decision
problem is thus to decide the values of each element
s
i
, i ∈ V
F
, that result in the largest value in Equation
(8). Because an element s
i
can be 1 or −1, each term
(u
T
i
s)
2
λ
i
, i ∈ V
F
, is maximized by setting s
i
as 1 if
u
i1
> 0 and as −1 if u
i1
< 0. In case u
i1
= 0, the choice
of s
i
does not change the value of the term. There-
fore, the resulting partition is P
F
= {c
1
, c
2
, . . . , c
|V
F
|
},
where c
i
= 1 when s
i
= −1 and c
i
= 2 when s
i
= 1,
for i ∈ V
F
.
4.1 Hierarchical Division of
Communities
In order to hierarchically divide the pair of commu-
nities found through the spectral decomposition ex-
plained in the earlier section, Newman (2006) sug-
gested creating subgraphs induced by the vertices of
each community. This approach, however, requires
the recalculation of the modularity matrix of the in-
duced graphs to consider the degree sequence of the
original graph.
In this paper, instead of analyzing the modularity
matrix of the induced graphs, we define the modula-
rity matrix of each community by selecting only the
rows and columns of the vertices that belong to the
community.
To show that the introduced strategy is correct, let
Z be a set containing the indices of the vertices that
belong to an arbitrary community labeled l
a
. Equation
(9) isolates the contribution of the vertices in Z to the
modularity measure.
Q(P
F
) =
1
2m
F
∑
i∈Z
∑
j∈Z
b f
i j
δ
c
i
c
j
+
1
2m
F
∑
i, j:{i, j}∈(V
F
×V
F
)−(Z×Z)
b f
i j
δ
c
i
c
j
(9)
where (V
F
×V
F
) − (Z × Z) has as elements all pairs
of vertices i, j such that both j and i does not belong
to Z.
The first term of Equation (9) is the contribution of
community labeled l
a
to the modularity. According
to this Equation, maximizing the first term does not
change the value of the second term in Equation (9).
Let D be a mapping between the vertices from Z
and elements of {1, 2, . . . , |Z|}, i.e.: D = {(i, υ) such
that i ∈ Z and υ is selected without replacement from
{1, 2, .., |Z|}}. Let B
Z
= [b f
υρ
] ∈ R
|Z|×|Z|
be the mo-
dularity matrix whose element b
υρ
has the value of
b
i j
, i : (i, υ) ∈ D and j : ( j, ρ) ∈ D.
Also, let z = [z
υ
] ∈ R
|Z|
be the vector whose ele-
ments z
υ
receive value 1 or −1 depending on which
community vertex i : (i, υ) ∈ D belong to. Thereby,
the modularity of the community labeled l
a
is given
by Q
Z
(z) =
1
2m
F
zB
Z
z.
Because the spectral decomposition of Q
Z
(z) is
analogous to the one performed on Q(s), the signs of
the eigenvectors associated with the leading eigenva-
lue of B
Z
can be used to choose the values of z that
maximize Q
Z
(z). After choosing z using the leading
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
310

eigenvalue approach, two new community labels are
selected for the vertices in Z.
5 VERTEX COMMUNITY
DETECTION IN LINE GRAPHS
The first step of the introduced strategy is to find a link
partition by applying a vertex community detection
algorithm to the corresponding line graph.
In addition to the introduced strategy to obtain ver-
tex partitions from link partitions, this paper also in-
troduces a divisive spectral community detection al-
gorithm.
5.1 Divisive Algorithm
The spectral divisive heuristic introduced in this paper
is strongly based on the leading eigenvalue algorithm
proposed by Newman (2006).
Algorithm 1 presents the heuristic, called Spe-
cDiv. It takes as input a graph F = (V
F
, E
F
), which
can be either the original graph G or its corresponding
line graph G
0
, the maximum number of communities
to be created, max_labels, and the minimum num-
ber of vertices required to further divide a community,
min_size. The algorithm returns a vertex partition for
the input graph F. Hence, in case F is the line graph,
the algorithm returns a link partition of the original
graph.
In line 1 of Algorithm 1 is constructed the mo-
dularity matrix B
F
according to Equation (1). Recall
that if F is a line graph, then the modularity matrix
of F is equivalent to the non-backtracking matrix of
the original graph. In line 3, a partition P
F
is created
wherein all vertices belong to the community labe-
led 0. In line 4 the list L which stores the labels of
the communities that can be further divided into two
communities is defined. Line 7 sets the modularity
matrix of the initial iteration, B
(1)
F
, as B
F
.
From lines 8 to 29, SpecDiv repeatedly breaks in
two each community in L until either there is no com-
munity left in L or a predefined maximum number of
communities is reached.
In lines 9 and 10, the set Z of indices of vertices
in the community labeled lr, chosen randomly from
L, is defined. In case the number of vertices indicated
by Z is greater than min_size, in line 12, the pairwise
mappings (i, υ) between vertices i ∈ Z and sequential
numbers υ ∈ {1, 2, . . . , |Z|} are assigned to set D. This
set is used to map the vertices of Z to indices that
correspond to the appropriate components of B
F
and
u. In line 13, B
(it)
F
is constructed by selecting only the
Algorithm 1: SpecDiv.
Input : F = (V
F
, E
F
), max_labels, min_size
Output: P
F
∗
1 B
F
:= compute the modularity matrix of F
according to Equation (1)
2 lb := 0
3 P
F
:= {c
1
= 0, c
2
= 0, . . . , c
|V
F
|
= 0}
4 L := {0}
5 P
F
∗ := P
F
6 it := 1
7 B
(1)
F
:= B
F
8 while L 6=
/
0 and number of communities of P
F
is less than max_labels do
9 lr := randomly chose a community label in
L
10 Z := {i such that c
i
= lr for i = 1, . . . , |V
F
|}
11 if |Z| > min_size then
12 D := {(i, υ) such that i ∈ Z and υ is
selected without replacement from
{1, 2, .., |Z|}}
13 B
(it)
F
:= Select only the rows and
columns of B
F
which to vertices in Z
according to Section 4.1
14 L := L\{lr}
15 λ, u
1
:= Compute the largest eigenvalue
and associated eigenvector of B
(it)
F
16 U
+
:= {i ∈ Z such that u
υ1
≥ 0,
υ : (i, υ) ∈ D}
17 U
−
:= {i ∈ Z such that u
υ1
< 0,
υ : (i, υ) ∈ D}
18 c
i
= lb, for i ∈ U
+
19 c
i
= lb + 1, for i ∈ U
−
20 Q(P
F
) := Calculate modularity according
to Equation (2).
21 repeat
22 P
F
, ∆Q := move each i ∈ Z to the
community labeled lb or lb + 1 that
results in the largest modularity gain
23 until ∆Q ≤ 0;
24 if Q(P
F
) > Q(P
F
∗) then P
F
∗ = P
F
;
25 if communities labeled lb and lb + 1 are
not empty then L := L ∪ {lb} ∪ {lb + 1}
;
26 lb := lb + 2
27 it := it + 1
28 repeat
29 P
F
∗, ∆Q∗ := move each i ∈ V
F
to the
community that results in the largest
modularity gain
30 until ∆Q∗ ≤ 0;
31 return P
F
∗
rows and columns of B
F
that correspond to vertices in
Z, according to Section 4.1.
In line 14, the selected element lr from the list L
is removed. In line 15, the largest eigenvalue, λ and
the respective eigenvector, u
1
, of B
(it)
F
are calculated.
We used the implicitly restarted Arnoldi method from
Spectral Algorithm for Line Graphs to Find Overlapping Communities in Social Networks
311

ARPACK library (Lehoucq et al., 1998) for this step
1
.
In lines 16 and 17, U
+
and U
−
are the sets of vertices
from Z whose corresponding signs of the components
of u
1
larger than or equal to zero are assigned to U
+
,
whereas those lower than 0 are assigned to U
−
. In
lines 18 and 19, vertices from U
+
and U
−
receive
two new community labels lb and lb + 1 in partition
P
F
, respectively. In case one of the sets is empty, the
community is not divided. Otherwise, the modularity
of partition P
F
is calculated according to Equation (2)
in line 21.
After that or when |Z| ≤ 8, a local search strategy
in line 23 moves each vertex in Z to the community
labeled lb or lb + 1 that results the largest modularity
gain. To avoid biased results, we select the vertices
to be moved in a random order. The local search is
repeated until there is no movement to improve the
modularity gain.
In line 25, the algorithm updates the best partition
found along the iterations, P
F
∗, to P
F
if Q(P
F
) is hig-
her than Q(P
F
∗). In line 27, the community labels lb
and lb +1 are inserted to the list L if both of them are
not empty, i.e., contain at least one vertex. In line 27,
the label of the next community to be created, lb, is
updated and in line 28 the number of iterations, it, is
incremented.
After defining a vertex partition P
F
∗ in F, Spe-
cDiv employs a local search strategy to improve it,
until there is no move that improves the modularity
value in line 31. Different from the local search per-
formed in line 23, the vertices can be moved to any
community. Finally, Algorithm 1 returns P
F
∗ as out-
put.
The next sections explain the proposed strategies
to find disjoint and overlapping communities.
5.2 Finding Disjoint Vertex Partitions
from Link Partitions
Algorithm 2 presents the strategy to find disjoint ver-
tex communities having as input a link partition. It
takes as input a connected graph G and a link parti-
tion P
0
obtained by some vertex community detection
algorithm applied to the line graph of G, here called
G
0
.
In line 1, the algorithm assigns to CV
i
the commu-
nity labels of the edges incident to vertex i ∈ V in G,
considering the link partition P
0
. In line 2, to define a
1
We required that |Z| must be higher than min_size = 8
due to conditions imposed by the number of iterations se-
lected for the implicitly restarted Arnoldi method to con-
verge. The local search procedures are capable of impro-
ving small communities with respect to the modularity va-
lue.
Algorithm 2: Disjoint community detection.
Input : Connected graph G = (V, E), link
partition P
0
Output: P ∗
1 CV
i
:= {c
0
(i, j)
∈ P
0
such that (i, j) ∈ E}, for
i ∈ V
2 c
i
= mode(CV
i
), for i ∈ V
3 P := {c
1
, c
2
, . . . , c
|V |
}
4 P ∗ := move each i ∈ V from community
labeled c
i
to that from CV
i
that results the
largest modularity gain
5 return P ∗
Algorithm 3: Overlapping community detection.
Input : Connected graph G = (V, E), link
partition P
0
Output: P V
1 CV
i
:= {c
0
(i, j)
∈ P
0
such that (i, j) ∈ E}, for
i ∈ V
2 P V := {CV
1
,CV
2
, . . . ,CV
|V |
}
3 X := set of community labels of vertices
from V that does not present overlapping in
P
0
4 forall i ∈ V such that |CV
i
| > 1 do
5 if |{ci ∈ CV
i
∩ X }| > 0 then
X i := {ci ∈ CV
i
∩ X };
6 else X i := CV
i
;
7 CV
i
:=
{ld ∈ X i|(
∑
j∈V such that c
j
=ld
b
i j
) > 0}
8 P V := {CV
1
,CV
2
, . . . ,CV
|V |
}
9 return P V
vertex partition, for each vertex i, mode(CV
i
) returns
to c
i
the most frequent label in CV
i
. The community
labels identified in line 2 define a vertex partition P
for G in line 3. In line 4, a local search procedure that
moves each vertex i ∈ V from community labeled c
i
to that from CV
i
that results in the largest modularity
gain is applied to P . Again, we select the vertices to
be moved in a random order. Finally, the algorithm
returns the refined vertex partition P ∗ in line 5.
5.3 Finding Overlapping Vertex
Partitions from Link Partitions
In Algorithm 3, we describe the strategy to identify
overlapping vertex communities from a link partition
given as input, along with a connected graph G.
In line 1, |V | sets of community labels according
to the link partition given as input are created. In line
2, a list of overlapping communities with the vertex
community labels assigned to CV
i
is defined.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
312

In line 3, set X with the community labels of the
vertices of G which are in only one community is con-
structed, i.e., vertices i ∈ V such that |CV
i
| = 1. We
shall refer to vertices that belong to more than one
community as overlapping vertices.
From lines 5 to 7, a post-processing strategy to de-
fine the community labels of each overlapping vertex
i,CV
i
> 0, is applied to P V . In line 5, elements of X i
are defined as the overlapping communities of vertex
i, CV
i
, in X . If CV
i
∩ X is empty, then X i := CV
i
in
line 6.
In line 7, the community labels of each overlap-
ping vertex i ∈ V are selected as those whose sum of
the modularity contributions between i and the verti-
ces of that community is higher than 0. We require
that a vertex is only moved to a community that exists
in X to avoid the creation of communities composed
only by overlapping vertices.
Finally, in line 10, the overlapping communities
P V with the community labels of each vertex defined
according to line 7 are returned.
6 CASE STUDY IN A TWITTER
NETWORK
Before presenting the computational experiments, in
this section, we study a practical application of over-
lapping community detection in a Twitter retweet net-
work constructed by Ribeiro et al. (2018). The aut-
hors of this network also classified users that used ha-
teful speech in Twitter.
The network presented here is the main connected
component of a small subgraph induced by 5000 ver-
tices and 10 hateful users selected randomly from the
network. The order of the selected subgraph was due
to computational performance restrictions of the pro-
posed spectral divisive heuristic. The resulting num-
bers of vertices and edges after extracting the main
connected component of this subgraph are 2885 and
4874, respectively.
Figure 1
2
illustrates the overlapping vertex com-
munities P V found using Algorithm 3 having as in-
put a link partition, obtained by SpecDiv applied to
the line graph. In this figure, the colors of the vertices
and edges identify the vertex and link communities.
The overlapping vertices are multi-colored according
to their community labels. The large-sized vertices
defined by the ‘*’ mark are the hateful users identi-
fied by Ribeiro et al. (2018). The large-sized vertices
2
Some of the vertices and edges of the graph were sup-
pressed to improve its readability.
without marks corresponds to the top 1% vertices with
the highest degrees.
Figure 1: Overlapping communities found in a sample of a
Twitter network.
The non-backtracking modularity of P V , i.e., the
modularity of the line graph, is 0.8384. The modula-
rity of the partition obtained from the link partition by
Algorithm 2 is 0.6371.
Approximately 36.05% of the vertices belong to
overlapping communities. Among them, 62.31%
have 2-overlapping community labels and only 5.1%
have more than 4 communities. The average number
of overlapping community labels is 2.59, with a stan-
dard deviation from the average of 0.91.
According to Figure 1, most of the top 1% highest
degree nodes do not belong to overlapping commu-
nities and many of them belong to the largest com-
munities. On the other hand, 4 of the 9 hateful users
belong to overlapping communities. In particular, 2
of them belong to 4-overlapping communities. At le-
ast one hateful user in each community also belongs
to another community that includes another hateful
user. Overall, 44.44% of the hateful users belong to
overlapping communities.
To ensure the consistency of the results, we repli-
cated the aforementioned experiment on 5 different
random subgraph sampling drawn from the original
network. The average number of vertices and edges
of the networks are 2868.8 and 4953.2, respectively.
The average modularity values for the line graph and
for the partition obtained from the link partition are
respectively 0.6193 and 0.8359. The average num-
ber of overlapping communities is 2.6. On average,
37.99% of the vertices in the networks belong to over-
lapping communities. Among them, 62.45% are in
2-overlapping communities and only 5.23% belong
to more than 4-overlapping communities, on average.
These results are consistent with those presented in
Figure 1.
In only one subgraph sampling the hateful users
do not belong to any overlapping communities. The
Spectral Algorithm for Line Graphs to Find Overlapping Communities in Social Networks
313

average percentage of hateful users that belong to
overlapping communities is 40.89% and presents the
large standard deviation value of 23.54%. In fact, this
experiment suggests that the subgraph sampling only
affects the distribution of hateful users in the commu-
nities.
An interesting application from these empiri-
cal observations based on overlapping communities
would be to study the influence of these overlapping
hateful users on other users of the network.
7 COMPUTATIONAL
EXPERIMENTS
This section presents the computational experiments
with sparse LFR networks with disjoint and overlap-
ping communities, generated using the software of
Lancichinetti et al. (2008).
All the LFR networks were generated having as
parameters: number of vertices equal to 1000, aver-
age and maximum degrees given by 3 and 10, respec-
tively and exponential distribution equal to 2. Table 1
presents the remaining characteristics that distinguish
the networks into sets: minimum and maximum num-
ber of vertices in the communities, minc and maxc,
respectively; number of overlapping vertices, OV n;
number of communities for the overlapping vertices,
OV m; and degree of mixture of the communities, µ.
Table 1: Characteristics of the generated LFR networks.
Set minc maxc OV n OV m µ
SD 10 50 0 - 0.1, 0.2, . . . , 0.8
LD 20 100 0 - 0.1, 0.2, . . . , 0.8
SOv 10 50 100 2 0.1, 0.2, . . . , 0.8
LOv 20 100 100 2 0.1, 0.2, . . . , 0.8
The disjoint networks are referred to as in sets SD
and LD, whereas the overlapping ones are said to be
in SOv and LOv sets. Networks from SD and SOv
are composed by small communities, whereas those
in LD and LOv are composed by large communities.
We generated 5 different networks for each set
and value of µ described in Table 1 and reported the
average results achieved over 5 independent executi-
ons. All the computational experiments were perfor-
med on a computer with a processor Intel Xeon E5-
1620 with 3.70Gz and main memory of 32 GB. The
disjoint and overlapping strategies were implemented
in R with igraph library (Csardi and Nepusz, 2006).
SpecDiv was implemented in C++ with ARPACK++
library. The parameter max_label of SpecDiv was set
to be 10% of the number of vertices in the graph and
the parameter min_size was set to 8.
7.1 Disjoint Communities
In this Section, we contrast the partitions found by
vertex community detection algorithms with those
obtained by the disjoint community detection strategy
that takes as input a link partition from the line graph
G
0
. To differentiate the strategies using line graphs
from those using the original graphs as inputs, we add
the suffixes "−G
0
" and "−G" to the names of the al-
gorithms.
To assess a disjoint partition, we employed the
Normalized Mutual Information (NMI) measure (Da-
non et al., 2005), which indicates the correlation be-
tween the partitions in a scale from 0 to 1, where 1
indicates a perfect correlation.
First, Figure 2 present the average NMI values
achieved by SpecDiv-G, SpecDiv-G’ and by the refe-
rence disjoint community detection algorithms Lou-
vain method, LP, Infomap and Walktrap. According
to these figures, SpecDiv-G’ outperformed SpecDiv-
G and presented better results than the algorithms
with the exception of Infomap and Walktrap. Despite
being worse than SpecDiv-G’, SpecDiv-G still obtai-
ned better results than Louvain and LP for networks
with µ ≥ 0.3.
0.0 0.2 0.4 0.6 0.8
0.0
0.2
0.4
0.6
0.8
1.0
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
SpecDiv−G'
SpecDiv−G
Louvain−G
LP−G
Infomap−G
Walktrap−G
NMI
µ
(a) Networks from SD.
0.0 0.2 0.4 0.6 0.8
0.0
0.2
0.4
0.6
0.8
1.0
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
SpecDiv−G'
SpecDiv−G
Louvain−G
LP−G
Infomap−G
Walktrap−G
NMI
µ
(b) Networks from LD.
Figure 2: Average NMI values over 5 executions of the met-
hods for detecting disjoint communities.
Figure 3 displays the average NMI values achie-
ved by SpecDiv-G’ and by the disjoint community
detection strategy taking as input the link partition
obtained by the reference algorithms applied to the
line graphs. It also presents the results of OSLOM
3
and of the disjoint version of SLPA.
The results of SpecDiv, Louvain, LP, Infomap
and Walktrap improved on average 9.93%, 14.95%,
3
OSLOM identified overlapping in some of the disjoint
networks. We chose one community label from each over-
lapping vertex to present its results.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
314
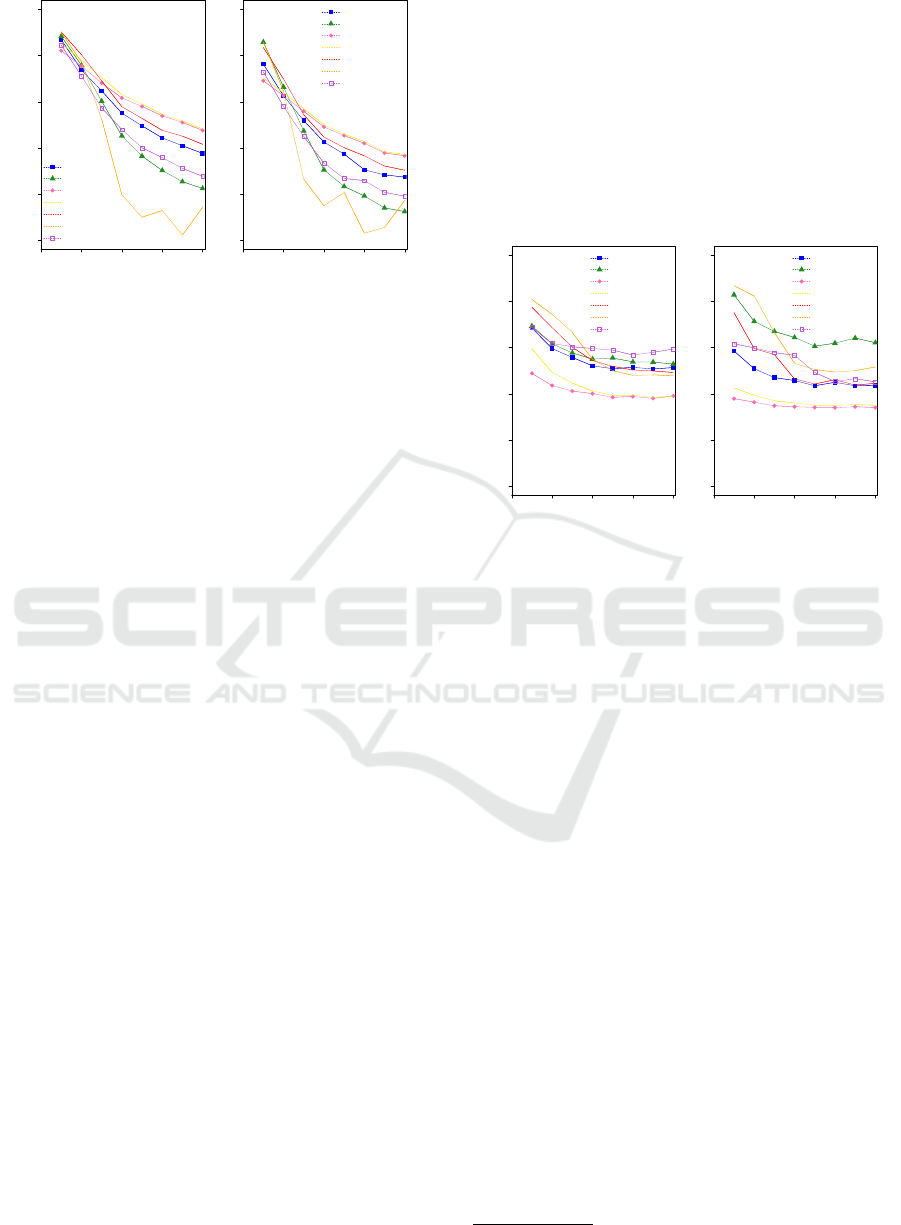
0.0 0.2 0.4 0.6 0.8
0.0
0.2
0.4
0.6
0.8
1.0
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
SpecDiv−G'
Louvain−G'
LP−G'
Infomap−G'
Walktrap−G'
OSLOM
SLPA
NMI
µ
(a) Networks from SD.
0.0 0.2 0.4 0.6 0.8
0.0
0.2
0.4
0.6
0.8
1.0
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
SpecDiv−G'
Louvain−G'
LP−G'
Infomap−G'
Walktrap−G'
OSLOM
SLPA
NMI
µ
(b) Networks from LD.
Figure 3: Average NMI values over 5 executions of the met-
hods for detecting disjoint communities using line graphs.
170.25%, 2.64% and 2.6%, respectively, when com-
pared to those for networks from SD presented in
Figure 2(a) and 16.62%, 20.32%, 258.57%, 4.64%
and 1.63%, respectively, when compared to those
for networks from LD presented in 2(b). LP, Info-
map and Walktrap were able to find better results
than SpecDiv-G’ by using the introduced link stra-
tegy. Moreover, the disjoint communities obtained
from the link partitions, with the exception of Lou-
vain, were better than those found by OSLOM and
SLPA for µ ≥ 0.3.
The maximum standard deviation values from the
presented averages results of LP and OSLOM were
0.19 and 0.27, respectively. The remaining algo-
rithms found results consistently closer to the average,
reporting standard deviations values lower than or
equal to 0.05.
These results allow us to conclude that even
though the introduced link strategy is mainly designed
to detect overlapping communities, it can improve the
detection of disjoint communities in networks.
7.2 Overlapping Communities
The traditional NMI employed in the previous section
is not capable of comparing overlapping communi-
ties. In this sense, we employed the extension of the
NMI introduced by Lancichinetti et al. (2009), called
oNMI, to assess the communities with respect to the
ground truth provided by the LFR software. The im-
plementation is due to McDaid et al. (2011).
In this section, we contrast the oNMI values achie-
ved by the introduced overlapping strategy having
as input link partitions obtained by SpecDiv, Lou-
vain method, Infomap, LP and Walktrap with those
achieved by the state-of-the-art overlapping methods
OSLOM and SLPA
4
.
Figure 4 reports the oNMI values obtained by the
algorithms. According to Figure 4(a), for µ ≤ 0.3,
OSLOM obtained the communities with the highest
oNMI values. For µ ≥ 0.4, SLPA found the com-
munities with the highest oNMI values. SpecDiv-
G’, Louvain-G
0
and Walktrap-G
0
achieved better re-
sults than OSLOM for networks with µ ≥ 0.5 and
SpecDiv-G’ was better than Walktrap-G
0
in networks
with µ ≥ 0.6.
0.0 0.2 0.4 0.6 0.8
0.0
0.2
0.4
0.6
0.8
1.0
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
SpecDiv−G'
Louvain−G'
LP−G'
Infomap−G'
Walktrap−G'
OSLOM
SLPA
oNMI
µ
(a) Networks from SOv.
0.0 0.2 0.4 0.6 0.8
0.0
0.2
0.4
0.6
0.8
1.0
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
SpecDiv−G'
Louvain−G'
LP−G'
Infomap−G'
Walktrap−G'
OSLOM
SLPA
oNMI
µ
(b) Networks from LOv.
Figure 4: Average oNMI values over 5 executions of the
methods for detecting overlapping communities.
On the other hand, Figure 4(b) shows that in net-
works with large overlapping communities, OSLOM
found the communities with the highest oNMI values
for µ ≤ 0.2 and Louvain-G
0
method found the com-
munities with the best oNMI values for µ ≥ 0.3.
The standard deviations of OSLOM and SLPA
from the average values in the large community net-
works, however, were in the intervals [0.02,0.06] and
[0.02, 0.23], respectively. Thereby, SLPA might not
find consistently good results in all its executions. On
the other hand, the standard deviations of the remai-
ning algorithms were lower than or equal to 0.05.
These values suggest the robustness of the algorithms
based on link partitions.
We, nonetheless, highlight that these networks are
very sparse and thus are different from the traditional
denser LFR networks considered in most of the expe-
riments performed in the literature.
7.3 Running Times
Table 2 summarizes the average running times of the
algorithms to detect disjoint and overlapping commu-
nities. The numbers presented between parentheses
are the standard deviation values from the averages.
4
The threshold parameter of SLPA was set to 0.1.
Spectral Algorithm for Line Graphs to Find Overlapping Communities in Social Networks
315

Table 2: Average running times of the algorithms in seconds.
Set SpecDiv-G’ Louvain-G
0
LP-G
0
Infomap-G
0
Walktrap-G
0
OSLOM SLPA
SD 370.88 (51.17) 32.05 (12.25) 45.92 (9.74) 45.17 (12.58) 38.49 (15.4) 37.86 (9.14) 1.74 (0.12)
LD 346.55 (38.36) 38.31 (10.53) 57.57 (4.89) 56.61 (5.6) 45.5 (13.2) 41.02 (4.34) 1.78 (0.16)
SOv 451.1 (70.05) 15.89 (3.59) 21.99 (2.03) 22.63 (3.31) 18.94 (4.64) 36.56 (8.24) 2.8 (0.22)
LOv 439.99 (30.43) 18.88 (4.06) 26 (2.52) 26.81 (2.57) 22.23 (4.9) 39.58 (3.79) 2.8 (0.28)
Despite the good results achieved by SpecDiv-G’ in
disjoint and overlapping communities, it is the most
time-consuming algorithm. Even though the fastest
algorithm to find overlapping communities is SLPA,
it obtained disjoint partitions worse than SpecDiv-G’.
We did not present the results of SpecDiv-G,
Louvain-G, LP-G, Infomap-G and Walktrap-G be-
cause they presented worse results than SpecDiv-G’,
Louvain-G
0
, LP-G
0
, Infomap-G
0
and Walktrap-G
0
, re-
spectively, and are not capable of finding overlapping
communities. However, we must point out that, with
the exception of SpecDiv-G, the remaining algorithms
required less than 2s to find disjoint communities.
SpecDiv-G required on average 48.8s and 47.55s to
find disjoint communities for SD and LD, respecti-
vely.
8 CONCLUSIONS
Overlapping community detection in networks is a
challenging problem explored by a few studies in the
literature. In particular, a research direction to appro-
ach it consists of applying community detection algo-
rithms to the line graphs of the networks under inves-
tigation.
In this paper, we propose a strategy to detect
overlapping communities in networks founded on de-
tecting link partitions in line graphs and hence de-
fining the overlapping communities by an algorithm
whose input is link partitions. As part of the strategy,
we suggest a spectral community detection algorithm
named SpecDiv.
The results of the experiments performed using
LFR networks showed that the overlapping commu-
nities found by the strategy based on line graphs
are competitive with state-of-the-art overlapping met-
hods.
Additional experiments were carried out using
disjoint LFR networks. As a result, the proposed stra-
tegy obtained better vertex partitions from the link
partitions than those obtained by SpecDiv and by the
reference algorithms applied to the original graphs.
In a case study using a Twitter network, we found
that most of the highest degree vertices do not belong
to overlapping communities. On the other hand, al-
most half of the users that use hateful speech belong
to overlapping communities. We have also observed
that hateful users belong to overlapping communities
which includes other hateful users. This observation
suggests the study of the influence of these users on
the rest of the network.
A major advantage of the introduced overlap-
ping strategy is its capability of obtaining overlapping
communities from any vertex community detection
algorithm.
The presented strategy is intended to be employed
in sparse networks when the number of vertices is ap-
proximately the number of edges. A lot of large-scale
networks have that characteristic. The high cost of the
methods based on line graphs makes them unsuitable
for large dense networks. To better approach this type
of networks, the strategy must be parallelized to be
more efficient in multi-core computers.
We suggest as a future work to reduce substanti-
ally the number of edges of line graphs by conside-
ring edge contraction strategies in the original or the
line graph itself. Another research direction is the ex-
tension of the presented methods to support directed
graphs.
ACKNOWLEDGEMENTS
This work was funded by São Paulo Research Foun-
dation (FAPESP), grant numbers: 2016/22688-2 and
2015/21660-4; and by Conselho Nacional de Desen-
volvimento Científico e Tecnológico (CNPq), grant
numbers: 448614/2014-6 and 308708/2015-6. The
second author is grateful to Leonardo V. Rosset for
giving her a hand.
REFERENCES
Ahn, Y.-Y., Bagrow, J. P., and Lehmann, S. (2010). Link
communities reveal multiscale complexity in net-
works. Nature, 466(7307):761.
Ali, H. T. and Couillet, R. (2017). Improved spectral
community detection in large heterogeneous net-
works. The Journal of Machine Learning Research,
18(1):8344–8392.
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., and Le-
febvre, E. (2008). Fast unfolding of communities
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
316

in large networks. Journal of Statistical Mechanics:
Theory and Experiment, 2008(10):P10008.
Brandes, U., Delling, D., Gaertler, M., Gorke, R., Hoefer,
M., Nikolosk, Z., and Wagner, D. (2008). On modula-
rity clustering. IEEE Transactions on Knowledge and
Data Engineering, 20:172–188.
Csardi, G. and Nepusz, T. (2006). The igraph software
package for complex network research. InterJournal,
Complex Systems:1695.
Danon, L., Diaz-Guilera, A., Duch, J., and Arenas, A.
(2005). Comparing community structure identifica-
tion. Journal of Statistical Mechanics: Theory and
Experiment, 2005(09):P09008.
Evans, T. S. and Lambiotte, R. (2009). Line graphs, link
partitions, and overlapping communities. Physical Re-
view E, 80:016105.
Fortunato, S. and Hric, D. (2016). Community detection in
networks: A user guide. Physics Reports, 659:1–44.
Gui, C., Zhang, R., Hu, R., Huang, G., and Wei, J. (2018).
Overlapping communities detection based on spectral
analysis of line graphs. Physica A: Statistical Mecha-
nics and its Applications, 498:50–65.
Jiang, J. Q. and McQuay, L. J. (2012). Modularity functions
maximization with nonnegative relaxation facilitates
community detection in networks. Physica A: Statisti-
cal Mechanics and its Applications, 391(3):854 – 865.
Krzakala, F., Moore, C., Mossel, E., Neeman, J., Sly, A.,
Zdeborová, L., and Zhang, P. (2013). Spectral re-
demption in clustering sparse networks. Proceedings
of the National Academy of Sciences, 110(52):20935–
20940.
Lancichinetti, A., Fortunato, S., and Kertész, J. (2009). De-
tecting the overlapping and hierarchical community
structure in complex networks. New Journal of Phy-
sics, 11(3):033015.
Lancichinetti, A., Fortunato, S., and Radicchi, F. (2008).
Benchmark graphs for testing community detection
algorithms. Physical Review E, 78(4):046110.
Lancichinetti, A., Radicchi, F., Ramasco, J. J., and Fortu-
nato, S. (2011). Finding statistically significant com-
munities in networks. PLOS ONE, 6(4):1–18.
Lehoucq, R. B., Sorensen, D. C., and Yang, C. (1998). AR-
PACK users’ guide: solution of large-scale eigenvalue
problems with implicitly restarted arnoldi methods.
volume 6 of Software, Environments, Tools. SIAM.
Li, M. and Liu, J. (2018). A link clustering based me-
metic algorithm for overlapping community detection.
Physica A: Statistical Mechanics and its Applications,
503:410–423.
McDaid, A. F., Greene, D., and Hurley, N. (2011).
Normalized mutual information to evaluate overlap-
ping community finding algorithms. arXiv preprint
arXiv:1110.2515.
Nascimento, M. C. and De Carvalho, A. C. (2011). Spectral
methods for graph clustering–a survey. European
Journal of Operational Research, 211(2):221–231.
Newman, M. (2013a). Spectral community detection in
sparse networks. arXiv preprint arXiv:1308.6494.
Newman, M. E. (2013b). Spectral methods for community
detection and graph partitioning. Physical Review E,
88(4):042822.
Newman, M. E. J. and Girvan, M. (2004). Finding and
evaluating community structure in networks. Physi-
cal Review E, 69(2):026113.
Newman, M. E. J. (2006). Finding community structure in
networks using the eigenvectors of matrices. Physical
Review E, 74(3):036104.
Nicosia, V., Mangioni, G., Carchiolo, V., and Malgeri, M.
(2009). Extending the definition of modularity to di-
rected graphs with overlapping communities. Jour-
nal of Statistical Mechanics: Theory and Experiment,
2009(03):P03024.
Pizzuti, C. (2009). Overlapped community detection in
complex networks. In Proceedings of the 11th An-
nual conference on Genetic and Evolutionary Com-
putation, pages 859–866. ACM.
Pons, P. and Latapy, M. (2005). Computing communities in
large networks using random walks. In International
Symposium on Computer and Information Sciences,
pages 284–293. Springer.
Raghavan, U. N., Albert, R., and Kumara, S. (2007).
Near linear time algorithm to detect community struc-
tures in large-scale networks. Physical Review E,
76(3):036106.
Ribeiro, M. H., Calais, P. H., Santos, Y. A., Almeida,
V. A., and Meira Jr, W. (2018). Characterizing and
detecting hateful users on twitter. arXiv preprint
arXiv:1803.08977.
Rosvall, M. and Bergstrom, C. T. (2007). An information-
theoretic framework for resolving community struc-
ture in complex networks. Proceedings of the Natio-
nal Academy of Sciences, 104(18):7327–7331.
Shi, C., Cai, Y., Fu, D., Dong, Y., and Wu, B. (2013). A link
clustering based overlapping community detection al-
gorithm. Data & Knowledge Engineering, 87:394–
404.
Singh, A. and Humphries, M. D. (2015). Finding commu-
nities in sparse networks. Scientific Reports, 5:8828.
Xie, J., Kelley, S., and Szymanski, B. K. (2013). Overlap-
ping community detection in networks: The state-of-
the-art and comparative study. ACM Computing Sur-
veys, 45(4):43:1–43:35.
Xie, J., Szymanski, B. K., and Liu, X. (2011). SLPA: Un-
covering overlapping communities in social networks
via a speaker-listener interaction dynamic process. In
Data Mining Workshops (ICDMW), 2011 IEEE 11th
International Conference on, pages 344–349. IEEE.
Yang, Z., Algesheimer, R., and Tessone, C. J. (2016).
A comparative analysis of community detection al-
gorithms on artificial networks. Scientific Reports,
6:30750.
Zhang, S., Wang, R.-S., and Zhang, X.-S. (2007). Identifi-
cation of overlapping community structure in complex
networks using fuzzy c-means clustering. Physica A:
Statistical Mechanics and its Applications, 374(1):483
– 490.
Zhang, X. and Newman, M. (2015). Multiway spectral
community detection in networks. Physical Review
E, 92(5):052808.
Zhou, X., Liu, Y., Wang, J., and Li, C. (2017). A density
based link clustering algorithm for overlapping com-
munity detection in networks. Physica A: Statistical
Mechanics and its Applications, 486:65–78.
Spectral Algorithm for Line Graphs to Find Overlapping Communities in Social Networks
317
