Hierarchical Reinforcement Learning Introducing Genetic Algorithm for

POMDPs Environments

Kohei Suzuki

and Shohei Kato

1, 2

Dept. of Computer Science and Engineering Nagoya Institute of Technology,

Gokiso-cho, Showa-ku, Nagoya 466-8555, Japan

Frontier Research Institute for Information Science, Nagoya Institute of Technology,

Gokiso-cho, Showa-ku, Nagoya 466-8555, Japan

Keywords:

Reinforcement Learning, Genetic Algorithm, Perceptual Aliasing.

Abstract:

Perceptual aliasing is one of the major problems in applying reinforcement learning to the real world. Percep-

tual aliasing occurs in the POMDPs environment, where agents cannot observe states correctly, which makes

reinforcement learning unsuccessful. HQ-learning is cited as a solution to perceptual aliasing. HQ-learning

solves perceptual aliasing by using subgoals and subagent. H owever, subagents learn independently and have

to r el earn each time when subgoals change. In addition, the number of subgoals is ﬁxed, and the number of

episodes in reinforcement learning increases unless the number of subgoals is appropriate. In this paper, we

propose the reinforcement learning method that generates subgoals using genetic algorithm. We also report

the effectiveness of our method by some experiments with partiall y observable mazes.

1 INTRODUCTION

There is a major problem in practical application of

reinfor c ement learning in the robotics ﬁeld. Many

studies of reinforc ement learning use Markov deci-

sion processes (MDPs), where agents observe sta-

tes correctly. However, it is not always possible for

agents to observe states accurately in real environ-

ments. For example, in case of autonomous mobile

robots, perceptual aliasing (Whitehea d and Ballard,

1991) arises from various factors such as sensor fai-

lure. Perceptual aliasing means that different states

are rec ognized as the same state. Because of this,

agents cannot learn the rou te correctly. This environ-

ment is called the partially observable Markov deci-

sion processes (POMDPs) (Whitehead and Ballard,

1990). A learning metho d under the POMDPs en-

vironm ent is necessary for practical use of reinforce-

ment learn ing in the real world.

There are many types of solutions to per cep-

tual aliasing: the methods u sin g sub goals (Wiering

and Schmidhuber, 1997; Nomura and Kato, 2015)

(Suzuki and Kato, 2017), the methods using proﬁt

sharing (PS) (Miyazaki and Kobayashi, 2003; Arai

and Sycara , 2001; Uemu ra et al., 2005) , the methods

using recurren t neural networks (Mnih et al., 2016;

Sridharan et a l., 2010; Sallab et al., 2017), the met-

hods using bayesian (Ross et al., 2008; Poupart et al.,

2006; Thomson and Young, 2010) a nd the methods

using state transition history (Chrisman, 199 2; Mc-

Callum, 1 993; McCallum, 1995). In this paper, we

focus on the methods usin g subgoals b ecause these

methods are able to adapt to c omplex tasks. HQ-

learning (Wiering and Schmidh uber, 1997) and First

Visit Proﬁt Sharing (FVPS) (Ara i and Sycara, 2001)

are cited as solutions to perceptual aliasing. HQ-

learning solves perceptual aliasing by using subgoals

and subagents. Th e subgoals are determined by HQ-

values, which are values of subg oals. However, sub-

agents learn independently and have to relearn each

time when subgoals change. In addition, the number

of subgoals is ﬁxed, and the number of episodes in-

creases unless the numbe r of subgoals is appropriate.

Therefore, learning efﬁciency is poor. FVPS is a m et-

hod that improves Proﬁt Sharing (PS), and updates

state-action pairs of each rule only once per one epi-

sode. However, it is difﬁcult for FVPS to set the ini-

tial value of the state-action pair s which is suitable for

the environment, moreover, FVPS accumulates value.

Therefore, there is a high possibility of falling into

local solution s.

In th is paper, we propose the reinforcement le-

arning method that generates subgoals using gen e-

tic algo rithm (GA). We explain perceptual aliasing in

Section 2, propose Subgoal Evolution-based Reinfor-

cement Learning (SERL) in Section 3, and conduct

experiments under POMDPs environm ent in Section

4. We propose Hy brid learning using PS and GA

318

Suzuki, K. and Kato, S.

Hierarchical Reinforcement Learning Introducing Genetic Algorithm for POMDPs Environments.

DOI: 10.5220/0007405403180327

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 318-327

ISBN: 978-989-758-350-6

Figure 1: A POMDP environment.

(HPG) that improves SE RL and report the effective-

ness of our method by some exp eriments with parti-

ally observable mazes in Section 5 and Section 6.

2 PERCEPTUAL ALIASING

In this paper, we consider the grid world as shown in

Figure 1. The ag ent can per ceive only eight neighbor

cells and performs self-localization by those cells.

There are four types of action: “up” “ down” “left”

and “right”. In Figure 1, the agent must go through

the states “A” and “B” to reach the goal state “G”

from the start state “S”. However, the agent is u na-

ble to distinguish between state “A” and “B” because

these states have the sam e eight neighbor cells. This

problem is called perceptual a liasing. This makes the

agent select “up” in state “A” becau se it selects “up”

in state “B” which is close to the goal. Therefore, the

agent falls into a loop in state “A”. In this paper, we

solve this problem.

3 SUBGOAL EVOLUTION-BASED

REINFORCEMENT LEARNIN G

(SERL)

SERL algorithm g e nerates agents that solve percep-

tual aliasing using GA. Each agent has subage nts and

subgoals represen ted in the binary string. Subgoals

divide a POMDPs environment into MDPs environ-

ments. Subagen ts perform reinforcement learning un-

der the MDPs environments. In acco rdance with the

result of the reinforcement learning, genetic operation

is perf ormed, and subgoals are generated. The over-

view of the proposed method is shown in Figure 2.

The procedure of SERL is shown below.

1. Initial population generation

Generate Y ag ents. Each agent has (X + 1) suba-

gents, which have a subgoal and Q-table. Subgo-

als are generated randomly.

2. Reinfo rcement learning

Subagents performs reinforcement learning using

Q-learning(Watkins and Dayan, 1992) in each

agent. Reinforc e ment learning is perfo rmed in or-

der of subagents. The order shifts to the next sub-

agent when the subagent has reach the subgoal.

3. Genetic operation

Subgoals are inherited by crossover and are gene-

rated by mutation.

4. Repeat the procedure 2 and 3 for the number of G

generations.

3.1 Initial Population Generation

Agents th a t have subagents and subgoals are ge -

nerated in initial population generation. Subgoals

are represented in th e binary string as shown in Fi-

gure 3, where “1” and “0” means a wall a nd a

road respe ctively, because the observation range of

the agent is eight neighbo r cells in th is paper. In

SERL, each agent randomly generates sub goals be-

cause the agents do not know what kinds of state exist

in unknown environment.

3.2 Reinforcement Learning

In reinforcement learning, subagents perform rein-

forcement le arning using Q -learning. SERL sets the

maximum number of steps in an episode an d ﬁnis-

hes reinforcement learning if the number of steps in

an episode reaches the maximum number. This is b e -

cause there is a possibility that the subagent does not

reach the subgoal which agents generated ran domly.

3.3 Genetic Operation

3.3.1 Fitness Calculation

After reinforcement lea rning, agents perform one epi-

sode using greedy selection in order to remove the

randomness of action selection. Fitness is calcula-

ted using the result of this one episode. The ﬁtness

function is shown below.

F1 =











Re +

Max

step − step

sub × a

(reach the goal)

goal

(not reach the goal)

, (1)

where, Re is the goal reward value; Max

step is

the maximum step number, step is the numb e r of

Hierarchical Reinforcement Learning Introducing Genetic Algorithm for POMDPs Environments

319

Figure 2: Overview of the proposed method.

Figure 3: Subgoal expression of state X.

steps taken to ob ta in rewards, sub is the numbe r of

subagents, goal is num ber of tim es th e agent reached

the goal during reinforcement learning, and a and b

are hyperparameter. The b is set to a value that

goal

does not exceed the go al reward Re. The goal is used

for ﬁtness calculation when the agent does not reach

the goal in one episode using the gree dy selection.

This is because, the agent is likely to have effective

subgoals if the agent reaches the goal during reinfor-

cement learning.

3.3.2 Crossover

SERL performs the fo llowing two kinds o f crossover.

Crossover 1 performs uniform crossover of subgo-

als as shown in Figure 4(a). Subgoals are inherited

and the state-action pairs are initialized. This is ex-

pected to avoid local solutions.

Crossover 2 performs single-point crossover of

subagents as shown in Figure 4(b). Subgoals and

the state-action pairs a re inherited. Lea rning efﬁ-

ciency incr e ases by inheriting the state-action pairs.

In addition, the crossover points of two parents are

not common points, but are random points in each

agent, which makes the number of subgoals d ynami-

cally changes an d is suitable for the environment.

In general, crossover generates two offspring fr om

two parents. However, SERL just selects one of two

offspring.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

320

(a) Crossover 1

(b) Crossover 2

Figure 4: Crossover.

Figure 5: Maze of Yamamura(Yamamura et al., 1995).

3.3.3 Mutation

There is a possibility that effective subgo als are not

generated in initial population generation. In this

case, mutation is important so as to avoid local solu-

tions. In muta tion, SERL inverts a part of the binary

string r andomly, which expresses the subgoal. In ad-

dition, SERL changes a p art of the binary string to

“don’t care”. “Don’t care” means either “0” or “1”,

that is, agent does not care whether correspon ding cell

is road or wall. This makes subgoals more diverse.

4 COMPARETIV E

EXPERIMENTS UNDER THE

POMDPS

We performed comparative experiments using maze

of Yamamura (Yamamura et al. , 1995) shown in Fi-

gure 5. Three methods are used: SERL, HQ-learning,

and FVPS. As explaine d in Section 2 , the ob servation

range of age nts is 8 neighbor cells, and the actions are

Table 1: Parameters.

Number of generations 10

Number of agents 20

Number of reinforcement learning episodes 30

Elite preservation (%) 20

Crossover 1 (%) 12.5

Crossover 2 (%) 87.5

Mutation rate (%) 5

Figure 6: The result in maze of Yamamura.

of four types “up” , “down”, “left” and “r ight”. Per-

ceptual aliasing occurs in the states, “A”, “B”, “C”,

“D” and “E”. The parameters for SERL is shown in

Table 1. The number of episodes of each method is

6,000. The maximum number of steps in an episode is

150. T he number of in itial subgoals of SERL and the

number of subgoals of HQ-learning are 2. The expe -

riments were performed in 100 runs for each method,

then the average value of results was calculated.

The experimental results a re shown in Figure 6.

The vertical axis of the graph shows the minimum

number of steps to reach the goal, and the horizon-

tal axis shows the number of reinforcement learning

episodes. SERL learned slower than the other two

methods. This is because subgoals were generated

randomly at the initial population generation, which

did not make m a ny subgoals suitable for the maze. In

addition, SE RL did not converge to th e optimal so -

lution. SERL took time to ﬁnd appropriate subgoals

because a new subgoal, which the initial individuals

do not h ave, is generated only by mutation. There-

fore, SERL shou ld generate effective subgoals at the

initial population generation.

Hierarchical Reinforcement Learning Introducing Genetic Algorithm for POMDPs Environments

321

5 HYBRID LEARNING PROFIT

SHARING AND GENETIC

ALGORITHM (HPG)

We pro pose HPG alg orithm that agents select subgo-

als among subgoal candidates at initial population ge-

neration. HPG judges aliased states as subgoal candi-

dates using PS. The ﬂow of HPG is the same as SERL.

HPG improves initial population generation and rein-

forcement learning in SERL.

5.1 Initial Population Generation

The procedure of initial generation population is

shown below.

1. A n agent per forms reinforcement learning using

PS.

2. Subgoal candidates are determined based o n state-

action pairs in each state.

3. Subgoals of each agent are determined randomly

among the subgoal candidates.

HPG makes su bgoal candidates using PS, which is a

kind of reinforceme nt learning.

PS (Miyazaki et al., 1994)(Grefenstette, 1988) is

an ofﬂine learning method which collectively updates

state-action pairs after earning rewards, and actio ns

are often determined by roulette selection. The upda-

ting formula for state-action pairs P(s

, a

) o f action

in the state s

is shown below.

P(s

, a

) ← P(s

, a

) + f (x), (2)

where, f (x) is a reinforcement function and x is the

number of steps to earn rewards. The re inforceme nt

function often uses a geometric decreasing function.

However, HPG changes the way of updating state-

action pair s to judge aliased states.

HPG equally updates the state-action pairs of ru-

les selected in th e same state. Because of that, ea c h

rule is updated only once in one episode, an d the rein-

forcement function does not depend on the x. It is

expressed by the following formula.

f (R, W ) =

, (3)

where, R is a reward and W is length of the episode.

We propose two methods to genera te initial popula-

tion using this PS: HPG using a ction selection proba-

bility and H PG using entropy o f action selection.

5.1.1 HPG Using Action Selection Probability

(HPG-a)

HPG-a determines sub goal candidates using action

selection probabilities. PS updates the rules equally

in each state. The value of state-action pairs are the

same when there are multiple essential rules to earn

the reward in a certain state. The value of state- a ction

pairs are equal if all actions have to be selected to earn

the reward. Then, the action selection probabilities P r

are the value of th e following formula.

Pr =

|Action|

, (4)

There is a possibility that effective subgo als are not

generated in initial population ge neration. In this

case, mutation is important so as to avoid local solu-

tions. In mutation, SERL inverts a part of the binary

string randomly, which expresses the subgoal. In ad-

dition, SERL changes a p art of the binary string to

“don’t care”. “Don’t care” means eith er “0” or “1 ”,

that is, agent does not care whether corr esponding cell

is road or wall. This makes subgoals m ore diverse.

where, Action is set of selectable actions in a state.

The action selec tion probability of the necessary ru-

les for earning rewards never falls below the value of

(4) because the state- action pairs of the necessary ru-

les are deﬁnitely upd ated every time when the agent

earns a reward. In othe r words, the agent has to se-

lect different actions because there is a hig h possibi-

lity that perceptual aliasing occurs when the action

selection probabilities of mu ltiple rules are over the

value of (4) in one state. Therefore, the states where

action selection probabilities of multiple rules exceed

the value of (4) are set as subgoal candida te s.

5.1.2 HPG Using Entropy of Action Selection

(HPG-e)

HPG-e determines the subgoal can didates using en-

tropy o f action selection and calculates the entropy

En(s) of action selection in each state s by th e follo-

wing formula.

En(s) = −

∑

a∈Act(s)

P(a)log

P(a), (5)

where, Act is set of selectable actions, P(a) is the

action selection p robability of action a. The value

of (5) decreases when the action selection proba bility

of one action increases. In contr ast, the value of (5)

increases when the action selection probability of all

actions are equal. In other words, entropy of action

selection exp resses uncertainty of policy and in c rea-

ses und er POMDPs.

When the agent has to select two action (a

, a

)

on an aliased state s

∗

, these action selection pro babi-

lities app roach

and the others approach 0. Then, the

entropy of a c tion selection is the value of following

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

322

formu la.

En(s

∗

) = −

∑

a∈Act(s

∗

)

P(a)log

P(a)

= −

∑

a∈{a

}

P(a)log

P(a)

= −(

log

)

= 1 (6)

The entropy of action selection do es not exceed (6)

when only one action selection probability in a state

is large. Whereas, the entropy exceeds (6) when the

agent has to select at least two actions to reach the

goal. It is highly likely to be aliased state when the

state h as the entropy exceeding (6). Therefore the

state is set as a subgoal candidate in HPG-e. Then,

each agen t randomly determines subgoals among the

subgoal cand idates.

5.2 Reinforcement Learning

In SERL, subagents perform reinforcement learn ing

using Q-learning (Watkins and Dayan, 1 992). Howe-

ver, In HPG, subagents perfo rm PS as described in

Section 5.1. Uemura et al. (Uemura et al. , 2005) sho-

wed tha t it is not inferior to random selection if the

agent can select all the n ecessary rules for rewards

with the sam e prob a bility in the state, where the agent

has to select multiple rules to reach the goal. HPG sa-

tisﬁes this c ondition and is able to solve perceptual

aliasing because HPG gives rewards equally to ru les

in the same state. Therefore, it is possible to reach the

goal even when subgoals do not divide the POMDPs

environment well.

HPG involves h ybrid learning usin g PS a nd GA.

By combining the PS and GA, HPG compensates for

their disadvantages: loca l optima and learning efﬁ-

ciency.

5.3 Peformance of Judgement of

Aliased States

We compared the two methods (HPG-a and HPG-e)

using the maze shown in Figure 7 and consider their

respective performances of judgement of aliased sta-

tes. Experimental setup is the same as in Section 4.

Perceptual aliasing occ urs in red cells in each maze.

The maze in Figure 7(a) is an environment that the

different actions must be selected in each red cell. I n

state “2”, the agent has to select “le ft”. However, In

state “1”, it has to select an action except “left”. The

maze in Figure 7(b) is an environment where the age nt

is able to go the route which the agent avoids percep-

tual aliasing. The number of PS episodes is set to

(a) Maze 1

(b) Maze 2

Figure 7: Mazes.

Table 2: Result of Maze 1.

(a) The number of times red cells is determined

to be subgoal candidates ( the sum of 100 r uns)

❳

Method

Reward

50 100 300

HPG-a 100 100 97

HPG-e 100 100 100

(b) The sum of subgoal candidates (the average of

100 runs)

❳

Method

Reward

50 100 300

HPG-a 1.16 1.06 1.06

HPG-e 6.80 5.42 4.55

1000, and the parameters for PS are uniﬁed in both

methods. T he a ll initial values of the state-action pairs

are set to 10 and th e goal reward was set to any of 50 ,

100 and 300.

The results of Maze 1 are shown in Table 2. Ta-

ble 2(a) shows the number of times red cells are jud-

ged to be aliased state in 100 runs. HPG-a and HPG-e

were able to judge red cells as aliased state almost cor-

rectly. However, HPG-a failed to jud ge aliased state

when reward was 300. In state “2”, “left” is selected

and, in state “1”, any action o f thre e action s (“up”

“down” and “right”) is selected to reach the goal. The

selection probability of “left” in red cells increased,

whereas the selection probabilities of the other three

actions were dispersed and did not exceed (4). There-

fore, HPG-a could not judge aliased states correctly.

Table 2(b) shows the average o f the to tal number of

subgoal candidates in 100 runs. In HPG-a, the num-

ber of su bgoal candidates was close to 1 which is an

ideal value. However, the number of subgo al candi-

dates was large in HPG-e. This is because the diffe-

rence in state-action pairs was small while reinforce-

Hierarchical Reinforcement Learning Introducing Genetic Algorithm for POMDPs Environments

323

Table 3: Result of Maze 2.

(a) The number of times red cells is determined

to be subgoal candidates ( the sum of 100 r uns)

❳

Method

Reward

50 100 300

HPG-a 65 72 76

HPG-e 100 100 100

(b) The sum of subgoal candidates (the average of

100 runs)

❳

Method

Reward

50 100 300

HPG-a 1.31 1.19 1.18

HPG-e 8.67 6.77 5.31

ment learning was in progress, which made the en-

tropy of action selection probabilities large. As value

of reward increased, the reinforceme nt learning was

completed early and the number of subgoal candida-

tes was small.

The results of Maze 2 are shown in Table 3. HPG-

a had poor precision for judgement of aliased state

compare d to result of Maze 1. There are two rou-

tes to the goal in Maze 2. The state-action p airs of

”left” became high in the red cell if the agent did not

go to the route wh ich through the state ”1”. In that

case, there were no more rules that exceed (4). As the

reward increased, the difference in state-action pairs

between the two routes became larger and the pr e ci-

sion increased. Whereas, although HPG-e had many

subgoal cand idates, red cells could be acc urately jud-

ged as aliased states. This is because HPG- e judged

the state where action selections were dispersed by

using entropy. In such a state, there is a high possibi-

lity that there are multiple effective rules. Therefore,

HPG could correctly judge aliased states.

HPG-a is able to correctly determine the aliased

states as lon g as PS does not fall into a local solution

at initial population gen eration. Although HPG- e has

a loose determination criterion for a liased state and

increases the number of subgoal candidates, HPG-e

does not miss the aliased states. Therefore, HPG- a is

more suitable for simple mazes and HPG-e is more

suitable for calculating optimal solution.

5.4 Effectiveness of Initial Population

Generation of HPG under the

POMDPs

We report the effectiveness of HPG-a and HPG-e

using the maze used in Section 4. Experimental se-

tup is also the same as in Section 5 .3. The number of

episodes of PS a t initial population generation is 100,

the number of generation s is 10, the number of agents

Figure 8: The result in maze of Yamamura.

Figure 9: The maze of Wiering (Wiering and Schmidhuber,

1997).

is 20, the numbe r of reinforcem ent learning episodes

in each agent is 30, a nd the nu mber of initial subgoals

is 2.

The result is shown in Figur e 8. HPG-a and HPG-

e lear ned faster than FVPS and obtained good results.

FVPS took tim e to learn because initial value of state-

action pairs was sma ll. HQ-learning did not ﬁnd ap-

propriate subg oals. This is because HQ-learning has

256 selectable subgoals, which is difﬁcult to ﬁnd ap-

propriate subgoals. Whereas, HPG-a and HPG-e ge-

nerated effective subgoa ls by PS at initial population

generation, and the subgoals made the maze easier.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

324

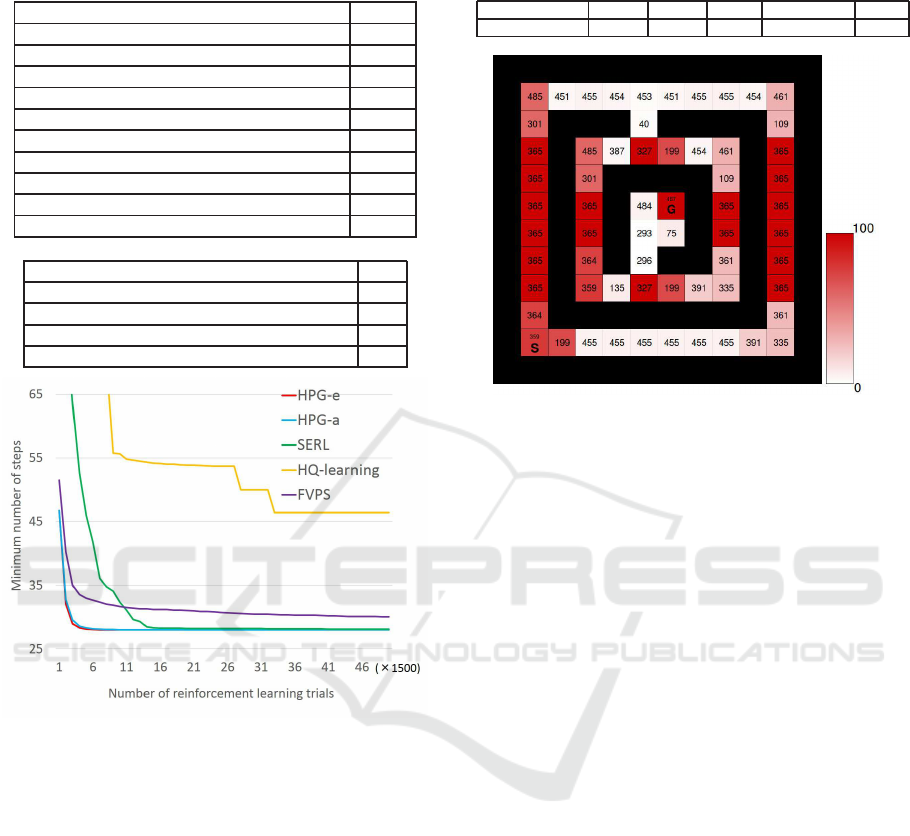
Table 4: Parameters.

(a) HPG-a and HPG-e

Number of PS episodes at initial population 15000

Number of generations 49

Number of agents 50

Number of reinforcement learning episodes 300

Elite preservation (%) 20

Crossover 1 (%) 12.5

Crossover 2 (%) 87.5

Mutation rate (%) 5

R (ﬁtness calculation) 100

a (ﬁtne ss c alculation) 0.2

b (ﬁtness calculation) 3

(b) SERL

Number of generations 50

Number of agents 50

Number of reinforcement learning episodes 300

Elite preservation (%) 30

Mutation rate (%) 5

Figure 10: T he result in a POMDP environment.

6 PERFORMANCE

EXPERIMENTS FOR A

POMDPS ENVIRONMENT

We performed experiments under the POMDPs en-

vironm ent using the maze of Wiering(Wiering and

Schmidhuber, 1997) sh own in Figure 9. The num-

bers in the cells represent observation information.

These number is obtained by converting 9-digit bi-

nary number, which expresses subgoal as shown in

Figure 3, into decimal number. The agent has to solve

the perceptual aliasing to reach the goal in this envi-

ronment. Perceptu al aliasing occurs in the red cells

and the blue cells on the shortest path indicated by

the red arrow. We per formed comparative experi-

ments with ﬁve methods: HPG-a , HPG-e, SERL, HQ-

learning and FVPS. The par ameters for each method

are shown in Table 4. The number of trials of each

Table 5: Minimum number of steps to reach t he goal (the

average of 100 runs).

HPG-a HPG-e SERL HQ-learning FVPS

Minimum steps 28.00 28.00 28.10 46.04 30.06

Figure 11: The distribution of subgoal candidates (HPG-a).

method is uniﬁed to 750,000 episodes. The sh ortest

step in this maze is 28, the maximum number of steps

in an episode is 150, a nd the number of initial subgo-

als is 3. The experiment was performed in 100 runs

for each method and the average value of results was

calculated.

The experimental results are shown in Figure 10

and Table 5. HPG-a and HPG-e converged to the sho r-

test step number. HPG-e obtained the optim a l solu-

tion in the sixth generation and HPG-a did in the 14th

generation. HPG-e completed learning in less than a

half of the trials of HPG-a. Whe reas, FVPS fell into

a local solutio n and SERL could n ot ﬁnd approp ri-

ate subgoals and did no t obtain an optimal solu tion.

HQ-learning had to relearn the p olicy each time when

the subgoal changed and failed to obtain the optimal

solution. It was conﬁrmed that the effectiveness of

subgoal gene ration by PS, a nd HPG-e is more suita-

ble than HPG-a in c omplicated environments where

there are multiple routes to the go al.

Figure 11 and Figure 12 show th e distribution of

subgoal candidates during 100 r uns. The deeper the

red, the greater the number of times the state is jud-

ged to be a subgoal candidate. Both metho ds accura-

tely judged red an d blue cells as aliased states in most

of th e runs. However, in HPG-a, “301” and “485”

were judged as subgoa l ca ndidates as not many as in

HPG-e. The agent h as to solve perceptual aliasing

occurring in these states to reach the goal in the shor-

test step. Whereas, HPG-e regarded these states as

subgoal candidates in more than 90% of experim ents.

Because of this, HPG-e got the optimal solution ear-

lier than HPG-a .

Hierarchical Reinforcement Learning Introducing Genetic Algorithm for POMDPs Environments

325

Figure 12: The distribution of subgoal candidates (HPG-e).

7 RELATED WORKS

7.1 HQ-learning

HQ-learning (Wiering and Schmidhuber, 1997) is a

hierarchical exten sion of Q -learning and divides task

into subtasks using subgoals. The agent has some

subagents which have Q-table independently. The

subagents perform Q(λ)-learning (Peng and Williams,

1994; Wiering and Schmidhuber, 1998) in order from

ﬁrst subagent and shift the next subagent when the

subagent reaches the subgoal. Action are selected ac-

cording to the Max-Bolzman n exp loration (Kaelbling

et al., 1996).

HQ-learning also learns appropriate sub goals.

The subgoals are determined by H Q -values which are

values of subgoals. HQ-value is updated when an

agent accomplish the task. The updating for mula for

HQ-value of subagent

is shown below.

i+1

−1

∑

t=t

t−t

R(s

, a

′

( ˆo

) ← R

+ γ

i+1

−t

[(1 − λ)max

′

∈O

i+1

′

)

+λHQ

′

i+1

( ˆo

i+1

( ˆo

) ← (1 − α)HQ

( ˆo

) + αHQ

′

( ˆo

), (7)

where, γ (0 ≤ γ ≤ 1) is the discount-rate, R is the re-

ward, HQ

(o) is HQ-value of state o, α is learning

rate, and λ (0 ≤ λ ≤ 1) is a constant. Subgoals are

selected using ε-greedy exploratio n (Sutton, 1996).

In HQ-learning, subagents have to relearn each

time when subgoals change. In addition, the number

of subgoals is ﬁxed. Therefore, learning efﬁciency is

poor. In HPG, State-action pairs are inherited by cros-

sover and the crossover points are random po ints in

each agent. Because of this, HPG obtained solutions

more quickly than HQ-learning as shown in Figure 8

and Figure 1 0.

7.2 First Visit Proﬁt Sharing

FVPS (Arai and Sycara, 2001) is an improved met-

hod of proﬁt sharing. FVPS changes reinforce ment

function and up dates state- action pairs of each rule

equally. The reinforcement function f (x) is shown

below.



(First time to update rule λ)

0 (Otherwise),

(8)

where, α

must be a constant value in state o

In FVPS, it is d ifﬁcult to set the initial value of

the state-action pairs, which is suitable for the envi-

ronment, moreover, FVPS accumulates the values of

state-action pairs. Therefore, FVPS often falls into

local solutions. In HPG, state-action p a irs ar e initi-

alized at crossover, which made HPG o btain o ptimal

solution as shown in Figure 10 and Table 5.

8 CONCLUSION

In this paper, we propo sed the reinforcement learnin g

method that generates subg oals using GA under the

POMDPs. SERL takes time to generate appropriate

subgoals. Therefore, we proposed HPG that genera-

tes subgoal candidates using PS. It was conﬁrmed that

HPG-a using action selection probability is suitable

for simple mazes and HPG-e using entropy of action

selection is suitable for comp licated mazes by some

experiments. However, HPG has a problem which

is appropriate subgoals are not found if PS cann ot

achieve the ta sk at initial population generation. To

solve the problem, we consider introducing swarm in-

telligence (Beni and Wang, 1993) to HPG. HPG intro-

duces swarm reinforcement learning (Iima and Kuroe,

2008) and shares state-action pairs, and deals with

complex problems.

In the future, we will improve the performan ce of

judgment of aliased states. We w ill a lso condu c t ex-

periments in the real world using mobile ro bots.

REFERENCES

Arai, S. and Sycara, K. (2001). Credit assignment method

for learning effective stochastic policies in uncertain

domains. In Proceedings of the 3rd Annual Confe-

rence on Genetic and Evolutionary Computation, pa-

ges 815–822. Morgan Kaufmann Publishers Inc.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

326

Beni, G. and Wang, J. (1993). Swarm intelligence in cellular

robotic systems. In Robots and B iological Systems:

Towards a New Bionics?, pages 703–712. Springer.

Chrisman, L. (1992). Reinforcement learning with percep-

tual aliasing: The perceptual distinctions approach. In

AAAI, pages 183–188.

Grefenstette, J. J. (1988). Credit assignment in rule disco-

very systems based on genetic algorithms. Machine

Learning, 3(2-3):225–245.

Iima, H. and Kuroe, Y. (2008). Swarm reinforcement le-

arning algorithms based on sarsa method. In SICE

Annual Conference, 2008, pages 2045–2049. I EEE.

Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996).

Reinforcement l earning: A survey. Journal of artiﬁ-

cial intelligence research, 4:237–285.

McCallum, R. A. (1993). Overcoming incomplete percep-

tion with utile distinction memory. In Proceedings of

the Tenth International Conference on Machine Lear-

ning, pages 190–196.

McCallum, R. A. (1995). Instance-based utile distinctions

for reinforcement learning with hidden state. In ICML,

pages 387–395.

Miyazaki, K. and Kobayashi, S. (2003). An extention of

proﬁt sharing to partially observable markov decision

processes : Proposition of ps-r* and its evaluation.

Journal of Japanese Society for Artiﬁcial Intelligence,

18(5):286–296.

Miyazaki, K., Yamamura, M., and Kobayashi, S. (1994).

A theory of proﬁt sharing i n reinforcement learning.

Journal of Japanese Society for Artiﬁcial Intelligence,

9(4):580–587. (in Japanese).

Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T.,

Harley, T., Silver, D., and Kavukcuoglu, K. (2016).

Asynchronous methods for deep reinforcement lear-

ning. In International conference on machine lear-

ning, pages 1928–1937.

Nomura, T. and Kato, S. (2015). Dynamic subgoal genera-

tion using evolutionary computation for reinforcement

learning under pomdp. International Symposium on

Artiﬁcial Life and Robotics, 2015(22):322–327.

Peng, J. and Williams, R. J. (1994). Incremental multi-st ep

q-learning. In Machine Learning Proceedings 1994,

pages 226–232. Elsevier.

Poupart, P., Vlassis, N., Hoey, J., and Regan, K. (2006).

An analytic solution t o discrete bayesian reinforce-

ment learning. In Proceedings of the 23rd internatio-

nal conference on Machine learning, pages 697–704.

ACM.

Ross, S., Chaib-draa, B., and Pineau, J. (2008). Bayesian

reinforcement learning in continuous pomdps. In In-

ternational Conference on Robotics and Automation

(ICRA).

Sallab, A. E., Abdou, M., Perot, E., and Yogamani,

S. (2017). Deep reinforcement learning frame-

work for autonomous driving. Electronic Imaging,

2017(19):70–76.

Sridharan, M., Wyatt, J., and Dearden, R. (2010). Plan-

ning to see: A hierarchical approach to planning vi-

sual actions on a robot using pomdps. Artiﬁcial Intel-

ligence, 174(11):704–725.

Sutton, R. S. (1996). Generalization in reinforcement le-

arning: Successful examples using sparse coarse co-

ding. In Advances in neural information processing

systems, pages 1038–1044.

Suzuki, K. and Kato, S. ( 2017). Hybrid learning using proﬁt

sharing and genetic algorithm for partially observable

markov decision processes. In International Confe-

rence on Network-Based Information Systems, pages

463–475. Springer.

Thomson, B. and Young, S. (2010). Bayesian update of dia-

logue state: A pomdp framework for spoken dialogue

systems. Computer Speech & Language, 24(4):562–

588.

Uemura, W., Ueno, A., and Tatsumi, S. (2005). An episode-

based proﬁt sharing method for pomdps. IEICE Tran-

sactions on Fundamentals of Electronics, Communi-

cations and Computer Sciences, 88(6):761–774. (in

Japanese).

Watkins, C. J. and Dayan, P. (1992). Q-learning. Machine

learning, 8(3-4):279–292.

Whitehead, S. D. and Ballard, D. H. (1990). Active percep-

tion and reinforcement learning. Neural Computation,

2(4):409–419.

Whitehead, S. D. and Ballard, D. H. (1991). Learning to

perceive and act by trial and error. Machine Learning,

7(1):45–83.

Wiering, M. and Schmidhuber, J. (1997). Hq-learning.

Adaptive Behavior, 6(2):219–246.

Wiering, M. and Schmidhuber, J. (1998). Fast online q (λ).

Machine Learning, 33(1):105–115.

Yamamura, M., Miyazaki, K., and Kobayashi, S. (1995). A

survey on learning for agents. The Japanese Society

for Artiﬁcial I ntelligence, 10(5):683–689.

Hierarchical Reinforcement Learning Introducing Genetic Algorithm for POMDPs Environments

327