Passive Path Imbalance Measurement in Fiber Optic Interferometer
using Homodyne PGC Scheme
Shubham Mirg and Pradeep Kumar K.
Department of Electrical Engineering, Indian Institute of Technology Kanpur, Kanpur-208016, India
Keywords:
Fiber Optic Interferometer, Homodyne PGC, Path Imbalance Measurement.
Abstract:
We demonstrate a passive measurement technique for interferometer path imbalance using homodyne PGC.
A 20.8 kHz frequency modulated optical source is employed to interrogate an unbalanced Michelson interfer-
ometer. The spectrum of the received photocurrent is then recorded for various frequency deviation values.
The variation in harmonic peak powers enables us to determine path imbalances. Different path imbalances
are estimated and verified against the pre-calibrated values. The measurement scheme proposed requires no
feedback and can be employed to passively measure path imbalances in interferometer sensor arrays already
laid out in the field.
1 INTRODUCTION
Fiber interferometeric sensors work by transducting
the measurand induced strain into a phase shift in the
optical carrier used for interrogation (Udd and Spill-
man Jr, 2011), (Santos and Farahi, 2014). The phase
shift can be converted into intensity changes by in-
ducing a path difference between the arms of the in-
terferometer.
The environmental perturbations from changes
in temperature, mechanical vibrations etc. cause a
slowly varying phase drift in the interferometer which
in turn severely alters the operating point of the inter-
ferometer thus hindering the linear recovery of high
frequency phase shifts. This problem is called the
fading problem (Sheem et al., 1982) and can be cir-
cumvented by employing passive interrogation tech-
niques(Cranch et al., 2003). Two of the most widely
used techniques for passive interrogation are homo-
dyne phase generated carrier (PGC) (Dandridge et al.,
1982) and differential delay heterodyne (Henning,
1983). Both of techniques employ unbalanced in-
terferometers and thus a passive technique to recali-
brate the sensors after they have been laid out in the
field is also required. Differential Delay Heterodyne
uses pulses at a temporal shift equal to the optical
path delay. Having a frequency shift between the two
pulse enables to have a phase modulated heterodyne
carrier output at the photodiode. The sine and co-
sine components of phase of interest are obtained by
synchronously mixing the photocurrent with in-phase
and quadrature version of heterodyne frequency. Ho-
modyne PGC scheme involves the frequency modu-
lation of the interrogating optical input and the re-
ceived signal involves extracting sine and cosine of
phase of interest from the harmonics of the received
signal by synchronously mixing them with appropri-
ate frequencies. From the sine and cosine of phase
of interest approaches like arctangent and Differen-
tiation and Cross multiplication (DCM) are used to
recover the signal of interest. Knowledge of path im-
balance is important in the above demodulation tech-
niques for appropriate scaling of the sine and cosine
terms by varying the frequency deviation suitably.
The path lengths of each arm can be calibrated
in lab environment and the difference can be used
to measure the path imbalance. However in sce-
narios where calibration in lab environment is not
feasible such as underwater fiber optic hydrophone
array (Cranch et al., 2003), a passive path imbal-
ance measurement technique is required. The ampli-
tudes of harmonic peaks in the spectrum of the re-
ceived photocurrent in homodyne PGC scheme are
in proportion to Bessel functions. The arguments of
whom are dependent on frequency deviation and im-
balance in the interferometer. By using properties
of Bessel’s J
n
recurrence relation (Sudarshanam and
Srinivasan, 1989), (Jin et al., 1991) and (Huang and
Lin, 2008), argument of Bessel function can be re-
covered. However this requires reading upto at least
four harmonics of the FM frequency, which in some
situations be limited by the bandwidth of the photode-
Mirg, S. and K., P.
Passive Path Imbalance Measurement in Fiber Optic Interferometer using Homodyne PGC Scheme.
DOI: 10.5220/0007407500730078
In Proceedings of the 7th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2019), pages 73-78
ISBN: 978-989-758-364-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
73

tectors employed. By varying frequency deviation
over a range of frequencies and fitting with appropri-
ate Bessel functions trace for only first two harmon-
ics, we demonstrate the argument can be obtained and
hence the path imbalance can be determined.
In this paper we demonstrate a passive path differ-
ence measuring technique by employing homodyne
PGC scheme for demodulation in a Michelson in-
terferometer setup with delay coils. By varying fre-
quency deviation over a 1 GHz range we record the
data for various path imbalances. Successful determi-
nation of path imbalances is shown and various po-
tential applications are discussed.
The rest of the paper is organized as follows. In
Section 2 we discuss the principle of operation and
mathematical analysis of homodyne PGC technique.
The experimental setup is discussed in Section 3 and
corresponding results are discussed in Section 4. Fi-
nally, we conclude our work by summarizing the re-
sults obtained in Section 5.
2 MATHEMATICAL ANALYSIS
The phase shift of an optical signal over a fiber of
length L is given by
φ =
2πnLv
c
, (1)
where n is the refractive index of the fiber, c is ve-
locity of light in free space and v is the frequency of
carrier. Differentiating (1) yields
∆φ
φ
=
2π
c

∆L
L
+
∆n
n
+
∆v
v

. (2)
From Eq. (2), it can be seen that changes in
length(∆L), refractive index (∆n) and frequency (∆v)
can induce a phase change in the optical carrier. The
first two changes can be induced by measurand in-
duced strain, hence creating a transduction mecha-
nism. Further the change in frequency can be used to
passively interrogate the optical fibers by modulating
the input frequency.
2.1 Homodyne PGC
Homodyne PGC scheme involves the interrogation of
an unbalanced interferometer with a frequency mod-
ulated(FM) optical carrier as the input signal. The
schematic is shown in Figure 1. A measurand induced
phase change φ
a
(t) is assumed in one arm of the inter-
ferometer. The modulated frequency ω(t) of the FM
optical carrier is given by
ω(t) = 2π[ f
o
+ ∆v
o
cos(ω
fm
t)] (3)
>ĂƐĞƌ
ĚŝŽĚĞ
&ZD
&ZD
L
ଵ
L
ଶ

௙௠

௢
W
W
Figure 1: Schematic diagram for homodyne PGC scheme
in a Michelson interferometer setup. PC: Polarization con-
troller, PD: Photodiode.
where f
o
is the carrier frequency and ∆v
o
is the
maximum frequency deviation. The equation of the
electric-field of the FM optical carrier E(t) is given
by
(4)
E(t) = E
o
exp

j

2π f
o
t +
2π∆v
o
ω
fm
sin(ω
fm
t)
+ φ
p
(t)

+ c.c,
where E
o
is the field amplitude and φ
p
(t) is the phase
noise. The net time delay τ in traversing each arm of
length difference (∆L = |L
1
−L
2
|) twice in the inter-
ferometer is given as
τ =
n2∆L
c
. (5)
The incident electric field at the photodetector input
(E
out
(t)) is then given by
E
out
(t) = E
1
(t) + E
2
(t + τ). (6)
Using Eqs. (3), (4) and (5) the photocurrent output
i
o
(t) of the interferometer is given by
i
o
(t) = R

P
1
+ P
2
+ 2V
√
P
1
P
2
cos(∆φ(t))

, (7)
where R is the responsivity of the photodiode, P
1
and
P
2
are the average powers from each arm in the ab-
sence of interference, V is the fringe visibility and the
phase difference (∆φ(t) = arg(E(t + τ)) −arg(E(t)))
between two arms is given by
(8)
∆φ(t) = 2π f
o
τ + φ
a
(t) + φ
n
(t)
+ φ
p
(t + τ) − φ
p
(t) + φ
fm
(t),
where φ
a
(t) is the phase change because of the mea-
surand, φ
n
(t) is the phase change due to environmen-
tal perturbations and φ
fm
(t) is given by
φ
fm
(t) =
2π∆v
o
ω
fm
[2cos(ω
fm
(t + τ/2))sin(ω
fm
τ/2)].
(9)
For small τ, Eq. (9) can be approximated as
φ
fm
(t) ≈
4πn∆v
o
∆L
c
cos(ω
fm
t). (10)
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
74

The photodetector current can then be written as
i
o
(t) = R[P
1
+P
2
+Pcos(µcos(ω
fm
t)+φ
o
(t))], (11)
where P=V
√
P
1
P
2
, µ=4πn∆v
o
∆L/c and
φ
o
(t)=(2πf
o
τ + φ
a
(t) + φ
n
(t) + φ
p
(t + τ) − φ
p
(t)).
It is noteworthy in Eq. (11), that φ
o
(t) contains
measurand information, while µ is in proportion to
the path imbalance. Eq. (11) can be expanded using
Bessel functions as
i
o
(t)
= R[P
1
+ P
2
] + RP
""
J
0
(µ)
+
n=∞
∑
n=1
J
2n
(µ)(−1)
n
cos(2nω
fm
t)
#
cos(φ
o
(t))
−
"
n=∞
∑
n=1
J
k
(µ)(−1)
n
cos((k)ω
fm
t)
#
sin(φ
o
(t))
#
,
(12)
where k=2n-1. The next step in the scheme involves
extracting the sine and cosine of phase φ
o
(t) by mix-
ing the current with cos(ω
fm
t) and cos(2ω
fm
t) fol-
lowed by low pass filtering as shown in Figure 2. The
two terms are given by
i
o1
(t) = RPJ
1
(µ)sin(φ
o
(t)), (13)
i
o2
(t) = −RPJ
2
(µ)cos(φ
o
(t)). (14)
Methods such as Arctangent and DCM are then em-
ployed to extract φ
o
(t). We instead obtain the spec-
trum of i
o
in Eq. (12) directly to find the harmonics
peak information, to determine the argument µ and
hence the path imbalance in the interferometer.
y
y
cos

2

௙௠


cos


௙௠


>W&
>W&

௢
RP
ଵ
 sin 
௢

RP
ଶ
 cos 
௢

Figure 2: Schematic diagram for obtaining in-phase and
quadrature phase of interest.
2.2 Path Imbalance Measurement
Argument of Bessel function (µ) is in direct propor-
tion to frequency deviation, therefore by varying fre-
quency deviation over a certain range the peak values
of the FM harmonics in the spectrum changes accord-
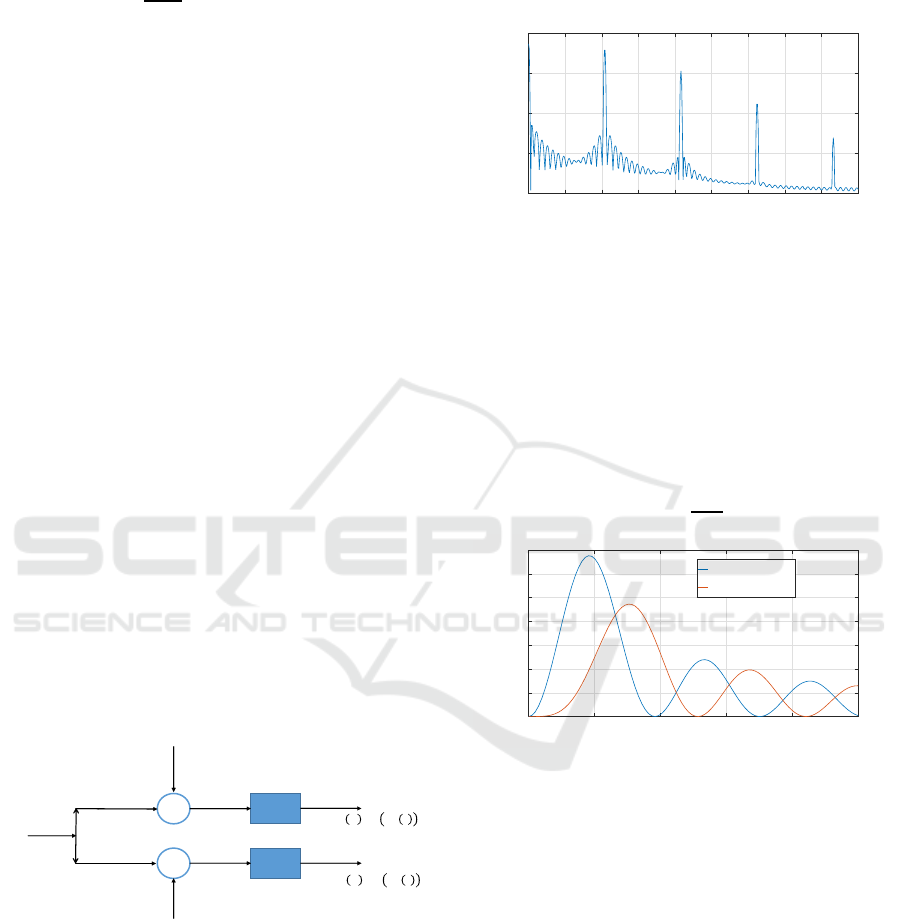
ingly. This is demonstrated by numerically plotting
the spectrum of i
o
(t) in Figure 3, assuming RPV=10
a.u, φ
o
(t) = π/4, µ=1, frequency modulation=20.8
kHz and sampling frequency in numerical calculation
was taken as 180 kHz.
Frequency (kHz)
0 10 20 30 40 50 60 70 80 90
Power (dB)
-60
-40
-20
0
20
Figure 3: Numerical plot of spectrum of photocurrent i
o
(t)
given in Eq. (12). F.M=20.8 kHz, µ=1, φ
o
(t) = π/4 and
RPV=10 a.u.
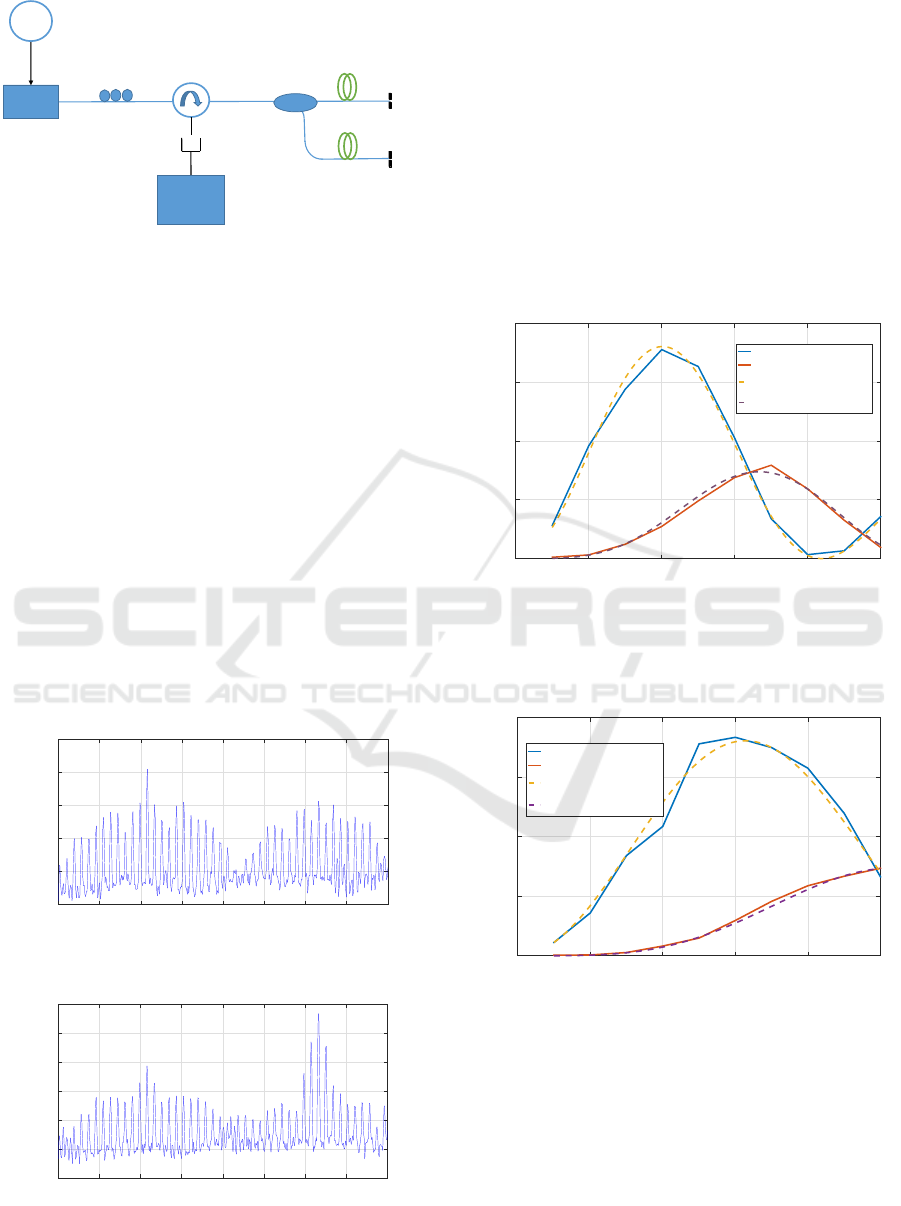
A frequency deviation sweep over a certain range
will lead to a change in peaks which follow J
2
n
(µ)
characteristics as shown in Figure 4 for J
2
1
(µ) and
J
2
2
(µ) where
µ = β∆v
o
(15)
and ∆L from Eq. (10) and (15) can then be found
using the expression
∆L =
βc
4πn
. (16)
Frequency deviation (GHz)
0 0.2 0.4 0.6 0.8 1
Power (a.u)
0
0.05
0.1
0.15
0.2
0.25
0.3
[J
1
(10*(∆ v(GHz))]
2
[J
2
(10*(∆ v(GHz))]
2
Figure 4: J
2
1
and J
2
2
plotted against frequency deviation with
β = 10 GHzˆ-1.
3 EXPERIMENTAL SETUP
Figure 5 shows the experimental setup. Keysight
N7714A Tunable laser source was employed with
20.8 kHz frequency modulation and frequency devi-
ation control over 0 to 1 GHz in steps of 0.1 GHz.
Tunable laser source also induces a 800 Hz dither fre-
quency modulation for frequency stabilization. The
effect of this dither frequency is reflected as side
bands to the harmonics of 20.8 kHz . This was fol-
lowed by a polarization controller to control the in-
put polarization of light. The optical carrier was then
input to port 1 of the circulator. Port 2 of the circula-
tor is connected to Michelson interferometer with two
Passive Path Imbalance Measurement in Fiber Optic Interferometer using Homodyne PGC Scheme
75

>ĂƐĞƌ
ĚŝŽĚĞ
&ZD
&ZD
L
ଵ
 15 
L
ଶ
 15 
20
.
8

^ƉĞĐƚƌƵŵ
ŶĂůLJƐĞƌ
ϯĚ
W
W
Figure 5: Experimental setup for path imbalance measure-
ment. PC: Polarization controller, PD: Photodiode.
delay coils of around 15 m initial lengths. The coils
were followed by Faraday rotating mirrors (FRM) to
circumvent polarization fading. At port 3 of the cir-
culator a photodiode converts the input signal to elec-
trical photocurrent which is then analysed using an
radio frequency (RF) spectrum analyser. The data is
acquired at the entire frequency deviation range of 0
to 1 GHz . The coil is then shortened and the amount
of length removed is noted. The readings are taken
at 5 different path imbalances. The obtained value of
length difference of two consecutive path imbalances
is then matched with calibrated length difference.
The variation in spectrum output at frequency de-
viation 0.1 GHz and 0.8 GHz is shown in Figure 6
and 7. The side bands of 800 Hz are due to the laser
source induced dither frequency modulation. The
peak power at 20.8 kHz and 41.6 kHz is averaged and
stored over the entire frequency deviation range.
Frequency (kHz)
10 15 20 25 30 35 40 45 50
Power (dBm)
-60
-50
-40
-30
-20
-10
Figure 6: Spectrum analyser output with frequency devia-
tion 0.1 GHz.
Frequency (kHz)
10 15 20 25 30 35 40 45 50
Power (dBm)
-70
-60
-50
-40
-30
-20
-10
Figure 7: Spectrum analyser output with frequency devia-
tion 0.8 GHz.
4 RESULTS AND DISCUSSIONS
The traces of first (20.8 kHz) and second harmonic
(41.6 kHz) peak powers are plotted against frequency
deviation upto 1 GHz in steps of 0.1 GHz for five
different path imbalances. The traces and curve
fit are shown in Figure 8-10 for three different
path imbalances in descending order. As the path
imbalance is decreased, the curves begin to expand
on the x axis, due to the direct proportion dependence
of arguments of Bessel function and path imbalance.
Traces are then fitted with both harmonics power
being in proportion to J
1
(β∆v
o
)
2
and J
2
(β∆v
o
)
2
.
Frequency deviation (GHz)
0 0.2 0.4 0.6 0.8 1
Power (mW)
0
2
4
6
8
20.8 kHz peak power
41.6 kHz peak power
21.33*(J
1
(4.5396*∆v
o
2))
2
12.49*(J
2
(4.5396*∆v
o
))
2
Figure 8: Path imbalance 1: Trace and appropriate curve fit-
tings for first two harmonic peak powers from the spectrum
of i
o
(t) for the frequency deviation range of 0.1-1 GHz. β
is obtained as 4.5396 GHz
−1
.
Frequency deviation (GHz)
0 0.2 0.4 0.6 0.8 1
Power (mW)
0
2
4
6
8
20.8 kHz peak power
41.6 kHz peak power
21.33*(J
1
(2.9351*∆v
o
))
2
12.49*(J
2
(2.9351*∆v
o
))
2
Figure 9: Path imbalance 2: Trace and appropriate curve fit-
tings for first two harmonic peak powers from the spectrum
of i
o
(t) for the frequency deviation range of 0.1-1 GHz. β
obtained as 2.9351 GHz
−1
.
The different value of β for different path imbal-
ance cases is shown in Table 1 and the estimated path
imbalance is calculated using Eq. (16) using n=1.445,
c=3 ×10
8
m/s, followed by estimated difference in
consecutive path imbalances (δ(∆L)) and the last col-
umn shows the calibrated length difference (δ(∆L)).
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
76

Frequency deviation (GHz)
0 0.2 0.4 0.6 0.8 1
Power (mW)
0
2
4
6
8
10
20.8 kHz peak power J
1
(x)
41.6 kHz peak power J
2
(x)
32.4*(J
1
(1.3728*∆v
o
))
2
27.06*(J
2
(1.3728*∆v
o
))
2
Figure 10: Path imbalance 4: Trace and appropriate curve
fittings for first two harmonic peak powers from the spec-
trum of i
o
(t) for the frequency deviation range of 0.1-1
GHz. β obtained as 1.3728 GHz
−1
.
The two values are mismatched, however as seen in
Table 2, the mismatch is a constant scaling factor with
a mean value of 0.34. This constant scaling factor can
then be employed to correct our path imbalance esti-
mation as seen in Table 3 using the equation
∆L
′
=
∆L
0.34
. (17)
We believe this scaling factor is inherent to the laser
diode’s frequency modulation through current modu-
lation, further study is needed to determine the root
cause of the scaling factor. A measure of path im-
balance without feedback is thus obtained using the
above scheme. The scaling factors can be calibrated
for the frequency modulated optical source and can
directly be implemented in the field passively using
just the received photocurrent spectrum in a homo-
dyne PGC setup.
5 CONCLUSIONS
In summary, we have demonstrated a path imbalance
measurement technique which can directly be em-
ployed in the field using the existing homodyne PGC
setup. We began by deriving the mathematical equa-
tions needed to predict the behaviour of the output
current spectrum in our PGC setup. Experimental es-
timation of multiple path imbalances were carried out
by tracing the first and second harmonic peaks in the
spectrum of i
o
(t) and then fitting them with appro-
priate curves on the basis of mathematical analysis, to
estimate the argument of the Bessel functions. A scal-
ing factor of 0.34 was obtained from comparing the
length difference of two consecutive path imbalances
estimated to the calibrated path difference. With the
frequency modulated optical source characterized and
Table 1: Values of β, Scaled path imbalance (∆L), Es-
timated length difference between consecutive configura-
tions (δ(∆L)) and Calibrated values of length difference
(δ(∆L)
cal
).
Case β ∆L δ(∆L) δ(∆L)
cal
(GHz
−1
) (cm) (cm) (cm)
1 4.5396 7.5 – –
2 2.9351 4.85 2.65 7.5
3 2.179 3.6 1.25 3.7
4 1.3728 2.27 1.33 3.9
5 0.7191 1.19 1.08 3.3
Table 2: Ration of estimated length difference to calibrated
length difference.
δ(∆L)(cm) δ(∆L)
cal
(cm)
δ(∆L)
δ(∆L)
cal
2.65 7.5 0.3533
1.25 3.7 0.3378
1.33 3.9 0.3410
1.08 3.3 0.3273
Table 3: Estimated path imbalance after appropriate scaling
(∆L
′
).
β(GHz
−1
) ∆L
′
(cm)
4.5396 22.059
2.9351 14.264
2.179 10.588
1.3728 6.676
0.7191 3.5
the scaling factor known, we estimated the different
path imbalances. The measurement involves no feed-
back and can be used in the field environment to esti-
mate path imbalances in the interferometers.
REFERENCES
Cranch, G. A., Nash, P. J., and Kirkendall, C. K. (2003).
Large-scale remotely interrogated arrays of fiber-optic
interferometric sensors for underwater acoustic appli-
cations. IEEE Sensors Journal, 3(1):19–30.
Dandridge, A., Tveten, A. B., and Giallorenzi, T. G. (1982).
Homodyne demodulation scheme for fiber optic sen-
sors using phase generated carrier. IEEE Transactions
on Microwave Theory and Techniques, 30(10):1635–
1641.
Henning, M. (1983). Optical fiber hydrophones with down
lead insensitivity. In Proc. First International Confer-
ence on Optical Fiber Sensors, London, 1983, pages
23–27.
Huang, S.-C. and Lin, H. (2008). Method for path imbal-
ance measurement of the two-arm fiber-optic interfer-
ometer. Appl. Opt., 47(28):5065–5073.
Passive Path Imbalance Measurement in Fiber Optic Interferometer using Homodyne PGC Scheme
77

Jin, W., Zhang, L. M., Uttamchandani, D., and Culshaw, B.
(1991). Modified j1 .. . j4 method for linear readout
of dynamic phase changes in a fiber-optic homodyne
interferometer. Appl. Opt., 30(31):4496–4499.
Santos, J. L. and Farahi, F. (2014). Handbook of optical
sensors. CRC Press.
Sheem, S. K., Giallorenzi, T. G., and Koo, K. (1982). Op-
tical techniques to solve the signal fading problem in
fiber interferometers. Appl. Opt., 21(4):689–693.
Sudarshanam, V. S. and Srinivasan, K. (1989). Linear read-
out of dynamic phase change in a fiber-optic homo-
dyne interferometer. Opt. Lett., 14(2):140–142.
Udd, E. and Spillman Jr, W. B. (2011). Fiber optic sensors:
an introduction for engineers and scientists. John Wi-
ley & Sons.
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
78