
A PSO based Approach to Assign Segments
for Reducing Excavated Soil in Shield Tunneling
Koya Ihara
1
, Shohei Kato
1,2
, Takehiko Nakaya
3
, Tomoaki Ogi
3
and Hiroichi Masuda
3
1
Dept. of Computer Science and Engineering, Graduate School of Engineering, Nagoya Institute of Technology,
Gokiso-cho, Showa-ku, Nagoya 466-8555, Japan
2
Frontier Research Institute for Information Science, Nagoya Institute of Technology,
Gokiso-cho, Showa-ku, Nagoya 466-8555, Japan
3
Shimizu Corporation, 2-16-1 Kyobashi, Chuo-ku, Tokyo 104-8370, Japan
Keywords:
Constrained Combinatorial Optimization, Genetic Algorithm, Particle Swarm Optimization, Shield Tunneling.
Abstract:
It is expected that artificial intelligence reduces labor and improves productivity of the shield tunneling, which
is one of tunnel construction methods. In a planning process of the shield tunneling, segments of a tunnel are
assigned along to a predetermined curve called the planning line. Conventionally, skilled engineers manually
assign the segments to minimize gaps between each segment and the planning line. Nevertheless, we have only
to reduce each gap less than a tolerance, and there is a demand to reduce the amount of soil excavated along
to the segments. Handling the reducing gaps as constraints and reducing the amount of excavated soil as an
objective, this paper addresses the segment assignment as a constrained combinatorial optimization problem.
These constraints are severe, and the problem has an extremely narrow feasible region. For this problem, we
proposed the ε constrained integer categorical particle swarm optimization (εICPSO), adapting a constraint
handling method called the ε constrained method to the integer categorical particle swarm optimization. The
effectiveness of the εICPSO to the segment assignment is shown by the two-dimensional simulator experiment
using real construction data. The experimental results show that the proposed method has a potential to reduce
the amount of excavated soil as compared to the conventional method (skilled engineer) while keeping the all
gaps between segments and the planning line falling within the tolerance. The εICPSO statistically performed
the best in all the test problems.
1 INTRODUCTION
In the construction industry of all over the world,
manpower shortage is serious problem. Windapo, A.
O. reported that a skilled labor shortage is preponde-
rant and it contributes to a decrease in productivity
and product quality in the South African construction
industry (Windapo, 2016).
The Japanese construction industry also has pro-
blems: manpower shortage, ageing workers, and de-
crease in international competitiveness. Since No-
vember 2015, the Japanese Ministry of Land, Infra-
structure, Transport and Tourism (MLIT) has been
promoted the i-Construction (Suzuki, 2016), an ef-
fort aiming to optimize and upgrade the whole pro-
cess from investigation and design, construction and
inspection, up to maintenance. Its major concepts are
utilization of information and communication techno-
logy and introducing innovative technology such as
artificial intelligence (AI) by cooperation between in-
dustries, governments, and academia. Our research
aims to develop a practical construction support sy-
stem according to the i-Construction.
The shield tunneling (Maidl et al., 2013; Japan
Society of Civil Engineers, 2007) is a tunnel con-
struction method used around the globe. It is neces-
sary to construct tunnels under sever conditions such
as urban areas. In the civil engineering and mechani-
cal engineering domains, the shield tunneling techni-
ques have been studied intensively (Koyama, 2003).
There are also a few studies (Suwansawat and Ein-
stein, 2006; Hasanipanah et al., 2016) about shield
tunneling in artificial intelligence domain. However
no studies have focused planning processes of shield
tunneling. In the planning process, segments of the
tunnel are assigned along to the predetermined plan-
ning line, where the tunnel is expected to be con-
structed. Conventionally, skilled engineers manually
assign the segments to minimize gaps between each
segment and the planning line. Nevertheless, we have
only to reduce each gap less than a tolerance, and
there is a demand to reduce the amount of soil ex-
cavated along to the segments.
It is assume that automation and optimization of
328
Ihara, K., Kato, S., Nakaya, T., Ogi, T. and Masuda, H.
A PSO based Approach to Assign Segments for Reducing Excavated Soil in Shield Tunneling.
DOI: 10.5220/0007407803280336
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 328-336
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

the segment assignment contribute to eliminate a skil-
led labor shortage and to improve productivity. This
paper addresses the segment assignment as a constrai-
ned combinatorial optimization problem. This pro-
blem has severe constraints, and its feasible region
is extremely narrow as compared with its large se-
arch space. For optimization problems having severe
constraints, Takahama and Sakai proposed the ε con-
strained method (Takahama and Sakai, 2005). The
ε constrained method is a method that adds the abi-
lity of constraint handling to the algorithms which
was originally designed for unconstrained optimiza-
tion problems. Although this method has been adap-
ted to several continuous optimizations (Takahama
and Sakai, 2010; Bonyadi et al., 2013; Yang et al.,
2014), there is no report of adapting it to discrete op-
timizations. Adapting the ε constrained method to
the Integer Categorical Particle Swarm Optimization
(ICPSO) (Strasser et al., 2016), we propose ε con-
strained ICPSO (εICPSO) for constrained combina-
torial optimization. We attempt to verify the effecti-
veness of the εICPSO to segment assignment through
the two-dimensional simulation experiment using real
construction data.
2 RELATED WORK
There are studies of adapting the ε constrained met-
hod to metaheuristics algorithms, e.g., particle swarm
optimization (PSO) (Kennedy, 2011), differential
evolution (DE) (Storn and Price, 1997), multiob-
jective evolutionary algorithm based on decomposi-
tion (MOEA/D) (Zhang and Li, 2007), and so on. Ta-
kahama and Sakai proposed an ε constrained differen-
tial evolution (εDE) (Takahama and Sakai, 2006), and
its extended version using an archive (Takahama and
Sakai, 2010). Takahama and Sakai proposed an ε con-
strained particle swarm optimizer (εPSO) (Takahama
and Sakai, 2005). Bonyadi, Li, and Michalewicz pro-
posed the hybrid method of εPSO and an other con-
straint handling method (Bonyadi et al., 2013). Yang,
Cai, and Fan introduced the ε constrained method into
MOEA/D in order to extend it for constrained multi-
objective optimization problems (Yang et al., 2014).
All of these methods are applicable to only continu-
ous optimization problems. Few researches have re-
ported on discrete constrained optimization methods
adapting the ε constrained method.
3 SEGMENT ASSIGNMENT
In this section, we explain the segment assignment
and its formulation as constrained combinatorial opti-
mization problem.
3.1 Shield Tunneling
The shield tunneling is a tunnel construction met-
hod using excavation machines called shield machi-
nes shown in Figure 1. The front surface of the shield
machine has cutters, called the cutter head, to exca-
vate grounds. The over cut, which is the external cut-
ter equipped outside of the front surface, is controlled
so that the machine body can pass without contacting
to ground wall. A shield machines is divided to a front
drum and a rear drum. The angle between the front
drum and the rear drum, called joint angle, is control-
led for the shield machine to go around curves. Seg-
ments are assembled at the rear of the shield machine.
The shield machine is propelled by the reaction force
given from its jack pushing the located segment.
3.2 Segment Assignment Problem
In planning process, multiple types of segments are
provided for each construction and they are assig-
ned along to the planning line consisting of straight
lines and curves so that the gaps between each seg-
ment and the planning line fall within a tolerance as
shown in Figure 2. Conventionally, skilled engineers
manually assign segments in order to minimize gaps
without considering construction costs. However, be-
cause this assignment roughly determine the excava-
tion route of shield machine, it is assumed that optimi-
zation of this assignment reduce shield construction
costs. Thus we focus on the segments assignment pro-
blems for reducing the amount of excavated soil.
There are following two demands in the segment
assignment. (1) To make the gaps between each seg-
ment and the planning line fall within the tolerance.
(2) To reduce the amount of soil excavated according
to the segments by the shield machine. In this paper,
the former is treated as an inequality constraint, and
the latter is treated as an objective function. We de-
fine segment assignment as the following constrained
combinatorial optimization problem.
minimize f (x
x
x),
subject to (g
i
(x
x
x) − g
t
) ≤ 0, (1)
x
i
∈ {1, ··· , k}, (i = 0, ··· , n)
where x
i
∈ {1, ·· · ,k} corresponds to the type of
the segment assigned to i-th position, and k is the
number of types. A decision variable vector x
x
x =
A PSO based Approach to Assign Segments for Reducing Excavated Soil in Shield Tunneling
329
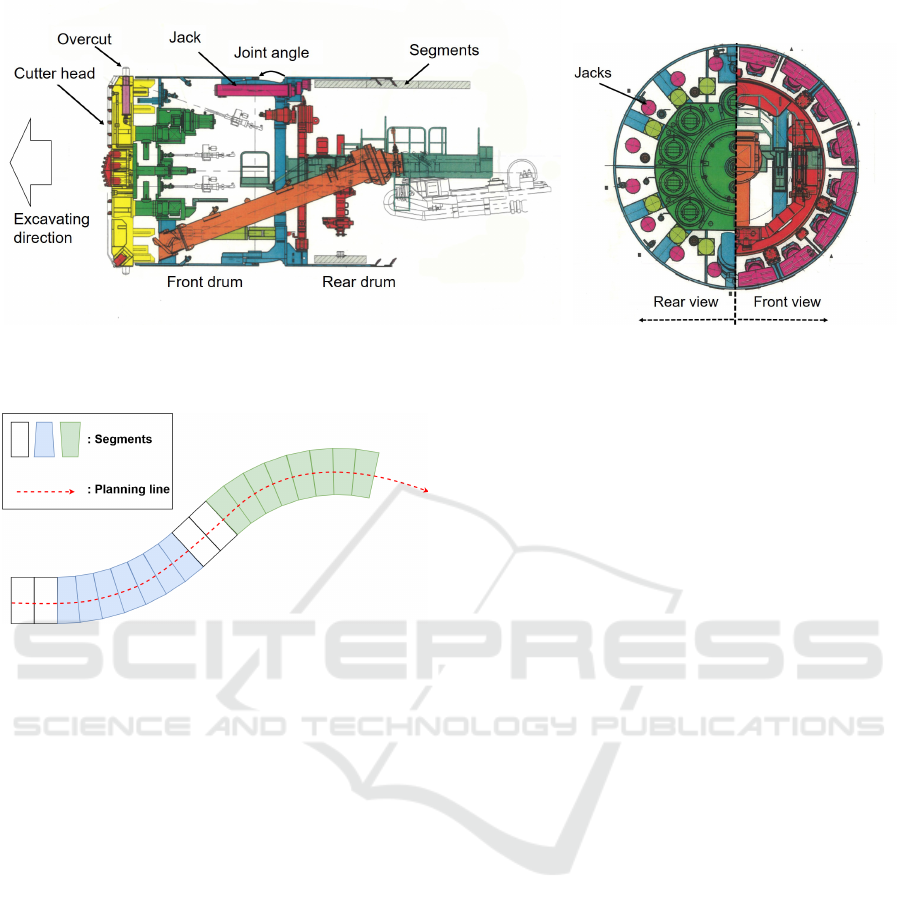
(a) Side View (b) Rear and Front View
Figure 1: An Example of Construction Diagrams of A Shield Machine.
Figure 2: An Example of Segment Assignment.
(x
1
, x
2
, · · ·x
n
) expresses the assigned segments. The
objective function f (x
x
x) is the amount of soil excava-
ted along to segments x
x
x by the shield machine; g
i
(x
x
x)
as the gap between the i-th segment and the planning
line; and g
t
is the gap tolerance.
This problem has n-dimensional decision variable
vector, and n is generally over several hundreds. The
problem has an extremely large search space. Howe-
ver, it is required to earn a solution in a short time,
because the segment assignment plan is should be re-
created when the practical construction deviates from
the plan. Population-based metaheuristics, such as
swarm intelligence (SI), is often used for optimiza-
tion problems in the real-world because of its ease
of parallelization and efficiency of its multi-point se-
arch (Hassanien and Emary, 2018; Soares et al., 2016;
Zhang et al., 2014; Glover and Kochenberger, 2006).
Although there are many discrete optimization algo-
rithms based on SI, they often only consider inte-
ger problems (Kennedy and Eberhart, 1995; Pampara
et al., 2005). The segment assignment has variables
whose values are not numerical but categorical and
unordered. The PSO is one of the most widely used
algorithm belonging to SI. Integer Categorical PSO
(ICPSO), presented in (Strasser et al., 2016), outper-
formed other discrete versions of PSO in unordered
discrete optimization. In addition, the gap tolerance
g
t
is commonly about 50 mm, whereas the diameter
of segments is around 10 m. The segment assignment
has n severe constraints. For handling the severe con-
straints, the ε constrained method is proposed by (Ta-
kahama and Sakai, 2005). Thus, we adapt the ε con-
strained method to ICPSO for constrained combina-
torial optimization.
4 PROPOSED METHOD
This section describes the considering constrained
combinatorial optimization problems, ε constrained
method, and εICPSO.
4.1 Problem Domain
In the proposed method, we consider the following
constrained optimization problem.
minimize f (x
x
x),
subject to g
j
(x
x
x) ≤ 0, ( j = 1, ··· , q)
h
j
(x
x
x) = 0, ( j = 1, ··· , r)
x
i
∈ {l
i
, · · · , u
i
}, (i = 1, ··· , n)
where x
x
x = (x
1
, · · · , x
n
) is an n-dimensional decision
variable vector; f (x
x
x) is a objective function; g
j
(x
x
x) ≤ 0
are q inequality constraints; and h
j
(x
x
x) = 0 are r equa-
lity constraints. f (x
x
x), g
j
(x
x
x), and h
j
(x
x
x) are real-valued
functions. The integer values l
i
, and u
i
are the lower
and upper bounds of x
i
respectively. The search space
is defined by the lower and upper bounds; the feasible
region is defined by the inequality and equality con-
straints.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
330

4.2 ε Constrained Method
The ε constrained method (Takahama and Sakai,
2005) adds the ability of constraint handling to the
algorithms originally designed for unconstrained op-
timization problems. This method introduces ε level
comparison, which is a comparison operator conside-
ring both the constraints and objective values for ran-
king candidate solutions. In this method, constraint
violation ϕ(x
x
x) is defined as a measure of how much
constraints a solution violates. The constraint viola-
tion can be given by the maximum of all constraints
of all constraints or the sum of all constraints.
ϕ(x
x
x) = max{max
j
{0, g
j
(x
x
x)}, max
j
|h
j
(x
x
x)|},
ϕ(x
x
x) =
∑
j
max{0, g
j
(x
x
x)}
p
+
∑
j
|h
j
(x
x
x)|
p
, (2)
where p is a positive number. In this paper, constrain
violation is given by (2), the sum of all constraints.
The ε level comparison (<
ε
,≤
ε
) is defined as an
order relation on the set of ( f (x
x
x), ϕ(x
x
x)). If f
1
( f
2
) and
ϕ
1
(ϕ
2
) are the objective values and the constraint vi-
olation of solution point x
1
(x
2
) respectively, then the
comparison operators <
ε
and ≤
ε
are defined by the
following:
( f
1
, ϕ
1
) <
ε
( f
2
, ϕ
2
) ⇔
f
1
< f
2
, (ϕ
1
, ϕ
2
≤ ε)
f
1
< f
2
, (ϕ
1
= ϕ
2
)
ϕ
1
< ϕ
2
, otherwise
( f
1
, ϕ
1
) ≤
ε
( f
2
, ϕ
2
) ⇔
f
1
≤ f
2
, (ϕ
1
, ϕ
2
≤ ε)
f
1
≤ f
2
, (ϕ
1
= ϕ
2
)
ϕ
1
< ϕ
2
, otherwise
This definition means that the ε level comparison
compares two solutions by constraint violation value
first. If both solutions have violation value under a
small threshold ε the two solutions are then compa-
red by the objective function value only.
4.3 εICPSO
The εICPSO is a constrained combinatorial optimiza-
tion algorithm based on ICPSO with candidate soluti-
ons ranked by the ε level comparison. The ICPSO is
a novel PSO algorithm that has been shown to surpass
other discrete PSO algorithms (Strasser et al., 2016).
In the PSO, particles search for the best position of the
search space. Particles have a position and a velocity,
and the position correspond to a candidate solution.
Original PSO assumes continuous state variables. In
the ICPSO, the representation of the particle’s posi-
tion is altered so that each attribute in a particle is a
distribution over its possible values rather than a va-
lue itself similarly to Estimation of Distribution Al-
gorithms (EDAs) (Larra
˜
naga and Lozano, 2002). A
particle is evaluated by sampling a candidate solution
from these distributions and then calculating its fit-
ness. In this subsection, the εICPSO is described in
more detail.
In the εICPSO, a particle p’s position X
p
is repre-
sented as
X
p
= [D
p,1
, D
p,2
, · · · , D
p,n
],
where each D
p,i
is the probability distribution for va-
riable X
i
. In other words, each component of the po-
sition vector is a set of probabilities
D
p,i
= [d
a
p,i
, d
b
p,i
, · · · , d
k
p,i
],
where d
j
p,i
denotes the probability that variable X
i
ta-
kes on value j for particle p. A particle p’s velocity
V
p
is a vector of n vector φ, which control the parti-
cle’s probability distributions.
V
p
= [φ
p,1
, φ
p,2
, · · · , φ
p,n
],
φ
p,1
= [ψ
a
p,i
, ψ
a
p,i
, · · · , ψ
a
p,n
],
where ψ
j
p,i
corresponds to velocity of particle p for
variable i in state j. The velocity and position update
equations are applied directly to the values in the dis-
tribution.
V
p
=ωV
p
+U(0, ϕ
1
) ⊗ (pBest − X
p
)
+U(0, ϕ
2
) ⊗ (gBest − X
p
),
X
p
=X
p
+V
p
,
where each operator is performed component-wise
over each variable in the vector; and U(0, ϕ
1
) and
U(0, ϕ
2
) are uniformly distributed random numbers
between 0 and ϕ
1
and 0 and ϕ
2
respectively. The vec-
tor pBest is the best position in the search space this
particle has ever reached; the gBest is the best po-
sition in the search space any particle in the swarm
has ever reached. The particle moves in the search
space by adding the updated velocity to the particle’s
position vector at the current iteration. The particle’s
behavior is controlled with adjusting the parameter ω,
ϕ
1
, and ϕ
2
known as inertia, the cognitive component
and the social component.
After the velocity and position update, any value
outside [0,1] is mapped to the nearest boundary in or-
der to maintain a valid probability. In addition, the
distribution is then normalized to ensure that its va-
lues sum to 1.
To evaluate a particle p, its distributions are
sampled to create a candidate solution S
p
=
[s
p,1
, s
p,2
, · · · , s
p,n
] where s
p, j
denotes the state of va-
riable X
j
. The samples are evaluated by the fitness
A PSO based Approach to Assign Segments for Reducing Excavated Soil in Shield Tunneling
331

function, and then the distributions are evaluated by
their own sample’s fitness value.
When a sample produced by a particle exceed the
global or local best in ε level comparison, the best
values are updated using both the distribution from
the particle position P
p
and the sample itself S
p
. For-
mally, for all states j ∈ Vals(X
i
) the global best’s pro-
bability is updated as
d
j
gB,i
=
ε × d
j
p,i
( j ̸= s
p,i
)
d
j
p,i
+
∑
k∈Vals(X
i
)
∧k̸= j
(1 − ε) × d
k
p,i
( j = s
p,i
)
where ε, the scaling factor, is a user-controlled para-
meter that determines the magnitude of the shift in the
distribution restricted to [0, 1), and d
j
gB,i
is the global
best position’s probability that variable X
i
takes value
j. This update increases the probability of the distri-
bution producing samples similar to the best sample,
while maintaining a valid probability distribution. In
other words, it ensures that the best position’s pro-
bability of producing a variable identical to the best
sample’s greater than 1−εwhich can be shown as fol-
lows:
d
k
gB,i
= d
k
p,i
+
∑
j∈S
v
(X
i
,k)
(1 − ε) × d
j
p,i
= ε × d
k
p,i
+ (1 − ε) × d
k
p,i
+
∑
j∈S
v
(X
i
,k)
(1 − ε) × d
j
p,i
= ε × d
k
p,i
+ (1 − ε),
where S
v
(X
i
, k) = { j| j ∈ Vals(X
i
) ∧ j ̸= k} and k =
s
p,i
. The scaling factor should be controlled accor-
ding to the dimension of the decision variable, since a
large dimension increases the difference between the
best sample and a sample expected to be produced by
the updated distribution. The local best is updated in
exactly the same way. At the end of the algorithm, the
global best sample is returned as the solution.
5 EXPERIMENT
We attempt to verify the effectiveness of εICPSO
to segment assignment through the two-dimensional
simulation experiment using real construction data
with comparison with the ε constrained genetic algo-
rithm (εDGA) (Ihara et al., 2018). Candidate solu-
tions (assigned segments) are evaluated by the two-
dimensional simulator we developed. Solutions are
encoded to particles and integer chromosome and
they are evolved by the εICPSO and εDGA.
Figure 3: Model of Shield Machines in the Two-
dimensional Simulator.
5.1 Two-dimensional Simulator for
Segment Assignment
In the two-dimensional simulator, we consider the
shield machines as shown in Figure 3. The simulator
evaluates segments by the area of the region a shield
machine passed along to the segments assuming that
the amount of excavated soils is in proportion to the
area. The area of the region through which the front
of the shield machine passes is determined by the pro-
duct of the width of the shield machine and the total
length of the planning line. Thus, We define the area
of the excavated field excluding this field as the fitness
because this field does not depend on segment assig-
nment. This fitness is equivalent to the amount of the
soil excavated by the overcut.
5.2 Conventional Method
In the construction site, segments are manually as-
signed by skilled engineers. However it is difficult
to compare with real skilled engineers’ assignment,
because engineers take a lot of time to assign seg-
ments in each problem. Since skilled engineers as-
sign in order to minimize the gaps without conside-
ring the amount of excavated soil, their methods are
approximately equivalent to the greedy method where
segments are assigned to minimize gaps. Thus we
compare the proposed methods to the greedy method
instead of skilled engineers.
5.3 εDGA
For the segment assignment problem, Ihara et al. pro-
posed the εDGA (Ihara et al., 2018), which is a com-
bination of the ε constraint method and discrete ge-
netic algorithm. The εDGA is basically based on
standard genetic algorithms, but in the algorithm, in-
dividuals are ranked by the ε level comparison with
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
332

(a) pl01
(b) pl02
(c) pl03
(d) segments
(e) shield machine
Figure 4: Dimensions [mm] of the planning lines, the segments, and the shield machine used in the experiments.
the ε level controlled in each generation. In particu-
lar, the parents are selected by selection methods ba-
sed on comparison of individuals such as tournament
selection (Miller et al., 1995) and ranking selection
(Goldberg and Deb, 1991) using the ε level compari-
son instead of general comparison. Elite individuals
are also selected by ε level comparison to carry over
to the next generation according to elitism. The flow
of the method is shown as follows:
1. Initialization: initial population is generated by
randomness or heuristics with population size of
N.
2. Determining terminate or not: If the termination
conditions satisfy, this algorithm terminates. In
this paper, the algorithm ends in the T th generati-
ons.
3. Controlling the ε level: the feasible region is tem-
porarily expanded by controlling the ε level. It is
desirable that ε level decrease as generations go
by.
4. Parents selection: individuals are ranked by ε le-
vel comparison, and selected by selection met-
hods only based on ranking solutions to insert into
a mating pool.
5. Crossover: crossover operators are applied to pa-
rents picked from the mating pool in order.
6. Mutation: when offspring are produced, each off-
spring has chance of mutation.
7. Replacement: N
e
elite individuals are selected to
carry out to the next generation instead of N
e
worst offspring selected by the ε level compari-
son.
8. Return to step 2.
5.4 Initialization
In the constrained optimization problem, it is desira-
ble search starts from in or near its feasible region,
especially when the feasible region is narrow. A feasi-
ble solution can be found easily by the greedy method
in the segment assignment as noted above. This ex-
periment uses the feasible solution discovered by the
greedy method for initializations. The εICPSO rand-
omly initialized velocity and position vectors, then as-
suming that the feasible solution is earned by sam-
pling a particle p’s position, the p’s local best and the
global best are updated. In the εDGA initial individu-
als are created by the applying the uniform mutation
to the feasible solution.
5.5 Experimental Setup
The algorithms tackle the constrained combinatorial
optimization problem defined in (1). Planning lines
are defined by the given series of curvature radius R
and length L. Figure 4a, 4b, and 4c show the planning
lines used in the experiment
pl01
,
pl02
, and
pl03
.
The segments are defined as shown in Figure 4d, and
we use the segment sets
sg01
and
sg02
, which in-
clude segments whose type number is from one to
three, and from one to five, respectively. The gap to-
lerance g
t
is set to 50 mm in each problem.
We conduct 50 trials of evolutions where fitness
evaluations are limited up to 500,000 times with both
the εICPSO and εDGA. The εICPSO uses a swarm of
size 100, and the swarm is evolved for 5, 000 itera-
tions, owing to the recommendation of (Engelbrecht,
2014), which demonstrated that a large swarm may,
counterintuitively, have difficulty exploring the search
space. The cognitive component ϕ
1
and social com-
ponent ϕ
2
are set to 1.49618, and the inertia ω is
0.729, which has been found to encourage convergent
A PSO based Approach to Assign Segments for Reducing Excavated Soil in Shield Tunneling
333
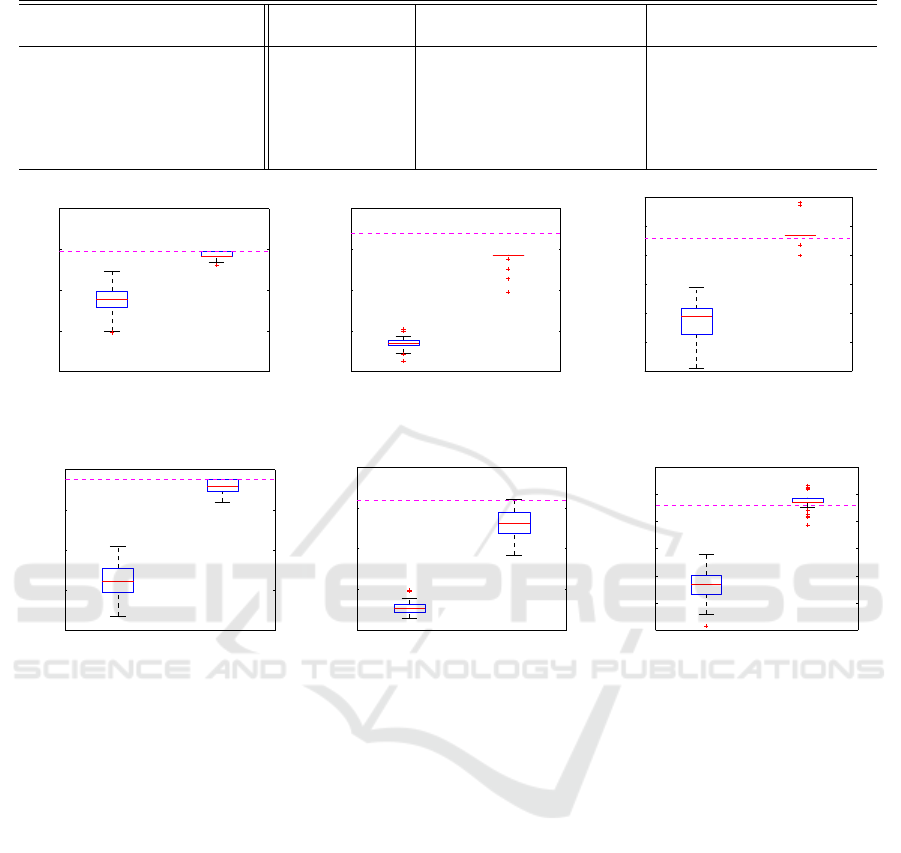
Table 1: Experimental Result [m
2
]50trials.
Problem Skilled engineer εICPSO εDGA
Segment set Planning line (greedy method) average best worst average best worst
sg01
(k = 3)
pl01
(n=267) 107.48 106.87 106.47 107.23 107.42 107.30 107.47
pl02
(n=210) 102.54 102.26 102.22 102.30 102.47 102.39 102.48
pl03
(n=325) 105.33 105.18 105.10 105.24 105.33 105.30 105.39
sg02
(k = 5)
pl01
(n=267) 107.35 106.84 106.67 107.01 107.32 107.24 107.35
pl02
(n=210) 102.52 102.25 102.22 102.29 102.46 102.38 102.52
pl03
(n=325) 105.08 104.93 104.85 104.99 105.08 105.04 105.11
106
106.5
107
107.5
108
Method
Fitness
Epsilon ICPSO Epsilon DGA
(a)
sg01
×
pl01
102.2
102.3
102.4
102.5
102.6
Method
Fitness
Epsilon ICPSO Epsilon DGA
(b)
sg01
×
pl02
105.1
105.15
105.2
105.25
105.3
105.35
105.4
Method
Fitness
Epsilon ICPSO Epsilon DGA
(c)
sg01
×
pl03
106.6
106.8
107
107.2
107.4
Method
Fitness
Epsilon ICPSO Epsilon DGA
(d)
sg02
×
pl01
102.2
102.3
102.4
102.5
102.6
Method
Fitness
Epsilon ICPSO Epsilon DGA
(e)
sg02
×
pl02
104.85
104.9
104.95
105
105.05
105.1
105.15
Method
Fitness
Epsilon ICPSO Epsilon DGA
(f)
sg02
×
pl03
Figure 5: Box plots of fitness scores of the εDGA and εICPSO for each problem with 50 trials, with horizontal dashed lines
representing the conventional method’s evaluations.
trajectories (Eberhart and Shi, 2000). In the
pl01
and
pl02
problems, the scaling factor ε = 5.0 × 10
−4
, and
in the
pl03
problems, ε = 1.0 × 10
−4
, due to large
dimensions of the problems. In the εDGA, populati-
ons are evolved for 500 generations, with a population
of size 1, 000. Uniform crossover (Syswerda, 1989)
is applied 95% of the time offspring are produced,
and each offspring does uniform mutation (Goldberg,
1989) where each gene has a 5% chance of change to
random value. Through the evolutions, ε level is set
to 0.
5.6 Experimental Results
The experimental results show that the proposed met-
hod have a potential to find the segment assignment
reducing the amount of excavated soil as compared
to the conventional method (skilled engineer) while
keeping the all gaps between segments and the plan-
ning line falling within the tolerance. Table 1 shows
the experimental results on the problems (Figure 4).
In the table, ”average”, “best”, and “worst” are the
average value, the best value, and the worst value of
50 trials on the each problem respectively. Bold va-
lues indicate algorithms that statistically significantly
outperformed all other methods (paired Student t-
Test, α = 0.01). Figure 5 illustrates the performance
of the εICPSO and εDGA. Their fitness scores are
shown as box plots, where the boxes represent the
25th to 75th percentiles, the lines within the boxes
represent the median, and the lines outside the boxes
represent the minimum and maximum values. The
conventional method’s scores are represented by the
horizontal dashed lines.
It is clear that the εICPSO has clear advantage
over the εDGA. In all the problems, the εICPSO sta-
tistically performs the best. In particular, the worst
scores of εICPSO exceed the εDGA’s best and the
skilled engineer’s score. In complex problems, with
large n or k, the difference in the performance is espe-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
334

cially remarkable. Although the εDGA has potential
to find the solution superior to the skilled engineer in
terms of the best score, the its score averagely almost
equivalent and at worst inferior in the
pl03
problems.
6 CONCLUSION
We addressed the segment assignment in shield tun-
neling as a constrained combinatorial optimization
problem. This paper proposed the εICPSO and de-
monstrated its effectiveness to segment assignment
problems. The experimental results showed its poten-
tial to reduce construction costs as compared with the
conventional method. In all the test problems, the pro-
posed method outperformed all the comparative met-
hods. In the future, we will make more experiments
using three-dimensional simulator for more accurate
evaluation of the proposed method.
REFERENCES
Bonyadi, M., Li, X., and Michalewicz, Z. (2013). A hy-
brid particle swarm with velocity mutation for con-
straint optimization problems. In Proceedings of the
15th annual conference on Genetic and evolutionary
computation, pages 1–8. ACM.
Eberhart, R. C. and Shi, Y. (2000). Comparing inertia weig-
hts and constriction factors in particle swarm optimi-
zation. In
Evolutionary Computation, 2000. Procee-
dings of the 2000 Congress on, volume 1, pages 84–
88. IEEE.
Engelbrecht, A. P. (2014). Fitness function evaluations: A
fair stopping condition? In Swarm Intelligence (SIS),
2014 IEEE Symposium on , pages 1–8. IEEE.
Glover, F. W. and Kochenberger, G. A. (2006). Handbook
of metaheuristics, volume 57. Springer Science & Bu-
siness Media.
Goldberg, D. (1989). Genetic algorithms in search, optimi-
zation and machine learning. Addison-Wesley, Rea-
ding, MA.
Goldberg, D. E. and Deb, K. (1991). A comparative analysis
of selection schemes used in genetic algorithms. In
Foundations of genetic algorithms, volume 1, pages
69–93. Elsevier.
Hasanipanah, M., Noorian-Bidgoli, M., Armaghani, D. J.,
and Khamesi, H. (2016). Feasibility of pso-ann model
for predicting surface settlement caused by tunneling.
Engineering with Computers, 32(4):705–715.
Hassanien, A. E. and Emary, E. (2018). Swarm intelligence:
principles, advances, and applications . CRC Press.
Ihara, K., Kato, S., Nakaya, T., and Ogi, T. (2018). Con-
strained GA based segment assignment in shield tun-
neling to minimize the amount of excavated soil. In
2018 IEEE 7th Global Conference on Consumer Elec-
tronics (GCCE), pages 229–230. IEEE.
Japan Society of Civil Engineers (2007). Standard speci-
fications for tunneling-2006: shield tunnels. Tunnel
Engineering Committee.
Kennedy, J. (2011). Particle swarm optimization. In Ency-
clopedia of machine learning, pages 760–766. Sprin-
ger.
Kennedy, J. and Eberhart, R. (1995). Particle swarm optimi-
zation. In IEEE International Conference on Neural
Networks, pages 1942–1948. IEEE.
Koyama, Y. (2003). Present status and technology of shield
tunneling method in japan. Tunnelling and Under-
ground Space Technology, 18(2-3):145–159.
Larra
˜
naga, P. and Lozano, J. A. (2002). Estimation of distri-
bution algorithms: A new tool for evolutionary com-
putation, volume 2. Springer Science & Business Me-
dia.
Maidl, B., Herrenknecht, M., Maidl, U., and Wehrmeyer, G.
(2013). Mechanised shield tunnelling. John Wiley &
Sons.
Miller, B. L., Goldberg, D. E., et al. (1995). Genetic algo-
rithms, tournament selection, and the effects of noise.
Complex systems, 9(3):193–212.
Pampara, G., Franken, N., and Engelbrecht, A. P. (2005).
Combining particle swarm optimisation with angle
modulation to solve binary problems. In Evolutionary
Computation, 2005. The 2005 IEEE Congress on, vo-
lume 1, pages 89–96. IEEE.
Soares, J., Ghazvini, M. A. F., Silva, M., and Vale,
Z. (2016). Multi-dimensional signaling method for
population-based metaheuristics: Solving the large-
scale scheduling problem in smart grids. Swarm and
Evolutionary Computation, 29:13–32.
Storn, R. and Price, K. (1997). Differential evolution–a
simple and efficient heuristic for global optimization
over continuous spaces. Journal of global optimiza-
tion, 11(4):341–359.
Strasser, S., Goodman, R., Sheppard, J., and Butcher, S.
(2016). A new discrete particle swarm optimization
algorithm. In Proceedings of the Genetic and Evo-
lutionary Computation Conference (GECCO), pages
53–60. ACM.
Suwansawat, S. and Einstein, H. H. (2006). Artificial neural
networks for predicting the maximum surface settle-
ment caused by epb shield tunneling. Tunnelling and
underground space technology, 21(2):133–150.
Suzuki, A. (2016). 2016 annual report of NILIM: Pro-
ductivity improvement in infrastrucure development
process using i-construction. http://www.nilim.go.jp/
english/annual/annual2016/ar2016e.html. Accessed:
2018-10-23.
Syswerda, G. (1989). Uniform crossover in genetic al-
gorithms. In Proceedings of the third international
conference on Genetic algorithms, pages 2–9. Morgan
Kaufmann Publishers.
Takahama, T. and Sakai, S. (2005). Constrained optimiza-
tion by ε constrained particle swarm optimizer with
ε-level control. In Soft computing as transdisciplinary
science and technology, pages 1019–1029. Springer.
Takahama, T. and Sakai, S. (2006). Constrained optimi-
zation by the ε constrained differential evolution with
A PSO based Approach to Assign Segments for Reducing Excavated Soil in Shield Tunneling
335

gradient-based mutation and feasible elites. In Evo-
lutionary Computation, 2006. CEC 2006. IEEE Con-
gress on, pages 1–8. IEEE.
Takahama, T. and Sakai, S. (2010). Constrained optimiza-
tion by the ε constrained differential evolution with an
archive and gradient-based mutation. In Evolutionary
Computation (CEC), 2010 IEEE Congress on, pages
1–9. IEEE.
Windapo, A. O. (2016). Skilled labour supply in the south
african construction industry: The nexus between cer-
tification, quality of work output and shortages. SA
Journal of Human Resource Management, 14(1):1–8.
Yang, Z., Cai, X., and Fan, Z. (2014). Epsilon constrai-
ned method for constrained multiobjective optimiza-
tion problems: some preliminary results. In Procee-
dings of the Companion Publication of the 2014 An-
nual Conference on Genetic and Evolutionary Com-
putation, pages 1181–1186. ACM.
Zhang, Q. and Li, H. (2007). MOEA/D: A multiob-
jective evolutionary algorithm based on decomposi-
tion. IEEE Transactions on evolutionary computation,
11(6):712–731.
Zhang, Z., Long, K., Wang, J., and Dressler, F. (2014).
On swarm intelligence inspired self-organized net-
working: its bionic mechanisms, designing principles
and optimization approaches. IEEE Communications
Surveys & Tutorials, 16(1):513–537.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
336
