A Framework for Discovering Frequent Event Graphs from Uncertain

Event-based Spatio-temporal Data

Piotr S. Maci ˛ag

Institute of Computer Science, Warsaw University of Technology, Nowowiejska 15/19, 00-665, Warsaw, Poland

Keywords:

Uncertain Spatio-temporal Data, Probabilistic Sequential Patterns, Fuzzy Microclustering.

Abstract:

The aim of this paper is to discuss a novel framework designed for discovering frequent event graphs from

uncertain spatio-temporal data. We consider the problem of discovering hidden relations between event types

and their set of uncertain spatio-temporal instances. For that purpose, we designed the following data mining

framework: microclustering of uncertain instances, generating set of possible worlds according to the possible

worlds semantic technique, creating a microclustering index for each world, generating a set of event graphs

from created microclusters and deﬁning apriori based algorithm mining frequent event graphs (EventGraph

Miner). To the best of our knowledge this is the ﬁrst approach to discover hidden patterns from event-type

spatio-temporal data when dataset contains uncertain instances. While the paper does not present experimental

results for the proposed framework, it presents its potential for futher studies in the topic.

1 INTRODUCTION

Discovering various forms of patterns from spatio-

temporal data is gaining attention of researchers

nowadays (Li, 2014). This fact is motivated by the

rapid development of sensing techniques, designing

new types of sensor networks and introducing new

types of spatial and temporal data. The classiﬁca-

tion of spatio-temporal data distinguishes two basic

types of such data: event-based and trajectory-based

(Li, 2014).

In the article, we refer to the second from men-

tioned type of data. The notion of sequential pattern

discovered from reliable event-based spatio-temporal

data has been introduced in (Huang et al., 2008). The

task is to discover all signiﬁcant sequences of event

types, where for any two consecutive types contained

in the sequence, instances of the preceding event type

attract in their spatio-temporal neighborhoods occur-

rences of instances of the following event type.

The problem of uncertainty is particularly impor-

tant for spatio-temporal data due to often unreliable

nature of sensors gathering physical or environmen-

tal signals, noise introduced by transmission proto-

cols or faults in data storage methods. Unfortunately,

the problem of discovering probabilistic patterns from

such type of data is still not well investigated. On

the other hand, the problem of discovering knowledge

from several types of uncertain data (e.g. transac-

tion databases) has been considered in the literature

((Chui et al., 2007; Aggarwal et al., 2009; Chui and

Kao, 2008; Aggarwal, 2009; Zhang et al., 2008; Ber-

necker et al., 2009; Leung and MacKinnon, 2014)).

An extensive overview of methods for mining uncer-

tain data is given in (Aggarwal, 2009). The problem

of discovering probabilistic sequential patterns from

uncertain trajectory data is considered in (Li et al.,

2013). A solution for querying uncertain trajectory

data is given in (Emrich et al., 2012). The problem

of discovering various types of patterns from spatial

co-location data under uncertainty is considered in

(Ouyang et al., 2017; Wang et al., 2016).

The common technique adapted for discovering

knowledge from uncertain data is possible worlds se-

mantic. The technique is based on generating possi-

ble worlds containing certain occurrences of instances

and calculating probability of an occurrence of the

world. Such probabilities are used in estimating sig-

niﬁcance of a pattern occurring over multiple worlds.

The notions important for our article are event

type and event instances. We assume existence of

event types set F = { f

, f

, . . . , f

} and corresponding

dataset of event instances D. Each instance e ∈ D is

associated with the following set of attributes: event

identiﬁer, event type and a list of possible locations

for both spatial and temporal domain, where each lo-

cation is given with certain probability of occurrence.

Additionally, probabilities of occurrences in each lo-

656

Maci ˛ag, P.

A Framework for Discovering Frequent Event Graphs from Uncertain Event-based Spatio-temporal Data.

DOI: 10.5220/0007411206560663

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 656-663

ISBN: 978-989-758-351-3

cations list sum to one. The task considered in the

paper is to discover hidden relations between event

types based on the set of their uncertain instances. As

an attempt to solve the problem we provide a novel

framework described in section 2.

In the paper, we introduce the notion of expected

frequent event graph and we give a framework for

mining such graphs. Frequent event graphs repre-

sent a patterns between event types in set F. De-

signed framework discovers expected frequent event

graphs in the following manner: ﬁrst the set of un-

certain instances and their possible locations are mi-

croclustered according to their event types. The aim

of microclustering is to reduce the size of dataset by

merging any locations of the same instance contained

in the microcluster. From the set of created micro-

clusters, we generate possible worlds according to

the possible worlds semantic. Then, for each world

and its set of microclusters, we create a microcluster-

ing index which contains the following information:

identiﬁers of microclusters in each world, a list of in-

stances contained in each microcluster, an event type

representative for the microcluster and centroid loca-

tion in both spatial and temporal aspects. Based on

the set of created microclusters for a particular world

we create event graphs. The event graph is a directed

acyclic graph which nodes correspond to microclus-

ters and their labels to event types. The edges of

the graph are created based on the user given speci-

ﬁcation of neighborhood spaces between microclus-

ters. The support of an event graph is the number of

isomorphic subgraphs of event graphs in a particular

world. The expected support of a given event graph

is the sum of supports of such graph in all generated

worlds weighted by the probabilities of occurrences

of these worlds. Frequent event graphs are those with

expected support greater than the given threshold.

The following parts of the article are organized

as follows. The proposed framework for mining fre-

quent event graphs is given in section 2. We provide

basic notions in section 2.1. In section 3, we give

an algorithm for microclustering uncertain instances.

The steps for generating possible worlds and micro-

clustering index for each world are described in sec-

tion 3.1. In section 4, our algorithm discovering fre-

quent event graphs is discussed. Section 5 contains

conclusions, discussion and possible future work.

2 A FRAMEWORK FOR MINING

FREQUENT EVENT GRAPHS

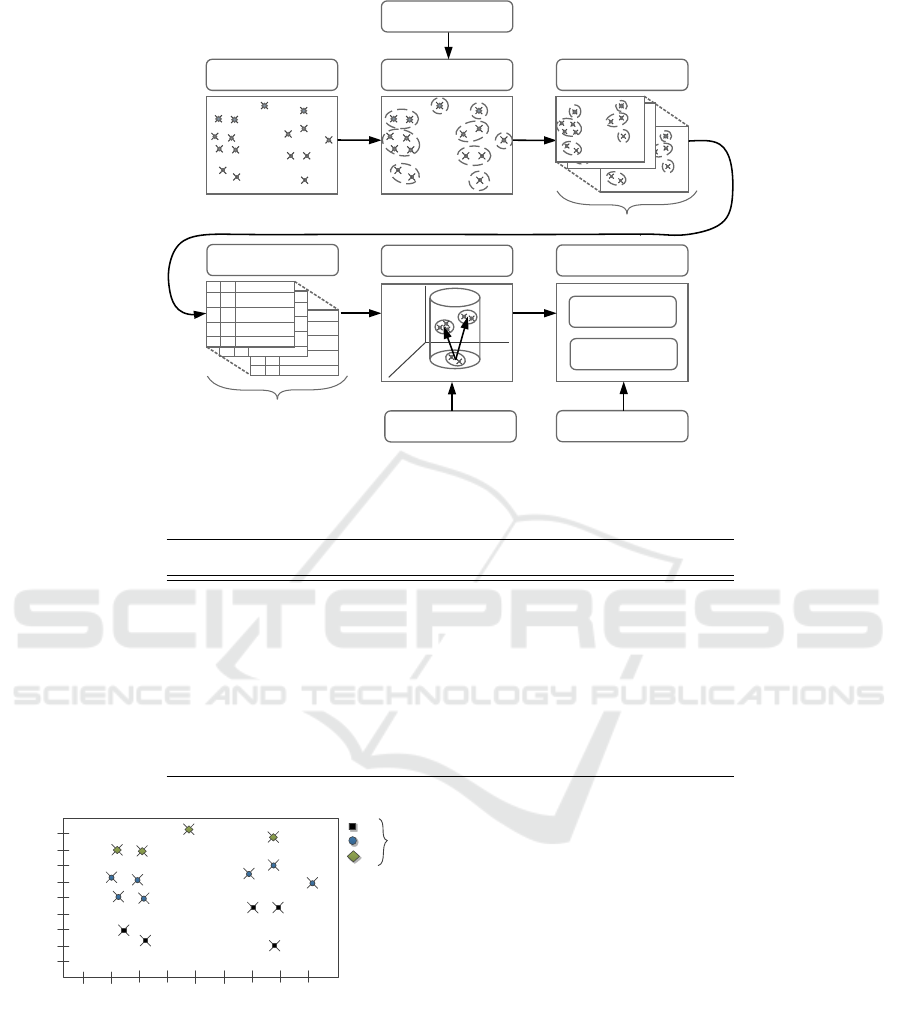
The process of mining expected frequent event graphs

is performed according to the framework shown in

Figure 1. In the designed framework, ﬁrst data is

compressed and transformed from the set of uncer-

tain event instances to the set of microclusters. In the

next step, the set of possible worlds is generated for

created microclusters. In section 4, we introduce an

event graph for created microclusters. The result of

the algorithm is the set of event graphs for which the

expected support is greater than the given minimum

support threshold (we deﬁne such graphs as frequent

event graphs).

2.1 Basic Notions

We provide elementary notions important for our for-

mulation of considered problem. The two sets are

provided: event types F = { f

, f

, . . . , f

} and dataset

of uncertain event instances D.

Deﬁnition 1 (Spatio-temporal Space V

). By V

denote the whole embedding spatio-temporal space

for a given problem.

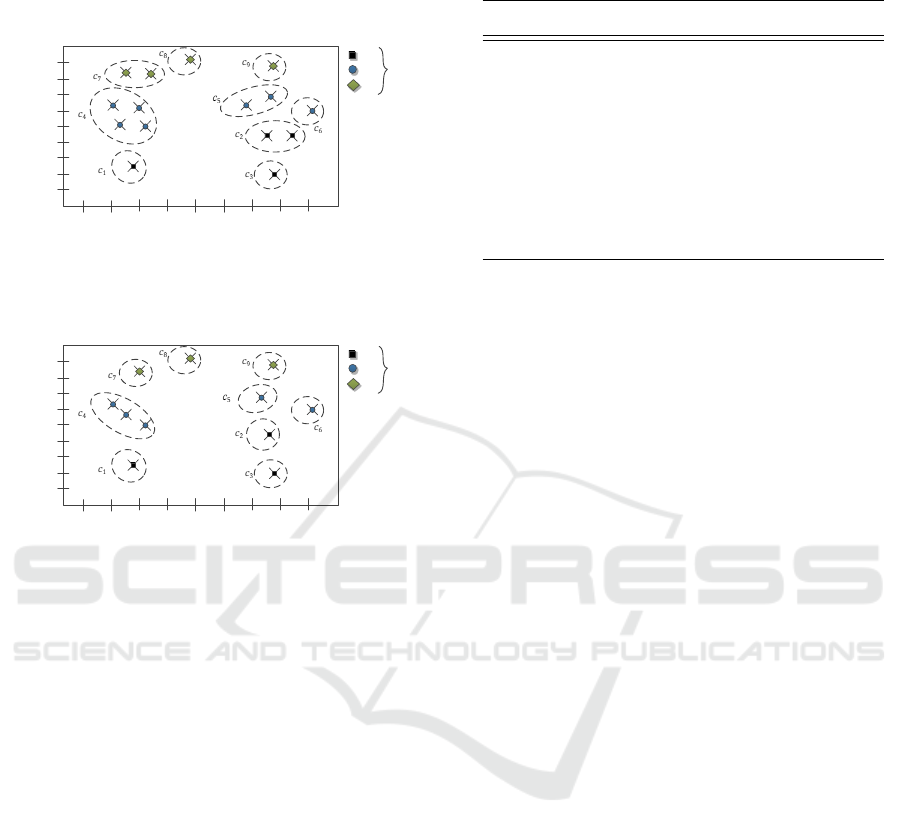
Let us consider an example given in Figure 2.

Note that the spatial area is usually given by two di-

mensions (i.e. longitude and latitude). For simplicity

we denote the spatial aspect in Figure 2 with only one

dimension. The number of event types in Figure 2 is

Deﬁnition 2 (Uncertain Event Instance). Uncertain

event instance e ∈ D is a triple associated with the

following constants: instance ID, event type and a

list of possible locations of e, where each location

is given with a certain probability of an occurrence.

We denote these constants using the following nota-

tion: e.ID, e.EventType, e.Locations = (l

, l

, . . . , l

Furthermore, for each possible location e.l, e.l.Loc

denotes spatial coordinates, e.l.Time occurrence time

and e.l.Probability probability of an occurrence.

Let us consider an example given in Figure 2. In-

stance e

is of type A and has two possible locations.

The two assumptions are important to note: (1) we

assume that each possible location is occurring in a

point, (2) probabilities of occurrences of locations

are summing to one (that is, having an instance e,

∑

∈e.Locations

(e.l

.Probability) = 1, where i is index-

ing locations of an instance e).

The common technique adapted for discovering

various types of patterns from uncertain data in data

mining is possible worlds semantic. In the technique,

possible worlds are generated as all possible combi-

nations of occurrences of instances locations: in each

word only one location of each uncertain instance

may occur. The probability of an occurrence of the

world is calculated as the product of probabilities of

A Framework for Discovering Frequent Event Graphs from Uncertain Event-based Spatio-temporal Data

657

ID ET Locations

1 A (0, 1, 1, 0.2 )

2 B (1, 2, 3, 0.6 )

3 B (1, 5, 5, 0.4 )

4 C (0, 3, 1, 0.7 )

ID ET Locations

1 A (0, 1, 1, 0.2 )

2 B (1, 2, 3, 0.6 )

3 B (1, 5, 5, 0.4 )

4 C (0, 3, 1, 0.7 )

Uncertain instances and their

possible locations

Uncertain microclustering of

locations / locations merging

ε1 and ε2 – user parameters

for microclustering

Generating possible worlds

M worlds

Generating microclustering

index for each world

M indexes

ID ET Locations

1 A (0, 1, 1, 0.2 )

2 B (1, 2, 3, 0.6 )

3 B (1, 5, 5, 0.4 )

4 C (0, 3, 1, 0.7 )

Creating set of event graphs

for each world

Mining expected frequent

event graphs

Minimal relative expected

support threshold

Longitude

Latitude

Time

Candidate generation

Isomorphism checking

Neighborhood space

specification

Figure 1: The framework for modelling and mining frequent event graphs.

Table 1: An example of event-based dataset with attributes: instance ID, event type, locations list.

ID Type Locations list (spatial coordinate, time, probability)

A l

= ((25, 3), 0.2), l

= ((33, 2), 0.8)

A l

= ((69, 4), 0.3), l

= ((78, 2), 0.5), l

= ((79, 4), 0.2)

B l

= ((33, 5), 1.0)

B l

= ((23, 5), 0.5), l

= ((31, 6), 0.5)

B l

= ((21, 6), 1.0)

B l

= ((72, 7), 0.4), l

= ((78, 7), 0.4), l

= ((92, 6), 0.2)

C l

= ((22, 8), 0.6), l

= ((33, 8), 0.4)

C l

= ((50, 9), 0.5), l

= ((78, 9), 0.5)

Time

Location

10 20 30 40 50 60 70 80 90

100

Event

Types

0.2

0.8

0.3

0.5

0.2

1.0

0.5

0.4

0.6

0.5

1.0

0.2

Figure 2: The visualization of the dataset given in Table 1.

occurrences of locations occurring in that world. Hav-

ing generated world, the support of a pattern discov-

ered in such world is weighted by the probability of

an occurrence of that world. The overall estimated

support of a pattern in the dataset D is the sum of

weighted supports of the pattern occurring in each

possible world.

Generating possible worlds directly from the set

of instances is in general infeasible. The number of

such worlds is bounded by |D|

Max

, where |D| denotes

the number of instances in D and Max denotes the

maximal number of possible locations among all in-

stances in D. An attempt to solve this problem is to

reduce the number of instances locations by perform-

ing microclustering of locations.

3 UNCERTAIN

MICROCLUSTERING

In this section, we consider the problem of uncer-

tain microclustering of instances locations. The idea

behind approach is: (1) to reduced dataset size; (2)

proceed with discovering patterns using created mi-

croclusters rather than particular instances. The set

of possible microclusters and locations contained in

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

658

them before generating possible worlds for dataset in

Figure 2 is given in Figure 4. By D( f ) in Algorithm 1,

we denote the set of instances of event type f in D.

Time

Location

10 20 30 40 50 60 70 80 90

100

Event

Types

1.0

0.5

0.3

0.2

0.4

0.5

1.0

0.5

1.0

0.4

0.6

0.5

Figure 3: A set of uncertain microclusters for dataset given

in Figure 2 before merging locations of the same instance

inside microclusters.

Time

Location

10 20 30 40 50 60 70 80 90

100

Event

Types

1.0

0.5

0.2

0.8

0.5

1.0

0.5

Figure 4: A set of uncertain microclusters for dataset given

in Figure 2 after merging locations of the same instance in-

side microclusters.

In Algorithm 1, ε

and ε

are the neighborhood

distances for the microclustering algorithm. Algo-

rithm 1 iteratively veriﬁes each possible location of

each instance and if that location is not in a micro-

cluster, then is inserted to the new microcluster. Al-

gorithm 2 retrieves all possible locations of instances

other than e.l, which are within distances ε

and ε

from e.l and are of the same type as e.EventType. All

these locations are inserted to the same microcluster

as e.l. ε

is the maximal spatial distance between spa-

tial coordinates e.l.Loc and spatial coordinates of any

other instance location (say p.l.Loc) of type f (that

is, p.l is considered to be the spatial neighbor of e.l

if distance(e.l.Loc, p.l.Loc) ≤ ε

). Distance function

is the Euclidean norm. ε

is the maximal temporal

interval between e.l.Time and any other possible lo-

cation of instances of type f . p.l is considered to be a

temporal neighbor of e.l if |e.l.Time− p.l.Time| ≤ ε

The purpose of step 9 in Algorithm 1 is to merge

all locations of the same instance occurring inside a

microcluster into one possible location. The proba-

bility of such location is the sum of probabilities of

merged locations and its spatial coordinates and oc-

currence time are calculated as averages of spatial co-

ordinates and occurrences times of merged locations.

Table 2: Uncertain microclusters generated for dataset

given in Table 1.

MCID Event Type Contained instances

A e

: 1.0

A e

: 0.5

A e

: 0.5

B e

: 1.0, e

: 1.0

B e

: 0.8

B e

: 0.2

C e

: 1.0

C e

: 0.5

C e

: 0.5

3.1 Generating Possible Worlds

Having a set of uncertain microclusters the next step

is to generate all possible worlds containing certain

occurrences of such microclusters. Table 2 contains

uncertain microclusters depicted in Figure 4. In-

stances e

, e

and e

may occur in different micro-

clusters and, due to that, there exist 8 possible worlds.

The ﬁrst world contains the following microclusters

and instances: w

= {c

= { e

}, c

= {e

}, c

, e

}, c

= {e

}, c

= {e

}, c

= {e

}}. The

second one is w

= {c

= {e

}, c

= {e

}, c

, e

}, c

= {e

}, c

= {e

}, c

= {e

}}, etc. The

probability of an occurrence of each possible world is

the product of probabilities of instances locations con-

tained in the microclusters generated for such world

and is calculated according to Eq. 1. Having gener-

ated M worlds for a given set of uncertain microclus-

ters

∑

i=1

(P(w

)) = 1.

P(w) =

∏

c∈w

∏

e.l∈c

e.l.Probability (1)

For each possible world and for its microclus-

ters we generate a microclustering index. The micro-

clustering index contains identiﬁers of microclusters,

event type contained in a particular microcluster, a list

of contained locations of instances and the centroid

location for a microcluster. In Table 3, we give a mi-

croclustering index for world 1.

4 DISCOVERING FREQUENT

EVENT GRAPHS

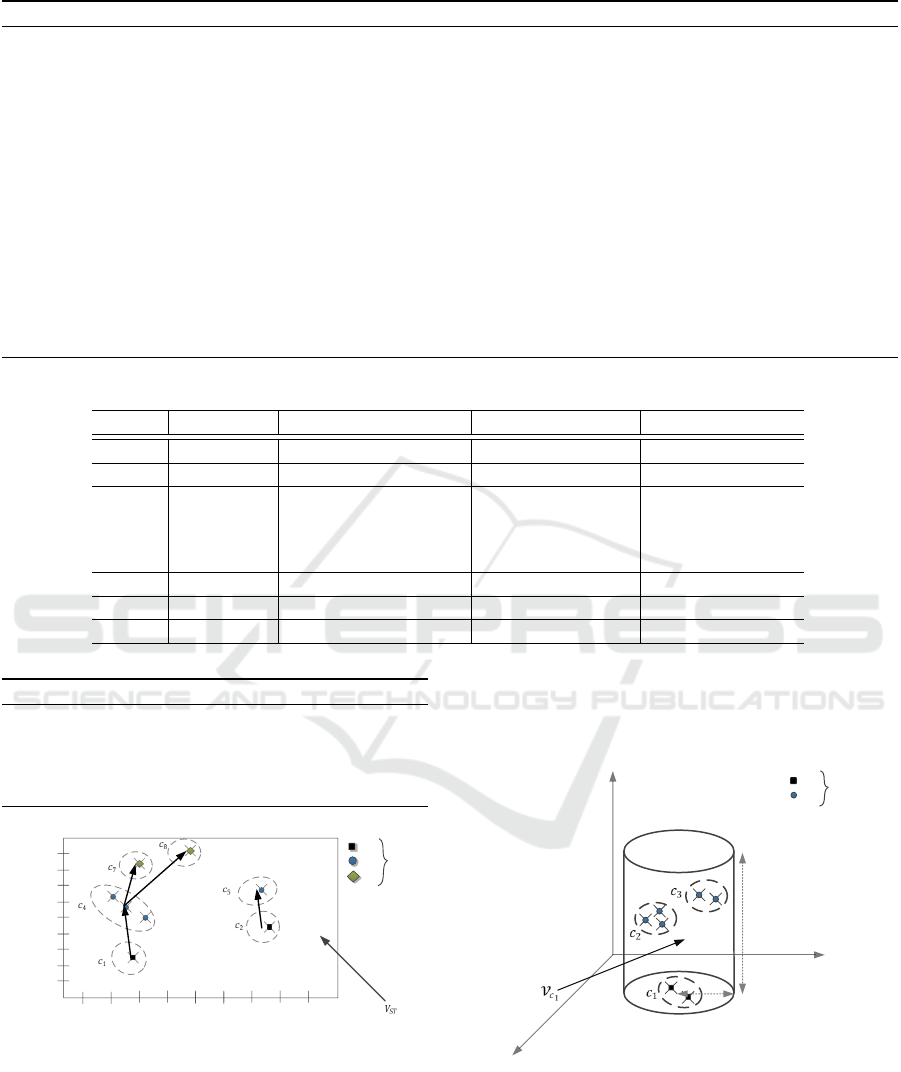
In Figure 5, we depict world w

which contains mi-

croclusters and instances locations generated accord-

ing to method proposed in subsection 3.1.

Deﬁnition 3 (Spatio-temporal Neighborhood Space).

For a microcluster c, its spatio-temporal neighbor-

A Framework for Discovering Frequent Event Graphs from Uncertain Event-based Spatio-temporal Data

659

Algorithm 1: Algorithm for generating uncertain microclusters.

Input: D - dataset of uncertain instances; ε

, ε

- neighborhood distances.

1: for each event type f ∈ F do

2: for each instance e ∈ D( f ) do

3: for each location l ∈ e.Locations do

4: if e.l does not belong to any microcluster then

5: Create new microcluster with MCID := MCID + 1.

6: Label e.l as belonging to the microcluster MCID.

7: X := RetrieveNeighbors(e.l, ε

, ε

)

8: Label each location p.l ∈ X as belonging to the microcluster MCID.

9: Merge all locations of the same instance in MCID into one location.

10: end if

11: end for

12: end for

13: end for

Table 3: The microclustering index created for microclusters of world 1 shown in Figure 5.

MCID Event type Contained locations Num. of locations Centroid location

A e

= ((28, 2), 1.0) 1 (28, 2)

A e

= ((75, 4), 0.5) 1 (75, 4)

= ((33, 5), 1.0),

= ((27, 5), 1.0),

= ((21, 6), 1.0) 3 (27, 5)

B e

= ((75, 7), 0.8) 1 (75, 7)

C e

= ((27, 8), 1.0) 1 (27, 8)

C e

= ((50, 9), 0.5) 1 (50, 9)

Algorithm 2: RetrieveNeighbors function.

Input: e.l - a possible location of instance e; ε

, ε

neighborhood distances.

1: Return all possible locations of instances other

than e.l within distance ε

and ε

from e.l.

Time

Location

10 20 30 40 50 60 70 80 90

100

Event

Types

Figure 5: Microclusters from world 1 and event graphs cre-

ated for them.

hood space V

is a cylindrical space deﬁned by spatial

radius R and temporal interval T . The centroid’s spa-

tial coordinates of the microcluster are the center of

spatial circle with radius R and temporal interval of

length T is deﬁned beginning with the time stamp of

centroid.

In Figure 6, we show spatio-temporal cylindrical

space for microcluster c

with parameters R = 4, T =

10.

Longitude

Latitude

Time

Event

Types

R = 4

T = 10

Figure 6: Spatio-temporal neighborhood space of micro-

cluster c

Deﬁnition 4. Given a microcluster c, its spatio-

temporal neighborhood space V

, we say all micro-

clusters which centroids are contained inside V

fol-

low c (in other words, there is a following relation

between such microclusters and c).

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

660

For microcluster c

and its neighborhood space

shown in Figure 6, microclusters c

, c

of event

type B are following c

Deﬁnition 5 (Set of Event Graphs G). Given gener-

ated world w and a set of microclusters for that world,

a set of graphs G

contains all directed acyclic graphs

with nodes corresponding to microclusters and edges

denoting the following relations between microclus-

ters. The graph G = (V, E, L, λ) ∈ G

is deﬁned as

follows:

1. V = (v

, v

, . . . , v

) is the set of vertices corre-

sponding to microclusters of a given world.

2. E = (x

, x

, . . . , x

) is the set of edges denoting

the following relation between microclusters.

3. L is the set of event types.

4. λ : V → L is the function assigning to each vertex

an event type of a microcluster represented by this

vertex.

Example 1. In Figure 5, we show microclusters gen-

erated for world 1. For this world G

contains two

directed acyclic graphs: G

• V

= {v

, v

• E

= {(v

, v

), (v

, v

), (v

, v

)}.

• L

= {A, B, C}

• λ

) = A, λ

) = B, λ

) = C, λ

) = C.

and G

• V

= {v

, v

• E

= {(v

, v

)}.

• L

= {A, B}.

• λ

) = A, λ

) = B.

Deﬁnition 6 (Supporting Graph of an Event Graph).

Given an event graph G, its supporting graph G

∈

is the graph which subgraph H is isomorphic to

G i.e. for the mapping φ of vertices between G and

H φ : V (G) → V (H) the following two conditions are

preserved:

1. Any vertices v

and v

with an edge (v

, v

) in G

also have an edge (φ(v

), φ(v

)) in H.

2. The event types of v

and v

are the same as φ(v

)

and φ(v

Deﬁnition 7 (Support and Relative Support of an

Event Graph). For a considered event graph G, the

support of G (sup

(G)) is the number of graphs in

supporting G in world w. The relative support of

G (relSup

(G)) is deﬁned as

sup

(G)

, where |G

| is

the number of graphs in G

Let us consider an event graph G = (V =

, v

}, E = {(v

, v

)}, lbl = {A, B}, (L(v

) =

A, L(v

) = B)). Its support for G given in Example 1

is 2 and relative support is 1.

Deﬁnition 8 (Expected Support and Relative Ex-

pected Support of an Event Graph). Having generated

M worlds, the expected support of an event graph G

is:

expSup(G) =

∑

i=1

P(w

) · sup

(G) (2)

where sup

(G) is support of G in world w

. The rel-

ative expected support of G is deﬁned as:

relExpSup(G) =

∑

i=1

P(w

) ·

sup

(G)

(3)

Deﬁnition 9 (Problem Deﬁnition). Given a dataset

of uncertain instances D, the task is to discover all

event graphs G with relExpSup(G) ≥ minSup. All

such graphs will be referred as frequent event graphs

and denoted by F .

4.1 Algorithm Discovering Frequent

Event Graphs

Algorithm 3 is inspired by the apriori-based strategy

to mine frequent graphs (Jiang et al., 2013). The car-

dinality of the graph is the number of its vertices.

First, the set F

is generated from event graphs sets

, G

, . . . , G

. Then, iteratively while F

k−1

is not

empty, the following operations are performed:

• A set of candidate event graphs of cardinality k

is generated from F

k−1

by procedure Candidate-

gen(F

k−1

• The support of each graph G ∈ C

in a world w

is calculated as the number of graphs isomorphic

with G in G

• The relative expected support of G is calculated

according to Deﬁnition 8.

• G is included in F

if its relative expected support

is greater than minSup threshold.

The candidate graphs may be generated accord-

ing to the procedure presented in (Kuramochi and

Karypis, 2004).

5 CONCLUSIONS AND

DISCUSSION

In the paper, we proposed a new framework for dis-

covering patterns from event-based spatio-temporal

data. The proposed framework consists of the follow-

ing steps: data microclustering, generating possible

worlds from uncertain microclusters and creating mi-

croclustering index for each generated world, then for

A Framework for Discovering Frequent Event Graphs from Uncertain Event-based Spatio-temporal Data

661

Algorithm 3: Apriori-based EventGraph Miner.

Input: G

, G

, . . . , G

- sets of event graphs for

worlds 1 . . . M; minSup - minimal relative ex-

pected support threshold.

Output: F

, F

, . . . , F

- sets of frequent event

graphs with cardinality 1 to k.

1: F

← sets of frequent event graphs of cardinality

1 detected for G

, G

, . . . , G

2: F

← sets of frequent event graphs of cardinality

2 detected for G

, G

, . . . , G

3: while F

k−1

0 do

4: F

←

5: C

← Candidate-gen(F

k−1

6: for each G ∈ C

7: relExpSup(G) ← 0.

8: for each event graphs set G

9: sup

(G) ← 0.

10: for each H ∈ G

11: if Is-isomorphism(G, H) then

12: sup

(G) ← sup

(G) + 1.

13: end if

14: end for

15: relExpSup(G) ← relExpSup(G) +

P(w

) ·

sup

(G)

16: end for

17: if relExpSup(G) ≥ minSup then

18: F

← F

∪ G.

19: end if

20: end for

21: end while

each world based on its microclustering index gener-

ating a set of event graphs and discovering expected

frequent event graphs from given dataset. The sev-

eral points of the proposed framework shall be further

discussed:

• The method for microclustering dataset. We pro-

posed rather simple method for dataset microclus-

tering. The more complex approaches may be to

apply one of the well known density based algo-

rithms (DBSCAN or OPTICS).

• For generating possible worlds and microcluster-

ing set. While the aim of microclustering is to

merge location of uncertain instances and reduce

the number of generated worlds, the number of

generated worlds still may be signiﬁcant. That can

make the algorithm discovering expected frequent

event graphs infeasible.

In our future work, we will focus on improving

the notions provided in the paper and performing ex-

perimental results showing efﬁciency and effective-

ness of the proposed algorithms. Some preliminary

experiments performed by us show that the possible

bottleneck of the proposed solution is the number of

generated possible worlds despite performing micro-

clustering step. In such a case, further improvements

of the solution should focus on more efﬁcient gen-

eration of possible worlds and calculating support of

event graphs.

REFERENCES

Aggarwal, C. C. (2009). Managing and Mining Uncertain

Data. Springer Publishing Company, Incorporated.

Aggarwal, C. C., Li, Y., Wang, J., and Wang, J. (2009). Fre-

quent pattern mining with uncertain data. In Proceed-

ings of the 15th ACM SIGKDD International Con-

ference on Knowledge Discovery and Data Mining,

KDD ’09, pages 29–38, New York, NY, USA. ACM.

Bernecker, T., Kriegel, H.-P., Renz, M., Verhein, F., and

Zueﬂe, A. (2009). Probabilistic frequent itemset min-

ing in uncertain databases. In Proceedings of the 15th

ACM SIGKDD International Conference on Knowl-

edge Discovery and Data Mining, KDD ’09, pages

119–128, New York, NY, USA. ACM.

Chui, C.-K. and Kao, B. (2008). A Decremental Approach

for Mining Frequent Itemsets from Uncertain Data,

pages 64–75. Springer Berlin Heidelberg, Berlin, Hei-

delberg.

Chui, C.-K., Kao, B., and Hung, E. (2007). Mining Fre-

quent Itemsets from Uncertain Data, pages 47–58.

Springer Berlin Heidelberg, Berlin, Heidelberg.

Emrich, T., Kriegel, H. P., Mamoulis, N., Renz, M., and

Zuﬂe, A. (2012). Querying uncertain spatio-temporal

data. In 2012 IEEE 28th International Conference on

Data Engineering, pages 354–365.

Huang, Y., Zhang, L., and Zhang, P. (2008). A framework

for mining sequential patterns from spatio-temporal

event data sets. IEEE Transactions on Knowledge and

Data Engineering, 20(4):433–448.

Jiang, C., Coenen, F., and Zito, M. (2013). A survey of

frequent subgraph mining algorithms. The Knowledge

Engineering Review, 28(1):75–105.

Kuramochi, M. and Karypis, G. (2004). An efﬁcient al-

gorithm for discovering frequent subgraphs. IEEE

Transactions on Knowledge and Data Engineering,

16(9):1038–1051.

Leung, C. K. S. and MacKinnon, R. K. (2014). Fast al-

gorithms for frequent itemset mining from uncertain

data. In 2014 IEEE International Conference on Data

Mining, pages 893–898.

Li, Y., Bailey, J., Kulik, L., and Pei, J. (2013). Mining

probabilistic frequent spatio-temporal sequential pat-

terns with gap constraints from uncertain databases.

In 2013 IEEE 13th International Conference on Data

Mining, pages 448–457.

Li, Z. (2014). Spatiotemporal Pattern Mining: Algorithms

and Applications, pages 283–306. Springer Interna-

tional Publishing, Cham.

Ouyang, Z., Wang, L., and Wu, P. (2017). Spatial co-

location pattern discovery from fuzzy objects. In-

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

662

ternational Journal on Artiﬁcial Intelligence Tools,

26(02):1750003.

Wang, L., Han, J., Chen, H., and Lu, J. (2016). Top-k

probabilistic prevalent co-location mining in spatially

uncertain data sets. Frontiers of Computer Science,

10(3):488–503.

Zhang, Q., Li, F., and Yi, K. (2008). Finding frequent items

in probabilistic data. In Proceedings of the 2008 ACM

SIGMOD International Conference on Management

of Data, SIGMOD ’08, pages 819–832, New York,

NY, USA. ACM.

A Framework for Discovering Frequent Event Graphs from Uncertain Event-based Spatio-temporal Data

663