Towards Hierarchical Probabilistic CTL Model Checking:

Theoretical Foundations

Norihiro Kamide and Yuki Yano

Teikyo University, Faculty of Science and Engineering, Department of Information and Electronic Engineering, Toyosatodai

1-1, Utsunomiya-shi, Tochigi 320-8551, Japan

Keywords:

Computation Tree Logic, Probabilistic Computation Tree Logic, Hierarchical Computation Tree Logic,

Embedding Theorem, Relative Decidability.

Abstract:

This study proposes a hierarchical probabilistic computation tree logic, HpCTL, which is an extension of the

standard probabilistic computation tree logic pCTL, as a theoretical basis for hierarchical probabilistic CTL

model checking. Hierarchical probabilistic model checking is a new paradigm that can appropriately verify

hierarchical randomized (or stochastic) systems. Furthermore, a probability-measure-independent translation

from HpCTL into pCTL is deﬁned, and a theorem for embedding HpCTL into pCTL is proved using this

translation. Finally, the relative decidability of HpCTL with respect to pCTL is proved using this embedding

theorem. These embedding and relative decidability results allow us to reuse the standard pCTL-based prob-

abilistic model checking algorithms to verify hierarchical randomized systems that can be described using

HpCTL.

1 INTRODUCTION

1.1 Aims

In this study, we develop a new temporal logic for

hierarchical probabilistic model checking, which is

a new model checking paradigm that can appropri-

ately verify hierarchical randomized (or stochastic)

systems. Model checking is a formal method for

automatically verifying concurrent systems (Clarke

and Emerson, 1981; Cavada et al., 2015; Holzmann,

2006; Clarke et al., 2018), and has been extended

to probabilistic model checking (Aziz et al., 1995;

Bianco and de Alfaro, 1995; Kwiatkowska et al.,

2011; Baier et al., 2018) and hierarchical model

checking (Kamide and Kaneiwa, 2009; Kaneiwa and

Kamide, 2011; Kamide, 2015; Kamide and Yano,

2017). Thus, the objective of this study is to in-

tegrate these extended model checking paradigms.

Computation tree logic (CTL) (Clarke and Emerson,

1981) has been typically used as a theoretical basis for

model checking. In fact, the model checker known as

NuSMV (Cavada et al., 2015) was developed based

on CTL. However, CTL is unsuitable for verifying hi-

erarchical randomized systems because it lacks the

constructors to represent “hierarchical randomized”

systems naturally. Thus, CTL has been extended

to probabilistic computation tree logics (Aziz et al.,

1995; Bianco and de Alfaro, 1995) and hierarchical

(or sequential) computation tree logics (Kamide and

Kaneiwa, 2009; Kaneiwa and Kamide, 2011; Kamide

and Yano, 2017; Kamide, 2018). The main aim of

this study is to integrate these extended logics for ob-

taining a theoretical basis for hierarchical probabilis-

tic model checking.

1.2 Probabilistic Computation Tree

Logic

Several probabilistic computation tree logics and their

variants have been studied to handle randomized

(or stochastic) systems (Aziz et al., 1995; Bianco

and de Alfaro, 1995; Kamide and Koizumi, 2015;

Kamide and Koizumi, 2016). A probabilistic com-

putation tree logic, pCTL, was studied by Aziz et

al. (Aziz et al., 1995) and Bianco and de Alfaro

(Bianco and de Alfaro, 1995). This pCTL was ob-

tained from CTL by adding some probabilistic or

probability operators, such as P

≥x

. The formulas of

the form P

≥x

α are intended to read “the probabil-

ity of α holding in the future evolution of the sys-

tem is at least x.” In (Bianco and de Alfaro, 1995),

the logic pCTL was studied to verify the reliabil-

ity properties and performance of the systems mod-

762

Kamide, N. and Yano, Y.

Towards Hierarchical Probabilistic CTL Model Checking: Theoretical Foundations.

DOI: 10.5220/0007456507620769

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 762-769

ISBN: 978-989-758-350-6

eled by discrete Markov chains, and the complexi-

ties of model-checking algorithms with regard to the

logic were also clariﬁed. In (Aziz et al., 1995), ef-

ﬁcient model checking algorithms for various exten-

sions of the previous settings of pCTL were pro-

posed to verify probabilistic non-deterministic con-

current systems, wherein probabilistic behavior coex-

ists with non-determinism. The difference between

the pCTL-settings of Aziz et al. (Aziz et al., 1995)

and those of Bianco and de Alfaro (Bianco and de Al-

faro, 1995) is the settings of the probability measures

within the probabilistic Kripke structures of pCTL. In

(Kamide and Koizumi, 2015; Kamide and Koizumi,

2016), the inconsistency-tolerant (or paraconsistent)

probabilistic computation tree logic, PpCTL, which

was obtained from pCTL by adding a paraconsis-

tent negation connective ∼, was developed on the ba-

sis of a probability-measure-independent translation

of PpCTL into pCTL. The theorem for embedding

PpCTL into pCTL was shown using this translation,

and entailed the relative decidability of PpCTL with

respect to pCTL. This result indicates that we can

reuse the existing pCTL-based model checking algo-

rithms of Aziz et al. (Aziz et al., 1995) and Bianco

and de Alfaro (Bianco and de Alfaro, 1995) to the

PpCTL-based model checking algorithms. Hence, the

aim of this study is to progress in this direction for hi-

erarchical probabilistic model checking.

1.3 Hierarchical Computation Tree

Logic

Several hierarchical (or sequential) computation tree

logics and their variants have been studied to han-

dle hierarchical systems (Kamide and Kaneiwa, 2009;

Kaneiwa and Kamide, 2011; Kamide, 2015; Kamide

and Yano, 2017; Kamide, 2018). A modal operator

called a sequence modal operator, which is denoted

as [b] where b is a sequence, is used in these hier-

archical computation tree logics. The formulas of the

form [b

; b

;···; b

]α intuitively mean that “α is true

based on a sequence b

; b

;···; b

of ordered pieces

of information.” For more information on [b], see Re-

mark 2.6 in Section 2. In (Kamide, 2015), an exten-

sion of CTL, which was called the sequence-indexed

paraconsistent computation-tree logic, SPCTL, was

introduced by adding [b] and ∼ to CTL. This logic

was used to verify clinical reasoning systems. In

(Kamide and Kaneiwa, 2009; Kaneiwa and Kamide,

2011), an extension of the full computation tree

logic (CTL

∗

), which was called CTLS

∗

, was devel-

oped by adding [b] to CTL

∗

. This logic was used

to represent conceptual hierarchies and ontologies.

In (Kaneiwa and Kamide, 2010), an extension of

the linear-time temporal logic (LTL) (Pnueli, 1977),

which was called the sequence-indexed linear-time

temporal logic, SLTL, was introduced by adding [b]

to LTL. In addition, a proof system for SLTL was de-

veloped to verify certain speciﬁcations of secure au-

thentication systems. In (Kamide and Yano, 2017;

Kamide, 2018), an extension of CTL, which was

called the sequential computation tree logic, sCTL,

was introduced by adding [b] to CTL. The logic sCTL

has a simple single satisfaction relation, which is

compatible with that of CTL. Thus, the aim of this

study is to move in this direction for hierarchical

probabilistic computation tree logic. In fact, the logic

proposed in this study is regarded as an extension of

sCTL.

1.4 Results

In this study, a simple new extended computation tree

logic called hierarchical probabilistic computation

tree logic, HpCTL, which can appropriately represent

hierarchical information and probabilistic phenom-

ena, is developed by extending pCTL and sCTL. Fur-

thermore, a probability-measure-independent transla-

tion from HpCTL into pCTL is deﬁned, and a theorem

for embedding HpCTL into pCTL is proved using this

translation. In addition, the relative decidability the-

orem of HpCTL with respect to pCTL is proved us-

ing this embedding theorem. This relative decidabil-

ity theorem indicates that the decidability of pCTL

implies the decidability of HpCTL. Moreover, these

embedding and relative decidability results allow the

efﬁcient reuse of the standard pCTL-based probabilis-

tic model checking algorithms to verify hierarchical

randomized systems that can be modeled and spec-

iﬁed using HpCTL. The previously proposed logics

CTLS

∗

(Kamide and Kaneiwa, 2009; Kaneiwa and

Kamide, 2011), SLTL (Kaneiwa and Kamide, 2010),

and SPCTL (Kamide, 2015) had complex multiple

sequence-indexed satisfaction relations |=

, where

represents sequences. On the other hand, the pro-

posed logic HpCTL has a simple single satisfaction

relation |=

, which is highly compatible with the stan-

dard single satisfaction relation of CTL. By using this

simple satisfaction relation, the theorem for embed-

ding HpCTL into pCTL can be simply proved, and the

sequence modal operator [b] can be formalized and

handled uniformly.

The remainder of this paper is organized as fol-

lows. In Section 2, we deﬁne pCTL and intro-

duce HpCTL based on the single satisfaction relation

. In Section 3, we deﬁne a probability-measure-

independent translation function from HpCTL into

pCTL, which is considered a simpliﬁcation of the

Towards Hierarchical Probabilistic CTL Model Checking: Theoretical Foundations

763

translation functions used in (Kamide and Kaneiwa,

2009; Kaneiwa and Kamide, 2010; Kaneiwa and

Kamide, 2011; Kamide, 2015). The theorem for em-

bedding HpCTL into pCTL is proved using the pro-

posed translation function, and the relative decidabil-

ity theorem for HpCTL is obtained using this em-

bedding theorem. In Section 4, we address some il-

lustrative examples for hierarchical probabilistic CTL

model checking based on HpCTL. In Section 5, we

present our concluding remarks.

2 LOGICS

Formulas of probabilistic computation tree logic

(pCTL) are constructed from countably many propo-

sitional variables, → (implication) ∧ (conjunction),

∨ (disjunction), ¬ (classical negation), X (next), G

(globally), F (eventually), U (until), R (release), A

(all computation paths), E (some computation path),

≤x

(less than or equal probability), P

≥x

(greater than

or equal probability), P

(less than probability), and

(greater than probability). The symbols X, G, F,

U, and R are called temporal operators, the symbols

A and E are called path quantiﬁers, and the symbols

≤x

, P

≥x

, P

, and P

are called probabilistic op-

erators or probability operators. A formula P

≤x

α is

intended to read “the probability of α is at least x.”

We use the symbol Φ to denote a non-empty set of

propositional variables. We use an expression A ≡ B

to denote the syntactical identity between A and B.

Deﬁnition 2.1. Formulas α of pCTL are deﬁned by

the following grammar, assuming p ∈ Φ and x ∈ [0,1]:

α ::= p | α→α | α ∧ α | α ∨ α | ¬α

| AXα | EXα | AGα | EGα | AFα | EFα

| A(αUα) | E(αUα) | A(αRα) | E(αRα)

| P

≤x

α | P

≥x

α | P

α.

In this deﬁnition, pairs of symbols like AG and

EU are indivisible, and the symbols X,G,F,U and R

cannot occur without being preceded by an A or an E.

Similarly, every A or E must have one of X, G, F, U

and R to accompany it.

Deﬁnition 2.2 (pCTL). A structure (S, S

,R,µ

,L) is

a probabilistic model iff

1. S is the set of states,

2. S

is a set of initial states and S

⊆ S,

3. R is a binary relation on S which satisﬁes the con-

dition:

∀s ∈ S ∃s

∈ S [(s, s

) ∈ R],

4. µ

is a certain probability measure (or probability

distribution) concerning s ∈ S: a set of paths be-

ginning at s is mapped into a real number in [0,1],

5. L is a mapping from S to the power set of Φ.

A path in a model is an inﬁnite sequence of states,

π = s

,... such that

∀i ≥ 0 [(s

i+1

) ∈ R].

A probabilistic satisfaction relation (M,s) |= α for

any formula α, where M is a probabilistic model

(S, S

,R, µ

,L) and s represents a state in S, is deﬁned

inductively by:

1. for any p ∈ Φ, (M, s) |= p iff p ∈ L(s),

2. (M, s) |= α ∧ β iff (M, s) |= α and (M, s) |= β,

3. (M, s) |= α ∨ β iff (M, s) |= α or (M, s) |= β,

4. (M, s) |= α→β iff (M, s) |= α implies (M, s) |= β,

5. (M, s) |= ¬α iff (M, s) 6|= α,

6. (M, s) |= AXα iff ∀s

∈ S [(s,s

) ∈ R implies (M,s

) |=

α],

7. (M, s) |= EXα iff ∃s

∈ S [(s,s

) ∈ R and (M, s

) |= α],

8. (M, s) |= AGα iff for all paths π ≡ s

,..., where

s ≡ s

, and all states s

along π, we have (M, s

) |= α,

9. (M, s) |= EGα iff there is a path π ≡ s

,..., where

s ≡ s

, and for all states s

along π, we have (M,s

) |= α,

10. (M, s) |= AFα iff for all paths π ≡ s

,..., where

s ≡ s

, there is a state s

along π such that (M,s

) |= α,

11. (M, s) |= EFα iff there is a path π ≡ s

,..., where

s ≡ s

, and for some state s

along π, we have (M, s

) |=

α,

12. (M, s) |= A(αUβ) iff for all paths π ≡ s

,...,

where s ≡ s

, there is a state s

along π such that

(M, s

) |= β and ∀0 ≤ k < j (M, s

) |= α,

13. (M, s) |= E(αUβ) iff there is a path π ≡ s

,...,

where s ≡ s

, and for some state s

along π, we have

(M, s

) |= β and ∀0 ≤ k < j (M, s

) |= α,

14. (M, s) |= A(αRβ) iff for all paths π ≡ s

,...,

where s ≡ s

, and all states s

along π, we have

(M, s

) |= β or ∃0 ≤ k < j (M, s

) |= α,

15. (M, s) |= E(αRβ) iff there is a path π ≡ s

,...,

where s ≡ s

, and for all states s

along π, we have

(M, s

) |= β or ∃0 ≤ k < j (M, s

) |= α,

16. for any x ∈ [0,1], M,s |= P

≤x

α iff µ

({w ∈ Ω

| M, s |=

α}) ≤ x,

17. for any x ∈ [0,1], M,s |= P

≥x

α iff µ

({w ∈ Ω

| M, s |=

α}) ≥ x,

18. for any x ∈ [0,1], M,s |= P

α iff µ

({w ∈ Ω

| M, s |=

α}) < x,

19. for any x ∈ [0,1], M,s |= P

α iff µ

({w ∈ Ω

| M, s |=

α}) > x.

A formula α is valid in pCTL iff (M, s) |= α holds

for any probabilistic model M := (S,S

,R, µ

,L), any

s ∈ S, and any probabilistic satisfaction relation |= on

Remark 2.3.

1. The deﬁnition of µ

is not precisely and explicitly

given in this paper. The reasons are as follows. (1)

the proposed translation from HpCTL into pCTL

is independent of the setting of µ

. (2) There are

many possibilities for deﬁning µ

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

764

2. In (Bianco and de Alfaro, 1995), two probability

measures µ

and µ

−

, called minimal probability

and maximal probability, respectively, are intro-

duced for pCTL. The measures µ

and µ

−

are

deﬁned on a Borel σ-algebra B

(⊆ 2

Ω

) as fol-

lows: for any ∆ ∈ B

, µ

(∆) = sup µ

s,η

(∆) and

−

(∆) = in f µ

s,η

(∆) where µ

s,η

with a strategy η

concerning nondeterminism is a unique probabil-

ity measure on B

3. In (Aziz et al., 1995), a probability measure µ

concerning some discrete Markov processes and

discrete generalized Markov processes is intro-

duced for pCTL. µ

is deﬁned as a mapping from

into [0, 1] where C

is a Borel sigma ﬁeld,

which is the class of subsets of the set of all in-

ﬁnite state sequences starting at s.

The language of hierarchical probabilistic com-

putation tree logic (HpCTL) is obtained from that

of pCTL by adding [b] (hierarchical operator or se-

quence modal operator) where b is a sequence. Se-

quences are constructed from atomic sequences,

(empty sequence) and ; (composition). The set of se-

quences (including the empty sequence

0) is denoted

as SE. Lower-case letters b, c, ... are used to denote

sequences. An expression [

0]α means α, and expres-

sions [

0 ; b]α and [b ;

0]α mean [b]α. The symbol

Φ is used to denote a non-empty set of propositional

variables, the symbol Φ

[d]

(d ∈ SE) is used to denote

the set {[d]p | p ∈ Φ}, and the symbol Φ

(d ∈ SE) is

used to denote the set {p

| p ∈ Φ} of propositional

variables where p

means p. Note that Φ

[

= Φ

= Φ.

Deﬁnition 2.4. Formulas α and sequences b of

HpCTL are deﬁned by the following grammar, as-

suming p and e represent propositional variables and

atomic sequences, respectively:

α ::= p | α→α | α ∧ α | α ∨ α | ¬α

| AXα | EXα | AGα | EGα | AFα | EFα

| A(αUα) | E(αUα) | A(αRα) | E(αRα)

| P

≤x

α | P

≥x

α | P

α.

b ::= e |

0 | b ; b.

We use an expression [d] to represent

][d

]· · · [d

] with i ∈ ω, d

∈ SE and d

≡

We remark that [d] can be the empty sequence, and

that [d] is not uniquely determined. For example,

if d ≡ d

; d

where d

, d

and d

are atomic

sequences, then [d] means [d

][d

], [d

; d

][d

; d

] or [d

; d

]. We also note that [d] can

be [d] (i.e., [d] includes [d]).

Deﬁnition 2.5 (HpCTL). A structure (S, S

,R, µ

)

is a hierarchical probabilistic model iff

1. S is the set of states,

2. S

is a set of initial states and S

⊆ S,

3. R is a binary relation on S which satisﬁes the con-

dition:

∀s ∈ S ∃s

∈ S [(s, s

) ∈ R],

4. µ

is a certain probability measure concerning s ∈

S: a set of paths beginning at s is mapped into a

real number in [0,1],

5. L

is a mapping from S to the power set of

[

d∈SE

[d]

A path in a hierarchical probabilistic model is an

inﬁnite sequence of states, π = s

,... such that

∀i ≥ 0 [(s

i+1

) ∈ R].

A hierarchical probabilistic satisfaction relation

(M, s) |=

α for any formula α, where M is a hierar-

chical probabilistic model (S, S

,R, µ

) and s rep-

resents a state in S, is deﬁned inductively by:

1. for any p ∈ Φ, (M, s) |=

[d]p iff [d]p ∈ L

(s),

2. (M, s) |=

[d][b]α iff (M,s) |=

[d ; b]α,

3. (M, s) |=

[d](α ∧ β) iff (M,s) |=

[d]α and (M, s) |=

[d]β,

4. (M, s) |=

[d](α ∨ β) iff (M,s) |=

[d]α or (M,s) |=

[d]β,

5. (M, s) |=

[d](α→β) iff (M, s) |=

[d]α implies

(M, s) |=

[d]β,

6. (M, s) |=

[d]¬α iff (M,s) 6|=

[d]α,

7. (M, s) |=

[d]AXα iff ∀s

∈ S [(s, s

) ∈ R implies

(M, s

) |=

[d]α],

8. (M, s) |=

[d]EXα iff ∃s

∈ S [(s,s

) ∈ R and

(M, s

) |=

[d]α],

9. (M, s) |=

[d]AGα iff for all paths π ≡ s

,...,

where s ≡ s

, and all states s

along π, we have

(M, s

) |=

[d]α,

10. (M, s) |=

[d]EGα iff there is a path π ≡ s

,...,

where s ≡ s

, and for all states s

along π, we have

(M, s

) |=

[d]α,

11. (M, s) |=

[d]AFα iff for all paths π ≡ s

,...,

where s ≡ s

, there is a state s

along π such that

(M, s

) |=

[d]α,

12. (M, s) |=

[d]EFα iff there is a path π ≡ s

,...,

where s ≡ s

, and for some state s

along π, we have

(M, s

) |=

[d]α,

13. (M, s) |=

[d]A(αUβ) iff for all paths π ≡ s

,...,

where s ≡ s

, there is a state s

along π such that

(M, s

) |=

[d]β and ∀0 ≤ k < j (M, s

) |=

[d]α,

14. (M, s) |=

[d]E(αUβ) iff there is a path π ≡ s

,...,

where s ≡ s

, and for some state s

along π, we have

(M, s

) |=

[d]β and ∀0 ≤ k < j (M, s

) |=

[d]α,

15. (M, s) |=

[d]A(αRβ) iff for all paths π ≡ s

,...,

where s ≡ s

, and all states s

along π, we have

(M, s

) |=

[d]β or ∃0 ≤ k < j (M, s

) |=

[d]α,

Towards Hierarchical Probabilistic CTL Model Checking: Theoretical Foundations

765

16. (M, s) |=

[d]E(αRβ) iff there is a path π ≡ s

,...,

where s ≡ s

, and for all states s

along π, we have

(M, s

) |=

[d]β or ∃0 ≤ k < j (M, s

) |=

[d]α,

17. for any x ∈ [0,1], M, s |=

[d]P

≤x

α iff µ

({w ∈

Ω

| M, s |=

[d]α}) ≤ x,

18. for any x ∈ [0,1], M, s |=

[d]P

≥x

α iff µ

({w ∈

Ω

| M, s |=

[d]α}) ≥ x,

19. for any x ∈ [0,1], M, s |=

[d]P

α iff µ

({w ∈

Ω

| M, s |=

[d]α}) < x,

20. for any x ∈ [0,1], M, s |=

[d]P

α iff µ

({w ∈

Ω

| M, s |=

[d]α}) > x.

A formula α is valid in HpCTL iff (M, s) |=

holds for any hierarchical probabilistic model M :=

(S, S

,R, µ

), any s ∈ S, and any hierarchical prob-

abilistic satisfaction relation |=

on M.

Remark 2.6.

1. The following clauses hold for any formula α, and

any sequences b,c and d,

(a) (M, s) |=

[b][c]α iff (M, s) |=

[b ; c]α,

(b) (M, s) |=

[d]α iff (M,s) |=

[d]α.

2. The following formulas are valid in HpCTL: For

any formulas α and β, and any sequences b,c and

(a) [b](α ] β) ↔ ([b]α) ] ([b]β)

where ] ∈ {∧,∨,→},

(b) [b]]α ↔ ][b]α

where ] ∈ {¬,AX,EX,AG,EG, AF, EF},

(d) [b](E(αUβ)) ↔ E(([b]α)U([b]β)),

(e) [b](A(αRβ)) ↔ A(([b]α)R([b]β)),

(f) [b](E(αRβ)) ↔ E(([b]α)R([b]β)),

(g) [b][c]α ↔ [b ; c]α,

(h) [d]α ↔ [d]α.

3. The operator [b] is useful for representing infor-

mative and highly complex hierarchical systems

with the concepts of hierarchical information, hi-

erarchical trees, orders, and ontologies. This

is plausible because a sequence structure gives

a monoid hM,;,

0i with the following informa-

tional interpretation (Wansing, 1993): (1) M is

a set of pieces of ordered information (i.e., a set

of sequences), (2) ; is a binary operator (on M)

that combines two pieces of information (i.e., it

is a concatenation operator on sequences), and

(3)

0 is an empty piece of information (i.e., an

empty sequence). Then, the formulas of the form

; b

;·· · ; b

]α intuitively mean that “α is true

based on a sequence b

; b

;·· · ; b

of ordered

pieces of information.” Furthermore, the formu-

las of the form [

0]α, which coincide with α, in-

tuitively mean that “α is true without any infor-

mation (i.e., it is an eternal truth in the sense of

classical logic).”

3 EMBEDDING AND RELATIVE

DECIDABILITY

Deﬁnition 3.1. The language L

(the set of formulas)

of HpCTL is deﬁned using Φ , →, ∧, ∨, ¬, X, G, F, U,

R, A, E, P

≤x

≥x

, and [b]. The language

L of pCTL is obtained from L

by adding Φ

and

deleting [b].

A mapping f from L

to L is deﬁned inductively

by:

1. for any p ∈ Φ, f ([d]p) := p

∈ Φ

, especially

f (p) := p,

2. f ([d][b]α) := f ([d ; b]α), especially f ([d]α) :=

f ([d]α),

3. f ([d](α ] β)) := f ([d]α) ] f ([d]β) where ] ∈

{→,∧, ∨},

4. f ([d]]α) := ] f ([d]α) where ] ∈ {¬, AX, EX, AG,

EG,AF, EF, P

≤x

≥x

5. f ([d]A(αUβ)) := A( f ([d]α)U f ([d]β)),

6. f ([d]E(αUβ)) := E( f ([d]α)U f ([d]β)),

7. f ([d]A(αRβ)) := A( f ([d]α)R f ([d]β)),

8. f ([d]E(αRβ)) := E( f ([d]α)R f ([d]β)).

Proposition 3.2. Let f be the mapping deﬁned in Def-

inition 3.1. The following conditions hold for any se-

quences b,c, d and k:

1. f ([d][b][c]α) = f ([d][b ; c]α),

2. f ([d][k]α) = f ([d][k]α).

Lemma 3.3. Let f be the mapping deﬁned in Deﬁ-

nition 3.1. For any hierarchical probabilistic model

M := (S, S

,R, µ

) of HpCTL and any hierarchical

probabilistic satisfaction relation |=

on M, we can

construct a probabilistic model N := (S, S

,R, µ

,L)

of pCTL and a probabilistic satisfaction relation |=

on N such that for any formula α in L

, any d ∈ SE,

and any state s in S,

(M, s) |=

[d]α iff (N,s) |= f ([d]α).

Proof. Suppose that M is a hierarchical proba-

bilistic model (S, S

,R, µ

) such that

is a mapping from S to the power set of

[

d∈SE

[d]

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

766

We then deﬁne a probabilistic model N :=

(S, S

,R, µ

,L) such that

1. L is a mapping from S to the power set of

[

d∈SE

2. for any s ∈ S and any p ∈ Φ,

[d]p ∈ L

(s) iff p

∈ L(s).

Then, this lemma is proved by induction on the

complexity of α.

• Base step:

Case α ≡ p where p ∈ Φ: We obtain: (M,s) |=

[d]p iff (M, s) |=

[d]p iff [d]p ∈ L

(s) iff p

∈

L(s) iff (N, s) |= p

iff (N, s) |= f ([d]p) (by the

deﬁnition of f ) iff (N, s) |= f ([d]p) (by the deﬁni-

tion of f ).

• Induction step: We show some cases.

1. Case α ≡ [b]β: (M, s) |=

[d][b]β iff (M, s) |=

[d ; b]β iff (N, s) |= f ([d ; b]β) (by induction hy-

pothesis) iff (N, s) |= f ([d ; b]β) (by the deﬁnition

of f ) iff (N, s) |= f ([d][b]β) (by the deﬁnition of

f ).

2. Case α ≡ β→γ: We obtain: (M, s) |=

[d](β→γ)

iff (M, s) |=

[d]β implies (M,s) |=

[d]γ iff

(N,s) |= f ([d]β) implies (N, s) |= f ([d]γ) (by in-

duction hypothesis) iff (N, s) |= f ([d]β)→ f ([d]γ)

iff (N, s) |= f ([d](β→γ)) (by the deﬁnition of f ).

3. Case α ≡ ¬β: We obtain: (M, s) |=

[d]¬β iff

(M, s) 6|=

[d]β iff (N, s) 6|= f ([d]β) (by induc-

tion hypothesis) iff (N,s) |= ¬ f ([d]β) iff (N, s) |=

f ([d]¬β) (by the deﬁnition of f ).

4. Case α ≡ AXβ: We obtain: (M,s) |=

[d]AXβ iff

∀s

∈ S [(s,s

) ∈ R implies (M,s

) |=

[d]β] iff

∀s

∈ S [(s, s

) ∈ R implies (N, s

) |= f ([d]β)] (by

induction hypothesis) iff (N, s) |= AX f ([d]β) iff

(N,s) |= f ([d]AXβ) (by the deﬁnition of f ).

5. Case α ≡ AGβ: We obtain:

(M, s) |=

[d]AGβ

iff for all paths π ≡ s

,..., where s ≡ s

, and

all states s

along π, we have (M, s

) |=

[d]β

iff for all paths π ≡ s

,..., where s ≡ s

, and

all states s

along π, we have (N, s

) |= f ([d]β)

(by induction hypothesis)

iff (N, s) |= AG f ([d]β)

iff (N, s) |= f ([d]AGβ) (by the deﬁnition of f ).

6. Case α ≡ A(βUγ): We obtain:

(M, s) |=

[d]A(βUγ)

iff for all paths π ≡ s

,..., where s ≡ s

, there

is a state s

along π such that (M, s

) |=

[d]γ

and ∀0 ≤ k < j (M,s

) |=

[d]β

iff for all paths π ≡ s

,..., where s ≡ s

, there

is a state s

along π such that (N, s

) |= f ([d]γ)

and ∀0 ≤ k < j (N,s

) |= f ([d]β) (by induction

hypothesis)

iff (N, s) |= A( f ([d]β)U f ([d]γ))

iff (N, s) |= f ([d]A(βUγ)) (by the deﬁnition of f ).

7. Case α ≡ P

≤x

β: We obtain: (M, s) |=

[d]P

≤x

β iff

({w ∈ Ω

| (M,w) |=

[d]β}) ≤ x iff µ

({w ∈

Ω

| (N,w) |= f ([d]β)}) ≤ x (by induction hy-

pothesis) iff (N, s) |= P

≤x

f ([d]β) iff (N, s) |=

f ([d]P

≤x

β) (by the deﬁnition of f ).

Lemma 3.4. Let f be the mapping deﬁned in Def-

inition 3.1. For any probabilistic model N :=

(S, S

,R, µ

,L) of pCTL and any probabilistic satis-

faction relation |= on N, we can construct a hier-

archical probabilistic model M := (S, S

,R, µ

) of

HpCTL and a hierarchical probabilistic satisfaction

relation |=

on M such that for any formula α in L

any d ∈ SE, and any state s in S,

(N,s) |= f ([d]α) iff (M,s) |=

[d]α.

Proof. Similar to the proof of Lemma 3.3.

Theorem 3.5 (Embedding). Let f be the mapping de-

ﬁned in Deﬁnition 3.1. For any formula α,

α is valid in HpCTL iff f (α) is valid in pCTL.

Proof. By Lemmas 3.3 and 3.4.

Theorem 3.6 (Relative decidability). If the model-

checking, validity, and satisﬁability problems for

pCTL with a probability measure are decidable, then

the model-checking, validity, and satisﬁability prob-

lems for HpCTL with the same probability measure

as that of pCTL are also decidable.

Proof. Suppose that the probability measure µ

in the hierarchical probabilistic model (S, S

,R, µ

) of HpCTL is the same as the probabilistic model

(S, S

,R, µ

, L) of pCTL. Suppose also that pCTL

with µ

is decidable. Then, by the mapping f deﬁned

in Deﬁnition 3.1, a formula α of HpCTL can be

transformed into the corresponding formula f (α) of

pCTL. By Lemmas 3.3 and 3.4 and Theorem 3.5, the

model checking, validity and satisﬁability problems

for HpCTL can be transformed into those of pCTL.

Since the model checking, validity and satisﬁability

problems for pCTL with µ

are decidable by the

assumption, the problems for HpCTL with µ

are also

decidable.

Towards Hierarchical Probabilistic CTL Model Checking: Theoretical Foundations

767

Remark 3.7.

1. The model checking problem for pCTL with the

probability measures µ

and µ

−

introduced by

Bianco and de Alfaro was shown to be decidable

in (Bianco and de Alfaro, 1995).

2. The model checking problem for pCTL with the

probability measure µ

introduced by Aziz et al.

was shown to be decidable in (Aziz et al., 1995).

3. An extension of HpCTL with the above-mentioned

probability measures by Bianco and de Alfaro or

by Aziz et al. is also decidable by Theorem 3.6.

4. The complexities of the decision procedures for

the model checking, validity, and satisﬁability

problems of HpCTL are the same as those of

pCTL, since the translation function f deﬁned in

Deﬁnition 3.1 is a polynomial time reduction.

4 ILLUSTRATIVE EXAMPLES

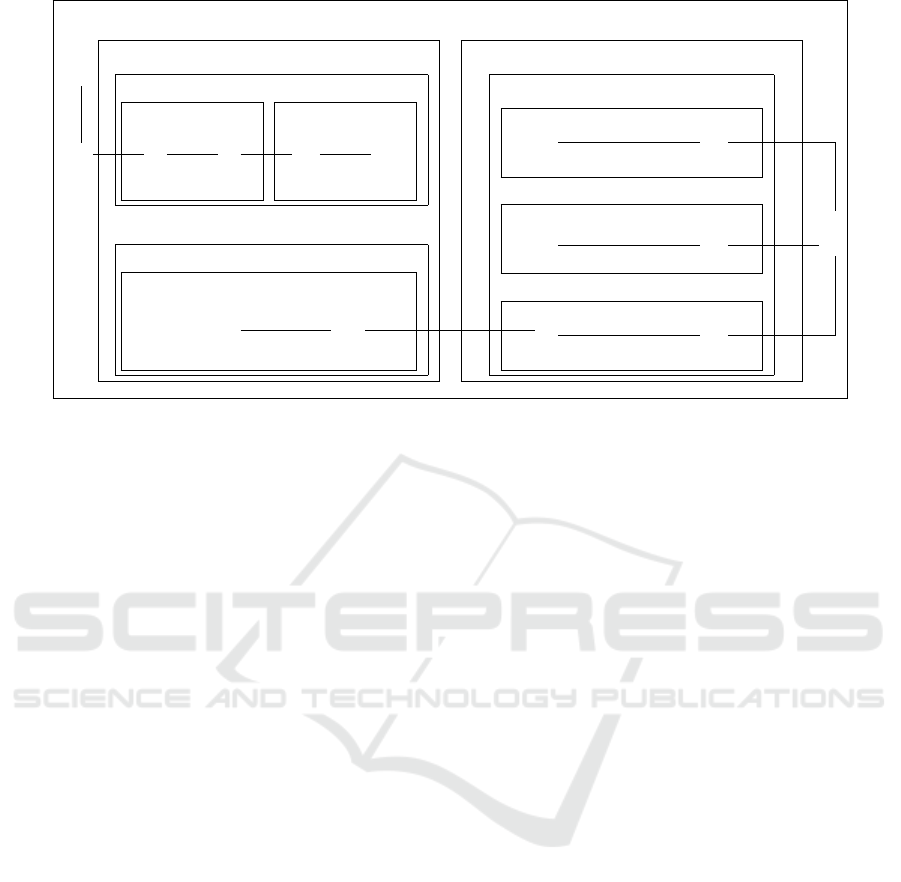
We present an illustrative example for hierarchical

probabilistic CTL model checking. Here, we consider

the scenario presented in Figure 1, which shows a

hierarchical probabilistic structure of students’ learn-

ing processes in a university setting. In this ﬁgure,

a student who is learning the natural sciences (e.g.,

physics) and engineering (e.g., electronics) will grad-

uate from the university. In this model, the entrance

examination pass rate is 60 % and the average exami-

nation pass rate varies among the courses.

In this example, we can declare the hierarchy of

the academic subjects: science, mathematics, anal-

ysis, vector analysis, electromagnetics, engineering,

electronics, power electronics, and semiconductor en-

gineering as the sequence modal operator:

1. [Science ; Mathematics ; Analysis ; Vector analysis],

2. [Science ; Physics ; Electromagnetics],

3. [Engineering ; Electronics ; Telecoms engineering],

4. [Engineering ; Electronics ; Power electronics],

5. [Engineering ; Electronics ; Semiconductor engineering].

The ﬁrst expression shows that the concept

Vector analysis is a subconcept of Analysis, the con-

cept of Analysis is a subconcept of Mathematics, and

Mathematics is a subconcept of Science.

We can use some probabilistic operators to repre-

sent certain probabilistic phenomena concerning the

learning process. As previously mentioned, the for-

mula of the form P

≥x

α is intended to read “the prob-

ability of α holding in the future evolution of the sys-

tem is at least x.” Thus, we can describe and verify

the following statement using HpCTL:

“If a student is learning in the second stage

of the subject of “Telecoms engineering” and

he or she understands the subject sufﬁciently,

then there is approximately an 80 % chance

that he or she will graduate some time in the

near future.”

This statement is true, and is expressed formally as:

[Engineering ; Electronics ; Telecoms engineering]

(AG(stage2 ∧ learning ∧ understand →

EF(P

≤0.85

graduate ∧ P

≥0.75

graduate)).

Moreover, if we can use the paraconsistent nega-

tion connective ∼, we can also express the nega-

tion of ambiguous concepts. If we cannot deter-

mine whether someone understands the underlying

subject, then the ambiguous concept understand can

be represented by asserting the following inconsistent

formula: understand ∧ ∼understand. However, the

classical negation connective ¬ is appropriate for de-

scribing the negation of the non-ambiguous concept

learning.

5 CONCLUDING REMARKS

In this study, the new logic HpCTL and its transla-

tion into the standard logic pCTL were developed to

obtain a theoretical foundation for hierarchical prob-

abilistic CTL model checking. We demonstrated that

the existing probabilistic model checking algorithms

for pCTL can be reused for hierarchical probabilis-

tic model checking as described using HpCTL. More-

over, we noted that the complexity of the model-

checking algorithms for HpCTL is the same as that of

pCTL. In addition, some illustrative examples for hi-

erarchical probabilistic CTL model checking was pre-

sented in this study.

Prospective courses of study may involve extend-

ing the proposed logic by adding a paraconsistent

negation connective. An extended hierarchical com-

putation tree logic with a paraconsistent negation con-

nective was studied in (Kamide, 2015). By combin-

ing our present work with that in (Kamide, 2015), we

hope to establish the theoretical foundations of hi-

erarchical inconsistency-tolerant probabilistic model

checking based on such an extended logic.

ACKNOWLEDGEMENTS

This research was supported by the Kayamori

Foundation of Informational Science Advancement,

JSPS KAKENHI Grant Numbers JP18K11171,

JP16KK0007 and JSPS Core-to-Core Program (A.

Advanced Research Networks).

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

768

[Science] [Engineering]

[Mathematics]

[Physics]

[Electronics]

[Analysis] [Vector analysis]

[Electromagnetics]

[Semiconductor engineering]

[Power electronics]

[Telecoms engineering]

enter

60%

stage1

learning

stage2 stage1

learning

stage2

95%

stage1

∼understand

understand

¬learning

stage2

understand

learning

90%

stage1

∼understand

stage2

understand

85%

stage1

∼understand

stage2

understand

stage1

∼understand

stage2

understand

85%

graduate

x x x x x

x x

- - - -





- 





- -



*

- -

Figure 1: A hierarchical learning process model for academic subjects.

REFERENCES

Aziz, A., Singhal, V., and Balarin, F. (1995). It usually

works: The temporal logic of stochastic systems. In

Proceedings of the 7th Int. Conf. on Computer Aided

Veriﬁcation (CAV 1995), Lecture Notes in Computer

Science 939, pages 155–165.

Baier, C., de Alfaro, L., Forejt, V., and Kwiatkowska, M.

(2018). Model Checking Probabilistic Systems, In:

Handbook of Model Checking, pp. 963-999. Springer.

Bianco, A. and de Alfaro, L. (1995). Model checking of

probabilistic and nondeterministic systems. In Pro-

ceedings of the 15th Conf. on Foundations of Soft-

ware Technology and Theoretical Computer Science

(FSTTCS 1995), Lecture Notes in Computer Science

1026, pages 499–513.

Cavada, R., Cimatti, A., Jochim, C., Keighren, G., Olivetti,

E., Pistore, M., Roveri, M., and Tchaltsev, A. (2015).

NuSMV 2.6 user manual, 144 pages. Online available.

Clarke, E. and Emerson, E. (1981). Design and synthesis of

synchronization skeletons using branching time tem-

poral logic. In Lecture Notes in Computer Science,

volume 131, pages 52–71.

Clarke, E., Henzinger, T., Veith, H., and Bloem, R. (2018).

Handbook of Model Checking. Springer.

Holzmann, G. (2006). The SPIN model checker: Primer

and reference manual. Addison-Wesley.

Kamide, N. (2015). Inconsistency-tolerant temporal rea-

soning with hierarchical information. Information Sci-

ences, 320:140–155.

Kamide, N. (2018). Logical foundations of hierarchical

model checking. Data Technologies and Applications,

52 (4):539–563.

Kamide, N. and Kaneiwa, K. (2009). Extended full

computation-tree logic with sequence modal operator:

Representing hierarchical tree structures. Proceedings

of the 22nd Australasian Joint Conference on Artiﬁ-

cial Intelligence (AI’09), Lecture Notes in Artiﬁcial

Intelligence, 5866:485–494.

Kamide, N. and Koizumi, D. (2015). Combining paracon-

sistency and probability in ctl. Proceedings of the 7th

International Conference on Agents and Artiﬁcial In-

telligence (ICAART 2015), 2:285–293.

Kamide, N. and Koizumi, D. (2016). Method for combin-

ing paraconsistency and probability in temporal rea-

soning. Journal of Advanced Computational Intelli-

gence and Intelligent Informatics, 20:813–827.

Kamide, N. and Yano, R. (2017). Logics and translations

for hierarchical model checking. Proceedings of the

21st International Conference on Knowledge-Based

and Intelligent Information and Engineering Systems

(KES2017), Procedia Computer Science, 112:31–40.

Kaneiwa, K. and Kamide, N. (2010). Sequence-indexed

linear-time temporal logic: Proof system and applica-

tion. Applied Artiﬁcial Intelligence, 24 (10):896–913.

Kaneiwa, K. and Kamide, N. (2011). Conceptual modeling

in full computation-tree logic with sequence modal

operator. International Journal of Intelligent Systems,

26 (7):636–651.

Kwiatkowska, M., Norman, G., and Parker, D. (2011).

Prism 4.0: Veriﬁcation of probabilistic real-time sys-

tems. Proceedings of the 23rd International Confer-

ence on Computer Aided Veriﬁcation (CAV 11), Lec-

ture Notes in Computer Science, 6806:585–591.

Pnueli, A. (1977). The temporal logic of programs. In Pro-

ceedings of the 18th IEEE Symposium on Foundations

of Computer Science, pages 46–57.

Wansing, H. (1993). The logic of information structures.

In Lecture Notes in Computer Science, volume 681,

pages 1–163.

Towards Hierarchical Probabilistic CTL Model Checking: Theoretical Foundations

769