Achromatic Cascade Optical System with Hybrid Lenses for

Distortion-compensated Multifocusing of Ultrashort Pulse Beams

Jun Amako and Hidetoshi Nakano

Faculty of Science and Engineering, Toyo University, 2100 Kujirai, Kawagoe, Saitama 350-8585, Japan

Keywords: Ultrafast Optics, Diffractive Optics, Hybrid Lens, Systems Design.

Abstract: We report an achromatic cascade optical system for multifocusing ultrashort pulse beams in its application

in high-precision materials processing. The challenge is to eliminate the beam-radius-dependent pulse

broadening or pulse front distortion from the arrayed pulses. We propose the inclusion of a pair of hybrid

refractive-diffractive lenses for chromatic aberration correction and dispersion management in the system.

From numerical analysis, we have realized that the hybridized system has enormous potential to improve

not only the spatial resolution but also the temporal resolution to their respective limits in generating

arrayed pulse beams. This pulse delivery system enables high-throughput material processing using

ultrashort-pulsed lasers.

1 INTRODUCTION

There has been growing interest in ultrashort-pulsed

laser for precision manufacturing. The deterministic

and reproducible nature of ultrashort pulses in light-

matter interaction is indispensable for micro and

nano-machining without thermal damages (Lenzner

et al, 1999; Chimier et al, 2011). On the other hand,

a material can be processed at multiple points

simultaneously with arrayed pulse beams to obtain a

high throughput. For arrayed irradiation, diffractive

beam splitters (DBSs) are extensively used with

nanosecond-pulsed lasers for a variety of laser-based

processes (Amako and Fujii, 2016).

A diffracted ultrashort pulse suffers chromatic

aberrations, however, due to its broad spectrum,

resulting in spatial and temporal pulse lengthening.

Such pulse broadening can be ignored by diffracting

and focusing the pulses near the optical axis but the

severely limited work areas remain challenging

(Kuroiwa et al, 2004; Hayasaki et al, 2005; Kelemen

et al, 2007; Sakakura et al, 2009; Jesacher and Booth,

2010). Although several efforts have been made to

fix the pulse distortions, temporal broadening

remains unfixed (Amako et al, 2002; Li et al, 2005;

Hasegawa and Hayasaki, 2014). Minguez-Vega et al.

proposed a diffractive-refractive lens triplet for

simultaneous compensation of spatio-temporal pulse

distortions (Minguez-Vega et al, 2006).

Multifocusing performance of the triplet was

evaluated in optical experiments (Martinez-Cuenca

et al, 2012; Torres-Peiro et al, 2013). According to

their report, it was the temporal distortion rather than

the spatial distortion restricting the outer-most angle

of pulse diffraction or the length of the beam array,

which determines the process throughput.

These prior studies motivated us to explore a

simple and practical method to design a pulse

delivery system for multifocusing ultrashort pulse

beams. We conceptualized a novel achromatic

cascade system, designed a prototype, and proved its

operation principle with 20-fs-pulses (Amako and

Nakano, 2018). Yet beam-diameter-dependent pulse

broadening or pulse front distortion was detected in

the transmitted pulses. These temporal distortions

can be minimized by narrowing the beam diameter,

but sacrificing the spatial resolution. Such parabolic

distortions are present due to the group-velocity

dispersions in the refractive lenses used in the

system and cannot be compensated by the action of

refractive lenses alone. Instead of refractive lenses,

hybrid lenses composed of a refractive and

diffractive surface can be employed for chromatic

aberration correction and dispersion management

(Stone and George, 1988; Piestun and Miller, 2001).

We here report on “hybridization” of the cascade

system for distortion-free multifocusing ultrashort

pulses.

Amako, J. and Nakano, H.

Achromatic Cascade Optical System with Hybrid Lenses for Distortion-compensated Multifocusing of Ultrashort Pulse Beams.

DOI: 10.5220/0007470202410247

In Proceedings of the 7th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2019), pages 241-247

ISBN: 978-989-758-364-3

241

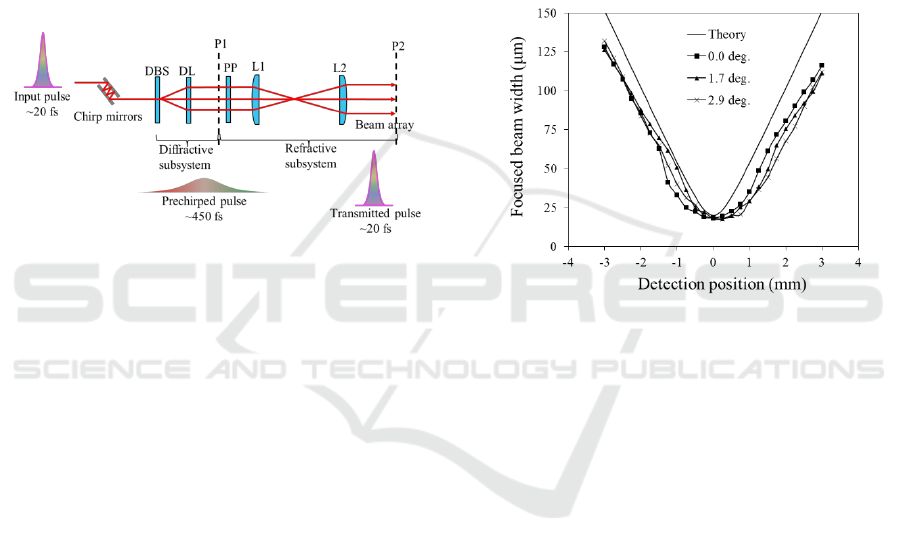
2 PROTOTYPE CONCEPT

Figure 1 shows the schematic of the prototype

cascade optical system. The diffractive subsystem

consists of a diffractive beam splitter (DBS) and a

diffractive lens (DL) of positive focal length. The

refractive subsystem, which is afocal, has a pair of

refractive lenses L

and L

with positive focal

lengths. These two subsystems are cascaded and a

phase plate (PP) is placed between them. Upon

entering the system, an ultrashort pulse beam is

divided by the DBS, producing a large angular

dispersion. This dispersion is the origin of chromatic

aberrations, which distorts the beam spot and

stretches the pulse.

Figure 1: Schematic configuration of the prototype

cascade system: DBS; diffractive beam splitter, DL;

diffractive lens, PP; phase plate, L

, L

; refractive lenses.

, P

are the intermediate plane and exit plane,

respectively.

Achromaticity of the system is the key to

simultaneous compensation of the spatio-temporal

pulse distortions. The diffractive subsystem is

designed to correct the lateral chromatic aberrations;

it forms an array of spatially identical pulse beams at

the intermediate plane, P

. The phase plate (PP)

eliminates the angular dispersions of the diffracted

pulse beams. The refractive subsystem is designed to

correct the longitudinal chromatic aberrations; it

generates an array of spatio-temporally identical

pulse beams at the exit plane P

, which is the work

area. Group delay dispersions primarily caused by

the refractive subsystem can be compensated for by

prechirping the input pulse and therefore, the

focused pulse at P

can be compressed back to the

initial pulse duration.

3 REMAINING ISSUE

For proof-of-principle, we designed a prototype

system and evaluated it with 20-fs-pulses by

characterizing the transmitted pulses at P

. In this

prototype, two lenses in the afocal subsystem were

made from E-FDS3 (HOYA), which was highly

dispersive with ν

= 17: ν

is the Abbe number

(HOYA’s Official Website). Figure 2 shows the

focused beam widths plotted against detection

positions for the diffraction angles of 0.0º, 1.7º and

2.9º. The solid line in the figure represents the

theoretically predicted beam widths for a Gaussian

beam with no aberrations (M

= 1). The pulse beams

on-axis and off-axis were tightly focused to a

diffraction limit, 20 μm, at the focal point. From

these results, we state that the cascade system is able

to correct chromatic aberrations introduced in the

diffracted 20-fs-pulse beams.

Figure 2: Focused beam widths vs. detection position.

Solid line represents a theoretical prediction and plots are

the measured data.

Another crucial issue in the prototype system can

be identified in the time domain. Figure 3 shows the

autocorrelation signals obtained from (a) the input

pulse, (b) the focused pulse at P

in the prototype

with two E-FDS3 refractive lenses, and (c) the

transmitted pulse through an 8.0-mm-thick parallel

plate of E-FDS3. The signal in Fig. 3(c) was

obtained by focusing the pulse with a parabolic

mirror. The plate thickness was set equal to the total

thickness of two refractive lenses. On comparing

these signals, we observed some distinctions: The

input pulse width was 22 fs, the pulse width at the

exit of the system was 35 fs, and the pulse width

after the parallel plate was 24 fs. In addition, ripple

structures were seen on the pedestal in Fig. 3(b).

Through this observation, we understand that the

temporal distortions in Fig. 3(b) were due to the

group-velocity dispersions in the lenses, which

introduced beam-radius-dependent pulse broadening

or pulse front distortion.

Pulse front distortion, which is in proportion to

the square of the beam radius, is given by

PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology

242

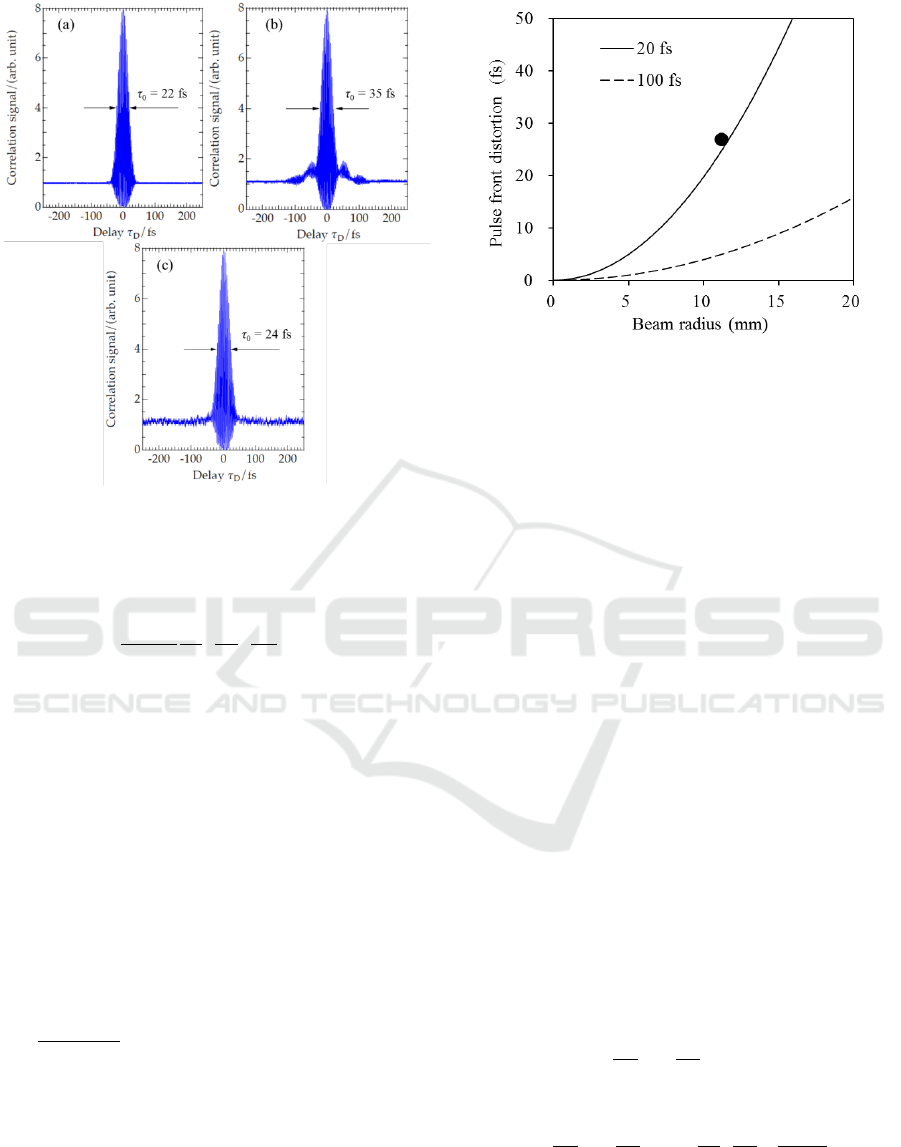
Figure 3: Auto-correlation signals obtained (a) from the

input pulse, (b) from transmitted pulse at P

in the cascade

system with the E-FDS3 refractive lenses, and (c) from the

transmitted pulse after the E-FDS3 parallel plate.

 









 

























where λ

is the center wavelength, ∆λ is the

wavelength bandwidth, n(λ) is the refractive index of

the lens glass, f

is the lens focal length at λ

, R is the

beam radius in the afocal system, and c is the speed

of light in vacuum. For a transform-limited pulse,

∆λτ

= 0.441λ

/c, where τ

is the full width at half

maximum (FWHM) of the pulse (Diels and Rudolph,

2006). As illustrated by Eq. (1), the distortion ∆τ is

inversely proportional to τ

. Computed distortions

are plotted against the beam radius in Fig. 4. The

estimated distortion from the signal in Fig. 3(b) is 27

fs, as plotted in Fig. 4, where λ

= 780 nm, ∆λ = ±23

nm, n

= 2.066 at λ

, f

= 278 mm at λ

, d/λ(dn/dλ) =

0.4885 μm

-2

at λ

, and R = 11.7 mm. Given temporal

distortions, the pulse width at P

can be estimated as











 



. Distortions may be negligible for a

100-fs pulse but need to be addressed for a 20-fs

pulse.

In order to eliminate such beam-radius-

dependent temporal distortions, the dispersion

management in the afocal subsystem is

indispensable. For that purpose, we have considered

a hybrid lens, which consists of a refractive lens and

a diffractive lens. As is well known, a combination

Figure 4: Computed pulse front distortions as a function of

beam radius in the afocal subsystem.

of two types of lenses can correct longitudinal

chromatic aberrations at the focus because the

aberrations presented by the two lenses are opposite

in sign. Likewise, two types of lenses, with

appropriate physical parameters, can get the phase

front and pulse front to coincide and further remove

the parabolic temporal distortions. There is a

temporal delay in the pulse front from the phase

front after passing through the refractive lens,

whereas the pulse front advances the phase front

after passing through the diffractive lens.

Although the wavelength dependence of

diffraction efficiency slightly narrows the spectral

profile of a pulse, for a 20-fs-pulse the pulse width is

scarcely affected.

4 SYSTEMS DESIGN

In design of the cascade system, the following two

conditions need to be satisfied at P

. Equation (1)

needs to be accepted to correct longitudinal

achromatic aberrations and Eq. (2) should be

honored to compensate for pulse front dispersions.

The two equations have some terms in common

through which space and time are entangled:

  









 





  

(2)

  









 





 



























 



where f

is the focal length of the diffractive lens and

F is the focal length of the hybrid lens. Equation (1)

Achromatic Cascade Optical System with Hybrid Lenses for Distortion-compensated Multifocusing of Ultrashort Pulse Beams

243

was derived by using the ray matrix (Yariv and Yeh,

2003) of the cascade system and Eq. (2) was derived

by applying an analytical model of pulse

propagation time (Bor, 1988; 1989) to the system.

Formula derivation was performed in a paraxial

regime. Equations (2) and (3) hold for the off-axis

beams as well as the on-axis beam, under first-order

approximation.

Figure 5: (a) Computed chromatic aberration and (b)

computed pulse front distortion plotted against f

, the

refractive focal length of the hybrid lens to be designed.

For a focal length F to satisfy the above

conditions,  needs to be a positive constant

and  needs to be zero across the spectral

band of the pulse. Provided that the focal lengths of

the refractive and diffractive lenses are f

(λ) and f

(λ),

respectively, F(λ) can be expressed as F = f

/(f

), where the two lenses are assumed to be

sufficiently thin. f

(λ) and f

(λ) are defined by











 





























 









 , where the

subscript 0 represents the focal length at λ

. If the

focal length f

is picked as the design variable, the

aberration can be zero at one focal length and the

pulse front distortion can be zero at another focal

length, as shown in Fig. 5. These two focal lengths

should match; this condition can be attained by

selecting a type of glass with a low dispersion degree

or a high Abbe number.

Figure 6: Dispersion properties of a designed hybrid lens.

(a) Focal length F, (b) first derivative of F, and (c) second

derivative of F plotted against wavelength, respectively.

5 RESULTS AND DISCUSSIONS

Assuming a pulse width of τ

= 20 fs with λ

= 780

nm and ∆λ = ±23 nm, we searched for a focal length

F, which satisfies both the conditions (1) and (2), by

scanning the focal length f

Other set conditions

were the incident beam width of 5.0 mm (2R = 15

mm), f

= 50 mm, and F

= 150 mm. As an example,

when fused silica

(ν

= 69) is selected as lens

material, we found f

= 133 mm and f

= −1144 mm

for ∆z = 0.0 mm using Eq. (2); we computed ∆τ =

PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology

244

0.87 fs and then τ = 20 fs from Eq. (3). The effective

Abbe number (Harm et al, 2014) of this hybrid lens

was calculated as 18. Figure 6 shows the dispersion

properties of the designed hybrid lens. F, ,

and  are plotted as a function of

wavelength in Fig. 6 (a), (b), and (c), respectively.

As illustrated by Fig. 6 (b),  has a minimum

in the spectral range of the pulse. Accordingly,

 comes close to zero around the center

wavelength of the pulse, thus nearly eliminating the

pulse front distortions for  = 0, as is seen from Eq.

(3).

In the prototype, a pair of refractive lenses made

from E-FDS3 (ν

= 17) were employed, for which

we found F

= f

= 278 mm (f

= ∞) for ∆z = 0.0

mm using Eq. (2) and we obtained ∆τ = 39 fs with

2R = 28 mm and thus τ = 44 fs using Eq. (3).

In this example design, there was a small gap

between the two f

values: one for zero aberration

and the other for zero distortion. That gap was filled

by selecting a type of glass that was much less

dispersive than fused silica, for example, FCD100

with ν

= 95, further reducing the temporal distortion

∆τ. However, we preferred to use fused silica

because of its compatibility with dry-etching

processes that we would rely on in fabrication of the

diffractive surface of a hybrid lens.

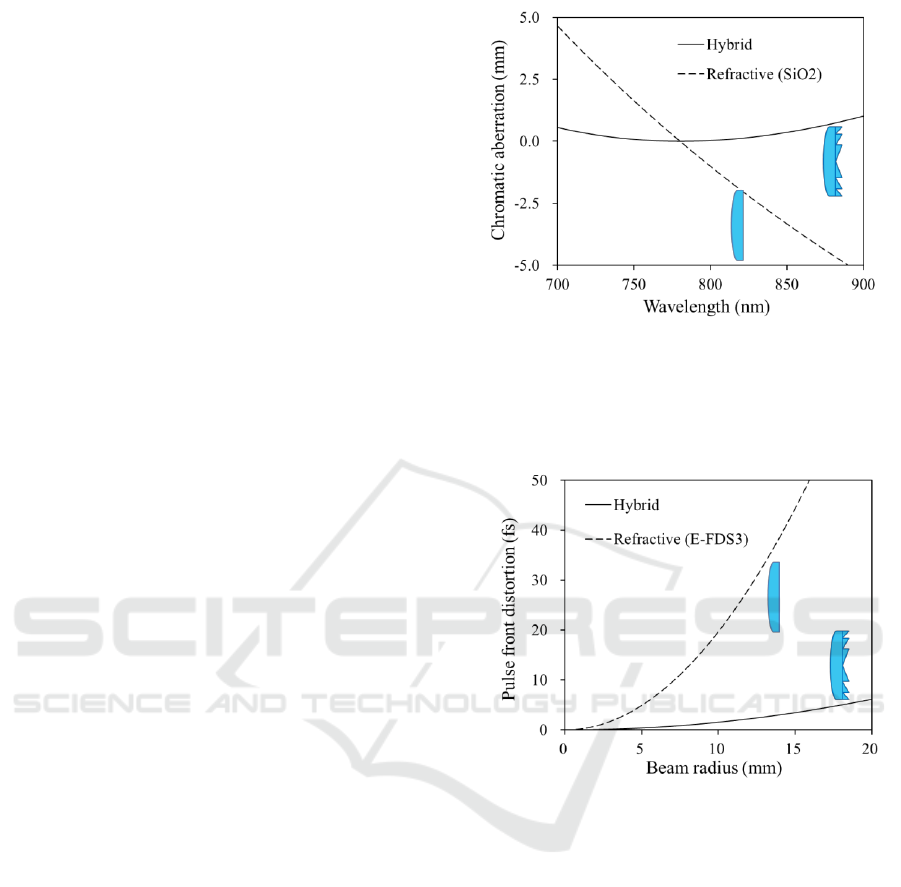
To verify the effects of the designed hybrid lens,

we conducted numerical analysis to study the

behaviors of the transmitted pulse. Computed focal

position deviations or longitudinal chromatic

aberrations at P

are plotted against the wavelength

in Fig. 7. The aberrations were computed by

applying the ray matrix of the cascade system. The

designed hybrid lens with 150-mm-focal length

allowed the transmitted pulse to focus at P

with a

deviation of 40 μm across the wavelength range of

780 nm ± 23 nm (solid line). In contrast, a refractive

singlet made from fused silica presented a lot of

longitudinal aberrations with a deviation of ±1.2 mm

across the wavelength range of interest (broken line).

Further, computed pulse front distortions are

plotted against the beam radius in Fig. 8. Distortions

were computed using Eq. (3). Employing a pair of

the designed hybrids kept the distortions sufficiently

small with increasing beam radius (solid line),

whereas employing a pair of the refractive lenses

made using E-FDS3 increased the distortions with

increasing beam radius (broken line).

From these results, we conclude that the hybrid

lens is able to compensate for spatio-temporal distor-

tions introduced by splitting and focusing ultrashort

pulse beams. In addition, a large diffractive dispersion

inherent in a hybrid, lens offers a small footprint of

Figure 7: Computed chromatic aberrations at P

(in Fig. 1)

against the wavelength. Solid line is for the cascade

system with the designed hybrid lenses and broken line is

for the cascade system with the fused silica refractive

lenses.

Figure 8: Computed pulse front distortions at P

(in Fig. 1)

against the beam radius in the afocal subsystem. Solid line

is for the cascade system with the designed hybrid lenses

and broken line is for the cascade system with the E-FDS3

refractive lenses.

the cascade system. The expected length of the

hybridized system is 700 mm, whereas the current

system is 1212 mm long. Small footprint may reduce

constraints on machine layouts of the cascaded

configuration.

To construct the hybrid lens, a plano-convex lens

and a diffractive lens can be produced independently

and then can be combined by optical contact

technique. This kind of binding method, which uses

no adhesive, avoids affecting the quality of

transmitted pulses. There is no particularly stringent

requirement in fabrication of the hybrid lens, except

for the focal length of its refractive surface, f

. The

error tolerance of f

is expected to be < 1% for

Achromatic Cascade Optical System with Hybrid Lenses for Distortion-compensated Multifocusing of Ultrashort Pulse Beams

245

sufficiently small chromatic aberrations. Stock

lenses usually have focal length errors of 1-2%. The

focal length f

should be fixed by prioritizing the

chromatic aberration over the pulse front distortion,

because the latter is much less sensitive to the focal

length error.

The proposed pulse delivery system will be in

operation with both temperature and humidity

controlled for a stable pulse generation. The optical

elements used in the system are made from

thermally stable glasses, such as fused silica, which

should be transparent over the wavelength range of

780 nm ± 23 nm for 20-fs-pulses.

6 CONCLUSIONS

We have proposed the use of hybrid lenses, instead

of refractive lenses, in an achromatic cascade optical

system that we developed for multifocusing

ultrashort pulse beams. We have realized through

numerical analysis that by constructing the afocal

subsystem with a pair of hybrid lenses, each

composed of a refractive lens and a diffractive lens,

spatial and temporal distortions can be compensated

for a 20-fs-pulse beam. Using this hybridized

cascade system, an ultrashort pulse beam can be

multifocused in significantly large array dimensions,

say, 5.0 mm across, while high resolutions are

accomplished in both space and time. The future

work is to fabricate a hybrid lens and validate its

effectiveness through experiments with 20-fs-pulses.

This pulse delivery system enables high-throughput

material-processing using ultrashort-pulsed lasers.

ACKNOWLEDGMENTS

This work was supported by the Amada Foundation

under grant AF-2017215.

REFERENCES

Lenzner, M., Kruger, J., Kautek, W., and Krausz, F.,

“Precision laser ablation of dielectrics in the 10-fs

regime,” Appl. Phys. A 68, 369–371 (1999).

Chimier, B., Uteza, O., Sanner, N., Sentis, M., Itina, T.,

Lassonde, P., Legare, F., Vidal, F., and Kieffer, J. C.,

“Damage and ablation threshold of fused-silica in

femtosecond regime,” Phys. Rev. B 84, 094104–

0941049 (2011).

Amako, J. and Fujii, E., “Beam delivery system with a

non-digitized diffractive beam splitter for laser drilling

of silicon,” Optics and Lasers in Eng. 77, 1–7 (2016)

and the references cited therein.

Kuroiwa, Y., Takeshima, N., Narita, Y., Tanaka, S., and

Hirao, K., “Arbitrary micropatterning method in

femtosecond laser microprocessing using diffractive

optical elements,” Opt. Express 12, 1908–1915 (2004).

Hayasaki, Y., Sugimoto, T., Takita, A., and Nishida, N.,

“Variable holographic femtosecond laser processing

by use of a spatial light modulator,” Appl. Phys. Lett.

87, 031101–031103 (2005).

Kelemen, L., Valkai, S., and Ormos, P., “Parallel

photopolymerisation with complex light patterns

generated by diffractive optical elements,” Opt.

Express 15, 14488–14497 (2007).

Sakakura, M., Sawano, T., Shimotsuma, Y., Miura, K.,

and Hirao, K., “Parallel drawing of multiple bent

optical waveguides by using a spatial light modulator,”

Jpn. J. Appl. Phys. 48, 126507–126511 (2009).

Jesacher, A. and Booth, M. J., “Parallel direct laser

writing in three dimensions with spatially dependent

aberration correction,” Opt. Express 18, 21090–21099

(2010).

Amako, J., Nagasaka, K., and Kazuhiro, N., “Chromatic-

distortion compensation in splitting and focusing of

femtosecond pulses by use of a pair of diffractive

optical elements,” Opt. Lett. 27, 969–971 (2002).

Li, G., Zhou, C., and Dai, E., “Splitting of femtosecond

laser pulses by using a Dammann grating and

compensating grating,” J. Opt. Soc. Am. A 22, 767–

772 (2005).

Hasegawa, S. and Hayasaki, Y., “Dynamic control of

spatial wavelength dispersion in holographic

femtosecond laser processing,” Opt. Lett. 39, 478–481

(2014).

Minguez-Vega, G., Lancis, J., Caraquitena, J., Torres-

Company, V., and Andres, P., “High spatiotemporal

resolution in multifocal processing with femtosecond

laser pulses,” Opt. Lett. 31, 2631–2633 (2006).

Martinez-Cuenca, R., Mendoza-Yero, O., Alonso, B., Sola,

I. J., Minguez-Vega, G., and Lancis, J., “Multibeam

second-harmonic generation by spatiotemporal

shaping of femtosecond pulses,” Opt. Lett. 7, 957–959

(2012).

Torres-Peiro, S., Gonzalez-Ausejo, J., Mendoza-Yero, O.,

Minguez-Vega, G., Angres, P., and Lancis, J.,

“Parallel laser micromachining based on diffractive

optical elements with dispersion compensated

femtosecond pulses,” Opt. Express 21, 31830–31835

(2013).

Amako, J. and Nakano, H., “Distortion-compensated

multifocusing of ultrashort pulse beams using cascade

optical system,” Appl. Opt. 57, 33–41 (2018).

Stone, T. and George, N., “Hybrid diffractive-refractive

lenses and achromats,” Appl. Opt. 27, 2960–2971

(1988).

Piestun, R., and Miller, D. A. B., “Spatiotemporal control

of ultrashort optical pulses by refractive-diffractive-

dispersive structured optical elements,” Opt. Lett. 26,

1373–1375 (2001).

PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology

246

Hoya’s Official Website, http://www.hoya-

opticalworld.com/english/datadownload/index.html.

Diels, J.–C.and Rudolph, W., Ultrashort Laser Pulse

Phenomena, 2nd ed. (Elsevier, 2006), p.10.

Yariv, Y. and Yeh, P., Optical Waves in Crystals (John

Wiley & Sons, 2003), p.34.

Bor, Z., “Distortion of femtosecond laser pulses in lenses

and lens systems,” J. Mod. Opt. 35, 1907–1918 (1988).

Bor, Z., “Distortion of femtosecond laser pulses in lenses,”

Opt. Lett. 14, 119–121 (1989).

Harm, W., Roider, C., jesacher, A., Bernet, S., and Ritsch-

Marte, M., “Dispersion tuning with a varifocal

diffractive-refractive hybrid lens,” Opt. Express 22,

5260-5269 (2014).

Achromatic Cascade Optical System with Hybrid Lenses for Distortion-compensated Multifocusing of Ultrashort Pulse Beams

247